A&A 366, 898-912 (2001)
DOI: 10.1051/0004-6361:20000269
N. Christlieb1 - L. Wisotzki2 - D. Reimers1 - D. Homeier3 - D. Koester3 - U. Heber4
1 - Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112,
21029 Hamburg, Germany
2 - Institut für Physik, Universität Potsdam, Am Neuen Palais 10,
14469 Potsdam, Germany
3 - Institut für Theoretische Physik und Astrophysik der
Christian-Albrechts-Universität Kiel, Leibnizstrasse 15, 24098 Kiel,
Germany
- Dr. Remeis Sternwarte, Universität Erlangen-Nürnberg,
Sternwartstrasse 7, 96049 Bamberg, Germany
Received 30 August 2000 / Accepted 14 November 2000
Abstract
We describe automatic procedures for the selection of DA white dwarfs in the
Hamburg/ESO objective-prism survey (HES). For this purpose, and the
selection of other stellar objects (e.g., metal-poor stars and carbon
stars), a flexible, robust algorithm for detection of stellar absorption and
emission lines in the digital spectra of the HES was developed. Broad band
(U-B, B-V) and intermediate band (Strömgren c1) colours can be derived
directly from HES spectra, with precisions of
![]() mag;
mag;
![]() mag;
mag;
![]() mag. We describe simulation techniques that allow one to convert model or slit spectra to HES spectra. These simulated objective-prism spectra are
used to determine quantitative selection criteria, and for the study of
selection functions. We present an atlas of simulated HES spectra of DA and
DB white dwarfs. Our current selection algorithm is tuned to yield maximum efficiency of the
candidate sample (minimum contamination with non-DAs). DA candidates are
selected in the B-V versus U-B and c1 versus
mag. We describe simulation techniques that allow one to convert model or slit spectra to HES spectra. These simulated objective-prism spectra are
used to determine quantitative selection criteria, and for the study of
selection functions. We present an atlas of simulated HES spectra of DA and
DB white dwarfs. Our current selection algorithm is tuned to yield maximum efficiency of the
candidate sample (minimum contamination with non-DAs). DA candidates are
selected in the B-V versus U-B and c1 versus
![]() parameter spaces. The contamination of the
resulting sample with hot subdwarfs is expected to be as low as
parameter spaces. The contamination of the
resulting sample with hot subdwarfs is expected to be as low as ![]() 8%, while there is essentially no contamination with main sequence or
horizontal branch stars. We estimate that with the present set of criteria,
8%, while there is essentially no contamination with main sequence or
horizontal branch stars. We estimate that with the present set of criteria,
![]() 80% of DAs present in the HES database are recovered. A yet higher
degree of internal completeness could be reached at the expense of higher
contamination. However, the external completeness is limited by additional
losses caused by proper motion effects and the epoch differences between
direct and spectral plates used in the HES.
80% of DAs present in the HES database are recovered. A yet higher
degree of internal completeness could be reached at the expense of higher
contamination. However, the external completeness is limited by additional
losses caused by proper motion effects and the epoch differences between
direct and spectral plates used in the HES.
Key words: surveys - methods: data analysis - white dwarfs
The Hamburg/ESO survey (HES) is an objective prism survey primarily targeting
bright quasars Wisotzki et al. (1996; Reimers & Wisotzki 1997; Wisotzki et al. 2000). However, because
its spectral resolution is typically 15Å FWHM at H![]() ,
it is also
possible to efficiently select a variety of interesting stellar
objects in the HES. These include, e.g., metal-poor halo stars, carbon stars,
cataclysmic variable stars, white dwarfs (WDs), subdwarf B stars (sdBs),
subdwarf O stars (sdOs), and field horizontal branch A- and B-type stars
(Christlieb 2000). In a series of papers, we will report on the
development of quantitative selection procedures for the systematic
exploitation of the stellar content of the HES, and their application to the
digital HES data base. In this paper, we report on an automatic algorithm for
the selection of DA white dwarfs (DAs).
,
it is also
possible to efficiently select a variety of interesting stellar
objects in the HES. These include, e.g., metal-poor halo stars, carbon stars,
cataclysmic variable stars, white dwarfs (WDs), subdwarf B stars (sdBs),
subdwarf O stars (sdOs), and field horizontal branch A- and B-type stars
(Christlieb 2000). In a series of papers, we will report on the
development of quantitative selection procedures for the systematic
exploitation of the stellar content of the HES, and their application to the
digital HES data base. In this paper, we report on an automatic algorithm for
the selection of DA white dwarfs (DAs).
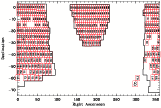 |
Figure 1:
Definition of HES area (framed) and numbers of fields in which the
exploitation of the stellar content of the HES is currently carried out.
For orientation, the position of the southern galactic pole is marked
with " |
| Open with DEXTER | |
The aim of the DA selection in the HES described in this paper is to test the
double-degenerate (DD) scenario for SN Ia progenitors, in which a binary
consisting of two WDs of large enough mass, merges and produces a
thermonuclear explosion. If this scenario is correct, SN Ia progenitor systems
should be present among DDs, the latter being identifiable by radial velocity
(RV) variations. Although several double degenerates have been found,
none of them is sufficiently massive to qualify as a viable SN Ia progenitor
(see Maxted & Marsh 1999). Note however that recently a system
consisting of a sdB and a massive white dwarf has been found, the total mass
of which exceeds the Chandrasekhar mass (Maxted et al. 2000). In order to
increase the sample of DDs, a Large Programme was proposed to (and
accepted by) the European Southern Observatory (ESO), aiming at observing a
large (![]() 1500) sample of WDs with VLT Unit Telescope 2 (UT2), and its
high resolution spectrograph UVES, at randomly chosen epochs, dictated by
observing conditions. That is, every time the weather is too bad to
carry out Service Mode observations for other programs, WDs are observed.
1500) sample of WDs with VLT Unit Telescope 2 (UT2), and its
high resolution spectrograph UVES, at randomly chosen epochs, dictated by
observing conditions. That is, every time the weather is too bad to
carry out Service Mode observations for other programs, WDs are observed.
A program like this requires a large catalog of targets spread all over the
accessible sky in order to be successful. From the "Catalog of
Spectroscopically Identified White Dwarfs'' of McCook & Sion (1999) it is
evident that the southern sky has not yet been surveyed as extensively for
white dwarfs as the northern sky: only 33% of the objects listed are
located at
![]() .
Therefore, we were aiming at selecting
additional targets in the data base of the HES.
.
Therefore, we were aiming at selecting
additional targets in the data base of the HES.
White dwarfs have been selected from wide angle surveys in the southern
hemisphere before, and also in the HES (see below). "Classical'' UV excess
surveys, like the Montreal-Cambridge-Tololo survey (MCT; Demers et al. 1986; Lamontagne et al. 2000), or the Edinburgh-Cape survey
(EC; Stobie et al. 1997; Kilkenny et al. 1997) can efficiently select
complete samples of hot stars, including WDs. However, completeness at the
cool end is either sacrificed for efficiency, as in the MCT (see Fig.
2), where only objects with U-B<-0.6 enter the sample of stars
for which follow-up spectroscopy is obtained (Lamontagne et al. 2000), or
efficiency is sacrificed for completeness, as in the EC. It has been shown
that the EC is 94% complete for objects of U-B<-0.4 down to B=16.5(Stobie et al. 1997). However, an intermediate selection step based on
photoelectric UBV photometry has to be used to eliminate the large fraction
(![]() 30%; see 1997) of "normal'' F and G type
stars.
30%; see 1997) of "normal'' F and G type
stars.
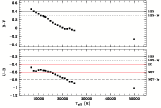 |
Figure 2:
U-B and B-V for DAs as a function of effective temperature,
determined with model spectra. Taking into account the rms error in
U-B of 0.18 mag in the MCT survey, the adopted selection criterion
of U-B<-0.6 leads to rejection of cool ( |
| Open with DEXTER | |
In the HES, WDs enter the quasar candidate sample if they have U-B<-0.18(Wisotzki et al. 2000). However, HES quasar candidates are inspected manually at
the computer screen, and in this process hot stars, and stars clearly
exhibiting stellar absorption lines (like e.g. DA white dwarfs, having strong,
broad lines over a wide temperature range; see Fig. B.1 in Appendix
B) are rejected, and follow-up spectroscopy is
not obtained for them in the course of the quasar survey. This results
in a very efficient quasar selection: typically 70% of the objects for
which follow-up spectroscopy is obtained are quasars
(Wisotzki et al. 2000). The remaining 30% are mainly hot subdwarfs, and cool
(
![]() K), helium-rich WDs
(DBs, DZs; see Friedrich et al. 2000). A couple of interesting peculiar objects,
e.g., magnetic DBs (Reimers et al. 1998) and magnetic DAs
(Reimers et al. 1994, 1996) have also been discovered in this way.
K), helium-rich WDs
(DBs, DZs; see Friedrich et al. 2000). A couple of interesting peculiar objects,
e.g., magnetic DBs (Reimers et al. 1998) and magnetic DAs
(Reimers et al. 1994, 1996) have also been discovered in this way.
The selection of white dwarf candidates described in this paper aims at an efficient selection; that is, the contamination of the sample with other objects (e.g., hot subdwarfs) shall be as clean as possible, in order not to waste any observing time at the VLT.
A description of the HES plate material, plate digitisation and data reduction can be found in Wisotzki et al. (2000). In this section we describe some survey properties that are particularily important for stellar work in more detail than it was done in Wisotzki et al. (2000), and we briefly repeat a general description of the HES, for better readability.
The HES is based on IIIa-J plates taken with the 1m ESO Schmidt telescope
and its ![]() prism. It covers the magnitude range
prism. It covers the magnitude range
![]() (Wisotzki et al. 2000). The magnitude limits depend on plate
quality. Note that the value given for the faint limit is the completeness
limit for quasar search, which we define as the magnitude corresponding to
average photographic density in the
(Wisotzki et al. 2000). The magnitude limits depend on plate
quality. Note that the value given for the faint limit is the completeness
limit for quasar search, which we define as the magnitude corresponding to
average photographic density in the ![]() band
band ![]() above the diffuse plate
background, where
above the diffuse plate
background, where ![]() is the background noise. The detection limit of the
HES is approximately one magnitude deeper than the completeness limit. For
stellar applications, the survey magnitude range depends on the object type
searched for. E.g., in our search for metal-poor stars, we only use spectra
that are not affected by saturation effects, which typically start to be
noticable at
is the background noise. The detection limit of the
HES is approximately one magnitude deeper than the completeness limit. For
stellar applications, the survey magnitude range depends on the object type
searched for. E.g., in our search for metal-poor stars, we only use spectra
that are not affected by saturation effects, which typically start to be
noticable at
![]() ,
and we only include spectra with S/N>10 (which
roughly corresponds to
,
and we only include spectra with S/N>10 (which
roughly corresponds to
![]() ), because at lower S/N an efficient
selection of metal-poor stars, by means of a weak or absent Ca K line, is not
feasible anymore. However, for most other object types, including DAs, we
adopt the
), because at lower S/N an efficient
selection of metal-poor stars, by means of a weak or absent Ca K line, is not
feasible anymore. However, for most other object types, including DAs, we
adopt the ![]() magnitude limit.
magnitude limit.
The atmospheric cutoff at the blue end, and the sharp sensitivity
cutoff of the IIIa-J emulsion ("red edge'') result in a wavelength
range of
![]() (see Fig. 3). The spectral resolution of the HES is
primarily seeing-limited. For plates taken during good seeing
conditions, the pixel spacings chosen in the digitization process
result in an under-sampling, so that in these cases the spectral
resolution is also limited by the sampling.
(see Fig. 3). The spectral resolution of the HES is
primarily seeing-limited. For plates taken during good seeing
conditions, the pixel spacings chosen in the digitization process
result in an under-sampling, so that in these cases the spectral
resolution is also limited by the sampling.
The definition of the HES survey area makes use of the mean star density and
average column density of neutral hydrogen for each ESO/SERC field
(Wisotzki et al. 2000). The adopted criteria roughly correspond to galactic
latitudes of
![]() .
The declination range covered by the HES is
.
The declination range covered by the HES is
![]() .
As a result, the survey area consists of 380 fields. Between 1989 and 1998, objective-prism plates were taken for all of
these, and the plates were subsequently digitized and reduced at Hamburger
Sternwarte. As one ESO Schmidt plate covers approximately
.
As a result, the survey area consists of 380 fields. Between 1989 and 1998, objective-prism plates were taken for all of
these, and the plates were subsequently digitized and reduced at Hamburger
Sternwarte. As one ESO Schmidt plate covers approximately
![]() on
the sky, the nominal survey area is
on
the sky, the nominal survey area is ![]() deg2, or the total southern
extragalactic sky. Note, however, that the effective survey area is
deg2, or the total southern
extragalactic sky. Note, however, that the effective survey area is
![]() 25% lower, mainly because of overlapping spectra
(Wisotzki et al. 2000).
25% lower, mainly because of overlapping spectra
(Wisotzki et al. 2000).
Overlapping spectra (hereafter shortly called overlaps) are detected
automatically using the direct plate data of the Digitized Sky Survey I
(DSS I). For each spectrum to be extracted, it is looked for objects in the
dispersion direction on the direct plate. If there is one, the automatic
procedure marks the corresponding spectrum, so that it can later be excluded
from further processing, if this is desired. It is desired for stellar
work, since the feature detection and object selection algorithms would get
confused otherwise, and a lot of "garbage'' would enter the candidate
samples. The digital HES data base for stellar work consists of ![]() 4 million extracted, overlap-free spectra with average S/N>5 in the
4 million extracted, overlap-free spectra with average S/N>5 in the ![]() band.
band.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10235f3.ps}
\end{figure}](/articles/aa/full/2001/06/aa10235/Timg31.gif) |
Figure 3:
Measurement of noise in an absorption line free spectral region of A-type
stars. Note that we plot HES objective prism spectra such that wavelengths
are decreasing towards the right, because the scan length x is
increasing in this direction. The sharp drop of the spectra at
the red end is due to the IIIa-J emulsion sensitivity cutoff at |
| Open with DEXTER | |
As described in Wisotzki et al. (2000), the calibration of HES ![]() magnitudes is done plate by plate with individual photometric
sequences. The
magnitudes is done plate by plate with individual photometric
sequences. The ![]() band is formally defined by the spectral
sensitivity curve of the Kodak IIIa-J emulsion multiplied with the
filter curve of a Schott GG395 filter. The overall errors of the HES
band is formally defined by the spectral
sensitivity curve of the Kodak IIIa-J emulsion multiplied with the
filter curve of a Schott GG395 filter. The overall errors of the HES
![]() magnitudes, including zero point errors, are less than
magnitudes, including zero point errors, are less than ![]() mag. Note that
mag. Note that ![]() can be converted to B using the formula
can be converted to B using the formula
A global dispersion relation for all HES plates was determined by using A-type
stars. In HES spectra of these stars the Balmer lines at least up to H10are resolved (see Fig. 3), so that a dispersion
relation can be derived by comparing the x-positions (scan length in
![]() m) of these lines with the known wavelengths. Borra et al. (1987)
used the position of the "red edge'' of objective-prism spectra to determine
the zero point of the wavelength calibration, but noticed that the position
depends on the energy distribution of the object. Therefore, in the HES we
decided to use a zero point specified by an astrometric transformation between
direct plates and spectral plates. The wavelength calibration is accurate to
m) of these lines with the known wavelengths. Borra et al. (1987)
used the position of the "red edge'' of objective-prism spectra to determine
the zero point of the wavelength calibration, but noticed that the position
depends on the energy distribution of the object. Therefore, in the HES we
decided to use a zero point specified by an astrometric transformation between
direct plates and spectral plates. The wavelength calibration is accurate to
![]() m. This corresponds to
m. This corresponds to ![]() Å at H
Å at H![]() and
and ![]() Å at
Å at
![]() Å.
Å.
Following the approach of Hewett et al. (1985), we determine the amplitude
of pixel-wise noise as a function of photographic density D plate by plate
using A- and F-type stars. A straight line fit is done to the spectral region
between H![]() and H
and H![]() (see Fig. 3).
The
(see Fig. 3).
The ![]() -scatter around this pseudo-continuum fit is taken as noise
amplitude. In this approach we assume that the scatter is mainly due to noise,
since in early-type stars the spectral region under consideration includes
only very few absorption lines at the spectral resolution of the HES.
Moreover, it is expected that the population of A- and F-type stars found at
high galactic latitudes is dominated by metal-poor stars, so that metal lines
are usually very weak. However, we cannot exclude that we overestimate the
noise by a few percent due to contributions of metal lines to the scatter
around the pseudo-continuum fit.
-scatter around this pseudo-continuum fit is taken as noise
amplitude. In this approach we assume that the scatter is mainly due to noise,
since in early-type stars the spectral region under consideration includes
only very few absorption lines at the spectral resolution of the HES.
Moreover, it is expected that the population of A- and F-type stars found at
high galactic latitudes is dominated by metal-poor stars, so that metal lines
are usually very weak. However, we cannot exclude that we overestimate the
noise by a few percent due to contributions of metal lines to the scatter
around the pseudo-continuum fit.
We measure the noise amplitude for all A- and F-type stars present on
each HES plate (typically several hundred per plate), and compute the mean
density D in the fit region. This yields data points
![]() ,
to
which a 2nd order polynomial is fitted, i.e.
,
to
which a 2nd order polynomial is fitted, i.e.
For the determination of the coefficients
![]() we use a robust fit
algorithm which minimizes the sum of absolute deviations, taking into account
the following set of boundary conditions:
we use a robust fit
algorithm which minimizes the sum of absolute deviations, taking into account
the following set of boundary conditions:
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10235f4.ps}
\end{figure}](/articles/aa/full/2001/06/aa10235/Timg52.gif) |
Figure 4:
Fitting of a 2nd order polynomial to data points
|
| Open with DEXTER | |
For simulations of spectra (see
Sect. 4) it is very important to know the form of the
distribution of noise. We investigated this by using 50 spectra of A-type
stars from eight plates with high sky background (
![]() ), and 60 spectra from seven plates with low background
(
), and 60 spectra from seven plates with low background
(
![]() ). These spectra were chosen by hand from the
sample of automatically selected A-type stars, in order to ensure that
misclassified spectra, and spectra for which the fit of the continuum between
H
). These spectra were chosen by hand from the
sample of automatically selected A-type stars, in order to ensure that
misclassified spectra, and spectra for which the fit of the continuum between
H![]() and H
and H![]() by a straight line is not fully adequate, do not
confuse the results. Five of the original set of 115 spectra were excluded in
the manual selection process.
by a straight line is not fully adequate, do not
confuse the results. Five of the original set of 115 spectra were excluded in
the manual selection process.
The deviations from the continuum fits were collected for each spectrum, shifted to a median of zero, and divided by the average of the absolute values of the upper and lower 50% quartile, so that a comparison of the noise distributions measured in different spectra (with different noise amplitude) is possible. The result is that the distribution of pixel-wise noise is almost perfectly Gaussian, independently of plate background (see Fig. 5).
Figure 6 shows the relation between average pixel-wise S/N in the
![]() band and
band and ![]() magnitudes for 589 not saturated point sources from many
different HES plates. The large scatter of S/N for given
magnitudes for 589 not saturated point sources from many
different HES plates. The large scatter of S/N for given ![]() shown in
this plot is due to varying plate background, and seeing.
shown in
this plot is due to varying plate background, and seeing.
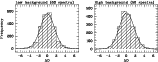 |
Figure 5: Distribution of pixel-wise noise in absorption line free regions of 60 spectra of A-type stars from seven plates with low sky background (left panel), and 50 spectra from eight plates with high background (right panel). For further explanation see text |
| Open with DEXTER | |
It is critical for all quantitative selection methods to have a set of reliable features at hand. The total set of available features should contain as much information of the objects to be classified as possible. Therefore, we implemented a flexible, robust algorithm which allows to detect stellar absorption and/or emission lines in HES spectra. Hewett et al. (1985) used a template matching technique to automatically detect absorption and emission lines in objective-prism spectra. Tests with HES spectra have shown that a fit algorithm involving a couple of boundary conditions (see below) is much more stable and leads to more accurate measurements of equivalent widths than template matching. The algorithm used in the HES consists of the following steps:
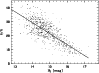 |
Figure 6:
Average pixel-wise S/N in the |
| Open with DEXTER | |
As already noticed by Hewett et al. (1985), relative colours can be determined quite accurately directly from objective-prism spectra. (Hewett et al. 1995) used so-called "half power points (hpps)'' to measure relative colours, that is, bisecting points of the photographic density distribution. hpps are equivalent to broad-band colours, but have the advantage of being more robust against noise. Wisotzki et al. (2000) introduced half power points that are computed only for a part of the spectrum (see Fig. 7). The half power points x_hpp1 and x_hpp2 are well correlated with U-B and B-V, respectively. Since it is helpful in many stellar applications to have not only relative, but calibrated U-B and B-V colours at hand, we established calibrations of x_hpp1 and x_hpp2 versus U-B and B-V, respectively.
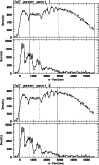 |
Figure 7: Illustration of spectral half power points x_hpp1 and x_hpp2. Solid lines mark the regions in which the hpps are computed; dotted lines indicate the position of the hpps |
| Open with DEXTER | |
A more precise colour calibration can be achieved when distances dx
to a cutoff line in a colour-magnitude diagram (see Fig. 8) is
used instead of x values (scan length in ![]() m) for the bisecting
point, because plate-to-plate variations of the spectral sensitivity curves
are compensated in this way. The cutoff line separates the bulk of "normal''
stars from UV-excess objects (or objects with unusually low B-V in case of
dx_hpp2). The cutoff is determined by a break finding algorithm.
m) for the bisecting
point, because plate-to-plate variations of the spectral sensitivity curves
are compensated in this way. The cutoff line separates the bulk of "normal''
stars from UV-excess objects (or objects with unusually low B-V in case of
dx_hpp2). The cutoff is determined by a break finding algorithm.
 |
Figure 8: Cutoff-line for bisecting point x_hpp1 on one HES plate |
| Open with DEXTER | |
Because the blue end of the HES spectra is sensitive to contamination by
overlaps, special care must be taken to exclude such spectra from the
calibration of dx_hpp1. This was done by applying stricter overlap
rejection criteria. In addition, an iterative
![]() -clipping with
-clipping with
![]() was employed to exclude overlaps unrecognized by the automatic
detection. 50 of the 623 spectra in the original data set were rejected, so
that the calibration uses spectra of 573 objects (see Fig. 9; a
similar plot was shown in Wisotzki et al. 2000).
was employed to exclude overlaps unrecognized by the automatic
detection. 50 of the 623 spectra in the original data set were rejected, so
that the calibration uses spectra of 573 objects (see Fig. 9; a
similar plot was shown in Wisotzki et al. 2000).
A potential problem for the B-V calibration is that the V band is not
fully covered by the HES wavelength range. Therefore, the calibration for very
red objects is inaccurate, or even impossible. As calibrators for red objects,
36 carbon stars were used, for which BV photometry was obtained
at the ESO 2.2m telescope in April 1999. Carbon stars with B-V>2.5were excluded from the fit. For
![]() ,
778 stars from the HK
survey of Beers et al. (1992), 354 FHB and other A-type stars of
Wilhelm et al. (1999), and 272 objects from the northern galactic cap
fields of the EC survey (Kilkenny et al. 1997) present on HES plates were
used. Linear fits in three colour regions were done separately, in
order to evaluate the scatter independently, and check consistency. Then, a
combined fit to all 1256 unique objects was done (see Fig. 9).
,
778 stars from the HK
survey of Beers et al. (1992), 354 FHB and other A-type stars of
Wilhelm et al. (1999), and 272 objects from the northern galactic cap
fields of the EC survey (Kilkenny et al. 1997) present on HES plates were
used. Linear fits in three colour regions were done separately, in
order to evaluate the scatter independently, and check consistency. Then, a
combined fit to all 1256 unique objects was done (see Fig. 9).
The results of the fits are summarized in Table 1. Note that a
single fit contains objects from a large fraction of the 329 stellar HES
plates, and a wide range of object types, e.g. carbon stars, metal-poor stars,
solar metallicity F- and G-type stars, field horizontal branch A-type stars,
"normal'' A-type stars, DAs, DBs, sdBs and quasars. The achieved accuracies
are
![]() mag, and
mag, and
![]() mag for the B-V fit
using all calibration objects together. The accuracy in B-V for red (
mag for the B-V fit
using all calibration objects together. The accuracy in B-V for red (
![]() )
and blue (
)
and blue (
![]() )
objects is a factor of
)
objects is a factor of ![]() 2
worse (
2
worse (
![]() mag and 0.12 mag, respectively) than for intermediate
B-V objects (
mag and 0.12 mag, respectively) than for intermediate
B-V objects (
![]() mag).
mag).
| Colour | valid range |
|
|
| B-V | -0.6<B-V<2.0 | 1259 | 0.095 |
| U-B | -1.4<U-B<0.8 | 573 | 0.092 |
| c1 | -0.4<c1<1.0 | 79 | 0.15 |
We obtain Strömgren coefficients
c1=(u-v)-(v-b) directly from HES spectra
by averaging the density in the Strömgren uvb bands, and computing
internal coefficients
![]() from that.
from that.
![]() was calibrated using a total of 79 stars not saturated in the HES,
from three different sources. 22 metal-poor stars were taken from Schuster et al.
(1996), 43 stars from Beers (2000, priv. comm.), of which 2
were rejected as outliers (see Fig. 10), and 16 hot subdwarfs
from an updated version of the catalog of Kilkenny et al. (1988). The
was calibrated using a total of 79 stars not saturated in the HES,
from three different sources. 22 metal-poor stars were taken from Schuster et al.
(1996), 43 stars from Beers (2000, priv. comm.), of which 2
were rejected as outliers (see Fig. 10), and 16 hot subdwarfs
from an updated version of the catalog of Kilkenny et al. (1988). The
![]() error of the calibration is 0.15 mag. c1 can be used as a
gravity indicator for early-type stars, since it measures the strength of the
Balmer discontinuity.
error of the calibration is 0.15 mag. c1 can be used as a
gravity indicator for early-type stars, since it measures the strength of the
Balmer discontinuity.
 |
Figure 9: Calibration of dx_hpp1 versus U-B using a sample of 573 objects from the EC and HK surveys present on HES plates (left panel); calibration of dx_hpp2 versus B-V using spectra of 1256 objects (right panel) |
| Open with DEXTER | |
In many stellar applications of the HES, it is not possible to generate large enough training and test samples from real spectra present on HES plates. This is because usually the target objects are very rare. Therefore, we have developed methods to generate artificial learning samples by simulations, using either model spectra, or slit spectra. In this paper we will use the simulations for the development of selection criteria. In later papers we will use sets of simulated spectra as learning samples for selection of e.g. metal-poor stars by automatic spectral classification.
The conversion of model spectra, or slit spectra, to objective-prism spectra consists of five steps:
Spectral sensitivity curves (SSCs) for HES plates were determined by
comparison of WD model spectra, rebinned to the wavelength dependent
pixel size
![]() of the objective-prism spectra, with
objective-prism spectra of DAs on HES plates. We do not use the slit spectra
directly as reference, because slit losses would produce erroneous results.
The theoretical DA spectra, taken from a standard grid of WD model atmospheres
(see Finley et al.1997 for a description), were fitted to the slit
spectra with methods described in Finley et al. (1997) and
Homeier et al. (1998). The spectra were taken with the Boller & Chivens
spectrograph attached to the ESO 1.52m telescope, and with DFOSC at the
ESO-Danish 1.54m telescope. The atmospheric parameters of the twelve objects
used in this investigation are listed in Table 2.
of the objective-prism spectra, with
objective-prism spectra of DAs on HES plates. We do not use the slit spectra
directly as reference, because slit losses would produce erroneous results.
The theoretical DA spectra, taken from a standard grid of WD model atmospheres
(see Finley et al.1997 for a description), were fitted to the slit
spectra with methods described in Finley et al. (1997) and
Homeier et al. (1998). The spectra were taken with the Boller & Chivens
spectrograph attached to the ESO 1.52m telescope, and with DFOSC at the
ESO-Danish 1.54m telescope. The atmospheric parameters of the twelve objects
used in this investigation are listed in Table 2.
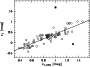 |
Figure 10: Calibration of Strömgren c1 measured in HES spectra. The two filled circles mark objects that were excluded from the fit |
| Open with DEXTER | |
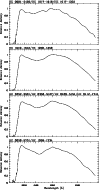 |
Figure 11: Averaged spectral sensitivity curves |
| Open with DEXTER | |
By comparing SSCs for plates from different plate batches, with different sky background, and generated with objects spanning a wide brightness range (see Table 3), but below the saturation threshold, we investigated the possible systematic influence of these characteristics on the shape of the SSCs. By comparing the shapes of the twelve resulting SSCs, we found that there is no systematic influence of object brightness, plate batch and sky background on SSC shape. The plate material of the HES is surprisingly homogenous; however, a slight variation of SSC shape is present, which hence must be attributed to another parameter. Since it is the blue part of the SSCs that varies, it is very likely that the time span between hypersensitization and development of the plate is responsible for the shape variations.
| Name |
|
McCook & Sion | |
| HE 0004-5403 |
|
|
|
| HE 0059-5701 |
|
|
|
| HE 0252-3501 |
|
|
WD 0252-350 |
| HE 0358-5127 |
|
|
|
| HE 0409-5154 |
|
|
|
| HE 0412-4744 |
|
|
|
| HE 0418-5326 |
|
|
|
| HE 1049-1552 |
|
|
WD 1049-158 |
| HE 1058-1258 |
|
|
WD 1058-129 |
| HE 1058-1334 |
|
|
|
| HE 1017-1618 |
|
|
WD 1017-163 |
| HE 1017-1352 |
|
|
We grouped the twelve SSCs into four SSC classes of similar shape, and averaged them within these classes (see Fig. 11). When converting model spectra or slit spectra to objective prism spectra, we use an SSC created by averaging the four averaged SSCs with randomly assigned weights.
| # | Name | Plate | bgr | Batch | |
| 1 | HE 0004-5403 | 16.2 | 12076 | 1123 | 1D4 |
| 1 | HE 1017-1618 | 15.8 | 8402 | 1363 | 1K6 |
| 1 | HE 1017-1352 | 14.4 | 8402 | 1363 | 1K6 |
| 2 | HE 1049-1552 | 14.2 | 9091 | 752 | 1C8 |
| 2 | HE 1058-1258 | 14.8 | 9091 | 752 | 1C8 |
| 3 | HE 0252-3501 | 16.0 | 11420 | 1039 | 1D4 |
| 3 | HE 0358-5127 | 15.4 | 10844 | 765 | 1I3 |
| 3 | HE 0409-5154 | 16.1 | 10844 | 765 | 1I3 |
| 3 | HE 0412-4744 | 16.5 | 10844 | 765 | 1I3 |
| 4 | HE 0059-5701 | 16.4 | 12052 | 1026 | 1D4 |
| 4 | HE 1058-1334 | 16.6 | 9091 | 752 | 1C8 |
We add artificial, normally distributed noise to the converted spectra, in
order to simulate objective-prism spectra of a desired brightness. We parameterize
the S/N of a spectrum by the mean S/N in the ![]() band,
band,
 |
Figure 12:
HES spectrum of HE0454-5446, a white
dwarf of type DA (left panel), in comparison with a model spectrum of a
DA with
|
| Open with DEXTER | |
Since we are aiming at a very efficient selection of white dwarf candidates, we investigated to what extent different types of hot stars can be distinguished in the HES in a two-colour diagram (U-B versus B-V), and in the two-dimensional feature space c1 versus balmsum. We also explored several other parameter combinations, including e.g. continuum shape parameters determined by principal component analysis, but found them to be less appropriate. Using various catalogs, we identified 521 hot stars in the HES. The catalogs are: (Kilkenny et al. 1997); Wilhelm et al. (1999), an updated version of the Kilkenny et al. (1988) subdwarf catalog, and McCook & Sion (1999). Additionally, 39 HES A-type stars with known stellar parameters were included.
It turned out that high gravity stars (WDs, sdBs, and sdOs) can be
distinguished quite reliably from lower gravity stars (main sequence and
horizontal branch stars). However, the separation between hot subdwarfs and
WDs is much more difficult, since they occupy similar regions in the parameter
space (see Fig. 13). The only way to obtain clean white dwarf
samples is to sacrifice completeness, as we will see below. Note however that
unlike in the EC, it is possible in the HES to compile candidate samples that
have no contamination with main sequence or horizontal branch stars.
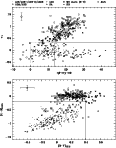 |
Figure 13: DA selection in colour-colour space and c1 versus Balmer line sum feature space. Solid lines: adopted selection box; dashed lines: additional parameter area included for the selection of the UVES sample. In the upper left corner, error bars for c1, U-B and B-V are displayed |
| Open with DEXTER | |
With the spectral features automatically detected in HES spectra up to now, it is not yet possible to select DB white dwarfs; in order to do this, Helium lines would have to be added to the line list. This is currently being done.
As a first step in developing selection criteria for DAs, selection boxes in the B-V versus U-B and c1 versus Balmer line sum parameter spaces were chosen such that all DAs were included (see Fig. 13). A first set of 47 HES DA candidates (hereafter referred to as the "UVES sample''; see Table A.1) selected in this way (and 72 additional WDs) were observed with VLT-UT2 and UVES between April 4 and June 6, 2000. This set includes seven re-discovered DAs listed in McCook & Sion (1999). Based on pipeline-reduced spectra, 19 of these were classified as DAs, 26 as hot subdwarfs (e.g., sdB, sdOB, sdO), two as DOs, and none as main sequence or horizontal branch star.
In order to decrease the contamination with hot subdwarfs, we examined if
"harder'' selection criteria could lead to reduced, but acceptable
completeness with respect to DA white dwarfs on the one hand, and a cleaner
candidate sample on the other hand.
Contamination and completeness in dependence of the cutoff in Balmer line
equivalent width sum was evaluated by using the subsample of those 200 stars
from the learning sample of 521 stars mentioned above that were located in the
selection boxes also applied to the UVES sample. The relative numbers of stars
were scaled such that the fraction of hot subdwarfs
and WDs did reflect the fractions in the UVES sample. As can be seen from the
results displayed in Fig. 14, it is possible to compile a 80%
complete sample of DA white dwarfs, which is contamined by only 8% hot
subdwarfs, if one confines the sample to objects with
![]() Å.
Å.
Selecting only the objects with very strong Balmer lines leads to
incompleteness at the hot end of the DA sample (see Fig. 15), whereas DAs at
![]() are very
likely to be selected even at faint magnitudes (that is, at low S/N).
are very
likely to be selected even at faint magnitudes (that is, at low S/N).
The final criteria,
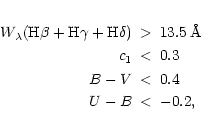
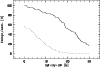 |
Figure 14: Completeness (solid line) and contamination (dotted line) of the DA candidate sample as a function of Balmer line equivalent sum |
| Open with DEXTER | |
 |
Figure 15:
Balmer line equivalent width sum and
Stroemgren c1 as a function of effective temperature, determined from
simulated HES spectra with S/N=10 (typically corresponding to
|
| Open with DEXTER | |
We evaluated the raw candidate selection by visually inspecting a
sample of 675 DA candidates at the computer screen. Visual inspection is a
mandatory step in the HES in order to identify plate artifacts, the few
overlaps that are not recognized by the automatic detection algorithm, and to
reject mis-classified and noisy spectra. The 675 candidates were selected from
the 1789792 overlap-free spectra with S/N>5 present on 225 HES plates.
We define the specifity of a selection as the fraction of candidate
spectra (
![]() )
drawn from the original set of spectra
(
)
drawn from the original set of spectra
(
![]() ); i.e.,
); i.e.,
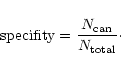 |
(5) |
| Specifity | 1/2652 |
| DA candidates (efficiency) | 71.6% |
| Uncertain DA candidates | 3.3% |
| main sequence stars (F or later) | 7.4% |
| Subdwarf B stars | 5.0% |
| Horizontal branch A- or B-type stars | 0.9% |
| Quasar candidates | 0.9% |
| Noisy spectra (no classification possible) | 4.7% |
| Spectra disturbed by artifacts | 4.1% |
| Overlaps | 2.1% |
The selection method described above allows a very efficient selection of DAs,
with a high completeness (![]() 80%). However, this completeness estimate
is based on a sample of objects that are part of the current HES data base of
spectra. It is expected that a significant fraction of WDs are not part of
that data base due to their proper motion (p.m.). This is because the input
catalog for extraction of objective-prism spectra is generated by using the
DSS I. Large proper motions and/or large epoch differences between HES and
DSS I plates (13.5 years on average) currently result in a mis-extraction of
spectra of objects having
80%). However, this completeness estimate
is based on a sample of objects that are part of the current HES data base of
spectra. It is expected that a significant fraction of WDs are not part of
that data base due to their proper motion (p.m.). This is because the input
catalog for extraction of objective-prism spectra is generated by using the
DSS I. Large proper motions and/or large epoch differences between HES and
DSS I plates (13.5 years on average) currently result in a mis-extraction of
spectra of objects having
![]() (i.e.,
(i.e.,
![]() pixels), because the spectrum of
the object is looked for at the wrong place. Proper motion in direction of
pixels), because the spectrum of
the object is looked for at the wrong place. Proper motion in direction of
![]() leads to an offset of the wavelength calibration zero point,
resulting in wrong equivalent width measurements (i.e., the measured widths
are too low).
leads to an offset of the wavelength calibration zero point,
resulting in wrong equivalent width measurements (i.e., the measured widths
are too low).
How large the incompleteness due to the epoch-difference problem is can
roughly be estimated from a cross-identification of the HES with the catalog
of McCook & Sion (1999). It lists 2187 objects. 1633 have an available
V measurement. Of these, 1295 (or 79.3%) lie in the HES magnitude
range (
![]() ,
assuming an average B-V of zero). 606 objects are located in the southern hemisphere (
,
assuming an average B-V of zero). 606 objects are located in the southern hemisphere (
![]() ),
and at high galactic latitude (
),
and at high galactic latitude (
![]() ). Assuming that 79.3% of
these are in the HES magnitude range, we expect
). Assuming that 79.3% of
these are in the HES magnitude range, we expect ![]() 480 WDs to be in the
HES area, and detectable in the HES. Taking into account a loss of 25%
due to overlapping spectra, we expect 360 known WDs to be found on all 380 HES
plates, and 310 WDs on the 329 plates used so far for the exploitation of the
stellar content. However, in a cross-identification procedure using a
480 WDs to be in the
HES area, and detectable in the HES. Taking into account a loss of 25%
due to overlapping spectra, we expect 360 known WDs to be found on all 380 HES
plates, and 310 WDs on the 329 plates used so far for the exploitation of the
stellar content. However, in a cross-identification procedure using a
![]() search box, to compensate for the sometimes very inaccurate
coordinates of McCook & Sion (1999), only 151 WDs (
search box, to compensate for the sometimes very inaccurate
coordinates of McCook & Sion (1999), only 151 WDs (![]() 50% of the
expected 310) were found.
50% of the
expected 310) were found.
At the chosen search box width a "saturation'' of identified objects was
reached; by using a larger box, no further WDs were found. However, the
experience from an identification of WDs from McCook & Sion (1999) in the
northern hemisphere sister project of the HES, the Hamburg Quasar Survey
(HQS; Hagen et al. 1995), is that 30-40% of the objects were
identified at positions more than 10''away from the nominal position; in
many cases much more (up to several arcminutes), which explains
why the identification saturation sets in already in for a
![]() search box.
search box.
Furthermore, we suspect that two effects may lead to an underestimate of the completeness of the present DA selection in the HES: First, many WDs listed in McCook & Sion (1999) were discovered in the course of proper motion surveys. Therefore, the catalog is very likely to be biased towards high p.m. objects, which makes the listed WDs less likely to be detected in the HES than the real population of WDs. Second, the peak of the magnitude distribution of the WDs from McCook & Sion (1999) is more than one magnitude brighter than that of the HES, so that on average closer WDs (with on average higher p.m.) are listed in McCook & Sion (1999).
We conclude that the true completeness of our selection is probably higher
than indicated by the simple cross-comparison. We conservatively estimate the
proper motion-induced losses of DAs in the HES to be not higher than ![]() 20%.
Special techniques to recover also high p.m. WDs are currently under
development. Such techniques will permit us to construct flux-limited samples
of DA white dwarfs with a very high degree of completeness, useful e.g. to
determine luminosity functions.
20%.
Special techniques to recover also high p.m. WDs are currently under
development. Such techniques will permit us to construct flux-limited samples
of DA white dwarfs with a very high degree of completeness, useful e.g. to
determine luminosity functions.
Another problem of WD selection in the HES might currently result from the fact that in the HES stellar feature detection algorithm the width of the absorption lines is held fixed at the measured width of the instrumental profile, in order to make the algorithm more robust. However, unlike in "normal'' stars, the absorption lines of WDs are so broad that they are usually resolved in the HES spectra. Therefore, the equivalent widths of their absorption lines are expected to be underestimated. Apart from more accurately measured equivalent widths, adding the line widths to the parameters to be fitted would result in the opportunity to employ a further criterion for the separation between hot subdwarfs and WDs: if the absorption lines in the spectrum of an object are significantly broader than the instrumental profile, the object is very likely to be a WD. A modification of the feature detection algorithm is in progress.
A further improvement of the selection can likely be achieved if instead of straight lines higher-order selection boundaries are used, as is the case e.g. in quadratic discriminant analysis. However, defining such selection boundaries requires large, and well-defined learning samples. A lack of model spectra for early-type stars (main sequence as well as horizontal branch stars) so far prevented us from using a learning sample of simulated objective-prism spectra for this purpose.
We described quantitative procedures for the selection of DA white dwarfs in the digital data base of the HES. Algorithms for the detection of stellar emission and absorption lines, broad- and intermediate-band colours were developed. These are not only used for the selection of DAs, but also for a couple of other interesting stars, e.g. metal-poor stars, and carbon stars. Simulation techniques allow us to convert model spectra to HES spectra, which is important for the development of selection criteria, for the compilation of learning samples used for automatic spectral classification, and for the determination of selection functions.
DAs can be selected very efficiently in the HES, as required by a currently ongoing Large Programme using VLT-UT2 and UVES, aiming at the detection of double degenerates. A first set of 440 DA candidates not listed in the catalog of McCook & Sion (1999) was identified on 225 HES plates (i.e., 59% of the survey).
We note that the UVES sample includes a double-lined DA+DA binary, and two further DAs with significant RV variations. The results will be reported elsewhere. Further investigation of these systems is in progress.
For investigations requiring complete samples of DAs (or other objects having high proper motions), special extraction techniques have to be employed to take into account the epoch differences between HES plates and the DSS I, since the latter is used for object detection in the HES. Such techniques are currently under development.
Acknowledgements
N. C. and D. H. acknowledge financial support from Deutsche Forschungsgemeinschaft under grants Re 353/40 and Ko 738/10-3, respectively. We thank V. Beckmann for observing a part of the DAs that were used to determine the HES spectral sensitivity curves. Precise, photoelectric UBV and Strömgren uvby photometry for HK survey stars was kindly provided by T. Beers before publication. We thank D. O'Donoghue for making EC survey photometry in digital form available to us. G. Pizarro kindly compiled a list of HES plate batches from the notes he made at the ESO Schmidt telescope. We thank the Paranal staff for carrying out the observations for the ESO Large Programme 165.H-0588 in Service Mode at VLT-UT2.
In Table A.1 we list coordinates, magnitudes, colours,
Balmer line equivalent width sums and classifications of the UVES sample of
47 DA candidates.
| HE name | RA | Dec | B | U-B | B-V | c1 | balmsum | Type | McCook & Sion |
| HE 0952+0227 | 09 55 34.6 | +02 12 48 | 14.7 | -1.04 | -0.17 | -0.10 | 6.6 | sdO | |
| HE 0956+0201 | 09 58 50.4 | +01 47 23 | 15.6 | -0.64 | 0.06 | -0.09 | 24.7 | DA | WD 0956+020 (DA3) |
| HE 0958-1151 | 10 00 42.6 | -12 05 59 | 13.7 | -1.05 | -0.11 | -0.15 | 2.9 | DAB | |
| HE 1008-1757 | 10 10 33.4 | -18 11 48 | 14.9 | -0.91 | -0.15 | -0.02 | 2.5 | DAO (sdO hot) | WD 1008-179 (DA) |
| HE 1012-0049 | 10 15 11.7 | -01 04 17 | 15.6 | -0.86 | 0.06 | -0.07 | 20.5 | DA | |
| HE 1026+0014 | 10 28 34.8 | -00 00 29 | 13.9 | -0.49 | 0.30 | -0.05 | 23.1 | DA+dM | WD 1026+002 (DA3) |
| HE 1033-2353 | 10 36 07.2 | -24 08 34 | 16.0 | -1.08 | -0.34 | -0.03 | 12.4 | sdB (sdOB) | |
| HE 1038-2326 | 10 40 36.9 | -23 42 39 | 15.9 | -0.86 | -0.13 | 0.00 | 10.7 | sdB+cool star? | |
| HE 1047-0436 | 10 50 26.9 | -04 52 36 | 14.7 | -0.96 | -0.21 | -0.01 | 10.0 | sdB | |
| HE 1047-0637 | 10 50 28.7 | -06 53 26 | 14.3 | -1.04 | -0.17 | -0.11 | 6.0 | sdO | |
| HE 1053-0914 | 10 55 45.4 | -09 30 58 | 16.4 | -0.74 | 0.07 | -0.12 | 30.3 | DA | |
| HE 1059-2735 | 11 01 24.9 | -27 51 42 | 15.1 | -1.23 | -0.35 | -0.19 | 10.6 | sdB (sdOB) | |
| HE 1117-0222 | 11 19 34.7 | -02 39 05 | 14.3 | -0.51 | 0.22 | -0.10 | 24.8 | DA | |
| HE 1130-0620 | 11 32 41.5 | -06 36 53 | 15.8 | -1.08 | -0.09 | -0.01 | 5.3 | sdB (sdOB) | |
| HE 1136-2504 | 11 39 10.2 | -25 20 55 | 13.8 | -1.09 | -0.17 | -0.15 | 9.5 | sdO | |
| HE 1142-2311 | 11 44 50.2 | -23 28 18 | 15.4 | -1.28 | -0.34 | -0.23 | 3.6 | sdO | |
| HE 1152-1244 | 11 54 34.9 | -13 01 17 | 15.8 | -0.47 | 0.08 | -0.13 | 28.4 | DA | |
| HE 1200-1924 | 12 02 40.1 | -19 41 08 | 14.3 | -0.95 | 0.21 | -0.26 | 3.0 | sdO | |
| HE 1204-3217 | 12 06 47.7 | -32 34 32 | 15.7 | -0.84 | -0.08 | -0.21 | 27.5 | DA | WD 1204-322 (DA) |
| HE 1221-2618 | 12 24 32.7 | -26 35 16 | 14.7 | -0.79 | 0.07 | -0.13 | 6.7 | sdB+cool star | |
| HE 1225+0038 | 12 28 07.8 | +00 22 17 | 15.2 | -0.45 | 0.34 | -0.10 | 22.5 | DA | |
| HE 1225-0758 | 12 27 47.5 | -08 14 38 | 14.6 | -0.85 | 0.06 | -0.09 | 1.8 | DAB, DBA? | WD 1225-079 (DZA) |
| HE 1229-0115 | 12 31 34.8 | -01 32 09 | 13.9 | -0.72 | 0.11 | -0.08 | 24.6 | DA | WD 1229-012 (DA4) |
| HE 1237-1408 | 12 39 56.5 | -14 24 48 | 16.1 | -1.13 | -0.07 | -0.19 | 12.0 | sdOB | |
| HE 1238-1745 | 12 41 01.1 | -18 01 58 | 14.3 | -0.95 | 0.11 | -0.16 | 6.1 | sdO | |
| HE 1247-1738 | 12 50 22.2 | -17 54 47 | 16.2 | -0.77 | 0.26 | -0.35 | 24.6 | DA+dM | WD 1247-176 (DA) |
| HE 1256-2738 | 12 59 01.4 | -27 54 19 | 16.1 | -1.30 | -0.31 | -0.36 | 4.7 | sdO | |
| HE 1257-2021 | 13 00 27.2 | -20 37 27 | 16.5 | -1.08 | 0.06 | -0.12 | 2.8 | DO/PG1159?? | |
| HE 1258+0113 | 13 00 59.2 | +00 57 10 | 16.5 | -0.95 | -0.01 | 0.00 | 4.2 | sdO | |
| HE 1258+0123 | 13 01 10.5 | +01 07 39 | 16.5 | -0.24 | 0.24 | 0.26 | 31.9 | DA | |
| HE 1309-1102 | 13 12 02.3 | -11 18 16 | 16.1 | -0.80 | -0.17 | 0.03 | 11.4 | sdB | |
| HE 1310-2733 | 13 12 50.6 | -27 49 02 | 14.3 | -1.23 | -0.25 | -0.28 | 8.2 | sdO | |
| HE 1314+0018 | 13 17 24.7 | +00 02 36 | 15.6 | -1.12 | 0.00 | -0.23 | 10.8 | DO | |
| HE 1315-1105 | 13 17 47.4 | -11 21 05 | 15.8 | -0.42 | 0.23 | 0.05 | 23.3 | DA | |
| HE 1318-2111 | 13 21 15.6 | -21 27 18 | 14.6 | -0.99 | -0.10 | -0.14 | 4.6 | sdOB | |
| HE 1325-0854 | 13 28 23.9 | -09 09 53 | 15.2 | -0.64 | 0.05 | 0.04 | 27.7 | DA | |
| HE 1333-0622 | 13 36 19.7 | -06 37 59 | 16.2 | -0.62 | 0.15 | 0.11 | 20.6 | DA+dM | |
| HE 1349-2320 | 13 52 15.0 | -23 34 57 | 15.1 | -1.20 | -0.04 | -0.33 | 10.2 | sdO | |
| HE 1352-1827 | 13 55 26.6 | -18 42 09 | 16.0 | -0.96 | -0.17 | -0.06 | 11.3 | sdB+cool star? | |
| HE 1355-0622 | 13 57 54.3 | -06 37 32 | 13.4 | -1.12 | -0.23 | -0.05 | 2.1 | sdO | |
| HE 1356-1613 | 13 59 12.5 | -16 28 01 | 16.1 | -1.21 | -0.35 | -0.23 | 7.9 | sdO | |
| HE 1419-1205 | 14 22 02.1 | -12 19 30 | 16.2 | -0.98 | -0.30 | -0.06 | 11.3 | sdB (sdOB) | |
| HE 1502-1019 | 15 05 22.7 | -10 31 26 | 15.6 | -1.04 | -0.17 | -0.25 | 7.3 | sdOB+cool star | |
| HE 1511-0448 | 15 14 12.9 | -04 59 33 | 15.3 | -1.14 | -0.32 | -0.05 | 6.8 | DA | |
| HE 1511-1103 | 15 14 17.0 | -11 14 13 | 14.7 | -1.12 | -0.25 | -0.11 | 1.7 | sdO | |
| HE 1512-0331 | 15 14 50.1 | -03 42 50 | 16.0 | -1.22 | -0.32 | -0.35 | 0.8 | sdO/DAO |
In Fig. B.1 we display model spectra of DAs and DBs, converted to
objective-prism spectra with the method described in
Sect. 4. The model spectra were computed by using
![]() .
.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{ms10235f18.ps}
\end{figure}](/articles/aa/full/2001/06/aa10235/Timg118.gif) |
Figure B.1: DA and DB white dwarf model spectra, converted to objective-prism spectra. Note that to these spectra no artificial noise has been added |