A&A 366, 558-564 (2001)
DOI: 10.1051/0004-6361:20000228

The early-type multiple system QZ Carinae[*]

P. Mayer1 - R. Lorenz2 - H. Drechsel2 - A. Abseim1


1 - Astronomical Institute, Charles University, V Holesovickách 2, 180 00 Praha 8, Czech Republic
2 - Dr. Remeis-Sternwarte, Astronomisches Institut der Universität Erlangen-Nürnberg, Sternwartstraße 7, 96049 Bamberg, Germany

Received 27 June 2000 / Accepted 7 November 2000

Abstract
We present an analysis of the early-type quadruple system QZ Car, consisting of an eclipsing and a non-eclipsing binary. The spectroscopic investigation is based on new high dispersion echelle and CAT/CES spectra of H and He lines. The elements for the orbit of the non-eclipsing pair could be refined. Lines of the brighter component of the eclipsing binary were detected in near-quadrature spectra, while signatures of the fainter component could be identified in only few spectra. Lines of the primary component of the non-eclipsing pair and of both components of the eclipsing pair were found to be variable in position and strength; in particular, the He II 4686 emission line of the brighter eclipsing component is strongly variable. An ephemeris for the eclipsing binary QZ Car valid at present was derived Prim. Min. = hel. JD $2448687.16 + 5\hbox{$.\!\!^{\rm d}$ }9991 \cdot E$. The relative orbit of the two binary constituents of the multiple system is discussed. In contrast to earlier investigations we found radial velocity changes of the systemic velocities of both binaries, which were used - together with an O-C analysis of the expected light-time effect - to derive approximate parameters of the mutual orbit of the two pairs. It is shown that this orbit and the distance to QZ Car can be further refined by minima timing and interferometry.

Key words: binaries: eclipsing - binaries: spectroscopic - stars: early-type - stars: individual: QZ Car


1 Introduction

HD 93206 is the brightest member of the open cluster Collinder 228 in the $\eta$ Carinae region; according to Lyngå (1987) the cluster distance is 2600 pc. A variable brightness of HD 93206 was first noted by Morgan et al. (1955). Several radial velocities were published by Feast et al. (1956) and Buscombe & Kennedy (1966). Walker & Marino (1972) determined the type and period of variability and published first photoelectric measurements. The multiple system HD 93206 contains the eclipsing pair QZ Car. Its period is very close to 6 days, depths of minima are 0 $.\!\!^{\rm m}$24 and 0 $.\!\!^{\rm m}$20 in V, maximum brightness is V = 6.22, and spectral type O 9.7 Ib:(n) according to Walborn (1973). Some photoelectric measurements were published by Moffat (1977). Two systems of periodically variable spectral lines were found by Morrison & Conti (1979): the period of the weaker lines corresponds to the eclipsing variable, and is different from that of the stronger lines of about 20 $.\!\!^{\rm d}$73. Therefore it is evident that HD 93206 is composed of two binaries, both single-lined. Recently, the cross-correlation method was applied to nine IUE spectra by Stickland (2000).

Morrison & Conti (1980; hereafter MC) remarked that it would be probably wise to spend ones resources on studying a less complicated binary than QZ Car. Certainly this is true when one tries to add new entries to the table of accurate stellar masses and radii. However, QZ Car is an especially remarkable case. Note, e.g., that there is no other star of such late type with the spectral "(f)'' characteristics among stars listed by Conti et al. (1977). The most similar case is perhaps MY Ser of type O8(f), which is another multiple system, and equally difficult to study.

The system was also studied by Leung et al. (1979; hereafter LMS), who confirmed the spectroscopic results of Morrison & Conti (1979). The mass functions suggest that the eclipsing binary component with so far undetected lines is more massive than its binary companion; in the non-eclipsing pair, which has a longer period, the invisible component is several times less massive than the primary component, and therefore probably has very weak, unobservable lines. LMS solved the light curve by Walker and Marino and found a luminosity ratio close to 3:1 for the two binary components, so supporting the hope that the secondary lines might be discernible in high resolution spectra of high S/N. MC analyzed a larger sample of spectra than LMS and found more reliable elements of both binaries. To avoid confusion, we will denote the two binaries in the following in the same way as MC: the long-period binary is called system A (its visible component A1), and the eclipsing binary is referred to as system B (with the brighter, but less massive component B1, and companion B2).


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H2289F1.PS}\end{figure} Figure 1: V photometry phased according to ephemeris (1). Crosses - our data, open circles - Christie, triangles - Moffat, points - Walker & Marino
Open with DEXTER

2 Photometry

An ephemeris for the eclipsing binary QZ Car valid at present was derived using the more recent minima (see Table 4), which will be used for the phasing of the eclipsing system B throughout this paper:

\begin{displaymath}{\rm Prim.\, Min. = hel.\, JD}\,\, 2448687.16 + 5\hbox{$.\!\!^{\rm d}$ }9991 \cdot E. \end{displaymath} (1)

Due to the particular, near integer day period of the eclipsing binary, no well-covered light curve obtained with ground-based telescopes exists. There are only very few measurements published by Walker & Marino (1972) and Moffat (1977). The present authors measured the star in UBV with the 50 cm ESO telescope at La Silla in 1992 and 1993; the light curve, however, also appears to be not suitable for solution. Some data were added by Christie (1998). In Fig. 1 these data are shown. Since a possible variability of the comparison star HD 93131 could not be excluded, our data were calibrated in terms of an all-sky photometry. Intrinsic variability of QZ Car is supported by these data, the type of which is in general agreement with the measurements by Walker & Marino and Moffat.

Perhaps the best quality light curve by now was obtained by HIPPARCOS (ESA 1997), see Fig. 2. Even this curve is affected by a rather large scatter, which might be due to the close vicinity of similarly bright stars; also short-term intrinsic variability of the star itself could contribute to the photometric scattering. Note that the best fit between photometry in the V bandpass and photometry by HIPPARCOS is obtained for $H_{\rm p}~=~V+0.01$.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H2289F2.PS}\end{figure} Figure 2: HIPPARCOS measurements phased according to ephemeris (1). Data of lower accuracy are plotted as opencircles
Open with DEXTER

3 Spectroscopy

We obtained high-resolution spectra with two telescopes and spectrographs at the ESO La Silla Observatory: in 1992 and 1993, the ESO 1.5 m telescope equipped with the ECHELEC spectrograph, in 1994 the 1.4 m CAT telescope with coudé echelle spectrograph (CES) were used. The spectra are listed in Table 1. They were reduced with the MIDAS package; details of the reduction procedure were described by Mayer et al. (1997). The S/N ratio of the ECHELEC spectra is about 150, in case of CAT/CES spectra about 250. The most pronounced lines are H$\beta$ and He I 4922. Unfortunately, a CCD defect between 4914 and 4917 Å was present close to the He I line in our 1992 spectra. The H$\beta$ line is rather wide, and the stellar components are more severely blended than in the case of the He I line, rendering H$\beta$ less suitable for radial velocity determinations. Examples for profiles of the He I 4922 line are presented in Fig. 3.

In one night, two spectra were obtained in the H$\alpha $ region (CAT 5.1 and 5.2 in Table 1; see Fig. 4 for CAT 5.2). These profiles confirm the presence of emission in the Balmer line, as already found by MC. The line is asymmetric - the red wing being less steep, with a peak emission of about 20% above continuum level at zero velocity. The spike at -10 kms-1 is probably due to the $\eta$ Carinae nebulae (MC give a nebular velocity of -27 kms-1). There is a P Cygni-type absorption component centered atabout -250 kms-1, which could be attributed to the expansion velocity of an envelope. On the red side the emission reaches about +500 kms-1. It is of course not possible to judge the nature and origin of the emission from only these two spectra.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H2289F3.eps}\end{figure} Figure 3: Examples of profiles of the He I 4922 line. Labels near profiles give phases according to ephemeris (1); the step width between continuum levels is 10% of the normalized flux
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H2289F4.PS}\end{figure} Figure 4: Profile of H$\alpha $ line (spectrum CAT 5.2)
Open with DEXTER


 

 
Table 1: Journal of QZ Car spectra and radial velocities of component A1
hel. JD [*] exposure $\Phi_{\rm A}$[*] $V_{\rm A}$ equivalent $\Phi_{\rm B}$[*] spectral range (Å) instrument [*] and
$-2\,400\,000$ (s)   (kms-1) width [*] (Å)   or observed line identification
48759.5206 3000 0.3975 -5.6 0.45 0.0617 4628-4953 ECH 1
48760.5324 4500 0.4463 4.0 0.28 0.2304 4628-4953 ECH 2
48760.5914 4500 0.4491 4.0 0.40 0.2402 4628-4953 ECH 3
48760.6511 4500 0.4520 0.3 0.34 0.2502 4628-4953 ECH 4
48761.5434 4500 0.4950 10.5 0.22 0.3989 4628-4953 ECH 5
48761.6011 4500 0.4978 -1.7 0.22 0.4085 4628-4953 ECH 6
48761.6629 4188 0.5008 -2.3 0.29 0.4188 4628-4953 ECH 7
48762.6087 3600 0.5464 17.0 0.25 0.5765 4628-4953 ECH 8
48762.6636 3600 0.5491 25.5 0.28 0.5856 4628-4953 ECH 9
48763.5482 3600 0.5917 13.1 0.34 0.7331 4628-4953 ECH 10
49023.5824 3600 0.1320 -65.8 0.29 0.0779 4628-4953 ECH 11
49024.5867 4200 0.1804 -53.7 0.24 0.2453 4628-4953 ECH 12
49025.7387 3000 0.2360 -26.4 0.40 0.4373 4628-4953 ECH 13
49026.7533 3600 0.2849 -15.5 0.28 0.6064 4628-4953 ECH 14
49027.5791 4200 0.3247 -15.6 0.30 0.7441 4628-4953 ECH 15
49027.6242 3600 0.3269 -14.4 0.31 0.7516 4628-4953 ECH 16
49027.7721 3600 0.3340 -9.5 0.31 0.7763 4628-4953 ECH 17
49028.6659 4800 0.3771 -14.6 0.32 0.9252 4628-4953 ECH 18
49147.4747 3600 0.1068 -79.0 0.24 0.7293 4826-5143 ECH 19
49148.5718 5400 0.1597 -71.9 0.31 0.9122 4826-5143 ECH 20
49448.5536 1800 0.6264 17.5 0.20 0.9159 He 4922 CAT 1
49449.6870 1800 0.6811 14.8 0.28 0.1048 He 4922 CAT 2
49450.5099 2400 0.7207 4.9 0.27 0.2419 He 4922 CAT 3
49451.5703 1800 0.7718 22.8 0.30 0.4187 He 4922 CAT 4
49452.5932 2100 0.8211     0.5893 H$\alpha $ CAT 5.1
49452.6398 1200 0.8234     0.5970 H$\alpha $ CAT 5.2
49453.5870 1800 0.8691 -10.6 0.21 0.7549 He 4922 CAT 6


3.1 The HeI 4922/OII 4925 line blend

As known from previous studies, the most prominent feature in the He I 4922 line profile corresponds to the primary component of the long-period binary (A1). In some spectra taken near quadratures of the short-period binary, it is apparent that lines of both stars are present. It is however also evident that all line components are changing their strengths with time or phase. The equivalent width of A1 lines is considerably larger than that of B1 and B2 lines, which makes the disentangling of spectral features a difficult task. We tried to use the KOREL code (Hadrava 1995) for this purpose. The line of star A1 was of course always dominant, and the orbit derived with the KOREL program had appropriate parameters. The short-period orbit is masked to such extent, that the automatic disentangling procedure was not able to extract its spectral features. Therefore, we tried to deconvolve the spectra by multiple Gaussian profile fitting (using MIDAS routines). The positions, depths and widths of the A1, B1 and B2 He I 4922 line components were iteratively optimized, while a fourth component in the blend was attributed to the O II 4925 line of star A1. In a paper on KX Vel (Mayer et al. 1997) we found that in this binary with a spectral type practically identical to A1 the equivalent width of the O II line equals approximately one sixth of the He I 4922 line. Therefore, we assumed the same relative strength for this line here too, and kept the ratio fixed at this value; for the two system B stars, we neglected any contribution of O II 4925 to the blend.

Being aware that automatic procedures can easily converge in local minima of the parameter space, we searched for a best fit solution following both the visual appearance of the computed profile blend and the value of sum of squared residuals O-C. We believe that the values given in Table 1 are the best obtainable. In some cases however it was not possible to fully reconstruct the profile using the four adapted line components. In cases close to conjunction of the short-period orbit, the Gaussian profile parameters have larger error margins than close to quadrature phases.

3.2 Other HeI and HeII lines

Among other lines, only He I 4713 and 5015 appear suitable for radial velocity determinations. Unfortunately, the B2 component cannot be identified reliably in any of them.

Conti et al. (1977) classified the integral spectrum as O9.5 Ib(f), i.e., they should have seen He II 4686 in emission. However, such emission is not mentioned in the MC paper, and also Walborn's classification does not refer to it. Our spectra can possibly explain this situation, because emission is also not always visible there. Several examples of the line profile are shown in Fig. 6. Due to the clear variability of the emission, the A1 contribution to the $\lambda$ 4686 line is unpredictably affected by the superimposed emission and hence not suitable for radial velocity measurements.


 

 
Table 2: Radial velocity curve solution - system A

Element		 MC solution MC &
  for He I present data

period		 20 $.\!\!^{\rm d}$73 20 $.\!\!^{\rm d}$73596
semi-amplitude K (kms-1) 49 49.6
MC systemic velocity (kms-1) -7 -8.1
present data systemic velocity (kms-1)   -19.1
eccentricity 0.34 0.342
longitude of periastron $\omega$ 131 $\hbox{$^\circ$ }$ 143.6 $\hbox{$^\circ$ }$
time of periastron 2442530.0 2442530.49
rms of MC data (kms-1)   11.9
rms of present data (kms-1)   6.9
$a \sin i$ (km) $1.31\, 10^7$ $1.33\, 10^7$
mass function ($M_{\odot}$) 0.21 0.218


4 Spectrophotometry

In Table 1, the equivalent widths of component A1 are given. For He I 4922, the values scatter around a mean value of 0.29 Å with a standard deviation of 0.06 Å, while the accuracy of individual values is certainly better than 10%, so some intrinsic variability of the line strengths has to be present. No dependence on phase is apparent. The average value of the width of the A1 component of He I 4713 is 0.27 Å.

The equivalent widths of He I 4713 and 4922 lines of other components are also variable, as is apparent from Fig. 3. For B1 the average value of He I 4922 is 0.10 Å. The maximum EW of the emission seen in the He II 4686 line of component B1 is 0.03 Å.

5 The long-period orbit

The period is known from previous studies with an accuracy of about 0.02 days. The mean time interval between the MC spectra and our data is 6200 days (300 periods; 17 years), so there is no problem with determining the number of intermediate epochs. As a matter of fact, periods corresponding to actual cycles $\pm$1 can already be ruled out by the MC data. Therefore, a definitely more precise period could be determined using the broad time base between the MC and our data sets without any bias.

We first tried to obtain a solution of our radial velocity data alone. However, due to a gap in the phase coverage of the velocity curve, the correlation among spectroscopic elements turned out to be strong, and solutions tended to be non-unique: e.g., possible solutions implied a relatively broad parameter range for K1. More decisive results were expected when our data were combined with the older published data. However, a combined solution of different data sets requires the assumption of different $\gamma $ velocities for widely separated epochs. In view of the long-term radial velocity changes due to the mutual orbit of the two binary systems A and B, different values of $\gamma $ velocities are to be expected for data with long time separations. MC also noted a discrepancy between $\gamma $ velocities obtained from different lines, so the intended combination of the MC and LMS data with our measurements required some caution. Therefore, we only considered He I measurements. Since LMS give velocities calculated from a combination of He I and Si IV lines, we restricted our data sample to the rather homogeneous set of He I velocities by MC and ourselves.

Our results are listed in Table 2 and compared with the original MC results. The solutions somewhat depend on the assumed data weighting. Since the rms values for MC velocities and for our data were about 12 and 7 kms-1, respectively, we gave the MC velocities a weight of 1, to ECHELEC velocities a weight of 2, and to CAT velocities a weight of 3. An independent solution of the MC data confirmed the original results by MC.

The large rms value of our high resolution data is somewhat unexpected and must be due to intrinsic variability of unknown nature. The error of fitting the Gaussians to line profiles is not larger than 2 kms-1. The deviations of the velocities from the anticipated orbital curve therefore represent real shifts of line positions.

In Fig. 5, velocities published by Feast et al. (1956) and Buscombe & Kennedy (1966) are also shown for comparison. Mean velocities per plate are used here in the case of Feast et al. data. They follow our A1 radial velocity curve reasonably, and their $\gamma $ velocity can be calculated as $-39.5 \pm 8.3$ kms-1. It is however difficult to comment on the data by Buscombe & Kennedy. The apparent difference in the $\gamma $ velocities will be discussed in Sect. 7.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H2289F5.PS}\end{figure} Figure 5: Radial velocities of the A1 component derived from He I lines. The theoretical curves are calculated according to elements in the last column of Table 2 for MC (full line) and present (dashed line) $\gamma $ velocities. Triangles correspond to MC data, plus signs to the present data, open circles to data by Feast et al., asterisks to those of Buscombe & Kennedy, and crosses are values by Stickland
Open with DEXTER

   
6 The short-period orbit

Lines of the component B1 of the eclipsing pair (which is the brighter, but less massive and cooler component) can always be recognized, however reliable velocities can only be obtained in phase ranges during which the lines are clearly separated from the A line and not affected by the CCD defect. These cases are compiled in Table 3. The resulting values of the semi-amplitude $K_{\rm B1}$ and systemic velocity $\gamma _{\rm B1}$could be rather accurately determined as:

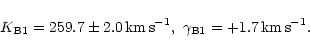
\begin{displaymath}K_{\rm B1} = 259.7 \pm 2.0\, {\rm km\,s}^{-1}, \ \gamma_{\rm B1} = +1.7\, {\rm km\,s}^{-1}. \end{displaymath}

In two cases (spectra ECH 12 and ECH 19) also tentative radial velocities of the secondary component were derived. Unfortunately, the positions of the fainter B2 lines, which are certainly present as deformations of the A line, are very difficult to measure. Note that in some cases, the integral profiles can even hardly be interpreted under our general assumptions: it happens that the depth of the 4922 line blend differs much from the expected values for certain phases, and also the O II 4925 line contribution must occasionally have changed its depth. From its general appearance one might expect that spectrum CAT 3 may yield a good value of the B2 velocity, but it turned out that the line component was too weak at this epoch to provide a reliable velocity value.


 

 
Table 3: Radial velocities of B components

Spectrum		 Phase $V_{\rm B1}$(kms-1) $V_{\rm B2}$(kms-1)

ECH 2		 0.2304 262  
ECH 3 0.2402 251  
ECH 4 0.2502 261  
ECH 12 0.2453 263 -219
CAT 3 0.2419 269  
ECH 14 0.6064 -195  
ECH 15 0.7441 -258  
ECH 16 0.7516 -257  
ECH 17 0.7763 -248  
ECH 19 0.7293 -271 83
CAT 6 0.7549 -251  



  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H2289F6.PS}\end{figure} Figure 6: Examples of profiles of the He II 4686 line. The dotted curves indicate the expected photospheric profiles, see text. The line at bottom center corresponds to the $\gamma _{\rm B1}$ velocity
Open with DEXTER

As already noted above, the line He II 4686 is strongly variable. For instance in one spectrum the line is clearly in emission (ECH 15), in another spectrum taken only one hour later (ECH 16) the profile does not rise above continuum at all, see Fig. 6. The photospheric profiles of He II 4686 are expected to be similar in shape (albeit of different depth) to those of He I 4922. As illustration, Fig. 6 depicts a few of such profiles; their depth has been decreased such that they fit that part of the line wing, which is not affected by emission. The width of the emission profiles is quite large. It is therefore suggested that the emission is not originating within a possible disk around the B1 component, but comes from a region closer to the B system mass center - e.g. from the L1point. Accordingly, it can be anticipated that no emission is present in spectra taken at phases near eclipse minima.

   
7 The mutual orbit of both binaries

From our detailed line blend fitting we found that the systemic velocities of both binaries changed on a time base of approximately 17 years by -11 and +36 kms-1 for systems A and B, respectively. The errors are difficult to estimate due to reasons discussed above, but the opposite sense of the changes supports the idea that it is due to the mutual orbital motion of the two binary constituents of the multiple system. MC noted that within three years no change was recognized; we therefore assume that the radial velocity change found by us has been monotonic in time, and its effect can be measured only on such a long time base. The amount of velocity changes strongly contradict the idea that masses of both binaries are nearly equal. But of course one should be aware that such conclusions depend on the essentially unknown uncertainty in determination of systemic velocities.

Therefore, only rough estimates for parameters of the mutual orbit can be given. The period might be of the order of several decades, not necessarily 25 years or shorter, as suggested by LMS. The $\gamma $velocity by Feast et al. (1956) does not contradict a period of about 50 years. Then the semi-axis might be larger than previously assumed, perhaps about 50 AU, and the hope that systems A and B can be separated by means of speckle interferometry increases. Note that Mason et al. (1998) made an attempt to resolve the system in 1994.31, and gave an upper limit for the separation of 0.30 mas.

7.1 Expected light-time effect

Caused by the orbital motion of both binaries around the common mass center, the light-time effect in times of eclipse minima of system B should be observable (see, e.g., Lorenz et al. 1998). Its semi-amplitude in days is

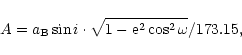
\begin{displaymath}A = a_{\rm B} \sin i \cdot \sqrt {1 -{\rm e}^2 \cos^2 \omega} /173.15, \end{displaymath}

where $ a_{\rm B}$ is the semimajor axis of the orbit of the binary B around the common mass center in AU, and e and $\omega$ are the elements of this orbit. The published times of minima are collected in Table 4. Values of O-C are calculated according to the ephemeris (Mayer et al. 1998)

\begin{displaymath}{\rm Prim.\, Min. = hel~JD}\,\,2441033.06 + 5\hbox{$.\!\!^{\rm d}$ }99857 \cdot E \end{displaymath} (2)

and plotted in Fig. 7. The curves in this graph were calculated mainly in order to demonstrate that good minimum timing is appropriate to find the orbital parameters. Since we are lacking a sufficient data sample to extract more precise information, circular orbits were assumed, and two trial curves were calculated for the following parameters: semi-amplitude $A = 0\hbox{$.\!\!^{\rm d}$ }20$, and;
1. $ P_{\rm mutual}$ = 40 years, time of conjunction JD 2449200;
2. $ P_{\rm mutual}$ = 50 years, time of conjunction JD 2450000.
In both cases, the linear ephemeris was optimized to fit the observations. Clearly, also shorter as well as longer periods would be compatible with the data.
 

 
Table 4: The published times of minima for QZ Car

HJD-2400000		 m.e. Epoch O-C Source

41033.06		 0.200 0.0 0.000 Walker & Marino 1972
42472.64 0.100 240.0 -0.077 Moffat 1977
43192.40 0.200 360.0 -0.145 Morrison & Conti 1980
48501.160 0.030 1245.0 -0.120 HIPPARCOS
48687.160 0.020 1276.0 -0.075 Mayer et al. 1992
49422.039 0.005 1398.5 -0.021 Mayer et al. 1998


The mutual orbit radial velocities are connected with the light-time effect parameters as $K_{\rm B} = 5156\,A/P_{\rm mutual}$, where $K_{\rm B}$ is in kms-1 and $ P_{\rm mutual}$ in years. In our examples, the semi-amplitudes are 25.8 and 20.6 kms-1, respectively. The radial velocity curve of the better observable component A1 should be shifted in phase by +90$^\circ$ against the O-C curve. It appears that the trend of the $\gamma $ velocities as given by the Feast et al. (1956), MC and in this paper does not contradict this expectation.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H2289F7.PS}\end{figure} Figure 7: O-C graph of times of minima published for QZ Car. The full line represents the light-time effect with an assumed period of 40 years, the dashed line with a period of 50 years (see text)
Open with DEXTER

   
8 Conclusions

Our spectroscopic analysis of QZ Car yielded valuable new information about the nature of this complicated multiple system being composed of two binary systems. We present refinements of the 20 day SB1 binary orbit, preliminary results on the short-period eclipsing binary, as well as a discussion of the long-term mutual orbit of both binaries. The orbital elements we found for the non-eclipsing system do not differ much from previous studies. The appearance and behaviour of lines of the eclipsing binary components can only be explained by the assumption that their equivalent widths are variable. In our case, the line disentangling was affected by an unfortunate CCD defect and by the superposition of the O II 4925 line on the profile of the crucial He I 4922 line. The mass function suggests that the invisible eclipsing binary component is more massive than its companion; hence it can be anticipated that this star will eventually be identified in high quality spectra.

Some conclusion about the mutual orbit of both binaries were reached. This orbit possesses a period of several decades, and it is demonstrated that it will be worth to further follow its evolution by evaluation of the light-time effect and probably also by speckle interferometry. A highly accurate distance will be found by a combination of these methods in the future. In this respect, the system is similar to SZ Cam (Mayer et al. 1994, Lorenz et al. 1998, Harries et al. 1998) and V505 Sgr (Mayer 1997; Ibanoglu et al. 2000).

Acknowledgements
The authors are indebted to Dr. Stickland for providing them a preliminary version of his study of QZ Car.

References

 
Copyright ESO 2001