A&A 366, 508-531 (2001)
DOI: 10.1051/0004-6361:20000022
S Doradus variables in the Galaxy and the Magellanic
Clouds![[*]](/icons/foot_motif.gif)
A. M. van Genderen
Leiden Observatory, Postbus 9513, 2300 RA Leiden,
The Netherlands
Received 6 June 2000 / Accepted 10 October 2000
Abstract
The goal in writing this paper is five fold: (1) to summarize the scientific achievements in the 20th century on S Dor variables (or LBVs); (2) to present an inventory of these variables in the Galaxy and the Magellanic Clouds with a description of their physical state and instability properties; (3) to emphasize the photometric achievements of the various types of instabilities. Generally this seems to be a neglected item resulting in a number of misunderstandings continuously wandering through literature; (4) to investigate the structure of the S Dor-area on the HR-diagram; (5) to estimate the total numbers of S Dor variables in the three stellar systems.
The position of the strong active S Dor variables in minimum brightness obey the following
linear relation on the HR-diagram:
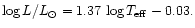 The relatively small dispersion of less active and supposed ex- and dormant S Dor variables with respect to this relation is twice as large at the blue side than at the red side. This might be caused by evolution to the WR stage and/or to high rotation.
S Dor variables can be subject to five types of instabilities: the very rare genuine eruptive episodes (the "SD-eruptions''), two different brightening phases caused by slow pulsations (the "SD-phases''): one on a time scale of years, the other on a time scale of decades at a more or less constant luminosity and two types of microvariations: one on a time scale of weeks, the other on a time scale of about 100d.
So far, no periodicities of light curve characteristics of any of these instabilities have ever been found.
The durations of active and non-active stages are estimated for about half of the sample based on scattered magnitude estimations such as from historical records, and on modern monitoring campaigns. It would be a misunderstanding to believe that all S Dor variables should be always spectacular. It is estimated that most of them will not be spectacular at all for at least 70% of their lifetime as an S Dor variable.
The relatively small dispersion of less active and supposed ex- and dormant S Dor variables with respect to this relation is twice as large at the blue side than at the red side. This might be caused by evolution to the WR stage and/or to high rotation.
S Dor variables can be subject to five types of instabilities: the very rare genuine eruptive episodes (the "SD-eruptions''), two different brightening phases caused by slow pulsations (the "SD-phases''): one on a time scale of years, the other on a time scale of decades at a more or less constant luminosity and two types of microvariations: one on a time scale of weeks, the other on a time scale of about 100d.
So far, no periodicities of light curve characteristics of any of these instabilities have ever been found.
The durations of active and non-active stages are estimated for about half of the sample based on scattered magnitude estimations such as from historical records, and on modern monitoring campaigns. It would be a misunderstanding to believe that all S Dor variables should be always spectacular. It is estimated that most of them will not be spectacular at all for at least 70% of their lifetime as an S Dor variable.
Key words: catalogue - stars: variables - stars: supergiants
Now, at the beginning of the 21st century it is appropriate to summarize the scientific achievements in the field of S Dor variables (or LBVs: Luminous Blue Variables) and to make an inventory of them in the Galaxy and the Magellanic Clouds.
When Humphreys & Davidson (1994) wrote their review paper on S Dor
variables entitled: "Astrophysical Geysers-The Luminous Blue Variables'', the
Galaxy numbered 5, the LMC 6 and the SMC 1 "confirmed'' of these variables. The
list of "candidates'' numbered 4, 4 and 0 stars, respectively. A few years later,
Parker (1997) listed 6 new candidates for the Galaxy and 2 confirmed
S Dor variables and 1 candidate for the LMC. The list presented by Bohannan
(1997) is very similar.
Apart from a concise description on the various aspects of S Dor variables (as I will call them throughout this paper, see Sect. 1.2), a list is presented of 34 confirmed members (including 8 so-called ex-/dormant members, see Sect. 1.2), 12 candidate members and 3 former candidates. Of the 46 objects (leaving out the 3 non-members) 21 belong to the Galaxy, 4 to the SMC and 21 to the LMC. They have been divided into four categories (defined in Sect. 2.1). For each category three tables are given listing a number of photometric and physical parameters, the reddening and the distance (all have been selected and/or have been made as homogeneous as possible), time scales and light amplitudes of the various types of instabilities, and whether ejecta are present. Each entry is accompanied by non-exhaustive reference numbers decoded in a separate table. It is not professed to be complete, after all, other references can be found in the quoted ones.
Further, for 18 objects a schematic light curve is presented, giving an impression of the past and present light variations. A few brightness estimates of LMC objects made in the 19th century are partly based on a compilation by Thackeray (1974) and partly on other sources such as the HD and HDE catalogues (the last one dated 1925). The ptm (photometric) and ptg (photographic) magnitudes of the HD catalogue are, depending on the declination, based on visual magnitudes of the Bonner Durchmusterung dated around 1850, of the Cordoba Durchmusterung and of the Cape Photographic Durchmusterung (both dated at the end of the 19th century) by applying a colour index correction if necessary (see the introduction to the HD catalogue).
A short discussion is devoted to a possible evolutionary connection between S Dor variables and the variable yellow hypergiants and some attention is paid to the present status of  Car.
The structure of the S Dor (SD)-area in the theoretical HR-diagram is analyzed for the four categories mentioned above.
Finally, a discussion is presented on the total numbers of estimated S Dor variables in the three stellar systems.
S Dor variables are a separate class of massive and very evolved stars. They are subject to a number of instabilities, often at the same time. Their origin is still largely a mystery, although there are a number of presumptions based on theories and models. Three types of photometrically observable instabilities belong to the "SD-phenomenon'', two others to the microvariations. One of the latters is typical for all variable super- and hypergiants: the
Car.
The structure of the S Dor (SD)-area in the theoretical HR-diagram is analyzed for the four categories mentioned above.
Finally, a discussion is presented on the total numbers of estimated S Dor variables in the three stellar systems.
S Dor variables are a separate class of massive and very evolved stars. They are subject to a number of instabilities, often at the same time. Their origin is still largely a mystery, although there are a number of presumptions based on theories and models. Three types of photometrically observable instabilities belong to the "SD-phenomenon'', two others to the microvariations. One of the latters is typical for all variable super- and hypergiants: the 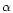 Cyg variables (thus including the S Dor
variables, see Sect. 1.6).
I prefer to call them "S Dor variables'' and not "LBVs'', because this is the traditional designation given by Kukarkin et al. (1974), (to be more specific: "hot S Dor variables'', since it is not excluded that also cooler supergiants can be subject to similar type of instabilities, see Sect. 3.2.5; de Jager & van Genderen 1989; van Genderen 1991a; Stahl et al. 1990). In this way confusing names like "yellow LBVs'' can be avoided.
An even more important reason not to call them LBVs is that all evolved massive stars are (micro-)variables, thus, also the blue ones, but only a very small fraction belongs to the S Dor variables.
The preference to keep the original name memorized, has been brought into practice by introducing the concept "S Dor (SD)-phase'' for the cyclic phases of brightening on a time scale of years to decades and light amplitudes up to a maximum of
Cyg variables (thus including the S Dor
variables, see Sect. 1.6).
I prefer to call them "S Dor variables'' and not "LBVs'', because this is the traditional designation given by Kukarkin et al. (1974), (to be more specific: "hot S Dor variables'', since it is not excluded that also cooler supergiants can be subject to similar type of instabilities, see Sect. 3.2.5; de Jager & van Genderen 1989; van Genderen 1991a; Stahl et al. 1990). In this way confusing names like "yellow LBVs'' can be avoided.
An even more important reason not to call them LBVs is that all evolved massive stars are (micro-)variables, thus, also the blue ones, but only a very small fraction belongs to the S Dor variables.
The preference to keep the original name memorized, has been brought into practice by introducing the concept "S Dor (SD)-phase'' for the cyclic phases of brightening on a time scale of years to decades and light amplitudes up to a maximum of
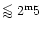 (van Genderen et al. 1997a,b; Sect. 3.4 of the present paper).
It should be avoided to call these cyclic SD-phases "eruptions'' or "outbursts'', because they suggest a period with violent mass ejections, which, as we know nowadays, is not the case (Sect. 1.5). The main cause of SD-phases are stellar radius and temperature variations. Sometimes, but not always, they are accompanied by a denser wind (Sects. 1.5 and 3.2.1). The few cases which showed genuine eruptions, called "SD-eruptions'' and witnessed the last few centuries (Sect. 1.4), are P Cyg (17th century),
(van Genderen et al. 1997a,b; Sect. 3.4 of the present paper).
It should be avoided to call these cyclic SD-phases "eruptions'' or "outbursts'', because they suggest a period with violent mass ejections, which, as we know nowadays, is not the case (Sect. 1.5). The main cause of SD-phases are stellar radius and temperature variations. Sometimes, but not always, they are accompanied by a denser wind (Sects. 1.5 and 3.2.1). The few cases which showed genuine eruptions, called "SD-eruptions'' and witnessed the last few centuries (Sect. 1.4), are P Cyg (17th century),  Car (19th century), perhaps HD5980 (1993-1995) in the SMC and a few in other galaxies (Humphreys 1999).
Humphreys (1999) suggested to name the just mentioned objects "
Car (19th century), perhaps HD5980 (1993-1995) in the SMC and a few in other galaxies (Humphreys 1999).
Humphreys (1999) suggested to name the just mentioned objects " Car-like variables'', not only because of the eruptions, but also because of an excess luminosity during the eruption (see for
Car-like variables'', not only because of the eruptions, but also because of an excess luminosity during the eruption (see for  Car: van Genderen & Thé 1984; for P Cyg: Lamers & de Groot 1992, de Groot & Lamers 1992; for V12 in NGC2403 and for SN1961V: Humphreys & Davidson 1994). After these eruptive periods, the four variables showed a post-maximum plateau, a second, lesser eruption and subsequently a strong obscuration by circumstellar dust (Humphreys et al. 2000). That these eruptive periods are fundamentally different from the SD-phases, which in the case of
Car: van Genderen & Thé 1984; for P Cyg: Lamers & de Groot 1992, de Groot & Lamers 1992; for V12 in NGC2403 and for SN1961V: Humphreys & Davidson 1994). After these eruptive periods, the four variables showed a post-maximum plateau, a second, lesser eruption and subsequently a strong obscuration by circumstellar dust (Humphreys et al. 2000). That these eruptive periods are fundamentally different from the SD-phases, which in the case of  Car are visible as small-amplitude light oscillations (several 0
Car are visible as small-amplitude light oscillations (several 0
 1) on a time scale of a few years, became obvious from a photometric analysis in 1984 by van Genderen & Thé (1984: Sects. 9.2 and 9.6), see also Whitelock et al. (1983) and van Genderen et al. (1999: Sect. 4.1).
Since many S Dor variables seem to suffer from such eruptive periods at least once in their life time (Sect. 1.8), I believe that a separate name for stars like
1) on a time scale of a few years, became obvious from a photometric analysis in 1984 by van Genderen & Thé (1984: Sects. 9.2 and 9.6), see also Whitelock et al. (1983) and van Genderen et al. (1999: Sect. 4.1).
Since many S Dor variables seem to suffer from such eruptive periods at least once in their life time (Sect. 1.8), I believe that a separate name for stars like  Car, P Cyg, etc., is not yet necessary, unless their light curves are really unique, i.e. when it will be shown in due course that other S Dor variables exhibit eruptive light curves different from those just mentioned. The eruptive light curve of the candidate S Dor variable HD5980 in the SMC (in 1992 and 1993) looks quite different indeed (see for references
Tables 11, 12 and 13). That e.g. the variable star hidden in
Car, P Cyg, etc., is not yet necessary, unless their light curves are really unique, i.e. when it will be shown in due course that other S Dor variables exhibit eruptive light curves different from those just mentioned. The eruptive light curve of the candidate S Dor variable HD5980 in the SMC (in 1992 and 1993) looks quite different indeed (see for references
Tables 11, 12 and 13). That e.g. the variable star hidden in  Car behaves as a normal S Dor variable also, is demonstrated by the 26yr (1974-2000) of multi-colour photometry undertaken by our group. It shows typical SD-phases with at times superimposed microvariations, although, often disturbed by a variable non-stellar light source (with especially in the near-UV peculiar periodicities). This light source could perhaps be a luminous accretion disk/hot spot system: see Sects. 3.2.2 and 3.2.6 and
Tables 4, 5 and 6; van Genderen et al. 1994, 1995, 1999; 2001; de Groot et al. 1997a; Sterken et al. 1996b, 1999a,b).
The criteria, or signatures for SD-membership are extensively discussed by Humphreys & Davidson (1994). Supplemented with new insights, they can be summarized as follows:
Car behaves as a normal S Dor variable also, is demonstrated by the 26yr (1974-2000) of multi-colour photometry undertaken by our group. It shows typical SD-phases with at times superimposed microvariations, although, often disturbed by a variable non-stellar light source (with especially in the near-UV peculiar periodicities). This light source could perhaps be a luminous accretion disk/hot spot system: see Sects. 3.2.2 and 3.2.6 and
Tables 4, 5 and 6; van Genderen et al. 1994, 1995, 1999; 2001; de Groot et al. 1997a; Sterken et al. 1996b, 1999a,b).
The criteria, or signatures for SD-membership are extensively discussed by Humphreys & Davidson (1994). Supplemented with new insights, they can be summarized as follows:
- a)
- visible ejecta (although only 40% of the present compilation has visible ejecta,
Sect. 1.8), likely caused by (an) SD-eruption(s);
- b)
- spectroscopic (variable) characteristics indicating a high luminosity,
a high mass loss rate (

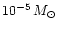 yr-1),
an extended atmosphere and ejecta containing CN or CNO processed material. This type of chemistry as well as the dust composition, is consistent with a RSG (red supergiant) origin (Sect. 1.7);
yr-1),
an extended atmosphere and ejecta containing CN or CNO processed material. This type of chemistry as well as the dust composition, is consistent with a RSG (red supergiant) origin (Sect. 1.7);
- c)
- a photometric variability of up to 2
 5 on a time scale of years to decades and even to centuries, the so-called SD-phases (Sects. 1.5 and 3.4). One of the typical characteristics is that the light variations show a large variety. The colour variations are crucial for the detection of the SD-phases and therefore a very strong diagnostic tool: due to the excursions on the HR-diagram at a more or less constant luminosity, the colour indices become red when the star (if hotter than
5 on a time scale of years to decades and even to centuries, the so-called SD-phases (Sects. 1.5 and 3.4). One of the typical characteristics is that the light variations show a large variety. The colour variations are crucial for the detection of the SD-phases and therefore a very strong diagnostic tool: due to the excursions on the HR-diagram at a more or less constant luminosity, the colour indices become red when the star (if hotter than  7000K) brightens and blue when the star becomes fainter. This habit appears to be easily detectable, even if the light ranges of SD-phases are as small as 0
7000K) brightens and blue when the star becomes fainter. This habit appears to be easily detectable, even if the light ranges of SD-phases are as small as 0
 1 or even smaller, thus, they should not be confused with the microvariations which have much shorter time scales (Sect. 1.6). In this way a number of candidates could be classified as genuine S Dor variables.
1 or even smaller, thus, they should not be confused with the microvariations which have much shorter time scales (Sect. 1.6). In this way a number of candidates could be classified as genuine S Dor variables.
Spectroscopically suspected S Dor variables turned out to fulfil without any exception the photometric criteria, if enough multi-colour photometric observations were made. Therefore, if spectroscopic observations, as well as a proof for ejecta are (still) lacking, I applied the reverse reasoning to identify S Dor variables only based on the photometric multi-colour behaviour.
Ofpe/WN9 stars will not be considered as suspected or candidate S Dor variables (such as S9), unless they show an N-enriched spectrum and stellar ejecta such like S61 (= Sk-69 266, see
Tables 8, 9 and 10). To cite Bohannan (1997): "... Ofpe/WN9
stars have been proposed as quiescent LBVs. As appealing as that is, this call cannot
be made on spectroscopic features alone''. Therefore, the stars studied spectroscopically
in the UV by Smith Neubig & Bruhweiler (1999), although showing
SD-characteristics in the UV, are not included in the present list of candidates, unless
they were already identified as genuine S Dor variables by other criteria.
The extremely powerful eruptions of a small number of S Dor variables mentioned in Sect. 1.2 released a total energy of 1047.3-1049.5ergs (Humphreys et al. 2000). There are different theoretical approaches to these SD-eruptions, although, to cite Davidson & Humphreys (1997): "Instabilities of this type are so complex that it is difficult to be sure that competing models are fundamentally different''. However, all authors agree that the L/M ratio is likely higher than for other stars at the same location on the HR-diagram, thus, they must have lost a lot of mass already.
Humphreys & Davidson (1994) discussed all views and models giving the state of affairs up to 1994. They believe that the sub-photospheric instability models are most promising (outer layers below 2 105K are dynamically isolated from the stellar interior because of the high opacity due to iron, and can easily become unstable). This is the hypothetical "modified Eddington limit'', in which "modified'' indicates that the opacity is temperature- and density-dependent. (The classical Eddington limit is an upper limit to the ratio L/M for a nearly static stellar atmosphere).
Since then a number of other models and mechanisms were proposed:
Langer et al. (1994) discussed a new scenario for the evolution of massive stars (
Ofpe/WN9
stars have been proposed as quiescent LBVs. As appealing as that is, this call cannot
be made on spectroscopic features alone''. Therefore, the stars studied spectroscopically
in the UV by Smith Neubig & Bruhweiler (1999), although showing
SD-characteristics in the UV, are not included in the present list of candidates, unless
they were already identified as genuine S Dor variables by other criteria.
The extremely powerful eruptions of a small number of S Dor variables mentioned in Sect. 1.2 released a total energy of 1047.3-1049.5ergs (Humphreys et al. 2000). There are different theoretical approaches to these SD-eruptions, although, to cite Davidson & Humphreys (1997): "Instabilities of this type are so complex that it is difficult to be sure that competing models are fundamentally different''. However, all authors agree that the L/M ratio is likely higher than for other stars at the same location on the HR-diagram, thus, they must have lost a lot of mass already.
Humphreys & Davidson (1994) discussed all views and models giving the state of affairs up to 1994. They believe that the sub-photospheric instability models are most promising (outer layers below 2 105K are dynamically isolated from the stellar interior because of the high opacity due to iron, and can easily become unstable). This is the hypothetical "modified Eddington limit'', in which "modified'' indicates that the opacity is temperature- and density-dependent. (The classical Eddington limit is an upper limit to the ratio L/M for a nearly static stellar atmosphere).
Since then a number of other models and mechanisms were proposed:
Langer et al. (1994) discussed a new scenario for the evolution of massive stars (
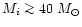 )
by introducing mass-loss in addition to the radiation-pressure driven wind, resulting in better agreement with the observations than previous scenarios.
Cox et al. (1997) gave a summary of the mechanisms proposed to destabilize S Dor-envelopes up to 1996.
Subsequently, Stothers & Chin (1997)
interpreted e.g.
)
by introducing mass-loss in addition to the radiation-pressure driven wind, resulting in better agreement with the observations than previous scenarios.
Cox et al. (1997) gave a summary of the mechanisms proposed to destabilize S Dor-envelopes up to 1996.
Subsequently, Stothers & Chin (1997)
interpreted e.g.  Car as a star burning hydrogen in its core,
while repeatedly encountering ionization-induced dynamical
instability, with a time scale of 3-6yr on the average.
This time scale for violent cycles agrees remarkable well with the
observed frequency of
Car as a star burning hydrogen in its core,
while repeatedly encountering ionization-induced dynamical
instability, with a time scale of 3-6yr on the average.
This time scale for violent cycles agrees remarkable well with the
observed frequency of 
 -peaks superimposed on the eruptive
light maximum between 1827 and 1857. Note that the light curve
(Fig. 11) shows a few gaps during this time interval of as long as
-peaks superimposed on the eruptive
light maximum between 1827 and 1857. Note that the light curve
(Fig. 11) shows a few gaps during this time interval of as long as
 5yr, so that more peaks may have occurred. Then, two more peaks appeared:
13yr later in 1870, and again 20yr later in 1890. Also the other cases discussed
by Humphreys et al. (2000), showed eruptive episodes characterized by a set of individual eruptions with a sharply declining frequency.
Owocki & Galay (1997) suggested that when an evolving star
responds to a super-Eddington condition, it will develop a convective outer layer which
will be blown up mimicking a RSG. This envelope may then become detached, due to a density
inversion, so that an S Dor variable is born.
A quite different possibility has been proposed by Sterken et al. (1997) based on the high noise, extending over a wide frequency range exhibited by the light variations of the ex- or dormant S Dor variable
5yr, so that more peaks may have occurred. Then, two more peaks appeared:
13yr later in 1870, and again 20yr later in 1890. Also the other cases discussed
by Humphreys et al. (2000), showed eruptive episodes characterized by a set of individual eruptions with a sharply declining frequency.
Owocki & Galay (1997) suggested that when an evolving star
responds to a super-Eddington condition, it will develop a convective outer layer which
will be blown up mimicking a RSG. This envelope may then become detached, due to a density
inversion, so that an S Dor variable is born.
A quite different possibility has been proposed by Sterken et al. (1997) based on the high noise, extending over a wide frequency range exhibited by the light variations of the ex- or dormant S Dor variable  Sco. The presence of this noise, unpredictable, but to some degree in step with the microvariations, could from time to time amplify the regular long-term oscillations beyond expectation leading to an eruption. Such amplification of weak signals by associated noise, known as stochastic resonance, could lead to unexpected triggerings when combined with long-period oscillations, especially when the star is in a state of dynamical instability.
In the proceedings of the IAU Coll. 169 held in Heidelberg in 1998, a number of papers were devoted to the instabilities in S Dor envelopes, in particular to the SD-eruptions (e.g. Guzik et al. 1999;
Sco. The presence of this noise, unpredictable, but to some degree in step with the microvariations, could from time to time amplify the regular long-term oscillations beyond expectation leading to an eruption. Such amplification of weak signals by associated noise, known as stochastic resonance, could lead to unexpected triggerings when combined with long-period oscillations, especially when the star is in a state of dynamical instability.
In the proceedings of the IAU Coll. 169 held in Heidelberg in 1998, a number of papers were devoted to the instabilities in S Dor envelopes, in particular to the SD-eruptions (e.g. Guzik et al. 1999;  degaard 1999) and all types of pulsations (the latter might play a role in the observed microvariations, see Sect. 1.6).
During the workshop on
degaard 1999) and all types of pulsations (the latter might play a role in the observed microvariations, see Sect. 1.6).
During the workshop on  Car, held in Montana 1998, special emphasis was given to its SD-eruption and the creation of the bipolar nebula. The model of Cassinelli (1999) includes binarity and that of Iben (1999) even a tertiary
companion. These models describe with straightforward physics SD-eruptions leading to a bipolar nebula. However, other S Dor variables excist with bipolar nebulae without being a binary as far as we know.
With hydrodynamical models of the evolution of bipolar ejecta, in particular that of
Car, held in Montana 1998, special emphasis was given to its SD-eruption and the creation of the bipolar nebula. The model of Cassinelli (1999) includes binarity and that of Iben (1999) even a tertiary
companion. These models describe with straightforward physics SD-eruptions leading to a bipolar nebula. However, other S Dor variables excist with bipolar nebulae without being a binary as far as we know.
With hydrodynamical models of the evolution of bipolar ejecta, in particular that of
 Car, Langer et al. (1999) find support for the general conjecture
that SD-eruptions occur when the stars approach the Eddington limit. Their models imply
that initial stellar rotation rate and angular momentum have influence on the occurrence
of SD-eruptions and that they are very important to the evolution of very massive
stars.
Stothers' (1999a) calculations show that rotation influences the hydrostatic structure as well, the course of the evolution and in an indirect way the star's L/M ratio and consequently the onset of dynamical instability, an appealing mechanism discovered by Stothers & Chin (1993, 1994, 1995, 1996).
All these models do not consider any possible influence of the frequently occurring SD-phases (which are in fact slow pulsations, Sect. 1.5) and the microvariations (which are always present, Sect. 1.6) on the eruptive instabilities and on the production of ejecta. An exception so far with respect to
Car, Langer et al. (1999) find support for the general conjecture
that SD-eruptions occur when the stars approach the Eddington limit. Their models imply
that initial stellar rotation rate and angular momentum have influence on the occurrence
of SD-eruptions and that they are very important to the evolution of very massive
stars.
Stothers' (1999a) calculations show that rotation influences the hydrostatic structure as well, the course of the evolution and in an indirect way the star's L/M ratio and consequently the onset of dynamical instability, an appealing mechanism discovered by Stothers & Chin (1993, 1994, 1995, 1996).
All these models do not consider any possible influence of the frequently occurring SD-phases (which are in fact slow pulsations, Sect. 1.5) and the microvariations (which are always present, Sect. 1.6) on the eruptive instabilities and on the production of ejecta. An exception so far with respect to  Car, is the study of Stothers (2000). He examines the effect of the enormous stellar wind on the envelope structure, assuming that
Car, is the study of Stothers (2000). He examines the effect of the enormous stellar wind on the envelope structure, assuming that  Car possesses a very massive hot main-sequence star, only slightly evolved. The high mass loss must dynamically perturb its outer envelope down to the two main iron convection zones of which the turbulent energy can be directly transformed into mass ejections. Besides, Stothers (2000) found that secular oscillations of the outer envelope, caused by the runaway mass loss, is potentially able to account not only for the cycles of visual brightenings (the SD-phases, Sect. 1.5), but also for the 1827-1857 eruptive period.
Whatever the truth is about the SD-eruptions, they seem to occur rarely in view of the low number of ejecta per S Dor variable. There are even S Dor variables without any ejecta (Sect. 1.8).
The SD-phases (see also Sect. 1.3, c) are presumably largely phases of variable radius and temperature. This was first suspected by van Genderen (1982), and later
confirmed by the study of Leitherer et al. (1989), while de Koter et al. (1996) showed that a reduced effective gravity should take part in the process. The luminosity stays more or less constant. One of the exceptions is S Dor; here the change in
Car possesses a very massive hot main-sequence star, only slightly evolved. The high mass loss must dynamically perturb its outer envelope down to the two main iron convection zones of which the turbulent energy can be directly transformed into mass ejections. Besides, Stothers (2000) found that secular oscillations of the outer envelope, caused by the runaway mass loss, is potentially able to account not only for the cycles of visual brightenings (the SD-phases, Sect. 1.5), but also for the 1827-1857 eruptive period.
Whatever the truth is about the SD-eruptions, they seem to occur rarely in view of the low number of ejecta per S Dor variable. There are even S Dor variables without any ejecta (Sect. 1.8).
The SD-phases (see also Sect. 1.3, c) are presumably largely phases of variable radius and temperature. This was first suspected by van Genderen (1982), and later
confirmed by the study of Leitherer et al. (1989), while de Koter et al. (1996) showed that a reduced effective gravity should take part in the process. The luminosity stays more or less constant. One of the exceptions is S Dor; here the change in
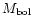 is close to
is close to 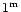 (van Genderen et al. 1997a). An SD-phase is apparently a kind of pulsation, especially by the envelope (see also Lamers et al. 1998: Sect. 5.3).
It appears that there are two types: one on a time scale of years and another one on a time scale of decades (Sect. 1.5.1).
The physical implications, amongst others with respect to the mass loss rate
(see below) are still not understood (Schmutz 1997). His suggestion is that an SD-phase "is a sort of small giant eruption that never makes it to infinity''. Most likely we see the stellar photosphere all the time from minimum to maximum light (and not an expanding optically thick pseudo-photosphere as thought formerly, however, see Sect. 3.2.1).
It is of interest to note that the S Dor-phases of
(van Genderen et al. 1997a). An SD-phase is apparently a kind of pulsation, especially by the envelope (see also Lamers et al. 1998: Sect. 5.3).
It appears that there are two types: one on a time scale of years and another one on a time scale of decades (Sect. 1.5.1).
The physical implications, amongst others with respect to the mass loss rate
(see below) are still not understood (Schmutz 1997). His suggestion is that an SD-phase "is a sort of small giant eruption that never makes it to infinity''. Most likely we see the stellar photosphere all the time from minimum to maximum light (and not an expanding optically thick pseudo-photosphere as thought formerly, however, see Sect. 3.2.1).
It is of interest to note that the S Dor-phases of  Car seem to be more or less sensitive for tidal forcing of a supposed companion with an excentric orbital revolution of 5.5yr (van Genderen et al. 2001): around the periastron passages the light is in, or close to a maximum. Such a possibility has been suggested by Stothers & Chin (2000).
It is doubtful whether the physical process of the SD-phases can be compared with a terrestrial geyser. This geyser model has been introduced by Maeder (1989, 1992). He elaborated the density inversion below the photospheres of cool supergiants (temperature below 9000K), discovered by Böhm-Vitense (1958), a probable cause of eruptive episodes. Although the S Dor variables discussed here are hotter, Humphreys & Davidson (1994) suggested that their characteristics allow the comparison with geysers. The duration of the quiescent period should be correlated with the size of the preceding eruption. However, the investigation of such a type of correlation for AG Car did not support that (van Genderen et al. 1997a). What we did find is that the durations of the SD-phases (on a time scale of years) appear to be linearly proportional to the visual light amplitude. The geyser model may be physically related to the dynamical unstable yellow/red SD-stage, as follows from the calculations of Stothers & Chin (1996) (see also Sect. 1.8 and the comments by Humphreys & Davidson 1994).
Contrary to former beliefs, a positive correlation between the brightness variation due to the SD-phases and the mass loss rate appeared to be not always true (Leitherer et al. 1989, 1994; de Koter et al. 1996). Whether M increases or decreases during an SD-phase depends on the temperature change, the proximity to the Atmospheric Eddington Limit (AEL, Lamers 1997), and the bistability jumps (Pauldrach & Puls 1990; Lamers 1997).
The study of a century of photometric observations of AG Car and S Dor revealed the presence of two different SD-phases. If both are present simultaneously, the shorter one, time scale of years: t< 10yr, is clearly superimposed on the longer one, time scale of decades:
Car seem to be more or less sensitive for tidal forcing of a supposed companion with an excentric orbital revolution of 5.5yr (van Genderen et al. 2001): around the periastron passages the light is in, or close to a maximum. Such a possibility has been suggested by Stothers & Chin (2000).
It is doubtful whether the physical process of the SD-phases can be compared with a terrestrial geyser. This geyser model has been introduced by Maeder (1989, 1992). He elaborated the density inversion below the photospheres of cool supergiants (temperature below 9000K), discovered by Böhm-Vitense (1958), a probable cause of eruptive episodes. Although the S Dor variables discussed here are hotter, Humphreys & Davidson (1994) suggested that their characteristics allow the comparison with geysers. The duration of the quiescent period should be correlated with the size of the preceding eruption. However, the investigation of such a type of correlation for AG Car did not support that (van Genderen et al. 1997a). What we did find is that the durations of the SD-phases (on a time scale of years) appear to be linearly proportional to the visual light amplitude. The geyser model may be physically related to the dynamical unstable yellow/red SD-stage, as follows from the calculations of Stothers & Chin (1996) (see also Sect. 1.8 and the comments by Humphreys & Davidson 1994).
Contrary to former beliefs, a positive correlation between the brightness variation due to the SD-phases and the mass loss rate appeared to be not always true (Leitherer et al. 1989, 1994; de Koter et al. 1996). Whether M increases or decreases during an SD-phase depends on the temperature change, the proximity to the Atmospheric Eddington Limit (AEL, Lamers 1997), and the bistability jumps (Pauldrach & Puls 1990; Lamers 1997).
The study of a century of photometric observations of AG Car and S Dor revealed the presence of two different SD-phases. If both are present simultaneously, the shorter one, time scale of years: t< 10yr, is clearly superimposed on the longer one, time scale of decades:
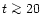 yr (van Genderen et al. 1997a). The first one was called a normal (N)-SD phase, the second one a very long-term (VLT)-SD phase. So far, no SD-phases were found with cycle lengths between 10-20yr. After having studied so many S Dor variables in more detail, I want to introduce the more convenient names: short (S)-SD and long (L)-SD phase, respectively.
SD-phases are probably caused by two different instability regions. This suspicion is
based on the fact that amplitude and shape of the S-SD phases are clearly
modulated by the ongoing L-SD phase (van Genderen et al. 1997a; Sterken et al.
1996a). So far, there is no theoretical support for this assumption.
In the models of Stothers & Chin (e.g. 1995) the "secular cycles''
can perhaps be identified as the SD-phases, but their models do not predict a sharp
physical (or even temporal) division between S- and L-SD phases. The actual length
of a particular "secular cycle'' depends on the dynamical mass-loss rate. However,
the observed S-SD cycle durations of the order of a year are too short to be attributed
to the secular cycles (Stothers, priv. comm.).
It is also possible that a period-modulation excists, i.e. that the L-SD phase influences the arrival times of the light maxima of the S-SD phases (Sects. 1.5.2 and 1.5.3). It appears that most of the S Dor variables are subject to both types of SD-phases, albeit not always simultaneously (see light curves presented by van Genderen et al. 1997b; van Genderen & Sterken 1996; Sterken et al. 1998).
Important for the interpretation and modelling of the SD-phases is the fact that multi-periodicities/-cyclicities have been found in the S-SD phases of a number of S Dor variables (van Genderen et al. 1997a,b; Sterken et al. 1996b, 1997a, 1998). AG Car shows a very pronounced primary periodicity of 371.4d with beat cycles (Sect. 1.5.3).
So far, no theoretical models predict two different types of SD-phases (Sect. 1.5.1), nor any (multi-) periodicity (e.g. Maeder 1989, 1992, 1997; Glatzel & Kiriakidis 1993; Cox et al. 1997, 1999; Guzik et al. 1997, 1999; Glatzel 1997). Stothers & Chin's (1995, 1996) models reveal a mechanism for dynamical instabilities. From their evolutionary models, "periods'' were predicted of the overall "secular cycles'' of
yr (van Genderen et al. 1997a). The first one was called a normal (N)-SD phase, the second one a very long-term (VLT)-SD phase. So far, no SD-phases were found with cycle lengths between 10-20yr. After having studied so many S Dor variables in more detail, I want to introduce the more convenient names: short (S)-SD and long (L)-SD phase, respectively.
SD-phases are probably caused by two different instability regions. This suspicion is
based on the fact that amplitude and shape of the S-SD phases are clearly
modulated by the ongoing L-SD phase (van Genderen et al. 1997a; Sterken et al.
1996a). So far, there is no theoretical support for this assumption.
In the models of Stothers & Chin (e.g. 1995) the "secular cycles''
can perhaps be identified as the SD-phases, but their models do not predict a sharp
physical (or even temporal) division between S- and L-SD phases. The actual length
of a particular "secular cycle'' depends on the dynamical mass-loss rate. However,
the observed S-SD cycle durations of the order of a year are too short to be attributed
to the secular cycles (Stothers, priv. comm.).
It is also possible that a period-modulation excists, i.e. that the L-SD phase influences the arrival times of the light maxima of the S-SD phases (Sects. 1.5.2 and 1.5.3). It appears that most of the S Dor variables are subject to both types of SD-phases, albeit not always simultaneously (see light curves presented by van Genderen et al. 1997b; van Genderen & Sterken 1996; Sterken et al. 1998).
Important for the interpretation and modelling of the SD-phases is the fact that multi-periodicities/-cyclicities have been found in the S-SD phases of a number of S Dor variables (van Genderen et al. 1997a,b; Sterken et al. 1996b, 1997a, 1998). AG Car shows a very pronounced primary periodicity of 371.4d with beat cycles (Sect. 1.5.3).
So far, no theoretical models predict two different types of SD-phases (Sect. 1.5.1), nor any (multi-) periodicity (e.g. Maeder 1989, 1992, 1997; Glatzel & Kiriakidis 1993; Cox et al. 1997, 1999; Guzik et al. 1997, 1999; Glatzel 1997). Stothers & Chin's (1995, 1996) models reveal a mechanism for dynamical instabilities. From their evolutionary models, "periods'' were predicted of the overall "secular cycles'' of  Car, AG Car and S Dor (i.e. the cycles from hot to cool portions of the dynamical unstable stage and vice versa), which agree with the observed ones (S-SD phases) to within a factor of two.
So far, no repetition of light curve characteristics has ever been found for the SD-phases. It seems that Dorfi & Feuchtlinger's (1998, priv. comm. to Guzik et al. 1999) models of S Dor-type envelopes exhibit regular pulsations.
Car, AG Car and S Dor (i.e. the cycles from hot to cool portions of the dynamical unstable stage and vice versa), which agree with the observed ones (S-SD phases) to within a factor of two.
So far, no repetition of light curve characteristics has ever been found for the SD-phases. It seems that Dorfi & Feuchtlinger's (1998, priv. comm. to Guzik et al. 1999) models of S Dor-type envelopes exhibit regular pulsations.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{sdfig1.eps} \end{figure}](/articles/aa/full/2001/05/aads1896/Timg21.gif) |
Figure 1:
From top to bottom: the (O-C)-,
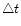 - and the schematic light curve of AG Car from maximum No. 30 onwards (full line; the dotted curve represents the underlying L-SD cycle) - and the schematic light curve of AG Car from maximum No. 30 onwards (full line; the dotted curve represents the underlying L-SD cycle) |
The primary period of the S-SD phases of AG Car appeared to have been stable during a century: P0 = 371.4d  0.6d (m.e. = mean error). The oscillating O-C (= observed epochs of maximum light minus the computed epochs of maximum light) values suggested the presence of a first beat period
0.6d (m.e. = mean error). The oscillating O-C (= observed epochs of maximum light minus the computed epochs of maximum light) values suggested the presence of a first beat period
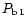 = 21.6yr and a possible second beat period
= 21.6yr and a possible second beat period
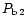 = 4.7yr (van Genderen et al. 1997a). New epochs of maximum light in 1995 and 1996 supported these results (Sterken et al. 1996a).
The last and most reliable part of the 21.6yr beat cycle
(represented by the O-C diagram, see below) appears to have
a similar shape as the L-SD cycle. I believe that this is suspect. Therefore,
it is possible
that
= 4.7yr (van Genderen et al. 1997a). New epochs of maximum light in 1995 and 1996 supported these results (Sterken et al. 1996a).
The last and most reliable part of the 21.6yr beat cycle
(represented by the O-C diagram, see below) appears to have
a similar shape as the L-SD cycle. I believe that this is suspect. Therefore,
it is possible
that
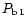 has been caused by the modulation of P0 by the
L-SD
cycle (
has been caused by the modulation of P0 by the
L-SD
cycle ( 20yr) instead of by a secondary period P1 =
390d. This is explained
in Fig. 1, from top to bottom:
Panel 1: the O-C curve for the S-SD phases (numbers from van Genderen et al. 1997a
and Sterken et al. 1996a), based on the linear ephemeris with P0 = 371.4d starting with maximum 30.
Panel 2: the trend of the duration
20yr) instead of by a secondary period P1 =
390d. This is explained
in Fig. 1, from top to bottom:
Panel 1: the O-C curve for the S-SD phases (numbers from van Genderen et al. 1997a
and Sterken et al. 1996a), based on the linear ephemeris with P0 = 371.4d starting with maximum 30.
Panel 2: the trend of the duration
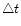 (d) between two successive maxima. It illustrates the secondary oscillations of Panel 1 more clearly, representing the possible beat cycle
(d) between two successive maxima. It illustrates the secondary oscillations of Panel 1 more clearly, representing the possible beat cycle
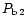 = 4.7yr. Each horizontal line piece, marked by the numbers of the two maxima has a length
= 4.7yr. Each horizontal line piece, marked by the numbers of the two maxima has a length
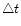 (d). The estimated error amounts to
(d). The estimated error amounts to 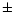 35d. It appears that
35d. It appears that
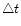 hovers between 200d and 540d. Using the formula
hovers between 200d and 540d. Using the formula
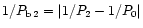 and depending on whether P2 (its meaning is explained below) is shorter or longer than P0, one finds P2 = 305d and 475d, respectively.
Panel 3: the schematic light curve from maximum 30 onwards. The dotted curve, touching most of the minima represents the shape of the underlying L-SD cycle on which the S-SD phases are superimposed.
The rising trend in the O-C values (Panel 1) between e.g. maxima 34 and 38 means that the maxima arrive progressively later due to the accumulation of too long S-SD cycles, thus, too large
and depending on whether P2 (its meaning is explained below) is shorter or longer than P0, one finds P2 = 305d and 475d, respectively.
Panel 3: the schematic light curve from maximum 30 onwards. The dotted curve, touching most of the minima represents the shape of the underlying L-SD cycle on which the S-SD phases are superimposed.
The rising trend in the O-C values (Panel 1) between e.g. maxima 34 and 38 means that the maxima arrive progressively later due to the accumulation of too long S-SD cycles, thus, too large
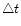 values compared to the average
values compared to the average
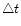 (= P0). The opposite appears for the subsequent steep decline after maximum 38. That the O-C curve in panel 1 and the dotted L-SD curve in panel 3 look similar is evident. This may not be accidental, and due to a modulation effect by the L-SD cycle on the periods P0 and P2. If this should be correct, the beat
(= P0). The opposite appears for the subsequent steep decline after maximum 38. That the O-C curve in panel 1 and the dotted L-SD curve in panel 3 look similar is evident. This may not be accidental, and due to a modulation effect by the L-SD cycle on the periods P0 and P2. If this should be correct, the beat
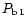 = 21.6yr has nothing to do with the interference of P0 with a secondary period P1 (= 390d). The latter is then obsolete, and P2 (305d or 475d) should be called P1.
The ratio between these two, P0 (= 371.4d) and P1 (= 305d or 475d), amounts to approximately 4/5 (if 305d is used), or 5/4 (if 475d is used), a ratio which is often found among multi-periodic pulsating stars.
All evolved massive stars, generally referred to as
= 21.6yr has nothing to do with the interference of P0 with a secondary period P1 (= 390d). The latter is then obsolete, and P2 (305d or 475d) should be called P1.
The ratio between these two, P0 (= 371.4d) and P1 (= 305d or 475d), amounts to approximately 4/5 (if 305d is used), or 5/4 (if 475d is used), a ratio which is often found among multi-periodic pulsating stars.
All evolved massive stars, generally referred to as 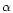 Cyg variables, including
the S Dor variables, show currently a photometric microvariability with light amplitudes
Cyg variables, including
the S Dor variables, show currently a photometric microvariability with light amplitudes
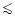 0
0
 2. Note that the light amplitude of the microvariations can be larger than that
of the S-SD phase (e.g. HD34664 = S22 in Fig. 16). The time scales, often called
semi- or
quasi-periods, are of the order of days (the hot members) to months (the cool members)
(van Genderen 1989, 1991a; Sterken 1989; van Leeuwen et al.
1998; van Genderen & Sterken 1999 and references therein).
Although the precise evolutionary connections and the physical
differences between
2. Note that the light amplitude of the microvariations can be larger than that
of the S-SD phase (e.g. HD34664 = S22 in Fig. 16). The time scales, often called
semi- or
quasi-periods, are of the order of days (the hot members) to months (the cool members)
(van Genderen 1989, 1991a; Sterken 1989; van Leeuwen et al.
1998; van Genderen & Sterken 1999 and references therein).
Although the precise evolutionary connections and the physical
differences between 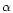 Cyg variables and S Dor variables
are still unclear, I tentatively considered the last ones as a
small sub-group of the first ones (van Genderen et al. 1988). The photometric behaviour of
the famous S Dor variable P Cyg seems to support this view. According to the models the star
should be dynamically stable at present (thus no SD-phases, but see Note added in proof;
Sect. 3.2.2), but it does show microvariations. It also appears that in
the same temperature domain S Dor variables and normal
Cyg variables and S Dor variables
are still unclear, I tentatively considered the last ones as a
small sub-group of the first ones (van Genderen et al. 1988). The photometric behaviour of
the famous S Dor variable P Cyg seems to support this view. According to the models the star
should be dynamically stable at present (thus no SD-phases, but see Note added in proof;
Sect. 3.2.2), but it does show microvariations. It also appears that in
the same temperature domain S Dor variables and normal 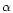 Cyg variables, show almost
the same type of microvariations. Often, the microvariations of S Dor variables near
minimum light show fewer secondary features, and the amplitudes (or the "maximum light
amplitudes'': MLA) appear to be somewhat larger (van Genderen 1989, 1991a;
van Genderen & Sterken 1996). Many S Dor variables near minimum light might still show very
weak SD-phases which contribute to the MLA's.
Analyzing the S Dor variables with a strong SD-activity, we noted a peculiar phenomenon. At or near minimum light they show
Cyg variables, show almost
the same type of microvariations. Often, the microvariations of S Dor variables near
minimum light show fewer secondary features, and the amplitudes (or the "maximum light
amplitudes'': MLA) appear to be somewhat larger (van Genderen 1989, 1991a;
van Genderen & Sterken 1996). Many S Dor variables near minimum light might still show very
weak SD-phases which contribute to the MLA's.
Analyzing the S Dor variables with a strong SD-activity, we noted a peculiar phenomenon. At or near minimum light they show 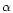 Cyg-type microvariations with quasi-periods of the order of days to weeks (like normal
Cyg-type microvariations with quasi-periods of the order of days to weeks (like normal 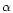 Cyg variables). As soon as they pass a certain temperature domain on their way to maximum light, somewhere between 20000K and 10000K, another type of microvariation emerges rather abruply (within a few months), with a much longer time scale: the "100d-type'' variation.
That is to say, the time scale is often of the order of 100d, but can range from 50d to 150d, of the same order as normal
Cyg variables). As soon as they pass a certain temperature domain on their way to maximum light, somewhere between 20000K and 10000K, another type of microvariation emerges rather abruply (within a few months), with a much longer time scale: the "100d-type'' variation.
That is to say, the time scale is often of the order of 100d, but can range from 50d to 150d, of the same order as normal 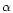 Cyg variables (non-S Dor variables) of the same temperature. The amplitudes are still
Cyg variables (non-S Dor variables) of the same temperature. The amplitudes are still
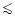 0
0
 2 (see references above). However, the colour behaviour of the 100d-type variations is often red in the light maxima instead of blue as for the shorter microvariations mentioned above (e.g. R40 in van Genderen et al. 1997b: Figs. 8-10) and often more chaotic (e.g. S Dor and R127 in van Genderen et al. 1997a and 1997b, respectively).
I speculate that they could correspond to the oscillations found by Stothers & Chin (1995, 1996) in their models and called "relaxation oscillations'' (a kind of pulsation superimposed on a dynamical unstable structure) due to the kappa-mechanism. They occur during the cool part of the "secular cycles'' in the models as well as in the observed maxima of the SD-phases. The predicted periods are also in the order of months! Stothers' (1999c) idealized hydrodynamical models reveal very small bolometric light amplitudes, less than 0
2 (see references above). However, the colour behaviour of the 100d-type variations is often red in the light maxima instead of blue as for the shorter microvariations mentioned above (e.g. R40 in van Genderen et al. 1997b: Figs. 8-10) and often more chaotic (e.g. S Dor and R127 in van Genderen et al. 1997a and 1997b, respectively).
I speculate that they could correspond to the oscillations found by Stothers & Chin (1995, 1996) in their models and called "relaxation oscillations'' (a kind of pulsation superimposed on a dynamical unstable structure) due to the kappa-mechanism. They occur during the cool part of the "secular cycles'' in the models as well as in the observed maxima of the SD-phases. The predicted periods are also in the order of months! Stothers' (1999c) idealized hydrodynamical models reveal very small bolometric light amplitudes, less than 0
 2, which is likely to be generally true, even for realistic models.
We found three S Dor variables where both types of microvariations were seen together: the short one superimposed on the long one. The first two are HR Car and R85 (Fig. 13), but only for a few months (van Genderen et al. 1990, 1997b, 1998b). The third is P Cyg,
but here both oscillations, 18.3d and 100d-type, are already seen together for many decades up to the present day (de Groot et al. 2001).
Obviously, the physical state of P Cyg is very close to the switching point for a long time. Apart from these two types of microvariations, P Cyg also shows a very low amplitude oscillation with a cycle length of
2, which is likely to be generally true, even for realistic models.
We found three S Dor variables where both types of microvariations were seen together: the short one superimposed on the long one. The first two are HR Car and R85 (Fig. 13), but only for a few months (van Genderen et al. 1990, 1997b, 1998b). The third is P Cyg,
but here both oscillations, 18.3d and 100d-type, are already seen together for many decades up to the present day (de Groot et al. 2001).
Obviously, the physical state of P Cyg is very close to the switching point for a long time. Apart from these two types of microvariations, P Cyg also shows a very low amplitude oscillation with a cycle length of  3000d (de Groot et al. 2001), which is presumably an S-SD phase (see
Table 6), and an apparent brightness rise due to evolution to the red (Lamers & de Groot 1992; de Groot & Lamers 1992). Thus, in more than one respect P Cyg is an exceptional case (see also Sects. 1.7 and 3.2.2).
Apart from the enigmatic way in which the two types of microvariations succeed each other,
the 100d-type ones offer another riddle: it is quite peculiar that the time scales of
e.g. R127 and HR Car, hardly changed during the brightness rise of
3000d (de Groot et al. 2001), which is presumably an S-SD phase (see
Table 6), and an apparent brightness rise due to evolution to the red (Lamers & de Groot 1992; de Groot & Lamers 1992). Thus, in more than one respect P Cyg is an exceptional case (see also Sects. 1.7 and 3.2.2).
Apart from the enigmatic way in which the two types of microvariations succeed each other,
the 100d-type ones offer another riddle: it is quite peculiar that the time scales of
e.g. R127 and HR Car, hardly changed during the brightness rise of  1
1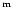 in
in  (van Genderen et al. 1997b: Sect. 4.2). This creates a paradox if one wants
to explain them as a result of stellar radial pulsations, non-radial pulsations offer an
acceptable alternative. But how to explain the (temporarily) simultaneous
excitation of both microvariations? So far, theoretical studies do not predict such
a phenomenon. The switch from one to the other could be explained by physical changes,
such as the density structure during expansion and contraction. However, this cannot
offer an explanation
for the simultaneous presence of both types of microvaraitions.
There are different views on the cause and the physical background of microvariations. Amongst others, they were linked with the "strange-mode'' instabilities (oscillation modes recovered in linear, non-adiabatic calculations for stars with high L/M ratios), see e.g. Kiriakidis et al. (1993, 1997), Soukup et al. (1994) and Cox et al. (1995). See also the reviews by Gautschy & Saio (1995, 1996).
Sterken (1989) was the first to suggest that the SD-domain on the
HR-diagram is an extension of the instability domains of the non-radial
(l>0) pulsators in the g-mode:
(van Genderen et al. 1997b: Sect. 4.2). This creates a paradox if one wants
to explain them as a result of stellar radial pulsations, non-radial pulsations offer an
acceptable alternative. But how to explain the (temporarily) simultaneous
excitation of both microvariations? So far, theoretical studies do not predict such
a phenomenon. The switch from one to the other could be explained by physical changes,
such as the density structure during expansion and contraction. However, this cannot
offer an explanation
for the simultaneous presence of both types of microvaraitions.
There are different views on the cause and the physical background of microvariations. Amongst others, they were linked with the "strange-mode'' instabilities (oscillation modes recovered in linear, non-adiabatic calculations for stars with high L/M ratios), see e.g. Kiriakidis et al. (1993, 1997), Soukup et al. (1994) and Cox et al. (1995). See also the reviews by Gautschy & Saio (1995, 1996).
Sterken (1989) was the first to suggest that the SD-domain on the
HR-diagram is an extension of the instability domains of the non-radial
(l>0) pulsators in the g-mode: 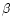 Cep variables and SPBs (slowly-pulsating B-type stars) (see also Waelkens et al. 1998; Lamers et al. 1998). This seems to be supported by theoretical calculations (Pamyatnykh 1998) which also indicate that the above mentioned instability domain covers a much wider region than predicted for the strange-modes. Further, Lamers et al. (1998) found that the observed periods of the microvariations (often near minimum brightness) are much longer than those caused by the strange modes.
According to Gäng's (2000) analysis of spectroscopic time series of HD160529, radial and non-radial pulsations are probably present.
Most of the variable supergiants can be found on the blue side of the HR-diagram. This agrees with the various theoretical models (e.g. Lovey et al. 1984; Stothers & Chin 1994, 1995, 1996; Schaller et al. 1992; Langer et al. 1994; Vanbeveren et al. 1998). The excess of blue supergiants is possibly due to the widening of the main sequence and their longer lifetimes.
S Dor variables are mainly concentrated in the blue part of the HR-diagram as well.
According to Stothers & Chin (1994, 1995,
1996) this is due to their much longer lifetime in their second (blue)
phase of dynamical instability (
Cep variables and SPBs (slowly-pulsating B-type stars) (see also Waelkens et al. 1998; Lamers et al. 1998). This seems to be supported by theoretical calculations (Pamyatnykh 1998) which also indicate that the above mentioned instability domain covers a much wider region than predicted for the strange-modes. Further, Lamers et al. (1998) found that the observed periods of the microvariations (often near minimum brightness) are much longer than those caused by the strange modes.
According to Gäng's (2000) analysis of spectroscopic time series of HD160529, radial and non-radial pulsations are probably present.
Most of the variable supergiants can be found on the blue side of the HR-diagram. This agrees with the various theoretical models (e.g. Lovey et al. 1984; Stothers & Chin 1994, 1995, 1996; Schaller et al. 1992; Langer et al. 1994; Vanbeveren et al. 1998). The excess of blue supergiants is possibly due to the widening of the main sequence and their longer lifetimes.
S Dor variables are mainly concentrated in the blue part of the HR-diagram as well.
According to Stothers & Chin (1994, 1995,
1996) this is due to their much longer lifetime in their second (blue)
phase of dynamical instability ( 104yr) than in their first as a yellow
supergiant (
104yr) than in their first as a yellow
supergiant ( 103yr). Supergiants on a blueward track, which are a
small minority due to their faster evolution, should show processed material at their
surface like presumably the
103yr). Supergiants on a blueward track, which are a
small minority due to their faster evolution, should show processed material at their
surface like presumably the 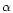 Cyg variable HD157038, a B1/2IaN-type
star (Lennon & Dufton 1986, see for its photometric variability
van Genderen et al. 1989).
Indeed, most of the S Dor variables show He- and N-enriched and O-poor circumstellar ejecta, pointing to CNO-processed material (e.g. L. Smith 1997). Also the dust composition of a number of S Dor variables (e.g. AG Car, WRA751, R71) points to an evolutionary connection with RSG (e.g. Viotti et al. 1988; Robberto et al. 1993; L. Smith et al. 1997, 1998; Voors 1999), although evolutionary tracks of e.g. Schaller et al. (1992) of stars with Mi
Cyg variable HD157038, a B1/2IaN-type
star (Lennon & Dufton 1986, see for its photometric variability
van Genderen et al. 1989).
Indeed, most of the S Dor variables show He- and N-enriched and O-poor circumstellar ejecta, pointing to CNO-processed material (e.g. L. Smith 1997). Also the dust composition of a number of S Dor variables (e.g. AG Car, WRA751, R71) points to an evolutionary connection with RSG (e.g. Viotti et al. 1988; Robberto et al. 1993; L. Smith et al. 1997, 1998; Voors 1999), although evolutionary tracks of e.g. Schaller et al. (1992) of stars with Mi
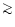 40
40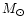 do not reach the RSG region at all, unless one introduces a mass loss in addition to the radiation pressure driven wind like Langer et al. (1994) did. Further support for a possible RSG-connection comes from the hydrodynamical models of the nebulae of e.g. P Cyg and AG Car by Garcia-Segura et al. (1996a,b), which imply that these stars evolved through what they call: a "blueward excursion''. Yet, P Cyg is the only S Dor variable which lacks any dust in its ejecta (Voors 1999). (It is however not clear whether they also mean an excursion starting right from the RSG domain. Their evolutionary track for a star with an initial mass of 60
do not reach the RSG region at all, unless one introduces a mass loss in addition to the radiation pressure driven wind like Langer et al. (1994) did. Further support for a possible RSG-connection comes from the hydrodynamical models of the nebulae of e.g. P Cyg and AG Car by Garcia-Segura et al. (1996a,b), which imply that these stars evolved through what they call: a "blueward excursion''. Yet, P Cyg is the only S Dor variable which lacks any dust in its ejecta (Voors 1999). (It is however not clear whether they also mean an excursion starting right from the RSG domain. Their evolutionary track for a star with an initial mass of 60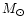 ,
does show a returning point in the RSG domain).
Initially, there was a discrepancy with regard to the H-content in mass (X) at the surfaces of S Dor variables amounting to
,
does show a returning point in the RSG domain).
Initially, there was a discrepancy with regard to the H-content in mass (X) at the surfaces of S Dor variables amounting to  0.36 (see the compilation by Stothers 1999b), while post-RSG should have 0.10-0.20 (Maeder 1997), or
0.36 (see the compilation by Stothers 1999b), while post-RSG should have 0.10-0.20 (Maeder 1997), or  0.18 (Stothers 1999b). However, this seems to have been solved now by Stothers & Chin (2000). If one adopts the Schwarzschild (temperature-gradient) criterion for convection instead of the Ledoux (density-gradient) criterion, a fully convective (thus chemically homogeneous) zone develops just above the H-burning shell, with X approximately equal to 0.35. The star would then be in the second (blue) S Dor stage.
On the other side, Maeder (1999) concluded that due to stellar rotation, some He- and N-enrichments at the stellar surface already occur during the MS-stage for not too high rotational velocities, thus it is not quite abnormal to find slightly enriched supergiants. Further, the computations indicate that rotation makes the star enter the WR-stage during the MS-stage, thus preventing an S Dor- and RSG-stage altogether.
Also with respect to the scheme of evolution of all massive stars, there is still no consensus: different sequences of stellar types exist (see e.g. Langer et al. 1994; Stothers & Chin 1996; Vanbeveren et al. 1998).
In Tables 1, 4, 8 and 11 it is indicated whether circumstellar gas and/or dust nebulae have been detected. It appears that only 40
0.18 (Stothers 1999b). However, this seems to have been solved now by Stothers & Chin (2000). If one adopts the Schwarzschild (temperature-gradient) criterion for convection instead of the Ledoux (density-gradient) criterion, a fully convective (thus chemically homogeneous) zone develops just above the H-burning shell, with X approximately equal to 0.35. The star would then be in the second (blue) S Dor stage.
On the other side, Maeder (1999) concluded that due to stellar rotation, some He- and N-enrichments at the stellar surface already occur during the MS-stage for not too high rotational velocities, thus it is not quite abnormal to find slightly enriched supergiants. Further, the computations indicate that rotation makes the star enter the WR-stage during the MS-stage, thus preventing an S Dor- and RSG-stage altogether.
Also with respect to the scheme of evolution of all massive stars, there is still no consensus: different sequences of stellar types exist (see e.g. Langer et al. 1994; Stothers & Chin 1996; Vanbeveren et al. 1998).
In Tables 1, 4, 8 and 11 it is indicated whether circumstellar gas and/or dust nebulae have been detected. It appears that only 40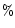 of the S Dor variables, including 8 candidates in these statistics for which the SD-membership is likely, possess with certainty one or more visible ejecta. (There is no statistically significant difference between the percentages of the different categories of S Dor variables defined in Sect. 2.1). It is not excluded that all have a neutral-H nebula, thus not easily detectable. Such nebulae are relics from previous evolutionary stages, such as e.g. a pseudo-RSG/super-Eddington phase with gentle ejections, as postulated by L. Smith et al. (1998). The visible ring nebulae around 25
of the S Dor variables, including 8 candidates in these statistics for which the SD-membership is likely, possess with certainty one or more visible ejecta. (There is no statistically significant difference between the percentages of the different categories of S Dor variables defined in Sect. 2.1). It is not excluded that all have a neutral-H nebula, thus not easily detectable. Such nebulae are relics from previous evolutionary stages, such as e.g. a pseudo-RSG/super-Eddington phase with gentle ejections, as postulated by L. Smith et al. (1998). The visible ring nebulae around 25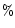 of the WR stars, generally supposed to be partly the descendants of S Dor variables, or at least closely related to them, may be caused by the interaction of the fast WR wind with the slower winds of the RSG- and SD-mass loss episodes (Marston et al. 1994; Marston 1999).
(It has also been suggested that the most luminous WNL stars may evolve into S Dor variables, rather than vice versa, after which they enter a second WR stage (Langer et al. 1994; Walborn 1989). Such a different history has consequences for the chemical composition of the WR nebulae, Garcia-Segura et al. 1996a,b.)
The great homogeneity of the properties of the ejecta generally suggest an interacting wind scenario by non-isotropic outflows. Thus, they are created by an interaction of fast moving gas overtaking slow moving gas (e.g. Icke 1981; Garcia-Segura et al. 1996a,b; L. Smith 1997; Dwarkas & Balick 1998; Langer et al. 1999).
The visible ejecta have dynamical ages between 102yr and
of the WR stars, generally supposed to be partly the descendants of S Dor variables, or at least closely related to them, may be caused by the interaction of the fast WR wind with the slower winds of the RSG- and SD-mass loss episodes (Marston et al. 1994; Marston 1999).
(It has also been suggested that the most luminous WNL stars may evolve into S Dor variables, rather than vice versa, after which they enter a second WR stage (Langer et al. 1994; Walborn 1989). Such a different history has consequences for the chemical composition of the WR nebulae, Garcia-Segura et al. 1996a,b.)
The great homogeneity of the properties of the ejecta generally suggest an interacting wind scenario by non-isotropic outflows. Thus, they are created by an interaction of fast moving gas overtaking slow moving gas (e.g. Icke 1981; Garcia-Segura et al. 1996a,b; L. Smith 1997; Dwarkas & Balick 1998; Langer et al. 1999).
The visible ejecta have dynamical ages between 102yr and 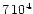 yr (e.g. Nota et al. 1995a; Nota & Clampin 1997; Smith et al. 1998). According to the dynamical evolution computations of Garcia-Segura et al. (1996a,b) visible ejecta have a lifetime of
yr (e.g. Nota et al. 1995a; Nota & Clampin 1997; Smith et al. 1998). According to the dynamical evolution computations of Garcia-Segura et al. (1996a,b) visible ejecta have a lifetime of  104yr, which is of the same order.
The masses of the visible ejecta are at most a few solar masses (e.g. Nota & Clampin 1997), thus not sufficient to explain the current relatively low masses of the S Dor variables. According to Stothers & Chin's calculations (1996) the present blue phase of instability is also too short: 103-104yr, for a substantial mass loss. Thus, the major mass losses should have occurred during the preceding dynamical instability stage in the yellow- or RSG-stage as well as by the normal stellar wind since the MS-stage. The intervening stage from the RSG- to the blue SD-stage is expected to last
104yr, which is of the same order.
The masses of the visible ejecta are at most a few solar masses (e.g. Nota & Clampin 1997), thus not sufficient to explain the current relatively low masses of the S Dor variables. According to Stothers & Chin's calculations (1996) the present blue phase of instability is also too short: 103-104yr, for a substantial mass loss. Thus, the major mass losses should have occurred during the preceding dynamical instability stage in the yellow- or RSG-stage as well as by the normal stellar wind since the MS-stage. The intervening stage from the RSG- to the blue SD-stage is expected to last
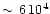 yr (Stothers & Chin 1996). In other words, most of the ejecta we observe today are presumably from the present blue SD-stage. Any ejecta formed in the yellow or red stage must have been dispersed into space.
As far as we know, most visible ejecta are single. There are a few exceptions: AG Car has two ejecta (Nota & Clampin 1997) like R127 (Appenzeller et al. 1987; L. Smith et al. 1998), HR Car has at least three ejecta (e.g. Voors 1999), P Cyg has four ejecta (Barlow et al. 1994; Meaburn et al. 1996; Skinner et al. 1998; see also the review on P Cyg by Israelian & de Groot 1999). The differences in dynamical ages amount to from a few centuries to
yr (Stothers & Chin 1996). In other words, most of the ejecta we observe today are presumably from the present blue SD-stage. Any ejecta formed in the yellow or red stage must have been dispersed into space.
As far as we know, most visible ejecta are single. There are a few exceptions: AG Car has two ejecta (Nota & Clampin 1997) like R127 (Appenzeller et al. 1987; L. Smith et al. 1998), HR Car has at least three ejecta (e.g. Voors 1999), P Cyg has four ejecta (Barlow et al. 1994; Meaburn et al. 1996; Skinner et al. 1998; see also the review on P Cyg by Israelian & de Groot 1999). The differences in dynamical ages amount to from a few centuries to 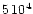 yr.
yr.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{sdfig11.eps} \end{figure}](/articles/aa/full/2001/05/aads1896/Timg35.gif) |
Figure 11:
The schematic light curve (ptm, ptg and  )
versus date of )
versus date of  Car between 1600 and 2000 (last observations made in February 2000). Note that the horizontal scale after 1900 is twice as large as before 1900.
Dashed curve: the "secular rise'' due to the decrease of circumstellar extinction (mainly self-extinction of the Homunculus) according to the model of van Genderen et al. (1994, see also van Genderen et al. 1995, 2001). Dots are averages of time series and the oscillating curve represents a series of monitored SD-phases sketched on scale.
See for further details the notes to Tables 4, 5 and 6 Car between 1600 and 2000 (last observations made in February 2000). Note that the horizontal scale after 1900 is twice as large as before 1900.
Dashed curve: the "secular rise'' due to the decrease of circumstellar extinction (mainly self-extinction of the Homunculus) according to the model of van Genderen et al. (1994, see also van Genderen et al. 1995, 2001). Dots are averages of time series and the oscillating curve represents a series of monitored SD-phases sketched on scale.
See for further details the notes to Tables 4, 5 and 6 |
The largest conundrum of all:  Car, with its bipolar Homunculus, 160yr old, and with N-rich fast moving knots and strings, must have been active on various occasions up to 1000yr ago (Walborn et al. 1978; Weis et al. 1999; Bohigas et al. 2000). A second, but older (a few 103yr) bipolar shell has been found by Bohigas et al. (2000), but its chemistry shows no trace of chemical processing.
The Homunculus has an onion-like structure, with sub-shells (Pantin & Le Mignant 2000). The light curve (Fig. 11) also suggests the occurrence of a series of
Car, with its bipolar Homunculus, 160yr old, and with N-rich fast moving knots and strings, must have been active on various occasions up to 1000yr ago (Walborn et al. 1978; Weis et al. 1999; Bohigas et al. 2000). A second, but older (a few 103yr) bipolar shell has been found by Bohigas et al. (2000), but its chemistry shows no trace of chemical processing.
The Homunculus has an onion-like structure, with sub-shells (Pantin & Le Mignant 2000). The light curve (Fig. 11) also suggests the occurrence of a series of
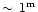 -eruptions between 1827 and 1857 with a repetition time
-eruptions between 1827 and 1857 with a repetition time
 5yr. Apart from that there were also SD-eruptions around 1870 and 1890 (Sect. 1.4). However, it seems that their ejecta have another morphology (e.g. Davidson et al. 1997; N. Smith et al. 1998).
It can be concluded that at least 40% of S Dor variables, suffer a small number of eruptive episodes during their present (second) blue lifetime. The observed eruptive episodes appear to last a few decades and consist of a set of distinct eruptions. These eruptions are visible as
5yr. Apart from that there were also SD-eruptions around 1870 and 1890 (Sect. 1.4). However, it seems that their ejecta have another morphology (e.g. Davidson et al. 1997; N. Smith et al. 1998).
It can be concluded that at least 40% of S Dor variables, suffer a small number of eruptive episodes during their present (second) blue lifetime. The observed eruptive episodes appear to last a few decades and consist of a set of distinct eruptions. These eruptions are visible as
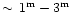 -peaks, in the beginning on top of an enhanced brightness. Subsequently the brightness drops, partly by circumstellar dust, and a few more eruptions occur (see light curves by Humphreys et al. 2000).
The interval between such eruptive episodes may amount to a few centuries up to a few 104yr.
The overall impression is that S Dor variables lose most of their mass in
previous evolutionary stages by the stellar wind and by eruptions caused by dynamical instabilities and not in their current lifetime as hot S Dor variables. The present visible ejecta are the relics of eruptive episodes from their present hot stage. S Dor variables which probably lack any ejecta, did not (yet) suffer from recent eruptions.
Lamers (1987) classified the individual SD-phases by means of the size of the light amplitude (note that they were called "eruptions'' by him as well as by most researchers, which I advise against). In the present paper, the S Dor variables are classified according to their maximum light amplitude reached in the 20th century. Thus, this is a classification on a centennial basis. It is quite possible that a few will enter another category in the 21st century. Some behaved differently in the 19th century. A reason to choose this kind of classification is to investigate whether the size of the instability has any influence on its present (at the turn of the 21st century) position on the theoretical HR-diagram.
Our knowledge of the photometric behaviour of S Dor variables is based on a strongly varying degree of coverage of the light curve. Variables like AG Car, S Dor,
-peaks, in the beginning on top of an enhanced brightness. Subsequently the brightness drops, partly by circumstellar dust, and a few more eruptions occur (see light curves by Humphreys et al. 2000).
The interval between such eruptive episodes may amount to a few centuries up to a few 104yr.
The overall impression is that S Dor variables lose most of their mass in
previous evolutionary stages by the stellar wind and by eruptions caused by dynamical instabilities and not in their current lifetime as hot S Dor variables. The present visible ejecta are the relics of eruptive episodes from their present hot stage. S Dor variables which probably lack any ejecta, did not (yet) suffer from recent eruptions.
Lamers (1987) classified the individual SD-phases by means of the size of the light amplitude (note that they were called "eruptions'' by him as well as by most researchers, which I advise against). In the present paper, the S Dor variables are classified according to their maximum light amplitude reached in the 20th century. Thus, this is a classification on a centennial basis. It is quite possible that a few will enter another category in the 21st century. Some behaved differently in the 19th century. A reason to choose this kind of classification is to investigate whether the size of the instability has any influence on its present (at the turn of the 21st century) position on the theoretical HR-diagram.
Our knowledge of the photometric behaviour of S Dor variables is based on a strongly varying degree of coverage of the light curve. Variables like AG Car, S Dor,  Car,
HR Car and P Cyg have been photometrically monitored for almost the whole 20th century. For others, only the last few decades were covered by photometric observations, while e.g. the HD and HDE catalogues furnish brightness data for earlier dates (Sect. 1.1). Thus, the knowledge of the photometric behaviour in the first half of the 20th century is often only fragmentary, so that some caution is appropriate.
The centennial classification is defined as follows:
Car,
HR Car and P Cyg have been photometrically monitored for almost the whole 20th century. For others, only the last few decades were covered by photometric observations, while e.g. the HD and HDE catalogues furnish brightness data for earlier dates (Sect. 1.1). Thus, the knowledge of the photometric behaviour in the first half of the 20th century is often only fragmentary, so that some caution is appropriate.
The centennial classification is defined as follows:
- a)
- The strong-active (s-a) members: light amplitudes >0
 5. The cycle lengths of the SD-phases are < 10yr and
5. The cycle lengths of the SD-phases are < 10yr and
 20yr (S-SD and L-SD phases, respectively). They are listed in
Tables 1, 2 and 3;
20yr (S-SD and L-SD phases, respectively). They are listed in
Tables 1, 2 and 3;
- b)
- The weak-active (w-a) members: light-amplitudes <0
 5. The cycle lengths of the SD-phases are < 10yr, thus they are S-SD phases. It is evident that the detection of low amplitude (say < 0
5. The cycle lengths of the SD-phases are < 10yr, thus they are S-SD phases. It is evident that the detection of low amplitude (say < 0
 2) variations on a time scale of decades (representing the L-SD phases) is difficult due to too short time bases of the observations. They are listed in
Tables 4, 5 and 6;
2) variations on a time scale of decades (representing the L-SD phases) is difficult due to too short time bases of the observations. They are listed in
Tables 4, 5 and 6;
- c)
- The ex- and dormant (ex-/dormant) members. These objects showed no SD-type photometric variability in the 20th century as far as the scattered observations allow such a conclusion (though they do show the microvariations like all
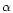 Cyg variables, if photometrically well observed). Usually, they are, or have been suspected members on account of one or two of the other criteria listed in Sect. 1.3. For some specimens a strong photometric variability in the 19th century, or even earlier, has been taken as an important criterium for membership. If they would have been monitored photometrically more extensive, a few might in fact be w-a S Dor variables. They are listed in
Tables 8, 9 and 10;
Cyg variables, if photometrically well observed). Usually, they are, or have been suspected members on account of one or two of the other criteria listed in Sect. 1.3. For some specimens a strong photometric variability in the 19th century, or even earlier, has been taken as an important criterium for membership. If they would have been monitored photometrically more extensive, a few might in fact be w-a S Dor variables. They are listed in
Tables 8, 9 and 10;
- d)
- Candidate SD variables (coined such in the literature) and former candidates
(candidates rejected in the present paper). This group is divided into three subgroups,
(1): the positive (+), (2): the negative (-) candidates (the first ones show a stronger
SD-signature than the second ones) and (3): the former, thus, non-candidates (0). It is now certain, or at least almost certain, that the last category do not belong to the S Dor variables. They all are listed in Tables 11, 12 and 13.
It must be stressed that the stars of the four categories a) to d) show almost without any exception microvariations as described in Sect. 1.6, at least if numerous photometric data are available.
Tables 14 and 15 decode the reference numbers given in Tables 1-6 and 8-13 below the header "ref.'' and mentioned in the notes below the tables, where they are bracketed.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{sdfig13.eps}\end{figure}](/articles/aa/full/2001/05/aads1896/Timg38.gif) |
Figure 13:
The schematic light curve ( )
versus JD-2400000
of the w-a S Dor variable R85 in the LMC. Note that
the magnitude HDEptg 1925 = 10.9 (Table 5) is not indicated in
the figure. The broken curve represents the L-SD phase.
The S-SD phase and the )
versus JD-2400000
of the w-a S Dor variable R85 in the LMC. Note that
the magnitude HDEptg 1925 = 10.9 (Table 5) is not indicated in
the figure. The broken curve represents the L-SD phase.
The S-SD phase and the 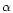 Cyg-type microvariations are
schematically sketched on scale (based on VBLUW monitoring,
while the dots are in most cases individual observations by various authors),
see for further details van Genderen et al. (1998b). The epochs of the three
spectral type determinations are indicated by arrows and are from Feast et al.
(1960), viz. around 1959, and Massey et al. (2000),
viz. in 1996 and 1999 (Tables 4, 5 and 6) Cyg-type microvariations are
schematically sketched on scale (based on VBLUW monitoring,
while the dots are in most cases individual observations by various authors),
see for further details van Genderen et al. (1998b). The epochs of the three
spectral type determinations are indicated by arrows and are from Feast et al.
(1960), viz. around 1959, and Massey et al. (2000),
viz. in 1996 and 1999 (Tables 4, 5 and 6) |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{sdfig16.eps}\end{figure}](/articles/aa/full/2001/05/aads1896/Timg39.gif) |
Figure 16:
The schematic light curve ( )
versus JD-2440000) of the w-a S Dor/B[e] variable HD34664 in the LMC. The dots are all averages of time series of VBLUW photometry and clearly represent an S-SD phase since the colours become red in the maximum (van Genderen & Sterken 1999). In order to illustrate the size of the )
versus JD-2440000) of the w-a S Dor/B[e] variable HD34664 in the LMC. The dots are all averages of time series of VBLUW photometry and clearly represent an S-SD phase since the colours become red in the maximum (van Genderen & Sterken 1999). In order to illustrate the size of the 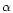 Cyg-type microvariations, a few of these time series are shown in detail, but only schematically sketched and on scale. Zickgraf et al. (1986) have given a compilation of scattered photometry, generally consisting of single observations, made between 1957 and 1984. These magnitudes Cyg-type microvariations, a few of these time series are shown in detail, but only schematically sketched and on scale. Zickgraf et al. (1986) have given a compilation of scattered photometry, generally consisting of single observations, made between 1957 and 1984. These magnitudes  hover between 11.72 and 11.85 and are not shown
hover between 11.72 and 11.85 and are not shown |
Photometric, spectroscopic and physical parameters for the same object often
vary significantly from author to author. This diversity is caused by differences in assumptions and calibrations, apart from the variability of the objects. The temperature and luminosity determination of an object based on different methods may lead to substantial differences, even when applied by the same author.
Uncertainties arise for example in assigned spectral types and spectral analyses and consequently in the temperature. Optical and UV spectral types sometimes disagree. Wind asymmetries might be a plausible reason (Pasquali 1997). Temperatures derived from the intrinsic colour
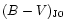 may be unreliable due to a flatter energy distribution, the cause of the extended atmosphere. Additionally, interstellar reddening determinations are
often uncertain.
Further, the chosen apparent magnitudes of the extrema in the light curve, or the average apparent magnitude, to obtain MV, as well as the applied
may be unreliable due to a flatter energy distribution, the cause of the extended atmosphere. Additionally, interstellar reddening determinations are
often uncertain.
Further, the chosen apparent magnitudes of the extrema in the light curve, or the average apparent magnitude, to obtain MV, as well as the applied
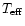 /BC calibration to find
/BC calibration to find
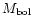 ,
may differ from author to author. And last but not least, the error in the distance can be considerable.
For galactic objects the errors in
,
may differ from author to author. And last but not least, the error in the distance can be considerable.
For galactic objects the errors in
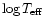 can easily amount to up to 0.05 (
can easily amount to up to 0.05 ( 4000K for high and
4000K for high and  1000K for low temperatures) and 0.2 in
1000K for low temperatures) and 0.2 in
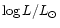 (0
(0
 5 in
5 in
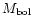 ). For the Magellanic Cloud objects the errors in
). For the Magellanic Cloud objects the errors in
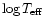 will be the same as above, but relative errors in
will be the same as above, but relative errors in
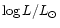 are much smaller than 0.2, say about 0.03 for the LMC and 0.06 for the SMC objects (the difference between the two stellar systems is caused by the difference in inclination angle).
The errors in the temperature mentioned above introduce errors via the BC in
are much smaller than 0.2, say about 0.03 for the LMC and 0.06 for the SMC objects (the difference between the two stellar systems is caused by the difference in inclination angle).
The errors in the temperature mentioned above introduce errors via the BC in
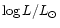 ,
thus
,
thus 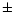 0.1 in
0.1 in
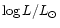 for the hottest S Dor variables, while it is negligible for the cool ones. This error should be incorporated into the error in the luminosity (for the hottest variables) given above.
Apart from that, relative errors in the distance moduli between galactic and Magellanic Clouds amounting to
for the hottest S Dor variables, while it is negligible for the cool ones. This error should be incorporated into the error in the luminosity (for the hottest variables) given above.
Apart from that, relative errors in the distance moduli between galactic and Magellanic Clouds amounting to  0
0
 15 cause an extra relative error in
15 cause an extra relative error in
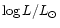 of
of  0.06.
In incidental cases the uncertainty in the distance of galactic objects is relatively larger, e.g. HD80077, Cyg OB2#12, WRA751, He3-519 and the Pistol Star. The error in
0.06.
In incidental cases the uncertainty in the distance of galactic objects is relatively larger, e.g. HD80077, Cyg OB2#12, WRA751, He3-519 and the Pistol Star. The error in
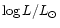 may then amount to 0.4 (
may then amount to 0.4 (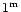 in
in
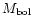 ). For
). For  Car, the MV and the circumstellar reddening of the hidden S Dor variable are the main uncertain parameters, affecting its error box on the HR-diagram.
Because of these problems, I list parameters which often are an average of various sources. Only the (hopefully) most reliable parameters were selected. References on which these data are partly or completely based, are given also. To get a more or less homogeneous set, many values from the literature, if necessary, were slightly revised by applying the relation
Car, the MV and the circumstellar reddening of the hidden S Dor variable are the main uncertain parameters, affecting its error box on the HR-diagram.
Because of these problems, I list parameters which often are an average of various sources. Only the (hopefully) most reliable parameters were selected. References on which these data are partly or completely based, are given also. To get a more or less homogeneous set, many values from the literature, if necessary, were slightly revised by applying the relation
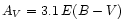 and taking
and taking
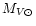 = 4.75. If no temperatures were known, the spectral type, or an average of literature spectra, served as a temperature indicator by applying the calibrations of de Jager & Nieuwenhuijzen (1987). The BC scale of Schmidt-Kaler (1982) was then used to derive M
= 4.75. If no temperatures were known, the spectral type, or an average of literature spectra, served as a temperature indicator by applying the calibrations of de Jager & Nieuwenhuijzen (1987). The BC scale of Schmidt-Kaler (1982) was then used to derive M
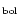 .
If no spectrum was known,
.
If no spectrum was known,
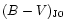 served as an temperature indicator.
Further, all Magellanic Cloud objects have been scaled to the same distance with the distance moduli 18.45 and 19.0 for LMC and SMC, respectively. This procedure may lead in some cases to smaller scatter, yet I will use the estimated errors given above for error bars on the
HR-diagram (Sect. 3).
Figure 20 shows the position of the four categories of objects on the HR-diagram in four separate panels. The error bars are based on estimates (Sect. 2.2). The bars at the left represent the relative errors for the objects within the same stellar system. There are two bars at the right labeled "extra''. The first one with the sublabel "dist'' is due to the error in the distances of the three stellar systems relative to each other. The second one with the sublabel "BC hot'' is the effect of an error in temperature on the luminosity via the BC. It is only appropriate for the hottest S Dor variables since the BC is negligible for the cooler ones. Both errors should be incorporated to the three at the left by adding them quadratically and taking the square root, if objects of one stellar system are compared with those in another one.
The dotted vertical line in each panel is the calculated threshold for dynamical instability when going from low to high temperatures according to Stothers & Chin (1996). Indeed, only a few objects lie on the left of it and within the estimated error.
served as an temperature indicator.
Further, all Magellanic Cloud objects have been scaled to the same distance with the distance moduli 18.45 and 19.0 for LMC and SMC, respectively. This procedure may lead in some cases to smaller scatter, yet I will use the estimated errors given above for error bars on the
HR-diagram (Sect. 3).
Figure 20 shows the position of the four categories of objects on the HR-diagram in four separate panels. The error bars are based on estimates (Sect. 2.2). The bars at the left represent the relative errors for the objects within the same stellar system. There are two bars at the right labeled "extra''. The first one with the sublabel "dist'' is due to the error in the distances of the three stellar systems relative to each other. The second one with the sublabel "BC hot'' is the effect of an error in temperature on the luminosity via the BC. It is only appropriate for the hottest S Dor variables since the BC is negligible for the cooler ones. Both errors should be incorporated to the three at the left by adding them quadratically and taking the square root, if objects of one stellar system are compared with those in another one.
The dotted vertical line in each panel is the calculated threshold for dynamical instability when going from low to high temperatures according to Stothers & Chin (1996). Indeed, only a few objects lie on the left of it and within the estimated error.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{sdfig20.eps}\end{figure}](/articles/aa/full/2001/05/aads1896/Timg47.gif) |
Figure 20:
The position of the four categories of S Dor variables on the theoretical HR-diagram. The fat dashed line in the four panels represents the SD-minimum strip. See for further explanation Sect. 3.2 |
The upper left panel of Fig. 20 shows the s-a variables: 4 galactic, 2 SMC and 8 LMC objects
(Tables 1, 2 and 3). To prevent crowding, not all designations are given. The minimum state (dots) and the maximum state (circles) are connected by a line. Most of these lines, representing schematically the displacement during SD-phases, run more or less horizontal as expected. The more luminous the star, the larger the shift in temperature and the visual amplitude.
For HDE269216 (LMC) only the average position is shown (open square), since no precise data for its extrema are known. For HDE269582 (LMC) only the minimum position could be derived (dot).
The thick dashed line sketched through the minima (3 galactic, 1 SMC and 7 LMC objects) represents the "s-a SD-minimum strip'', which will be called from now on the "SD-minimum strip''. Such a relation has been first pointed out by Wolf (1989). The dashed line has been copied into the three other panels, which will be discussed hereafter.
WRA751 (uncertain distance) and R4 (SMC; see below) have been ignored. The equation for the strip is:
It must be stressed that this strip is not necessarily the same as where the SD-eruptions originate. However, see the discussion on P Cyg in Sect. 3.2.2.
The small scatter is surprising. It can partly be explained by the fact that errors in temperature cause a change in luminosity via the BC, which runs along almost the same inclination as the strip. If the small scatter is not accidental and intrinsic to the strip, then the distances are apparently rather reliable.
The SMC object R4 (including an A-type companion) is much too faint: about 2
 5 (bolometric) compared to other S Dor variables with the same temperature. This must be intrinsic. Whether this has anything to do with the fact that it also is a B[e] star
(Tables 1 and 2; see also van Genderen & Sterken 1999) is unknown. B[e] stars are likely rapid rotators and according to Langer (1999) such stars should have a lower luminosity. On the other hand Langer & Heger (1998) concluded from the morphology and chemical enrichment of the nebula that R4 was originally composed of a close binary and a third star (the A-type companion). The close binary merged into a single star: the present B[e]/S Dor companion. In this model, supported by observations of the nebula by Pasquali et al. (2000), the merger star would be expected to add a large amount of He to the interior of the combined object, giving it a very large L/M ratio. However, how should this be reconciled with the unusual low luminosity of R4?
The evolutionary tracks of stars on the verge of becoming a WR star leave the SD-area by bending down to the left (the most massive ones), or leaving it horizontally to the left (the less massive ones). Thus, R4 could be such a case.
The second SMC object in this group, R40, lies only slightly above the SD-minimum strip. Clear systematic differences between the objects of the three stellar systems due to differences in metal content, are obviously absent. Perhaps R40 is the only one that to some extent responds to the expectation, since with low Z L goes up and
5 (bolometric) compared to other S Dor variables with the same temperature. This must be intrinsic. Whether this has anything to do with the fact that it also is a B[e] star
(Tables 1 and 2; see also van Genderen & Sterken 1999) is unknown. B[e] stars are likely rapid rotators and according to Langer (1999) such stars should have a lower luminosity. On the other hand Langer & Heger (1998) concluded from the morphology and chemical enrichment of the nebula that R4 was originally composed of a close binary and a third star (the A-type companion). The close binary merged into a single star: the present B[e]/S Dor companion. In this model, supported by observations of the nebula by Pasquali et al. (2000), the merger star would be expected to add a large amount of He to the interior of the combined object, giving it a very large L/M ratio. However, how should this be reconciled with the unusual low luminosity of R4?
The evolutionary tracks of stars on the verge of becoming a WR star leave the SD-area by bending down to the left (the most massive ones), or leaving it horizontally to the left (the less massive ones). Thus, R4 could be such a case.
The second SMC object in this group, R40, lies only slightly above the SD-minimum strip. Clear systematic differences between the objects of the three stellar systems due to differences in metal content, are obviously absent. Perhaps R40 is the only one that to some extent responds to the expectation, since with low Z L goes up and
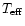 drops (Stothers & Chin 1996) and the location of the photospheric Eddington limit goes up (Lamers & Noordhoek 1993). However, the observed deviation is not significant.
According to the opaque-wind model of Davidson (1987) the maximum visual brightness cannot surpass the temperature limit to the red between 7000K and 8000K. Although an SD-phase is basically caused by an expanding radius and a decreasing temperature, rather than by an expanding pseudo-photosphere due to an increasing wind density, this group (and the other ones to be discussed
below) seems to have a limit at
drops (Stothers & Chin 1996) and the location of the photospheric Eddington limit goes up (Lamers & Noordhoek 1993). However, the observed deviation is not significant.
According to the opaque-wind model of Davidson (1987) the maximum visual brightness cannot surpass the temperature limit to the red between 7000K and 8000K. Although an SD-phase is basically caused by an expanding radius and a decreasing temperature, rather than by an expanding pseudo-photosphere due to an increasing wind density, this group (and the other ones to be discussed
below) seems to have a limit at  7000K. Perhaps the SD-phase is not only caused by
a radius and temperature variation alone, but might at times be a mixture of an expanding radius/decreasing temperature and an
expanding pseudo-photosphere, see van Genderen et al. (1998b, Sect. 4.5
7000K. Perhaps the SD-phase is not only caused by
a radius and temperature variation alone, but might at times be a mixture of an expanding radius/decreasing temperature and an
expanding pseudo-photosphere, see van Genderen et al. (1998b, Sect. 4.5![[*]](/icons/foot_motif.gif) )
The SD-minimum strip lies roughly at the same location as that of the dynamical unstable blue models of Stothers & Chin (1996), viz. between
)
The SD-minimum strip lies roughly at the same location as that of the dynamical unstable blue models of Stothers & Chin (1996), viz. between
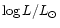
 6.1 and
6.1 and
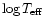
 4.5, and
4.5, and
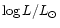
 5.4 and
5.4 and
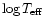
 3.9.
Further, it should be noted that the red side of the SD-area overlaps the "Yellow Void'', a region of atmospheric instability of yellow hypergiants, investigated by Nieuwenhuijzen & de Jager (1995, 2000) and de Jager (1998), see Sect. 3.2.5 of the present paper.
The upper right panel shows the w-a members: 4 galactic and 8 LMC objects (Tables 4, 5 and 6). For most of these stars the parameters have been plotted as averages, since the extrema are not precisely known. HD38489 is the only one with a relative large range: minimum (dot) and maximum (circle) are connected by a line, although the light variation is poorly known. R85 has a small range, minimum (dot) and maximum (circle) are connected by a line. That the long-term low-amplitude variation represents an SD-phase indeed is obvious from the three spectral type determinations indicated in Fig. 13: at minimum the star is hotter than at the maximum.
Two famous objects:
3.9.
Further, it should be noted that the red side of the SD-area overlaps the "Yellow Void'', a region of atmospheric instability of yellow hypergiants, investigated by Nieuwenhuijzen & de Jager (1995, 2000) and de Jager (1998), see Sect. 3.2.5 of the present paper.
The upper right panel shows the w-a members: 4 galactic and 8 LMC objects (Tables 4, 5 and 6). For most of these stars the parameters have been plotted as averages, since the extrema are not precisely known. HD38489 is the only one with a relative large range: minimum (dot) and maximum (circle) are connected by a line, although the light variation is poorly known. R85 has a small range, minimum (dot) and maximum (circle) are connected by a line. That the long-term low-amplitude variation represents an SD-phase indeed is obvious from the three spectral type determinations indicated in Fig. 13: at minimum the star is hotter than at the maximum.
Two famous objects:  Car (Fig. 11) and P Cyg, belong to this group. The S Dor variable connected to the first object is hidden in a lot of circumstellar material, so its brightness and temperature are only roughly known
(Table 4).
According to the principle of a "Chinese lantern'' any light variation of the variable is imitated by the bipolar reflection nebula (mainly by the dominant SE part more or less pointing to us,
van Genderen et al. 1999). It appears that the light variation in the visual during the interval 1992-1994 showed strong similarities with that of R85 during 1984-1986: both S Dor variables showed a cycle of an S-SD phase with microvariations superimposed (van Genderen et al. 1999). This proves that the S Dor variable hidden in
Car (Fig. 11) and P Cyg, belong to this group. The S Dor variable connected to the first object is hidden in a lot of circumstellar material, so its brightness and temperature are only roughly known
(Table 4).
According to the principle of a "Chinese lantern'' any light variation of the variable is imitated by the bipolar reflection nebula (mainly by the dominant SE part more or less pointing to us,
van Genderen et al. 1999). It appears that the light variation in the visual during the interval 1992-1994 showed strong similarities with that of R85 during 1984-1986: both S Dor variables showed a cycle of an S-SD phase with microvariations superimposed (van Genderen et al. 1999). This proves that the S Dor variable hidden in  Car must also be a normal S Dor variable. This is supported by the spectrum which looks like that of P Cyg (Ebbets et al. 1997).
Its most probable position is outlined by the dashed-dotted error box. The cause of the large uncertainty is explained in the notes to Table 4. The present status of
Car must also be a normal S Dor variable. This is supported by the spectrum which looks like that of P Cyg (Ebbets et al. 1997).
Its most probable position is outlined by the dashed-dotted error box. The cause of the large uncertainty is explained in the notes to Table 4. The present status of  Car is discussed in Sect. 3.2.6.
After the SD-eruptions in the 17th century, P Cyg's total displacement in
Car is discussed in Sect. 3.2.6.
After the SD-eruptions in the 17th century, P Cyg's total displacement in
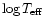 to the right on the HR-diagram amounts to 0.046, assuming constant luminosity (Lamers & de Groot 1992; de Groot & Lamers 1992). This is indicated by the short horizontal line in Fig. 20. If this is not much in error, the eruptions occurred close to its present position and according to the model of Langer et al. (1994), P Cyg ought to be at the beginning of an S Dor stage.
It is of interest to note that the age of the oldest shell of P Cyg, possibly a relic of an eruption, amounts to some 2 104yr (Meaburn et al. 1999). This suggests that P Cyg has been that long an S Dor variable. According to Stothers's (1999b) prediction, P Cyg is now exactly in a state of marginal dynamical instability, as is indeed observed by de Groot et al. (2001) (see Sect. 1.6 and Table 6 in the present paper). Only microvariations are present and a possible very low-amplitude SD-cycle.
The Stothers & Chin (1995) models do not predict much variation in the luminosity, either during or directly after the mass-loss episodes. In the course of the "blue loop'' after a mass-loss episode, the star, in this case P Cyg, should be (nearly) inactive, as is observed.
Thus, the observations of P Cyg support my view that S Dor variables are a sub-class of
the
to the right on the HR-diagram amounts to 0.046, assuming constant luminosity (Lamers & de Groot 1992; de Groot & Lamers 1992). This is indicated by the short horizontal line in Fig. 20. If this is not much in error, the eruptions occurred close to its present position and according to the model of Langer et al. (1994), P Cyg ought to be at the beginning of an S Dor stage.
It is of interest to note that the age of the oldest shell of P Cyg, possibly a relic of an eruption, amounts to some 2 104yr (Meaburn et al. 1999). This suggests that P Cyg has been that long an S Dor variable. According to Stothers's (1999b) prediction, P Cyg is now exactly in a state of marginal dynamical instability, as is indeed observed by de Groot et al. (2001) (see Sect. 1.6 and Table 6 in the present paper). Only microvariations are present and a possible very low-amplitude SD-cycle.
The Stothers & Chin (1995) models do not predict much variation in the luminosity, either during or directly after the mass-loss episodes. In the course of the "blue loop'' after a mass-loss episode, the star, in this case P Cyg, should be (nearly) inactive, as is observed.
Thus, the observations of P Cyg support my view that S Dor variables are a sub-class of
the 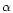 Cyg variables (Sect. 1.6). It seems obvious that the microvariations are
hardly influenced by the various SD-instabilities: they are present when the star is
not, or at most an extremely weak-active S Dor variable, or they are imperturbably
present during high-amplitude SD-phases. Presumably they should be considered as small-scale
instabilities of the outer layers, typical for
Cyg variables (Sect. 1.6). It seems obvious that the microvariations are
hardly influenced by the various SD-instabilities: they are present when the star is
not, or at most an extremely weak-active S Dor variable, or they are imperturbably
present during high-amplitude SD-phases. Presumably they should be considered as small-scale
instabilities of the outer layers, typical for 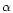 Cyg variables in general.
If the
Cyg variables in general.
If the
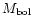 of P Cyg was a magnitude brighter during the eruption of the 17th
century, which is not certain at all (Lamers & de Groot 1992), the
displacement followed an inclination steeper than the SD- minimum strip. The model of
Langer et al. (1994) does not predict such a large variation in the
luminosity.
With a few exceptions, the w-a members obey the SD-minimum strip, but with more scatter. Most of them are Be stars and/or are suspected of having a gaseous disk e.g. R99 and R123 in the LMC
(Table 4).
R149 (Be+neb, LMC) is like R4 (B[e], SMC) in the previous panel, much too faint, which could be intrinsic (Sect. 3.2.1).
I suspect that most of the w-a variables should fit the SD-minimum strip because they are supposed to be in a minimum of both types of SD-phases. The s-a variable HR Car experienced such a minimum lasting about 20yr and the s-a variable R71 has now (1999) been in such a state for 15yr, only showing weak-active SD phases (Fig. 4; van Genderen et al. 1997b; Sterken et al. 1997b). Such minima might even last much longer. Note that R81 (B2.5eqIa+, LMC) and R123 (Bpec, LMC), were s-a variables in the previous century (Figs. 12 and 15, respectively).
The bottom panel at the left of Fig. 20, shows the ex-/dormant variables: 5 galactic and 3 LMC objects (Tables 8, 9 and 10). Most of them lie below the SD-minimum strip. Whether this is accidental or intrinsic (e.g. due to further evolution to the blue, see Sect. 3.2.1) is unknown. Again, there is one object with a much too low luminosity, the galactic object HDE326823. Lopes et al. (1992) and Sterken et al. (1995b) suspect that it is on its way to the WN stage. One could speculate that the same is true for R4 and R149 discussed in Sects. 3.2.1 and 3.2.2, respectively.
According to Weis (1999) S119 has a shell typical for an S Dor variable, although the age may amount up to
of P Cyg was a magnitude brighter during the eruption of the 17th
century, which is not certain at all (Lamers & de Groot 1992), the
displacement followed an inclination steeper than the SD- minimum strip. The model of
Langer et al. (1994) does not predict such a large variation in the
luminosity.
With a few exceptions, the w-a members obey the SD-minimum strip, but with more scatter. Most of them are Be stars and/or are suspected of having a gaseous disk e.g. R99 and R123 in the LMC
(Table 4).
R149 (Be+neb, LMC) is like R4 (B[e], SMC) in the previous panel, much too faint, which could be intrinsic (Sect. 3.2.1).
I suspect that most of the w-a variables should fit the SD-minimum strip because they are supposed to be in a minimum of both types of SD-phases. The s-a variable HR Car experienced such a minimum lasting about 20yr and the s-a variable R71 has now (1999) been in such a state for 15yr, only showing weak-active SD phases (Fig. 4; van Genderen et al. 1997b; Sterken et al. 1997b). Such minima might even last much longer. Note that R81 (B2.5eqIa+, LMC) and R123 (Bpec, LMC), were s-a variables in the previous century (Figs. 12 and 15, respectively).
The bottom panel at the left of Fig. 20, shows the ex-/dormant variables: 5 galactic and 3 LMC objects (Tables 8, 9 and 10). Most of them lie below the SD-minimum strip. Whether this is accidental or intrinsic (e.g. due to further evolution to the blue, see Sect. 3.2.1) is unknown. Again, there is one object with a much too low luminosity, the galactic object HDE326823. Lopes et al. (1992) and Sterken et al. (1995b) suspect that it is on its way to the WN stage. One could speculate that the same is true for R4 and R149 discussed in Sects. 3.2.1 and 3.2.2, respectively.
According to Weis (1999) S119 has a shell typical for an S Dor variable, although the age may amount up to  105yr, which is relatively high.
The bottom panel at the right of Fig. 20 shows the candidate S Dor variables, at least those for which luminosity and temperature are known: 6 positive candidates (+ sign, bracketed if the position is very uncertain) and 4 negative candidates (- sign) (Tables 11, 12 and 13). The Pistol Star (PS) is represented by two models. Their positions far from the SD-minimum strip could point to a large uncertainty in the distance and/or the reddening, just like for most of the other candidates. Further, 3 non-candidates (dots) are also plotted.
The positive candidate IRC+10420 is the only object which was situated on the left side of the 7000-8000K border (discussed in Sect. 3.2.1) some decades ago, but which evolved quickly to about 7900K in 1994
(Oudmaijer 1995; Nieuwenhuijzen & de Jager 2000). The star has been plotted in Fig. 20 with the last-mentioned temperature. This object might still be a yellow hypergiant. See for a further discussion on the possible relationship between the two types of variables Sect. 3.2.5.
According to de Jager (1998) IRC+10420 is a yellow hypergiant, like
105yr, which is relatively high.
The bottom panel at the right of Fig. 20 shows the candidate S Dor variables, at least those for which luminosity and temperature are known: 6 positive candidates (+ sign, bracketed if the position is very uncertain) and 4 negative candidates (- sign) (Tables 11, 12 and 13). The Pistol Star (PS) is represented by two models. Their positions far from the SD-minimum strip could point to a large uncertainty in the distance and/or the reddening, just like for most of the other candidates. Further, 3 non-candidates (dots) are also plotted.
The positive candidate IRC+10420 is the only object which was situated on the left side of the 7000-8000K border (discussed in Sect. 3.2.1) some decades ago, but which evolved quickly to about 7900K in 1994
(Oudmaijer 1995; Nieuwenhuijzen & de Jager 2000). The star has been plotted in Fig. 20 with the last-mentioned temperature. This object might still be a yellow hypergiant. See for a further discussion on the possible relationship between the two types of variables Sect. 3.2.5.
According to de Jager (1998) IRC+10420 is a yellow hypergiant, like 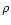 Cas and HR8752. HR8752 appeared to have evolved quickly to the blue during the 20th century (Zsoldos 1986), like IRC+10420 (e.g. Kastner et al. 1995;
Oudmaijer 1995; Nieuwenhuijzen & de Jager 2000).
Cas and HR8752. HR8752 appeared to have evolved quickly to the blue during the 20th century (Zsoldos 1986), like IRC+10420 (e.g. Kastner et al. 1995;
Oudmaijer 1995; Nieuwenhuijzen & de Jager 2000). 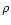 Cas may be doing the same, although its behaviour is more chaotic.
The observations and calculations of Nieuwenhuijzen & de Jager (1995, 2000) and de Jager (1998) indicate that HR8752 and
Cas may be doing the same, although its behaviour is more chaotic.
The observations and calculations of Nieuwenhuijzen & de Jager (1995, 2000) and de Jager (1998) indicate that HR8752 and 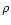 Cas are now bouncing against the cool border (
Cas are now bouncing against the cool border ( 7500K) of the Yellow Void, a region of atmospheric instability, which overlaps the cool side of the SD-area (although no S Dor variables reside in the Void, just at its lower boundary, see Fig. 21). This is accompanied by enhanced mass ejections. For HR8752 the bouncing occurs in possible cycles of
7500K) of the Yellow Void, a region of atmospheric instability, which overlaps the cool side of the SD-area (although no S Dor variables reside in the Void, just at its lower boundary, see Fig. 21). This is accompanied by enhanced mass ejections. For HR8752 the bouncing occurs in possible cycles of  10yr. It is unknown how and when these objects will cross this border to enter the Yellow Void. With other words: are these fast evolving yellow hypergiants in fact proto-S Dor variables? The opposite question has been posed by de Jager (1998: Sect. 2).
According to Garcia-Segura et al.'s (1996b) evolutionary model for a 35
10yr. It is unknown how and when these objects will cross this border to enter the Yellow Void. With other words: are these fast evolving yellow hypergiants in fact proto-S Dor variables? The opposite question has been posed by de Jager (1998: Sect. 2).
According to Garcia-Segura et al.'s (1996b) evolutionary model for a 35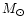 star: possibly not. Their model predicts an extremely rapid evolution from the yellow hypergiant stage to the WR stage: about 100yr!
However, as de Jager & Nieuwenhuijzen (see above) have demonstrated, the evolution of the yellow hypergiants to the blue will be stopped by the Yellow Void for some time, but it is unknown for how long. Once they have passed, or avoided this barrier somehow, there is perhaps not much time left for a (blue) S Dor stage. On the other hand, note that the S Dor variables like the w-a variables HD168607, R85, R74, the s-a variable R110 and the ex-/dormant variable HD168625 in Fig. 20, lie just at the lower edge of the Yellow Void (Fig. 21) and that not one S Dor variable is situated right inside the Void, (only the s-a variables cross the Void during SD-phases and are obviously not in a normal state then).
Therefore, we may assume that once the envelopes of the yellow hypergiants have lost so much mass that it results in more atmospheric stability, they become low-luminous S Dor variables after all and for a time long enough to be observed.
Note that both types of variables are generally blueward evolving stars and that the masses of the yellow hypergiants (Nieuwenhuijzen & de Jager 2000) are most likely of the same order as that of the S Dor variables like R110: 10
star: possibly not. Their model predicts an extremely rapid evolution from the yellow hypergiant stage to the WR stage: about 100yr!
However, as de Jager & Nieuwenhuijzen (see above) have demonstrated, the evolution of the yellow hypergiants to the blue will be stopped by the Yellow Void for some time, but it is unknown for how long. Once they have passed, or avoided this barrier somehow, there is perhaps not much time left for a (blue) S Dor stage. On the other hand, note that the S Dor variables like the w-a variables HD168607, R85, R74, the s-a variable R110 and the ex-/dormant variable HD168625 in Fig. 20, lie just at the lower edge of the Yellow Void (Fig. 21) and that not one S Dor variable is situated right inside the Void, (only the s-a variables cross the Void during SD-phases and are obviously not in a normal state then).
Therefore, we may assume that once the envelopes of the yellow hypergiants have lost so much mass that it results in more atmospheric stability, they become low-luminous S Dor variables after all and for a time long enough to be observed.
Note that both types of variables are generally blueward evolving stars and that the masses of the yellow hypergiants (Nieuwenhuijzen & de Jager 2000) are most likely of the same order as that of the S Dor variables like R110: 10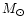 (Stahl et al. 1990), HD160529: 13
(Stahl et al. 1990), HD160529: 13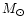 (Sterken et al. 1991) and HD168625: 10
(Sterken et al. 1991) and HD168625: 10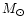 (Robberto & Herbst 1998). Consequently, in some respects, yellow hypergiants could be very well proto-S Dor variables, consistent with de Jager's (1998) supposition.
Besides, the cycles of mass ejections of the yellow hypergiants and the SD-phases of S Dor variables may be related instability mechanisms.
It should be noted that yellow hypergiants also belong to the
(Robberto & Herbst 1998). Consequently, in some respects, yellow hypergiants could be very well proto-S Dor variables, consistent with de Jager's (1998) supposition.
Besides, the cycles of mass ejections of the yellow hypergiants and the SD-phases of S Dor variables may be related instability mechanisms.
It should be noted that yellow hypergiants also belong to the 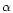 Cyg variables, viz. the cool ones, showing microvariations on a time scale of hundreds of days.
Cyg variables, viz. the cool ones, showing microvariations on a time scale of hundreds of days.
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{1896F21new.eps} %
\end{figure}](/articles/aa/full/2001/05/aads1896/Timg50.gif) |
Figure 21:
The structure of the S Dor area on the HR-diagram. It shows amongst others the SD-triangle in which the s-a S Dor variables move to-and-fro during the SD-phases, the SD-minimum strip (fat dashed line) with the thinly dashed lines as its bandwidth, and the Yellow Void |
The fact that all S Dor variables with reasonable reliable distances and reddenings lie on a relatively narrow band on the HR-diagram, can have consequences for an object like  Car. Its distance (2.3kpc), foreground reddening (0
Car. Its distance (2.3kpc), foreground reddening (0
 50) and total luminosity (
50) and total luminosity (
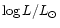 = 6.65, or
= 6.65, or
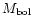 = -11.9) seem to be reliable as well. Nevertheless, its position if plotted in Fig. 20 is too far above the S Dor area, whatever temperature is used. Note that more than 90% of the luminosity is due to IR radiation. Thus, apart from the S Dor variable, more IR sources, or sources leading to heating of dust and gas complexes (such like explosive events in the past, accreting mass processes, etc.), might be present inside
= -11.9) seem to be reliable as well. Nevertheless, its position if plotted in Fig. 20 is too far above the S Dor area, whatever temperature is used. Note that more than 90% of the luminosity is due to IR radiation. Thus, apart from the S Dor variable, more IR sources, or sources leading to heating of dust and gas complexes (such like explosive events in the past, accreting mass processes, etc.), might be present inside  Car (van Genderen et al.
1994, 1995
Car (van Genderen et al.
1994, 1995![[*]](/icons/foot_motif.gif) , 1999, 2001).
Note that the radial velocity curve based on lines of the Paschen series is useless and that
according to Davidson et al. (2000) the binary hypothesis is weak, in contrast with the view of Damineli et al. (2000). The justification of serious doubt on the radial velocity curve of Damineli et al. (1997) is certainly not new: two years before the study of Davidson et al. (2000),
de Groot & Henderson (1998, quoted by van Genderen et al. 1999) already expressed their
serious concern. They found that the HeI 5875Å and 6678Å lines (presumably originating deeper in the wind) gave radial velocities completely different from those on which the excisting binary models were based.
The "spectroscopic events'', the X-ray observations and the spectroscopy suggest a colliding-wind binary (Damineli et al. 1997, 2000; Pittard 2000). Another indication that
, 1999, 2001).
Note that the radial velocity curve based on lines of the Paschen series is useless and that
according to Davidson et al. (2000) the binary hypothesis is weak, in contrast with the view of Damineli et al. (2000). The justification of serious doubt on the radial velocity curve of Damineli et al. (1997) is certainly not new: two years before the study of Davidson et al. (2000),
de Groot & Henderson (1998, quoted by van Genderen et al. 1999) already expressed their
serious concern. They found that the HeI 5875Å and 6678Å lines (presumably originating deeper in the wind) gave radial velocities completely different from those on which the excisting binary models were based.
The "spectroscopic events'', the X-ray observations and the spectroscopy suggest a colliding-wind binary (Damineli et al. 1997, 2000; Pittard 2000). Another indication that  Car hides a secret is based on the detection of peculiar light variations of non-stellar origin, sometimes only clearly present in the near-UV, sometimes also detectable in V and B and deviating from the normal SD-variability. Most striking are the periodicities in the near-UV, detected by our multi-photometric monitoring campaigns. They could point to the presence of a luminous accretion disk which can occur in semi-detached binaries (van Genderen et al. 1994, 1995, 1999, 2001). Calculations based on formulae derived from energy balance arguments (Bath 1979; Bath & Pringle 1985) show that variations in such a disk can be measurable. This would imply the presence of a semi-detached binary, but other scenarios without a semi-detached binary are not impossible as well (van Genderen et al. in prep.).
Our photometric analysis revealed that the nett rising trend of the brightness from the near-IR (see also Whitelock et al. 1994) to the near-UV between 1974 and 1992 is not due to a star's photosphere, but due to variations in the amount of circumstellar hot gas and dust (van Genderen et al. 1994). This is supported by a near-IR study of Smith & Gehrz (2000). They conclude that the near-IR variations are mainly due to morphological changes of the ejecta in the core and their variable illumination. In this respect it is of interest to mention that according to Viotti & Rossi (1999) the core is likely enshrouded by a
Car hides a secret is based on the detection of peculiar light variations of non-stellar origin, sometimes only clearly present in the near-UV, sometimes also detectable in V and B and deviating from the normal SD-variability. Most striking are the periodicities in the near-UV, detected by our multi-photometric monitoring campaigns. They could point to the presence of a luminous accretion disk which can occur in semi-detached binaries (van Genderen et al. 1994, 1995, 1999, 2001). Calculations based on formulae derived from energy balance arguments (Bath 1979; Bath & Pringle 1985) show that variations in such a disk can be measurable. This would imply the presence of a semi-detached binary, but other scenarios without a semi-detached binary are not impossible as well (van Genderen et al. in prep.).
Our photometric analysis revealed that the nett rising trend of the brightness from the near-IR (see also Whitelock et al. 1994) to the near-UV between 1974 and 1992 is not due to a star's photosphere, but due to variations in the amount of circumstellar hot gas and dust (van Genderen et al. 1994). This is supported by a near-IR study of Smith & Gehrz (2000). They conclude that the near-IR variations are mainly due to morphological changes of the ejecta in the core and their variable illumination. In this respect it is of interest to mention that according to Viotti & Rossi (1999) the core is likely enshrouded by a
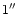 -
-
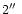 dense circumstellar cloud. They believe also that in the immediate surroundings of the core, dust is at present condensating from the stellar wind at a very high rate.
See for a bipolar nebula older than the Homunculus, Sect. 1.8.
Figure 21 summarizes the structure of the SD-area.
It shows the HD-limit, the triangle in which the s-a variables move to and fro during the SD-phases, the SD-minimum strip with its limits (thinly dashed lines) in which most of the S Dor variables reside, and the Yellow Void for yellow hypergiants.
The SD-area between the thinly dashed lines is 0.6 wide in
dense circumstellar cloud. They believe also that in the immediate surroundings of the core, dust is at present condensating from the stellar wind at a very high rate.
See for a bipolar nebula older than the Homunculus, Sect. 1.8.
Figure 21 summarizes the structure of the SD-area.
It shows the HD-limit, the triangle in which the s-a variables move to and fro during the SD-phases, the SD-minimum strip with its limits (thinly dashed lines) in which most of the S Dor variables reside, and the Yellow Void for yellow hypergiants.
The SD-area between the thinly dashed lines is 0.6 wide in
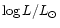 ,
or 1
,
or 1
 5 in
5 in
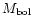 and confined to the right of the instability boundary of Stothers & Chin (1996) (vertical dotted line).
The close similarity between the slopes of the SD-area and the oblique part of the empirical HD-limit indicates that the SD-phenomenon is somehow related to the Eddington limit as expected (the locus where
and confined to the right of the instability boundary of Stothers & Chin (1996) (vertical dotted line).
The close similarity between the slopes of the SD-area and the oblique part of the empirical HD-limit indicates that the SD-phenomenon is somehow related to the Eddington limit as expected (the locus where
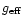 = 0, a situation favourable for instability and increasing mass loss, e.g. Lamers & Noordhoek 1993; de Koter 1993; Humphreys & Davidson 1994). The SD-upper limit slopes down more deeply to the red than the HD-limit.
Figure 21 also shows the atmospheric Eddington limits (AEL) for post-mainsequence stars (PMS) for constant Eddington factors
= 0, a situation favourable for instability and increasing mass loss, e.g. Lamers & Noordhoek 1993; de Koter 1993; Humphreys & Davidson 1994). The SD-upper limit slopes down more deeply to the red than the HD-limit.
Figure 21 also shows the atmospheric Eddington limits (AEL) for post-mainsequence stars (PMS) for constant Eddington factors 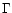 = 0.90 and 0.95 (Z = 0.02). Those for Z = 0.008 are not very different (Lamers 1997). Between and above these lines, the atmospheres are expected to become losely bound, thus, for
= 0.90 and 0.95 (Z = 0.02). Those for Z = 0.008 are not very different (Lamers 1997). Between and above these lines, the atmospheres are expected to become losely bound, thus, for
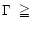 0.9. These lines fit the upper part of the SD-minimum strip very well (contrary to the lower part). Lamers (1997) speculated that the objects with low luminosity do not come directly from the MS, but should be post-RSG, as opposed to those belonging to the upper part. According to the chemical abundances of the ejecta, with the exception of that of P Cyg, all could be post-RSG (Sect. 1.7). The calculations of Stothers & Chin (1996) predict that most S Dor variables are in their second (thus hot/blue) SD-instability stage, thus, post-RSG, supporting many observational findings. Thus, the reason why the high luminous variables do fit the AEL for PMS stars, while they are possibly post-RSG, is not clear.
In Fig. 22, the relation between the observed maximum light amplitude
(
0.9. These lines fit the upper part of the SD-minimum strip very well (contrary to the lower part). Lamers (1997) speculated that the objects with low luminosity do not come directly from the MS, but should be post-RSG, as opposed to those belonging to the upper part. According to the chemical abundances of the ejecta, with the exception of that of P Cyg, all could be post-RSG (Sect. 1.7). The calculations of Stothers & Chin (1996) predict that most S Dor variables are in their second (thus hot/blue) SD-instability stage, thus, post-RSG, supporting many observational findings. Thus, the reason why the high luminous variables do fit the AEL for PMS stars, while they are possibly post-RSG, is not clear.
In Fig. 22, the relation between the observed maximum light amplitude
(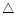
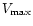 ), largely based on the schematic light curves presented here, see also Table 16 to be discussed in Sect. 3.5) and the luminosity at minimum apparent brightness (
), largely based on the schematic light curves presented here, see also Table 16 to be discussed in Sect. 3.5) and the luminosity at minimum apparent brightness (
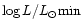 )
is investigated. Note that such a relation has already been investigated by Wolf (1989) and called the "amplitude-luminosity'' relation.
The figure shows 12 s-a- (dots), 3 w-a- (circles) and 1 ex-/dormant (square) S Dor variables. Since most of the observed light amplitudes are lower limits (unless the objects were observed for a century or so, in which case the amplitude can be considered as statistically reliable upper limits), the arrows point to the right. Objects with unreliable parameters have not been plotted.
The curve represents the maximum excursions in the s-a SD-triangle from the
SD-minimum strip to the boundary at
)
is investigated. Note that such a relation has already been investigated by Wolf (1989) and called the "amplitude-luminosity'' relation.
The figure shows 12 s-a- (dots), 3 w-a- (circles) and 1 ex-/dormant (square) S Dor variables. Since most of the observed light amplitudes are lower limits (unless the objects were observed for a century or so, in which case the amplitude can be considered as statistically reliable upper limits), the arrows point to the right. Objects with unreliable parameters have not been plotted.
The curve represents the maximum excursions in the s-a SD-triangle from the
SD-minimum strip to the boundary at
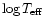 = 3.84 at constant luminosity.
Thus, from the maximum observed shift in temperature follows
= 3.84 at constant luminosity.
Thus, from the maximum observed shift in temperature follows  BC
BC
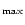 ,
which is therefore equal to
,
which is therefore equal to 
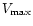 .
The higher the luminosity, the
larger the expected light amplitude (which agrees more or less with the observations),
since the radiation pressure is an important agent of the SD-instability.
.
The higher the luminosity, the
larger the expected light amplitude (which agrees more or less with the observations),
since the radiation pressure is an important agent of the SD-instability.
![\begin{figure}
\par\includegraphics[width=10.5cm,clip]{sdfig22.eps}\end{figure}](/articles/aa/full/2001/05/aads1896/Timg58.gif) |
Figure 22:
The maximum observed light amplitude as a function of the luminosity at minimum apparent brightness. The relation between maximum light amplitudes in the s-a SD-triangle for genuine horizontal displacements on the HR-diagram (thus, then 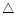
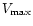 =
=
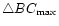 )
is represented by the curved line )
is represented by the curved line |
Most of the objects lie close to the curve. Part of the scatter must be caused by the fact that 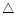
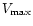 is not always equal to
is not always equal to  BC
BC
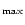 (thus, no precise horizontal displacement in the HR-diagram). Another part is due to errors in the physical parameters and the fact that the genuine maximum amplitude has not been observed.
Evidently, this maximum amplitude due to the sum of the two SD-phases (S-SD and L-SD phases) can amount to about 2
(thus, no precise horizontal displacement in the HR-diagram). Another part is due to errors in the physical parameters and the fact that the genuine maximum amplitude has not been observed.
Evidently, this maximum amplitude due to the sum of the two SD-phases (S-SD and L-SD phases) can amount to about 2
 5. Note that this is only slightly less than that for the SD-eruptions of
5. Note that this is only slightly less than that for the SD-eruptions of  Car and P Cyg!
Variables currently in or close to minimum state, especially the w-a and ex-/dormant variables, may be on the verge of ending their S Dor-life, or may have just ended it.
However, the probability that this is so, is low, as may be concluded from
the following discussion. This seems to indicate that their
relative quiescence is in most cases only temporary.
Table 16 lists the variables, ordered according to category, of which the probable apparent brightness before 1950 could be traced.
The header brightness/activity is divided into two columns: <1950 and 1950-2000, listing whether the objects were in a "high'' or "low'' state. The column "ampl'' lists the observed total light range of the SD-phases, which inevitably is in most cases a lower limit. The column "
Car and P Cyg!
Variables currently in or close to minimum state, especially the w-a and ex-/dormant variables, may be on the verge of ending their S Dor-life, or may have just ended it.
However, the probability that this is so, is low, as may be concluded from
the following discussion. This seems to indicate that their
relative quiescence is in most cases only temporary.
Table 16 lists the variables, ordered according to category, of which the probable apparent brightness before 1950 could be traced.
The header brightness/activity is divided into two columns: <1950 and 1950-2000, listing whether the objects were in a "high'' or "low'' state. The column "ampl'' lists the observed total light range of the SD-phases, which inevitably is in most cases a lower limit. The column "
 '' lists the probable limit of the duration between "high'' and "low'' brightness of the SD-activity, or vice versa. The column "
'' lists the probable limit of the duration between "high'' and "low'' brightness of the SD-activity, or vice versa. The column "
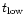 '' lists the duration of the "low'' state. The last column lists the reference numbers, or refers to a figure, or tables, in the present paper.
It appears that at least 8 objects: viz. 5 s-a-, 2 w-a- and 1 ex-/dormant objects (uncertain cases are bracketed and are not included in this statistic), were presumably "high'' before, in some cases long before, 1950. At least 4 objects: viz. 2 s-a-, 1 w-a- and 1 ex-/dormant objects were presumably "low'' before, or long before, 1950. Of two specimens of the latter group, R40 and R127, together with R110 ("low'' state before 1950 uncertain) we witnessed their developing SD-phases in the last few decades. This means that the precise durations of the "high'' and "low'' states before 1950 are unknown because of the lack of observations.
It appears that most of the time scales of the declines and rises (
'' lists the duration of the "low'' state. The last column lists the reference numbers, or refers to a figure, or tables, in the present paper.
It appears that at least 8 objects: viz. 5 s-a-, 2 w-a- and 1 ex-/dormant objects (uncertain cases are bracketed and are not included in this statistic), were presumably "high'' before, in some cases long before, 1950. At least 4 objects: viz. 2 s-a-, 1 w-a- and 1 ex-/dormant objects were presumably "low'' before, or long before, 1950. Of two specimens of the latter group, R40 and R127, together with R110 ("low'' state before 1950 uncertain) we witnessed their developing SD-phases in the last few decades. This means that the precise durations of the "high'' and "low'' states before 1950 are unknown because of the lack of observations.
It appears that most of the time scales of the declines and rises (
 )
lie
between 20 and 50yr. The durations of the observed non-active stages (
)
lie
between 20 and 50yr. The durations of the observed non-active stages (
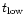 )
are of the same order.
)
are of the same order. 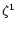 Sco has already been low for 100yr (Sterken et al. 1997a). For HD160529 the "high'' state (
Sco has already been low for 100yr (Sterken et al. 1997a). For HD160529 the "high'' state (
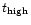 not listed in Table 16) already has lasted 110yr (Fig. 2). To this sample P Cyg can be added, which seems to have been hardly active for perhaps 300yr (however, a very low amplitude oscillation with a time scale of 8yr has been detected by
de Groot et al. 2001; this could be an S-SD cycle, see Table 6).
Most of the objects have not been monitored photometrically for longer than a few decades (since 1950), thus, it is quite thinkable that most of the current (1950-2000) "low'' or "nearly low'' states are only temporary. It is therefore impossible to say which of the ex-/dormant variables are really "ex'' and on their way to become a WN-type star.
If the numbers of variables are counted showing a low activity in the last two-three
decades, say with light amplitudes
not listed in Table 16) already has lasted 110yr (Fig. 2). To this sample P Cyg can be added, which seems to have been hardly active for perhaps 300yr (however, a very low amplitude oscillation with a time scale of 8yr has been detected by
de Groot et al. 2001; this could be an S-SD cycle, see Table 6).
Most of the objects have not been monitored photometrically for longer than a few decades (since 1950), thus, it is quite thinkable that most of the current (1950-2000) "low'' or "nearly low'' states are only temporary. It is therefore impossible to say which of the ex-/dormant variables are really "ex'' and on their way to become a WN-type star.
If the numbers of variables are counted showing a low activity in the last two-three
decades, say with light amplitudes
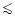 0
0
 2, (thus, difficult to discover), one finds about 24 (5 s-a-, 10 w-a-, 8 ex-/dormant and 1 positive candidate, viz. HD80077). The total number of variables amount to 35 (excluding the other 7 positive candidates, because there is no information on any light variation: most of them are still shrouded by dense circumstellar material).
On the other hand, there are only a few which turned out to have been highly, or moderately active for 110yr or more, viz. AG Car (van Genderen et al. 1997a), HR Car (but with a long lasting inactive interval, van Genderen et al. 1997b) and HD160529 (see above), while S Dor (not listed in Table 16) has been active for at least 165yr (to be more precise since at least
2, (thus, difficult to discover), one finds about 24 (5 s-a-, 10 w-a-, 8 ex-/dormant and 1 positive candidate, viz. HD80077). The total number of variables amount to 35 (excluding the other 7 positive candidates, because there is no information on any light variation: most of them are still shrouded by dense circumstellar material).
On the other hand, there are only a few which turned out to have been highly, or moderately active for 110yr or more, viz. AG Car (van Genderen et al. 1997a), HR Car (but with a long lasting inactive interval, van Genderen et al. 1997b) and HD160529 (see above), while S Dor (not listed in Table 16) has been active for at least 165yr (to be more precise since at least  1834, see Thackeray 1974; van Genderen et al. 1997a). Some of the S Dor variables in M 31 and M 33 also show an activity lasting at least 100yr (AF And in M 31, Var.A in M 33), others are only active at intervals of 20yr (e.g. Var.C in M 33) in between periods of quiescence lasting a few decades (Hubble & Sandage 1953; Sharov 1975, 1990; Rosino & Bianchini 1973; Humphreys et al. 1988).
Consequently, the numbers and examples above suggest that S Dor variables are for most
of their lifetime (
1834, see Thackeray 1974; van Genderen et al. 1997a). Some of the S Dor variables in M 31 and M 33 also show an activity lasting at least 100yr (AF And in M 31, Var.A in M 33), others are only active at intervals of 20yr (e.g. Var.C in M 33) in between periods of quiescence lasting a few decades (Hubble & Sandage 1953; Sharov 1975, 1990; Rosino & Bianchini 1973; Humphreys et al. 1988).
Consequently, the numbers and examples above suggest that S Dor variables are for most
of their lifetime ( 70%) close to (= w-a),
or in a minimum (= dormant) state. Long-lasting active stages
(thus, with frequent SD-phases) are rare. Whether S Dor variables can be very active for most of their lifetime is unknown, but obviously such objects are rare too.
If the numbers of the three categories (s-a, w-a and ex-/dormant) are complete for the volume of the galactic disc around the Sun (maximum radii 6kpc for the s-a- and 2.5kpc for the other two groups, excluding He3-519 with a possible distance of 8kpc, see Table 9), then the total numbers in the galactic disk can be estimated.
Table 17 summarizes the results. For the determination of the multiplication factors ("mult.f.'') the radius of the galactic disk has been taken to be 12kpc with a negligible thickness. There should then be about 200 S Dor variables. If the number for the LMC is complete, which is not certain at all, there are 10 times more S Dor variables in the Galaxy than in the LMC. However, considering that the mass ratio between galactic disk and the LMC is presumably of the same order (80 and
70%) close to (= w-a),
or in a minimum (= dormant) state. Long-lasting active stages
(thus, with frequent SD-phases) are rare. Whether S Dor variables can be very active for most of their lifetime is unknown, but obviously such objects are rare too.
If the numbers of the three categories (s-a, w-a and ex-/dormant) are complete for the volume of the galactic disc around the Sun (maximum radii 6kpc for the s-a- and 2.5kpc for the other two groups, excluding He3-519 with a possible distance of 8kpc, see Table 9), then the total numbers in the galactic disk can be estimated.
Table 17 summarizes the results. For the determination of the multiplication factors ("mult.f.'') the radius of the galactic disk has been taken to be 12kpc with a negligible thickness. There should then be about 200 S Dor variables. If the number for the LMC is complete, which is not certain at all, there are 10 times more S Dor variables in the Galaxy than in the LMC. However, considering that the mass ratio between galactic disk and the LMC is presumably of the same order (80 and
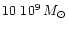 ,
respectively), there is not much difference in their frequency.
Assuming that the incompleteness is the same for both Magellanic Clouds, the ratio found for the numbers of S Dor variables as well as for the masses of the two stellar systems one finds LMC/SMC
,
respectively), there is not much difference in their frequency.
Assuming that the incompleteness is the same for both Magellanic Clouds, the ratio found for the numbers of S Dor variables as well as for the masses of the two stellar systems one finds LMC/SMC  6 (the mass for the SMC amounts to
6 (the mass for the SMC amounts to
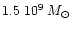 ).
Due to the low number of variables in the SMC, this result is not very reliable.
It was my intention to give a concise overview of the current knowledge on S Dor variables up to the beginning of the 21st century, complemented with an inventory of all confirmed and suspected members and members in quiescence. I also felt the need to put much emphasis on the photometric achievements of the various types of instabilities, because usually not enough light is shed thereon and besides a number of misunderstandings, continuously wandering through literature, needed clarification and correction.
S Dor variables exhibit a number of instabilities which, together with their precise evolutionary
state, are highly of interest, but badly understood. None are strictly periodic like Cepheids and
the like. The instabilities comprise:
).
Due to the low number of variables in the SMC, this result is not very reliable.
It was my intention to give a concise overview of the current knowledge on S Dor variables up to the beginning of the 21st century, complemented with an inventory of all confirmed and suspected members and members in quiescence. I also felt the need to put much emphasis on the photometric achievements of the various types of instabilities, because usually not enough light is shed thereon and besides a number of misunderstandings, continuously wandering through literature, needed clarification and correction.
S Dor variables exhibit a number of instabilities which, together with their precise evolutionary
state, are highly of interest, but badly understood. None are strictly periodic like Cepheids and
the like. The instabilities comprise:
1. the rare SD-eruptions (Sect. 1.4). Is stochastic resonance a cause, as tentatively suggested by
Sterken et al. (1997a), possibly in connection with the dynamical ionization-induced
dynamical instability discovered by Stothers & Chin (1996)?
2. the frequent SD-phases (Sect. 1.5) consisting of two types with different time scales
(t < 10yr and
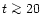 yr, the short (S)-SD- and long (L)-SD phases, respectively)
which are often superimposed on each other
(Sect. 1.5.1). Is there any connection between these two and the SD-eruptions? Where and how do
they originate and how should the multi-periodic character of the SD-phases of e.g. AG Car be
explained
(Sects. 1.5.2 and 1.5.3)? Presumably, the SD-phases, the "secular cycles'' according to Stothers
& Chin (1995, see Sect. 1.5.1 of the present paper) originate deeper in the
stellar interior than the microvariations, otherwise the latters should not remain so imperturbably
present on the ongoing SD-phases;
yr, the short (S)-SD- and long (L)-SD phases, respectively)
which are often superimposed on each other
(Sect. 1.5.1). Is there any connection between these two and the SD-eruptions? Where and how do
they originate and how should the multi-periodic character of the SD-phases of e.g. AG Car be
explained
(Sects. 1.5.2 and 1.5.3)? Presumably, the SD-phases, the "secular cycles'' according to Stothers
& Chin (1995, see Sect. 1.5.1 of the present paper) originate deeper in the
stellar interior than the microvariations, otherwise the latters should not remain so imperturbably
present on the ongoing SD-phases;
3. the two types of microvariations
(Sect. 1.6) with different timescales (weeks: near minimum light, and about 100d:
near maximum light). Within a certain temperature interval (20000-10000K)
they can be seen superimposed on each other. This suggests that they originate in different
layers. Subsequently, e.g. when the SD-phase is on its way to maximum light, the short one quickly disappears (within a few months or
shorter), the longer one continues. This must be due to changing physical conditions of the outer layers by the expansion.
Thus, it appears that S Dor variables form a well-equipped laboratory for a number of photospheric and atmospheric pulsations and instabilities, but theoretically they are still badly understood. To cite Stothers (2000, priv. comm.): "A great difficulty right now seems to be the problem of correlating what the stellar models predict with what the observations show. This will continue to be a problem until theoretical models can be produced that are more sophisticated''. Therefore, the modeling should continue, with the emphasis on the explanation for the photometric phenomena and to answer the question: will all 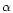 Cyg variables pass through a blue S Dor-stage?
Topics as well are the origin, the chemical and dynamical characteristics of their circumstellar ejecta which are usually much better understood. It appears that the chemistry and the dynamics of the ejecta are important for the interpretation of the evolutionary stage of S Dor variables: in most cases they point to a post-RSG stage, even for the most luminous variables.
The inventory is complemented with physical and photometric parameters (made as homogeneous as possible) and other characteristics for all members and suspected members, collected from literature. Attention was given to errors in temperature and luminosity, of crucial importance for the interpretation of their position on the theoretical HR-diagram.
The inventory contains 46 SDor variables among which 12 candidates
and additionally it contains 3 rejected candidates. It is
differentiated into four categories according to the size of
the maximum light amplitude of the SD-phases exhibited in the 20th century.
It appears that the strong-active S Dor variables obey the relation, called the SD-minimum strip:
Cyg variables pass through a blue S Dor-stage?
Topics as well are the origin, the chemical and dynamical characteristics of their circumstellar ejecta which are usually much better understood. It appears that the chemistry and the dynamics of the ejecta are important for the interpretation of the evolutionary stage of S Dor variables: in most cases they point to a post-RSG stage, even for the most luminous variables.
The inventory is complemented with physical and photometric parameters (made as homogeneous as possible) and other characteristics for all members and suspected members, collected from literature. Attention was given to errors in temperature and luminosity, of crucial importance for the interpretation of their position on the theoretical HR-diagram.
The inventory contains 46 SDor variables among which 12 candidates
and additionally it contains 3 rejected candidates. It is
differentiated into four categories according to the size of
the maximum light amplitude of the SD-phases exhibited in the 20th century.
It appears that the strong-active S Dor variables obey the relation, called the SD-minimum strip:
The other categories obey the same relation, but with more scatter which is twice as large on the blue side than on the red side. This could point to evolutionary effects, or high rotation velocities. The occasional specimens even show a substantial and significant deviation from the narrow S Dor area (R4 in the SMC, R149 and HDE326823 in the LMC).
Thus, according to the observations, the S Dor stage occupies only a small portion of the blue part of the evolutionary tracks of massive stars.
In Sect. 3.2.5 a short discussion is given of the possible evolutionary connection between S Dor variables and the variable yellow hypergiants. These may be proto-low-luminous S Dor variables.
In Sect. 3.2.6 the present status of  Car is discussed (see also Sect. 1.8). It has been confirmed that the reliability of the radial velocity curve on which the existing binary models were based, is highly questionable.
It would be a misunderstanding to believe that all S Dor variables are, or should be, spectacular during most of their lifetime. The majority appears to be low-amplitude (< 0
Car is discussed (see also Sect. 1.8). It has been confirmed that the reliability of the radial velocity curve on which the existing binary models were based, is highly questionable.
It would be a misunderstanding to believe that all S Dor variables are, or should be, spectacular during most of their lifetime. The majority appears to be low-amplitude (< 0
 5) variables, or are close to the minimum state. It is estimated that for more than 70
5) variables, or are close to the minimum state. It is estimated that for more than 70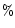 of their lifetime as a hot S Dor variable, they are not spectacular at all. It was the happy few, like
of their lifetime as a hot S Dor variable, they are not spectacular at all. It was the happy few, like  Car, P Cyg, S Dor, AG Car, etc., which gave the S Dor variables their famous reputation.
The estimated total number of S Dor variables in the Galaxy amounts to
Car, P Cyg, S Dor, AG Car, etc., which gave the S Dor variables their famous reputation.
The estimated total number of S Dor variables in the Galaxy amounts to  200.
It seems that the frequency of S Dor variables in the Galaxy, the LMC and the SMC is more or less equal, although the frequency in the SMC is based on low-number statistic.
All reseachers interested in these variables should look eagerly forwards to surprises which the unpredictable S Dor variables have instore for us in the 21st century.
200.
It seems that the frequency of S Dor variables in the Galaxy, the LMC and the SMC is more or less equal, although the frequency in the SMC is based on low-number statistic.
All reseachers interested in these variables should look eagerly forwards to surprises which the unpredictable S Dor variables have instore for us in the 21st century.
Note added in proof:
It is quite well possible that P Cyg is yet slightly instable in view of the possible very
low-amplitude SD-phase with a time scale of about 8y (Table 6). Very recent research by
Markova and collaborators has demonstrated that for this variation a correlation excists
between brightness, temperature and radius, similar to those of other S Dor variables during
SD-phases. Further, it appeared that the massloss rate increased with increasing radius
(like R71 and S Dor) (Markova, N. 2000, ASP Conf. Ser., 204, 117; Markova, N. 2001,
ASP Conf. Ser. on P Cyg, Armagh, in press;
Markova, N.,
Morrison, N., Kolka, I., & de Groot, M.
2001,
in press; Markova, N.,
Scuderi, S., de Groot, M., & Panagia, N. 2001,
A&A, in prep.).
This 8y variation and a 500d variation are possibly cyclic, at least spectroscopically
(Markova, N.,
Morrison, N., Kolka, I., & de Groot, M.
2001, in prep.).
Further, it appeared that the 100d microvariation of P Cyg
(Table 6) has a counterpart in
the wind variability
(Markova, N., 2000, A&AS, 144, 391;
Markova, N.,
Scuderi, S., de Groot, M., & Panagia, N.
2001, in prep).
The inner nebula within a few arcsec from HR Car (see Table 1) has been studied by Hulbert,
S., Nota, A., Clampin, M., et al. 1999, IAU Coll., 169, 103,
and White, S. M. 2000, ApJ, 539,
851.
R143 (see Table 1) appears to have a
clump of material which is definitely ejected by an
SD-eruption according to Smith, L. J., Nota, A., Pasquali, A., et al. 1998, ApJ, 503, 278.
A dust model for the ejected nebula of G79.29+0.46 (see Table 11) has been presented by
Trams, N. R., van Tuyll, C. I., Voors, R. H. M., et al. 1999, IAU Coll.,
169, 71, and more proof of
its membership as an S Dor variable has been offered by
Voors, R. H. M., Geballe, T. R., Waters,
L. B. F. M., et al. 2000, A&A, 326, 236.
Both references suggest for the central star
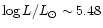 and
and
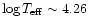 ,
thus, different from the values
listed in Table 11.
,
thus, different from the values
listed in Table 11.
A bipolar shell has been discovered recently around G25.5+0.2 (see Table 11)
by Clark, J. S.,
Steele, I. A., & Langer, N. 2000, ApJ, 541, L67.
Acknowledgements
I am much indebted to the following colleagues for their invaluable remarks and comments: Drs. R. B. Stothers, C. de Jager, C. Sterken, I. Salamanca and B. Wolf. I am also very grateful to Dr. J. K. Katgert-Merkelijn for improving the language.
-
Allen, D. A., & Glass, I. 1976, ApJ, 210, 666
In the text
NASA ADS
-
Allen, D. A., & Hillier, D. J. 1993, Proc. Astron. Soc. Aust., 10, 338
In the text
NASA ADS
-
Appenzeller, I., & Wolf, B. 1979, A&AS, 38, 51
In the text
NASA ADS
-
Appenzeller, I., Wolf, B., & Stahl, O. 1987, in Instabilities in Luminous Early Type
Stars, ed. H. J. G. L. M. Lamers, & C. W. H. de Loore (Reidel), 241
In the text
-
Ardeberg, A., Brunet, J. P., Maurice, E., & Prévot, L. 1972, A&AS, 6, 249
In the text
NASA ADS
-
Azzopardi, M., & Vigneau, J. 1975, A&AS, 22, 285
In the text
NASA ADS
-
Barba, R. H., Niemela, V. S., Baume, G., & Vasquez, R. A. 1995, ApJ, 446, L23
In the text
NASA ADS
-
Barba, R. H., Niemela, V. S., & Morel, N. 1997, ASP Conf. Ser., 120, 238, ed. A. Nota,
& H. J. G. L. M Lamers
In the text
-
Barlow, M. J., Drew, J. E., Meaburn, J., & Massey, R. M. 1994, MNRAS, 268, L29
In the text
NASA ADS
-
Bateson, F. M., & Jones, A. F. 1994, Publ. Var. Star Sect. RASNZ, 19
In the text
-
Bath, G. T. 1979, Nature, 282, 274
In the text
NASA ADS
-
Bath, G. T., & Pringle, J. E. 1985, in Interacting Binary Stars, ed. J. E. Pringle, & R. A. Wade
(Cambridge Univ. Press), 177
In the text
-
Bieging, J. H., Abbott, D. C., & Churchwell, E. B. 1989, ApJ, 340, 518
In the text
NASA ADS
-
Blöcker, T., Balega, Y., Hofmann, K. H., et al. 1999, A&A, 348, 805
In the text
NASA ADS
-
Bohannan, B. 1997, ASP Conf. Ser., 120, 3, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Bohannan, B., & Walborn, N. R. 1989, PASP, 101, 520
In the text
NASA ADS
-
Bohigas, J., Tapia, M., Ruiz, M. T., & Roth, M. 2000, MNRAS, 312, 295
In the text
NASA ADS
-
Breysacher, J. 1997, ASP Conf. Ser., 120, 227, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Breysacher, J., & Perrier, C. 1991, IAU Coll., 143, 229, ed. K. A. van der Hucht, & B. Hidayat
In the text
-
Brunet, J. P. 1975, A&A, 43, 345
In the text
NASA ADS
-
Burgarella, D., & Paresce, F. 1991, A&A, 241, 595
In the text
NASA ADS
-
Burki, G., Heck, A., Bianchi, L., & Cassatella, A. 1982, A&A, 107, 205
In the text
NASA ADS
-
Carpay, J., de Jager, C., Nieuwenhuijzen, H., & Moffat, A. F. J. 1989, A&A, 216, 143
In the text
NASA ADS
-
Carpay, J., de Jager, C., & Nieuwenhuijzen, H. 1991, A&A, 248, 475
In the text
NASA ADS
-
Cassinelli, J. P. 1999, ASP Conf. Ser., 179, 258, ed. J. A. Morse, R. M. Humphreys, & A. Damineli
In the text
-
Catchpole, R. M., Whitelock, P. A., & Glass, I. 1990, MNRAS, 247, 479
In the text
NASA ADS
-
Chentsov, E. L., & Luud, L. 1990, Astrophys., 31, 415
In the text
NASA ADS
-
Chini, R., Elsasser, H., & Neckel, Th. 1980, A&A, 91, 186
In the text
NASA ADS
-
Clampin, M., Schulte-Ladbeck, R. E., Nota, A., et al. 1995, AJ, 110, 251
In the text
NASA ADS
-
Clayton, G. C., & Martin, P. G. 1985, ApJ, 288, 558
In the text
NASA ADS
-
Code, A. D., & Houck, T. E. 1958, PASP, 70, 261
In the text
NASA ADS
-
Conti, P. S., Garmany, C. D., & Massey, P. 1986, AJ, 92, 48
In the text
NASA ADS
-
Corcoran, M. F., Swank, J. H., Petre, R., et al. 1999, ASP Conf. Ser., 179, 46, ed. J. A. Morse, R. M.
Humphreys, & A. Damineli
In the text
-
Cotera, A. S., Erickson, E. F., Colgan, S. W. J., et al. 1996, ApJ, 461, 750
In the text
NASA ADS
-
Cox, A. N., Guzik, J. A., & Soukup, M. S. 1995, ASP Conf. Ser., 83, 192, ed. R. S. Stobie, & P. A. Whitelock
In the text
-
Cox, A. N., Guzik, J. A., & Soukup, M. S. 1997, ASP Conf. Ser., 120, 133, ed. A. Nota, & H. J. G. L. M.
Lamers
In the text
-
Cox, P., Mezger, P. G., Sievers, A., et al. 1995, A&A, 297, 168
In the text
NASA ADS
-
Crowther, P. A., Hillier, D. J., & Smith, L. J. 1995, A&A, 293, 172
In the text
NASA ADS
-
Crowther, P. A., & Smith, L. J. 1997, A&A, 320, 500
In the text
NASA ADS
-
Damineli, A. 1996, ApJ, 460, L49
In the text
NASA ADS
-
Damineli, A., Conti, P. S., & Lopes, D. F. 1997, New Astron., 2, 107
In the text
NASA ADS
-
Damineli, A., Kaufer, A., Wolf, B., et al. 2000, ApJ, 528, L101
In the text
NASA ADS
-
Davidson, K. 1987, ApJ, 317, 760
In the text
NASA ADS
-
Davidson, K. 1989, IAU Coll., 113, ed. K. Davidson, A. F. J. Moffat, & H. J. G. L. M. Lamers
-
Davidson, K., & Humphreys, R. M. 1997, ARA&A, 35, 1
In the text
NASA ADS
-
Davidson, K., Ebbets, D., Johansson, S., et al. 1997, AJ, 113, 335
NASA ADS
-
Davidson, K., Humphreys, R. M., Hajian, A., & Terzian, Y. 1993, ApJ, 411, 336
In the text
NASA ADS
-
Davidson, K., Gull, T. R., Humphreys, R. M., et al. 1999, AJ, 118, 1777
In the text
NASA ADS
-
Davidson, K., Ishibashi, K., Gull, T. R., et al. 2000, ApJ, 530, L107
In the text
NASA ADS
-
Dong, Y. S., & Hu, J. Y. 1991, Chin A&A, 15, 275
In the text
-
Dufour, R. J., & Duval, J. E. 1975, PASP, 87, 769
In the text
NASA ADS
-
Duncan, R. A., White, S. M., Reynolds, J. E., & Lim, J. 1999, ASP Conf. Ser., 179, 54,
ed. J. A. Morse, R. M. Humphreys, & A. Damineli
In the text
-
Duschl, W. J., Hofmann, K. H., Rigaut, F., & Weigelt, G., 1995, Rev. Mex. AA SDc, 2, 41
In the text
-
Dwarkadas, V. V., & Balick, B. 1998, AJ, 116, 829
NASA ADS
-
Ebbets, D., Morse, J., Davidson, K., & Walborn, N. R. 1997, ApJ, 489, L161
In the text
NASA ADS
-
Feast, M. W., Thackeray, A. D., & Wesselink, A. J. 1960, MNRAS, 121, 337
In the text
NASA ADS
-
Figer, D. F., Najarro, F., Morris, M., et al. 1998, ApJ, 506, 384
In the text
NASA ADS
-
Friedjung, M., & Muratorio, G. 1980, A&A, 85, 233
In the text
NASA ADS
-
Gäng, T. 2000, Thesis Univ. of Heidelberg
In the text
-
Garcia-Lario, P., Riera, A., & Manchado, A. 1998, A&A, 334, 1007
In the text
NASA ADS
-
Garcia-Segura, G., Mac Low, M. M., & Langer, N. 1996a, A&A, 305, 229
In the text
NASA ADS
-
Garcia-Segura, G., Langer, N., & Mac Low, M. M. 1996b, A&A, 316, 133
In the text
NASA ADS
-
Gautschy, A., & Saio, H. 1995, ARA&A, 33, 75
In the text
NASA ADS
-
Gautschy, A., & Saio, H. 1996, ARA&A, 34, 551
In the text
NASA ADS
-
van Genderen, A. M. 1970, A&A, 7, 49
NASA ADS
-
van Genderen, A. M. 1979a, A&AS, 38, 249
-
van Genderen, A. M. 1979b, A&AS, 38, 381
NASA ADS
-
van Genderen, A. M. 1989, A&A, 208, 135
NASA ADS
-
van Genderen, A. M. 1991a, in ESO Workshop on Rapid Variability of OB Stars: Nature and Diagnostic Value,
ed. D. Baade, 117
-
van Genderen, A. M. 1991b, IAU Symp., 143, 563, ed. K. A. van der Hucht, & B. Hidayat
-
van Genderen, A. M. 2000, J. Astron. Data, 4
-
van Genderen, A. M., & Sterken, C. 1996, A&A, 308, 763
NASA ADS
-
van Genderen, A. M., & Sterken, C. 1999, A&A, 349, 537
NASA ADS
-
van Genderen, A. M., & Sterken, C. 2001, in preparation
-
van Genderen, A. M., & Thé, P. S. 1984, Sp. Sc. Rev., 39, 317
NASA ADS
-
van Genderen, A. M., van Leeuwen, F., & Brand, J. 1982, A&AS, 47, 591
NASA ADS
-
van Genderen, A. M., Groot, M., & Thé, P. S., 1983, A&A, 117, 53
NASA ADS
-
van Genderen, A. M., Bijleveld, W., & van Groningen, E. 1984, A&AS, 58, 537
NASA ADS
-
van Genderen, A. M., Steemers, W. J. G., Feldbrugge, P. T. M., et al. 1985, A&A, 153, 163
NASA ADS
-
van Genderen, A. M., Thé, P. S., Augusteijn, Th., et al. 1988, A&AS, 74, 453
NASA ADS
-
van Genderen, A. M., Bovenschen, H., Engelsman, E. C., et al. 1989, A&AS, 79, 263
NASA ADS
-
van Genderen, A. M., Thé, P. S., Heemskerk, M., et al. 1990, A&AS, 82, 189
NASA ADS
-
van Genderen, A. M., Robijn, F. H. A., van Esch, B. P. M., & Lamers, H. J. G. L. M. 1991, A&A, 246, 407
NASA ADS
-
van Genderen, A. M., Thé, P. S., de Winter, D., et al. 1992a, A&A, 258, 316
NASA ADS
-
van Genderen, A. M., van den Bosch, F. C., Dessing, F., et al. 1992b, A&A, 264, 88
NASA ADS
-
van Genderen, A. M., de Groot, M., & Thé, P. S. 1994, A&A, 283, 89
NASA ADS
-
van Genderen, A. M., Sterken, C., de Groot, M., et al. 1995, A&A, 304, 415
NASA ADS
-
van Genderen, A. M., Sterken, C., & de Groot, M. 1997a, A&A, 318, 81
NASA ADS
-
van Genderen, A. M., de Groot, M., & Sterken, C. 1997b, A&AS, 124, 517
NASA ADS
-
van Genderen, A. M., Sterken, C., de Groot, M., & Reijns, R. A. 1998a, A&A, 332, 857
NASA ADS
-
van Genderen, A. M., Sterken, C., & de Groot, M. 1998b, A&A, 337, 393
NASA ADS
-
van Genderen, A. M., Sterken, C., de Groot, M., & Burki, G. 1999, A&A, 343, 847
NASA ADS
-
van Genderen, A. M., de Groot, M., & Sterken, C. 2001, ASP Conf. Ser., in press
-
van Gent, R. H., & Lamers, H. J. G. L. M. 1986, A&A, 158, 335
NASA ADS
-
Glatzel, W. 1997, ASP Conf. Ser., 120, 128, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Glatzel, W., & Kiriakidis, M. 1993, MNRAS, 263, 375
In the text
NASA ADS
-
Glover, T. W., Dufour, R. J., Hester, J. J., et al. 1997, ASP Conf. Ser., 120, 296,
ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Gottlieb, E. W., & Liller, Wm. 1978, ApJ, 225, 488
In the text
NASA ADS
-
de Groot, M. 1969, BAN, 20, 225
NASA ADS
-
de Groot, M., & Lamers, H. J. G. L. M. 1992, Nature, 355, 422
NASA ADS
-
de Groot, M., van Genderen, A. M., & Sterken, C. 1996, Irish Astron. J., 23, 187
NASA ADS
-
de Groot, M., van Genderen, A. M., & Sterken, C. 1997a, Astron. Astrophys. Trans., 14, 35
-
de Groot, M., van Genderen, A. M., & Sterken, C. 1997b, AAVSO Conf. Proc. (May 1997, Switserland)
-
de Groot, M., Sterken, C., & van Genderen, A. M. 2001, in preparation
-
Guzik, J. A., Cox, A. N., Despain, K. M., & Soukup, M. S. 1997, ASP Conf. Ser., 120, 138,
ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Guzik, J. A., Cox., A. N., Despain, K. M., & Soukup, M. S. 1999, IAU Coll., 169, 337,
ed. B. Wolf, O. Stahl, & A. W. Fullerton
In the text
-
Hamann, F., De Poy, D. L., Johansson, S., & Elias, J. 1994, ApJ, 422, 626
In the text
NASA ADS
-
Henize, K. G. 1952, ApJ, 115, 133
In the text
NASA ADS
-
Henize, K. G. 1976, ApJS, 30, 491
In the text
NASA ADS
-
Heydari-Malayeri, M., Rauw, G., Esslinger, O., & Beuzit, J. L. 1997a, A&A, 322, 554
In the text
NASA ADS
-
Heydari-Malayeri, M., Courbin, F., Rauw, G., et al. 1997b, A&A, 326, 143
In the text
NASA ADS
-
Higgs, L. A., Wendker, H. J., & Landecker, T. L. 1994, A&A, 291, 295
In the text
NASA ADS
-
Hillier, D. J., & Allen, D. A. 1992, A&A, 262, 153
In the text
NASA ADS
-
Hillier, D. J., Crowther, P. A., Najarro, F., & Fullerton, A. W. 1998, A&A, 340, 483
In the text
NASA ADS
-
Hiltner, W. A. 1954, ApJ, 120, 41
In the text
NASA ADS
-
Hiltner, W. A. 1956, ApJS, 2, 389
In the text
NASA ADS
-
Hoekzema, N., Lamers, H. J. G. L. M., & van Genderen, A. M. 1992, A&A, 257, 118
In the text
NASA ADS
-
Hoekzema, N., Lamers, H. J. G. L. M., & van Genderen, A. M. 1993, A&AS, 98, 505
In the text
NASA ADS
-
Hoffleit, D. 1933, Harv. Bull., 892, 19
-
Hoffleit, D. 1940, Harv. Bull., 913, 4
-
Hu, J. Y., de Winter, D., Thé P. S., & Pérez, M. R. 1990, A&A, 227, L17
In the text
NASA ADS
-
Hubble, E., & Sandage, A. 1953, ApJ, 118, 353
In the text
NASA ADS
-
Humphreys, R. M. 1978, ApJS, 38, 309
In the text
NASA ADS
-
Humphreys, R. M. 1999, IAU Coll., 169, 243, ed. B. Wolf, O. Stahl, & A. W. Fullerton
In the text
-
Humphreys, R. M., & Davidson, K. 1994, PASP, 106, 1025
In the text
NASA ADS
-
Humphreys, R. M., Davidson, K., & Smith, N. 2000, PASP, 111, 1124
In the text
-
Humphreys, R. M., Lamers, H. J. G. L. M., Hoekzema, N., & Cassatella, A. 1989, A&A, 218, L17
In the text
NASA ADS
-
Humphreys, R. M., Leitherer, C., Stahl, O., et al. 1988, A&A, 203, 306
In the text
NASA ADS
-
Hutsemékers, D. 1997, ASP Conf. Ser., 120, 316, ed. A. Nota, & H. J. G. L. M. Lamers
-
Hutsemékers, D., & van Drom, E. 1991, A&A, 248, 141
NASA ADS
-
Hutsemékers, D., van Drom, E., Gosset, E., & Melnick, J. 1994, A&A, 290, 900
-
Iben Jr., I. 1999, ASP Conf. Ser., 179, 367, ed. J. A. Morse, R. M. Humphreys, & A.
Damineli
In the text
-
Icke, V. 1981, ApJ, 247, 152
In the text
NASA ADS
-
Innes, R. T. A. 1903, Cape Ann., 9, 75B
In the text
-
Israelian, G., & de Groot, M. 1999, Sp. Sc. Rev., 90, 493
In the text
NASA ADS
-
Isserstedt, J. 1975, A&AS, 19, 259
In the text
NASA ADS
-
de Jager, C. 1998, A&A Rev., 8, 145
-
de Jager, C., & van Genderen, A. M. 1989, IAU Coll., 113, 127, ed. K. Davidson, H. J. G. L. M. Lamers, &
A. F. J. Moffat
-
de Jager, C., & Nieuwenhuijzen, H. 1987, A&A, 177, 217
NASA ADS
-
Jones, A., & Sterken, C. 1997, J. Astron. Data, 3, 1
In the text
-
Jones, C. A., Chetin, T., & Liller, W. 1974, ApJ, 190, L1
In the text
NASA ADS
-
Jones, T. J., Humphreys, R. M., Gehrz, R. D., et al. 1993, ApJ, 411, 323
In the text
NASA ADS
-
Kaper, L., Lamers, H. J. G. L. M., Raymakers, E., et al. 1995, A&A, 300, 446
In the text
NASA ADS
-
Kaplan, S. A., &
Pikelner, S. B. 1970, The Interstellar Medium, Cambridge, Harvard Univ.
Press, 50
In the text
-
Kastner, J. H., & Weintraub, D. A. 1995, ApJ, 452, 833
In the text
NASA ADS
-
Kiriakidis, M., Chernigovski, S., Fricke, K. J., &
Glatzel, W. 1997, ASP Conf. Ser., 120,
150, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Kiriakidis, M., Fricke, K. J., & Glatzel, W. 1993, MNRAS, 264, 50
In the text
NASA ADS
-
Klochkova, V. G., Chentsov, E. L., & Panchuk, V. E. 1997, MNRAS, 292, 19
In the text
NASA ADS
-
Knoechel, G., & Moffat, A. F. J. 1982, A&A, 110, 263
In the text
NASA ADS
-
Koenigsberger, G., Auer, L. H., Georgiev, L., & Guinan, E. 1998a, ApJ, 496, 934
In the text
NASA ADS
-
Koenigsberger, G., Pena, M., & Schmutz, W. 1998b, ApJ, 499, 889
In the text
NASA ADS
-
Kolka, I. 1983, Esti NSV Tead. Akad. Toim. Fuus. Matem., 32, 51
In the text
-
Kolka, I. 1999, IAU Coll., 169, 268, ed. B. Wolf, O. Stahl, & A. W. Fullerton
In the text
-
de Koter, A. 1993, Thesis Univ. Utrecht
In the text
-
de Koter, A., Scholten, G. G. J., & Lamers, H. J. G. L. M. 1993a, Chap. 5 in Thesis de Koter (1993)
In the text
-
de Koter, A., & Lamers, H. J. G. L. M. 1993b, Chap. 7 in Thesis de Koter (1993)
In the text
-
de Koter, A., Lamers, H. J. G. L. M., & Schmutz, W. 1996, A&A, 306, 501
In the text
NASA ADS
-
Kozak, J. R. 1985, A&AS, 62, 7
In the text
NASA ADS
-
Kukarkin, B. V., Kholopov, P. N., & Efremov, Yu. N. 1974, Sec. Suppl. Third Edition Gen. Cat. Var.
Stars, Nauka, Moscow, 10
In the text
-
Lamers, H. J. G. L. M. 1987, in Instabilities in Luminous Early-Type Stars, ed. H. J. G. L. M. Lamers, &
C. W. H. de Loore (Reidel), 99
In the text
-
Lamers, H. J. G. L. M. 1995, ASP Conf. Ser., 83, 176, ed. R. S. Stobie, & P. A. Whitelock
In the text
-
Lamers, H. J. G. L. M. 1997, ASP Conf. Ser., 120, 76, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Lamers, H. J. G. L. M., & de Groot, M. 1992, A&A, 257, 153
In the text
NASA ADS
-
Lamers, H. J. G. L. M., & Noordhoek, R. 1993, ASP Conf. Ser., 35, 517, ed. J. Cassinelli, & E.
Churchwell
In the text
-
Lamers, H. J. G. L. M., de Groot, M., & Cassatella, A. 1983, A&A, 128, 299
In the text
NASA ADS
-
Lamers, H. J. G. L. M., Hoekzema, N., Trams, N., et al. 1989, IAU Coll., 113, 271, ed. K. Davidson, A.
F. J. Moffat, & H. J. G. L. M. Lamers
In the text
-
Lamers, H. J. G. L. M., Bastiaanse, M. V., Aerts, C., & Spoon, H. W. W. 1998, A&A, 335, 605
In the text
NASA ADS
-
Langer, N. 1999, IAU Coll., 169, 359, ed. B. Wolf, O. Stahl, & A. W. Fullerton
In the text
-
Langer, N., Garcia-Segura, G., & Mac Low, M. M. 1999, ApJ, 520, L49
In the text
NASA ADS
-
Langer, N., Hamann, W. R., Lennon, M., et al. 1994, A&A, 290, 819
In the text
NASA ADS
-
Langer, N., & Heger, A. 1998, in B[e] Stars, ed. A. M. Hubert, & C. Jaschek, ASSL 233, 235
In the text
NASA ADS
-
van Leeuwen, F., van Genderen, A. M., & Zegelaar, I. 1998, A&AS, 127, 1
In the text
NASA ADS
-
Leitherer, C. 1997, ASP Conf. Ser., 120, 213, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Leitherer, C., & Chavarria, K. C. 1987, A&A, 175, 208
In the text
NASA ADS
-
Leitherer, C., & Wolf, B. 1984, A&A, 132, 151
In the text
NASA ADS
-
Leitherer, C., Allen, R., Altner, B., et al. 1994, ApJ, 428, 292
In the text
NASA ADS
-
Leitherer, C., Appenzeller, I., Klare, G., et al. 1985, A&A, 153, 168
In the text
NASA ADS
-
Leitherer, C., Schmutz, W., Abbott, D. C., et al. 1989, ApJ, 346, 919
In the text
NASA ADS
-
Lennon, D. J., & Dufour, P. L. 1986, A&A, 155, 79
In the text
NASA ADS
-
Lennon, D. J., Wobig, D., Kudritzki, R. P., & Stahl, O. 1994, Sp. Sci. Rev., 66, 207
In the text
-
Lester, J. B., Gray, R. O., & Kurucz, R. L. 1986, ApJS, 61, 509
In the text
NASA ADS
-
Lopes, D. F., Damineli Neto, A., & de Freitas Pacheco, J. A. 1992, A&A, 261, 482
In the text
NASA ADS
-
Lovey, D., Maeder, A., Noëls, A., & Gabriël, M. 1984, A&A, 133, 307
In the text
NASA ADS
-
Maeder, A. 1989, in Physics of Luminous Blue Variables, ed. K. Davidson, A. F. J. Moffat, & H. J. G. L.
M. Lamers (Kluwer), 15
In the text
-
Maeder, A. 1992, in Instabilities in Evolved Super- and Hypergiants, ed. C. de Jager, & H. Nieuwenhuijzen
(North-Holland), 138
In the text
-
Maeder, A. 1997, ASP Conf. Ser., 120, 374, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Maeder, A. 1999, IAU Symp., 193, 177, ed. K. A. van der Hucht, G. Koenigsberger, & P. R. J. Eenens
In the text
NASA ADS
-
Manfroid, J., Sterken, C., Bruch, A., et al. 1991, A&AS, 87, 481
In the text
NASA ADS
-
Manfroid, J., Sterken, C., Conuw, B., et al. 1994, A&AS, 109, 329
In the text
NASA ADS
-
Markova, N. 1986, A&A, 162, L3
In the text
NASA ADS
-
Markova, N., & de Groot, M. 1997, A&A, 326, 1111
In the text
NASA ADS
-
Markova, N., & Tomov, N. 1998, IBVS, 4641
In the text
-
Marston, A. P. 1999, IAU Symp., 193, 306, ed. K. A. van der Hucht, G. Koenigsberger, & P. R. J. Eenens
In the text
NASA ADS
-
Marston, A. P., Yocum, D. R., Garcia-Segura, G., & Chu, Y. H. 1994, ApJ, 95, 151
In the text
-
Martini, A. 1969, A&A, 3, 443
In the text
NASA ADS
-
Massey, P. 2000, PASP, 112, 144
In the text
NASA ADS
-
Massey, P., & Thompson, A. B. 1991, AJ, 101, 1408
In the text
NASA ADS
-
Massey, P., Waterhouse, E., & Degioia-Eastwood, K. 2000, in press
In the text
-
McGregor, P. J., Hyland, A. R., & Hillier, D. J. 1988a, ApJ, 324, 1071
In the text
NASA ADS
-
McGregor, P. J., Finlayson, K., Hyland, A. R., et al. 1988b, ApJ, 329, 874
In the text
NASA ADS
-
McGregor, P. J., Hyland, A. R., & McGinn, M. T. 1989, A&A, 223, 237
In the text
NASA ADS
-
Meaburn, J., Walsh, J. R., & Wolstencroft, R. D. 1993, A&A, 268, 283
In the text
NASA ADS
-
Meaburn, J., Lopez, J. A., Barlow, M. J., & Drew, J. E. 1996, MNRAS, 283, L69
In the text
NASA ADS
-
Meaburn, J., Lopez, J. A., & O'Connor, J. 1999, ApJ, 516, L29
In the text
NASA ADS
-
Mendoza, V. E. E. 1970, Bol. Obs. Tonantzintla Tacubaja, 5, 269
In the text
NASA ADS
-
Menshchikov, A. B. 1989, AN, 310, 335
In the text
NASA ADS
-
Miroschnichenko, A. S. 1996, A&A, 312, 941
In the text
NASA ADS
-
Miroschnichenko, A. S., Chentsov, E. L., & Klochkova, V. G. 1999, IAU Coll., 169, 272, ed. B. Wolf, O.
Stahl, & A. W. Fullerton
In the text
-
Moffat, A. F. J., & FitzGerald, M. 1977, A&A, 54, 263
In the text
NASA ADS
-
Moffat, A. F. J., Marchenko, S. V., Bartzakos, P., et al. 1998, ApJ, 497, 896
In the text
NASA ADS
-
Morris, P. W., Waters, L. B. F. M., Barlow, M. J., et al. 1999, Nature, 402, 502
In the text
NASA ADS
-
Muratorio, G., & Friedjung, G. 1988, A&A, 190, 103
In the text
NASA ADS
-
Najarro, F., Hillier, D. J., & Stahl, O. 1997, A&A, 326, 1117
In the text
NASA ADS
-
Nieuwenhuijzen, H., & de Jager, C. 1995, A&A, 302, 811
In the text
NASA ADS
-
Nieuwenhuijzen, H., & de Jager, C. 2000, A&A, 353, 163
In the text
NASA ADS
-
Nota, A. 1999, IAU Coll., 169, 62, ed. B. Wolf, O. Stahl, & A. W. Fullerton
-
Nota, A., & Clampin, M. 1997, ASP Conf. Ser., 120, 303, ed. A. Nota, & H. J. G. L. M. Lamers
-
Nota, A., Drissen, L., Clampin, M., et al. 1994, in Circumstellar Media in the Late Stages of Stellar
Evolution, ed. R. Clegg, et al., Cambridge, 89
In the text
-
Nota, A., Livio, M., & Schulte-Ladbeck, R. E. 1995a, ApJ, 448, 788
In the text
NASA ADS
-
Nota, A., Pasquali, A., Drissen, L., et al. 1995b, ApJS, 102, 383
In the text
NASA ADS
-
Nota, A., Pasquali, A., Clampin, M., et al. 1996a, ApJ, 473, 946
In the text
NASA ADS
-
Nota, A., Pasquali, A., Clampin, M., et al. 1996b, Proc. 33rd Liège Inst. Astr. Coll., Wolf-Rayet
Stars in the Frame Work of Stellar Evolution, ed. J. M. Vreux, et al., 453
In the text
-
Nota, A., Smith, L., Pasquali, A., et al. 1997, ApJ, 486, 338
NASA ADS
-
Ødegaard, K. J. R. 1999, IAU Coll., 169, 353, ed. B. Wolf, O. Stahl, & A. W. Fullerton
In the text
-
Oudmaijer, R. D. 1995, Thesis, Univ. Groningen
In the text
-
Oudmaijer, R. D., 1998, A&AS, 129, 541
In the text
NASA ADS
-
Oudmaijer, R. D., Geballe, T. R., Waters, L. B. F. M., & Sahu, K. C. 1994, A&A, 281, L33
In the text
NASA ADS
-
Oudmaijer, R. D., Groenewegen, M. A. T., Matthews, H. E., et al. 1996, MNRAS, 280, 1062
In the text
NASA ADS
-
Owocki, S. P., & Gayley, K. G. 1997, ASP Conf. Ser., 120, 121, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Pacheco, J. A., Neto, A. D., Costa, R. D. D., & Viotti, R. 1992, A&A, 266, 360
In the text
NASA ADS
-
Pamyathnykh, A. A. 1998, ASP Conf. Ser., 135, 268, ed. P. A. Bradley, & J. A. Guzik
In the text
-
Pantin, E., & Le Mignant, D. 2000, A&A, 355, 155
In the text
NASA ADS
-
Parker, J. W. 1997, ASP Conf. Ser., 120, 368, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Parker, J. W., Clayton, G. C., Winge, C., et al. 1993, ApJ, 409, 770
In the text
NASA ADS
-
Pasquali, A. 1997, ASP Conf. Ser., 120, 13, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Pasquali, A., Langer, N., Schmutz, W., et al. 1997a, ApJ, 478, 340
In the text
NASA ADS
-
Pasquali, A., Schmutz, W., Nota, A., & Origlia, L. 1997b, A&A, 327, 265
In the text
NASA ADS
-
Pasquali, A., Nota, A., & Clampin, M. 1999, A&A, 343, 536
In the text
NASA ADS
-
Pasquali, A., Nota, A., Langer, N., et al. 2000, AJ, 119, 1352
In the text
NASA ADS
-
Pauldrach, A. W. A., & Puls, J. 1990, A&A, 237, 409
In the text
NASA ADS
-
Percy, J. R., Napke, A. E., Richer, M. G., et al. 1988, A&A, 191, 248
In the text
NASA ADS
-
Perry, C. L., Hill, G., & Christodoulou, D. M. 1991, A&AS, 90, 195
NASA ADS
-
Pittard, J. M. 2000, Thesis, Univ. of Birmingham
In the text
-
Polomsk, E. F., Telesco, C. M., Piña, R. K., & Fisher, R. S. 1999, AJ, 118, 2369
NASA ADS
-
Pottasch, S. R., Wesselius, P. R., & van Duinen, R. J. 1976, A&A, 47, 443
In the text
NASA ADS
-
Prinja, R. K., & Schild, H. 1991, A&A, 249, 428
In the text
NASA ADS
-
Reddish, V. C., Lawrence, L. C., & Pratt, M. N. 1967, Publ. R. Obs. Edinburgh, 5, 111
In the text
NASA ADS
-
Rivinius, Th., Stahl, O., Wolf, B., et al. 1997, A&A, 318, 819
In the text
NASA ADS
-
Robberto, M., Ferrari, A., Nota, A., & Paresce, F. 1993, A&A, 269, 330
In the text
NASA ADS
-
Robberto, M., & Herbst, T. M. 1998, ApJ, 498, 400
In the text
NASA ADS
-
Rosino, L., & Bianchini, A. 1973, A&A, 22, 453
In the text
NASA ADS
-
Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269
In the text
NASA ADS
-
Schild, H. 1987, A&A, 173, 405
In the text
NASA ADS
-
Schild, H., Hiltner, W. A., & Sanduleak, N. 1969, ApJ, 156, 609
In the text
NASA ADS
-
Schmidt-Kaler, Th. 1982, Landolt-Börnstein, Gruppe IV, Band 2
In the text
-
Schmutz, W. 1997, ASP Conf. Ser., 120, 115, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Schmutz, W., Leitherer, C., Hubeny, I., et al. 1991, ApJ, 372, 664
In the text
NASA ADS
-
Schulte, D. H. 1958, ApJ, 128, 41
In the text
NASA ADS
-
Schulte-Ladbeck, R. E., & Clayton, G. C. 1993, AJ, 106, 790
In the text
NASA ADS
-
Schulte-Ladbeck, R. E., Clayton, G. C., Hillier, D. J., et al. 1994, ApJ, 429, 846
In the text
NASA ADS
-
Sharov, A. S. 1973, IAU Symp., 67, 275, ed. V. E. Sherwood, & L. Plaut
-
Shore, S. N. 1990, IAU Circ., 5009
In the text
-
Shore, S. N. 1992, in Nonisotropic and Variable Outflows from Stars, ed. L. Drissen, C. Leitherer, & A.
Nota, 342
In the text
-
Shore, S. N., & Sanduleak, N. 1984, ApJS, 55, 1
In the text
NASA ADS
-
Shore, S. N., Sanduleak, N., & Allen, D. A. 1987, A&A, 176, 59
In the text
NASA ADS
-
Shore, S. N., Brown, D. N., Bopp, B. W., et al. 1990, ApJS, 73, 461
In the text
NASA ADS
-
Shore, S. N., Altner, B., & Waxin, I. 1996, AJ, 112, 2744
In the text
NASA ADS
-
Skinner, C. J. 1997, ASP Conf. Ser., 120, 322, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Skinner, C., Becker, R. H., White, R. L., et al. 1998, MNRAS, 296, 669
In the text
NASA ADS
-
Smith, L. J. 1997, ASP Conf. Ser., 120, 310, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Smith, L. J., Crowther, P. A., & Prinja, R. K. 1994, A&A, 281, 833
In the text
NASA ADS
-
Smith, L. J., Stroud, M. P., Esteban, C., & Vilchez, J. M. 1997, MNRAS, 290, 265
In the text
NASA ADS
-
Smith, L. J., Nota, A., Pasquali, A., et al. 1998, ApJ, 503, 278
In the text
NASA ADS
-
Smith, N., Gehrz, R. D., & Krautter, J. 1998, AJ, 116, 1332
In the text
NASA ADS
-
Smith, N., & Gehrz, R. D. 2000, ApJ, 529, L99
In the text
NASA ADS
-
Smith Neubig, M. M., & Bruhweiler, F. C. 1999, AJ, 117, 2856
In the text
NASA ADS
-
Soukup, M. S., Cox, A. N., Guzik, J. A., & Morgan, S. M. 1994, BAAS, 26, 907
In the text
NASA ADS
-
Souza, S. P., & Lutz, B. L. 1980, ApJ, 235, L87
In the text
NASA ADS
-
Spoon, H. W. W., de Koter, A., Sterken, C., et al. A&AS, 106, 141
In the text
-
Stahl, O. 1986, A&A, 164, 321
In the text
NASA ADS
-
Stahl, O., & Wolf, B. 1982, A&A, 110, 272
In the text
NASA ADS
-
Stahl, O., & Wolf, B. 1986, A&A, 154, 243
In the text
NASA ADS
-
Stahl, O., & Wolf, B. 1987, A&A, 181, 293
In the text
NASA ADS
-
Stahl, O., Wolf, B., Klare, G., et al. 1983, A&A, 127, 49
In the text
NASA ADS
-
Stahl, O., Leitherer, C., Wolf, B., & Zickgraf, F. J. 1984a, A&A, 131, L5
In the text
NASA ADS
-
Stahl, O., Wolf, B., Leitherer, C., et al. 1984b, A&A, 140, 459
NASA ADS
-
Stahl, O., Wolf, B., de Groot, M., et al. 1985, A&AS, 61, 237
In the text
NASA ADS
-
Stahl, O., Wolf, B., & Zickgraf, F. J. 1987, A&A, 184, 193
In the text
NASA ADS
-
Stahl, O., Wolf, B., Klare, G., et al. 1990, A&A, 228, 379
In the text
NASA ADS
-
Steemers, W. J. G., & van Genderen, A. M. 1986, A&A, 154, 308
In the text
NASA ADS
-
Sterken, C. 1976, A&A, 47, 453
In the text
NASA ADS
-
Sterken, C. 1977, A&A, 57, 361
In the text
NASA ADS
-
Sterken, C. 1981, in The Most Massive Stars, ESO Workshop, ed. S. D'Odorico, D. Baade, & K. Kjär, 147
In the text
-
Sterken, C., IAU Coll., 113, 59, ed. K. Davidson, A. F. J. Moffat, & H. J. G. L. M. Lamers
In the text
-
Sterken, C., & Breysacher, J. 1997, A&A, 328, 269
In the text
NASA ADS
-
Sterken, C., Gosset, E., Jüttner, A., et al. 1991, A&A, 247, 383
In the text
NASA ADS
-
Sterken, C., Manfroid, J., Anton, K., et al. 1993, A&AS, 102, 79
In the text
NASA ADS
-
Sterken, C., Manfroid, J., Beele, D., et al. 1995a, A&AS, 113, 31
In the text
NASA ADS
-
Sterken, C., Stahl, O., Wolf, B., et al. 1995b, A&A, 303, 766
In the text
NASA ADS
-
Sterken, C., Jones, A., Vos, B., et al. 1996a, IAU Circ., 4401
In the text
-
Sterken, C., de Groot, M., & van Genderen, A. M. 1996b, A&AS, 116, 9
In the text
NASA ADS
-
Sterken, C., Jones, A., van Genderen, A. M., & de Groot, M. 1996c, Australian J. Astr., 6, 199
In the text
-
Sterken, C., de Groot, M., & van Genderen, A. M. 1997a, A&A, 326, 640
In the text
NASA ADS
-
Sterken, C., van Genderen, A. M., & de Groot, M. 1997b, ASP Conf. Ser., 120, 35, ed. A. Nota, & H. J.
G. L. M. Lamers
In the text
-
Sterken, C., de Groot, M., & van Genderen, A. M. 1998, A&A, 333, 565
In the text
NASA ADS
-
Sterken, C., Freyhammer, L., Arentoft, T., & van Genderen, A. M. 1999a, A&A, 346, L33
In the text
NASA ADS
-
Sterken, C., van Genderen, A. M., de Groot, M., & Burki, G. 1999b, ASP Conf. Ser., 179, 200, ed. J. A.
Morse, R. M. Humphreys, & A. Damineli
In the text
-
Sterken, C., Arentoft, T., Duerbeck, H. W., & Brogt, E. 1999c, A&A, 349, 537
In the text
NASA ADS
-
Sterken, C., et al. 2001, A&A, in preparation
In the text
-
Stothers, R. B. 1999a, ApJ, 513, 460
In the text
NASA ADS
-
Stothers, R. B. 1999b, ApJ, 516, 366
In the text
NASA ADS
-
Stothers, R. B. 1999c, MNRAS, 305, 365
In the text
NASA ADS
-
Stothers, R. B. 2000, ApJ, 530, L103
NASA ADS
-
Stothers, R. B., & Chin, C. W. 1993, ApJ, 408, L85
In the text
NASA ADS
-
Stothers, R. B., & Chin, C. W. 1994, ApJ, 426, L43
In the text
NASA ADS
-
Stothers, R. B., & Chin, C. W. 1995, ApJ, 451, L61
In the text
NASA ADS
-
Stothers, R. B., & Chin, C. W. 1996, ApJ, 468, 842
In the text
NASA ADS
-
Stothers, R. B., & Chin, C. W. 1997, ApJ, 489, 319
In the text
NASA ADS
-
Stothers, R. B., & Chin, C. W. 1999, ApJ, 522, 960
NASA ADS
-
Stothers, R. B., & Chin, C. W. 2000, ApJ, 540, 1041
In the text
NASA ADS
-
Stroud, M. P. 1997, ASP Conf. Ser., 120, 350, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Subrahmanyan, R., Ekers, R. D., Wilson, W. E., et al. 1993, MNRAS, 263, 868
NASA ADS
-
Szeifert, Th., Stahl, O., Wolf, B., et al. 1993, A&A, 280, 508
In the text
NASA ADS
-
Thackeray, A. D. 1974, MNRAS, 168, 221
In the text
NASA ADS
-
Thompson, G. I., Nandy, K., Morgan, D. H., et al. 1982, MNRAS, 200, 551
In the text
NASA ADS
-
Torres-Dodgen, A. V., Tapia, M., & Carroll M. 1991, MNRAS, 249, 1
In the text
NASA ADS
-
Turner, D. G. 1985, A&A, 144, 241
In the text
NASA ADS
-
Vacca, W. D., & Torres-Dodgen, A. V. 1990, ApJS, 73, 685
In the text
NASA ADS
-
Vakili, F., Mourard, D., Stee, P., & Bonneau, D. 1999, IAU Coll., 169, 87, ed. B. Wolf, O. Stahl, & A.
W. Fullerton
In the text
-
Vanbeveren, D., van Rensbergen, W., & de Loore, C. 1998, The Brightest Binaries, Sect. 4 (Kluwer)
In the text
-
de Vaucouleurs, G., & Eggen, D. J. 1952, PASP, 64, 185
In the text
NASA ADS
-
van der Veen, W. E. C. J., Waters, L. B. F. M., Trams, N. R., & Mathews, H. E. 1994, A&A, 285, 551
In the text
NASA ADS
-
Venn, K. 1997, ASP Conf. Ser., 120, 95, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Viotti, R. 1971, PASP, 83, 170
In the text
NASA ADS
-
Viotti, R., & Rossi, C. 1999, ASP Conf. Ser., 179, 211, ed. J. A. Morse, R. M. Humphreys, & A. Damineli
In the text
-
Viotti, R., Cassatella, A., Ponz, D., & Thé, P. S. 1988, A&A, 190, 333
In the text
NASA ADS
-
Viotti, R., Rossi, L., Cassatella, A., et al. 1989, ApJS, 71, 983
In the text
NASA ADS
-
Voors, R. H. M. 1999, Thesis Univ. Utrecht
In the text
-
Voors, R. H. M., Waters, L. B. F. M., Trams, N. R., & Käufl, H. U. 1997, A&A, 321, L21
In the text
NASA ADS
-
Voors, R. H. M., Waters, L. B. F. M., Morris, P. W., et al. 1999, A&A, 341, L67
In the text
NASA ADS
-
Voors, R. H. M., Waters, L. B. F. M., de Koter, A., et al. 2000, Obs., in press
In the text
-
Waelkens, C., Aerts, C., Kestens, E., et al. 1998, A&A, 330, 215
In the text
NASA ADS
-
Walborn, N. R. 1982, ApJ, 256, 452
In the text
NASA ADS
-
Walborn, N. R. 1989, IAU Coll., 113, 250, ed. K. Davidson, A. F. J. Moffat, & H. J. G. L. M. Lamers
In the text
-
Walborn, N. R., & Blades, J. C. 1997, ApJS, 112, 457
In the text
NASA ADS
-
Walborn, N. R., Blanco, B. M., & Thackeray, A. D. 1978, ApJ, 219, 498
In the text
NASA ADS
-
Walborn, N. R., Evans, I. N., Fitzpatrick, E. L., et al. 1991, IAU Symp., 143, 505, ed. K. A. van der Hucht, & B. Hidayat
In the text
NASA ADS
-
Walraven, Th., & Walraven, J. H. 1977, A&AS, 30, 245
In the text
NASA ADS
-
Walsh, J. R., & Ageorges, N. 2000, A&A, 357, 255
In the text
NASA ADS
-
Warren, P. R., & Penfold, J. E. 1975, MNRAS, 172, 41P
In the text
-
Waters, L. B. F. M., Izumiura, H., Zaal, P. A., et al. 1996, A&A, 313, 866
In the text
NASA ADS
-
Weis, K. 1996, Diplomarbeit, Ruprecht-Karls-Univ., Heidelberg
In the text
-
Weis, K. 1999, Inaugural-Dissertation, Ruprecht-Karls-Univ., Heidelberg, AA, in press
In the text
-
Weis, K. 2000, A&A, 357, 938
In the text
NASA ADS
-
Weis, K., Bomans, D. J., Chu, Y. H., et al. 1995, Rev. Mex. A. A. Ser. Conf., 3, 237
In the text
NASA ADS
-
Weis, K., Duschl, W. J., Bomans, D. J., et al. 1997, A&A, 320, 568
In the text
NASA ADS
-
Weis, K., Duschl, W. J., & Chu, Y. H. 1999, A&A, 349, 467
In the text
NASA ADS
-
Westerlund, B. E. 1961, Uppsala Astron. Obs. Ann., 5, 1
In the text
NASA ADS
-
Whitelock, P. A., Feast, M. W., Carter, B. S., et al. 1983a, MNRAS, 203, 385
In the text
NASA ADS
-
Whitelock, P. A., Carter, B. S., Roberts, G., et al. 1983b, MNRAS, 205, 577
In the text
NASA ADS
-
Whitelock, P. A., Feast, M. W., Koen, C., et al. 1994, MNRAS, 270, 364
In the text
NASA ADS
-
de Winter, D. 1996, Thesis Univ. Amsterdam
In the text
-
de Winter, D., Pérez, M. R., Hu, J. Y., & Thé, P. S. 1992, A&A, 257, 632
In the text
NASA ADS
-
Wisse, P. N. J., & Wisse, M. 1971, A&A, 12, 149
In the text
NASA ADS
-
Wolf, B. 1989, A&A, 217, 87
In the text
NASA ADS
-
Wolf, B., Stahl, O., de Groot, M., & Sterken, C. 1981, A&A, 99, 351
In the text
NASA ADS
-
Wray, J. 1966, Ph.D. Thesis, North Western Univ.
In the text
-
Zickgraf, F. J. 1997, ASP Conf. Ser., 120, 173, ed. A. Nota, & H. J. G. L. M. Lamers
In the text
-
Zickgraf, F. J., Wolf, B., Stahl, O., et al. 1985, A&A, 143, 421
In the text
NASA ADS
-
Zickgraf, F. J., Wolf, B., Stahl, O., et al. 1986, A&A, 163, 119
In the text
NASA ADS
-
Zickgraf, F. J., & Schulte-Ladbeck, R. E. 1989a, A&A, 214, 274
In the text
NASA ADS
-
Zickgraf, F. J., Wolf, B., Stahl, O., & Humphreys, R. M. 1989b, A&A, 220, 206
In the text
NASA ADS
-
Zickgraf, F. J., Kovács, J., Wolf, B., et al. 1996a, A&A, 309, 505
In the text
NASA ADS
-
Zickgraf, F. J., Humphreys, R. M., Lamers, H. J. G. L. M., et al. 1996b, A&A, 315, 510
In the text
NASA ADS
-
Zsoldos, E. 1986, Obs., 106, 156
In the text
NASA ADS
All sources indicated by reference numbers, in the tables below the header "ref'', are codified in
Tables 14 and 15. Uncertain data in the tables have been bracketed.
Below the tables special notes are given with bracketed reference numbers.
Table 1
Column 1: Most popular designations by a name and/or a catalogue number, for 4 galactic-, 2 SMC- and 8 LMC s-a S Dor variables, respectively.
Column 2: Approximate dates of the extrema for which the physical and photometric parameters in this table and Table 2 are applicable.
Columns 3, 4 and 5: Effective temperature, absolute visual magnitude and luminosity, respectively. Blanks: no parameters could be derived with any certainty.
Column 6: Reference numbers on which the parameters in Cols. 3-5 are partly, or completely based; pp = present paper.
Column 7: Gas nebula (g), or dust nebula (d) present? y = yes, n = no, ? = still uncertain, blank = unknown.
Column 8: Reference numbers concerning Col. 7, discussing and/or summarizing physical,
chemical and geometrical parameters and giving references.
Table 2
Column 1: A selected designation (see Table 1).
Columns 2 and 3: Reddening (the subscript J refers to the UBV system of Johnson) and reference numbers respectively.
Columns 4 and 5: The distance in kpc for the galactic objects and reference numbers, respectively. pp = present paper. See for the distance moduli of the SMC and LMC Sect. 2.2.
Columns 6, 7 and 8: The apparent visual magnitude  (the subscript J refers to the V of the UBV system of Johnson) of the extrema (dates listed in Table 1) and the reference numbers, respectively.
Column 9: A selected list of additional reference numbers dealing with photometry, spectroscopy and /or on various aspects of possible SD-signatures. Remarks on early magnitude determinations are given in square brackets, see for more (44).
They are important for the determination of a possible long-term light variation. However, an uncertainty of a few tenths of a magnitude should be taken into account.
(the subscript J refers to the V of the UBV system of Johnson) of the extrema (dates listed in Table 1) and the reference numbers, respectively.
Column 9: A selected list of additional reference numbers dealing with photometry, spectroscopy and /or on various aspects of possible SD-signatures. Remarks on early magnitude determinations are given in square brackets, see for more (44).
They are important for the determination of a possible long-term light variation. However, an uncertainty of a few tenths of a magnitude should be taken into account.
Table 3
Column 1: A selected designation (see Table 1).
Column 2: Approximate time scale (first line) and amplitude (second line) of the L-SD phases.
Column 3: The same as in Col. 2, but now for the S-SD phases.
Column 4: The same as in Cols. 2 and 3, but now for the microvariations.
Column 5: Reference numbers concerning Cols. 2, 3 and 4.
Column 6: A reference to figures with a schematic light curve and to Table 16 with some information on a possible long-term light variation.
Table 4
Column 1: Most popular designations by a name and/or a catalogue number, for 4 galactic- and 8 LMC w-a S Dor variables, respectively.
Column 2: A selected spectral classification.
Column 3: Approximate date(s), or approximate time interval, for which the physical and photometric parameters in this table and Table 5 are applicable.
Columns 4, 5 and 6: The effective temperature, the absolute visual magnitude (the apparent visual magnitude used is listed in Table 5 in italics) and the luminosity, respectively.
Column 7: Reference numbers on which the parameters in Cols. 4, 5 and 6 are partly, or completely based. pp = present paper.
Columns 8 and 9: The same as Cols. 7 and 8 in Table 1.
Table 5
Column 1: A selected designation (see Table 4).
Columns 2, 3, 4 and 5: The same as in Table 2.
Columns 6, 7 and 8: The mean (Col. 6) and/or minimum apparent visual magnitude (Col. 7) and reference numbers, respectively. The magnitudes in italics have been used for MV and
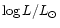 in Table 4. The maximum apparent magnitude can be easily derived from the difference between the minimum and the mean magnitudes.
Column 9: The same as in Table 2.
in Table 4. The maximum apparent magnitude can be easily derived from the difference between the minimum and the mean magnitudes.
Column 9: The same as in Table 2.
Table 6
Column 1: A selected designation (see Table 4).
Columns 2, 3, 4, 5 and 6: The same as in Table 3.
Table 8
Column 1: Most popular designations by a name, or by a catalogue number, for 5 galactic- and 3 LMC ex-/dormant S Dor variables, respectively.
Column 2: A selected spectral classification.
Column 3: Approximate time interval for which the physical and photometric
parameters in this table and Table 9 are applicable.
Columns 4, 5 and 6: The effective temperature, the absolute visual
magnitude (the mean apparent visual magnitude used is listed in Table 9)
and the luminosity, respectively.
Column 7: Reference numbers on which the parameters in Cols. 4, 5 and 6 are partly or completely based. pp = present paper.
Columns 8 and 9: The same as Cols. 7 and 8, respectively, in Table 1.
Table 9
Column 1: A selected designation (see Table 8).
Columns 2, 3, 4 and 5: The same as in Table 2.
Columns 6 and 7: The mean apparent visual magnitude and reference numbers, respectively.
Column 8: The same as Col. 9 in Table 2.
Table 10
Column 1: A selected designation (see Table 8).
Column 2, 3, 4, 5 and 6: The same as in Table 3.
Table 11
Column 1: Most popular designation by a name and/or a catalogue number for 8 galactic-, 2 SMC- and 2 LMC candidate S Dor variables and 3
former candidates (marked by a "0'': 1 star in the Galaxy and 2 stars in the LMC).
Column 2: A selected spectral classification.
Column 3: The weight for the candidate membership: "+'' = indications for a possible S Dor-membership; "-'' = indications are weaker than for the previous category; "0'' = most likely no S Dor variable, but it is a normal 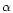 Cyg variable.
Cyg variable.
Column 4: Approximate date, or time interval, for which the photometric and physical parameters in this table and in Table 12 are applicable.
Columns 5, 6, 7 and 8: The same as Cols. 4, 5, 6 and 7, respectively, in Table 8.
Columns 9 and 10: The same as Cols. 7 and 8 in Table 1.
Table 12
Columns 1: A selected designation (see Table 11).
Columns 2, 3, 4 and 5: The same as in Table 2.
Columns 6 and 7: The mean apparent visual magnitude and reference numbers, respectively.
Column 8: The same as Col. 9 in Table 2.
Table 13
Column 1: A selected designation (see Table 11).
Column 2: The same as Col. 3 in Table 11.
Column 3: The approximate time scales, or quasi-periods (first line) and amplitudes (second line) of the microvariations.
Column 4: Reference numbers concerning Col. 3.
Column 5: A reference to figures with a schematic light curve.
Table 1:
Selected particulars of the s-a S Dor variables
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
| designation |
date |
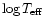 |
MV |
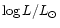 |
ref. |
g?d? |
ref. |
| HD/HDE |
|
|
|
|
|
|
|
| AG Car |
min 1985-1990 |
4.46a |
-7.7 |
6.14 |
96,103 |
y y |
173, 196, 251, 254, 264, 273, 291 |
| = 94910 |
max 1982 |
4.13 |
-9.8 |
6.22 |
96 |
|
|
| HR Carb |
min 1970 |
4.34 |
-8.0 |
5.90 |
pp |
y y |
120, 173, 196, 250, 251 |
| = 90177 |
max 1992 |
3.90 |
-9.3 |
5.62 |
pp |
|
|
| 160529 |
min 1989.5 |
4.00 |
-8.4 |
5.46 |
77 |
n n |
173, 250 |
| = 164G Sco |
max 1972-1980 |
3.90 |
-8.9 |
5.46 |
77 |
|
|
| WRA751 |
min 1989-1991 |
4.48 |
(-6.0) |
(5.50) |
pp,114,126 |
y y |
126, 173, 196, 250, 291, 297 |
| |
max 1949-1951 |
|
|
|
|
|
|
| R4c |
min  1984 1984 |
4.43 |
-5.3d |
5.06 |
67 |
y y |
95, 275 |
| = S6 |
max  1988 1988 |
|
|
|
|
|
|
| A-comp |
|
3.98 |
-5.2d |
4.14 |
67 |
|
|
| R40 |
min  1959 1959 |
4.05 |
-8.7 |
5.66 |
9 |
|
|
| = 6884 |
max 1996.3 |
3.90 |
-9.5 |
5.70 |
137,138 |
|
|
| R71 |
min 1982, 1989 |
4.24 |
-8.0 |
5.80 |
42 |
y y |
173, 196, 250 |
| = 269006 |
max 1975 |
4.10 |
-9.2 |
5.92 |
42 |
|
|
| S Dor |
min 1965 |
4.54e |
-7.6 |
6.30 |
70 |
? ? |
173, 250 |
| = R88 |
max 1989 |
3.93e |
-10.0 |
5.96 |
70 |
|
|
| = 35343 |
|
|
|
|
|
|
|
| R110 |
min 1957-1962 |
3.96 |
-8.4 |
5.36 |
7,63 |
? ? |
173, 250 |
| = 269662 |
max 1993 |
3.84 |
-9.2 |
5.56 |
7,63 |
|
|
| R116f |
min 1989-1990 |
4.29 |
-8.4 |
5.92 |
pp |
|
|
| = 269700 |
max  1900 1900 |
|
|
|
|
|
|
| R127 |
min 1969.9 |
4.46 |
-7.4g |
6.00 |
5,7 |
y y |
173, 250, 256 |
| = 269858f |
max 1989.8 |
3.87 |
-10.0 |
5.92 |
7 |
|
|
| R143 |
min 1981-1995 |
4.23 |
-8.2 |
5.70 |
pp |
? ? |
173, 250 |
| = 269929 |
max 1957 |
3.90 |
-9.4 |
5.72 |
pp |
|
|
| 269216h |
mean 1970-1993 |
4.08 |
-8.2 |
5.44 |
64,66 |
|
|
= Sk
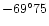 |
|
|
|
|
|
|
|
| HV5495i |
min 1988-1993 |
4.46 |
-7.0 |
5.80 |
22 |
? ? |
173, 250 |
| = 269582 |
max  1990 1990 |
|
|
|
|
|
|
| = BE294 |
|
|
|
|
|
|
|
| = MWC112 |
|
|
|
|
|
|
|
Notes to Table 1:
a See the discussion on the temperature scale (70).
b In the maximum of 1992 (
b-
y) = 0.83 and with
E(
b-
y) = 0.78E
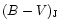
= 0.78,
(
b-
y)
0 = 0.05. Adopting
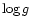

1 and a solar abundance,
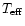

8000K (259).
c R4 consists of two components: an LBV/B[e] star and an A-type star. The latter is presumably constant. See note
d in Table 3.
d Adopted value by (67).
e The temperatures at the visual minimum of 1965 and the visual maximum in 1989 have been derived from the estimated colour
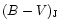

-0.1 (74) and the observed colour
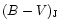
= 0.28, respectively, and corrected for E
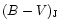
= 0.20. Vennix et al. (quoted by (71)) using Kurucz models and a different distance and reddening for the same visual maximum found:
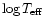
= 3.95 and
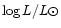
= 5.85. Note that the epoch of our chosen visual minimum is not the same as theirs.
f The spectral type in the visual minimum is according to (9): B1.5Iaeq.
g The visual minimum which has been used for the determination of
MV has been corrected for the faint companion, see note
d in Table 2.
h Spectral type according to (64) and (65) B8I.
i Spectral type close to visual minimum (

= 11.88) WN10h by (22).
Table 2:
Selected particulars of the s-a S Dor variables
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
(9) |
| designation |
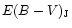 |
ref. |
r |
ref. |
 |
 |
ref. |
add. ref. |
| HD/HDE |
|
|
(kpc) |
|
min |
max |
|
[Remarks] |
| AG Car |
0.63 |
97 |
6 |
97,98 |
8.1 |
6.0 |
70 |
29,46,57,76,78,83,99, |
| |
|
|
|
|
|
|
|
101,109,113,114,116,119, |
| |
|
|
|
|
|
|
|
121,124,125,127,128,131, |
| |
|
|
|
|
|
|
|
196,198-201,263 |
| HR Car |
1.00 |
102,107 |
5.2 |
110,111 |
8.7 |
7.4 |
7,108 |
32,46,57,109,112, |
| |
|
|
|
|
|
|
|
113,114,116,122,123, |
| |
|
|
|
|
|
|
|
128,196,198-201 |
| 160529 |
1.10 |
77 |
2.5 |
77 |
6.95 |
6.4 |
77 |
79,80,81,82,198-201,281,293 |
| |
|
|
|
|
|
|
|
[See for BD and |
| |
|
|
|
|
|
|
|
HD mag note a] |
| WRA751 |
1.6 |
114,115, |
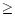 4.5 4.5 |
114,115, |
12.3 |
10.3 |
114,115, |
196 |
| |
|
126 |
|
126 |
|
|
117,118 |
|
| R4 |
0.07 |
67 |
|
|
13.0b |
12.5b |
67 |
95,134 |
| R40c |
0.14 |
136 |
|
|
10.7c |
9.9 |
9,137 |
57,83,119,198-201,281 |
| |
|
|
|
|
|
|
|
[HDptg 1900 = 10.8] |
| R71 |
0.20 |
42 |
|
|
11.0 |
9.9 |
43,74,197 |
44,46,47,57,78,83,119,168, |
| |
|
|
|
|
|
|
|
196,198-201,281 |
| |
|
|
|
|
|
|
|
[HDEptg 1925 = 9.2] |
| S Dor |
0.20 |
70 |
|
|
11.4 |
9.0 |
70 |
44,57,71,72,73,74,75,78, |
| |
|
|
|
|
|
|
|
168,198-201,271,281 |
| R110 |
0.15 |
62 |
|
|
10.6 |
9.7 |
3,7 |
10,23,51,57,199-201,281 |
| |
|
|
|
|
|
|
|
[HDEptg 1925 = 10.8] |
| R116 |
0.15 |
8 |
|
|
10.6 |
|
8 |
9,10,44,50,51,52 |
| |
|
|
|
|
|
|
|
[HDEptg 1925 = 10.4] |
| R127 |
0.12 |
103 |
|
|
11.2d |
8.8 |
7,88 |
1,6,9,46,57,76,78,87, |
| |
|
|
|
|
|
|
|
198-201 |
| |
|
|
|
|
|
|
|
[HDEptg 1925 = 11.1] |
| R143 |
0.54 |
1 |
|
|
12.0 |
10.6 |
1,2,85, |
3,4,9 |
| |
|
|
|
|
|
|
86 |
|
| 269216 |
0.12 |
66 |
|
|
10.7e |
|
66 |
49,65 |
| |
|
|
|
|
|
|
|
[HDEptg 1925 = 11.0] |
| HV5495 |
0.24 |
39 |
|
|
12.2 |
11.7 |
22,39,40, |
12,23,131,199-201 |
| |
|
|
|
|
|
|
41 |
|
Notes to Table 2:
a BD visual magnitude (

1850) = 6.9. Three HD photometric magnitudes (ptm) in 1897 with an average 6.69 and two in 1899 with an average 6.68. The averages and (the small) residuals are given in H.A.45 and 46, respectively. The HDptg 1900 = 7.6 is more or less consistent with respect to the HDptm above in view of the high reddening amounting to 1.10 (Col. 2).
b Both components together, see note
d in Table 3.
c Note that the HDptg magnitude (see Col. 9) and the

1959 magnitude

= 10.73 by (9), are roughly equal. Thus, considering the low reddening, the star was at both epochs at roughly the same minimum brightness. Note that the current SD-activity started after 1959, see (7) and (137).
d This is the magnitude including the faint field star nearby. After correction

= 11.4.
e This is the mean apparent magnitude.
Table 3:
Time scales and amplitudes of the light variations of the s-a S Dor variables
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
| designation |
L-SD |
S-SD |
microvar. |
ref. |
light curve/ |
| HD/HDE |
(yr, mag) |
(yr, mag) |
(d, mag) |
|
light history |
| AG Car |
25 |
1a |
10-41 |
43,70,78,84,100, |
Fig. 1 |
| |
1-2 |
0.2-1.5 |
0.1 |
102,247,248 |
|
| HR Car |
10-20 |
2-3 |
20-40 |
7,78,247 |
|
| |
0.5 |
0.5 |
0.15 |
|
|
| |
|
|
100 |
|
|
| |
|
|
0.2 |
|
|
| 160529 |
30-50 |
2.7 |
45-57 |
77,78,84,b |
Fig. 2 |
| |
0.5 |
0.1 |
0.1 |
|
|
| WRA751c |
c |
c |
30.5 |
115 |
Fig. 3, Table 16 |
| |
|
|
0.15 |
|
|
| R4d |
(25) |
|
|
67 |
|
| |
(1) |
|
|
|
|
| R40 |
25 |
3.5 |
46; 99; 121 |
7,66,137,247 |
Table 16 |
| |
0.2-0.6 |
0.02 |
0.1 |
|
|
| R71 |
10 |
3, 6 |
14-24; 76 |
7,43,69,76,84,247 |
Fig. 4, Table 16 |
| |
1 |
0.25 |
0.1 |
|
|
| |
|
|
100-200 |
|
|
| |
|
|
0.2 |
|
|
| S Dore |
35 |
6.8e |
 100; 131; 195 100; 131; 195 |
70,76,247,248 |
|
| |
1-2 |
0.5-1.2 |
0.2 |
|
|
| R110 |
20 |
2-3 |
50-100 |
7,63,247 |
Fig. 5, Table 16 |
| |
0.3-0.6 |
0.1-0.3 |
0.02-0.1 |
|
|
| R116 |
(25-50) |
|
(10-40) |
8 |
Fig. 6, Table 16 |
| |
1.4 |
|
|
|
|
| R127 |
>13 |
1.4 |
 100; 111 100; 111 |
7,78,247 |
Fig. 7, Table 16 |
| |
1.7 |
0.5 |
0.1 |
|
|
| R143 |
>30 |
|
|
|
Fig. 8, Table 16 |
| |
(1.5) |
|
|
|
|
| 269216 |
|
1.6 |
(16) |
66 |
Fig. 9 |
| |
|
0.4 |
0.1 |
|
|
| HV5495 |
20 |
2.2 |
|
39,40,41 |
Fig. 10, Table 16 |
| |
1.2 |
0.3-0.5 |
|
|
|
Notes to Table 3:
a The primary period
P0 = 371.4d shows a beat of 21.6yr (70), see Fig. 1 and Sect. 1.5.3.
b According to the analysis of spectroscopic time series (293), a dominant period of 92.5d is present for the photospheric line profile variations, which is about twice the photometric periods, and a period of 114-127d for the wind line profile vriations.
c It is unknown to what type of SD-phase (S-SD or L-SD) the long-term light variation belongs with an approximate amplitude of
(Fig. 3).
e Although the colour index
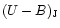
becomes bluer during brightening (67), while this should be just like the
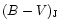
redder, we are yet most likely dealing with an SD-phase. This blueing can be explained by the presence of the A-type companion of which the contribution in the UV channels becomes dominant when the S Dor star becomes cooler than its companion. For example: if

(S Dor star in min) = 13.9, and

(A star) = 14.0, the blueing in
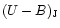
can be explained if the rise in the visual due to an SD-phase amounts to

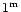
.
d The reported brightening in 1999 by (271) is nothing else then a new S-SD phase, confirming the established cyclicity amounting to on the average 6.8yr (70).
Table 4:
Selected particulars of the w-a S Dor variables
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
(9) |
| designation |
Sp. |
date |
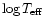 |
MV |
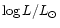 |
ref. |
g?d? |
ref. |
| HD/HDE |
|
|
|
|
|
|
|
|
 Cara Cara |
|
1970-2000 |
4.36-4.18 |
-7--9 |
5.14-6.34 |
181,182,183, |
y y |
b |
| = 93308 |
|
|
|
|
|
184,186,194 |
|
|
| P Cyg |
B1Ia+ |
min 1980-2000 |
4.26 |
-7.9 |
5.70 |
142 |
y n |
149,173,196, |
| = 193237 |
|
|
|
|
|
|
|
240,250,255 |
| 168607 |
B9.4Ia+ |
1970-1990 |
3.97 |
-8.4 |
5.38 |
38,48 |
n n |
173 |
| = V4029 Sgr |
|
|
|
|
|
|
|
|
| Cyg OB2#12 |
B5Ie |
1990 |
4.11 |
(-10.4) |
(6.42) |
162 |
|
|
| R74 |
BIe |
1988-1990 |
4.11 |
-7.8 |
5.40 |
8 |
|
|
| = 268939 |
|
|
|
|
|
|
|
|
| R81 |
B2.5eqIa+ |
min 1960-1995c |
4.30 |
-8.6 |
6.04 |
139 |
|
|
| = 269128 |
|
|
|
|
|
|
|
|
| R85d |
B5Iaed |
min 1960 |
4.13 |
-8.2 |
5.54 |
pp,9 |
|
|
| = 269321 |
|
max 1983-1990 |
4.00 |
-8.5 |
5.50 |
pp,63,272 |
|
|
| R99e |
WN10 |
1960-1990 |
4.50 |
-8.3 |
6.42 |
93 |
? ? |
173,250 |
| = 269445 |
|
|
|
|
|
|
|
|
| R123e |
Bpec |
1980-1990 |
4.54 |
-8.5 |
6.60 |
94 |
|
|
| = 37836 |
|
|
|
|
|
|
|
|
| R149 |
Be+neb |
1960-1985 |
4.30 |
-6.4 |
5.16 |
pp |
|
|
= -69 476f 476f |
|
|
|
|
|
|
|
|
| 34664 |
B[e] |
1982-1990 |
(4.39)g |
-7.4 |
(5.80)g |
pp |
- y |
21 |
| = S22 |
|
|
4.18h |
-7.4 |
5.32h |
pp |
|
|
| 38489i |
Be |
min 1960 & 1984 |
4.52 |
-8.0 |
6.36 |
pp |
- y |
95 |
| = S134 |
|
max 1966 |
4.05 |
-8.4 |
5.52 |
pp |
|
|
Notes to Table 4:
a Total luminosity
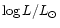
= 6.65 (
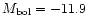
).
Physical and photometric parameters in the table are only for the S Dor variable hidden in

Car. Their large uncertainty is due to the following facts: (i) most of the visual light is reflected light from the core by the Homunculus; (ii) the internal reddening in the Homunculus is highly uncertain; (iii) the S Dor variable is presumably not single (e.g. 185). The peculiar non-stellar variability
(Sect. 3.2.6) is perhaps due to the varying physical conditions of a luminous
accretion disk according to (298), perhaps around a hot nearby companion of the S Dor star.
The error box in Fig. 20 has been computed from the estimated temperature- and
MV limits of the S Dor star. The spectral type of that object looks like that of P Cyg (186), (294). See for more information the notes to Tables 5 and 6 and Sects. 3.2.2 and 3.2.6.
b The literature on the Homunculus is overwhelming, see ``add.ref.'' in Table 5 and references therein.
c Presumably the star is at present in a minimum of SD-phases, but the parameters were taken outside the eclipse (Fig. 12), since R81 is an eclipsing binary (140) of which the revised period
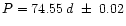
d m.e. (66).
d The spectral type is from (9) and presumably for the date
.
According to (272) the spectral type was AIe in October 1996 and somewhat hotter in January 1999: B8Ie. The trend of these three spectral types supports the presumable trend of the L-SD cycle sketched in Fig. 13, thus, in the minimum the star is hotter than in the maximum. For the temperature and luminosity during the maximum (1983-1990), a spectral type A0Ia has been adopted, inspired by the spectrum made some years later by (272). The minimum and maximum apparent magnitudes used for the two
MV values are 10.8 and 10.5, respectively.
e Possibly having a disk, see references in Col. 7.
f CPD number. The maximum light amplitude, MLA = 0

3, is too high for a normal
Cyg variable, thus, supporting the S Dor membership based on (10) and observations listed in Table 7, see note
e in Table 5 and note
f in Table 6.
g If the spectral type is B0-0.5 according to (14).
h If the spectral type is B4 according to (13), which agrees better with the photometry than the previous spectral type in note
g, therefore, the star has been plotted with the matching
and
L on the HR-diagram in Fig. 20.
i See Fig. 18 for a correlation

/
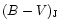
which supports the S Dor membership. However, the track on the HR-diagram is abnormally steep (Fig. 20). Perhaps inadequate photometry and/or the presence of much circumstellar material is the cause of its abnormality.
Table 5:
Selected particulars of the w-a S Dor variables
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
(9) |
| designation |
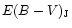 |
ref. |
r |
ref. |
 |
 |
ref. |
add.ref. |
| HD/HDE |
|
|
(kpc) |
|
mean |
min |
|
[Remarks] |
 Cara Cara |
0.50 |
178,179, |
2.3 |
189,194 |
a |
a |
|
83,119,190,191,193,195,198-201, |
| |
|
180,181 |
|
|
|
|
|
202,203,206,242,243,269,276, |
| |
|
|
|
|
|
|
|
278,279,282,283,287,288,289, |
| |
|
|
|
|
|
|
|
290,292,294,295,296,298,299 |
| P Cyg |
0.51 |
142,145 |
1.7 |
142 |
|
4.9 |
147,169, |
143,144,146,149,150,151, |
| |
|
|
|
|
|
|
204 |
152,224,237,238,239,240, |
| |
|
|
|
|
|
|
|
241,249,280,281 |
| 168607b |
1.55 |
38 |
2.2 |
132,133 |
8.2b |
|
38,66, |
48,198-201 |
| |
|
|
|
|
|
|
80,253 |
[HDptm 1900 = 8.9; |
| |
|
|
|
|
|
|
|
 (1956) = 8.29 (89)] (1956) = 8.29 (89)] |
| CygOB2#12 |
3.4 |
159,162 |
(1.7) |
161,162 |
11.5 |
|
163 |
160,164 |
| R74 |
0.15 |
|
|
|
11.0 |
|
8 |
9,10,11,12 |
| |
|
|
|
|
|
|
|
[HDEptg 1925 = 10.6] |
| R81 |
0.14 |
66,139, |
|
|
|
10.3c |
198-201 |
3,9,44,51,66,119 |
| |
|
141 |
|
|
|
|
|
|
| R85 |
0.17d |
pp |
|
|
10.65 |
10.8 |
63 |
10,57,198-201,272 |
| |
|
|
|
|
|
|
|
[HDEptg 1925 = 10.9] |
| R99 |
0.42 |
91,94, |
|
|
11.45 |
|
91 |
10,22,57,92 |
| |
|
95 |
|
|
|
|
|
[HDEptg 1925 = 11.6] |
| R123 |
0.20 |
94 |
|
|
10.55 |
10.7 |
91 |
10,44,57,87,93 |
| R149 |
0.10 |
|
|
|
12.4e |
|
10 |
9,165,166,167 |
| 34664 |
0.28 |
15 |
|
|
11.8 |
|
8,15 |
11,16,17,18,19,20,21 |
| 38489 |
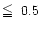 |
87 |
|
|
11.85f |
12.1f |
8,85, |
10,95 |
| |
|
|
|
|
|
|
87 |
[HDptg 1900 = 11.6] |
Notes to Table 5:
a The apparent visual magnitude of the S Dor variable inside

Car is very uncertain, see note
a below Table 4. See for the integrated magnitudes (thus including the bipolar nebula) the references (182), (178), (188), (187), (184), (192) and (243). Note that the constructed

scale in (188), (187), (184) and (192) is about 0

15 fainter than the constructed

scale in (182) and (178) and about 0

2 fainter than the

,
directly obtained with an
UBV photometer, from (243). The cause is the use of different filter systems,
clearly expressed by the transformation formula and is not due to errors in the photometry. For instance, it is easy to see from the zero points in the transformation equations given for
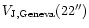
and
y in Sect. 2 of (184) that the difference between the two systems amounts to 0

213. The first is brighter than the second magnitude scale and consequently close to

directly measured by an
UBV photometer. The cause is the emission spectrum of

Car and the narrowness of the
y passband. See also (277).
b Note that the HDptg 1900 = 8.7, listed in the HD catalogue, has been derived from the HDptm, by adding the colour index -0.2 (see the Introduction to the HD catalogue), assuming zero reddening. Since the reddening appears to be substantial (Col. 2), the HDptg 1900 must be considered as erroneous.
c This is the outside-eclipse magnitude, but supposed to be the minimum of possible S Dor phases.
d Based on the spectral types in minimum light (B5Iae) and maximum light (A0Ia, see note
d in Table 4) and
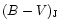
= 0.1 (9) and 0.18 (63), respectively.
e VBLUW photometry, made in eight nights in 1975 and 1976 are listed in Table 7. The

given above is an average based on a compilation in (10), complemented with the data in Table 7 and in (165), (166) and (167).
f At maximum light the apparent magnitude

= 11.6. In view of the reddening (Col. 2), the ``HDptm'' could have been between 11.1 and 11.6.
Table 6:
Time scales and amplitudes of the light variations of the w-a S Dor variables
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
| designation |
L-SD |
S-SD |
microvar. |
ref. |
light curve/ |
| HD/HDE |
(yr, mag) |
(yr, mag) |
(d, mag) |
|
light history |
 Cara Cara |
|
1-6 |
58.6 |
84,184,187,188,192,195,205, |
Fig. 11b |
| |
|
0.2-0.4 |
0.04-0.08 |
245,246,247,248,277,298 |
|
| P Cygc |
|
8.2d |
17.3 |
147,148,169,204 |
|
| |
|
0.06 |
0.05-0.15 |
|
|
| |
|
|
70-150 |
|
|
| |
|
|
0.2 |
|
|
| 168607e |
|
1.8d |
62 |
80,253 |
Table 16 |
| |
|
0.2 |
0.2 |
|
|
| CygOB2#12 |
(50) |
|
? |
163 |
|
| |
(0.2) |
|
0.3 |
|
|
| R74 |
|
|
42.1 |
8 |
|
| |
|
|
0.25 |
|
|
| R81 |
>50? |
|
24.1 |
38 |
Fig. 12, |
| |
>1 |
|
0.17 |
|
Table 16 |
| R85 |
30-40 |
1.1 |
15-180 |
63 |
Fig. 13 |
| |
0.3 |
0.1 |
0.01-0.2 |
|
|
| R99 |
30 |
|
2.1, 10 |
91 |
Fig. 14 |
| |
0.3 |
|
0.15 |
|
|
| R123 |
|
0.8 |
3.9; 1.3 |
91 |
Fig. 15, |
| |
|
0.2 |
0.13 |
|
Table 16 |
| R149 |
|
>0.5? |
? |
166 |
|
| |
|
0.1 |
(0.3)f |
|
|
| 34664g |
|
7 |
47.2 |
8 |
Fig. 16 |
| |
|
0.04 |
0.14 |
|
|
| 38489h |
|
|
|
10 |
Fig. 17 |
Notes to Table 6:
a Showed a number of presumable SD-eruptions between 1827 and 1857, and a single SD-eruption around 1870 and once more around
1890, see next note.
b The historical observations (until 1910) include a few observations between 1600 and 1800. After 1935 a gradual rise set in, called the ``secular rise'' and has been interpreted as largely caused by a decrease of circumstellar extinction by the expanding bipolar nebula (178), see also (206) and (274). In Fig. 11, showing a schematic light curve, all observations after 1970 which are not measured by an
UBV photometer are corrected according to our transformation equations to fit the

directly measured by an
UBV photometer. See note
a in Table 5 and (277).
Superimposed on the secular rise (after 1960) the frequent SD-phases with a time scale of 1-6 yr and an amplitude of about 0

2 are schematically indicated. The last one of 1999-2000 has an amplitude twice as high (192), (243), (277), (298).
c Showed a number of SD-eruptions between 1600 and 1700 (150), (151). Balmerline shell ejections were observed on a time scale of a few months to half a year (152), (237), (238) and (249).
d This very low-amplitude oscillation is possibly an SD-phase: the
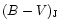
tends to be red in the maxima and blue in the minima. See for P Cyg the discussion in Sect. 3.2.2.
e Note that the star was possibly fainter around 1900, see Table 5. The 640d (1.8yr) peak in the Fourier analysis is likely due to an S-SD phase, clearly visible in Fig. 5 of (253) and not an artifact.
f This relative high amplitude, based on the references mentioned in note
e in Table 5, may be partly caused by the SD-phase mentioned in Col. 3 of Table 6.
g Note that the amplitude of the microvariations is larger than that of the S-SD phase, see Fig. 16.
h It is uncertain to what type the probable long-term light variation (with unknown time scale) with an amplitude of 0

5 belongs, see also Fig. 17 and notes
i and
f
in Tables 4 and 5, respectively.
Table 7:
VBLUW photometry of R149 (in log intensity scale) and the transformed values in the UBV system (in magnitude scale) with subscript J, made in 1975 and 1976
| JD - |
V |
V-B |
B-U |
U-W |
B-L |
 |
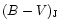 |
| 2440000 |
|
|
|
|
|
|
|
| 2712.555 |
-2.202 |
-0.003 |
-0.072 |
0.13 |
-0.030 |
12.39 |
-0.02 |
| 2714.552 |
-2.208 |
0.002 |
-0.080 |
0.08 |
-0.042 |
12.41 |
0.00 |
| 2813.382 |
-2.200 |
-0.008 |
-0.097 |
|
-0.047 |
12.39 |
-0.03 |
| 2818.362 |
-2.212 |
-0.005 |
-0.074 |
|
-0.040 |
12.42 |
-0.02 |
| 2830.282 |
-2.216 |
-0.012 |
-0.103 |
|
-0.042 |
12.43 |
-0.04 |
| 2838.299 |
-2.205 |
0.005 |
-0.089 |
|
-0.033 |
12.40 |
0.00 |
| 2862.288 |
-2.191 |
0.017 |
-0.085 |
|
-0.026 |
12.36 |
0.03 |
| 2869.344 |
-2.218 |
-0.004 |
-0.090 |
|
-0.040 |
12.43 |
-0.02 |
Table 8:
Selected particulars of the ex-/dormant S Dor variables
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
(9) |
| designation |
Sp |
date |
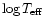 |
MV |
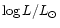 |
ref. |
g?d? |
ref. |
| HD/HDE |
|
|
|
|
|
|
|
|
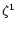 Sco Sco |
B1.5Ia+ |
1985-1995 |
4.29 |
-8.5 |
6.02 |
56,pp |
|
|
| = 152236 |
|
|
|
|
|
|
|
|
| 168625 |
B5.6/8Ia+ |
1982-2000 |
4.15 |
-7.3 |
5.23 |
36 |
y y |
173,250,252 |
| = V4030 Sgr |
|
|
|
|
|
|
|
|
| 326823 |
B1.5Ie |
1960-1990 |
4.29 |
-6.0 |
4.98 |
68,106 |
|
|
=
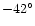 11834a 11834a |
|
|
|
|
|
|
|
|
| He3-519 |
WN11 |
1985-1992 |
4.48 |
(-7.9) |
(6.26) |
29,129, |
y y |
135,173,250,251 |
| |
|
|
|
|
|
257 |
|
|
| 316285 |
BIe |
1984-1996 |
4.18 |
-8.4 |
5.44 |
33 |
|
|
| = He3-1482 |
|
|
|
|
|
|
|
|
| S61 |
Ofpe/WN9 |
1970-2000 |
4.45 |
-7.0 |
5.84 |
pp,154 |
y y |
173,250 |
= Sk
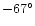 266 266 |
|
|
|
|
|
|
|
|
Sk
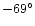 279 279 |
O9f |
1980-2000 |
4.48 |
-6.4 |
5.68 |
158,pp |
y |
155,156,279 |
| S119 |
WN11h |
1970-2000 |
4.44 |
-6.8 |
5.80 |
22b |
y ? |
173,250,251,279 |
| = 269687 |
|
|
|
|
|
|
|
|
Notes to Table 8:
a CoD number.
b Model B.
Table 9:
Selected particulars of the ex-/dormant S Dor variables
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
| designation |
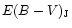 |
ref |
r |
ref. |
 |
ref. |
add.ref. |
| HD/HDE |
|
|
(kpc) |
|
mean |
|
[Remarks] |
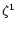 Scoa Scoa |
0.65 |
53,55, |
1.8 |
53,54, |
4.75a |
57,58, |
59,80,207 |
| |
|
208 |
|
209 |
|
198-201 |
|
| 168625b |
1.7 |
34 |
1.2 |
36 |
8.4b |
38,89, |
35,37,48,66,198-201 |
| |
|
|
|
|
|
66,80, |
[HDptm 1900 = 9.2, |
| |
|
|
|
|
|
253 |
VJ 1956 = 8.41 (89)] |
| 326823c |
1.15 |
105,106 |
2 |
106 |
9.1 |
105 |
32,83,119 |
| He3-519d |
1.3 |
29,129, |
(8) |
129 |
11.0d |
29,131 |
24,135 |
| |
|
257 |
|
|
|
|
[m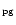 1949-1950 1949-1950  |
| |
|
|
|
|
|
|
10.5 (130)] |
| 316285 |
1.81 |
33 |
1.85 |
33 |
9.1 |
33 |
32,211 |
| S61 |
0.18 |
92,153 |
|
|
12.0 |
49 |
154 |
Sk
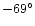 279 279 |
0.25 |
pp |
|
|
12.8 |
23 |
157,244 |
| S119e |
0.09 |
1 |
|
|
11.95e |
1,23 |
24,25,244 |
| |
|
|
|
|
|
|
[HDEptg 1925 = 11.4] |
Notes to Table 9:
a The star was much brighter in the 18th and 19th century, see (58).
b Note that the HDptg = 9.0 (listed in the HD catalogue) has been derived from the HDptm = 9.2 by adding the estimated colour index -0.2, assuming that the reddening is zero. Since the reddening appears to be substantial (Col. 2), the HDptg is erroneous. The HDptm 1900 = 9.2 suggests that the star was

0

8 fainter around 1900 than at present.
c According to (104) and (105) perhaps an ex-S Dor variable on its way to the WN-stage, see note
c in Table 10.
d According to (130) the star was possibly brighter in the interval 1949-1950, see [Remarks]. If this is the case, the star could be a w-a S Dor variable.
e It is not certain whether the magnitude difference with the HDEptg 1925, see the [Remarks], should be taken seriously.
Table 10:
Time scales and amplitudes of the light variations of the ex-/dormant S Dor variables
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
| designation |
L-SD |
S-SD |
microvar. |
ref. |
light curve/ |
| HD/HDE |
(yr, mag) |
(yr, mag) |
(d, mag) |
|
light history |
 Sco Sco |
|
|
2000a |
56,58,84 |
Table 16 |
| |
|
|
0.02 |
|
|
| |
|
|
32 |
|
|
| |
|
|
0.1 |
|
|
| |
|
|
25.7 |
|
|
| |
|
|
0.1 |
|
|
| 168625b |
|
|
35 |
38,66,80,253 |
Table 16 |
| |
|
|
0.06 |
|
|
| 326823c |
|
|
6 |
105,119 |
|
| |
|
|
0.1 |
|
|
| He3-519d |
|
|
|
|
Table 16 |
| 316285e |
|
|
? |
33 |
|
| |
|
|
 0.1 0.1 |
|
|
| S61 |
|
|
|
|
|
Sk
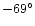 279 279 |
|
|
|
|
|
| S119 |
|
|
|
|
|
Notes to Table 10
a The colour becomes bluer in the light maximum, thus, this periodicity/cyclicity is presumably no SD-phase.
b See note
b in Table 9 on a possible long-term light variation.
c While the object showed an increasing trend of the brightness between 1990 and 1994, the colour became bluer which is unlike an SD-phase, see note
c in Table 9. Further, the photometric observations by (105) show a long-term oscillation of 396d and an amplitude of 0

2, but it is unknown whether they should be classified as an S-SD phase, in which case the object should be a w-a S Dor variable.
d See note
d in Table 9 on a possible long-term light variation.
e According to (33) hardly variable (
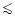
0.1) since 1890, also according to the Hipparcos data quoted by (103).
Table 11:
Selected particulars of the candidate (+ and -) and former candidate (0) S Dor variables
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
(9) |
(10) |
| designation |
Sp. |
cand. |
date |
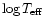 |
MV |
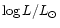 |
ref. |
g?d? |
ref. |
| HD/HDE |
|
|
|
|
|
|
|
|
|
| 80077 |
B2/3Ia+ |
+ |
1975-1995 |
4.23 |
(-9.4) |
(6.30) |
38,236 |
|
|
| 148937 |
O6.5f |
- |
1960-1995 |
4.58 |
-6.0 |
5.68 |
132,170, |
|
|
| |
|
|
|
|
|
|
171 |
|
|
| WRA977 |
B1.5Ia+ |
0 |
1970-1995 |
4.28 |
-8.7 |
6.06 |
39,59 |
|
|
| = BP Cru |
|
|
|
|
|
|
|
|
|
| = Hen788 |
|
|
|
|
|
|
|
|
|
| AS314 |
B9Ia |
+ |
1983-1997 |
4.01 |
(-7.0) |
(4.9) |
222 |
y y |
222,223 |
| = V452 Sct |
|
|
|
|
|
|
|
|
|
| = LS5017 |
|
|
|
|
|
|
|
|
|
| IRC+10420a |
F8Ia+- |
+ |
1975-1994 |
3.90b |
(-10.0) |
(5.80) |
260,284 |
y y |
176,260,261,262, |
| |
mid-Ab |
|
|
|
|
|
|
|
286 |
| MWC314 |
< B2 |
+ |
1954-1995 |
4.48 |
(-8.2) |
(6.34) |
210,222 |
|
|
| = V1492 Aql |
|
|
|
|
|
|
|
|
|
| = BD+14 3887 |
|
|
|
|
|
|
|
|
|
| G79.29+0.46 |
|
+ |
1983-2000 |
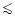 4.40 4.40 |
|
(6.3) |
60 |
y |
250 |
| G25.5+0.2c |
|
+ |
1983-1993 |
|
c |
|
172 |
y |
250 |
| Pistol Star |
|
+ |
1994-1998 |
4.15d |
-10.8 |
6.61d |
265 |
y y |
265 |
| |
|
|
|
4.33e |
-11.3 |
7.20e |
265 |
|
|
| S18 |
B[e] |
- |
1975-1995 |
4.40 |
-6.7 |
5.58 |
226 |
|
|
| 5980f |
WN3+OB |
+ |
min of |
|
|
|
218,219, |
|
|
| = R14 |
|
|
1950-1980 |
|
|
|
220 |
|
|
| |
WN11+OB |
|
max of |
|
(-10.7) |
|
pp |
|
|
| |
|
|
1994.8 |
|
|
|
|
|
|
| R78 |
B0Ia |
- |
1960-1990 |
4.41 |
-7.4 |
5.80 |
45 |
|
|
| = 269050 |
|
|
|
|
|
|
|
|
|
| R84 |
WN9 |
- |
1960-1995 |
4.46 |
-6.8g |
5.77 |
22 |
? ? |
173,250 |
| = 269227 |
|
|
|
|
|
|
|
|
|
| 269604 |
A1Ia+ |
0 |
1970-1985 |
3.96 |
-8.0 |
5.20 |
pp |
|
|
| R128 |
B2Ia |
0 |
1960-1995 |
4.24 |
-8.2 |
5.76 |
90 |
|
|
| = 269859 |
|
|
|
|
|
|
|
|
|
Notes to Table 11:
a Considered as a variable yellow hypergiant by (270) and (284). See the discussion in Sect. 3.2.5 of the present paper.
b According to (285) the spectral type evolved to mid-A in 1994. The temperature has been determined from that spectrum by (284). See also the discussion in Sect. 3.2.5 of the present paper.
c MK = -7 according to (172).
d Model L of (265).
e Model H of (265).
f Showed two SD-type eruptions, one in 1993 and a second in 1994. Since the true nature of the multiple star (including an eclipsing binary), is far from being understood, no proper physical and photometric parameters on the possible S Dor variable in the system can be given.
g The apparent visual magnitude has been corrected for the faint field stars in the aperture, see (8).
Table 12:
Selected particulars of the candidate and former candidate S Dor variables
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
| designation |
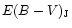 |
ref. |
r |
ref. |
 |
ref. |
add.ref. |
| HD/HDE |
|
|
(kpc) |
|
mean |
|
[Remarks] |
| 80077 |
1.47 |
38,235 |
(3) |
232,233 |
7.5 |
38,232 |
66,234 |
| |
|
|
|
|
|
|
[HDptm 1900 = 7.9; |
| |
|
|
|
|
|
|
HDptg 1900 = 9.0] |
| 148937 |
0.60 |
pp,171 |
1.38 |
132 |
6.7 |
170 |
174 |
| WRA977 |
1.65 |
39,59 |
5-8 |
39,59 |
10.9 |
39 |
|
| AS314 |
0.9 |
222 |
(8) |
222 |
|
|
|
| IRC+10420 |
2.2 |
175 |
(5) |
175 |
11.0 |
175 |
176,177,270 |
| MWC314 |
1.84 |
210 |
(3) |
222 |
9.9 |
210 |
|
| G79.29+0.46 |
5-2 |
60,196 |
2-4 |
60,196 |
|
|
61 |
| G25.5+0.2 |
10 |
172 |
(14.5) |
172 |
|
|
173 |
| Pistol Star |
8-11 |
266 |
8 |
268 |
|
|
267 |
| S18a |
0.4 |
225 |
|
|
13.55a |
227 |
228,229,230,231 |
| 5980b |
0.07 |
218 |
|
|
c |
|
213,214,216,217,220,221 |
| R78 |
0.15 |
pp |
|
|
11.7 |
8 |
9,10,49 |
| |
|
|
|
|
|
|
[HDptg 1925 = 11.2] |
| R84 |
0.18 |
26 |
|
|
12.1d |
8,27 |
10,11,21,28,29,30,31 |
| |
|
|
|
|
|
|
[HDEptg 1925 = 11.6] |
| 269604 |
0.10 |
pp |
|
|
10.8 |
10 |
|
| R128 |
0.12 |
90 |
|
|
10.6 |
90,91 |
10,57 |
| |
|
|
|
|
|
|
[HDEptg 1925 = 10.9] |
Notes to Table 12:
a Star strongly variable, see Table 13 and Fig. 19.
b There is an eclipsing binary in the system (215), with
P = 19.2654d and an amplitude amounting to

0

2 (212).
c 
(min) = 11.7,

(max) = 8.5 (83), (213).
d Corrected for the field stars in the aperture.
Table 13:
Time scales and amplitudes of the light variations of the candidate and former candidate S Dor variables
| (1) |
(2) |
(3) |
(4) |
(5) |
| designation |
cand |
microvar. |
ref. |
light curve |
| HD/HDE |
|
(d, mag) |
|
|
| 80077a |
+ |
41-66 |
38,66 |
|
| |
|
0.2a |
|
|
| 148937b |
- |
|
170 |
|
| WRA977 |
0 |
11.90c |
90 |
|
| |
|
0.14 |
|
|
| AS314 |
+ |
|
|
|
| IRC+10420 |
+ |
|
|
|
| MWC314d |
+ |
4.16? |
210 |
|
| |
|
0.1 |
|
|
| G79.29+0.46 |
+ |
|
|
|
| G25.5+0.2 |
+ |
|
|
|
| Pistol Stare |
+ |
|
|
|
| S18f |
- |
|
|
Fig. 19 |
| 5980g |
+ |
0.25g |
212 |
|
| |
|
0.1 |
|
|
| R78 |
- |
3.6-3.9? |
8,9 |
|
| |
|
0.1 |
|
|
| R84 |
- |
h |
8 |
|
| 269604 |
0 |
? |
10 |
|
| |
|
0.18 |
|
|
| R128 |
0 |
3.444 |
91 |
|
| |
|
0.25 |
|
|
Notes to Table 13:
a The maximum light amplitude, MLA = 0

2, is too high for a normal
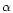
Cyg variable (39). Therefore, it is not excluded that it may be partly due to a very weak SD-phase (38). Thus, this is in conflict with the supposition of (235) and (236) that it is no S Dor variable, but a hot blue hypergiant.
b The apparent magnitude

became gradually brighter on a long-term basis by

0

1 between 1960 and 1987. Between 1981 and 1987 the star showed microvariations
0

01
exclusively in blue and ultraviolet light on a time scale of months (170).
c This is a quasi-period which appeared to be stable on a time basis of 17yr (39).
d According to a compilation of optical photometry made between 1954 and 1992 by (210),

varied by

0

1. However, it is unknown whether this is caused by a long-term variation, or by microvariations, see Col. 3.
e The light variations in the
H and
K passbands lie barely outside the errors of the data (265).
f The long-term light variations with a time scale of months and an amplitude of
,
are no SD-phases, see Fig. 19. These observations are based on preliminary
VBLUW photometry. The
V of this system has been transformed to the
V of the
UBV system (with subscript J) (231).
g It is uncertain which of the stars in the system is responsible for the this pulsation-type of light variation (212).
h No significant light variation was detected during the photometric monitoring between 1988 and 1991.
Table 14:
Bibliographical references mentioned in the Tables 1-6 and 8-13 are codified as follows
| No. |
Reference |
No. |
Reference |
No. |
Reference |
| 1 |
L. Smith et al. 1998 |
50 |
van Genderen et al. 1982 |
101 |
de Koter et al. 1996 |
| 2 |
Parker et al. 1993 |
51 |
Appenzeller et al. 1979 |
102 |
van Genderen et al. 1990 |
| 3 |
Walraven et al. 1977 |
53 |
van Genderen et al. 1984 |
103 |
de Koter et al. 1993b |
| 4 |
Walborn et al. 1997 |
54 |
Percy et al. 1991 |
104 |
Lopes et al. 1992 |
| 5 |
Stahl et al. 1983 |
55 |
Leitherer et al. 1984 |
105 |
Sterken et al. 1995b |
| 6 |
Stahl et al. 1986 |
56 |
Rivinius et al. 1997 |
106 |
Kozak 1985 |
| 7 |
van Genderen et al. 1997b |
57 |
van Genderen 2000 |
107 |
Viotti 1971 |
| 8 |
van Genderen/Sterken 1999 |
58 |
Sterken et al. 1997a |
108 |
Wisse et al. 1971 |
| 9 |
Feast et al. 1960 |
59 |
Kaper et al. 1995 |
109 |
de Koter et al. 1993a |
| 10 |
Stahl et al. 1984a |
60 |
Higgs et al. 1994 |
110 |
Hutsemékers et al. 1991 |
| 11 |
Stahl et al. 1985 |
61 |
Waters et al. 1996 |
111 |
van Genderen et al. 1991 |
| 12 |
Shore et al. 1984 |
62 |
Stahl et al. 1990 |
112 |
Clampin et al. 1995 |
| 13 |
Muratorio et al. 1988 |
63 |
van Genderen et al. 1998b |
113 |
de Winter et al. 1992 |
| 14 |
Zickgraf et al. 1996b |
64 |
Prinja et al. 1991 |
114 |
Hu et al. 1990 |
| 15 |
Zickgraf et al. 1986 |
65 |
Schild 1987 |
115 |
van Genderen et al. 1992a |
| 16 |
Zickgraf et al. 1985 |
66 |
van Leeuwen et al. 1998 |
116 |
de Winter 1996 |
| 17 |
Friedjung et al. 1980 |
67 |
Zickgraf et al. 1996a |
117 |
Wray 1966 |
| 18 |
Shore 1990 |
68 |
McGregor et al. 1988a |
118 |
Henize 1976 |
| 19 |
Shore 1992 |
69 |
van Genderen et al. 1985 |
119 |
A. Jones et al. 1997 |
| 20 |
Schulte-Ladbeck et al. 1993 |
70 |
van Genderen et al. 1997a |
120 |
Weis et al. 1997 |
| 21 |
Allen et al. 1976 |
71 |
Lamers 1995 |
121 |
McGregor et al. 1988b |
| 22 |
Crowther et al. 1997 |
72 |
Stahl et al. 1982 |
122 |
Nota et al. 1997 |
| 23 |
Isserstedt 1975 |
73 |
Leitherer et al. 1985 |
123 |
Voors et al. 1997 |
| 24 |
Nota et al. 1995a |
74 |
van Genderen 1979b |
124 |
L Smith et al. 1997 |
| 25 |
Nota et al. 1994 |
75 |
Martini 1969 |
125 |
Whitelock et al. 1983b |
| 26 |
Crowther et al. 1995 |
76 |
de Koter 1993 |
126 |
Garcia-Lario et al. 1998 |
| 27 |
Heydari-Malayeri et al. 1997b |
77 |
Sterken et al. 1991 |
127 |
Schulte-Ladbeck et al. 1994 |
| 28 |
Vacca et al. 1990 |
78 |
Lamers et al. 1998 |
128 |
Shore et al. 1996 |
| 29 |
L. Smith et al. 1994 |
79 |
Hiltner 1954 |
129 |
Davidson et al. 1993 |
| 30 |
Walborn 1982 |
80 |
Sterken 1977 |
130 |
Henize 1952 |
| 31 |
Schmutz et al. 1991 |
81 |
Sterken 1981 |
131 |
Stahl 1986 |
| 32 |
Shore et al. 1990 |
82 |
Sterken 1976 |
132 |
Humphreys 1978 |
| 33 |
Hillier et al. 1998 |
83 |
Sterken et al. 1996c |
133 |
Chini et al. 1980 |
| 34 |
Nota et al. 1996a |
84 |
Sterken et al. 1997b |
134 |
Zickgraf 1997 |
| 35 |
Nota et al. 1996b |
85 |
Westerlund 1961 |
135 |
Stroud 1997 |
| 36 |
Robberto et al. 1998 |
86 |
Clayton et al. 1985 |
136 |
Szeifert et al. 1993 |
| 37 |
Hutsemékers et al. 1994 |
87 |
van Genderen 1970 |
137 |
Sterken et al. 1998 |
| 38 |
van Genderen et al. 1992b |
88 |
Mendoza 1970 |
138 |
Venn 1997 |
| 39 |
van Genderen et al. 1996 |
89 |
Hiltner 1956 |
139 |
Wolf et al. 1981 |
| 40 |
Hofleit 1933 |
90 |
Walborn et al. 1991 |
140 |
Stahl et al. 1987 |
| 41 |
Hofleit 1940 |
91 |
van Genderen et al. 1998a |
141 |
Brunet 1975 |
| 42 |
Lennon et al. 1994 |
92 |
Pasquali et al. 1997a |
142 |
Najarro et al. 1997 |
| 43 |
van Genderen et al. 1988 |
93 |
Pasquali et al. 1997b |
143 |
Lamers et al. 1983 |
| 44 |
Thackeray 1974 |
94 |
Stahl/Wolf 1987 |
144 |
Markova et al. 1997 |
| 45 |
van Genderen et al. 1983 |
95 |
Stahl et al. 1984a |
145 |
Turner 1985 |
| 46 |
Spoon et al. 1994 |
96 |
Lamers et al. 1989 |
146 |
de Groot 1969 |
| 47 |
Voors et al. 1999 |
97 |
Humphreys et al. 1989 |
147 |
de Groot et al. 2001 |
| 48 |
Chentsov et al. 1990 |
98 |
Hoekzema et al. 1992 |
148 |
van Genderen 1991b |
| 49 |
Ardeberg et al. 1972 |
99 |
Leitherer et al. 1994 |
149 |
Meaburn et al. 1996 |
| 50 |
Code et al. 1958 |
100 |
Sterken et al. 1996a |
150 |
Lamers et al. 1992 |
Table 15:
Continuation of Table 14
| No. |
Reference |
No. |
Reference |
No. |
Reference |
| 151 |
de Groot et al. 1992 |
201 |
Sterken et al. 1995a |
251 |
L. Smith 1997 |
| 152 |
van Gent et al. 1986 |
202 |
Innes 1903 |
252 |
Skinner 1997 |
| 153 |
Pasquali et al. 1999 |
203 |
de Vaucouleurs et al. 1952 |
253 |
Sterken et al. 1999c |
| 154 |
Bohannan et al. 1989 |
204 |
Percy et al. 1988 |
254 |
Pacheco et al. 1992 |
| 155 |
Weis et al. 1995 |
205 |
Whitelock et al. 1983 |
255 |
Skinner et al. 1998 |
| 156 |
Weis 1996 |
206 |
Whitelock et al. 1994 |
256 |
Appenzeller et al. 1987 |
| 157 |
Conti et al. 1986 |
207 |
Burki et al. 1982 |
257 |
Humphreys et al. 1994 |
| 158 |
Thompson et al. 1982 |
208 |
Schild et al. 1969 |
258 |
Walborn et al. 1978 |
| 159 |
Schulte 1958 |
209 |
Bieging et al. 1989 |
259 |
Lester et al. 1986 |
| 160 |
Reddish et al. 1967 |
210 |
Miroschnichenko 1996 |
260 |
Blöcker et al. 1999 |
| 161 |
Torres-Dodgen et al. 1991 |
211 |
van der Veen et al. 1994 |
261 |
Oudmaijer et al. 1994 |
| 162 |
Massey et al. 1991 |
212 |
Sterken et al. 1997 |
262 |
Klochkova et al. 1997 |
| 163 |
Gottlieb et al. 1978 |
213 |
Bateson et al. 1994 |
263 |
Hoekzema et al. 1993 |
| 164 |
Souza et al. 1980 |
214 |
Breysacher 1997 |
264 |
Viotti et al. 1988 |
| 165 |
Dufour et al. 1975 |
215 |
Breysacher et al. 1991 |
265 |
Figer et al. 1998 |
| 166 |
Warren et al. 1975 |
216 |
Moffat et al. 1998 |
266 |
Catchpole et al. 1990 |
| 167 |
C. Jones et al. 1974 |
217 |
Heydari-Malayeri et al. 1997a |
267 |
Cotera et al. 1996 |
| 168 |
van Genderen et al. 1982 |
218 |
Koenigsberger et al. 1998b |
268 |
Kaplan et al. 1970 |
| 169 |
Markova et al. 1998 |
219 |
Koenigsberger et al. 1998a |
269 |
Hamann et al. 1994 |
| 170 |
van Genderen et al. 1989 |
220 |
Barba et al. 1995 |
270 |
de Jager 1998 |
| 171 |
Leitherer et al. 1987 |
221 |
Barba et al. 1997 |
271 |
Massey 2000 |
| 172 |
Subrahmanyari et al. 1993 |
222 |
Miroschnichenko et al. 1999 |
272 |
Massey et al. 2000 |
| 173 |
Hutsemékers 1997 |
223 |
Dong et al. 1991 |
273 |
Robberto et al. 1993 |
| 174 |
Leitherer et al. 1997 |
224 |
Vakili et al. 1999 |
274 |
Menshchikov 1989 |
| 175 |
T. Jones et al. 1993 |
225 |
Zickgraf et al. 1989a |
275 |
Pasquali et al. 2000 |
| 176 |
Kastner et al. 1995 |
226 |
Zickgraf et al. 1989b |
276 |
Polomski et al. 1999 |
| 177 |
Oudmaijer et al. 1996 |
227 |
Azzopardi et al. 1975 |
277 |
Sterken et al. 2001 |
| 178 |
van Genderen et al. 1994 |
228 |
McGregor et al. 1989 |
278 |
Morris et al. 1999 |
| 179 |
Burgarella et al. 1991 |
229 |
Shore et al. 1987 |
279 |
Weis 1999 |
| 180 |
Pottasch et al. 1976 |
230 |
Nota et al. 1995b |
280 |
Langer et al. 1994 |
| 181 |
Davidson/Humphreys 1997 |
231 |
van Genderen/Sterken 2001 |
281 |
Stothers 1999b |
| 182 |
van Genderen et al. 1984 |
232 |
Steemers et al. 1986 |
282 |
Bohigas et al. 2000 |
| 183 |
P. Cox et al. 1995 |
233 |
Moffat et al. 1977 |
283 |
Icke 1981 |
| 184 |
van Genderen et al. 1999 |
234 |
Knoechel et al. 1982 |
284 |
Nieuwenhuijzen et al. 2000 |
| 185 |
Damineli et al. 1997 |
235 |
Carpay et al. 1989 |
285 |
Oudmaijer 1998 |
| 186 |
Ebbets et al. 1997 |
236 |
Carpay et al. 1991 |
286 |
Oudmaijer 1995 |
| 187 |
Sterken et al. 1996b |
237 |
Markova 1986 |
287 |
Damineli et al. 2000 |
| 188 |
van Genderen et al. 1995 |
238 |
Kolka 1983 |
288 |
Davidson et al. 2000 |
| 189 |
Meaburn et al. 1993 |
239 |
Israelian et al. 1999 |
289 |
N. Smith et al. 2000 |
| 190 |
Hillier et al. 1992 |
240 |
Barlow et al. 1994 |
290 |
Pantin et al. 2000 |
| 191 |
Viotti et al. 1989 |
241 |
Meaburn et al. 1999 |
291 |
Voors et al. 2000 |
| 192 |
Sterken et al. 1999a |
242 |
Glover et al. 1997 |
292 |
Duschl et al. 1995 |
| 193 |
Damineli 1996 |
243 |
Davidson et al. 1999 |
293 |
Gäng 2000 |
| 194 |
Allen et al. 1993 |
244 |
Smith-Neubig et al. 1999 |
294 |
Viotti et al. 1999 |
| 195 |
Stothers et al. 1997 |
245 |
Sterken et al. 1999b |
295 |
Corcoran et al. 1999 |
| 196 |
Voors 1999 |
246 |
de Groot et al. 1997a |
296 |
Duncan et al. 1999 |
| 197 |
van Genderen 1979a |
247 |
de Groot et al. 1997b |
297 |
Weis 2000 |
| 198 |
Manfroid et al. 1991 |
248 |
de Groot et al. 1996b |
298 |
van Genderen et al. 2001 |
| 199 |
Sterken et al. 1993 |
249 |
Kolka 1999 |
299 |
Walsh et al. 2000 |
| 200 |
Manfroid et al. 1994 |
250 |
Nota/Clampin 1997 |
|
|
Table 16:
Overview of the presumable trends of the brightness in the intervals before 1950 and between 1950 and 2000, their amplitudes, the duration of the low stages and the time scales, for 17 S Dor variables
| designation |
category |
brightness/activity |
ampl. |
 |
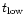 |
references |
| HD/HDE |
|
<1950 |
1950-2000 |
(mag) |
(yr) |
(yr) |
|
| 160529a |
s-a |
(high) |
high |
0.5 |
|
|
Fig. 2 |
| WRA751 |
s-a |
high |
low |
2 |
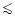 35 35 |
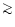 10 10 |
Fig. 3 |
| R40 |
s-a |
low |
high |
0.8 |
35 |
|
7,137; Tables 2 and 3 |
| R71b |
s-a |
high |
lowb |
1.7 |
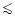 25 25 |
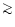 15 15 |
Fig. 4 |
| R110 |
s-a |
(low) |
high |
1.1 |
35 |
|
Fig. 5 |
| R116 |
s-a |
high |
low |
1.2 |
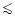 40 40 |
40-70 |
Fig. 6 |
| R127 |
s-a |
low |
high |
2.4 |
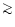 20 20 |
10 |
Fig. 7 |
| R143 |
s-a |
high |
low |
1.4 |
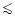 20 20 |
 10 10 |
Fig. 8 |
| HV5495 |
s-a |
high |
low |
1.5 |
|
(
 20) 20) |
Fig. 10 |
| P Cygc |
w-a |
|
low |
|
|
 300 300 |
147,150,151 |
| 168607 |
w-a |
low |
high |
0.7 |
 55 55 |
|
38,66,80,253; |
| |
|
|
|
|
|
|
Tables 5 and 6 |
| R81 |
w-a |
high |
low |
0.9 |
 70 70 |
50 |
Fig. 12 |
| R123 |
w-a |
high |
low |
1.2 |
 50 50 |
 20 20 |
Fig. 15 |
 Sco Sco |
ex/d |
high |
low |
2 |
 100 100 |
100 |
58; Tables 9 and 10 |
| 168625d |
ex/d |
low |
high |
0.8 |
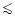 55 55 |
|
38,66,80,253; |
| |
|
|
|
|
|
|
Tables 9 and 10 |
| He3-519 |
ex/d |
(high) |
(low) |
(0.5) |
(
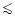 35) 35) |
|
Tables 9 and 10 |
| S119 |
ex/d |
(high) |
(low) |
(0.5) |
(
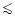 45) 45) |
|
Tables 9 and 10 |
Notes to Table 16:
a According to Fig. 2, the star is probably active since at least 1890, thus
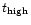

110yr.
b The star was also ``high'' between 1970 and 1980, but much less than before 1950. After 1980 and until 1995 the star behaved as a w-a S Dor variable. New observations have been made by Sterken after 1995. The results will be published in due course.
c It is unknown whether the ``high'' state in the 17th century was only due to SD-eruptions, or whether also SD-phases were involved.
d This star seems to be brighter at present (thus, in the interval 1950-2000) than around 1900, but there is no SD-activity detected in the present photometry.
![]() The relatively small dispersion of less active and supposed ex- and dormant S Dor variables with respect to this relation is twice as large at the blue side than at the red side. This might be caused by evolution to the WR stage and/or to high rotation.
S Dor variables can be subject to five types of instabilities: the very rare genuine eruptive episodes (the "SD-eruptions''), two different brightening phases caused by slow pulsations (the "SD-phases''): one on a time scale of years, the other on a time scale of decades at a more or less constant luminosity and two types of microvariations: one on a time scale of weeks, the other on a time scale of about 100d.
So far, no periodicities of light curve characteristics of any of these instabilities have ever been found.
The durations of active and non-active stages are estimated for about half of the sample based on scattered magnitude estimations such as from historical records, and on modern monitoring campaigns. It would be a misunderstanding to believe that all S Dor variables should be always spectacular. It is estimated that most of them will not be spectacular at all for at least 70% of their lifetime as an S Dor variable.
The relatively small dispersion of less active and supposed ex- and dormant S Dor variables with respect to this relation is twice as large at the blue side than at the red side. This might be caused by evolution to the WR stage and/or to high rotation.
S Dor variables can be subject to five types of instabilities: the very rare genuine eruptive episodes (the "SD-eruptions''), two different brightening phases caused by slow pulsations (the "SD-phases''): one on a time scale of years, the other on a time scale of decades at a more or less constant luminosity and two types of microvariations: one on a time scale of weeks, the other on a time scale of about 100d.
So far, no periodicities of light curve characteristics of any of these instabilities have ever been found.
The durations of active and non-active stages are estimated for about half of the sample based on scattered magnitude estimations such as from historical records, and on modern monitoring campaigns. It would be a misunderstanding to believe that all S Dor variables should be always spectacular. It is estimated that most of them will not be spectacular at all for at least 70% of their lifetime as an S Dor variable.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{sdfig1.eps} \end{figure}](/articles/aa/full/2001/05/aads1896/Timg21.gif)
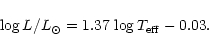
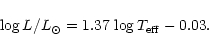
![]() and
and
![]() ,
thus, different from the values
listed in Table 11.
,
thus, different from the values
listed in Table 11.
![\begin{figure}
\includegraphics[width=6.5cm,clip]{sdfig3.eps} \end{figure}](/articles/aa/full/2001/05/aads1896/Timg87.gif)
![\begin{figure}
\includegraphics[width=8cm,clip]{sdfig7.eps}\end{figure}](/articles/aa/full/2001/05/aads1896/Timg91.gif)