A&A 366, 708-716 (2001)
DOI: 10.1051/0004-6361:20000110
Wavefront coherence time seasonal variability and forecasting
at the San Pedro Mártir site
E. Masciadri
- T. Garfias
Instituto de Astronomía, Universidad Nacional Autónoma de Mexico,
Apartado Postal 70-264, 04510 D.F.,
Mexico
Received 30 August 2000 / Accepted 14 November 2000
Abstract
In order to efficiently use the recent astronomy high angular resolution techniques
(Adaptive Optics and Interferometry) to correct the perturbed wavefront arriving at the
telescope pupil, it is necessary to characterize a set of astroclimatic parameters. One of
these is the wavefront coherence time
 .
It is an integral parameter, defining the
maximum temporal correlation of the perturbed wavefront and it depends on the optical
turbulence
.
It is an integral parameter, defining the
maximum temporal correlation of the perturbed wavefront and it depends on the optical
turbulence
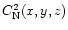 and the wind intensity
and the wind intensity 
 (x, y, z)
(x, y, z) in
the whole troposphere. In this paper we use an atmospheric non-hydrostatic model (Meso-NH)
conceived to simulate the classical meteorological parameters (p, T and
in
the whole troposphere. In this paper we use an atmospheric non-hydrostatic model (Meso-NH)
conceived to simulate the classical meteorological parameters (p, T and
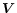 )
and adapted to simulate the optical turbulence (
)
and adapted to simulate the optical turbulence (
 )
to characterize the
)
to characterize the
 in a
region of some kilometers around the astronomical site of San Pedro Mártir (SPM)
in Baja California (Mexico). We study the seasonal variability of the wind intensity in the
whole atmosphere (20 km) above the SPM site during one year. We show that, using the
in a
region of some kilometers around the astronomical site of San Pedro Mártir (SPM)
in Baja California (Mexico). We study the seasonal variability of the wind intensity in the
whole atmosphere (20 km) above the SPM site during one year. We show that, using the
 profiles simulated by Meso-Nh initialized with ECMWF (European Center for Medium Weather
Forecasts) data, we obtain typical
profiles simulated by Meso-Nh initialized with ECMWF (European Center for Medium Weather
Forecasts) data, we obtain typical
 values in the V band (
values in the V band (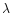 = 0.5
= 0.5 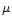 m).
We calculate the seasonal variability of the
m).
We calculate the seasonal variability of the
 in SPM and also some preliminary
results about the seasonal variability of
in SPM and also some preliminary
results about the seasonal variability of
 .
Moreover, we suggest a physical
explication of these variabilities. Finally we investigate the possibility of forecasting
.
Moreover, we suggest a physical
explication of these variabilities. Finally we investigate the possibility of forecasting
 .
.
Key words: atmospheric effets - site testing - instrumentation:
interferometers; adaptive optics
1 Introduction
A detailed characterization of the atmospheric optical turbulence is necessary in order to
successfully apply the modern techniques of High Angular Resolution observations such as
Adaptive Optics and Interferometry. Actually, a set of astroclimatic parameters are used to
describe the atmospheric turbulence state (the seeing
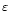 ,
the wavefront coherence time
,
the wavefront coherence time
 ,
the scintillation rate
,
the scintillation rate
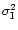 ,
the isoplanatic angle
,
the isoplanatic angle
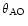 and the spatial
wavefront outer scale
and the spatial
wavefront outer scale
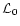 ). These parameters provide different information. For
example the seeing, which is the integral of the turbulence (
). These parameters provide different information. For
example the seeing, which is the integral of the turbulence (
 profiles) along lines of
sight, gives us quantitative information about the total turbulence in the atmosphere.
The wavefront coherence time
profiles) along lines of
sight, gives us quantitative information about the total turbulence in the atmosphere.
The wavefront coherence time
 gives the velocity turbulence characteristics. For a
single turbulence shear moving with a horizontal velocity V,
gives the velocity turbulence characteristics. For a
single turbulence shear moving with a horizontal velocity V,
 is the time
that the wavefront needs to cover the distance of r0. This last parameter is the
wavefront spatial coherence that is the typical size over which the wavefront
perturbations are correlated.
is the time
that the wavefront needs to cover the distance of r0. This last parameter is the
wavefront spatial coherence that is the typical size over which the wavefront
perturbations are correlated.
 fixes the minimum
exposure time for a detection system
if we want a free temporal filtering signal. In the case of Interferometry
(Buscher 1994; Davis
fixes the minimum
exposure time for a detection system
if we want a free temporal filtering signal. In the case of Interferometry
(Buscher 1994; Davis  Tango 1996; Roddier
Tango 1996; Roddier  Lena
1984), if the wavefront perturbations change consistently during
the exposure time, the fringe visibility is reduced and this can result in an incorrect image
interpretation. In the case of Adaptive Optics, if the correction system frequency
is lower than
Lena
1984), if the wavefront perturbations change consistently during
the exposure time, the fringe visibility is reduced and this can result in an incorrect image
interpretation. In the case of Adaptive Optics, if the correction system frequency
is lower than
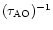 we obtain only a partial wavefront correction. In this article
we consider the following expression of the Fried parameter r0 (Roddier
1981):
we obtain only a partial wavefront correction. In this article
we consider the following expression of the Fried parameter r0 (Roddier
1981):
![\begin{displaymath}
r_{0}=\left[ 0.423\left( \frac{2\pi }{\lambda }\right)
^{2}...
...\infty }C_{\rm N}^{2}\left( h\right) {\rm d}h\right] ^{-3/5},
\end{displaymath}](/articles/aa/full/2001/05/aa10238/img16.gif) |
(1) |
which is proportional to
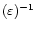 ,
and of the wavefront
coherence time
(Roddier et al. 1982):
,
and of the wavefront
coherence time
(Roddier et al. 1982):
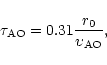 |
(2) |
where
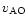 is the horizontal equivalent velocity:
is the horizontal equivalent velocity:
![\begin{displaymath}
\upsilon _{\rm AO}=\left[ \frac{\int\limits_{0}^{\infty }\le...
...ty }C_{\rm N}^{2}\left(
h\right) {\rm d}h}\right] ^{3/5}\cdot
\end{displaymath}](/articles/aa/full/2001/05/aa10238/img19.gif) |
(3) |
We should note that many different definitions of
 exist in the literature (Greenwood 1977; Tango
exist in the literature (Greenwood 1977; Tango  Twiss 1980; Buscher 1988; Nightingale
Twiss 1980; Buscher 1988; Nightingale  Buscher 1991). The wavefront coherence time values can be different depending on the kind of filter function used to compute
Buscher 1991). The wavefront coherence time values can be different depending on the kind of filter function used to compute
 .
We refer to the Buscher (Buscher 1994) for a more exhaustive discussion about this.
.
We refer to the Buscher (Buscher 1994) for a more exhaustive discussion about this.
Equations (2-3) show how
 depends on the vertical spatial distribution of the turbulence and on the wind intensity. It is easy to see that, for the same detector, a low turbulence concentrated in very fast shears can have a stronger effect on the observations than a larger turbulence distributed in slow shears.
Moreover,
depends on the vertical spatial distribution of the turbulence and on the wind intensity. It is easy to see that, for the same detector, a low turbulence concentrated in very fast shears can have a stronger effect on the observations than a larger turbulence distributed in slow shears.
Moreover,
 is a chromatic parameter which depends on the wavelength to a 6/5 power. In
Table 1 typical
is a chromatic parameter which depends on the wavelength to a 6/5 power. In
Table 1 typical
 values related to different observational bands and to different seeing conditions are listed. We computed
values related to different observational bands and to different seeing conditions are listed. We computed
 using a typical value of
using a typical value of
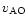 = 12 m/s (Vernin et al. 2000).
= 12 m/s (Vernin et al. 2000).
The detectors normally used in adaptive optics work with an average exposure time
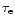
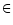 [1-20] msec. In Table 1, one sees that, for the medium and far infrared range (M and N bands)
[1-20] msec. In Table 1, one sees that, for the medium and far infrared range (M and N bands)
 is greater than
is greater than
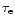 .
In this case therefore, the signal is not filtered temporally. In the near-infrared range (K band), if we are in a good site (
.
In this case therefore, the signal is not filtered temporally. In the near-infrared range (K band), if we are in a good site (
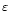
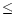 0.7 arcsec),
0.7 arcsec),
 is still greater than
is still greater than
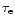 .
In the optical range
(V band), on the contrary, the typical
.
In the optical range
(V band), on the contrary, the typical
 is in the [1-10] msec range. In this case,
is in the [1-10] msec range. In this case,
 can determine the temporal filtration in adaptive optics and interferometry applications.
can determine the temporal filtration in adaptive optics and interferometry applications.
It is difficult to measure
 because the signal can easily be
filtered during the measurements. If the exposure time is larger than the
because the signal can easily be
filtered during the measurements. If the exposure time is larger than the
 ,
all the
frequencies higher than
,
all the
frequencies higher than
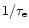 can be eliminated in the signal.
Some instruments
were recently employed to measure
can be eliminated in the signal.
Some instruments
were recently employed to measure
 ,
for example the technique based
on fringe visibility measurements of the Sydney University Stellar Interferometry (SUSI)
(Davis 1996), the Scidar technique (Vernin et al. 2000;
Avila et al. 2000) and the Generalized Scale Monitor (GSM) (Martin et al.
2000). However, a systematic monitoring of the
,
for example the technique based
on fringe visibility measurements of the Sydney University Stellar Interferometry (SUSI)
(Davis 1996), the Scidar technique (Vernin et al. 2000;
Avila et al. 2000) and the Generalized Scale Monitor (GSM) (Martin et al.
2000). However, a systematic monitoring of the
 has never
been done in any astronomical observatory. The advantage of numerical atmospherical
models is
that they can give the
has never
been done in any astronomical observatory. The advantage of numerical atmospherical
models is
that they can give the
 (x, y, z) and wind intensity
(x, y, z) and wind intensity
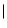
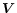 (x, y, z)
(x, y, z)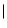 profiles sampled with the vertical resolution of the model levels in a region around
the telescope. Moreover, the numerical models can provide, at the same time, a 2D spatial
characterization, a seasonal characterization and a forecasting of
profiles sampled with the vertical resolution of the model levels in a region around
the telescope. Moreover, the numerical models can provide, at the same time, a 2D spatial
characterization, a seasonal characterization and a forecasting of
 .
.
In this study we use a non-hydrostatic atmospheric model (Meso-NH) (Lafore et al. 1998) adapted to simulate the optical turbulence (Masciadri et al. 1999a). The ability of the model to simulate
 profiles was successfully tested in previous articles (Masciadri et al. 1999b; Masciadri et al. 2000a). The typical spatial and temporal fluctuations of the wind are larger than the optical turbulence fluctuations so it is relatively easy to simulate the wind profiles with a meteorological model such as Meso-Nh.
profiles was successfully tested in previous articles (Masciadri et al. 1999b; Masciadri et al. 2000a). The typical spatial and temporal fluctuations of the wind are larger than the optical turbulence fluctuations so it is relatively easy to simulate the wind profiles with a meteorological model such as Meso-Nh.
In Sect. 2 we investigate the wind intensity seasonal variability in the whole atmosphere (20 km) over the San Pedro Mártir region during one year (1997). To do this, we use ECMWF (European Center for Medium Weather Forecasting) meteorological data (MARS catalog). We prove that the
 profiles simulated by the model provide typical values of
profiles simulated by the model provide typical values of
 for
for 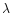 = 0.5
= 0.5 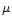 m. In Sect. 3 we study the importance of the
m. In Sect. 3 we study the importance of the
 in the
in the
 simulations and, in Sect. 4, we investigate the possibilities of forecasting
simulations and, in Sect. 4, we investigate the possibilities of forecasting
 .
.
2 Wind and
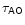 seasonal variability
seasonal variability
In order to characterize the wind intensity in the whole troposphere (20 km) in a region above the San Pedro Mártir Observatory (31.0441 N, 115.4569 W) we studied 156 vertical profiles of analysis wind intensity provided by the ECMWF climatological model (horizontal resolution of 0.5 degrees). These profiles are evenly distributed over the 1997 year and are computed at 00:00 hours U.T. on each night in the geographic coordinates (31 N, 116 W). In the following we will call this point AE (analysis extracted). More information about the analysis can be found in the Annex of (Masciadri et al. 1999b). Although the distance between the AE point and the Observatory is about 50 km, we can assume that, above 4 km (altitude), the analysis wind is representative of the flow above the Observatory. The AE point is at a 553 m above the ground, the San Pedro Mártir site is at 2780 m above the ground. We prefered to choose AE in the west side respect with the astronomical site because it is in an upstream position in respect to the wind. At these altitudes the wind temporal and spatial fluctuations scales are larger in the horizontal direction than in the vertical one so we judge that this hypothesis is acceptable for a seasonal wind characterization. In the first 4 km above the ground, which are affected by orographic effects and are therefore not well described by the analysis data, we use wind intensities measured at the San Pedro Mártir Observatory (Alvarez 1969).
![\begin{figure}
\par\includegraphics[width=13cm,clip]{10238f1.eps}\end{figure}](/articles/aa/full/2001/05/aa10238/Timg25.gif) |
Figure 1:
Daily (left column) and monthly (right column) wind intensity values during the 1997 year in the (31 N, 116 W) grid point. From top to bottom: [4-7] km, [7-11] km, [11-14] km and [14-18] km from the ground. The numbers on the top left corner (left column) are the model levels corresponding to the different altitudes expressed in kilometers |
| Open with DEXTER |
We averaged the wind intensity in 4 different atmospheric regions [4-7] km,
[7-11] km, [11-14] km and [14-18] km over the whole year. In Fig. 1 are shown the daily values (left column) and the monthly values (right) averaged over each region.
A clear seasonal variability is
evident in each atmospheric region, especially in
the right column where the daily fluctuations are filtered. During the (December - February)
months one can observe a stronger wind than during the (July - September) months.
In Fig. 2 we show the vertical wind profiles averaged over the winter period (December
- February: right) and over the summer period (July - September: left). At
an altitude of about 12 km, that is the region with the strongest wind, one can
observe a typical difference between the two periods of about 25 m/s. This is in a good
agreement with the values found in general climatological studies (Holton 1992).
![\begin{figure}
\par\includegraphics[width=13cm,clip]{10238f2.eps}\end{figure}](/articles/aa/full/2001/05/aa10238/Timg26.gif) |
Figure 2:
At the top the vertical wind profiles averaged over the summer time (July - September:
left) and over the winter time (December - February: right) are shown. The values are provided by the ECMWF analysis computed in the (31 N, -116 W) grid point at 00:00 hours in 156 nights sampled over the 1997 year. At the bottom a
 profile simulated by the Meso-Nh model over the San Pedro Martir Observatory is shown
profile simulated by the Meso-Nh model over the San Pedro Martir Observatory is shown |
| Open with DEXTER |
In the first 4 km we used the values of 7.26 m/s and 2.92 m/s, respectively, for the winter and summer period provided by a climatological wind study done by Alvarez (1969).
![\begin{figure}
\par\includegraphics[width=13cm,clip]{10238f3.eps}\end{figure}](/articles/aa/full/2001/05/aa10238/Timg27.gif) |
Figure 3:
Simulation outputs related to the 16/5/93 night (left column) and
25/5/93 night (right column) done above the Paranal site (Chile). From top to bottom:
1) the vertical sections of
 isolines. The color table (in the Web) shows a
strong
isolines. The color table (in the Web) shows a
strong
 near the ground and a lower and stratified
near the ground and a lower and stratified
 above 5 km. 2)-3) the vertical wind and
above 5 km. 2)-3) the vertical wind and
 profiles simulated above the Paranal site. 4) the vertical
profiles simulated above the Paranal site. 4) the vertical
 sections centered above the Paranal site. (This figure is available in color in electronic form)
sections centered above the Paranal site. (This figure is available in color in electronic form) |
| Open with DEXTER |
In order to compute
 we use a typical
we use a typical
 profile simulated by Meso-Nh (also shown in Fig. 2). This
profile simulated by Meso-Nh (also shown in Fig. 2). This
 profile is related to a seeing of 0.65 arcsec and is obtained by averaging the simulation over 3 hours in the same night. We used vertical (p, T and
profile is related to a seeing of 0.65 arcsec and is obtained by averaging the simulation over 3 hours in the same night. We used vertical (p, T and
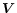 )
profiles provided by ECMWF data to initialize Meso-Nh. More details about the Meso-Nh initialization technique can be found in Masciadri et al. (1999a). We find, for the winter period
)
profiles provided by ECMWF data to initialize Meso-Nh. More details about the Meso-Nh initialization technique can be found in Masciadri et al. (1999a). We find, for the winter period
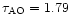 msec,
msec,
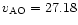 m/s, and for the summer period
m/s, and for the summer period
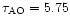 msec,
msec,
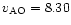 m/s. The spatial and temporal fluctuations of the optical turbulence are smaller than the ones of the classical meteorological parameters like the wind velocity and they are not considered in this estimation. In the same way we do not consider in this section the
m/s. The spatial and temporal fluctuations of the optical turbulence are smaller than the ones of the classical meteorological parameters like the wind velocity and they are not considered in this estimation. In the same way we do not consider in this section the
 seasonal variability in the sense of variations induced by climatological large scale phenomena. We note that no studies of the
seasonal variability in the sense of variations induced by climatological large scale phenomena. We note that no studies of the
 seasonal variability in the troposphere during such a long period have ever been published. We therefore make the following hypothesis: that the high frequency
seasonal variability in the troposphere during such a long period have ever been published. We therefore make the following hypothesis: that the high frequency
 fluctuations exist and that they are equally distributed in the year and that the intensity of these fluctuations can modify locally the
fluctuations exist and that they are equally distributed in the year and that the intensity of these fluctuations can modify locally the
 value but do not modify the seasonal variability of
value but do not modify the seasonal variability of
 .
In the following section we will describe this in a more detailed way.
We therefore conclude that, under these conditions, the model can simulate typical values of
.
In the following section we will describe this in a more detailed way.
We therefore conclude that, under these conditions, the model can simulate typical values of
 in the visible range. At the same time, we find that in the San Pedro Mártir site,
in the visible range. At the same time, we find that in the San Pedro Mártir site,
 has a clear seasonal variability. We estimate a
has a clear seasonal variability. We estimate a
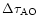 = 3.96 ms difference between the summer and winter time.
= 3.96 ms difference between the summer and winter time.
3 Discussion
Here we try to answer the following two questions:
- Can the
 vertical distribution affect locally the
vertical distribution affect locally the
 value? Here locally means in a temporal scale smaller than a season, for example a night or, better, a part of a night;
value? Here locally means in a temporal scale smaller than a season, for example a night or, better, a part of a night;
- Can the
 vertical distribution affect the season variability of
vertical distribution affect the season variability of
 ?
?
In order to answer to the first question we show an example in Fig. 3.
These are the simulation outputs that we obtained over the Paranal site (Chile) in a precedent study (Masciadri et al. 1999b). We choose this example because it is representative of what we want to prove.
In the left column the outputs related to the 16/5/93 night and in the right column the 25/5/93
night ones are shown. From top to bottom we show: the vertical sections (East-West direction
extended over 40 km, the Paranal site is in the centre) of the
 isolines (1), the vertical
wind intensity and
isolines (1), the vertical
wind intensity and
 profiles simulated above the Paranal site (2)-(3). Finally, the vertical sections of
profiles simulated above the Paranal site (2)-(3). Finally, the vertical sections of
 along the same direction (4) are shown.
The general characteristics of these simulations are: horizontal resolution of 500 m for a surface of
along the same direction (4) are shown.
The general characteristics of these simulations are: horizontal resolution of 500 m for a surface of
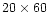 km.
km.
In Table 2 we give the integral parameters (r0,
 and
and
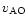 )
computed above the Paranal site from these two simulations.
One can see (first two lines of Table 2) that the optical turbulence is stronger in the 16/5 night (the values of r0 are very different in the two nights). On the contrary, the values of
)
computed above the Paranal site from these two simulations.
One can see (first two lines of Table 2) that the optical turbulence is stronger in the 16/5 night (the values of r0 are very different in the two nights). On the contrary, the values of
 are comparable in the two nights. In the last column one can observe that the turbulence is distributed in a homogeneous way over the whole troposphere in the 25/5 night. On the contrary, in the 16/5 night the turbulence is concentrated near the ground. The wind intensity difference between the two nights at 12 km is of about 15 m/s. The wind intensity near the ground is comparable and not higher than 10 m/s. How do the wind and the
are comparable in the two nights. In the last column one can observe that the turbulence is distributed in a homogeneous way over the whole troposphere in the 25/5 night. On the contrary, in the 16/5 night the turbulence is concentrated near the ground. The wind intensity difference between the two nights at 12 km is of about 15 m/s. The wind intensity near the ground is comparable and not higher than 10 m/s. How do the wind and the
 contribute to the
contribute to the
 estimation? One can observe that the
estimation? One can observe that the
 has comparable values in the [5-20] km region and over the whole atmosphere in the 25/5 night. On the contrary, in the 16/5 night, the
has comparable values in the [5-20] km region and over the whole atmosphere in the 25/5 night. On the contrary, in the 16/5 night, the
 in the [5-20] km region is two time larger than over the whole atmosphere. This means that in the 25/5 night the strong wind at high altitudes that principally affects the
in the [5-20] km region is two time larger than over the whole atmosphere. This means that in the 25/5 night the strong wind at high altitudes that principally affects the
 .
In the 16/5 night, on the contrary, the strong turbulence near the ground determine the values of
.
In the 16/5 night, on the contrary, the strong turbulence near the ground determine the values of
 .
Comparing the [0-5] km and the [5-20] km regions in the 16/5 night, one can see that r0 increases by a larger factor (85/5.7
.
Comparing the [0-5] km and the [5-20] km regions in the 16/5 night, one can see that r0 increases by a larger factor (85/5.7 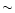 15) than
15) than
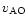 (
17.24/5.29
(
17.24/5.29 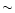 3).
3).
We can therefore answer the first question, concluding that
 can affect locally the
can affect locally the
 .
In the example shown, the strong turbulence near the ground is probably caused by an orographic effect more easily related to a local meteorological condition than to general climatologic phenomena
.
In the example shown, the strong turbulence near the ground is probably caused by an orographic effect more easily related to a local meteorological condition than to general climatologic phenomena
It is more difficult to answer to the second question. The
 is characterized, at the same time, by two different kind of fluctuations: the natural high frequency turbulence fluctuations and a slower seasonal fluctuation. Here we are interested to the second one. Measurements extended over 3 years in the San Pedro Mártir Observatory (Echevarría et al. 1998) show a seasonal variability of the seeing, which seems to be better during the summer time. The seeing is an integrated parameter so we cannot know a priori whether this variability is caused by large scale phenomena or by local ones. The large scale phenomena principally affect the
is characterized, at the same time, by two different kind of fluctuations: the natural high frequency turbulence fluctuations and a slower seasonal fluctuation. Here we are interested to the second one. Measurements extended over 3 years in the San Pedro Mártir Observatory (Echevarría et al. 1998) show a seasonal variability of the seeing, which seems to be better during the summer time. The seeing is an integrated parameter so we cannot know a priori whether this variability is caused by large scale phenomena or by local ones. The large scale phenomena principally affect the
 at high altitudes while the short scale phenomena affect the
at high altitudes while the short scale phenomena affect the
 at low altitudes. We have computed, using the Meso-Nh model, a set of simulations (4 nights in the summer time and 4 in the winter time). We computed (Table 3) the seeing contributions at high altitudes (
at low altitudes. We have computed, using the Meso-Nh model, a set of simulations (4 nights in the summer time and 4 in the winter time). We computed (Table 3) the seeing contributions at high altitudes (
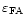 ), at low altitudes (
), at low altitudes (
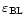 )
and over the whole 20 km range (
)
and over the whole 20 km range (
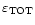 ). In the summer time, the average seeing is
). In the summer time, the average seeing is
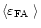 = 0.38 arcsec. In the winter time we obtain
= 0.38 arcsec. In the winter time we obtain
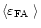 = 0.55 arcsec. Moreover, each night shows the same tendency at high altitudes: a larger optical turbulence during the winter time. This preliminary result shows a seasonal
= 0.55 arcsec. Moreover, each night shows the same tendency at high altitudes: a larger optical turbulence during the winter time. This preliminary result shows a seasonal
 variability at high altitudes at large climatological scales. In the last column of the Table 3 are reported the
variability at high altitudes at large climatological scales. In the last column of the Table 3 are reported the
 obtained using the wind profils of Fig. 2. In the winter, the average
obtained using the wind profils of Fig. 2. In the winter, the average
 is equal to 1.41 msec, in the summer is equal to 6.89 msec. The difference of
is equal to 1.41 msec, in the summer is equal to 6.89 msec. The difference of
 between winter and summer time previous estimated (3.96 msec) is therefore enhanced (5.48 msec). This results indicate that the seasonal variability of the
between winter and summer time previous estimated (3.96 msec) is therefore enhanced (5.48 msec). This results indicate that the seasonal variability of the
 probably affect the
probably affect the
 seasonal variability. Obviously, this same experiment should be extended to the whole year to have a richer statistical sample, but it is not possible at the present time because of limited computational resources.
seasonal variability. Obviously, this same experiment should be extended to the whole year to have a richer statistical sample, but it is not possible at the present time because of limited computational resources.
To give an idea of the
 modulation over the astronomical site we show in Fig. 5, as an example, a simulated
modulation over the astronomical site we show in Fig. 5, as an example, a simulated
 map related to the 27 July 1997 night. The whole surface is
map related to the 27 July 1997 night. The whole surface is
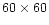 km centered on the Observatory. The black lines are the level isolines (orographic structure). On the right of the Observatory, along a North-West versus South-East direction, one can observe the maximum slope mountain chain. The gray scale shows different
km centered on the Observatory. The black lines are the level isolines (orographic structure). On the right of the Observatory, along a North-West versus South-East direction, one can observe the maximum slope mountain chain. The gray scale shows different
 values. We observe small
values. We observe small
 values above the maximum slope, that is the place where the turbulence production is probably larger. All around the Observatory, the
values above the maximum slope, that is the place where the turbulence production is probably larger. All around the Observatory, the
 map presents modulations in a range of about 6 msec.
map presents modulations in a range of about 6 msec.
We suggest now a physical explication of the
 seasonal variation. We know that the deterministic turbulence production in the atmosphere depends on the Richardson number:
seasonal variation. We know that the deterministic turbulence production in the atmosphere depends on the Richardson number:
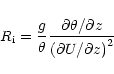 |
(4) |
where 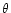 is the potential temperature and U is the horizontal wind component.
is the potential temperature and U is the horizontal wind component.
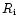 describes the stability level of the atmosphere. In the night time, the atmosphere is generally stable (
describes the stability level of the atmosphere. In the night time, the atmosphere is generally stable (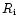 > 1/4) and it is difficult to detect the dynamical instability (
> 1/4) and it is difficult to detect the dynamical instability (
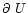 /
/
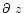
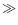 1 and
1 and
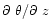 < 1) that causes the turbulence in strongly stratified shears. Following a statistical approach (Van Zandt et al. 1978; Van Zandt et al. 1981) we can replace the deterministic
< 1) that causes the turbulence in strongly stratified shears. Following a statistical approach (Van Zandt et al. 1978; Van Zandt et al. 1981) we can replace the deterministic 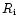 with a probability density function describing the stability and instability factors in the atmosphere provided by climatological data.
In this stochastic context it was proved (Van Zandt et al. 1978) that the probability
function to find dynamical instabilities depends on the wind and potential temperature vertical
gradient at large scales (of a few kilometers). In Fig. 2 it is evident that during the
winter time the vertical wind gradient is stronger than during the summer time. In
Fig. 4 we show the potential temperature vertical profiles obtained averaging the ECMWF
data described in Sect. 2 over the winter period (December - February, bold line)
and over the summer period (July - September, thin line). The potential temperature gradient is not too different during the winter and summer time. We therefore conclude that, during the winter time, the probability to generate dynamical instabilities is higher than during the summer time. We find a further confirmation of this hypothesis in the Cerro Pachón site campaign results (Vernin et al. 2000) which is, at our best knowledge, the longest site testing campaign ever done measuring directly the
with a probability density function describing the stability and instability factors in the atmosphere provided by climatological data.
In this stochastic context it was proved (Van Zandt et al. 1978) that the probability
function to find dynamical instabilities depends on the wind and potential temperature vertical
gradient at large scales (of a few kilometers). In Fig. 2 it is evident that during the
winter time the vertical wind gradient is stronger than during the summer time. In
Fig. 4 we show the potential temperature vertical profiles obtained averaging the ECMWF
data described in Sect. 2 over the winter period (December - February, bold line)
and over the summer period (July - September, thin line). The potential temperature gradient is not too different during the winter and summer time. We therefore conclude that, during the winter time, the probability to generate dynamical instabilities is higher than during the summer time. We find a further confirmation of this hypothesis in the Cerro Pachón site campaign results (Vernin et al. 2000) which is, at our best knowledge, the longest site testing campaign ever done measuring directly the
 profiles (4 weeks equally distributed over the year). From the results of this campaign it was found that the average free atmosphere seeing in the austral summer is 0.49 arcsec and in the winter time is 0.87 arcsec. Moreover, the
profiles (4 weeks equally distributed over the year). From the results of this campaign it was found that the average free atmosphere seeing in the austral summer is 0.49 arcsec and in the winter time is 0.87 arcsec. Moreover, the
 estimated in this campaign in the winter time is 7.25 msec and in the summer time is 1.65 msec. The seasonal difference is so 5.6 msec absolutely comparable with that found by our model in San Pedro Mártir.
estimated in this campaign in the winter time is 7.25 msec and in the summer time is 1.65 msec. The seasonal difference is so 5.6 msec absolutely comparable with that found by our model in San Pedro Mártir.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10238f4.eps}\end{figure}](/articles/aa/full/2001/05/aa10238/Timg48.gif) |
Figure 4:
Vertical potential temperature profiles of the ECMWF analysis averaged over the winter time (bold line) and over the summer time (thin line). The data are related to the (31 N, 116 W) grid point |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10238f5.eps}\end{figure}](/articles/aa/full/2001/05/aa10238/Timg49.gif) |
Figure 5:
 map simulated above the San Pedro Martir Observatory (central black point) the 27 July 1997 night. The North is at the top of the figure. The black lines are the levels isolines
map simulated above the San Pedro Martir Observatory (central black point) the 27 July 1997 night. The North is at the top of the figure. The black lines are the levels isolines |
| Open with DEXTER |
We proved that, neglecting the contribution of the
 fluctuations, the
fluctuations, the
 difference between the winter and summer time is of about 5.48 msec. Probably, this difference is reinforced by the 5/3 wind power (Eq. (2)). We find that, considering the contributions of the
difference between the winter and summer time is of about 5.48 msec. Probably, this difference is reinforced by the 5/3 wind power (Eq. (2)). We find that, considering the contributions of the
 fluctuations, this difference is statistically enhanced. At the same time, we saw in Sect. 3 that particular
fluctuations, this difference is statistically enhanced. At the same time, we saw in Sect. 3 that particular
 and wind values can affect the
and wind values can affect the
 and modify locally its seasonal characteristics. It is therefore very important, at the same time, to characterize the seasonal variability of
and modify locally its seasonal characteristics. It is therefore very important, at the same time, to characterize the seasonal variability of
 and to forecast the
and to forecast the
 values. The critical points related to the model ability to forecast
values. The critical points related to the model ability to forecast
 in an operational mode are:
in an operational mode are:
- the Meso-Nh reliability in simulating
 profiles
profiles
- the representative level of the atmospheric flow of the initialization data.
We can characterize the
 reliability comparing the dispersion of the measurements obtained with different instruments (
reliability comparing the dispersion of the measurements obtained with different instruments (
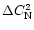 )
with the dispersion between the average of measurements and simulations (
)
with the dispersion between the average of measurements and simulations (
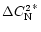 ). In a previous article (Masciadri et al. 2000a) we proved that
). In a previous article (Masciadri et al. 2000a) we proved that
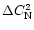 and
and
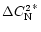 are comparable. Moreover, we recently tested a new method for the model calibration that seems to improve the Meso-Nh reliability. A preliminary result shows a difference between measurements and simulations of 8%. A forthcoming article will describe these results in detail.
are comparable. Moreover, we recently tested a new method for the model calibration that seems to improve the Meso-Nh reliability. A preliminary result shows a difference between measurements and simulations of 8%. A forthcoming article will describe these results in detail.
Table 4:
Estimation of the average relative errors computed between the analysis and the forecasts at 6 and 12 hours during the whole of 1997
| Parameter |
Forecasts |
err (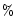 )
[4-17.5] km )
[4-17.5] km |
err (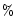 )
[0-4] km )
[0-4] km |
| Wind Intensity |
6 |
8 |
21.68 |
| |
12 |
14 |
26.5 |
| Wind Direction |
6 |
10.15 |
14.7 |
| |
12 |
10.36 |
15.70 |
| Absolute Temperature |
6 |
0.2 |
0.185 |
| |
12 |
0.3 |
0.265 |
| Dew point Temperature |
6 |
1 |
1 |
| |
12 |
1.18 |
1.2 |
In order to characterize the initialization
data quality we compared (Fig. 6) the analysis profiles of meteorological
parameters (p, T and
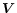 )
computed at 00:00 U.T.
hours of the day J with the
forecasted profiles at 6 and 12 hours of the same parameters
computed, respectively, at 18:00 and 12:00 U.T. hours of the day (J-1). Both the
analysis and the forecasts are computed in the AE grid point in an
up-stream position respect to the San Pedro Mártir Observatory. We suppose that the
analysis represent the "real'' state of the atmospheric flow
and we analyze the dispersion of the forecasts. Doing so we estimate how realistic are the
initialization data. Table 4 shows, for each meteorological
parameter, the relative error (
)
computed at 00:00 U.T.
hours of the day J with the
forecasted profiles at 6 and 12 hours of the same parameters
computed, respectively, at 18:00 and 12:00 U.T. hours of the day (J-1). Both the
analysis and the forecasts are computed in the AE grid point in an
up-stream position respect to the San Pedro Mártir Observatory. We suppose that the
analysis represent the "real'' state of the atmospheric flow
and we analyze the dispersion of the forecasts. Doing so we estimate how realistic are the
initialization data. Table 4 shows, for each meteorological
parameter, the relative error (
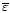 )
between the analysis and the
forecasts at 6 hours (first line) and the analysis and forecasts at 12 hours (second
line). The third column is related to the high atmosphere [4-17.5] km
and the fourth to the low atmosphere [0-4] km. The results shown are computed
considering the dispersion at each model level for 156 nights. The four analyzed
parameters are used to initialize Meso-Nh. We can observe that the absolute temperature and
the dew point temperature are well correlated. The wind intensity and direction show
a larger dispersion. In general, we find a larger dispersion for the forecasts at 12 hours
than for the forecasts at 6 hours. Above 4 km the largest wind intensity and
direction average relative errors are, respectively, 14% and 10.36%. In the low
atmosphere the relative errors grow because the orographic effects are not well
represented by the ECMWF climatological model. Anyway, the worst statistical dispersion is of
26.5 (
)
between the analysis and the
forecasts at 6 hours (first line) and the analysis and forecasts at 12 hours (second
line). The third column is related to the high atmosphere [4-17.5] km
and the fourth to the low atmosphere [0-4] km. The results shown are computed
considering the dispersion at each model level for 156 nights. The four analyzed
parameters are used to initialize Meso-Nh. We can observe that the absolute temperature and
the dew point temperature are well correlated. The wind intensity and direction show
a larger dispersion. In general, we find a larger dispersion for the forecasts at 12 hours
than for the forecasts at 6 hours. Above 4 km the largest wind intensity and
direction average relative errors are, respectively, 14% and 10.36%. In the low
atmosphere the relative errors grow because the orographic effects are not well
represented by the ECMWF climatological model. Anyway, the worst statistical dispersion is of
26.5 (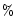 )
which we judge acceptable for our present studies.
)
which we judge acceptable for our present studies.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10238f6.eps}\end{figure}](/articles/aa/full/2001/05/aa10238/Timg54.gif) |
Figure 6:
Schematic drawing showing the meteorological initialization data (analysis and forecasts) used for the statistical analysis described in Sect. 4. The analysis at 00:00 U.T are compared to the forecasts at 6 hours (computed at 18:00 U.T. of the (J-1) day) and forecasts at 12 hours (computed at 12:00 U.T. of the (J-1) day) |
| Open with DEXTER |
5 Conclusions
We used 156 wind intensity profiles provided by the ECMWF data bank
evenly distributed in the year 1997 and representative of
the atmospheric flow over the San Pedro Mártir site to carry out a
 seasonal
variability study. We proved that, using
seasonal
variability study. We proved that, using
 profiles simulated by the non-hydrostatic model Meso-NH, and neglecting the high frequency fluctuations of the
profiles simulated by the non-hydrostatic model Meso-NH, and neglecting the high frequency fluctuations of the
 profiles, we obtain typical
profiles, we obtain typical
 values for the wavelength
values for the wavelength
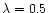
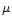 m. Under this hypothesis, the
m. Under this hypothesis, the
 amplitude seasonal variability at San Pedro Mártir site is of about 5.48 msec. We investigated the
amplitude seasonal variability at San Pedro Mártir site is of about 5.48 msec. We investigated the
 seasonal variability (slow frequency variability) using
seasonal variability (slow frequency variability) using
 simulations provided by Meso-NH (4 nights in the summer time, 4 nights in the winter time). Our preliminary results show that such a variability, probably, exists and it has a tendency to enhance the previously reported
simulations provided by Meso-NH (4 nights in the summer time, 4 nights in the winter time). Our preliminary results show that such a variability, probably, exists and it has a tendency to enhance the previously reported
 difference. In Sect. 3 we have suggested a physical stochastic explanation for this phenomenon. Some
difference. In Sect. 3 we have suggested a physical stochastic explanation for this phenomenon. Some
 measurements done in the past (Vernin et al. 2000) confirm the
measurements done in the past (Vernin et al. 2000) confirm the
 difference in winter and summer time at high altitudes. The interesting result of this paper is that the numerical models are indeed able to reproduce this effect.
difference in winter and summer time at high altitudes. The interesting result of this paper is that the numerical models are indeed able to reproduce this effect.
We showed that, locally, the
 can modify the
can modify the
 .
This means that it is fundamental to be able to forecast
.
This means that it is fundamental to be able to forecast
 .
We investigated so the Meso-Nh potential ability to do it. We analyzed the two more critical points: (1) the model reliability in simulating
.
We investigated so the Meso-Nh potential ability to do it. We analyzed the two more critical points: (1) the model reliability in simulating
 profiles (2) that the initialization meteorological forecasting represent well the atmospheric flow over the site. Relating to the first point we can affirm that the average dispersion between the simulations and the average of the measurements is comparable to the dispersion between the measurements obtained with different instruments. Relating to the second point, we proved that the meteorological forecasts (at 6 and 12 hours) that we could use to initialize the model in an operational configuration, are well correlated to the analysis (considered here as the "real'' atmospheric flow representation). The maximum average error (26.5%) is obtained for the wind intensity between the forecasts at 12 hours and the analysis.
profiles (2) that the initialization meteorological forecasting represent well the atmospheric flow over the site. Relating to the first point we can affirm that the average dispersion between the simulations and the average of the measurements is comparable to the dispersion between the measurements obtained with different instruments. Relating to the second point, we proved that the meteorological forecasts (at 6 and 12 hours) that we could use to initialize the model in an operational configuration, are well correlated to the analysis (considered here as the "real'' atmospheric flow representation). The maximum average error (26.5%) is obtained for the wind intensity between the forecasts at 12 hours and the analysis.
These results open new perspectives in the site testing studies and the
flexible-scheduling of the telescope instruments and scientific programs.
Ambitious projects to build a new class of telescopes now exist (OWL:
Overwhelmingly Large Telescope - D = 100 m, Hubin et al. 2000; CELT
California Extremely Large Telescope - D = 30 m). For these projects, excellent sites are
necessary and numerical models could be used to choose the best of all possible sites. We
found that, in the San Pedro Mártir site, the summer time is the potentially
better period for
 .
This means that, the best scientific programs requiring high
angular resolution could be scheduled in this period. Moreover, we remember
that one of the critical points for the successful application of some of the adaptive optics
techniques such as the tomographic one (Ragazzoni et al. 1999;
Ragazzoni et al. 2000) or the Multiconjugated Adaptive Optics MCAO (Fusco
et al. 1999; Fusco et al. 2000) is the characterization
of the
.
This means that, the best scientific programs requiring high
angular resolution could be scheduled in this period. Moreover, we remember
that one of the critical points for the successful application of some of the adaptive optics
techniques such as the tomographic one (Ragazzoni et al. 1999;
Ragazzoni et al. 2000) or the Multiconjugated Adaptive Optics MCAO (Fusco
et al. 1999; Fusco et al. 2000) is the characterization
of the
 during a long period and in a whole 3D domain around the telescope. Indeed, the
optical turbulence has a typically non-uniform distribution in the atmosphere and
the model indicates that different lines of sight can provide large differences in the
seeing estimation (Masciadri et al. 2000b). The numerical modeling
technique is, in our opinion, probably one of the best candidates for obtaining such a 3D
characterization of the atmosphere turbulence. Some of the advantages with respect to other techniques are: it has no limitations in the vertical resolution, it does not suffer of exposure time limitations, it supplies 3D
during a long period and in a whole 3D domain around the telescope. Indeed, the
optical turbulence has a typically non-uniform distribution in the atmosphere and
the model indicates that different lines of sight can provide large differences in the
seeing estimation (Masciadri et al. 2000b). The numerical modeling
technique is, in our opinion, probably one of the best candidates for obtaining such a 3D
characterization of the atmosphere turbulence. Some of the advantages with respect to other techniques are: it has no limitations in the vertical resolution, it does not suffer of exposure time limitations, it supplies 3D
 maps and 2D integrated parameters (as
maps and 2D integrated parameters (as
 )
maps.
)
maps.
Acknowledgements
This work was support by the TIM (Telescope Infrarojo
Mexicano) Project, the CONACYT grants (J32412E) and the DGAPA grants
(IN118199). The Meso-Nh simulations were run on the Fujitsu VPP5000
supercomputer (CNRM - Meteo France - Toulouse, Fr). We
thank P. Bougeault for kindly supplying CPU time for this study.
We are grateful to P. Jabouille and J. Stein for helpful discussions about
the Meso-Nh code. We are grateful to F. Angeles and L. Morales for providing
the vegetation model implemented in the Meso-Nh model. Special thanks to A. Raga
for useful discussions.
-
Alvarez, M. 1969, Reporte IA-UNAM
In the text
-
Avila, R., et al. 2000,
Adaptive Optical System Technology, SPIE Proc., 4007, Munich 2000
In the text
-
Buscher, D. F. 1988, MNRAS, 235, 1203
In the text
NASA ADS
-
Buscher, D. F. 1994, SPIE, 2200, 260
In the text
-
Davis, J., & Tango, W. J. 1996, PASP, 108, 456
In the text
NASA ADS
-
Echevarria, J., et al. 1998, RMxAA, 34, 47
In the text
NASA ADS
-
Fusco, T., et al. 1999, Opt. Lett., 24, (N.21), 1
In the text
-
Fusco, T., et al. 2000, Adaptive Optical System Technology, SPIE Proc., 4007, Munich 2000
In the text
-
Greenwood, D. P. 1977, JOSA, 67, 390
In the text
-
Holton, 1992, An introduction to Dynamic Meteorology (Academic Press)
In the text
-
Hubin, N., et al. 2000,
Adaptive Optical System Technology, SPIE Proc., 4007, Munich 2000
In the text
-
Lafore, J. P., et al. 1998, Ann. Geophys., 16, 90
In the text
-
Martin, F., et al. 2000, A&A, in press
In the text
-
Masciadri, E., et al. 1999a,
A&AS, 137, 185
In the text
NASA ADS
-
Masciadri, E., et al. 1999b,
A&AS, 137, 203
In the text
NASA ADS
-
Masciadri, E., et al. 2000a, A&A, in press
In the text
-
Masciadri, E., et al. 2000b,
Interferometry in Optical Astronomy, SPIE Proc., 4006, Munich 2000
In the text
-
Nightingale, N. S., & Buscher, D. F. 1991,
MNRAS, 251, 155
In the text
NASA ADS
-
Ragazzoni, R., et al. 1999,
A&AL, 342, L53
In the text
-
Ragazzoni, R., et al. 2000,
Nature, 403, 54
In the text
NASA ADS
-
Roddier, F., & Lena, P. 1984,
J. Opt. Paris, 15, 171
In the text
-
Roddier, F. 1981, Prog. Opt., XIX, 283
In the text
-
Roddier, F., et al. 1982, J. Opt. Paris, 13, 263
In the text
-
Tango, W. J., & Twiss, R. Q. 1980, Prog. Opt., XVII
In the text
-
VanZandt, T. E., et al. 1978, Radio Sci., 13, 819
In the text
NASA ADS
-
VanZandt, T. E., et al. 1981,
20th Radar Meteor. Conference - Boston, American Meteorological Society
In the text
-
Vernin, J., et al. 2000,
Gemini Report, Web Page: In the text
http://www.gemini.edu/sciops/instruments
/adaptiveOptics/
Copyright ESO 2001
![\begin{displaymath}
r_{0}=\left[ 0.423\left( \frac{2\pi }{\lambda }\right)
^{2}...
...\infty }C_{\rm N}^{2}\left( h\right) {\rm d}h\right] ^{-3/5},
\end{displaymath}](/articles/aa/full/2001/05/aa10238/img16.gif)
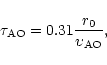
![\begin{displaymath}
\upsilon _{\rm AO}=\left[ \frac{\int\limits_{0}^{\infty }\le...
...ty }C_{\rm N}^{2}\left(
h\right) {\rm d}h}\right] ^{3/5}\cdot
\end{displaymath}](/articles/aa/full/2001/05/aa10238/img19.gif)
![\begin{figure}
\par\includegraphics[width=13cm,clip]{10238f1.eps}\end{figure}](/articles/aa/full/2001/05/aa10238/Timg25.gif)
![\begin{figure}
\par\includegraphics[width=13cm,clip]{10238f2.eps}\end{figure}](/articles/aa/full/2001/05/aa10238/Timg26.gif)
![\begin{figure}
\par\includegraphics[width=13cm,clip]{10238f3.eps}\end{figure}](/articles/aa/full/2001/05/aa10238/Timg27.gif)
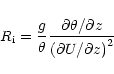
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10238f4.eps}\end{figure}](/articles/aa/full/2001/05/aa10238/Timg48.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10238f5.eps}\end{figure}](/articles/aa/full/2001/05/aa10238/Timg49.gif)