A&A 366, 306-310 (2001)
DOI: 10.1051/0004-6361:20000027

Fast magnetoacoustic waves in a randomly structured solar corona

K. Murawski1 - V. M. Nakariakov2 - E. N. Pelinovsky3


1 - Technical University of Lublin, Department of Environmental Physics, ul. Nadbystrzycka 40,
20-618 Lublin, Poland
2 - Physics Department, University of Warwick, Coventry CV4 7AL, UK
3 - Institute of Applied Physics, 46 Ul'anova Street 603600, Nizhny Novgorod, Russia

Received 9 June 2000 / Accepted 3 November 2000

Abstract
The propagation of fast magnetoacoustic waves in a randomly structured solar corona is considered in the linear and cold plasma limits. The random field is assumed to be static and associated with plasma density inhomogeneities only. A transcendental dispersion relation for the fast magnetoacoustic waves which propagate perpendicularly to the magnetic field is derived in the weak random field approximation. It is shown analytically that the fast magnetosonic waves experience acceleration, attenuation, and dispersion in comparison to the homogeneous case. These analytical findings are essentially confirmed by numerical simulations for a wide-spectrum pulse, except that the waves were found decelerated. It is concluded that the coronal Moreton waves can be applied to MHD seismology of the solar corona.

Key words: oscillations MHD waves - methods: analytical - Sun: corona


1 Introduction

MHD waves play an important role in the dynamics and formation of the solar corona as they are believed to be associated with the long-standing problem of the plasma heating and the solar wind acceleration. The EUV imaging telescopes onboard SOHO (EIT) and TRACE spacecrafts made it possible to directly observe the MHD waves in the corona. In particular, compressive longitudinal waves were detected in the polar plumes (Deforest & Gurman 1998; Ofman et al. 1999). These waves were interpreted as slow magnetoacoustic waves (Ofman et al. 1999; Ofman et al. 2000). Similar waves were detected in long coronal loops (Berghmans & Clette 1999).

Recently, Thompson et al. (1999) reported observations of the so-called coronal Moreton waves (or flare waves). These waves are seen as perturbations of the EUV emission intensity, propagating predominantly radially from a flare site. Most probably, these waves are fast magnetoacoustic waves because they are compressive and they propagate essentially isotropically in the low-$\beta$ coronal plasma. They are believed to be a manifestation of the waves which were discovered in the chromosphere in the H$_\alpha$ line (1961). These waves provide a unique tool for MHD seismology of the solar corona. Indeed, measuring parameters of these waves, e.g. the evolution of the wave amplitude and speed as a function of the distance from the epicenter, one can build up a map of the local Alfvén speed. However, application of this method requires a well-developed theory of MHD wave propagation in the corona.

Theoretical analysis of MHD waves in the corona shows that a key element of the coronal wave theory is interaction of the waves with coronal structures (e.g., Roberts 1991; Roberts & Ulmschneider 1997) which affect the MHD waves by a number of different ways: they can guide the waves due to refraction and reflection, resonantly absorb the wave energy when the wave phase speed coincides with local Alfvén or tube speeds, make the waves dispersive, lead to linear coupling of the waves and enhance efficiency of their nonlinear coupling. These and other aspects of the interaction of MHD waves with coronal structures are well-understood in the case of a deterministic structuring.

Recent interest in the effect of a random field on coronal MHD waves is arising in connection with the significant progress in the spatial and temporal resolution of coronal observations. For a wide band of large-scale wave motions, the coronal plasma is a randomly structured medium. Indeed, the typical scale of the inhomogeneity across the magnetic field is determined by the cross-section diameter of coronal loops, which randomly varies around a few Mm. This fact can dramatically affect the MHD wave dynamics. In particular, a random field leads to the attenuation of wave amplitude, dispersion, and to enhanced coupling of MHD modes. Valley (1971, 1974) derived dispersion relations for MHD waves propagating through plasma with a randomly structured magnetic field. He found that random irregularities in the magnetic field strength lead to attenuation of the waves. However, his choice of an analytically inconvenient correlation function did not allow him to estimate the effect quantitatively (see the discussion at the end of his Sect. V). Lou & Rosner (1986) reconsidered Valley's results for damping of incompressible MHD (pure Alfvén) waves in plasma with time-dependent fluctuations of the magnetic and velocity fields. Li & Zweibel (1987) developed the previous studies by considering time-dependent random irregularities. They found that as a consequence of the random field, an efficient conversion of Alfvén waves into compressive magnetoacoustic waves occurs.

This paper is organized as follows. The physical model is described in Sect. 2. The dispersion relation is derived and analyzed in Sect. 3. Numerical simulations for the wave equation are described in Sect. 4. Possible implications of these studies for the coronal Moreton waves are discussed in Sect. 5.

2 Physical model

We consider a fast magnetoacoustic wave that propagates perpendicularly to the ambient magnetic field. As a consequence of this we can assume that the coronal plasma is cold. The fast magnetosonic waves are described then by cold ideal MHD equations, viz.


 
$\displaystyle \frac{\partial}{\partial t}\varrho+\nabla\cdot({\varrho\vec V}) =0,$     (1)


 
$\displaystyle \varrho\left[\frac{\partial}{\partial t}\vec V+(\vec V\cdot \nabla)\vec V\right] = -\frac{1}{\mu}\vec B\times (\nabla\times \vec B),$     (2)


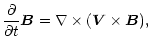$\displaystyle \frac{\partial}{\partial t}\vec B = \nabla\times (\vec V\times \vec B),$     (3)


 
$\displaystyle \nabla\cdot\vec B = 0.$     (4)

Here, $\varrho$ is the mass density, $\vec V$ is the velocity, $\vec B$ is the magnetic field, and $\mu$ is the magnetic permeability.

The solar coronal plasma consists of randomly distributed coronal loops. Consequently, for the fast magnetoacoustic waves, the corona is a random environment with a characteristic spatial scale (the correlation length lz) of a few Mm (the coronal loop cross-section diameter) and a density ratio $\kappa\leq 10$ (the density ratio inside and outside the loop).

In what follows we assume one-dimensional motions with $\partial/\partial x=\partial/\partial y=0$ and Vx=Vy=0 and consider the equilibrium state, in which the magnetic field $\vec B_0$ points in the x-direction and is uniform. The equilibrium quantities are given by

$\displaystyle \varrho=\varrho_0+\varrho_{\rm r}(z), \hspace{3mm} \vec V_0=0, \hspace{3mm} \vec B_0=B_0 \hat x,$     (5)

where $\varrho_{\rm r}$ is a random function of z such that $<\varrho_{\rm r}(z)> = 0$. Here, the symbol <> denotes the ensemble average. In this model, we neglected the effects of temporal variation of $\varrho_{\rm r}$. This assumption is justified, as typical times of the temporal evolution of coronal loops are a few hours while the wave periods are less then several minutes.

The standard linearization procedure of Eqs. (1-4) leads to the following wave equation:

  \begin{displaymath} (1+\kappa(z))\frac{\partial^2}{\partial t^2}{V_z}- V_{A0}^2\frac{\partial^2}{\partial z^2}{V_z} = 0, \end{displaymath} (6)

where Vz is the perturbed velocity in the direction of the wave propagation, $V_{A0} = B_0/\sqrt{\mu \varrho_0}$ is the Alfvén speed, and the density ratio $\kappa$ is defined as

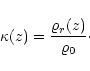\begin{displaymath}\kappa(z) = \frac{\varrho_r(z)}{\varrho_0}\cdot \end{displaymath} (7)

When the structuring is a deterministic periodic function, Eq. (6) coincides with the magnetoacoustic wave equation derived by Berton & Heyvaerts (1987) who showed that periodic structuring leads to the appearance of wave dispersion and deceleration. In this paper we consider the effects of a random field instead.

3 Dispersion relation

Following Howe (1971), we use the expansion

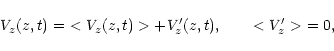\begin{displaymath}V_z(z,t) =\ <V_z(z,t)>+V_z'(z,t),\qquad <V_z'>\ = 0, \end{displaymath} (8)

where the primes denote the perturbations of the averaged state. Substituting this expansion into Eq. (6), we get

 \begin{displaymath} (1+\kappa)\frac{\partial^2}{\partial t^2}(<V_z>+{V_z'}) = V_{A0}^2\frac{\partial^2}{\partial z^2}(<V_z>+{V_z'})\cdot \end{displaymath} (9)

By taking the ensemble average of this equation, we obtain the equation which governs the evolution of the coherent field


 \begin{displaymath} \frac{\partial^2}{\partial t^2}<V_z>-V_{A0}^2\frac{\partial^... ... z^2} <V_z>\ = -\frac{\partial^2}{\partial t^2}<\kappa V_z'>. \end{displaymath} (10)

An equation for the random field is obtained by subtracting Eq. (10) from Eq. (9). The assumption of a weak random field yields


  \begin{displaymath} \frac{\partial^2}{\partial t^2}{V'_z}-V_{A0}^2\frac{\partial... ... z^2} {V'_z}=-\kappa \frac{\partial^2}{\partial t^2}<V_z>\cdot \end{displaymath} (11)

Working out Eqs. (10) and (11) leads to the dispersion relation

 \begin{displaymath} \omega^2-V_{A0}^2k^2 = \omega^4 \int_{-\infty}^{\infty}\frac{E(k-\bar k)}{\omega^2-V_{A0}^2\bar k^2} {\rm d}\bar k, \end{displaymath} (12)

where $\omega$ is the frequency, k is the wavenumber, and E(k) is the Fourier transform of the correlation function

 \begin{displaymath} E(z_1-z_2)\ =\ <\kappa(z_1)\kappa(z_2)> \end{displaymath} (13)

of the density ratio $\kappa(z)$.

From the dispersion relation (12) it follows that the dependence of the cyclic frequency $\omega$ on the wave number k differs from the coherent dispersion relation, $\omega_0^2=V_{A0}^2k^2$. A random field leads to the appearance of dispersion. This dispersion is described by the real part of $\omega$. As a consequence of scattering by turbulent flow, the energy of the fast magnetoacoustic wave is partially transformed into the turbulent field. This phenomenon is associated with the imaginary part of the frequency, ${\rm Im}(\omega)$.

We introduce dimensionless variables

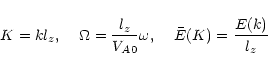\begin{displaymath}K= k l_z,\hspace{4mm} \Omega = \frac{l_z}{V_{A0}}\omega, \hspace{4mm} \bar E(K)=\frac{E(k)}{l_z} \end{displaymath} (14)

and assume that the random spectrum is Gaussian, e.g.

 \begin{displaymath} \bar E(K) = \frac{\sigma^2}{\pi}\exp(-K^2), \end{displaymath} (15)

where $\sigma $ is the variance which represents a departure of the local plasma density from the average value. In the dimensionless variables, Eq. (12) can be rewritten as:

 \begin{displaymath}\Omega^2-K^2 = -\frac{\sigma^2}{2\sqrt{\pi}}\Omega^3 [Z(\Omega-K)+ Z(\Omega+K)], \end{displaymath} (16)

where

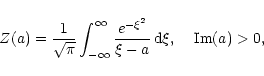
\begin{displaymath}Z(a)=\frac{1}{\sqrt{\pi}}\int_{-\infty}^{\infty} \frac{e^{-\xi^2}}{\xi-a}\,{\rm d}\xi,\hspace{4mm} {\rm Im}(a)>0, \end{displaymath}

is the plasma dispersion function (Fried & Conte 1961). In the case of a homogeneous medium, $\sigma=0$, dispersion relation (16) reduces to the fast wave dispersion relation for the cold plasma, $\Omega_0^2-K^2 = 0$. For finite structuring, $\sigma > 0$, the fast magnetoacoustic waves experience dispersion due to a non-zero righthand side of (16). For a more detailed discussion of this dispersion relation see Nocera et al. (2000).

In principle, one can consider solutions of Eq. (16) in some limiting cases, applying asymptotic expansions for the plasma dispersion function (Fried & Conte 1961). However, in the general case, determination of the dependency of the wave frequency $\Omega $ on the wave number K requires numerical methods.

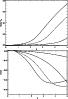  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{aah2261.f1a.ps}}\par\resizebox{\hsize}{!}{\includegraphics{aah2261.f1b.ps}}\end{figure} Figure 1: The difference between the real parts of the fast magnetoacoustic wave frequency for the random ($\Omega $) and homogeneous ($\Omega _0$) media (top panel) and imaginary part of $\Omega $ (bottom panel) as functions of the wave number K. Different curves correspond to different variances: $\sigma =0.4$ (solid), $\sigma =0.3$ (broken), $\sigma =0.2$ (dash-dotted), and $\sigma =0.1$ (dash-dot-dot-dot). The cyclic frequency $\Omega $ and the wavenumber K are shown in units of lz/VA0 and lz, respectively
Open with DEXTER

Figure 1 (top panel) displays the difference between the real part of $\Omega $ that is evaluated from Eq. (16) and $\Omega _0$, as a function of the wave number K. A more intensive random field (with a higher value of $\sigma $) increases more significantly the frequency of the fast magnetoacoustic wave with respect to the homogeneous medium case. This increase is also higher for higher values of K. For low values of $\sigma $ and K the influence of the random field is negligible. In the case of $\sigma =0.2$ and $\sigma =0.4$ the real part of the cyclic frequency $\Omega $ departs significantly from $\Omega _0$ for K>4 and K>2, respectively.

Figure 1 (bottom panel) illustrates the imaginary part of the frequency $\Omega $. It is noteworthy that ${\rm Im}(\Omega)$ always attains negative values which correspond to the wave damping. A higher damping occurs for higher values of $\sigma $ which represents a stronger random field. This result confirms the qualitative conclusions of Valley (1971). It is interesting that the damping decrement has a minimum value for a certain value of the wave number K, prescribed by the variance $\sigma $. For a higher $\sigma $, the minimum of ${\rm Im}(\Omega)$, which corresponds to the strongest damping, is shifted towards lower K.

4 Numerical illustration for pulse propagation

To illustrate the theory developed above, we perform numerical simulations of Eq. (6). Attention is paid to evolution of a wide-spectrum pulse. As different spectral components of the pulse propagate with different phase and group speeds, due to a dispersion brought by the random field, the pulse shape evolves in time. Our aim is to determine a typical profile of the small-amplitude pulse which interacts with randomly distributed coronal structures. A typical profile of the Alfvén speed is shown in Fig.  2. The average Alfvén speed is unity.

  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{aah2261.f2.ps}}\end{figure} Figure 2: A typical profile of the local Alfvén speed
Open with DEXTER

The numerical simulations are performed with the use of the existing and well-tested solver to the problem (LeVeque 1997). The code utilizes the Godunov-type method which yields accurate results near steep profiles and complex flows. The computational domain has a typical dimension $(0,\ 200l_z)$ and is divided into a grid of at least 20000 cells. The boundaries of the simulation region are set at z=0 and z=200lz. At the left and right boundaries free-streaming conditions are applied. Tests were performed with larger domains and a finer numerical grid to ensure grid convergence and to be sure that the accuracy of the results was not being compromised by the grid size. Initially, at t=0, an impulse in the perturbed velocity Vz is launched at the initial position z = 5lz to excite waves which propagate through the simulation region.

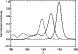  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{aah2261.f3.eps}}\end{figure} Figure 3: The profiles of the fast magnetoacoustic pulses at $t=190 l_z/V_{\rm A0}$. The solid line corresponds to $\sigma =0.01$, dotted to $\sigma =0.2$ and dashed to $\sigma =0.3$. The pulse amplitude is normalized to the initial amplitude at t=0
Open with DEXTER


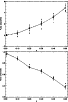  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{aah2261.f4a.ps}} \resizebox{\hsize}{!}{\includegraphics{aah2261.f4b.ps}}\end{figure} Figure 4: The delay (top) and attenuation (bottom) of the fast magnetoacoustic pulse in randomly structured medium with respect to the non-structured case for different values of the parameter $\sigma $. The crosses correspond to particular realizations results. The ensemble averaged data is joined by the dashed lines
Open with DEXTER

Figure 3 shows typical profiles of the initially Gaussian pulse at the time $t=190 l_z/V_{\rm A0}$. In the case of almost uniform medium (the variance of the random field is negligibly small, $\sigma =0.01$), the pulse approximately keeps its Gaussian form and initial amplitude (solid curve). In a randomly structured medium, the pulse is attenuated and decelerated (dotted and dashed curves). The tails appearing behind the pulses are typical manifestations of the effect of dispersion.

The deceleration and attenuation of the pulse are obviously proportional to the variance of the random field. Figure 4 (top) shows the relative delay of the pulse, defined as follows:

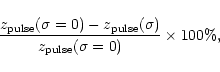
\begin{displaymath}\frac{z_{\rm pulse}(\sigma=0) - z_{\rm pulse}(\sigma)}{z_{\rm pulse}(\sigma=0)}\times 100\%, \end{displaymath}

where $z_{\rm pulse}(\sigma)$ is the coordinate of the pulse, determined as the position of highest amplitude, at the time $t=190 l_z/V_{\rm A0}$. The crosses represent results for particular realizations of the random field. The dashed lines join ensemble averaged data. It is noteworthy that $z_{\rm pulse}(\sigma=0)=195l_z$. The relative delay grows with the strength of the random field of the density, $\sigma $. In disagreement with Fig. 1 (top panel), the random inhomogeneity of the coronal plasma leads to deceleration of the fast magnetoacoustic waves. The reason of this disagreement is discussed by Nocera et al. (2000).

The attenuation of the pulse due to a random field is shown in Fig. 4 (bottom). The relative amplitude of the pulses is shown as a function of the variance $\sigma $at $t=190 l_z/V_{\rm A0}$. The amplitude is normalized by the pulse amplitude in the case of a homogeneous medium $\sigma=0$. We see that a random field leads to very efficient attenuation of the fast magnetoacoustic pulse amplitude, about 50% for $\sigma =0.4$.

5 Conclusions

We considered a simple 1D model of a perpendicular fast magnetoacoustic wave interaction with randomly distributed coronal structures. Our findings can be summarized as follows: a) even a relatively weak random density field, with variance less than 0.5, leads to significant (up to 50%) attenuation of the fast wave amplitude. This effect is stronger for wavelengths shorter than the correlation length of the random field. b) Numerical results reveal that fast waves are decelerated by random field. However, this effect is less pronounced than attenuation. For $\sigma< 0.5$, the deceleration can be about 25% for some Fourier components. A total deceleration of the wide-spectrum pulse is found to be $4\%$ for $\sigma=0.5$. c) A fast magnetoacoustic pulse experiences a dispersion that is introduced by the random field.

Our results are in qualitative agreement with the numerical findings by Shapiro & Kneib (1993) who have shown that a random pulse experiences broadening, decaying, and its spectrum is shifted towards lower frequencies as well as by Karweit & Blanc-Benon (1995) who have observed retardation of random waves.

These results suggest that the theory of interaction of MHD waves with randomly distributed coronal structures can be applied to seismology of the corona. Indeed, observing the damping and attenuation of coronal waves and applying the theory developed above, we obtain an additional tool for the determination of physical parameters of the solar corona, such as the coronal loop filling factor (associated with the correlation length lz and the variance $\sigma $).

There are several physical effects which have been left out of the model: in particular, coupling of the waves with slow and Alfvén modes and refraction. These neglected mechanisms can also lead to deceleration of the fast waves and the amplitude attenuation. However, consideration of these effects has to be at least 2D and so requires a much more developed technique. Also, any analytical treatment of such problems does not seem to be possible. From this point of view, this work can be considered as a first step toward the construction of the theory for wave interaction with a randomly structured corona.

One interesting application of the coronal MHD wave theory is the explanation of the coronal Moreton wave speed determined observationally as about 200-600 kms-1 (Thomson et al. 1999). As is discussed above, these waves are believed to be fast magnetoacoustic waves. In the low-$\beta$coronal plasma, the fast magnetoacoustic wave speed has to be between the Alfvén speed VA0 and $\sqrt{V_{A0}^2+c^2}$, depending upon the angle between the wave vector and the local magnetic field. Here, c is the sound speed. So, the wave speed has to be slightly higher than the Alfvén speed. But, according to accepted estimations, the coronal Alfvén speed is over 700-800 kms-1, which is supported by recent observational findings (Nakariakov et al. 1999). As a consequence of that the coronal Moreton waves propagate with speeds significantly lower than the expected speed. This discrepancy is to be explained.

The numerical simulations presented above suggest that the fast magnetoacoustic waves are indeed decelerated in a randomly structured medium. These simulations provide a qualitative explanation of the Moreton wave speed. An extension of the simulations which allow the quantitative comparison with the observations will have to incorporate 2D effects such as a random orientation of the magnetic field along the path of the wave.

Acknowledgements
The authors express their sincere thanks to Dr. Luigi Nocera and to Prof. Bernard Roberts for the stimulating discussions. K. M.'s work was financially supported by the KBN grant No. 2 PO3D 017 17. The work of K. M. and V. M. N. was in the frame of the Nato grant PST.CLG.976135, while V. M. N. and E. N. P. acknowledge the INTAS grant 97 31931. A part of the numerical calculations have been performed on a SUN workstation at the Institute of Physics, UMCS Lublin.

References

 

Copyright ESO 2001