14 behind-the-limb flares with occulted footpoints, well-observed by Yohkoh, have been carefully selected (Table 1). None of these events coincides in time with another flare. This ensures that the observations of the whole-Sun instruments (Yohkoh/BCS, CGRO/BATSE, GOES) can be used for additional investigation of the loop-top area. The LDE events lasting longer than 2.5 hours have been omitted in this paper.
To estimate the actual height of the flaring structure, a projection along the line-of-sight has been calculated. For this purpose, a plot time-versus-longitude for all flares in the active region during its solar disc passage before or after the investigated flare has been made (Masuda 1994). A linear fit to this plot allows us to estimate the longitude of the behind-the-limb event (see Table 1).
![\begin{figure}
\par\includegraphics[width=12.3cm,clip]{h2243f2.eps}\end{figure}](/articles/aa/full/2001/04/aah2243/Timg20.gif) |
Figure 2: The HXT light curves of the 13 January 1992 flare (event No. 3) in the channels L and M1 (two upper panels) and the temperatures estimated from the M1/L hardness ratio (bottom panel) are presented. The background was subtracted. The 7-minutes interval around the maximum was selected when impulses were the strongest. Two different smooth components are seen. For other details - see the caption of Fig. 1 |
For events from Table 1 it is reasonable to assume that the total hard X-ray radiation detected by the HXT comes from the loop-top area. This offered an unique chance to derive some parameters of loop-top HXR emission sources without the necessity of image reconstruction. Because of this, the obtained results have a better time resolution, up to the data sampling (0.5 s) and are not charged with the errors of the image reconstruction method.
| Maximum count rate f | Number of smooth | |||||||
| No. | Date | [cts/s/SC] |
components and | FWHM duration |
Contribution | |||
| L | M1 | M2 | H | their FWHM | [sec] of impulses | of impulses
|
||
| duration |
||||||||
| 1 |
21-Oct.-91 | 51.7 | 12.5 | 3.4 | 9.7 | 2: 1.5-2, 2.5-3 | 9.5-16 | medium |
| 2 | 10-Dec.-91 | 12.8 | 4.3 | 2.5 | 9.2 | 1: 2.3 | 5.5-8.5 | medium |
| 3 | 13-Jan.-92 | 14.8 | 4.0 | 2.6 | 9.5 | 2:
|
6-13 | weak |
| 4 | 6-Feb.-92 | 122.9 | 18.3 | 3.6 | 10.6 | 2:
|
13.5-16, 20.5-28 | medium |
| 5 | 19-Feb.-92 | 19.7 | 6.8 | 2.8 | 9.1 | 1: 7.5 | 12-28.5 | strong |
| 6 |
18-Jul.-92 | 57.8 | 7.0 | 2.9 | 9.6 | 1: 3-4 | 5-10.5 | weak |
| 7 | 24-Nov.-92 | 13.9 | 6.3 | 3.1 | 9.4 | 1: 2.3 | 8.5-13.5 | medium |
| 8 | 24-Nov.-92 | 4.6 | 3.2 | 2.6 | 9.6 | 1: 8 | 8.5-9.5 | strong |
| 9 | 24-Nov.-92 | 4.3 | 3.1 | 2.6 | 9.3 | 2: 5.5-6, 6 | 13-19.5 | strong |
| 10 |
24-Nov.-92 | 23.7 | 6.3 | 3.1 | 9.9 | 1: 6-7 | 12.5-23.5 | weak |
| 11 | 1-Feb.-93 | 39.8 | 11.9 | 5.0 | 10.6 | 3:
|
7.5-8.5, 13.5-24.5 | medium |
| 12 | 11-Nov.-93 | 9.2 | 6.7 | 4.1 | 11.2 | 2: 2.3, 6.6-7 | 5.5-8.5, 12-15.5 | strong |
| 13 | 29-Jan.-94 | 125.6 | 35.6 | 6.3 | 11.1 | 2: 4.5-5.5, 2.2 | 7-17 | medium |
| 14 |
29-Jan.-94 | 9.4 | 4.7 | 3.4 | 11.3 | 1: 7.5-9 | 10.5-17.5 | strong |
|
|
In spite of the physical variety of the investigated flares, their HXR light curves show evident similarity. First, most of the emission occurs in the low energy channels: L (14-23 keV) and M1 (23-33 keV), only exceptionally reaching higher energy bands: M2 (33-53 keV), and H (53-93 keV) - see Table 2. Second, the light curves show two kinds of variability: a slow, long-term variability and a rapid, short-term variability (see Figs. 1 and 2). The first type will be called "a smooth component'', the second type, "an impulsive component''. For half of the events, more than one (2 or 3) smooth component was detected (see Table 2 and Fig. 2).
The smooth and the impulsive components have been separated by subtracting a
constant background, ![]() :
:
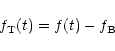 |
(1) |
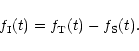 |
(2) |
On the basis of this separation several observational characteristics, i.e., peak flux, time of maximum, FWHM duration, time profile, and relative contribution to the total flux have been obtained for both components and for all investigated flares. Results for the individual event are presented in Table 2. Because of greater number of counts, the values obtained in the channel L have better quality.
Smooth components have quasi-symmetrical time profiles. This property allows us to resolve multi-parts smooth components and to estimate their duration if observations were not complete. Obtained values of the FWHM duration were from about 2 min to about 8 min (Table 2).
To lower the statistical noise, the light curves of the impulsive components were smoothed first by central-moving-averages of 5 s duration. The impulsive components consisted of many individual impulses which appeared randomly during the whole evolution of smooth components. Sometimes they grouped into clusters from which it was difficult to isolate individual episodes (e.g. the middle panel in Fig. 2). The number of impulses increases if we consider weaker ones. The impulses were evidently weaker than the smooth component, as their maximum contribution to the total flux only rarely reached about 25-30%. For individual flares the relative contribution of impulses to the total flux was usually similar (Table 2).
Almost all isolated impulses were symmetrical. This property helped resolve impulses for which a rising or decaying wing was superimposed by other impulses. The histogram of the FWHM duration of 104 impulses that have been resolved in all investigated events is shown in Fig. 3. Obtained values fall within the interval of 5-30 s. Shorter durations were more frequent than the longer durations. Impulses shorter than 5 seconds have been smoothed by central-moving-averages of the light curves, so that the short-period cutoff is artificial. As a rule, impulses resolved in the same flare fall within narrower intervals of FWHM duration values than the whole population (Table 2). Therefore, the peaks at 8- and 12-s in the histogram (Fig. 3) can be explained as a result of an observational selection.
| No. | Total | Smooth | Impulsive |
| flux |
component |
component |
|
| 1 | 38 | 34 | 67 |
| 2 | 37.5 | 34 | 60 |
| 3 | 33 | 29 | 65 |
| 4 | 38 | 33 | 49 |
| 5 | 39 | 32.5 | 68 |
| 6 | 26 | 25 | 40 |
| 7 | 67.5 | 59 | 97 |
| 8 | 28 | 28 | N/A |
| 9 | 31 | 31 | N/A |
| 10 | 37 | 32 | 94 |
| 11 | 48.5 | 43.5 | 92 |
| 12 | 60.5 | 55 | 115 |
| 13 | 47 | 41 | 87 |
| 14 | 36 | 32 | 50 |
|
|
|
|
In the next step the time evolution of the hardness ratio M1/L for all investigated events was investigated. The calculations have been made for the total flux as well as for the smooth and the impulsive components. In the case of the total flux and the smooth component time accumulation was adopted to lower the relative error of individual values below 5 percent. To achieve this, for one M1/L value 11-18 counts per subcollimator in the channel M1 were needed. For the majority of impulses the number of counts was too low to fulfill such a criterion. Therefore the flux was accumulated over the FWHM duration and one value for one impulse was calculated. For weak impulses the flux was accumulated throughout the whole cluster of impulses. Assuming a specific model of hard X-ray emission and considering the spectral response of the HXT (Kosugi et al. 1991), the physical condition of emitting plasma was estimated from the calculated hardness ratio. For further presentation of results the hardness ratio M1/L and the fluxes are expressed in terms of the temperature T and the emission measure EM.
Examples of the temperature evolution are presented in bottom panels of Figs. 1 and 2. We see that impulses were responsible for temporal jumps of temperature estimated from the total flux (plots with boxes). After the separation of them, the temperature evolution was smooth (plots with diamonds) and the obtained values were slightly lower. From this observation we can conclude qualitatively that plasma producing impulses was hotter and less frequent than plasma emitting the smooth component. Temperatures obtained from the total flux were mainly within the interval 20-50 MK, only exceptionally reaching higher values, up to 70 MK (Table 3). Temperatures of the smooth component were about several MK lower. The temperatures of the impulses were higher by the factor of 1.2-2.4 than the temperatures estimated for the smooth component (Fig. 4). From the bottom panel of this figure we see that emission measure of impulses were 1-3 orders lower than emission measure of the smooth component.
Copyright ESO 2001