We work with flat 2-dimensional disc models. In a cylindrical coordinate
system
![]() centred on the central star,
the disc rotation axis and the
central star-companion object orbital angular momentum vectors are
in the z direction.
The equations of motion that describe the
disc are the vertically
integrated Navier-Stokes equations.
The disc evolves in the
combined gravitational field of the star and companion, and
as a result of pressure and viscous forces. The star-companion orbit
evolves under their mutual gravitational interaction
and the gravitational field of the disc.
For the calculations reported here, the companion gravitational
potential was taken
to be that of a softened point
mass with softening parameter equal to
centred on the central star,
the disc rotation axis and the
central star-companion object orbital angular momentum vectors are
in the z direction.
The equations of motion that describe the
disc are the vertically
integrated Navier-Stokes equations.
The disc evolves in the
combined gravitational field of the star and companion, and
as a result of pressure and viscous forces. The star-companion orbit
evolves under their mutual gravitational interaction
and the gravitational field of the disc.
For the calculations reported here, the companion gravitational
potential was taken
to be that of a softened point
mass with softening parameter equal to
![]()
![]() being the Roche lobe radius.
As with similar cases dealt with in NPMK,
the companion was not permitted to accrete mass
but could maintain a static atmosphere.
being the Roche lobe radius.
As with similar cases dealt with in NPMK,
the companion was not permitted to accrete mass
but could maintain a static atmosphere.
We use a locally isothermal equation of state, and prescribe
the local sound speed
![]() to be such that the disc aspect ratio
H/r=0.05 throughout the disc,
to be such that the disc aspect ratio
H/r=0.05 throughout the disc,
![]() being the Keplerian velocity.
Thus the disc Mach number is 20 everywhere.
We employ
a constant value of the kinematic viscosity
being the Keplerian velocity.
Thus the disc Mach number is 20 everywhere.
We employ
a constant value of the kinematic viscosity
![]() in dimensionless
units (described below). The assumption implicit within this formalism is that
the process that causes angular momentum transport in
astrophysical discs may be modeled simply using an anomalous
viscosity coefficient in the Navier-Stokes equations,
even though it probably arises through complicated processes such
as MHD turbulence generated by the Balbus-Hawley instability (Balbus & Hawley
1991, 1998).
in dimensionless
units (described below). The assumption implicit within this formalism is that
the process that causes angular momentum transport in
astrophysical discs may be modeled simply using an anomalous
viscosity coefficient in the Navier-Stokes equations,
even though it probably arises through complicated processes such
as MHD turbulence generated by the Balbus-Hawley instability (Balbus & Hawley
1991, 1998).
For computational convenience we adopt dimensionless
units. The unit of mass is taken to be the sum
of the mass of the central star (M*) and companion (![]() ).
The unit of length
is taken to be the initial orbital radius of the companion,
).
The unit of length
is taken to be the initial orbital radius of the companion, ![]() .
The gravitational constant G=1, so that the natural unit of time becomes
.
The gravitational constant G=1, so that the natural unit of time becomes
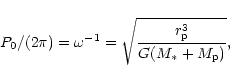
The disc models used in all simulations
had uniform surface density, ![]() with an imposed taper near the
disc edge, initially.
The value of
with an imposed taper near the
disc edge, initially.
The value of ![]() was chosen such that when
was chosen such that when
![]() there exists the equivalent of
2 Jupiter masses
there exists the equivalent of
2 Jupiter masses
![]() in the disc interior to the initial
orbital radius of the companion.
Then
in the disc interior to the initial
orbital radius of the companion.
Then
![]() in our dimensionless units.
in our dimensionless units.
Different mass ratios between the companion and the
central star
![]() ,
were considered, such that
,
were considered, such that
![]() .
For
.
For
![]() the lower end of this range
corresponds to a Jupiter mass protoplanet and
the upper end to a Brown Dwarf of mass
the lower end of this range
corresponds to a Jupiter mass protoplanet and
the upper end to a Brown Dwarf of mass
![]() The inner radius of the disc was located at r=0.4 and the outer radius
at r=6.
The inner radius of the disc was located at r=0.4 and the outer radius
at r=6.
Copyright ESO 2001