A&A 366, 263-275 (2001)
DOI: 10.1051/0004-6361:20000011
Orbital eccentricity growth through disc-companion tidal interaction
J. C. B. Papaloizou - R. P. Nelson - F. Masset
Astronomy Unit, Queen Mary & Westfield College, Mile End Rd, London E1 4NS, UK
Received 8 June 2000 / Accepted 15 November 2000
Abstract
We investigate the driving of orbital eccentricity of giant protoplanets and
brown dwarfs through disc-companion tidal interactions
by means of two dimensional numerical simulations. We consider disc
models that are thought to be typical of protostellar discs during the
planet forming epoch, with characteristic surface densities similar to
standard minimum mass solar nebula models. We consider
companions, ranging in mass between 1 and 30 Jupiter masses
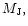 that are initially
embedded within the discs on circular orbits about a central solar mass.
We find that a transition in orbital behaviour
occurs at a mass in the range 10-20
that are initially
embedded within the discs on circular orbits about a central solar mass.
We find that a transition in orbital behaviour
occurs at a mass in the range 10-20
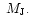 For low mass
planetary companions,
we find that the orbit remains essentially
circular. However, for companion masses
For low mass
planetary companions,
we find that the orbit remains essentially
circular. However, for companion masses
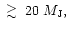 we find that non
steady behaviour of the orbit occurs,
characterised by a growth
in eccentricity to values of
we find that non
steady behaviour of the orbit occurs,
characterised by a growth
in eccentricity to values of
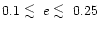 .
Analysis of the disc response to the presence of a perturbing companion
indicates that for the higher masses, the inner parts of the disc
that lie exterior to the companion orbit
become eccentric through an instability driven by the
coupling of an initially
small disc eccentricity to the companion's
tidal potential. This coupling leads to the excitation
of an m=2 spiral wave at the 1:3 outer eccentric Lindblad resonance,
which transports angular momentum outwards,
leading to a growth of the disc eccentricity.
The interaction of the companion with this eccentric disc, and
the driving produced by direct resonant wave excitation at the 1:3 resonance,
can lead to the growth of orbital eccentricity, with the driving
provided by the eccentric disc being the stronger. Eccentricity growth
occurs when the tidally induced gap width is such that eccentricity damping
caused by corotating Lindblad resonances is inoperative.
These simulations indicate that for standard disc models,
gaps become wide enough for the 1:3 resonance to dominate,
such that the transition from circular orbits can occur, only
for masses in the brown dwarf range. However, the transition
mass might be reduced into the range for extrasolar planets
if the disc viscosity is significantly lower enabling
wider gaps to occur for these masses.
Another possibility is that an eccentric disc is produced
by an alternative mechanism, such as viscous
overstability resulting in a slowly
precessing non axisymmetric mass distribution.
A large eccentricity
in a planet orbit contained within an inner cavity
might then be produced.
.
Analysis of the disc response to the presence of a perturbing companion
indicates that for the higher masses, the inner parts of the disc
that lie exterior to the companion orbit
become eccentric through an instability driven by the
coupling of an initially
small disc eccentricity to the companion's
tidal potential. This coupling leads to the excitation
of an m=2 spiral wave at the 1:3 outer eccentric Lindblad resonance,
which transports angular momentum outwards,
leading to a growth of the disc eccentricity.
The interaction of the companion with this eccentric disc, and
the driving produced by direct resonant wave excitation at the 1:3 resonance,
can lead to the growth of orbital eccentricity, with the driving
provided by the eccentric disc being the stronger. Eccentricity growth
occurs when the tidally induced gap width is such that eccentricity damping
caused by corotating Lindblad resonances is inoperative.
These simulations indicate that for standard disc models,
gaps become wide enough for the 1:3 resonance to dominate,
such that the transition from circular orbits can occur, only
for masses in the brown dwarf range. However, the transition
mass might be reduced into the range for extrasolar planets
if the disc viscosity is significantly lower enabling
wider gaps to occur for these masses.
Another possibility is that an eccentric disc is produced
by an alternative mechanism, such as viscous
overstability resulting in a slowly
precessing non axisymmetric mass distribution.
A large eccentricity
in a planet orbit contained within an inner cavity
might then be produced.
Key words: accretion, accretion disks - methods: numerical - stars: planetary systems
1 Introduction
Disc-companion interactions are important in a variety of
astrophysical contexts ranging from orbital evolution, tidal interaction,
and accretion in close binary systems (e.g. Lin & Papaloizou 1979;
Artymowicz & Lubow 1994; Papaloizou & Terquem 1995; Larwood & Papaloizou 1997)
to the evolution of black hole binary pairs in active
galaxies (Begelman et al. 1980; Ivanov et al. 1999).
The recent discovery of a number of extrasolar giant planets orbiting around
nearby solar-type stars (Marcy & Butler 1998, 2000) has stimulated renewed interest in the
theory of planet formation and disc-companion interaction.
These planetary objects have masses, 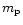 ,
that
are comparable to that of Jupiter
(
,
that
are comparable to that of Jupiter
(
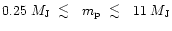 ),
have orbital semi-major axes in the range
),
have orbital semi-major axes in the range
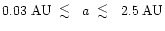 ,
and orbital
eccentricities in the range
,
and orbital
eccentricities in the range
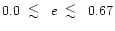 (Marcy & Butler 2000). Explaining these data is one of the major
challenges faced by planet formation theory.
(Marcy & Butler 2000). Explaining these data is one of the major
challenges faced by planet formation theory.
The presence of the brown dwarf
Gliese 229B with mass 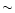 45
45 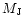 in a binary system indicates the potential
existence of a separate population, at the one percent
incidence level, of brown dwarfs
(Oppenheimer et al. 2000)
which could also form from discs, possibly
through a different mechanism to that for extrasolar planets.
in a binary system indicates the potential
existence of a separate population, at the one percent
incidence level, of brown dwarfs
(Oppenheimer et al. 2000)
which could also form from discs, possibly
through a different mechanism to that for extrasolar planets.
Recent simulations of protoplanets in the observed
mass range (Kley 1999; Bryden et al. 1999; Lubow et al. 1999)
interacting with a disc with parameters thought to be typical
of protoplanetary discs, indicate gap formation and
upper mass limit consistent with the observations. In addition
simulations by Nelson et al. (2000) (hereafter NPMK) which
allowed the protoplanet orbit to change
found inward migration on near circular orbits leaving
the observed eccentricities of extrasolar planets unexplained.
However, previous discussions of this problem (Artymowicz 1992;
Lin & Papaloizou 1993a) have indicated that orbital eccentricity
might be driven by disc-companion interactions.
This might be expected from the general theory of tidal interaction.
Jeffreys (1961) showed that a body in circular orbit around
a rapidly rotating central object could have an instability
driving orbital eccentricity. A similar instability might be
expected for a body orbiting inside a rotating disc.
In this case resonant wave excitation at the inner and outer eccentric
Lindblad resonances leads to the excitation of eccentricity.
However, a sufficiently wide gap is required to exclude
coorbital and near coorbital disc material
which would damp the eccentricity through coorbital Lindblad
torques (Artymowicz 1993). Thus an eccentric instability
would only be expected for a mass sufficiently large to clear a wide gap.
The mass above which eccentric orbits might be excited is expected
to be a function of the disc parameters.
Determination of this mass is important for the theory of disc-companion
interactions and its implications for binary systems and the formation
theory of planets and brown dwarfs.
We find that the transition to an eccentric orbit can be linked
to the driving of an eccentric disc, and it appears that the interaction
between the companion and this disc eccentricity produces eccentricity driving
that moderately exceeds that due to direct resonant wave excitation at the
1:3 outer eccentric Lindblad resonance discussed above.
As the behaviour of the disc
then also has a transition, different predictions
for the mass spectrum
and orbital distribution of more massive objects
above the transition mass may result.
In this paper we
investigate the driving of orbital eccentricity of giant protoplanets and
brown dwarfs through disc-companion tidal interactions
by means of two dimensional numerical simulations.
We examined the evolution of
companions ranging in mass between 1 and 30 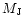 orbiting within protoplanetary discs about a central solar mass.
For standard parameters, we find the transition to eccentric orbits
occurs for companion masses that are greater than
orbiting within protoplanetary discs about a central solar mass.
For standard parameters, we find the transition to eccentric orbits
occurs for companion masses that are greater than 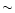 20
20
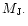 In these cases the inner disc has accreted onto the central star.
The inner parts of the disc
that lie exterior to the companion orbit were found to
become eccentric.
This latter process is associated with the excitation
of a m=2 spiral wave at the 1:3 outer eccentric Lindblad resonance.
This effect has a counterpart in the modelling of
discs in Cataclysmic binaries. Here, in the lower companion mass range,
an eccentric circumprimary disc has been seen (Whitehurst 1988;
Hirose & Osaki 1990; Lubow 1991).
This in turn is related to the excitation
of a m=2 spiral wave at the 3:1 inner eccentric Lindblad resonance,
as described by Lubow (1991).
In these cases the inner disc has accreted onto the central star.
The inner parts of the disc
that lie exterior to the companion orbit were found to
become eccentric.
This latter process is associated with the excitation
of a m=2 spiral wave at the 1:3 outer eccentric Lindblad resonance.
This effect has a counterpart in the modelling of
discs in Cataclysmic binaries. Here, in the lower companion mass range,
an eccentric circumprimary disc has been seen (Whitehurst 1988;
Hirose & Osaki 1990; Lubow 1991).
This in turn is related to the excitation
of a m=2 spiral wave at the 3:1 inner eccentric Lindblad resonance,
as described by Lubow (1991).
Our present results indicate
eccentric orbits only
for masses in the brown dwarf range. However, the transition
mass might be reduced into the range for extrasolar planets
if
wider gaps or more extensive disc clearance
occurs while allowing an outer eccentric
disc to still exist.
The plan of the paper is as follows. In Sect. 2
we describe the physical model of the disc-companion system used.
In Sect. 3 we describe the numerical methods.
In Sect. 4 we present the numerical results
which indicate the transition from circular companion orbit
to eccentric companion orbit together with an eccentric outer disc
for companion masses exceeding  20
20
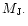 In Sect. 5 we give a simple analytic model
illustrating how the eccentricity can be driven both
in the companion orbit and exterior disc by an instability
operating through density wave excitation at the outer 1:3
Lindblad resonance leading to a pattern rotating
with 1/2 the companion orbital frequency as seen in the numerical
calculations. A similar analysis for the driving of eccentricity in
circumstellar discs, but with fixed circular
companion orbit, is discussed in
Lubow (1991). Finally in Sect. 6 we discuss
our results and speculate on how eccentric discs
might produce eccentric orbits for masses in the planetary range.
In Sect. 5 we give a simple analytic model
illustrating how the eccentricity can be driven both
in the companion orbit and exterior disc by an instability
operating through density wave excitation at the outer 1:3
Lindblad resonance leading to a pattern rotating
with 1/2 the companion orbital frequency as seen in the numerical
calculations. A similar analysis for the driving of eccentricity in
circumstellar discs, but with fixed circular
companion orbit, is discussed in
Lubow (1991). Finally in Sect. 6 we discuss
our results and speculate on how eccentric discs
might produce eccentric orbits for masses in the planetary range.
2 The physical model
We solve the time dependent evolution equations for a system
composed of a primary star, small mass companion, and viscous disc.
The equations of motion and numerical
procedures adopted are described
in NPMK. For the sake of brevity we refer the reader to that paper
for details.
We work with flat 2-dimensional disc models. In a cylindrical coordinate
system
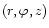 centred on the central star,
the disc rotation axis and the
central star-companion object orbital angular momentum vectors are
in the z direction.
The equations of motion that describe the
disc are the vertically
integrated Navier-Stokes equations.
The disc evolves in the
combined gravitational field of the star and companion, and
as a result of pressure and viscous forces. The star-companion orbit
evolves under their mutual gravitational interaction
and the gravitational field of the disc.
For the calculations reported here, the companion gravitational
potential was taken
to be that of a softened point
mass with softening parameter equal to
centred on the central star,
the disc rotation axis and the
central star-companion object orbital angular momentum vectors are
in the z direction.
The equations of motion that describe the
disc are the vertically
integrated Navier-Stokes equations.
The disc evolves in the
combined gravitational field of the star and companion, and
as a result of pressure and viscous forces. The star-companion orbit
evolves under their mutual gravitational interaction
and the gravitational field of the disc.
For the calculations reported here, the companion gravitational
potential was taken
to be that of a softened point
mass with softening parameter equal to
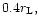
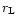 being the Roche lobe radius.
As with similar cases dealt with in NPMK,
the companion was not permitted to accrete mass
but could maintain a static atmosphere.
being the Roche lobe radius.
As with similar cases dealt with in NPMK,
the companion was not permitted to accrete mass
but could maintain a static atmosphere.
We use a locally isothermal equation of state, and prescribe
the local sound speed
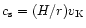 to be such that the disc aspect ratio
H/r=0.05 throughout the disc,
to be such that the disc aspect ratio
H/r=0.05 throughout the disc,
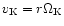 being the Keplerian velocity.
Thus the disc Mach number is 20 everywhere.
We employ
a constant value of the kinematic viscosity
being the Keplerian velocity.
Thus the disc Mach number is 20 everywhere.
We employ
a constant value of the kinematic viscosity
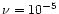 in dimensionless
units (described below). The assumption implicit within this formalism is that
the process that causes angular momentum transport in
astrophysical discs may be modeled simply using an anomalous
viscosity coefficient in the Navier-Stokes equations,
even though it probably arises through complicated processes such
as MHD turbulence generated by the Balbus-Hawley instability (Balbus & Hawley
1991, 1998).
in dimensionless
units (described below). The assumption implicit within this formalism is that
the process that causes angular momentum transport in
astrophysical discs may be modeled simply using an anomalous
viscosity coefficient in the Navier-Stokes equations,
even though it probably arises through complicated processes such
as MHD turbulence generated by the Balbus-Hawley instability (Balbus & Hawley
1991, 1998).
For computational convenience we adopt dimensionless
units. The unit of mass is taken to be the sum
of the mass of the central star (M*) and companion (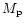 ).
The unit of length
is taken to be the initial orbital radius of the companion,
).
The unit of length
is taken to be the initial orbital radius of the companion, 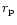 .
The gravitational constant G=1, so that the natural unit of time becomes
.
The gravitational constant G=1, so that the natural unit of time becomes
with P0 being
the initial orbital period of the binary, which in all cases was initiated
on a circular orbit.
2.1 Initial conditions
The disc models used in all simulations
had uniform surface density, 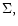 with an imposed taper near the
disc edge, initially.
The value of
with an imposed taper near the
disc edge, initially.
The value of 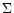 was chosen such that when
was chosen such that when
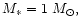 there exists the equivalent of
2 Jupiter masses
there exists the equivalent of
2 Jupiter masses
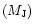 in the disc interior to the initial
orbital radius of the companion.
Then
in the disc interior to the initial
orbital radius of the companion.
Then
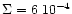 in our dimensionless units.
in our dimensionless units.
Different mass ratios between the companion and the
central star
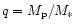 ,
were considered, such that
,
were considered, such that
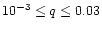 .
For
.
For
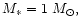 the lower end of this range
corresponds to a Jupiter mass protoplanet and
the upper end to a Brown Dwarf of mass
the lower end of this range
corresponds to a Jupiter mass protoplanet and
the upper end to a Brown Dwarf of mass
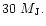 The inner radius of the disc was located at r=0.4 and the outer radius
at r=6.
The inner radius of the disc was located at r=0.4 and the outer radius
at r=6.
Since material in a viscous
accretion disc will naturally flow onto the
central star, an outflow condition
was applied at the inner boundary.
The outer boundary condition was the same as that described in NPMK.
3 Hydrodynamic codes
The calculations
presented here were performed
with the three dimensional MHD code NIRVANA (here adapted to 2D) that
has
been described in depth elsewhere (Ziegler & Yorke 1997).
Viscous forces have been added as described
by Kley (1998).
In each case the equations are solved using a finite difference scheme on a
discretised computational domain containing
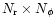 grid cells, where the grid spacing in the
grid cells, where the grid spacing in the
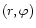 coordinates is uniform.
coordinates is uniform.
For the calculations
presented here and listed in Table 1,
no accretion onto the companion was allowed and
three different resolutions have been used.
The run with
q=10-3, listed as N1 in Table 1 used
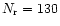 and
and
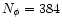 .
The other lower resolution runs used
.
The other lower resolution runs used
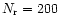 and
and
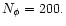 One higher resolution run used
One higher resolution run used
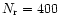 and
and
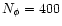 .
The numerical method is based on
the monotonic transport algorithm of
Van Leer (1977), leading to the global conservation of mass and angular
momentum.
The evolution of the companion orbit was computed using a standard leapfrog
integrator.
.
The numerical method is based on
the monotonic transport algorithm of
Van Leer (1977), leading to the global conservation of mass and angular
momentum.
The evolution of the companion orbit was computed using a standard leapfrog
integrator.
NIRVANA has been applied to a number of different problems including
that of an accreting protoplanet embedded in a protostellar disc (NPMK).
It was found to give results that are very similar to those obtained with
other finite difference codes including FARGO (described in Masset 2000)
and RH2D (described in Kley 1999).
In order to establish the reliability
of the numerical results,
simulations were also performed
using
an alternative code based on the FARGO
fast advection method (see Masset 2000, NPMK).
In this scheme, which is able to operate with longer time steps
than NIRVANA,
a fourth-order
Runge Kutta scheme was used as orbit integrator.
Results obtained with the two codes were very similar.
4 Numerical calculations
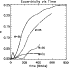 |
Figure 1:
This figure shows the evolution of the eccentricity versus time
(measured in units of P0) for the calculations, N2, N3, N4, N5 listed
in Table 1. The lines corresponding to each companion of different
mass are indicated on the figure in units of 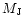
|
| Open with DEXTER |
Recent simulations of protoplanets with
0.001 < q < 0.01,interacting with
discs with physical parameters similar to those adopted
here, being thought to be appropriate to protoplanetary
discs, have been carried out by Bryden et al. (1999), Kley (1999),
and Lubow et al. (1999). Fixed circular orbits were
assumed. It was found that a gap was formed that deepened
and widened with increasing q. The disc interior to the orbit
accreted onto the central star forming an inner cavity.
Subsequent work by NPMK which allowed the orbit to evolve
found that it remained essentially circular while migrating
towards the central star.
We remark that Artymowicz (1992) indicated that
orbital eccentricity growth might occur for sufficiently large
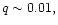 while Lin & Papaloizou (1993a) argued that for sufficiently wide gaps,
eccentricity growth could be induced by interaction at the 1:3
resonance in the outer disc and the 3:1 resonance in the inner disc.
As the latter is absent in the work presented here, only
the 1:3 resonance in the outer disc will concern us.
while Lin & Papaloizou (1993a) argued that for sufficiently wide gaps,
eccentricity growth could be induced by interaction at the 1:3
resonance in the outer disc and the 3:1 resonance in the inner disc.
As the latter is absent in the work presented here, only
the 1:3 resonance in the outer disc will concern us.
The aim of the work presented here is to examine for what value of
the companion-star mass ratio, if any, eccentricity growth of the companion
orbit is induced by its interaction with the disc model that we assume.
Should it occur, we wish
to understand the dominant mechanism by which growth occurs
and in particular whether the 1:3 resonance is involved.
The numerical calculations are summarised in Table 1.
The case of q=10-3 was considered in some detail in NPMK.
The planet/companion in this case was found to migrate in towards the central
star on a time scale given by the viscous evolution time at the initial
position of the planet (also see Lin & Papaloizou 1986)
remaining on an essentially circular orbit.
We will not give further discussion here on this case, since eccentricity
growth was not observed.
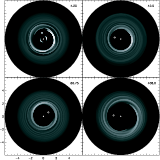 |
Figure 2:
This figure shows the evolution of the surface density
profile of the disc in calculation N5 described in Table 1. The time,
in units of P0, is shown at the top right hand corner of each panel.
The initial clearing of a gap is shown in the first and second
panel, and the growth of
eccentricity of the disc interior to the 1:3 resonance (located at
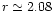 )
may be observed in the third panel. The fourth panel shows the
disc at a later time when the companion has developed an eccentricity of )
may be observed in the third panel. The fourth panel shows the
disc at a later time when the companion has developed an eccentricity of
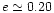 ,
and indicates that the behaviour of the disc becomes
more complicated and unsteady during these later times ,
and indicates that the behaviour of the disc becomes
more complicated and unsteady during these later times |
| Open with DEXTER |
The evolution of the eccentricity for the remaining cases listed
in Table 1 is shown in Fig. 1. It is apparent
from this figure that strong eccentricity growth occurs for
mass ratios in the range
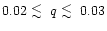 ,
with the strongest eccentricity
growth being observed at the higher end of this range. From here onwards we
will concentrate on describing the evolution of the q=0.03 case.
,
with the strongest eccentricity
growth being observed at the higher end of this range. From here onwards we
will concentrate on describing the evolution of the q=0.03 case.
A plot of the surface density evolution of run N5 described in Table 1
is shown in Fig. 2. The times corresponding to each panel
are shown in the top right hand corner in units of P0.
It can be seen that the disc interior to
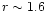 is cleared out
by the action of the companion tides on a relatively short
time scale, and remains tidally truncated.
Further evolution of the system leads to the formation
of an eccentric outer disc, as may be observed in the third panel of
Fig. 2. Figure 4 also shows the formation of an eccentric
disc for a companion on a fixed circular orbit, and is described below.
As the eccentricity of the companion increases
beyond
is cleared out
by the action of the companion tides on a relatively short
time scale, and remains tidally truncated.
Further evolution of the system leads to the formation
of an eccentric outer disc, as may be observed in the third panel of
Fig. 2. Figure 4 also shows the formation of an eccentric
disc for a companion on a fixed circular orbit, and is described below.
As the eccentricity of the companion increases
beyond
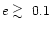 ,
we observe
that the disc response becomes non steady as the companion orbits between
apocentre and pericentre. The evolution of the orbital radius of
the companion and its eccentricity evolution (on both linear and log scales)
are presented in Fig. 3.
This figure shows that the eccentricity undergoes a period
of rapid growth after a time of
,
we observe
that the disc response becomes non steady as the companion orbits between
apocentre and pericentre. The evolution of the orbital radius of
the companion and its eccentricity evolution (on both linear and log scales)
are presented in Fig. 3.
This figure shows that the eccentricity undergoes a period
of rapid growth after a time of 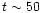 P0. The logarithmic
plot of e versus t shown in the second panel of this figure shows that
the growth rate is initially constant (approximately), but then decreases as
the system evolves beyond
P0. The logarithmic
plot of e versus t shown in the second panel of this figure shows that
the growth rate is initially constant (approximately), but then decreases as
the system evolves beyond
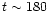 P0, indicating exponential growth
during these early stages. Analysis of the torques being exerted
on the companion between the times
P0, indicating exponential growth
during these early stages. Analysis of the torques being exerted
on the companion between the times
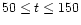 P0 shows that the
angular momentum is removed from the companion orbit
and transferred to the disc as it approaches
apocentre, leading to further growth of the orbital
eccentricity. This, however,
does not explain why the disc itself becomes eccentric during its early
evolution. At a later time
P0 shows that the
angular momentum is removed from the companion orbit
and transferred to the disc as it approaches
apocentre, leading to further growth of the orbital
eccentricity. This, however,
does not explain why the disc itself becomes eccentric during its early
evolution. At a later time
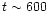 P0, the eccentricity
reaches a maximum value
P0, the eccentricity
reaches a maximum value 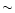 0.25. It subsequently enters
into a sequence of cyclic variations, decreasing
to small values at
0.25. It subsequently enters
into a sequence of cyclic variations, decreasing
to small values at
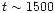 P0, before increasing again.
After the initial saturation the disc is always very eccentric
and in contact with the companion at some orbital phases.
This interaction of the companion
with material with higher specific
angular momentum causes the early net inward orbital migration
to reverse such that the final semi-major axis
at
P0, before increasing again.
After the initial saturation the disc is always very eccentric
and in contact with the companion at some orbital phases.
This interaction of the companion
with material with higher specific
angular momentum causes the early net inward orbital migration
to reverse such that the final semi-major axis
at
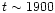 P0 exceeds the initial one.
But note that the details of this evolution depend
on the manner in which the disc interacts with the companion
and will be discussed by one of us in a future publication.
Clearly the disc-companion interaction is very
different in the brown dwarf regime from the planetary one.
P0 exceeds the initial one.
But note that the details of this evolution depend
on the manner in which the disc interacts with the companion
and will be discussed by one of us in a future publication.
Clearly the disc-companion interaction is very
different in the brown dwarf regime from the planetary one.
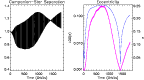 |
Figure 3:
This figure shows the evolution of the companion-star
orbital separation as a function of time in the first panel,
and the orbital eccentricity plotted as a log function (dotted line)
and linear function (solid line) in the second panel.
It is apparent that the eccentricity undergoes a period
of rapid growth after 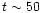 P0. Between
P0. Between 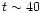 and 100 P0,
the growth is approximately exponential, as indicated by the plot
of
and 100 P0,
the growth is approximately exponential, as indicated by the plot
of  in the second panel which is close to being a straight line
during these times. At later times, the growth rate decreases and the plots
show a change of behaviour at
in the second panel which is close to being a straight line
during these times. At later times, the growth rate decreases and the plots
show a change of behaviour at
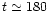 P0 when
P0 when
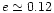 .
This change in the growth of e is accompanied by a change in the behaviour
of the disc surface density response, which becomes very unsteady.
This latter point was discussed
in the caption of Fig. 2.
On average there is net inward orbital migration
until .
This change in the growth of e is accompanied by a change in the behaviour
of the disc surface density response, which becomes very unsteady.
This latter point was discussed
in the caption of Fig. 2.
On average there is net inward orbital migration
until
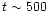 P0. After this time the eccentricity
starts to decrease before increasing again in a cyclic variation.
During these later phases
the companion has contact with material with higher specific
angular momentum from the eccentric disc. The interaction
causes the inward migration to reverse
P0. After this time the eccentricity
starts to decrease before increasing again in a cyclic variation.
During these later phases
the companion has contact with material with higher specific
angular momentum from the eccentric disc. The interaction
causes the inward migration to reverse |
| Open with DEXTER |
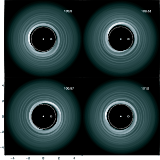 |
Figure 4:
This figure shows the eccentricity of the inner parts
of the outer disc for a run in which the companion was maintained on a
fixed circular orbit, with
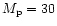
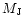 .
The times of each panel are shown
in the top right corner in units of the orbital period. The figure is plotted
in a frame that is corotating with the binary orbit, and the dotted line
indicates the position of the 1:2 outer Lindblad resonance .
The times of each panel are shown
in the top right corner in units of the orbital period. The figure is plotted
in a frame that is corotating with the binary orbit, and the dotted line
indicates the position of the 1:2 outer Lindblad resonance |
| Open with DEXTER |
 |
Figure 5:
This figure shows the evolution of the m=2 component
of the Fourier transform of the surface density, in the inertial frame,
for the case of
a
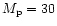
 companion on a fixed circular orbit.
The time elapsed when moving between the panels is shown in
the top right hand corner, in units of P0, where we have arbitrarily
denoted the time of the first panel to be t=0.0.
From the discussion in the text, it is expected that an m=2 spiral density wave will be excited at the 1:3 outer eccentric
Lindblad resonance, located at
companion on a fixed circular orbit.
The time elapsed when moving between the panels is shown in
the top right hand corner, in units of P0, where we have arbitrarily
denoted the time of the first panel to be t=0.0.
From the discussion in the text, it is expected that an m=2 spiral density wave will be excited at the 1:3 outer eccentric
Lindblad resonance, located at
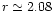 (shown by the dashed line), if the
eccentricity growth of the disc arises because
of a period doubling instability.
This wave should have a pattern speed
(shown by the dashed line), if the
eccentricity growth of the disc arises because
of a period doubling instability.
This wave should have a pattern speed
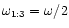 .
For an m=2 feature, the observed pattern should
repeat every P0, but not
every P0/2 (as would be the case if the wave had a frequency .
For an m=2 feature, the observed pattern should
repeat every P0, but not
every P0/2 (as would be the case if the wave had a frequency
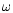 ).
Comparing the first and fifth panels, it is apparent that the m=2 pattern does indeed repeat after every P0. Comparing the
first and third panels, it is obvious that the m=2 feature does not repeat
every P0/2 ).
Comparing the first and fifth panels, it is apparent that the m=2 pattern does indeed repeat after every P0. Comparing the
first and third panels, it is obvious that the m=2 feature does not repeat
every P0/2 |
| Open with DEXTER |
In order to explore why the disc itself becomes eccentric, an identical
simulation to N5 was performed, except that the companion was maintained
on a fixed circular orbit. According to
the discussion given below,
non linear coupling between an eccentric disc mode (with small e)
corresponding to an essentially time independent m=1 pattern
and the m=1component of the tidal potential and its disc response
propagating with pattern speed equal to the orbital frequency,
is expected to give rise to the excitation of an
m=2 spiral density wave emitted at the 1:3 outer eccentric
Lindblad resonance. The pattern speed of this wave is half the orbital
frequency. This wave can in turn couple back through the tidal
potential to produce a time independent wave and associated
potential with m=1. The removal of angular momentum from the disc
through such a potential
will cause the disc eccentricity to increase. This is because
no energy is removed along with the angular momentum,
from the fluid orbits, so they cannot remain circular.
If a wave with pattern speed equal to half the orbital frequency
is present and launched from the 1:3 resonance,
in a simulation with a companion on a fixed circular orbit, then it
accounts naturally for
the growth of disc eccentricity. Wave excitation is also expected
to cause a growth in orbital eccentricity when that is present
(see Lin & Papaloizou 1993a, and below).
The excited wave is expected to have a
pattern speed equal to
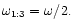 Because the disc configuration changes to one in which
the pattern rotation period has doubled, the instability
produces a period doubling and so resembles a parametric instability.
Because the disc configuration changes to one in which
the pattern rotation period has doubled, the instability
produces a period doubling and so resembles a parametric instability.
A plot of the disc surface density for the run with the companion on a fixed
circular orbit is shown in Fig. 4, in a frame corotating with the orbit.
The panels are separated by one third of the orbital period.
The 1:2 outer Lindblad resonance is shown by the dotted line, and the
eccentricity of the inner parts of the disc that lie just exterior
to this resonance may be observed.
The disc surface density that resulted from the simulation
in which the companion remained on a fixed circular orbit
was Fourier transformed in azimuth, and the m=2 component was examined.
In line with our expectations, it was observed that once the inner disc was
cleared of material, the presence of the m=2 wave being launched from
the 1:3 outer eccentric Lindblad resonance became apparent, travelling with
a pattern speed 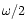 .
This m=2 component of
.
This m=2 component of 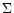 is plotted in Fig. 5 at different
times during an orbit.
Comparison between the first, fifth, and ninth panels, which are separated by an
orbital period of the star-companion system, show that the pattern does indeed
repeat after this time interval. Comparison between panels separated by
half an orbital period, such as the first and third, shows that the pattern
does not repeat after half an orbital period. An m=2 wave travelling
with the orbital frequency
is plotted in Fig. 5 at different
times during an orbit.
Comparison between the first, fifth, and ninth panels, which are separated by an
orbital period of the star-companion system, show that the pattern does indeed
repeat after this time interval. Comparison between panels separated by
half an orbital period, such as the first and third, shows that the pattern
does not repeat after half an orbital period. An m=2 wave travelling
with the orbital frequency 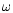 would repeat after every half an orbital
period. The fact that the m=2 wave only repeats after every orbital period
indicates that it is being excited at the 1:3 resonance (indicated by the dashed
line in Fig. 5) with a pattern speed
would repeat after every half an orbital
period. The fact that the m=2 wave only repeats after every orbital period
indicates that it is being excited at the 1:3 resonance (indicated by the dashed
line in Fig. 5) with a pattern speed
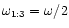 .
We conclude that a parametric instability is operating to excite this wave,
giving rise to an eccentric disc.
In calculation N5 where the star-companion orbit
is able to evolve, the interaction between the companion and the eccentric
disc leads to the growth of eccentricity of the companion orbit.
.
We conclude that a parametric instability is operating to excite this wave,
giving rise to an eccentric disc.
In calculation N5 where the star-companion orbit
is able to evolve, the interaction between the companion and the eccentric
disc leads to the growth of eccentricity of the companion orbit.
As described above, previous work on orbital eccentricity growth through
disc-companion interactions indicated that direct resonant wave excitation at
inner and outer eccentric Lindblad resonances should drive eccentricity, whereas
interaction with material at corotating Lindblad resonances should cause
it to damp (Artymowicz 1993; Lin & Papaloizou 1993a). In the simulations
presented here, only the outer 1:3 resonance is important, and it is of
interest to ask whether direct wave excitation at this resonance, or
interaction with the disc eccentricity, is primarily responsible for
the eccentricity growth of the companion orbit. To address this question,
we performed simulations
similar to run N5, but in which the surface density of the disc was
Fourier analysed in azimuth. In these calculations the gravitational
force of the disc acting on the star-companion orbit only included a
contribution from an individual Fourier component (m=1, 2, 3, or 4),
though the full potential of the star-companion system acting on the disc was
included. We expect that if the interaction of the companion with the disc
eccentricity is dominant in driving the companion eccentricity then the
calculation including only the m=1 component of the disc gravitational
potential will show more rapid growth of orbital eccentricity.
Conversely, if resonant wave excitation of an m=2 wave at the 1:3 resonance was
primarily responsible, then the calculation
including only the m=2 component of the disc
potential will show more rapid eccentricity growth.
In fact, we find that the m=1 run showed a moderately larger eccentricity
growth than the m=2 run, suggesting that the orbital
interaction with the eccentric disc
produces the stronger growth. This conclusion is further suggested
by the estimates of the eccentricity growth rates presented in Sect. 5.10.
The runs including only the m=3 and m=4 terms showed negligible
eccentricity growth.
5 A simple analytic model
In order to help understand some of the simulation results
described above, we consider a simplified model system
of primary, orbiting companion and disc.
We suppose the companion orbits inside a disc with truncated
inner edge. We make the additional simplification
that the central star remains fixed at the origin
of the coordinate system. The disc itself is taken to be inviscid with
a simple relation between vertically integrated pressure, Pand surface density, 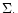 Much of the complex nonlinear dynamics involving
the balance between tides and viscosity determining
the structure of the inner disc edge is thus omitted.
However, enough content remains in order
to display an instability leading to eccentricity growth
in both disc and companion orbit, as well as the excitation
of an outward propagating density wave with half the pattern speed.
The existence of this has been described above.
Much of the complex nonlinear dynamics involving
the balance between tides and viscosity determining
the structure of the inner disc edge is thus omitted.
However, enough content remains in order
to display an instability leading to eccentricity growth
in both disc and companion orbit, as well as the excitation
of an outward propagating density wave with half the pattern speed.
The existence of this has been described above.
We are concerned here with the situation when the companion
orbit becomes eccentric. In general it will
precess with a period very much longer than
the orbital period. In an inertial frame the
time averaged orbit then appears as a perturbation
of the unperturbed circular orbit with azimuthal
mode number m=1.
Because we are interested in modes that appear to change slowly
in the inertial frame, we adopt the approach of secular perturbation theory.
We thus perform a time average over an interval
long compared to the orbital period
but short compared to the orbital precession period.
The companion then acts gravitationally as if
it mass were continuously
distributed along its orbit with line density inversely
proportional to its speed. In an average sense it behaves
like a continuous mass distribution and can be regarded as an infinitesimally
thin annular extension of the disc. In this respect we suppose that
we have a disc with well defined inner edge, interior to which there
is a gap or hole
in which the companion orbits. In the secular theory, we shall regard
the companion as equivalent to an annular extension of the disc orbiting
inside the
gap and consider an eccentric companion orbit as
a non axisymmetric perturbation of the initially
axisymmetric combined disc-companion system.
In this way an eccentric disc is produced also as comprising the normal mode.
Good coupling results in eccentricities of comparable magnitudes
in both components, while weak coupling enables them to exhibit
eccentricities separately. The condition for good coupling is that
the precession period induced in disc orbits by the companion
and its own pressure and self-gravity
be comparable to the precession period induced in the companion orbit
by the disc. This is met when the disc mass,
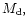 contained in a radial
scale
comparable to the gap radius (or 1:3 resonance radius as
taken below) is comparable to the mass of the companion.
When these masses are very different, the situation will favour
either an eccentric companion orbit or an eccentric disc.
contained in a radial
scale
comparable to the gap radius (or 1:3 resonance radius as
taken below) is comparable to the mass of the companion.
When these masses are very different, the situation will favour
either an eccentric companion orbit or an eccentric disc.
This occurs because the
slowly precessing nonaxisymmetric pattern in the disc
makes it behave similarly to a planet of mass
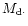 From standard secular perturbation theory (Brouwer & Clemence 1961)
eccentricity is freely exchanged between this planet and the companion
when their orbital angular momenta are comparable, a situation
that occurs here when the masses are comparable.
From standard secular perturbation theory (Brouwer & Clemence 1961)
eccentricity is freely exchanged between this planet and the companion
when their orbital angular momenta are comparable, a situation
that occurs here when the masses are comparable.
The slowly varying m=1 modes described above are found to be negative
angular momentum modes. This means that if they induce an angular
momentum transfer
to outer disc material from the region where they are located,
they will grow unstably.
Within the framework of secular perturbation theory of an initially
axisymmetric
disc this does not occur. However, if the high frequency components
of the companion potential are now allowed to act, their coupling
with the m=1 secular mode induces an angular momentum loss and hence growth.
This occurs through the coupling of the m=1 low frequency mode
with an m=1 potential component with pattern speed equal to the orbital
frequency. This produces a forcing potential with m=2 and pattern speed
one half the orbital frequency. As we shall see this can produce
a density wave resonantly excited at the 1:3 resonance located at
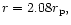
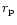 being the companion semi-major axis,
provided that resonance is contained within the disc, and hence mode growth.
A favourable situation occurs when the gap or inner hole is large enough that
possibly stabilizing corotation resonances are absent (Goldreich & Tremaine
1980; Artymowicz 1993; Lin & Papaloizou 1993a).
When growth occurs we find two limiting cases. When the companion mass
dominates that of the disc, an eccentric disc is produced.
This situation is illustrated by our run in which the companion
was maintained on a fixed circular orbit. In the opposite case,
an eccentric companion orbit is expected as has
been previously discussed by e.g. Artymowicz (1992) and
Lin & Papaloizou (1993a).
In the intermediate case
eccentricities in both components are produced.
We consider linear perturbations of a two dimensional
flat axisymmetric disc and time averaged planet.
The dependence on time, t, and azimuthal angle,
being the companion semi-major axis,
provided that resonance is contained within the disc, and hence mode growth.
A favourable situation occurs when the gap or inner hole is large enough that
possibly stabilizing corotation resonances are absent (Goldreich & Tremaine
1980; Artymowicz 1993; Lin & Papaloizou 1993a).
When growth occurs we find two limiting cases. When the companion mass
dominates that of the disc, an eccentric disc is produced.
This situation is illustrated by our run in which the companion
was maintained on a fixed circular orbit. In the opposite case,
an eccentric companion orbit is expected as has
been previously discussed by e.g. Artymowicz (1992) and
Lin & Papaloizou (1993a).
In the intermediate case
eccentricities in both components are produced.
We consider linear perturbations of a two dimensional
flat axisymmetric disc and time averaged planet.
The dependence on time, t, and azimuthal angle, 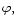 is taken
to be through a factor
is taken
to be through a factor
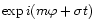 henceforth
taken as read. Here the
azimuthal mode number m=1 and the mode frequency
henceforth
taken as read. Here the
azimuthal mode number m=1 and the mode frequency
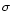 is such that
is such that
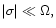 where
where 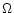 is the angular
velocity
in the unperturbed disc
where the unperturbed surface density is
is the angular
velocity
in the unperturbed disc
where the unperturbed surface density is 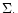 The Lagrangian displacement
The Lagrangian displacement
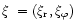 obeys the perturbed equations of motion
obeys the perturbed equations of motion
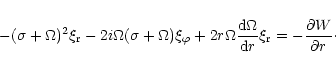 |
(1) |
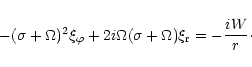 |
(2) |
Equations (1) and (2) can be combined to give
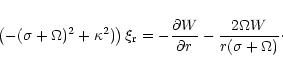 |
(3) |
Here
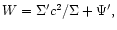 where
where 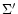 and
and 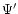 are the
surface density and gravitational potential perturbations respectively.
The vertically integrated pressure P is assumed to be a function of
are the
surface density and gravitational potential perturbations respectively.
The vertically integrated pressure P is assumed to be a function of
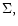
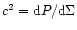 is the square of the sound speed,
and
is the square of the sound speed,
and
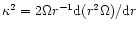 is the square of
the epicyclic frequency.
The perturbation to the gravitational
potential
may be written (temporarily restoring the
is the square of
the epicyclic frequency.
The perturbation to the gravitational
potential
may be written (temporarily restoring the 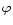 dependence)
dependence)
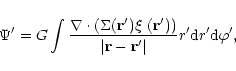 |
(4) |
where this and similar integrals are taken over the active mass distribution.
We may apply (4) to both the distributed disc
mass and the separated, time averaged, but initially
radially localized companion mass
for which
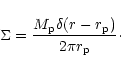 |
(5) |
Here 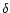 denotes a delta function and
denotes a delta function and 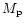 the companion mass.
Before so doing, we use the fact that
the companion mass.
Before so doing, we use the fact that
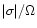 is small to
make some simplifications. In this limit and for a thin disc
for which forces due to internal pressure and self-gravity
are small, Eq. (2) becomes
is small to
make some simplifications. In this limit and for a thin disc
for which forces due to internal pressure and self-gravity
are small, Eq. (2) becomes
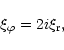 |
(6) |
which is the limiting form for purely epicyclic motion.
We use this to evaluate the pressure and self-gravity terms
on the right hand side of (3). The error in doing this, for a
gravitationally
stable disc, is measured
by the greater of
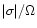 and H/r, where H is the semi-thickness
of the disc.
Then we have
and H/r, where H is the semi-thickness
of the disc.
Then we have
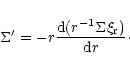 |
(7) |
Equation (4) can then be written
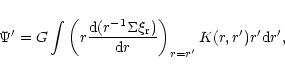 |
(8) |
with
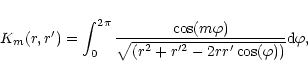 |
(9) |
and noting that for m=1 we shall drop the subscript from
Km(r,r'),thus
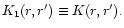 We finally obtain a normal mode equation for
We finally obtain a normal mode equation for
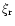 by using
(8),
and (7) in (3) in the form
by using
(8),
and (7) in (3) in the form
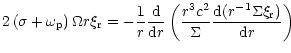 |
|
|
|
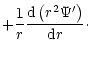 |
|
|
(10) |
Here we have used the fact that
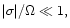 and the precession frequency
and the precession frequency
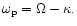
Although Eq. (10) applies to the joint disc and companion system,
we shall separate the contributions to the potential from
the companion and disc, writing
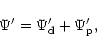 |
(11) |
where
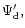 and
and
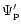 are the contributions
from the disc and planet obtained from the appropriate
surface density distributions respectively.
Using (5), we find
are the contributions
from the disc and planet obtained from the appropriate
surface density distributions respectively.
Using (5), we find
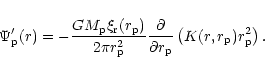 |
(12) |
Here the eccentricity of the companion orbit is related to the displacement by
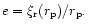
If we replace 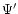 in (10) by the disc contribution
in (10) by the disc contribution
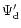 only, we obtain an equation for the normal modes of the
disc only. In fact under reasonable boundary conditions
that
only, we obtain an equation for the normal modes of the
disc only. In fact under reasonable boundary conditions
that
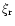 is well behaved at the inner boundary and vanishes
at large distances, (10) gives a self-adjoint eigenvalue problem
for the eigenvalue
is well behaved at the inner boundary and vanishes
at large distances, (10) gives a self-adjoint eigenvalue problem
for the eigenvalue 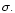 The right hand side gives a self-adjoint
operator with weight
The right hand side gives a self-adjoint
operator with weight 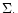 Denoting, the eigenvalues by
Denoting, the eigenvalues by 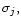 and corresponding eigenfunctions,
and corresponding eigenfunctions,
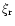 by
uj, j= 1,2,...,we have the orthogonality condition
by
uj, j= 1,2,...,we have the orthogonality condition
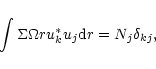 |
(13) |
with this and later integrals being taken over the disc.
We comment that the eigenvalues are all real and the local dispersion relation
associated with (10) is the low frequency limit
of the well known relation for spiral density waves (Lin & Shu 1964)
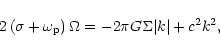 |
(14) |
where k is the radial wavenumber and of course m=1.Each mode propagates with a prograde pattern speed
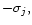 which is also the precession frequency.
which is also the precession frequency.
The effect of the companion may be incorporated by adding
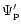 into
into 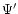 in (10). Regarding the companion potential so added
as giving an external forcing term, Eq. (10) may be solved using the
standard method of eigenfunction expansion to give interior to the disc
in (10). Regarding the companion potential so added
as giving an external forcing term, Eq. (10) may be solved using the
standard method of eigenfunction expansion to give interior to the disc
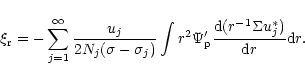 |
(15) |
Omitting the pressure term, Eq. (10) gives
for the equation of motion of the companion
![\begin{displaymath}2\left[\sigma + \omega_{\rm p}(r_{\rm p}) \right] \Omega(r_{\...
...si'_{\rm d}(r) \right) \over {\rm d} r}
\right]_{r=r_{\rm p}}
\end{displaymath}](/articles/aa/full/2001/04/aa9988/img114.gif) |
(16) |
with
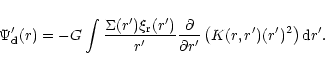 |
(17) |
Combining (16), (15) and (17)
gives an equation for the eigenvalue 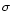 for the joint
normal mode in the form
for the joint
normal mode in the form
![\begin{displaymath}\left[\sigma + \omega_{\rm p}(r_{\rm p}) \right] \Omega(r_{\r...
...t^2 M_{\rm p} \over 8\pi r_{\rm p}^2 N_j (\sigma - \sigma_j)},
\end{displaymath}](/articles/aa/full/2001/04/aa9988/img116.gif) |
(18) |
with the coupling coefficient given by
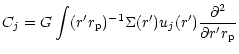 |
|
|
|
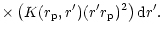 |
|
|
(19) |
The schematic behaviour of the eigenvalues is that, when the coupling
coefficient Cj is negligible, the solutions are
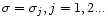 and
and
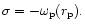 In this case the companion
and disc are
decoupled
and precess independently. In contrast when the coupling is non negligible
the precession of companion orbit and disc are linked. One induces
eccentricity in the other. To estimate when this occurs, one needs that
In this case the companion
and disc are
decoupled
and precess independently. In contrast when the coupling is non negligible
the precession of companion orbit and disc are linked. One induces
eccentricity in the other. To estimate when this occurs, one needs that
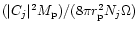 be
of the same order as the square of the difference in disc
and companion orbit
precession frequencies
be
of the same order as the square of the difference in disc
and companion orbit
precession frequencies
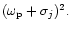 If the companion
and disc mutually induce eccentricity and precession,
simple
estimates, assuming there is a single radial scale length, indicate
this requires that
If the companion
and disc mutually induce eccentricity and precession,
simple
estimates, assuming there is a single radial scale length, indicate
this requires that
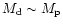 for good coupling.
for good coupling.
We comment that although the gravity
of the disc acting on both itself and the companion
has been included in the above formalism, the self-interaction
only affects the precise determination of the 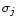 and uj.The above discussion still applies if that is neglected,
as long as the interaction
with the companion is retained. This is the case for the simulations
presented here.
and uj.The above discussion still applies if that is neglected,
as long as the interaction
with the companion is retained. This is the case for the simulations
presented here.
The effective angular momentum content in the joint mode can be
evaluated using standard methods (e.g. Goodman & Ryu 1992;
Lin & Papaloizou 1993b).
For the low frequency modes considered here, we obtain after
a straightforward calculation
 |
(20) |
where the integral is over the entire system.
We comment that, using (5), the contribution from the companion
to
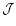 is
is
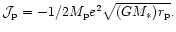 This is negative corresponding to a negative
angular momentum mode and it is also minus the radial action.
If angular momentum is drained from the mode, the companion orbit
eccentricity
and radial action grow. In general the total angular momentum content
is
This is negative corresponding to a negative
angular momentum mode and it is also minus the radial action.
If angular momentum is drained from the mode, the companion orbit
eccentricity
and radial action grow. In general the total angular momentum content
is
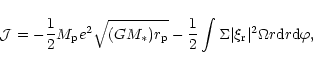 |
(21) |
where the second contribution now comes from the disc only, involving
the radial component of the Lagrangian displacement
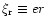 there.
there.
5.10 Angular momentum loss due to resonant torques
The modes discussed above, in the time averaging approximation,
do not lose angular momentum. However,
only the time averaged potential due to the companion has been included.
When the effects of the full potential are included,
additional perturbation of the disc occurs. This can lead to
angular momentum loss through resonant torques
(Goldreich & Tremaine 1978).
In that case, the mode eccentricities grow and instability occurs.
The full potential due to the companion located
at
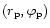 can be written
can be written
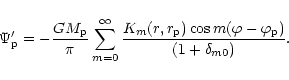 |
(22) |
When the disc and companion orbit are eccentric, with small eccentricities,
to evaluate the companion potential at the location of a perturbed fluid
element in the disc,
we set
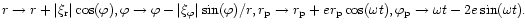 Here, arbitrary phases are chosen
such that all ellipses have apsidal lines aligned at
Here, arbitrary phases are chosen
such that all ellipses have apsidal lines aligned at
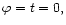 consistently with the joint mode. The orbital frequency is
consistently with the joint mode. The orbital frequency is 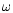 and we have neglected the small precession frequency.
The simulations suggest an alignment such the eccentricities of the
disc and orbit are of opposite sign. In this case the disc pericentre
is closest to the orbital apocentre.
The contribution
to the companion potential that is first order in the eccentricities
and we have neglected the small precession frequency.
The simulations suggest an alignment such the eccentricities of the
disc and orbit are of opposite sign. In this case the disc pericentre
is closest to the orbital apocentre.
The contribution
to the companion potential that is first order in the eccentricities
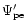 is given by
is given by
where
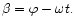 We comment that for zero eccentricities, all time dependent
components of the companion
potential have pattern speed
We comment that for zero eccentricities, all time dependent
components of the companion
potential have pattern speed 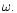 In the outer disc, there are
possible outer Lindblad resonances where
In the outer disc, there are
possible outer Lindblad resonances where
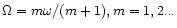 However, as the inner edge approaches the 1:2 resonance,
only the resonance with m=1 remains eventually.
When eccentricities are included,
contributions occur in (23) with pattern speeds
However, as the inner edge approaches the 1:2 resonance,
only the resonance with m=1 remains eventually.
When eccentricities are included,
contributions occur in (23) with pattern speeds
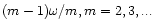 The outer Lindblad resonances associated with these are at
The outer Lindblad resonances associated with these are at
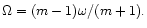 For m=2, this gives
the smallest value of
For m=2, this gives
the smallest value of
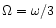 which
occurs at the 1:3 resonance.
The corresponding pattern speed of the resonant forcing is
which
occurs at the 1:3 resonance.
The corresponding pattern speed of the resonant forcing is 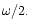 As the material at the outer Lindblad
resonance rotates more slowly than the pattern speed,
resonant torques cause angular momentum loss leading to
eccentricity growth of the joint disc-companion system.
For discs with inner edges approaching the 1:2 resonance
such that the disc surface density becomes depressed there, potentially
damping corotation torques (Goldreich & Tremaine 1980)
and coorbital Lindblad torques (Artymowicz 1993) are weakened.
Here we shall assume that
only the 1:3 resonance needs to be considered.
The resonant forcing occurs through terms produced by
a nonlinear coupling
between the secular m=1 mode and disturbances with m=1moving with the orbital pattern speed
As the material at the outer Lindblad
resonance rotates more slowly than the pattern speed,
resonant torques cause angular momentum loss leading to
eccentricity growth of the joint disc-companion system.
For discs with inner edges approaching the 1:2 resonance
such that the disc surface density becomes depressed there, potentially
damping corotation torques (Goldreich & Tremaine 1980)
and coorbital Lindblad torques (Artymowicz 1993) are weakened.
Here we shall assume that
only the 1:3 resonance needs to be considered.
The resonant forcing occurs through terms produced by
a nonlinear coupling
between the secular m=1 mode and disturbances with m=1moving with the orbital pattern speed
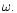 We begin by
calculating the resonant forcing using (23)
as a forcing potential on the unperturbed axisymmetric disc.
However, it is important
to note that not all the effective forcing terms are included in this way.
They arise also by coupling between the secular m=1 mode
and the tidal distortion of the disc produced by
the circular orbit tide propagating with a pattern speed
We begin by
calculating the resonant forcing using (23)
as a forcing potential on the unperturbed axisymmetric disc.
However, it is important
to note that not all the effective forcing terms are included in this way.
They arise also by coupling between the secular m=1 mode
and the tidal distortion of the disc produced by
the circular orbit tide propagating with a pattern speed 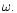 Evaluation of these is lengthy and depends on the detailed disc model which
has here been simplified.
Instead of such evaluation,
we replace the disc eccentricity in (23) by
Evaluation of these is lengthy and depends on the detailed disc model which
has here been simplified.
Instead of such evaluation,
we replace the disc eccentricity in (23) by
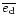 to indicate additional forcing. Although such forcing is not necessarily
through a potential, it can still be taken into account by defining
a suitable
to indicate additional forcing. Although such forcing is not necessarily
through a potential, it can still be taken into account by defining
a suitable
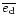 which is proportional to the
disc eccentricity
amplitude (see Eq. [24]).
This procedure will enable eccentricity growth rates
to be qualitatively discussed and estimated.
The component of (23) with pattern speed
which is proportional to the
disc eccentricity
amplitude (see Eq. [24]).
This procedure will enable eccentricity growth rates
to be qualitatively discussed and estimated.
The component of (23) with pattern speed
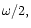 is then given by
is then given by
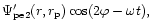 where
where
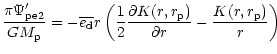 |
|
|
|
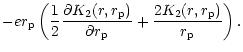 |
|
|
(24) |
Here we have set
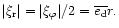 We calculate the rate of loss of angular momentum as a result
of resonant torques using the torque formula of
Goldreich & Tremaine (1978, 1980) to obtain
We calculate the rate of loss of angular momentum as a result
of resonant torques using the torque formula of
Goldreich & Tremaine (1978, 1980) to obtain
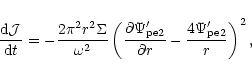 |
(25) |
where r and the disc quantities are evaluated at the 1:3 resonance.
The angular momentum is transported outwards via a wave with pattern speed
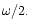 It has to be extracted from the m=1 joint mode
and the companion orbit which have combined together to give
the resonant forcing.
It has to be extracted from the m=1 joint mode
and the companion orbit which have combined together to give
the resonant forcing.
Extraction from an eccentric companion orbit can occur directly through
the excited m=2 wave.
Extraction from the m=1 mode can occur through a recoupling of the
m=2 wave with
the tidal potential with pattern speed 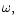 to produce a time independent forcing with m=1.
Similarly extraction from the orbit can occur through recoupling of the m=2wave to
the m=1 joint mode to produce an m=1 disturbance with the circular
orbit pattern speed
to produce a time independent forcing with m=1.
Similarly extraction from the orbit can occur through recoupling of the m=2wave to
the m=1 joint mode to produce an m=1 disturbance with the circular
orbit pattern speed 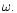
If the resonantly excited m=2 wave carries an angular momentum
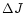 ,
the associated energy is
,
the associated energy is
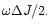 If this energy is supplied by the circular orbit tide, then
the angular momentum supplied along with it will be
If this energy is supplied by the circular orbit tide, then
the angular momentum supplied along with it will be
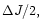 leaving
leaving
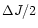 to be extracted from the joint m=1 mode.
to be extracted from the joint m=1 mode.
The above discussion suggests
the growth rate of this mode can be obtained by
assuming half the
resonantly induced angular momentum loss
is extracted from it.
The growth rate of the combined mode is then estimated as
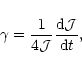 |
(26) |
with
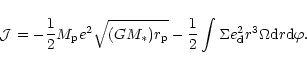 |
(27) |
Evaluating (25) we obtain
where
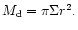
Note that here we neglect any change in the companion
semi-major axis due to the time dependent terms in the disc potential.
To set the magnitudes of typical growth rates, we first
set the terms involving the disc eccentricity
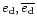 to zero.
We find from (28)
that for the 1:3 resonance with
to zero.
We find from (28)
that for the 1:3 resonance with
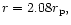
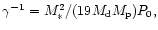 with P0 being the
orbital period. Thus for
with P0 being the
orbital period. Thus for
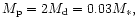 here we allow a factor of two surface density enhancement above
the initial value at the 1:3 resonance,
we find a growth time
here we allow a factor of two surface density enhancement above
the initial value at the 1:3 resonance,
we find a growth time
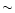 120 companion orbital periods.
This is comparable, but a factor of
120 companion orbital periods.
This is comparable, but a factor of 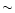 3 smaller,
than the eccentricity growth rate
obtained for calculation N5, and is consistent with the idea
that the orbital
eccentricity driving arises through effects due to
both the orbital eccentricity itself and the eccentricity
induced in the disc,
the latter actually giving stronger effects.
We comment that for these parameters the disc and companion orbit
eccentricities are likely to be coupled. This is because
typically
3 smaller,
than the eccentricity growth rate
obtained for calculation N5, and is consistent with the idea
that the orbital
eccentricity driving arises through effects due to
both the orbital eccentricity itself and the eccentricity
induced in the disc,
the latter actually giving stronger effects.
We comment that for these parameters the disc and companion orbit
eccentricities are likely to be coupled. This is because
typically
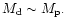 Then the precession frequency
induced by the companion in externally orbiting disc matter
is given by
Then the precession frequency
induced by the companion in externally orbiting disc matter
is given by
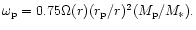 Similarly the precession frequency induced by the
disc (assumed to have constant surface density)
in the companion orbit is
Similarly the precession frequency induced by the
disc (assumed to have constant surface density)
in the companion orbit is
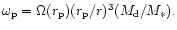 These are comparable leading to the likely setting up of a joint mode.
We comment that this condition is the same as
requiring that the companion orbital angular momentum and the orbital
angular momentum contained in
These are comparable leading to the likely setting up of a joint mode.
We comment that this condition is the same as
requiring that the companion orbital angular momentum and the orbital
angular momentum contained in 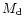 assumed in circular orbit
be comparable.
assumed in circular orbit
be comparable.
Under the conditions of the simulations considered here,
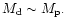 Then it is also likely that the radial action in the disc is comparable
to that of the companion and so modifies the growth rate.
However, as long as they are comparable our estimate is probably
reasonable. Note that
Then it is also likely that the radial action in the disc is comparable
to that of the companion and so modifies the growth rate.
However, as long as they are comparable our estimate is probably
reasonable. Note that
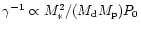 as long as
as long as 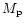 is comparable to or less than
is comparable to or less than
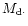 If the companion mass dominates, so fixing it in a circular orbit,
then e=0, in (28) and
If the companion mass dominates, so fixing it in a circular orbit,
then e=0, in (28) and
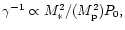 attaining a limiting value independent of the disc mass.
Our simulation with fixed
companion orbit indicates that the growth rate does not change very much
as
attaining a limiting value independent of the disc mass.
Our simulation with fixed
companion orbit indicates that the growth rate does not change very much
as 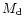 is reduced significantly below
is reduced significantly below
6 Discussion
In this paper we have
investigated the driving of orbital eccentricity of giant protoplanets and
brown dwarfs through disc-companion tidal interactions
by means of two dimensional numerical simulations. Disc
models thought to be typical of protostellar discs during the
planet forming epoch, with characteristic surface densities similar to
standard minimum mass solar nebula models were considered.
We examined the evolution of
companions ranging in mass between 1 and 30 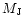 initially
embedded within the discs on circular orbits.
For low mass companions,
typical of giant planets, we found, in agreement with our
previous work (NPMK)
that the orbit remains essentially
circular. For companion masses that are greater than
initially
embedded within the discs on circular orbits.
For low mass companions,
typical of giant planets, we found, in agreement with our
previous work (NPMK)
that the orbit remains essentially
circular. For companion masses that are greater than 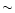 20
20 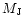 ,
however, we found that a transition occurs, leading to a
non steady behaviour of the companion orbit. This is
characterised by a growth in eccentricity such that
,
however, we found that a transition occurs, leading to a
non steady behaviour of the companion orbit. This is
characterised by a growth in eccentricity such that
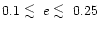 .
.
The inner parts of the disc
that lie exterior to the companion orbit
become eccentric through an instability driven through the
coupling of the non circular motions associated with a
small disc eccentricity to the companion's
tidal potential. This coupling leads to the excitation
of an m=2 spiral wave at the 1:3 outer eccentric Lindblad resonance,
which transports angular momentum outwards.
A similar picture of disc eccentricity driving
for inner discs has been discussed
by Lubow (1991) in the context of Cataclysmic Variables.
As the disc eccentricity corresponds to a negative angular
momentum mode, this angular momentum loss
leads to a growth of the disc eccentricity.
In addition to the effects of
resonant wave excitation at the 1:3 resonance produced
by the direct forcing of the companion in its eccentric orbit,
the gravitational interaction of the
companion with this eccentric disc leads to the growth of eccentricity
of the companion orbit, where this latter effect is found to be moderately
larger.
For a companion orbiting within a disc, the effects of the 1:3
resonance lead to growth of the eccentricity while
the effects of corotation and coorbital Lindblad resonances lead to
its damping (e.g. Artymowicz 1993; Ward & Hahn 2000).
For a very wide gap or isolation of the companion
from the disc material, the effects of the 1:3 resonance win
and the eccentricity grows (Lin & Papaloizou 1993a).
However, our simulations indicate that for standard disc models,
sufficient clearance due to the companion tides occurs only
for masses in the brown dwarf range. However, the transition
mass might be reduced into the range for extrasolar planets
if the disc viscosity is significantly lower enabling
wider gaps to occur. One can estimate
the viscosity required by noting that
the gap must extend out to the 1:2 resonance.
For
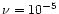 as adopted here
the gap half width is
as adopted here
the gap half width is 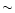 0.2 for
0.2 for
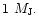 To reach the 1:2 resonance this has to be three times
larger. From Lin & Papaloizou (1993a) and Bryden et al. (1999),
the tidal torque, which varies as the inverse cube
of the gap width, is then reduced by a factor of 27.
To prevent the gap filling the viscosity would have to
be reduced by at least the same factor requiring
To reach the 1:2 resonance this has to be three times
larger. From Lin & Papaloizou (1993a) and Bryden et al. (1999),
the tidal torque, which varies as the inverse cube
of the gap width, is then reduced by a factor of 27.
To prevent the gap filling the viscosity would have to
be reduced by at least the same factor requiring
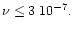 This corresponds to
the Shakura & Sunyaev (1973) viscosity parameter,
This corresponds to
the Shakura & Sunyaev (1973) viscosity parameter,
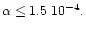 Note that this is
significantly
smaller than values normally adopted for protostellar discs
(e.g. Papaloizou & Terquem 1999).
Note that this is
significantly
smaller than values normally adopted for protostellar discs
(e.g. Papaloizou & Terquem 1999).
We also found that when the angular momentum content of
the disc material within a scale characteristic of the inner
edge radius is comparable to that of the companion in a circular
orbit, the eccentricity of the disc and companion are coupled.
This behaviour occurs because the gravitational potential
produced by the disc is similar to that of another companion
in eccentric orbit. A coupling is then expected from standard
secular perturbation theory.
When the companion and disc masses are disparate, orbital eccentricity
would be expected only for the smaller of the two.
Although the extrasolar planet mass range is too small (Marcy & Butler 2000)
for eccentricity driving due to the 1:3 resonance assuming
standard disc parameters, it is possible that
it could be produced if the protoplanet orbits in a cavity with an eccentric
external disc. This would require disc
m=1 modes to be excited
by some other mechanism e.g. viscous overstability (Kato 1978;
Papaloizou & Lin 1988).
A slowly
precessing non axisymmetric mass distribution would then be produced.
A configuration like the one described above might be produced
during the phase of disc clearance. There is observational
evidence that this occurs on a 105 yr time scale working
from the inside out (Shu et al. 1993).
The precession period of the nonaxisymmetric mass distribution
would be time variable and could potentially equal that
of the inner protoplanet orbit at some stage.
Because the average disc and protoplanet
orbits would then maintain a fixed orientation,
a large eccentricity
in the protoplanet orbit can be produced by
gravitational torques on the precession time scale.
Notably the effect need not be correlated with the protoplanet mass.
A mechanism operating on the same principle has been proposed
by Ward et al. (1976) as a mechanism for
producing the eccentricity of Mercury.
The precession frequency induced by the
disc (assumed to have constant surface density)
in the protoplanet orbit is
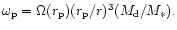 For
For
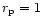 au, r =10 au,
au, r =10 au,
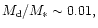 this
gives a precession period of
this
gives a precession period of  105 yr
comparable to estimated disc dispersal times (Shu et al. 1993).
105 yr
comparable to estimated disc dispersal times (Shu et al. 1993).
Finally, the presence of the brown dwarf
Gliese 229B with mass 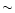 45
45 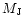 in a binary system indicates the potential
existence of a separate population, at the one percent incidence
level, of brown dwarfs
(Oppenheimer et al. 2000) which could form from discs.
The simulations presented here indicate
eccentricity excitation due to the effects
of the 1:3 resonance plays a role for these masses.
The different type of disc behaviour could
result in a distinct orbital and mass distribution
for these objects as compared to extrasolar planets.
in a binary system indicates the potential
existence of a separate population, at the one percent incidence
level, of brown dwarfs
(Oppenheimer et al. 2000) which could form from discs.
The simulations presented here indicate
eccentricity excitation due to the effects
of the 1:3 resonance plays a role for these masses.
The different type of disc behaviour could
result in a distinct orbital and mass distribution
for these objects as compared to extrasolar planets.
Acknowledgements
This work was supported by
PPARC grant number PPARC GR/L 39094.
It was also supported in part (F.M.) by the European
Commission under contract number ERBFMRX-CT98-0195
(TMR network "Accretion onto black holes, compact stars
and protostars'').
We thank Udo Ziegler for making a FORTRAN Version of his code NIRVANA
publicly available.
The calculations reported here were carried out using GRAND, a high
performance computing facility funded by PPARC.
-
Artymowicz, P. 1992, PASP, 104, 769
In the text
NASA ADS
-
Artymowicz, P. 1993, ApJ, 419, 155
NASA ADS
-
Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651
NASA ADS
-
Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214
In the text
NASA ADS
-
Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1
In the text
NASA ADS
-
Begelman, M. C., Blandford, R. D., & Rees, M. J. 1980,
Nature, 287, 307
In the text
NASA ADS
-
Brouwer, D., & Clemence, G. M. 1961, Methods of Celestial Mechanics
(New York, Academic press)
In the text
-
Bryden, G., Chen, X., Lin, D. N. C., Nelson, R. P., & Papaloizou, J. C. B. 1999, ApJ, 514, 344
In the text
NASA ADS
-
Goldreich, P., & Tremaine, S. 1978, Icarus, 34, 227
In the text
NASA ADS
-
Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425
In the text
NASA ADS
-
Goodman, J., & Ryu, D. 1992, ApJ, 388, 438
In the text
-
Hirose, M., & Osaki, Y. 1990, PASJ, 42, 135
In the text
NASA ADS
-
Ivanov, P. B., Papaloizou, J. C. B., & Polnarev, A. G. 1999, MNRAS, 307, 79
In the text
NASA ADS
-
Jeffreys, H. 1961, MNRAS, 122, 239
In the text
NASA ADS
-
Kato, S. 1978, MNRAS, 185, 629
In the text
NASA ADS
-
Kley, W. 1989, A&A, 208, 98
NASA ADS
-
Kley, W. 1998, A&A, 338, L37
In the text
NASA ADS
-
Kley, W. 1999, MNRAS, 303, 696
In the text
NASA ADS
-
Larwood, J. D., & Papaloizou, J. C. B. 1997, MNRAS, 285, 288
In the text
NASA ADS
-
Lin, C. C., & Shu, F. H. 1964, ApJ, 140, 646
In the text
NASA ADS
-
Lin, D. N. C., & Papaloizou, J. C. B. 1979, MNRAS, 188, 191
In the text
NASA ADS
-
Lin, D. N. C., & Papaloizou, J. C. B. 1986, ApJ, 309, 846
In the text
NASA ADS
-
Lin, D. N. C., & Papaloizou, J. C. B. 1993a, Protostars and Planets III, 749
In the text
-
Lin, D. N. C., & Papaloizou, J. C. B. 1993b, ApJ, 416, 689
In the text
NASA ADS
-
Lubow, S. H. 1991, ApJ, 381, 259
In the text
NASA ADS
-
Lubow, S. H., Seibert, M., & Artymowicz, P. 1999, ApJ, 526, 1001
In the text
NASA ADS
-
Marcy, G. W., & Butler, R. P. 1998, ARA&A, 36
In the text
-
Marcy, G. W., & Butler, R. P. 2000, PASP, 112, 137
In the text
NASA ADS
-
Masset, F. S. 2000, A&A, 141, 165
In the text
-
Nelson, R. P., Papaloizou, J. C. B., Masset, F. S., & Kley, W. 2000,
MNRAS, 318, 18
In the text
NASA ADS
-
Oppenheimer, B. R., Kulkarni, S. R., & Stauffer, J. R. 2000, To appear in
Protostars and Planets IV,
Tucson, AZ (University of Arizona Press)
In the text
-
Papaloizou, J. C. B., & Terquem, C. 1995, MNRAS, 274, 987
In the text
NASA ADS
-
Papaloizou, J. C. B., & Lin, D. N. C. 1988, ApJ, 331, 838
In the text
NASA ADS
-
Papaloizou, J. C. B., & Terquem, C. 1999, ApJ, 521, 823
In the text
NASA ADS
-
Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337
In the text
NASA ADS
-
Shu, F., Johnstone, D., & Hollenbach, D. 1993, Icarus, 106, 92
In the text
NASA ADS
-
Van Leer, B. 1977, J. Comp. Phys., 23, 276
In the text
NASA ADS
-
Ward, W. R., Columbo, G., & Franklin, F. A. 1976, Icarus, 28, 441
In the text
NASA ADS
-
Ward, W. R., & Hahn, J. M. 2000, To appear in
Protostars and Planets IV,
Tuscon, AZ (University of Arizona Press)
In the text
-
Whitehurst, R. 1988, MNRAS, 232, 35
In the text
NASA ADS
-
Ziegler, U., & Yorke, H. W. 1997, Comp. Phys. Comp., 101, 54
In the text
Copyright ESO 2001
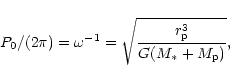





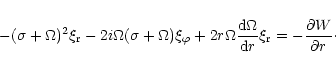
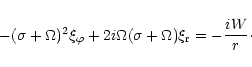
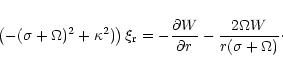
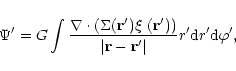
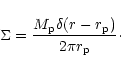
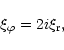
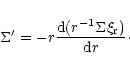
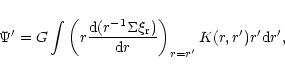
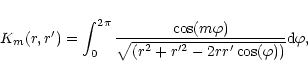
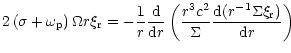
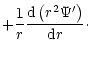
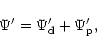
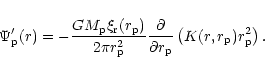
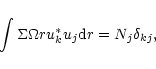
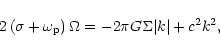
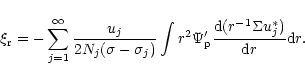
![\begin{displaymath}2\left[\sigma + \omega_{\rm p}(r_{\rm p}) \right] \Omega(r_{\...
...si'_{\rm d}(r) \right) \over {\rm d} r}
\right]_{r=r_{\rm p}}
\end{displaymath}](/articles/aa/full/2001/04/aa9988/img114.gif)
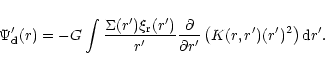
![\begin{displaymath}\left[\sigma + \omega_{\rm p}(r_{\rm p}) \right] \Omega(r_{\r...
...t^2 M_{\rm p} \over 8\pi r_{\rm p}^2 N_j (\sigma - \sigma_j)},
\end{displaymath}](/articles/aa/full/2001/04/aa9988/img116.gif)
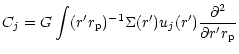

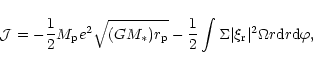
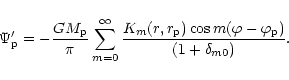
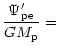
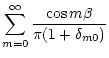
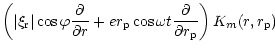
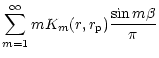
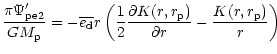
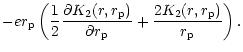
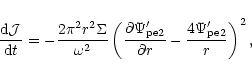
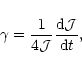
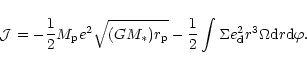
![$\displaystyle {9\pi
\left[(4{\overline{e_{\rm d}}}
- {2r\over3} {{\rm d}{\overl...
...\pi \Sigma e_{\rm d}^2 r^3\Omega {\rm d}r/(M_{\rm p}\omega r_{\rm p}^2)\right]}$](/articles/aa/full/2001/04/aa9988/img164.gif)