A&A 366, 166-173 (2001)
DOI: 10.1051/0004-6361:20000219
M. A. Dupret
Institut d'Astrophysique et de Géophysique de l'Université de Liège, avenue de Cointe 5, 4000 Liège, Belgium
Received 25 February 2000 / Accepted 7 November 2000
Abstract
A new general method for the computation
of nonradial nonadiabatic oscillations of a given stellar model is
presented for a linear approximation.
A simple and useful modelling of the atmosphere is included,
allowing to obtain credible values for the eigenfunctions
in the atmosphere.
Some of the results obtained for a
![]() model are shown as an illustration.
Our study opens the way to different applications.
Better theoretical line-profile variations
could be obtained from our method, allowing a more detailed
comparison with observations.
More generally, our study is relevant for asteroseismology,
giving a way for a better knowledge of stellar interiors.
model are shown as an illustration.
Our study opens the way to different applications.
Better theoretical line-profile variations
could be obtained from our method, allowing a more detailed
comparison with observations.
More generally, our study is relevant for asteroseismology,
giving a way for a better knowledge of stellar interiors.
Key words: stars: interiors - stars: oscillations
The problem of finding precise theoretical values for the nonradial nonadiabatic eigenfunctions of a given stellar model has become very interesting and useful for astronomers. Great progress in the study of pulsating stars has been made from an observational point of view. On the one hand, precise periods for multiperiodically pulsating stars have been recently detected from photometric data (e.g. Breger et al. 1999). On the other hand, the observation and analysis of line-profile variations for variable stars is in great development. In those observations, a trace of nonradial oscillations is now clearly admitted, and methods of mode identification have been developed (Aerts 1996; Telting & Schrijvers 1997). So, a confrontation with theory, followed by the improvement of stellar interiors' knowledge (asteroseismology) becomes possible. First steps in this way have already been made (Dziembowsky & Jerzykiewicz 1996; Shibahashi & Aerts 2000).
Concerning the study of line profiles, methods have been
developed in order to obtain theoretical line-profile variations
comparable with observations.
As data for these methods, theoretical values
of the nonradial eigenfunctions in the atmosphere are necessary.
Until now, only adiabatic eigenfunctions have been used.
It is well known, however, that in the atmosphere of a star, the
adiabatic approximation gives inaccurate results for some
eigenfunctions (
![]() ,
,
![]() ,
,
![]() ...). The development of a code computing
the nonradial eigenfunctions of a stellar model in the linear
nonadiabatic case and giving credible values in the atmosphere
implies an important step forward. This is the goal of our study.
...). The development of a code computing
the nonradial eigenfunctions of a stellar model in the linear
nonadiabatic case and giving credible values in the atmosphere
implies an important step forward. This is the goal of our study.
Dziembowski (1977) was one of the first to study
the computation of nonradial nonadiabatic modes.
Since then, other authors have worked on the problem
(Saio & Cox 1980;
Pesnell 1990). In comparison with those previous works, the
particularity of our study is, on the one hand, that it puts
the emphasis on a new, clear and complete presentation
of the problem (Sects. 2 and 4)
and of the method of solution
(Sect. 5), using a pure Lagrangian formalism;
and on the other hand,
that it includes a useful treatment of the perturbed equations in the
atmosphere (Sect. 3). The results in Sect. 6 are given
as an illustration of the quality and the possibilities of our
method. We have chosen a
![]() model near the turn-off
for this application, which is a good candidate for the modelling of a
model near the turn-off
for this application, which is a good candidate for the modelling of a
![]() Cephei variable star. We do not propose a modelling
of the perturbed convection in this study, so it is not applicable
for stars having an important superficial convection zone as the Sun.
The presence of a central convection zone (as for
Cephei variable star. We do not propose a modelling
of the perturbed convection in this study, so it is not applicable
for stars having an important superficial convection zone as the Sun.
The presence of a central convection zone (as for ![]() Cephei stars)
does not pose a problem, for it is located in the quasi-adiabatic
region.
Cephei stars)
does not pose a problem, for it is located in the quasi-adiabatic
region.
We examine the equations governing the behaviour of
a given nonradial mode for which the angular dependence
can be expressed by the spherical harmonic
![]() and the time dependence by the factor
and the time dependence by the factor
![]() .
We use the notation
.
We use the notation ![]() for the
Lagrangian variation of X.
First we have the conservation of momentum equations:
for the
Lagrangian variation of X.
First we have the conservation of momentum equations:
![\begin{displaymath}\delta\rho + \rho \left[ \frac{1}{r^2}\frac{\partial}{\partia...
...ight)
+ \frac{\partial\delta\phi}{\partial\phi} \right] = 0 ,
\end{displaymath}](/articles/aa/full/2001/04/aa9682/img26.gif) |
(4) |
And finally, perturbing the conservation of energy equation
![]() with
with
![]() ,
we find:
2pt
,
we find:
2pt
(![]() is the rate of gain of heat per unit mass due to
the thermonuclear reactions, T is the temperature, L the
luminosity at radius r and, in the diffusion approximation,
is the rate of gain of heat per unit mass due to
the thermonuclear reactions, T is the temperature, L the
luminosity at radius r and, in the diffusion approximation,
![]() ).
).
Equations (6) and (7) could seem complicated
in comparison with their Eulerian formulation. But we think,
our goal being a precise numerical solution of the problem,
that a Lagrangian formulation of the equations is better.
The reasons are that the surface boundary
conditions and the perturbed equations of state
appear naturally in a Lagrangian description.
Let us consider for example the relation
![]() .
The factor
.
The factor
![]() is very large
in some parts of a star,
going up to values of the order of 103. So a small value of
is very large
in some parts of a star,
going up to values of the order of 103. So a small value of
![]() could lead to a large value of P' and a
first order approximation would no longer be good in an Eulerian
description.
could lead to a large value of P' and a
first order approximation would no longer be good in an Eulerian
description.
In what follows, the star will be subdivided in two parts:
the interior from the center to
a chosen optical depth
![]() ,
and the atmosphere from
this optical depth to
,
and the atmosphere from
this optical depth to
![]() .
The frontier between interior and atmosphere will be named
the connecting layer and the last layer of the model
(at
.
The frontier between interior and atmosphere will be named
the connecting layer and the last layer of the model
(at
![]() )
the surface.
)
the surface.
In the interior of a massive near main sequence star,
except for the central convection zone, we can use the diffusion
approximation
We propose to treat the atmosphere in the following way.
The starting approximation is to suppose that the atmosphere is always
in thermal equilibrium during the pulsation. This approximation can
be justified by comparing the fundamental pulsation period of a star,
![]() ,
to the thermal relaxation time of its atmosphere,
,
to the thermal relaxation time of its atmosphere,
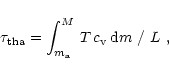 |
(9) |
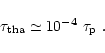
Next, we examine the definition of ![]() in the perturbed
model. More precisely, we have
in the perturbed
model. More precisely, we have
![]() ,
but what is
the direction of
,
but what is
the direction of ![]() we take?
We could choose that
we take?
We could choose that ![]() has the same direction as the
flux vector or that it is
perpendicular to the constant
T surface or that it is purely radial, etc.
But in all these definitions, the angle
between
has the same direction as the
flux vector or that it is
perpendicular to the constant
T surface or that it is purely radial, etc.
But in all these definitions, the angle
between ![]() and
and ![]() is
of the first order and so (using the "
is
of the first order and so (using the "![]() ''
for Eulerian variations)
''
for Eulerian variations)
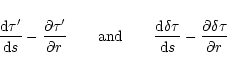
This is the equation we will use instead of Eq. (7) in the atmosphere.
In our approximation, the flux can be obtained
by the diffusion approximation in the interior of the star,
but not in the atmosphere. So the only place where a boundary
condition can be imposed on the flux is at the connecting layer
between atmosphere and interior. From the diffusion approximation,
we have on the one hand:
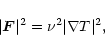 |
(14) |
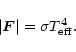 |
(15) |
Let us consider now the dynamic boundary conditions.
We define R and M as the values of r and m at the surface.
For the Eqs. (1) and (5), we proceed as suggested by
Cox (1980, Sect. 17.6b).
We obtain the boundary conditions assuming that
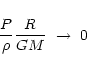
The central boundary conditions are obtained by imposing the
solutions to be regular at the center (finite values for the
perturbed variables and their derivatives).
After some algebra, it can be shown
that the different variables can be rewritten in the following form:
| = | 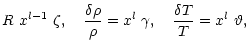 |
||
| = | 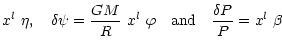 |
(22) |
| = | 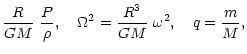 |
||
| x | = | 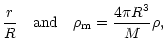 |
the Eqs. (1), (5), (6), (7) and (13)
can be rewritten in a dimensionless form.
We keep only the r
dependent part of the variables, so the partial derivatives are
transformed into simple derivatives. In what follows, a prime will
denote the derivative with respect to x(for example:
![]() ).
We assume that all the variables
have a derivative equal to zero at the centre, which gives
(here for
).
We assume that all the variables
have a derivative equal to zero at the centre, which gives
(here for ![]() ):
):
![]() .
.
Equation (1) gives then:
It can be shown that
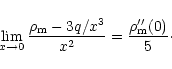 |
(28) |
| k | = | 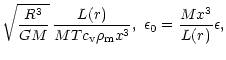 |
|
| = | 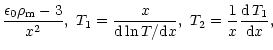 |
||
| = | 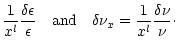 |
Noting that k,
![]() ,
T1 and T2
have finite values when
,
T1 and T2
have finite values when ![]() ,
we find at the center:
2pt
,
we find at the center:
2pt
The appearance of first and second derivatives with respect
to x in the coefficient T1 and T2 needs to
be very careful in order to avoid numerical noise in their estimation.
A good way to proceed
is to use the analytical values given either by the diffusion
approximation in radiative zones or by the adiabatic gradient
in convective zones. More precisely, we have
in a radiative zone:
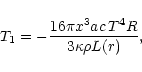 |
(32) |
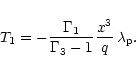 |
(33) |
We use the notation
![]() for the value of
for the value of ![]() at the surface and
at the surface and
![]() for the
value of
for the
value of ![]() at the
connecting layer.
Finally, Eq. (16) gives:
at the
connecting layer.
Finally, Eq. (16) gives:
To all these differential
equations we have to add some algebraic equations.
They consist of the perturbed state equations:
The way to obtain
![]() and
and
![]() is explained in Ledoux & Walraven (1958, Sect. 66).
As we can see,
is explained in Ledoux & Walraven (1958, Sect. 66).
As we can see,
![]() was obtained from the
perturbation of the diffusion approximation (Eq. (8)).
When a convection zone is present, we use the same equation.
Such a simplification does not
pose a problem in central convection zones, for they are located in
a quasi-adiabatic region where
the conservation of energy equation plays a very small role.
was obtained from the
perturbation of the diffusion approximation (Eq. (8)).
When a convection zone is present, we use the same equation.
Such a simplification does not
pose a problem in central convection zones, for they are located in
a quasi-adiabatic region where
the conservation of energy equation plays a very small role.
Equations (23), (25), (27) and (30)
(or (34) in the atmosphere) form a system of 4 linear
ordinary differential equations of first and second order with 4
boundary conditions at the centre (Eqs. (24), (26),
(29) and (31)), 3 boundary conditions at the surface
(dimensionless form of Eqs. (18), (19) and (21))
and 1 condition at the connecting layer
(Eq. (35)). Using Eqs. (36), (37)
and (38), we can express these 4 differential equations
in terms of the 4 unknown functions ![]() ,
,
![]() ,
,
![]() and
and ![]() .
Because of the presence of the factor
.
Because of the presence of the factor ![]() ,
this system of
equations can be seen as an eigenvalue problem.
It can be shown that the number of boundary conditions is in agreement
with the number of differential equations and their order
(some of the central conditions,
Eqs. (26), (29) and (31),
are not really boundary conditions
in the usual sense, their order
being the same or larger than the one of the differential equations).
,
this system of
equations can be seen as an eigenvalue problem.
It can be shown that the number of boundary conditions is in agreement
with the number of differential equations and their order
(some of the central conditions,
Eqs. (26), (29) and (31),
are not really boundary conditions
in the usual sense, their order
being the same or larger than the one of the differential equations).
Let us examine now how we solve numerically this problem.
We use a finite differences method in order to express our
problem as a finite dimensional eigenvalue problem. So first we have
to choose a good grid
![]() ,
,
![]() ,
,
![]() where
the discrete variables will be defined. Then we have to approximate
at each point of the grid the derivatives appearing in the differential
equations by finite differences between these variables,
and our problem will be rewritten as a difference scheme.
Finally, introducing 2 additional variables, it will
take the canonical form
where
the discrete variables will be defined. Then we have to approximate
at each point of the grid the derivatives appearing in the differential
equations by finite differences between these variables,
and our problem will be rewritten as a difference scheme.
Finally, introducing 2 additional variables, it will
take the canonical form
Let us examine first the choice of the number of layers (N)
and of the distribution of the different points
![]() .
In order to have sufficiently precise results, the number of layers
has to be larger than the one usually used in evolution codes.
A number
.
In order to have sufficiently precise results, the number of layers
has to be larger than the one usually used in evolution codes.
A number
![]() turns out to be appropriate and leads to
calculation times quite reasonable (
turns out to be appropriate and leads to
calculation times quite reasonable (![]() 10 s for one mode).
10 s for one mode).
Let us examine now the discretization of the differential equations.
The most important quality criterion of a difference scheme is
its stability, which is even more important than its precision.
We insist on this point
because in our case the difference scheme obtained is easily
subject to instabilities, which can lead to completely
wrong results.
This is the case, for example, if we use the estimation
Finally, our problem can be rewritten as a difference scheme
consisting of a system of 4 N+2 linear equations with 4 N+2
unknowns. More precisely, let ![]() be the index of the
connecting layer, we have the
following variables:
be the index of the
connecting layer, we have the
following variables:
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() and concerning the equations, we have:
N equations for the discretization
of the Poisson equation and its boundary conditions (Eqs. (27), (29) and (21)),
N equations for the discretization of the radial component of the
equation of motion
and its boundary conditions (Eqs. (23), (24) and (18)),
N equations for the discretization of the continuity equation
and its boundary conditions (Eqs. (25), (26) and (19)),
and concerning the equations, we have:
N equations for the discretization
of the Poisson equation and its boundary conditions (Eqs. (27), (29) and (21)),
N equations for the discretization of the radial component of the
equation of motion
and its boundary conditions (Eqs. (23), (24) and (18)),
N equations for the discretization of the continuity equation
and its boundary conditions (Eqs. (25), (26) and (19)),
![]() equations for the discretization of the conservation of
Energy equation in the interior and its central boundary condition
(Eqs. (30) and (31)),
equations for the discretization of the conservation of
Energy equation in the interior and its central boundary condition
(Eqs. (30) and (31)),
![]() equations for the discretization
of the thermal equation
we use in the atmosphere (Eq. (34)), 1 equation for the
discretization of the flux boundary condition (Eq. (35))
and 2 equations for the linking between
equations for the discretization
of the thermal equation
we use in the atmosphere (Eq. (34)), 1 equation for the
discretization of the flux boundary condition (Eq. (35))
and 2 equations for the linking between ![]() and
and ![]() at the connecting point between interior and atmosphere.
An inaccurate way to proceed is to eliminate the N equations
corresponding
to the Poisson equation and the N variables
at the connecting point between interior and atmosphere.
An inaccurate way to proceed is to eliminate the N equations
corresponding
to the Poisson equation and the N variables ![]() ,
substituting in the other equations the value
of
,
substituting in the other equations the value
of ![]() given by the discretization of Eq. (27).
The principal reason is that this substitution corresponds to a very
bad pivot choice in the superficial layers of a star
(
given by the discretization of Eq. (27).
The principal reason is that this substitution corresponds to a very
bad pivot choice in the superficial layers of a star
(
![]() in these layers).
in these layers).
As we have said, we want to express our problem in the canonical
form
![]() .
In order to do this, we have to introduce
two additional variables at each layer. More precisely,
an
.
In order to do this, we have to introduce
two additional variables at each layer. More precisely,
an ![]() dependence
appears in the discretization of the radial component of the
equation of motion
and of the continuity equation.
For the former equation, we eliminate it introducing
the new variables
dependence
appears in the discretization of the radial component of the
equation of motion
and of the continuity equation.
For the former equation, we eliminate it introducing
the new variables
![]() ,
and for the latter equation, we
eliminate it by splitting at each layer i the equation
,
and for the latter equation, we
eliminate it by splitting at each layer i the equation
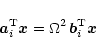 |
(43) |
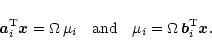 |
(44) |
In order to solve Eq. (39) we use a
generalization of the inverse iteration algorithm. Departing from
the estimation ![]() of the eigenvector at the step k
and the initial estimation
of the eigenvector at the step k
and the initial estimation ![]() of the eigenvalue,
the next estimation is obtained by the formula
of the eigenvalue,
the next estimation is obtained by the formula
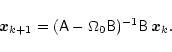 |
(45) |
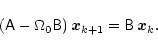 |
(46) |
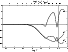 |
Figure 1:
Real parts of the nonadiabatic eigenfunctions
|
| Open with DEXTER | |
We now describe some of the results obtained for a
![]() model with Z=0.02.
We have chosen a model at the end of the central hydrogen burning,
for it
corresponds to a region of the HR diagram
where
model with Z=0.02.
We have chosen a model at the end of the central hydrogen burning,
for it
corresponds to a region of the HR diagram
where ![]() Cephei variable stars
are found. More precisely, it represents a star with
Cephei variable stars
are found. More precisely, it represents a star with
![]() ,
,
![]() and for which
the age after the beginning of
the hydrogen burning is
and for which
the age after the beginning of
the hydrogen burning is
![]() years.
As it is well known, many
years.
As it is well known, many ![]() Cephei stars have
simultaneous radial and nonradial pulsations.
Cephei stars have
simultaneous radial and nonradial pulsations.
In Figs. 1 and 2,
we give the graphs of the real parts of
the nonadiabatic eigenfunctions
![]() and
and
![]() .
We give also for a comparison the graphs of
.
We give also for a comparison the graphs of
![]() obtained in the adiabatic approximation
(refered to by
obtained in the adiabatic approximation
(refered to by
![]() ).
Figure 1 corresponds to the nonradial mode p1 with l=1and Fig. 2 to the fundamental radial mode.
The labels at the bottom correspond to the
logarithm of the equilibrium
temperature. The labels at the top correspond to the logarithm of the
thermal relaxation time of the upper layers
(
).
Figure 1 corresponds to the nonradial mode p1 with l=1and Fig. 2 to the fundamental radial mode.
The labels at the bottom correspond to the
logarithm of the equilibrium
temperature. The labels at the top correspond to the logarithm of the
thermal relaxation time of the upper layers
(
![]() )
divided by the
dynamical time of the star
(
)
divided by the
dynamical time of the star
(
![]() ).
Those functions are normalized in such a way
that
).
Those functions are normalized in such a way
that
![]() at the surface.
In Fig. 2, we have also given
at the surface.
In Fig. 2, we have also given
![]() (divided by 5).
The graphs of
(divided by 5).
The graphs of
![]() show that from the center
to
show that from the center
to
![]() ,
the adiabatic approximation is valid. The comparison between the
adiabatic and nonadiabatic values of
,
the adiabatic approximation is valid. The comparison between the
adiabatic and nonadiabatic values of
![]() shows that the
adiabatic approximation gives wrong results from
shows that the
adiabatic approximation gives wrong results from
![]() to the surface. From a qualitative point of view, the shapes of
the eigenfunctions
to the surface. From a qualitative point of view, the shapes of
the eigenfunctions
![]() and
and
![]() (positions of the zeros and sign
of the derivatives)
are approximately the same for the different modes
we have examined (compare for example
Figs. 1 and 2).
(positions of the zeros and sign
of the derivatives)
are approximately the same for the different modes
we have examined (compare for example
Figs. 1 and 2).
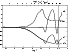 |
Figure 2:
Real parts of the nonadiabatic eigenfunctions
|
| Open with DEXTER | |
If the discretization is done carefully, the derivatives
of the eigenfunctions are continuous at the connecting layer
between interior and atmosphere and the solutions are not dependent
on the choice of this layer. In our application, we took it at
![]() but the results are virtually the same (indistinguishable
on a graph) if we take it for
example at
but the results are virtually the same (indistinguishable
on a graph) if we take it for
example at ![]() or
or ![]() .
In Fig. 3,
we give the graphs of
.
In Fig. 3,
we give the graphs of
![]() in the atmosphere
for the first 3 nonradial p modes of order l=1 (p1, p2
and p3). The abscissa corresponds to the logarithm of the
equilibrium optical depth (Rossland mean). In Figs. 1, 2 and 3, the vertical line corresponds to the connecting layer between interior and atmosphere.
in the atmosphere
for the first 3 nonradial p modes of order l=1 (p1, p2
and p3). The abscissa corresponds to the logarithm of the
equilibrium optical depth (Rossland mean). In Figs. 1, 2 and 3, the vertical line corresponds to the connecting layer between interior and atmosphere.
| |
Figure 3:
Values of
|
| Open with DEXTER | |
| mode |
|
|
|
f ( |
|
|
| 2.62 | 2.39 | 3.78 | 2.818 | 55.89 |
|
| 4.66 | 2.92 | 5.40 | 3.092 | 74.27 |
|
| 7.75 | 3.52 | 6.85 | -2.909 | 91.66 |
|
| 4.56 | 2.79 | 5.97 | 3.131 | 78.02 |
|
| 6.39 | 3.09 | 7.09 | -3.015 | 90.35 |
|
| 8.62 | 3.30 | 8.21 | -2.876 | 102.70 |
|
| 6.35 | 3.10 | 6.97 | -3.016 | 90.36 |
|
| 7.50 | 3.23 | 7.69 | -2.942 | 96.93 |
|
| 9.52 | 3.35 | 9.12 | -2.825 | 107.27 |
|
| 14.86 | 3.29 | 7.90 | -2.558 | 130.22 |
|
| 7.26 | 3.23 | 7.52 | -2.956 | 95.88 |
|
| 10.87 | 3.40 | 9.24 | -2.754 | 113.69 |
|
| 13.25 | 3.37 | 9.04 | -2.636 | 123.84 |
In Table 1, the results obtained for different modes
of the same model are examined.
In the second column, we give the value of
![]() at the photosphere (
at the photosphere (![]() ).
In the third column,
we give the value of
).
In the third column,
we give the value of
![]() .
For the comparison, we give in the fourth column
the value of
.
For the comparison, we give in the fourth column
the value of
![]() obtained in the adiabatic approximation
at the photosphere.
In the fifth column, we give the phase of
obtained in the adiabatic approximation
at the photosphere.
In the fifth column, we give the phase of
![]() in Radians (
in Radians (
![]() ).
In the last column, we give the frequency of the mode (real part)
in
).
In the last column, we give the frequency of the mode (real part)
in ![]() Hz.
We see that, systematically, the value of
Hz.
We see that, systematically, the value of
![]() is smaller than
the value of
is smaller than
the value of
![]() obtained in the adiabatic approximation.
These differences are significant and could have a great effect
on the obtaining of accurate theoretical line-profile variations.
We see also that the phase of
obtained in the adiabatic approximation.
These differences are significant and could have a great effect
on the obtaining of accurate theoretical line-profile variations.
We see also that the phase of
![]() is not exactly equal to
is not exactly equal to
![]() as it was the case in the adiabatic approximation.
as it was the case in the adiabatic approximation.
Another interesting function is
the work integral. Demonstrating the Hermiticity
of the linear adiabatic
wave equation (see Cox 1980 or Unno et al. 1989),
it is shown that the imaginary part of the eigenvalue
![]() can be obtained by an integral
expression similar to the well known one of the radial case. Using
our dimensionless formulation, we have
can be obtained by an integral
expression similar to the well known one of the radial case. Using
our dimensionless formulation, we have
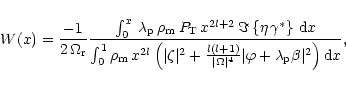 |
(47) |
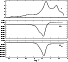 |
Figure 4:
Work integrals of the fundamental radial mode
( |
| Open with DEXTER | |
The results shown in this section permit to see clearly that
a pulsating star can be subdivided in three different parts.
From the center to
the surface, we have first the adiabatic region
where the thermal capacity is so large that luminosity imbalances
have not the time to change significantly the entropy of the matter
(see the thermal relaxation times and the graphs of
![]() given in Figs. 1 and 2).
Then we have the transition region
(between
given in Figs. 1 and 2).
Then we have the transition region
(between
![]() and
and ![]() in this example), in which
the thermal relaxation time is of the same order as the dynamical
time. In this region, the pulsation becomes clearly nonadiabatic
and the heat capacity remains sufficiently important, so that driving
and damping mechanisms can influence the all pulsation,
making the star stable or unstable (see Fig. 4).
And finally we have a region
of small heat capacity, where very small luminosity imbalances
are sufficient to change significantly the entropy of the matter.
In this region,
in this example), in which
the thermal relaxation time is of the same order as the dynamical
time. In this region, the pulsation becomes clearly nonadiabatic
and the heat capacity remains sufficiently important, so that driving
and damping mechanisms can influence the all pulsation,
making the star stable or unstable (see Fig. 4).
And finally we have a region
of small heat capacity, where very small luminosity imbalances
are sufficient to change significantly the entropy of the matter.
In this region,
![]() becomes
quasi-constant (as function of r) and the
hypothesis of thermal equilibrium becomes thus perfectly acceptable
(see the thermal relaxation times and the graph of
becomes
quasi-constant (as function of r) and the
hypothesis of thermal equilibrium becomes thus perfectly acceptable
(see the thermal relaxation times and the graph of
![]() in Fig. 2).
in Fig. 2).
In conclusion, the method we have developed opens the way to interesting bridges between theory and observations. Our new treatment of the outer atmosphere to calculate the eigenfunctions of a nonradially pulsating stars is a fruitful starting point to improve the current methods of analysis of pulsating stars. Up to now, e.g., the nonadiabatic character of the pulsation was treated with an ad hoc parameter in all mode-identification methods based on multicolour photometry (see e.g. Watson 1988; Heynderickx et al. 1994; Garrido 2000).
Also, the available codes for the calculation of theoretical line-profile variations (e.g. Townsend 1997) rely on adiabatic eigenfunctions. It has been claimed in the literature (Balona 1987; Lee et al. 1992) that nonadiabatic effects in the calculation of a line profile are much more important than the pulsational velocity effects in rapid rotators. However, these results are based on an (each time different) arbitrary parametrization of the eigenfunction of the temperature. Moreover, the discrepancies between observed and theoretical line-profile variations is sometimes ascribed to the neglect of temperature effects (e.g. Aerts et al. 1992). Our method allows us to justify or contradict all these suggestions on a much firmer base than was possible before. To find an answer to the question whether or not it is necessary to use nonadiabatic eigenfunctions in the calculation of line-profile variations would be an important step forward in the interpretation of such kind of data and thus also in the application of asteroseismology. We will elaborate on this problem in a forthcoming paper.
Acknowledgements
This work was supported by the F.R.I.A. (Fonds de Recherche pour l'Industrie et l'Agriculture). We express our thanks to R. Scuflaire who helped us greatly in this study and to A. Noels who proposed us to work on this subject. We would also like to thank C. Aerts who encouraged us to write this paper and J. De Ridder who gave us with C. Aerts useful comments about it. And finally, we thank P. Bradley who gave us also useful comments.