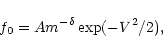 |
(1) |
A&A 366, 276-280 (2001)
DOI: 10.1051/0004-6361:20000347
V. G. Ortega1 - E. Volkov2,1 - I. Monte-Lima1
Received 21 February 2000 / Accepted 3 October 2000
Abstract
Starting from an axisymmetric, differentially rotating thin
disc at equilibrium, in which the velocity dispersion is not large
and in which the particles are characterized by a mass distribution
and by a relationship between mass and velocity dispersion, we consider
the stability of such a configuration against small axisymmetric
disturbances. The analysis is performed kinetically and the behaviour of
the marginal stability curves for different values of the
system's parameters is investigated. Specifically, we consider the
implications of changes in the parameters characterizing the mass
spectrum range and the law relating the mass and velocity dispersion.
Our results show that the characteristics of the system
can significantly affect the critical stability parameters.
We point out that such effects may strongly influence the evolution
of the interstellar medium in disc galaxies.
Key words: ISM: kinematics and dynamics - ISM: clouds - ISM: molecules
In the present paper, we employ the kinetic approach to investigate the stability of a flat, thin, differentially rotating disc configuration against local radial disturbances. We obtain the dispersion equation for such disturbances and compute the curves of marginal stability. These curves, calculated for several values of the parameters characterizing the mass spectrum and the particle dynamics, are compared with Toomre's (1964) well known curves. The behaviour of Toomre's stability parameter under various conditions and the possible role of certain instability conditions on the gas distributions observed in spiral galaxies are also considered.
We consider a differentially rotating thin disc with an undisturbed
distribution function of the Schwarzschild type:
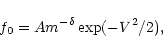 |
(1) |
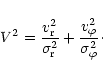
In the epicyclic approximation the components
![]() and
and
![]() of the velocity dispersion obey the relation
of the velocity dispersion obey the relation
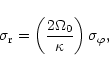
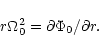
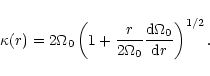
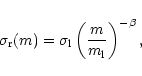 |
(2) |
![\begin{displaymath}f_0 = Am^{-\delta}\exp\left[-\frac{V_1^2}{2\sigma_{\rm r}^2}(\xi^2+\eta^2)\right] .
\end{displaymath}](/articles/aa/full/2001/04/aa9667/img30.gif) |
(3) |
Given such a system we wish to find its response to small perturbations
of the undisturbed potential ![]() ,
considered to be axisymmetric. It is
well known (Lin et al. 1969) that an asymptotic (WKBJ) solution of the
linearized collisionless Boltzmann equation for disturbances of the
type
,
considered to be axisymmetric. It is
well known (Lin et al. 1969) that an asymptotic (WKBJ) solution of the
linearized collisionless Boltzmann equation for disturbances of the
type
![\begin{displaymath}\Phi_1 \propto \exp \left[i( \omega t - n\varphi + \chi )\right] ,
\end{displaymath}](/articles/aa/full/2001/04/aa9667/img31.gif)
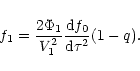 |
(4) |
Here f1 is the perturbed distribution function,
![]() and q is given by the expression
and q is given by the expression
![\begin{displaymath}q=\frac{\nu}{2\sin(\nu\pi)}\int_{-\pi}^{\pi}{\rm e}^{i
\left[\nu s -\theta\xi \sin s +\theta\eta(1 + \cos s)\right]}{\rm d}s.
\end{displaymath}](/articles/aa/full/2001/04/aa9667/img37.gif) |
(5) |
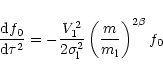 |
(6) |
and using (2) it follows that
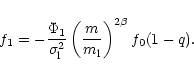 |
(7) |
Defining further the surface density
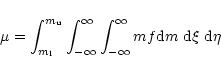 |
(8) |
it can be shown that the perturbed ![]() and undisturbed
and undisturbed
![]() densities are related by
densities are related by
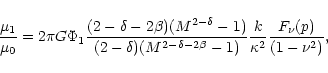 |
(9) |
where
![]() ,
,
![]() and
and
![]() is
a function which we define below.
Inserting in the last equation the potential
is
a function which we define below.
Inserting in the last equation the potential
![]() obtained from Poisson's equation we get the dispersion relation
obtained from Poisson's equation we get the dispersion relation
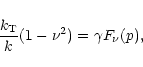 |
(10) |
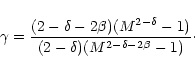 |
(11) |
![\begin{displaymath}F_{\nu }(p)= \frac{1- \nu^2}{p}\left[1 - \frac{\nu}{2\sin(\nu \pi)}
\int_{- \pi}^{\pi}\cos(\nu s)D_{\rm s}(p){\rm d}s\right] ,
\end{displaymath}](/articles/aa/full/2001/04/aa9667/img57.gif) |
(12) |
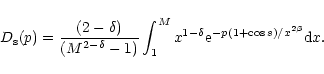 |
(13) |
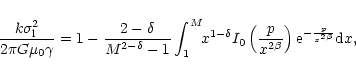 |
(14) |
where I0 is the modified Bessel function.
For the limiting case of a cold disc (
![]() ),
this equation gives, as expected, the Toomre critical wavenumber
),
this equation gives, as expected, the Toomre critical wavenumber
![]() .
For the limiting case of a rotationless hot disc
(
.
For the limiting case of a rotationless hot disc
(
![]() ), we obtain
), we obtain
![]() .
The velocity dispersion
.
The velocity dispersion
![]() may be expressed in terms of the average
radial velocity dispersion
may be expressed in terms of the average
radial velocity dispersion
![]() .
To do this, we fix the
density,
.
To do this, we fix the
density, ![]() ,
and the total specific random energy,
,
and the total specific random energy,
![]() ,
,
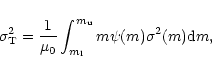 |
(15) |
where ![]() is the velocity dispersion of particles of
mass m and
is the velocity dispersion of particles of
mass m and ![]() the mass distribution function
the mass distribution function
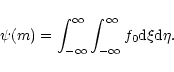
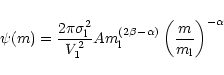 |
(16) |
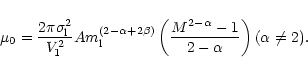 |
(17) |
Here
![]() is the spectral index of the mass
distribution. Thus, the value of
is the spectral index of the mass
distribution. Thus, the value of ![]() is known once
is known once ![]() and
and ![]() are given.
When
are given.
When
![]() the last formula becomes
the last formula becomes
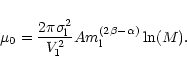 |
(18) |
![\begin{displaymath}\sigma^2(m) = \sigma_{\rm r}^2(m)\left[1+\left(\frac{\kappa}{2\Omega_0}\right)^2
\right] ,
\end{displaymath}](/articles/aa/full/2001/04/aa9667/img78.gif)
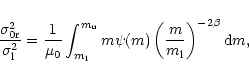 |
(19) |
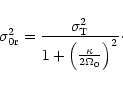
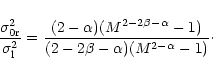 |
(20) |
| (21) |
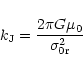
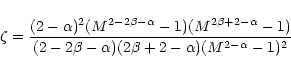 |
(22) |
![\begin{displaymath}y_0 = \gamma \zeta \hat \lambda
\left[1- \left(\frac{2-\alpha +2\beta}{M^{2- \alpha +2\beta}-1}\right) L_{\rm s} \right].
\end{displaymath}](/articles/aa/full/2001/04/aa9667/img86.gif) |
(23) |
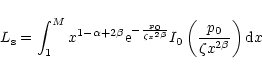 |
(24) |
Formulae (21), (22) establish the relationship between Jeans' wavenumbers for non-rotating homogeneous and heterogeneous discs. A similar result was obtained by Volkov & Ortega (2000) by generalizing the case, previously investigated by Grishchuk & Zel'dovich (1981), of systems composed of a certain discrete number of sub-systems. Here it arises as a particular case of Eq. (14).
As shown by Toomre (1964), it is possible to compute the maximum
value of the quantity y0 from the dispersion equation. This value
determines the critical velocity dispersion which stabilizes the
disc against radial disturbances. We note that for ![]() ,
that is, in the absence of any correlation between the mass and
the velocity dispersion, Eq. (23) coincides with the marginal
stability relation established by Toomre (1964), independent of the
existence of a mass spectrum in the system.
In order to explicitly show the effect of the mass spectrum when
,
that is, in the absence of any correlation between the mass and
the velocity dispersion, Eq. (23) coincides with the marginal
stability relation established by Toomre (1964), independent of the
existence of a mass spectrum in the system.
In order to explicitly show the effect of the mass spectrum when
![]() ,
we present in Fig. 1 plots of y0 vs.
,
we present in Fig. 1 plots of y0 vs.
![]() for three values of the parameter
for three values of the parameter ![]() (
(
![]() ).
For each value of
).
For each value of ![]() ,
marginal stability curves are plotted for
,
marginal stability curves are plotted for
![]() corresponding to equipartition and for the mass spectrum ranges M = 100and M =1000. The stability proves to be very sensitive to changes in the
parameter M determining the mass range. We note from Fig. 1
that compared with the homogeneous (Toomre) system, the neutral
stability curves have their peak values shifted in the direction of decreasing
wavelengths
corresponding to equipartition and for the mass spectrum ranges M = 100and M =1000. The stability proves to be very sensitive to changes in the
parameter M determining the mass range. We note from Fig. 1
that compared with the homogeneous (Toomre) system, the neutral
stability curves have their peak values shifted in the direction of decreasing
wavelengths
![]() .
A heterogeneous disc under the conditions
investigated here is capable of becoming unstable against perturbations
of smaller wavelengths
.
A heterogeneous disc under the conditions
investigated here is capable of becoming unstable against perturbations
of smaller wavelengths
![]() .
In fact, it allows instability
even for perturbations of wavelengths smaller than the conventional Jeans
length
.
In fact, it allows instability
even for perturbations of wavelengths smaller than the conventional Jeans
length
![]() .
This is also apparent in Fig. 2, where for more
clarity we use Jeans wavelength
.
This is also apparent in Fig. 2, where for more
clarity we use Jeans wavelength
![]() (in units of
(in units of
![]() )
as ordinate and where we have drawn the
straight lines corresponding to the limiting rotationless case with
)
as ordinate and where we have drawn the
straight lines corresponding to the limiting rotationless case with
![]() and with
and with
![]() .
.
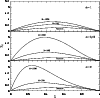 |
Figure 1:
Marginal stability curves for some
values of the parameters |
| Open with DEXTER | |
Toomre's parameter, defined as
![]() ,
where
,
where
![]() is the critical velocity dispersion, is widely employed
as a measure of stability in gaseous and stellar discs. From the
maximum values of y0 in the plots we can estimate the ratio
is the critical velocity dispersion, is widely employed
as a measure of stability in gaseous and stellar discs. From the
maximum values of y0 in the plots we can estimate the ratio
![]() between Toomre's parameter calculated both for
between Toomre's parameter calculated both for
![]() (
(
![]() )
and for
)
and for ![]() (
(![]() ). In Fig. 3 we
have plotted this quantity as a function of the mass spectrum range for two
values of the parameter
). In Fig. 3 we
have plotted this quantity as a function of the mass spectrum range for two
values of the parameter ![]() using
using
![]() .
We notice the
significant decline of this ratio with the mass spectrum range M.
.
We notice the
significant decline of this ratio with the mass spectrum range M.
From the above result, we observe that for a heterogeneous thin disc with a mass spectrum and in which the random velocity and the mass of the elements are anticorrelated, the use of an average Toomre's parameter as indicator of stability may be misleading. For instance, the star formation threshold may be affected if we take the view that the onset of gravitational axisymmetric instability is a determinant of such a process (Kennicutt 1989; Chamcham et al. 1993). We note, however, that star formation is a complex process in which additional non-gravitational effects may be important and even dominant.
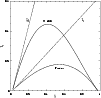 |
Figure 2:
Jeans' length as a function of wavelength.
|
| Open with DEXTER | |
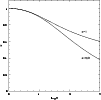 |
Figure 3:
Ratio of Toomre's parameter for |
| Open with DEXTER | |
Our results may be of interest in studies on the dynamics of spiral
galaxies where considerable structure is observed.
In the case of our Galaxy, observations of the molecular clouds' kinematics
(e.g., Stark 1984; Stark & Brand 1989) have shown that the cloud velocity
dispersion averaged over masses contained in a certain range yields
approximately equal values in low (
![]() )
and high
(
)
and high
(
![]() )
mass spectrum regions. For more massive
clouds (
)
mass spectrum regions. For more massive
clouds (
![]() ), Stark (1983) finds that the Z component
of the cloud velocity dispersion decreases with mass approximately as
m-0.5. An analogous result, consistent with equipartition, was obtained
by Scoville et al. (1987) from a sample of clouds with masses within the
range
), Stark (1983) finds that the Z component
of the cloud velocity dispersion decreases with mass approximately as
m-0.5. An analogous result, consistent with equipartition, was obtained
by Scoville et al. (1987) from a sample of clouds with masses within the
range
![]() .
Such a behaviour of the cloud
velocity dispersion in the disc of the Galaxy has been investigated by several
authors. Fukunaga (1984) and Tosa & Fukunaga (1986) introduced
gravitational viscosity, i.e. the transfer of energy from differential
rotation to random motions as a heating source for molecular clouds.
Considering this mechanism as the main process responsible for supporting
the velocity dispersion of the clouds and equating its enery input to the
losses due to inelastic collisions, Jog & Ostriker (1988) (see also
Gammie et al. 1991) obtained the equilibrium, steady-state cloud velocity
dispersion. The estimated value turned out to be independent of mass and in
good agreement with the observations. It has to be pointed out, however,
that other equally important ingredients of the molecular cloud ensemble,
such as the existence of a mass spectrum, its evolution through cloud
coalescence and its effect on dissipation and shear, were not considered in
these calculations. The collisional buildup of molecular clouds in the
disk of the Galaxy was numerically investigated by Das & Jog (1996). In this
study, inelastic collisions, as well as the gravitational interaction between
the clouds, were taken into account. Starting with a random mass distribution,
a power-law mass spectrum (with
.
Such a behaviour of the cloud
velocity dispersion in the disc of the Galaxy has been investigated by several
authors. Fukunaga (1984) and Tosa & Fukunaga (1986) introduced
gravitational viscosity, i.e. the transfer of energy from differential
rotation to random motions as a heating source for molecular clouds.
Considering this mechanism as the main process responsible for supporting
the velocity dispersion of the clouds and equating its enery input to the
losses due to inelastic collisions, Jog & Ostriker (1988) (see also
Gammie et al. 1991) obtained the equilibrium, steady-state cloud velocity
dispersion. The estimated value turned out to be independent of mass and in
good agreement with the observations. It has to be pointed out, however,
that other equally important ingredients of the molecular cloud ensemble,
such as the existence of a mass spectrum, its evolution through cloud
coalescence and its effect on dissipation and shear, were not considered in
these calculations. The collisional buildup of molecular clouds in the
disk of the Galaxy was numerically investigated by Das & Jog (1996). In this
study, inelastic collisions, as well as the gravitational interaction between
the clouds, were taken into account. Starting with a random mass distribution,
a power-law mass spectrum (with
![]() )
was obtained. The
resulting random velocity of the clouds was
)
was obtained. The
resulting random velocity of the clouds was ![]() 8-10 kms-1,
independent of cloud mass, in good accord with the observations by
Stark (1984) and Stark & Brand (1989) in the solar vicinity
(
8-10 kms-1,
independent of cloud mass, in good accord with the observations by
Stark (1984) and Stark & Brand (1989) in the solar vicinity
(
![]() 3 kpc). The energetics of molecular cloud systems was tackled
also by Sotnikova & Volkov (1994) on the basis of a model of selective
cloud coagulation. Their solutions for the velocity dispersion spectrum
contain two separate regions, one of constancy followed by another of
abrupt fall-off for large masses. The transition depends on the initial
velocity dispersion but occurs at
3 kpc). The energetics of molecular cloud systems was tackled
also by Sotnikova & Volkov (1994) on the basis of a model of selective
cloud coagulation. Their solutions for the velocity dispersion spectrum
contain two separate regions, one of constancy followed by another of
abrupt fall-off for large masses. The transition depends on the initial
velocity dispersion but occurs at
![]() for input
values in the interval
( 7.5-15 ) kms-1.
If we consider the response of such a system to radial perturbations, then,
according to our results, it is expected to be subject to the destabilizing
effect discussed above. We here note one important characteristic of the
molecular cloud ensemble in our Galaxy. The observations in the disc of the
Galaxy (e.g. Solomon & Sanders 1980) indicate that most of the mass of
the molecular cloud system resides at the high end of the spectrum.
This can also be estimated from our formula (8) for the surface
density by computing, for fixed values of the parameter
for input
values in the interval
( 7.5-15 ) kms-1.
If we consider the response of such a system to radial perturbations, then,
according to our results, it is expected to be subject to the destabilizing
effect discussed above. We here note one important characteristic of the
molecular cloud ensemble in our Galaxy. The observations in the disc of the
Galaxy (e.g. Solomon & Sanders 1980) indicate that most of the mass of
the molecular cloud system resides at the high end of the spectrum.
This can also be estimated from our formula (8) for the surface
density by computing, for fixed values of the parameter ![]() ,
the mass fraction due to clouds with masses within a given interval.
For values of
,
the mass fraction due to clouds with masses within a given interval.
For values of ![]() lying between 1.5 and 2, we obtain that in average
lying between 1.5 and 2, we obtain that in average
![]() of the total mass corresponds to clouds with masses in the
range
of the total mass corresponds to clouds with masses in the
range
![]() .
It is possible that this kind of instability is responsible for
the formation of the large gas concentrations with masses
.
It is possible that this kind of instability is responsible for
the formation of the large gas concentrations with masses
![]() in our Galaxy and also in other disc galaxies
where giant molecular associations have been observed (e.g. Rand &
Kulkarni 1989).
in our Galaxy and also in other disc galaxies
where giant molecular associations have been observed (e.g. Rand &
Kulkarni 1989).
Using the kinetic approach we have investigated the stability
conditions in a flat, nonmagnetic differentially rotating disc. The disc
is assumed to be made up of an ensemble of particles possessing
a certain mass spectrum and obeying a specific law between the velocity
dispersion and mass. In the present paper it is assumed that the
velocity dispersion and the mass are related through the power-law
given by Eq. (2). We have assumed that the velocity dispersion of
the particles is small compared to the equilibrium rotational
velocity of the motion around the centre of the disc,
thus, it is valid to apply the epicyclic approximation.
We consider the case where the unperturbed velocity distribution
is of the form described by expression (1) which is a simple
generalization of the usual Schwarzschild velocity distribution,
frequently used in dynamical studies of disc configurations.
Having so defined the disc configuration, we considered the reaction of
this system to axisymmetric disturbances in the short-wave approximation.
Of prime importance in this kind of problem is the analysis
of the marginal states. Marginal stability curves were obtained
from the general dispersion equation for time-independent radial
perturbations. Different values of the parameters M, ![]() and
and ![]() were used in order to ascertain their influence upon
the stability of the system. Our choice of the values M = 100 and
M = 1000 was motivated by the fact that most giant molecular clouds
are observed to be comprised in the mass range
were used in order to ascertain their influence upon
the stability of the system. Our choice of the values M = 100 and
M = 1000 was motivated by the fact that most giant molecular clouds
are observed to be comprised in the mass range
![]() .
As for the parameter
.
As for the parameter ![]() ,
we have employed for this quantity
the value
,
we have employed for this quantity
the value
![]() .
Although other values of
.
Although other values of ![]() ,
greater
than 0.5, appear to be possible in the numerical work of Sotnikova
& Volkov (1994), we have used the equipartition value because of
its clear and simple physical meaning.
Our results lead to the conclusion that the neutral stability curves
are quite sensitive to variations in the mass spectrum range M and
of the parameter
,
greater
than 0.5, appear to be possible in the numerical work of Sotnikova
& Volkov (1994), we have used the equipartition value because of
its clear and simple physical meaning.
Our results lead to the conclusion that the neutral stability curves
are quite sensitive to variations in the mass spectrum range M and
of the parameter ![]() .
As shown in Figs. 1 and 3 the effect is already quite significant for
.
As shown in Figs. 1 and 3 the effect is already quite significant for
![]() ,
especially if
,
especially if ![]() .
.
In conclusion our analysis has shown that:
a) Enhanced instability may be produced in certain regions
of the mass spectrum. A somewhat more general treatment of this problem
would be to find solutions for the dispersion equation allowing the
parameter ![]() to vary with the mass spectrum;
to vary with the mass spectrum;
b) The instability can take place in smaller scales as compared to the homogeneous case;
c) Toomre's stability parameter can be significantly decreased. This point suggests that the gravitational effect investigated here may be able to affect considerably the evolution of the interstellar medium in disc galaxies;
d) Our results are consistent with those obtained in Volkov & Ortega (2000) where the hydrodynamic approach was used. Nevertheless, we think that, in the present case, the kinetic method offers a more direct way to obtain the main quantities which characterize the stability conditions of the system.
Acknowledgements
One of the authors (EV) thanks CNPq (Brazil) for financial support under the contract No. 301632195-2(RE). EV also acknowledges partial support from the Russian Basic Research (project 99-02-17087).