A&A 366, 157-165 (2001)
DOI: 10.1051/0004-6361:20000217
A. Skopal
Astronomical Institute, Slovak Academy of Sciences,
05960 Tatranská Lomnica, Slovakia
Received 17 February 2000 / Accepted 19 October 2000
Abstract
We discuss the origin of a periodic wave-like variation as a function
of the orbital phase observed in the light curves (LC) of symbiotic stars.
It is shown that this type of variability cannot be ascribed to
a reflection effect. For example, the observed amplitudes of the LCs are
far larger than those calculated within a model of the reflection effect.
Here, the nature of the orbitally related changes in the optical continuum
is outlined within an ionization model of symbiotic binaries.
Key words: stars: binaries: symbiotic
Symbiotic stars are interacting binaries consisting of a cool giant and a hot compact star. Typical orbital periods run between 1-3 years. The giant component losses mass, part of which is accreted by its companion. The hot star ionizes a portion of the giant's wind, giving rise to nebular emission. As a result the spectrum of symbiotic stars consists of basically three components of radiation - two stellar and one nebular. Such composition of the spectrum was demonstrated well for ZAnd, BFCyg and AGDra (Nussbaumer & Vogel 1989; Fernandéz-Castro et al. 1990; Greiner et al. 1997). In many cases the nebular radiation dominates the optical.
A very significant feature of LCs of many symbiotic stars is a
periodic wave-like variation along the orbital motion
(see Fig. 1).
It displays a large amplitude (i.e. magnitude difference between
the maximum and minimum of the light),
![]() 1mag or more,
which is a function of the wavelength - we always observe
1mag or more,
which is a function of the wavelength - we always observe
![]() .
The period is approximately equal
to the orbital period, and a minimum occurs at/around the inferior
conjunction of the cool component. These properties relate this type
of variations to the orbital motion. Originally, Boyarchuck (1966)
and Belyakina (1970) suggested a reflection effect as responsible for
such variability in the AGPeg LC. In this model, the hot star irradiates
and heats up the facing giant's hemisphere that causes variation in
the star's brightness when viewing the binary at different orbital phases.
This natural explanation was adopted by many authors (e.g. Kenyon
1986) and it is still popular (e.g. Munari 1989,
1992; Dobrzycka et al. 1993;
Proga et al. 1996, 1998).
On the other hand, some authors have never used the reflection effect
and/or found it to be problematic to interpret their data.
For example, Nussbaumer & Vogel (1987) suggested a new approach
to symbiotic stars based on the interaction of the hot star radiation
with the cool stellar wind.
Formiggini & Leibowitz (1990) found that the reflection effect
requires an extremely high bolometric luminosity of the hot component,
to explain the light variation in AGDra, AXPer and AGPeg.
Schmutz et al. (1994) did not find any
irradiation effect in the red giant spectrum of SYMus, although
its visual LC varies with an amplitude of 0.6mag.
Recently Skopal (1996) demonstrated that the reflection effect
is not a reliable interpretation of the wave-like variation in the optical
continuum of V443Her.
.
The period is approximately equal
to the orbital period, and a minimum occurs at/around the inferior
conjunction of the cool component. These properties relate this type
of variations to the orbital motion. Originally, Boyarchuck (1966)
and Belyakina (1970) suggested a reflection effect as responsible for
such variability in the AGPeg LC. In this model, the hot star irradiates
and heats up the facing giant's hemisphere that causes variation in
the star's brightness when viewing the binary at different orbital phases.
This natural explanation was adopted by many authors (e.g. Kenyon
1986) and it is still popular (e.g. Munari 1989,
1992; Dobrzycka et al. 1993;
Proga et al. 1996, 1998).
On the other hand, some authors have never used the reflection effect
and/or found it to be problematic to interpret their data.
For example, Nussbaumer & Vogel (1987) suggested a new approach
to symbiotic stars based on the interaction of the hot star radiation
with the cool stellar wind.
Formiggini & Leibowitz (1990) found that the reflection effect
requires an extremely high bolometric luminosity of the hot component,
to explain the light variation in AGDra, AXPer and AGPeg.
Schmutz et al. (1994) did not find any
irradiation effect in the red giant spectrum of SYMus, although
its visual LC varies with an amplitude of 0.6mag.
Recently Skopal (1996) demonstrated that the reflection effect
is not a reliable interpretation of the wave-like variation in the optical
continuum of V443Her.
Accordingly we show that the reflection effect cannot explain the orbitally related wave-like modulation of LCs of symbiotic binaries. To demonstrate this, we compare basic observational properties of this variation to those caused by the reflection effect (Sect. 3). In Sect. 4 we describe a simple ionization model, which could be responsible for such variation.
Figure 1 shows examples of the periodic wave-like variation in
the UBV LCs for selected symbiotic stars. Table 1 summarizes its
basic characteristics - the amplitude, ![]() ,
and the profile
through a parameter a (Sect. 3.2). Photometric UBV observations
used in this paper has been extracted from the literature and are
also referred in Table 1.
,
and the profile
through a parameter a (Sect. 3.2). Photometric UBV observations
used in this paper has been extracted from the literature and are
also referred in Table 1.
 |
Figure 1:
Examples of periodic wave-like variation in the LCs of selected
symbiotic binaries. Symbols, |
| Object |
|
|
aU aB aV | Obs. | Note | |
| AXPer | 680 |
|
0.8 0.6 0.5 | 0.6 0.7 0.8 | 1 | |
| BFCyg | 757 |
|
1.1 0.9 0.8 | 0.5 0.6 0.6 | 2 | ss |
| CICyg | 855 |
|
1.2 0.7 0.5 | 0.8 0.8 0.9 | 3 | ss |
| EGAnd | 482 |
|
0.6 0.3 0.2 | 1.0 1.0 1.0 | 4 | sss |
| AGDra | 550 |
|
1.0 0.2 0.1 | 0.5 0.5 0.5 | 5 | |
| V1329Cyg | 958 | 0.18 -0.47 | 1.8 1.3 1.2 | 0.5 0.5 0.5 | 6 | |
| He2-467 | 479 | 0.07 -0.2 | 2.2 0.6 0.3 | 0.6 0.6 1.0 | 7 | s |
| ZAnd | 759 |
|
1.5 1.0 0.7 | 0.5 0.5 0.6 | 8 | ss |
| V443Her | 594 | 0.7 0.4 0.3 | 0.6 0.7 0.8 | 9 | ||
| AGPeg | 813 | 1.1 0.6 0.5 | 0.5 0.5 0.5 | 10 |
In this section we compare the observed parameters of the wave-like variation - its amplitude and profile - to those given by the reflection effect.
The largest amplitude, between ![]() 0.5 and
0.5 and ![]() 2.5mag, is observed
in the U band (Fig. 1, Table 1). In the model of the reflection effect,
it is given by the luminosity ratio of the illuminated to the
non-illuminated giant's hemisphere. The upper limit (
2.5mag, is observed
in the U band (Fig. 1, Table 1). In the model of the reflection effect,
it is given by the luminosity ratio of the illuminated to the
non-illuminated giant's hemisphere. The upper limit (
![]() )
of
the magnitude difference between the two hemispheres,
)
of
the magnitude difference between the two hemispheres,
![]() ,
can be expressed as
,
can be expressed as
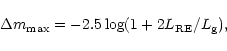 |
(1) |
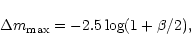 |
(2) |
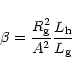 |
(3) |
![\begin{figure}
\par\includegraphics[width=8cm]{ms9660f2r.eps} \end{figure}](/articles/aa/full/2001/04/aa9660/Timg39.gif) |
Figure 2:
Profiles of LCs given by the reflection function
for inclination of the orbit
|
However, this problem should be treated by solving the radiation
transfer of a very hot light (
![]() )
throughout a very cool atmosphere
(
)
throughout a very cool atmosphere
(
![]() )
to learn how the reprocessed UV/EUV radiation contributes into
the Balmer and Paschen continua. An exact approach to the reflection
effect was outlined by
Vaz & Nordlund (1985) and Nordlund & Vaz (1990)
for similar effective temperatures of the component stars, but not for
very cool stars, where the TiO absorption bands are important.
Recently, Proga et al. (1996) treated this problem for symbiotic
binary stars using a non-LTE photoionization model, but also without
including molecules. According to their model, significant changes
in the structure of the red giant atmosphere are expected for
)
to learn how the reprocessed UV/EUV radiation contributes into
the Balmer and Paschen continua. An exact approach to the reflection
effect was outlined by
Vaz & Nordlund (1985) and Nordlund & Vaz (1990)
for similar effective temperatures of the component stars, but not for
very cool stars, where the TiO absorption bands are important.
Recently, Proga et al. (1996) treated this problem for symbiotic
binary stars using a non-LTE photoionization model, but also without
including molecules. According to their model, significant changes
in the structure of the red giant atmosphere are expected for
![]() 1 and negligible when
1 and negligible when ![]() 1.
Their calculations showed that the magnitude difference between
the illuminated and non-illuminated hemisphere
1.
Their calculations showed that the magnitude difference between
the illuminated and non-illuminated hemisphere
![]() mag
in the range of considered temperatures between 20000 and 200000K
for
mag
in the range of considered temperatures between 20000 and 200000K
for ![]() = 10, 1, 0.1 and 0.01 (cf. their Fig. 6).
Also according to this study, the theoretical differences
in broadband magnitudes between the opposite hemispheres of an
illuminated red giant are also very small,
= 10, 1, 0.1 and 0.01 (cf. their Fig. 6).
Also according to this study, the theoretical differences
in broadband magnitudes between the opposite hemispheres of an
illuminated red giant are also very small,
![]() mag,
far from those observed.
mag,
far from those observed.
To characterize the shape of the observed LC we introduce
a parameter a as
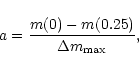 |
(4) |
Shaping of LCs caused by the reflection effect is determined
by a reflection function. To construct such a LC we assume that
the observed luminosity of the binary,
![]() ,
is given by
the sum of a constant part of the system luminosity,
,
is given by
the sum of a constant part of the system luminosity,
![]() ,
given mainly by stellar components, and a phase dependent variable
light,
,
given mainly by stellar components, and a phase dependent variable
light,
![]() ,
given by the reflection function.
Then we can write
,
given by the reflection function.
Then we can write
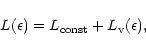 |
(5) |
![\begin{displaymath}m(\epsilon) = - 2.5\log\left[1+\frac{L_{\rm v}(\epsilon)}{L_{\rm const}}
\right]+m_{\rm const}.
\end{displaymath}](/articles/aa/full/2001/04/aa9660/img56.gif) |
(6) |
We conclude that the observational characteristics of the LCs of symbiotic binaries - the large amplitude, the profile of minima and variation in their positions - cannot be reproduced by the reflection effect.
To get a better idea of the origin of the orbitally related wave-like variation we discuss it within the basic model of symbiotic binaries - the cool giant losing material via the stellar wind and the hot luminous compact object ionizing a portion of the neutral wind. Such composition creates a strong source of nebular emission in the binary, which often dominates the optical region (e.g. BFCyg, AG Dra, He2-467, AS338). Therefore we discuss the apparent variation in the optical continuum within an ionization model.
First, we introduce the simplest model of the ionization structure in symbiotic binaries.
| Object |
|
Ref. |
|
|
|
|
| [ergcm-2s-1Å-1] | [cm-3] | [cm-3] | [cm-3] | [cm-3] | ||
| ZAnd | 7.5a | 1 | 3.4
|
2.9
|
1.7
|
|
| ZAnd | 2.4 - 9.6b | Fig. 1 |
|
|
||
| BFCyg | 5.0a | 2 | 3.8
|
2.9
|
d | |
| BFCyg | 2.7 - 7.9b | Fig. 1 |
|
|
||
| AGDra | 2.4 a | 3 | 1.5
|
1.5
|
1.1
|
|
| AGDra | 0.9 - 2.2b | Fig. 1 |
|
|
||
| AXPer | 2.0a | 4 | 2.1
|
1.2
|
d | |
| AXPer | 1.0 - 2.5b | Fig. 1 |
|
|
||
| V443Her | 2.1a | 5 | 3.0
|
4.2
|
1.9
|
|
| V443Her | 1.1 - 2.1b | Fig. 1 |
|
|
| a - from the energy distribution in the spectrum at
b - from the dereddened U-magnitude at minimum and maximum, respectively: ZAnd: U = 12.3 - 10.8, EB-V = 0.35, d = 1.12kpc, BFCyg: U = 12.4 - 11.3, EB-V = 0.4, d = 4.6kpc, AGDra: U = 12.0 - 11.0, EB-V = 0.05, d = 1.0kpc (Appendix A), AXPer: U = 12.9 - 11.9, EB-V = 0.27, d = 1.73kpc, V443Her: U = 12.2 - 11.5, EB-V = 0.15, d = 2.0kpc. |
c - the range of the observed EM referred in the literature.
d - not applicable. Ref.: 1 - Fig. 1 of Fernández-Castro et al. (1988), 2 - Fig. 3b of Fernández-Castro et al. (1990), Skopal et al. (1997), 3 - Fig. 3 of Mikolajewska et al. (1995), Appendix A, 4 - Fig. 2 of Mikolajewska & Kenyon (1992), Skopal (2000), 5 - Fig. 1 of Dobrzycka et al. (1993). |
![\begin{figure}
\par\includegraphics[width=8cm]{ms9660f3r.eps} \end{figure}](/articles/aa/full/2001/04/aa9660/Timg75.gif) |
Figure 3:
The Hi/Hii boundary calculated for
X = 0.3, 1, 10, the stellar wind model characterized by the parameters
|
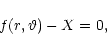 |
(7) |
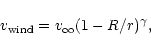 |
(8) |
We now test if the amount of emission produced by this model is consistent with observations.
We investigate the balance between the observed nebular
emission in the continuum and that produced by the ionization model.
The nebular flux largely depends on the number of hydrogen
recombinations, and is proportional to
![]() ,
(the so called emission measure - EM); n+ and
,
(the so called emission measure - EM); n+ and ![]() is
the concentration of ions (protons) and electrons, respectively.
is
the concentration of ions (protons) and electrons, respectively.
(i) Observations: The quantity of the EM can be estimated,
for example, from the measured flux,
![]() (
(
![]() ), of the nebular continuum
at the wavelength
), of the nebular continuum
at the wavelength ![]() ,
according to the equation
,
according to the equation
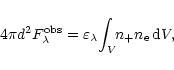 |
(9) |
(ii) Model: The source of the nebular radiation in the model
is the ionized region, in which the rate of ionization/recombination
processes is balanced by the rate of photons,
![]() (photonss-1), capable of ionizing the element under
consideration. In the case of pure hydrogen we can write
the equilibrium condition as
(photonss-1), capable of ionizing the element under
consideration. In the case of pure hydrogen we can write
the equilibrium condition as
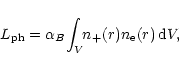 |
(10) |
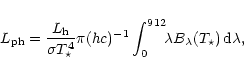 |
(11) |
We can calculate the EM directly by integrating emission
contributions throughout the volume of the ionized zone defined by
the model (Eq. 7). The calculation of the Hi/Hii and
Hei/Heii boundary in 2-D representation can be found
in STB and Nussbaumer & Vogel (1987), respectively. Using
Nussbaumer & Vogel (1989), we derive an upper limit to the modeled
EM assuming the sphere around the cool star to be fully ionized from
r = Q to
![]() .
The parameter Q is the location of
the Hi/Hii boundary on the line joining the cool and the hot
star (
.
The parameter Q is the location of
the Hi/Hii boundary on the line joining the cool and the hot
star (
![]() ). The particle density n(r) is given
by the mass-loss rate of the wind
). The particle density n(r) is given
by the mass-loss rate of the wind
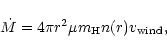 |
(12) |
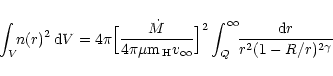
![\begin{displaymath}=4\pi\Big[\frac{\dot M}{4\pi\mu {\rm m}_{\,\rm H}
v_{\infty...
...ma)}
\Big[1-\Big(1-\frac{R}{Q}\Big)^{1-2\gamma}\Big]\nonumber
\end{displaymath}](/articles/aa/full/2001/04/aa9660/img107.gif)
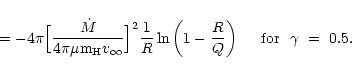 |
(13) |
We find that the observed EM is consistent with that
produced by the ionization model. This implies that all
the
![]() photons consumed by the particles of the giant wind
are needed to produce the observed nebular flux. However, in the model
of the reflection effect only a small part of ionizing photons,
photons consumed by the particles of the giant wind
are needed to produce the observed nebular flux. However, in the model
of the reflection effect only a small part of ionizing photons,
![]() (Sect. 3), can be used to
produce the nebular radiation. This causes the discrepancy
between the
(Sect. 3), can be used to
produce the nebular radiation. This causes the discrepancy
between the ![]() parameter given by observations and much
larger value, required by models of reflection effect to explain
the amplitude of the LCs.
parameter given by observations and much
larger value, required by models of reflection effect to explain
the amplitude of the LCs.
We now will demonstrate that the variation in the EM is responsible for the investigated wave-like variation in the LCs.
The quantity of the EM in the continuum also varies as a function of
the orbital phase (e.g. Fernandez-Castro et al. 1988;
Mikolajewska et al. 1989; Mikolajewska & Kenyon 1992;
Dobrzycka et al. 1993). To investigate this variability
we express Eq. (9) in the scale of magnitudes
(
![]() )
as
)
as
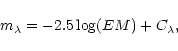 |
(14) |
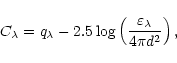 |
(15) |
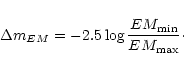 |
(16) |
Note that the decrease of the LC amplitude with wavelength is caused
by an increase of the cool giant contribution, which does not
vary with the orbital phase. The same effect takes place towards
the short wavelengths due to an increase in the stellar contribution
from the hot star (see Fig. 4 of Kenyon et al. 1993).
![\begin{figure}
\par\includegraphics[width=7.3cm]{ms9660f4ar.eps} \includegraphics[width=7.3cm]{ms9660f4br.eps} \end{figure}](/articles/aa/full/2001/04/aa9660/Timg119.gif) |
Figure 4: Top: variation in the EM of BFCyg as a function of the orbital phase. The data (Mikolajewska et al. 1989) were converted into the B-magnitudes according to Eq. (14). Compared is the LC in the B band obtained photometrically during the same period, between JD 2445700 and 2446718 (Hric et al. 1993). Bottom: the same as the top, but for ZAnd. Measurements of the EM were taken from Fernandez-Castro et al. (1988), and photometric B-magnitudes from Fig. 1, but omitting the active phase. These results show that the variation in the EM is fully responsible for the variation in the LCs |
Together with the periodic variation in the nebular continuum,
the same type of variability is observed in fluxes of Balmer lines.
The source of hydrogen emission in lines is also the Hii region.
Therefore the variation in both the hydrogen continuum and the lines
should be of the same nature.
So the EM derived from the hydrogen continuum should be consistent
with that given by the Balmer lines, assuming an optically
thin regime and the case B of recombination. In Table 3
we summarize results for the line H![]() .
.
| Object |
|
Ref. |
|
| [ergcm-2s-1] | [cm-3] | ||
| ZAnd | 37.3 | 1 | 4.5
|
| BFCyg | 18 - 65 | 2 | 0.4
|
| AGDra | 6.4 - 9.4 | 3 | 6.2
|
| AXPer | 7.2 - 22 | 4 | 2.1
|
| V443Her | 6.5 - 15 | 5 | 2.5
|
| a - dereddened fluxes with EB-V referred in Table 2. Ref.: 1 - Mikolajewska & Kenyon (1996), 2 - Mikolajewska et al. (1989), 3 - Mikolajewska et al. (1995), 4 - Mikolajewska & Kenyon (1992), 5 - Dobrzycka et al. (1993). |
As the variation in the emission of the Balmer lines is connected with the Hii region - the dominant source of the optical/near-UV continuum - the observed periodic wave-like variation in the continuum should always be followed by a similar variation in Balmer lines.
To produce the wave-like variation in the LCs along the orbital cycle,
the nebula - the main source of the optical continuum in symbiotic
binaries - has to be partially optically thick and of a non-spherical
shape. In our simple ionization model the opacity, ![]() ,
of
the ionized emission medium decreases with the distance from the cool
star, since
,
of
the ionized emission medium decreases with the distance from the cool
star, since
![]() (i.e. its parts nearest to the giant's surface will be most opaque).
It is probable that the observed emission will also depend
on the extension of the ionized region. Below we give a qualitative
description on how, or whether, it is possible to produce the observed
profile of LCs within the ionization model mentioned above.
(i.e. its parts nearest to the giant's surface will be most opaque).
It is probable that the observed emission will also depend
on the extension of the ionized region. Below we give a qualitative
description on how, or whether, it is possible to produce the observed
profile of LCs within the ionization model mentioned above.
(i) In the case of an oval shape of the Hii zone (Fig. 3;
a small parameter X), its total emission will be atenuated more
at positions of the inferior and superior conjunction of the cool
star (the orbital phase ![]() = 0 and 0.5, respectively) than
at positions of
= 0 and 0.5, respectively) than
at positions of ![]() = 0.25 and 0.75, respectively. Such
apparent variation in the EM will produce both the primary and
the secondary minimum in the LC and will thus mimic the ellipsoidal
effect in binaries containing a giant star. This type of LC profile
corresponds to the parameter
= 0.25 and 0.75, respectively. Such
apparent variation in the EM will produce both the primary and
the secondary minimum in the LC and will thus mimic the ellipsoidal
effect in binaries containing a giant star. This type of LC profile
corresponds to the parameter ![]() (right panels of Fig. 1).
(right panels of Fig. 1).
(ii) A gradual opening of the Hii zone (approximately
![]() )
will make it optically thinner behind the hot
star (outside the binary around
)
will make it optically thinner behind the hot
star (outside the binary around ![]() = 0.5). Thus, more of
the nebular radiation, relative to the case (i), will be observed
at the position of
= 0.5). Thus, more of
the nebular radiation, relative to the case (i), will be observed
at the position of
![]() .
The secondary minimum in LCs
will therefore become less pronounced or flat, and/or a maximum at
.
The secondary minimum in LCs
will therefore become less pronounced or flat, and/or a maximum at
![]() can arise. The LC profile here should be
characterized by the parameter a > 0.5 (mid panels of Fig. 1).
can arise. The LC profile here should be
characterized by the parameter a > 0.5 (mid panels of Fig. 1).
(iii) Given an extensive emission zone (X > 10) one can imagine
the partially optically thick portion of the Hii region as
a cap on the Hi/Hii boundary around the binary axis.
This resembles the geometry of the reflection effect, but
the emission region causing the light variation is physically
displaced from the giant's surface (see also a sketch in
Baratta & Viotti (1990), who drawn such regions for
Feii and Ciii lines). In these cases the LC profile
is similar to that of the reflection effect, i.e. the parameter
![]() (left panels of Fig. 1).
(left panels of Fig. 1).
A relationship between the parameters a and X supports the connection between the shape of the LC and the extent of the symbiotic nebula mentioned above (Fig. 5, Appendix B).
However, the real structure of the ionized region in symbiotic binaries is probably much more complex. Currently it is being intensively investigated (e.g. Schmid 1998). For example, the observed systematic variation in the minima position (i.e. an apparent change of the orbital period) requires an asymmetrical shape of the Hii zone with respect to the binary axis (see Sect. 4.1 of Skopal 1998a in more detail). A modification of the STB model, which includes effects of the orbital motion, is outlined in Appendix C.
We find that:
Acknowledgements
This research has been supported by the Slovak Academy of Science under a grant No. 5038/2000 and the Alexander von Humboldt foundation under project No. SLA/1039115. The author would like to thank his anonymous referee for constructive comments that allowed him to improve the original version of the present work.
The ![]() parameter (Eq. 3) is defined by the luminosity ratio
parameter (Eq. 3) is defined by the luminosity ratio
![]() and the giant radius in units of the separation of the components,
and the giant radius in units of the separation of the components,
![]() .
To determine these quantities we used published parameters and/or
made appropriate estimates. If applicable, we used spectral types
of the cool components in symbiotic binaries of
Mürset & Schmid (1999) and empirically determined dependencies
of effective temperature and linear radius upon the spectral type
given by van Belle et al. (1999). Table 4 summarizes the resulting
parameters. Their uncertainties represent mean square errors of
the mean value given by Eq. (3). A brief explanation to Table 4 is
given below for individual objects.
.
To determine these quantities we used published parameters and/or
made appropriate estimates. If applicable, we used spectral types
of the cool components in symbiotic binaries of
Mürset & Schmid (1999) and empirically determined dependencies
of effective temperature and linear radius upon the spectral type
given by van Belle et al. (1999). Table 4 summarizes the resulting
parameters. Their uncertainties represent mean square errors of
the mean value given by Eq. (3). A brief explanation to Table 4 is
given below for individual objects.
AXPer:
Skopal (1994) determined
![]() .
The luminosity of the giant,
.
The luminosity of the giant,
![]() for the distance
for the distance
![]() pc (Skopal 2000).
The hot star luminosity,
pc (Skopal 2000).
The hot star luminosity,
![]() (Mürset et al. 1991) with the uncertainty resulting from that
of d.
(Mürset et al. 1991) with the uncertainty resulting from that
of d.
BFCyg:
Parameters
![]() and
and
![]() (Skopal et al. 1997). The uncertainty of the luminosity
ratio is
(Skopal et al. 1997). The uncertainty of the luminosity
ratio is ![]() 30%, which is relevant to its determination from
the observed fluxes.
30%, which is relevant to its determination from
the observed fluxes.
CICyg:
Kenyon et al. (1991) estimated
![]() .
Adopting their estimate of the total mass of the binary,
.
Adopting their estimate of the total mass of the binary,
![]() ,
we get
A =
,
we get
A =
![]() for
for
![]() = 855.25 days (Aller 1954),
which yields
= 855.25 days (Aller 1954),
which yields
![]() .
The spectral type (ST) of the red giant in CICyg, M5.5,
corresponds to its effective temperature,
.
The spectral type (ST) of the red giant in CICyg, M5.5,
corresponds to its effective temperature,
![]() K,
which then yields
K,
which then yields
![]() .
Finally, Mürset et al. (1991) determined
.
Finally, Mürset et al. (1991) determined
![]() (d/1.5kpc)2.
(d/1.5kpc)2.
EGAnd:
From the contact times of a minimum observed in continuum fluxes
at ![]() 1320Å (Pereira 1996) we determined
1320Å (Pereira 1996) we determined
![]() for the orbital period,
for the orbital period,
![]() = 482 days (Skopal 1997)
and a circular orbit. As the minimum is caused by Rayleigh
scattering of the hot star radiation on the neutral atoms of
the cool giant wind, this is an upper limit.
The luminosity ratio for the two stars,
= 482 days (Skopal 1997)
and a circular orbit. As the minimum is caused by Rayleigh
scattering of the hot star radiation on the neutral atoms of
the cool giant wind, this is an upper limit.
The luminosity ratio for the two stars,
![]() (Vogel et al. 1992).
The uncertainty of this ratio is assumed to be of 30%.
(Vogel et al. 1992).
The uncertainty of this ratio is assumed to be of 30%.
AGDra:
From the energy distribution in the spectrum during quiescence
(Greiner et al. 1997) we estimated the observed fluxes
![]() and
and
![]() ergcm-2s-1,
i.e.
ergcm-2s-1,
i.e.
![]() .
Smith et al. (1996) estimated the surface gravity as
.
Smith et al. (1996) estimated the surface gravity as
![]() (g in units of cms-2), which for
the cool component mass of 1.5
(g in units of cms-2), which for
the cool component mass of 1.5 ![]() (Mikolajewska et al. 1995),
yields
(Mikolajewska et al. 1995),
yields
![]() .
This value is also consistent with that corresponding to the recent
.
This value is also consistent with that corresponding to the recent
![]() dependencies. For
dependencies. For
![]() and
and
![]() = 550 days (Gális et al. 1999)
we have
= 550 days (Gális et al. 1999)
we have
![]() and thus
and thus
![]() .
We can also estimate the distance to AGDra
.
We can also estimate the distance to AGDra
![]() pc from
pc from
![]() (
(
![]() as for K3-4III giant) and
as for K3-4III giant) and
![]() .
.
V1329Cyg:
The maximum width of the pre-outburst eclipses
(Fig. 1 of Schild & Schmid 1997),
| Object |
|
|
|
| AXPer |
|
|
|
| BFCyg |
|
|
|
| CICyg |
|
|
|
| EGAnd |
|
|
|
| AGDra |
|
|
|
| V1329Cyg | 3.1-1.2 | <0.39 | 0.18 - 0.47 |
| He2-467 | 0.05-0.03 | 0.07 - 0.2 | |
| ZAnd |
|
|
|
| V443Her | |||
| AGPeg |
Here we investigate the suggested connection between the parameters
a and X (Sect. 4.2). STB derived the parameter X as
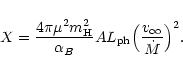 |
(B.1) |
![\begin{figure}
\par\includegraphics[width=6.6cm]{ms9660f5r.eps} \end{figure}](/articles/aa/full/2001/04/aa9660/Timg224.gif) |
Figure B.1: A correlation between the shape of the LC characterized by the parameter a (Sect. 3.2) and the extent of the symbiotic nebula given by the parameter X |
| Object | Ref. |
|
a | X | |
| AGPeg | 2.0 | 7.2 | 0.50 | >15 | |
| ZAnd | 2.0 | 1 | 3.5 | 0.53 | |
| AGDra | 2.0 | 2 | 2.6 | 0.50 | 11 |
| V1329Cyg | 15 | 56 | 0.50 | ||
| BFCyg | 50 | 0.57 | |||
| CICyg | >4 | 3.7 | 0.83 | <5 | |
| AXPer | 3 | 2.2 | 0.70 | ||
| EGAnd | 2.0 | 4 | 0.077 | 1.0 | 0.3 |
| Ref.: 1 - Fernández-Castro et al. (1988),
2 - Mikolajewska et al. (1995),
3 - Skopal et al. (in press), 4 - Vogel (1991): this value is needed to explain the nebular continuum. In contrast, the value of 3-4 |
In spite of these problems the present knowledge of the fundamental parameters of symbiotic binaries makes a correlation between a and X possible (Fig. 5). However, further investigation is needed to determine more accurate parameters, mainly the mass-loss rate via the wind from cool giants in binaries, to verify the relationship between the profile of the LC and the extent of the symbiotic nebula.
In this appendix we introduce a modification of the STB model
accounting for the additional ionizations due to the inflow of neutral
material into the ionized region through the ionization front due to
the orbital motion and the velocity of the giant wind.
At a boundary point, ![]() ,
the rate of particles,
,
the rate of particles,
![]() ,
crosses the area of the front,
dS = d
,
crosses the area of the front,
dS = d
![]() ,
where d
,
where d![]() is
a small angle around the vector r pointing to
is
a small angle around the vector r pointing to ![]() from the hot star and
from the hot star and ![]() is the velocity of atoms in the
direction of S (i.e. perpendicular to the boundary at the
point
is the velocity of atoms in the
direction of S (i.e. perpendicular to the boundary at the
point ![]() ).
Thus, within the Hii region, the rate of photons,
).
Thus, within the Hii region, the rate of photons,
![]() ,
capable of ionizing hydrogen, has to balance a surplus of
,
capable of ionizing hydrogen, has to balance a surplus of
![]() recombinations
in addition to the steady state situation;
recombinations
in addition to the steady state situation;
![]() stands for
the total hydrogenic recombination coefficient for case B.
The distance
stands for
the total hydrogenic recombination coefficient for case B.
The distance ![]() from the hot star of the modified
ionization front is then given by the equilibrium condition
from the hot star of the modified
ionization front is then given by the equilibrium condition
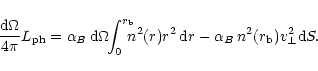 |
(C.1) |