Along with the surface brightness profiles, the method
mentioned above also provides the ellipticity ![]() and
position angle PA of each isophote. For each image, mean
and
position angle PA of each isophote. For each image, mean
![]() and PA were calculated with the values of the
isophotes between 23 and 24 magarcsec-2 and are
listed in Table 2. Since the outer isophotes of many of
our galaxies were distorted by different structures, such as
bars, rings, spiral arms, bright HII regions, some of these
averages were corrupted, so a visual inspection of each image
was carried out in order to exclude from the averaging the
distorted zones and get more indicative values.
and PA were calculated with the values of the
isophotes between 23 and 24 magarcsec-2 and are
listed in Table 2. Since the outer isophotes of many of
our galaxies were distorted by different structures, such as
bars, rings, spiral arms, bright HII regions, some of these
averages were corrupted, so a visual inspection of each image
was carried out in order to exclude from the averaging the
distorted zones and get more indicative values.
Light distributions of spiral galaxies are commonly modeled using two components: a central concentration of luminosity (the bulge) and an outer plane structure (the disk). This simple scheme can be far from the real component mixture of the galaxy. Features such as bars, rings or bright starbursts affect dramatically the light distribution and make bulge-disk decomposition a nearly impossible task. These features are supposed to be more frequent in late Hubble type galaxies and extremely relevant in starburst galaxies, becoming dominant at high-redshifts.
Bulge-disk decomposition can be undertaken using several techniques and fitting functions. Several authors are now using the entire galaxy image to perform two dimensional fittings of the flux (see, e.g., de Jong 1996b); this technique is better for galaxies with peculiar structures such as bars or rings, which are masqueraded in the azimuthally averaged plots.
We have carried out the morphology study of the sample using
one-dimensional surface brightness profiles. These profiles
were checked visually in order to exclude from the fitting
algorithm those regions dominated by artifacts, which are
revealed through bumps and dips in the radial
profiles. Besides, the algorithm only utilizes the points with
![]() lower than the detection threshold, which was measured
as the surface brightness corresponding to the standard
deviation of the sky; the values of this threshold ranged from
24 to 26 magarcsec-2, depending on the observation
campaign. Some of the galaxies showed very irregular
morphologies and extremely perturbed profiles due to
interaction companions or starbursts; consequently, these
galaxies were excluded from this bulge-disk study.
lower than the detection threshold, which was measured
as the surface brightness corresponding to the standard
deviation of the sky; the values of this threshold ranged from
24 to 26 magarcsec-2, depending on the observation
campaign. Some of the galaxies showed very irregular
morphologies and extremely perturbed profiles due to
interaction companions or starbursts; consequently, these
galaxies were excluded from this bulge-disk study.
A great variety of fitting functions are available in the
literature. Some authors adjust exponential laws to both bulge
and disk or other more complicated functions. We have
attempted the decompositions using the empirical bulge law
established by de Vaucouleurs (1948):
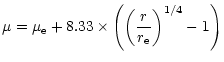 |
(1) |
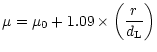 |
(2) |
During the performance of bulge-disk decomposition, special
care should be taken when dealing with the inner parts of the
galaxy profile, since these zones are affected by atmospheric
seeing. Most authors exclude from the fit the part of the
galaxy dominated by seeing (e.g., Baggett et al. 1998;
Schombert & Bothun 1987; Chatzichristou
1999). To account for this effect, we used in the
fitting procedure a seeing-convolved formula for the light
profile in the inner parts of the galaxy (Pritchet & Kline
1981). This procedure copes with the uncomfortable
r1/4 bulge law, that tends to infinity as r approaches
0. Assuming radial symmetry and a Gaussian description of the
PSF, the seeing convolved profile can be expressed as:
The main problem involved with seeing is the determination of the seeing-dominated zone of the profile, where Eq. (3) has to be used. This parameter was set free until a best fit was achieved.
The decomposition procedure followed to obtain the bulge and disk parameters is the following:
Equal weights were used for all the points during the fits. The outermost points of the profiles have larger errors due to the uncertainties in the determination of the sky, artifacts, etc. This should lead to assign greater weights to the innermost points, as some authors do in the literature (Baggett et al. 1998; Chatzichristou 1999; Hunt et al. 1999). However, in our profiles there were more points in the inner parts of the plots than in the outer ones; when weights were introduced in the fitting algorithm, wrong estimates of the parameters (the bulge parameters are the most affected ones) occurred; therefore, the equi-weighting scheme was chosen.
The method described above was tested in several artificial
galaxies. They were built with known and representative bulge
and disk parameters. We chose typical profiles for this test,
including: (a) those with well-defined bulge and disk, (b)
with a dominant disk, (c) with a dominant bulge, (d) a nearly
linear profile (fitted with a disk by our method) and (e) a
curved profile (identified as a bulge by our method). The
artificial profiles were convolved with a common seeing value
of
![]() ;
the zone where this convolution was made was
set randomly inside the typical interval of the true
fits. Standard values of noise were added to the profile,
based on real data. In Table 1 some of the input
and output bulge and disk parameters are shown. The initial
parameters seem to be well recovered by our technique; the
largest differences correspond to profiles where the disk
dominates although there is some contribution of a bulge
component (test number 2, corresponding to a late-type
spiral); these profiles were identified as an isolate disk by
our method. Discrepancies were also present when one of the
components is dominant (examples number 4 or 7, corresponding
to a late-type spiral and an early-type galaxy, respectively);
in this case, the parameters of the other component do not
contribute much to the total profile and our method of
decomposition does not recover the initial values (the errors
of the B/D ratio are specially affected and are not shown in
the result table - they are substituted by three dots -),
although this fact is irrelevant. We took special care with
these types of profile during morphological classification
based on bulge-disk decomposition.
;
the zone where this convolution was made was
set randomly inside the typical interval of the true
fits. Standard values of noise were added to the profile,
based on real data. In Table 1 some of the input
and output bulge and disk parameters are shown. The initial
parameters seem to be well recovered by our technique; the
largest differences correspond to profiles where the disk
dominates although there is some contribution of a bulge
component (test number 2, corresponding to a late-type
spiral); these profiles were identified as an isolate disk by
our method. Discrepancies were also present when one of the
components is dominant (examples number 4 or 7, corresponding
to a late-type spiral and an early-type galaxy, respectively);
in this case, the parameters of the other component do not
contribute much to the total profile and our method of
decomposition does not recover the initial values (the errors
of the B/D ratio are specially affected and are not shown in
the result table - they are substituted by three dots -),
although this fact is irrelevant. We took special care with
these types of profile during morphological classification
based on bulge-disk decomposition.
| Profile type |
|
|
|
|
|
| (1) | (2) | (3) | (4) | (5) | (6) |
| a | 19.50 | 0.90 | 21.60 | 5.50 | 0.67 |
|
|
|
|
|
|
|
| b | 26.00 | 13.80 | 21.50 | 4.60 | 0.51 |
|
|
|
|
|
|
|
| c | 23.30 | 5.30 | 21.80 | 6.90 | 0.54 |
|
|
|
|
|
|
|
| d | 31.20 | 4.60 | 18.70 | 1.30 | 0.00 |
|
|
|
|
|
|
|
| d | 24.10 | 4.40 | 19.20 | 2.40 | 0.13 |
|
|
|
|
|
|
|
| e | 20.80 | 3.40 | 21.60 | 6.80 | 1.88 |
|
|
|
|
|
1.84 |
|
| e | 21.50 | 3.50 | 22.90 | 4.90 | 6.68 |
|
|
|
|
|
|
| Results for the test of the bulge-disk decomposition procedure on seven artificial galaxies. Input parameters are in the first row and output results and their corresponding errors in the second one. Columns: (1) Profile type as explained in the text. (2) Effective surface brightness of the bulge in magarcsec-2. (3) Effective radius of the bulge in arcsec. (4) Typical surface brightness of the disk in magarcsec-2. (5) Exponential scale of the disk in arcsec. (6) Bulge-to-disk ratio. | |
One of the main problems during profile fitting is the fact
that the hypersurface in the four parameters space
(
![]() )
has many local minima. The
minimization method must be able to determine the real
absolute minimum, whose parameters must have physical
meaning. To achieve this, all the initial parameters were
varied randomly before attempting the fit; we also used
several fractional convergence tolerances in each individual
fit and boundaries on each parameter were taken in order to
avoid solutions with no physical meaning.
)
has many local minima. The
minimization method must be able to determine the real
absolute minimum, whose parameters must have physical
meaning. To achieve this, all the initial parameters were
varied randomly before attempting the fit; we also used
several fractional convergence tolerances in each individual
fit and boundaries on each parameter were taken in order to
avoid solutions with no physical meaning.
With the four parameters of the disk-bulge decomposition, the
bulge-to-disk luminosity ratio was calculated as follows:
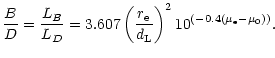 |
(4) |
![\begin{table}
\par\includegraphics[width=16.8cm,clip]{t21.ps}\end{table}](/articles/aa/full/2001/03/aah2366/img71.gif) |
We have calculated for the whole sample three concentration indices in the same way that Vitores et al. (1996a) did for the Gunn r bandpass:
where
![]() is the detection threshold (set to 24.5 magarcsec-2, mean value in our images) and
is the detection threshold (set to 24.5 magarcsec-2, mean value in our images) and
![]() a parameter
a parameter
![]() ,
appropriately chosen (it
was set to 0.3, optimal value as described in Doi et
al. 1993).
,
appropriately chosen (it
was set to 0.3, optimal value as described in Doi et
al. 1993).
All these parameters are listed in Table 3. It was not possible to obtain reliable parameters for two objects, since their images were of very bad quality.
An asymmetry parameter A was computed for each galaxy
according to the definition established by Abraham et
al. (1996). Each image was first smoothed with a
Gaussian kernel of ![]() pixel. After smoothing, it was
rotated 180
pixel. After smoothing, it was
rotated 180![]() around the center of the object (this center
was determined as the average of the inner isophotes of the
galaxy). Finally, the rotated image was subtracted from the
original. The parameter A was calculated as:
around the center of the object (this center
was determined as the average of the inner isophotes of the
galaxy). Finally, the rotated image was subtracted from the
original. The parameter A was calculated as:
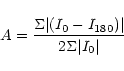 |
(8) |
Copyright ESO 2001