A&A 365, 370-391 (2001)
DOI: 10.1051/0004-6361:20000153
P. G. Pérez-González - J. Gallego - J. Zamorano - A. Gil de Paz
Send offprint request: P. G. Pérez-González
Departamento de Astrofísica, Universidad
Complutense de Madrid, Av. Complutense s/n. 28040 Madrid, Spain
e-mail: pag@astrax.fis.ucm.es; jgm@astrax.fis.ucm.es; jaz@astrax.fis.ucm.es; gil@astrax.fis.ucm.es
Received 2 August 2000 / Accepted 16 October 2000
Abstract
We present Johnson B surface photometry for the UCM Survey
galaxies. One-dimensional bulge-disk decomposition is
attempted, discussing on fitting functions and computational
procedures. The results from this decomposition, jointly with
concentration indices and an asymmetry coefficient, are
employed to study the morphological properties of these
galaxies. We also compare our results with the previous
morphological classification established using Gunn r imaging data and with other samples of galaxies. No major
statistical differences in morphology are found between red
and blue data, although some characteristics such as size and
luminosity concentration vary. We find a correlation between
luminosity and size. Several parameters are used to segregate
the objects according to their morphological type.
Key words: galaxies: photometry - galaxies: fundamental parameters - surveys-galaxies-spiral, galaxies-starburst - methods: data analysis
The Universidad Complutense de Madrid Survey (UCM Survey list I, Zamorano et al. 1994; list II, Zamorano et al. 1996; list III, Alonso et al. 1999) constitutes a representative and fairly complete sample of current star-forming galaxies in the Local Universe (Gallego 1999). Its main purposes are to identify and study new young, low metallicity galaxies and to quantify the properties of the current star formation in the Local Universe. Another key goal is also to provide a reference sample for the studies of high-redshift populations, mainly dominated by star-forming galaxies (see, e.g., Hu et al. 1998; Steidel et al. 1999).
Specific details of the UCM sample concerning spectroscopic properties were presented in Gallego et al. (1995, 1996, 1997). Photometric properties in the Gunn r band can be found in Vitores et al. (1996a, 1996b) and near-infrarred data are available in Alonso-Herrero et al. (1996) and Gil de Paz et al. (2000).
In Pérez-González et al. (2000, hereafter Paper I), integrated Johnson B photometry for the whole sample was presented. In this paper we will study the spatial concentration of the B luminosity in these objects. This will allow us to obtain information about morphology and the different structures embedded in the galaxies. The effects of the photometric band on the determination of galaxy morphology will be evaluated through the comparison of the results presented here with those achieved with the Gunn r data (Vitores et al. 1996a, 1996b).
The study of large-scale characteristics of the galaxies involves the quantitative measurement of structural parameters and light distribution. These parameters, which must describe the different components of galaxies (i.e., bulges, disks, bars), may be used to perform a morphological classification of the objects.
In this sense, we will attempt bulge-disk decomposition in one dimensional surface photometry radial profiles. Calculation of concentration indices and an asymmetry coefficient will also be done. All these data will be utilized to classify the galaxies according to their Hubble type.
The paper is structured as follows: we introduce the sample of galaxies and the Johnson B observations in Sect. 2. In Sect. 3 the method used in this surface photometry study is detailed, including the explanation of the procedures followed in the bulge-disk decomposition and in the calculation of concentration indices and the asymmetry coefficient. The results and discussion about morphology are located in Sect. 4. Finally, Sect. 5 presents the correlations found between several photometric parameters. A Hubble constant H0=50kms-1Mpc-1 and a deceleration parameter q0=0.5 have been used throughout this paper.
The UCM Survey galaxies lie at an averaged redshift of
0.026. The sample is dominated by low-excitation,
high-metallicity starburst-like galaxies (57% of the sample);
high-excitation, low-metallicity HII-like galaxies are also
present (32%) with a fraction of AGN objects (8%) (Gallego
et al. 1996). The averaged B magnitude and standard
deviation of the sample are
![]() and the mean B-r colour
and the mean B-r colour
![]() (Pérez-González et al. 2000),
corresponding to a morphological type of Sbc, according to
Fukugita et al. (1995).
(Pérez-González et al. 2000),
corresponding to a morphological type of Sbc, according to
Fukugita et al. (1995).
Along with the surface brightness profiles, the method
mentioned above also provides the ellipticity ![]() and
position angle PA of each isophote. For each image, mean
and
position angle PA of each isophote. For each image, mean
![]() and PA were calculated with the values of the
isophotes between 23 and 24 magarcsec-2 and are
listed in Table 2. Since the outer isophotes of many of
our galaxies were distorted by different structures, such as
bars, rings, spiral arms, bright HII regions, some of these
averages were corrupted, so a visual inspection of each image
was carried out in order to exclude from the averaging the
distorted zones and get more indicative values.
and PA were calculated with the values of the
isophotes between 23 and 24 magarcsec-2 and are
listed in Table 2. Since the outer isophotes of many of
our galaxies were distorted by different structures, such as
bars, rings, spiral arms, bright HII regions, some of these
averages were corrupted, so a visual inspection of each image
was carried out in order to exclude from the averaging the
distorted zones and get more indicative values.
Light distributions of spiral galaxies are commonly modeled using two components: a central concentration of luminosity (the bulge) and an outer plane structure (the disk). This simple scheme can be far from the real component mixture of the galaxy. Features such as bars, rings or bright starbursts affect dramatically the light distribution and make bulge-disk decomposition a nearly impossible task. These features are supposed to be more frequent in late Hubble type galaxies and extremely relevant in starburst galaxies, becoming dominant at high-redshifts.
Bulge-disk decomposition can be undertaken using several techniques and fitting functions. Several authors are now using the entire galaxy image to perform two dimensional fittings of the flux (see, e.g., de Jong 1996b); this technique is better for galaxies with peculiar structures such as bars or rings, which are masqueraded in the azimuthally averaged plots.
We have carried out the morphology study of the sample using
one-dimensional surface brightness profiles. These profiles
were checked visually in order to exclude from the fitting
algorithm those regions dominated by artifacts, which are
revealed through bumps and dips in the radial
profiles. Besides, the algorithm only utilizes the points with
![]() lower than the detection threshold, which was measured
as the surface brightness corresponding to the standard
deviation of the sky; the values of this threshold ranged from
24 to 26 magarcsec-2, depending on the observation
campaign. Some of the galaxies showed very irregular
morphologies and extremely perturbed profiles due to
interaction companions or starbursts; consequently, these
galaxies were excluded from this bulge-disk study.
lower than the detection threshold, which was measured
as the surface brightness corresponding to the standard
deviation of the sky; the values of this threshold ranged from
24 to 26 magarcsec-2, depending on the observation
campaign. Some of the galaxies showed very irregular
morphologies and extremely perturbed profiles due to
interaction companions or starbursts; consequently, these
galaxies were excluded from this bulge-disk study.
A great variety of fitting functions are available in the
literature. Some authors adjust exponential laws to both bulge
and disk or other more complicated functions. We have
attempted the decompositions using the empirical bulge law
established by de Vaucouleurs (1948):
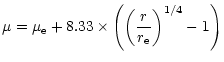 |
(1) |
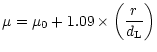 |
(2) |
During the performance of bulge-disk decomposition, special
care should be taken when dealing with the inner parts of the
galaxy profile, since these zones are affected by atmospheric
seeing. Most authors exclude from the fit the part of the
galaxy dominated by seeing (e.g., Baggett et al. 1998;
Schombert & Bothun 1987; Chatzichristou
1999). To account for this effect, we used in the
fitting procedure a seeing-convolved formula for the light
profile in the inner parts of the galaxy (Pritchet & Kline
1981). This procedure copes with the uncomfortable
r1/4 bulge law, that tends to infinity as r approaches
0. Assuming radial symmetry and a Gaussian description of the
PSF, the seeing convolved profile can be expressed as:
The main problem involved with seeing is the determination of the seeing-dominated zone of the profile, where Eq. (3) has to be used. This parameter was set free until a best fit was achieved.
The decomposition procedure followed to obtain the bulge and disk parameters is the following:
Equal weights were used for all the points during the fits. The outermost points of the profiles have larger errors due to the uncertainties in the determination of the sky, artifacts, etc. This should lead to assign greater weights to the innermost points, as some authors do in the literature (Baggett et al. 1998; Chatzichristou 1999; Hunt et al. 1999). However, in our profiles there were more points in the inner parts of the plots than in the outer ones; when weights were introduced in the fitting algorithm, wrong estimates of the parameters (the bulge parameters are the most affected ones) occurred; therefore, the equi-weighting scheme was chosen.
The method described above was tested in several artificial
galaxies. They were built with known and representative bulge
and disk parameters. We chose typical profiles for this test,
including: (a) those with well-defined bulge and disk, (b)
with a dominant disk, (c) with a dominant bulge, (d) a nearly
linear profile (fitted with a disk by our method) and (e) a
curved profile (identified as a bulge by our method). The
artificial profiles were convolved with a common seeing value
of
![]() ;
the zone where this convolution was made was
set randomly inside the typical interval of the true
fits. Standard values of noise were added to the profile,
based on real data. In Table 1 some of the input
and output bulge and disk parameters are shown. The initial
parameters seem to be well recovered by our technique; the
largest differences correspond to profiles where the disk
dominates although there is some contribution of a bulge
component (test number 2, corresponding to a late-type
spiral); these profiles were identified as an isolate disk by
our method. Discrepancies were also present when one of the
components is dominant (examples number 4 or 7, corresponding
to a late-type spiral and an early-type galaxy, respectively);
in this case, the parameters of the other component do not
contribute much to the total profile and our method of
decomposition does not recover the initial values (the errors
of the B/D ratio are specially affected and are not shown in
the result table - they are substituted by three dots -),
although this fact is irrelevant. We took special care with
these types of profile during morphological classification
based on bulge-disk decomposition.
;
the zone where this convolution was made was
set randomly inside the typical interval of the true
fits. Standard values of noise were added to the profile,
based on real data. In Table 1 some of the input
and output bulge and disk parameters are shown. The initial
parameters seem to be well recovered by our technique; the
largest differences correspond to profiles where the disk
dominates although there is some contribution of a bulge
component (test number 2, corresponding to a late-type
spiral); these profiles were identified as an isolate disk by
our method. Discrepancies were also present when one of the
components is dominant (examples number 4 or 7, corresponding
to a late-type spiral and an early-type galaxy, respectively);
in this case, the parameters of the other component do not
contribute much to the total profile and our method of
decomposition does not recover the initial values (the errors
of the B/D ratio are specially affected and are not shown in
the result table - they are substituted by three dots -),
although this fact is irrelevant. We took special care with
these types of profile during morphological classification
based on bulge-disk decomposition.
| Profile type |
|
|
|
|
|
| (1) | (2) | (3) | (4) | (5) | (6) |
| a | 19.50 | 0.90 | 21.60 | 5.50 | 0.67 |
|
|
|
|
|
|
|
| b | 26.00 | 13.80 | 21.50 | 4.60 | 0.51 |
|
|
|
|
|
|
|
| c | 23.30 | 5.30 | 21.80 | 6.90 | 0.54 |
|
|
|
|
|
|
|
| d | 31.20 | 4.60 | 18.70 | 1.30 | 0.00 |
|
|
|
|
|
|
|
| d | 24.10 | 4.40 | 19.20 | 2.40 | 0.13 |
|
|
|
|
|
|
|
| e | 20.80 | 3.40 | 21.60 | 6.80 | 1.88 |
|
|
|
|
|
1.84 |
|
| e | 21.50 | 3.50 | 22.90 | 4.90 | 6.68 |
|
|
|
|
|
|
| Results for the test of the bulge-disk decomposition procedure on seven artificial galaxies. Input parameters are in the first row and output results and their corresponding errors in the second one. Columns: (1) Profile type as explained in the text. (2) Effective surface brightness of the bulge in magarcsec-2. (3) Effective radius of the bulge in arcsec. (4) Typical surface brightness of the disk in magarcsec-2. (5) Exponential scale of the disk in arcsec. (6) Bulge-to-disk ratio. | |
One of the main problems during profile fitting is the fact
that the hypersurface in the four parameters space
(
![]() )
has many local minima. The
minimization method must be able to determine the real
absolute minimum, whose parameters must have physical
meaning. To achieve this, all the initial parameters were
varied randomly before attempting the fit; we also used
several fractional convergence tolerances in each individual
fit and boundaries on each parameter were taken in order to
avoid solutions with no physical meaning.
)
has many local minima. The
minimization method must be able to determine the real
absolute minimum, whose parameters must have physical
meaning. To achieve this, all the initial parameters were
varied randomly before attempting the fit; we also used
several fractional convergence tolerances in each individual
fit and boundaries on each parameter were taken in order to
avoid solutions with no physical meaning.
With the four parameters of the disk-bulge decomposition, the
bulge-to-disk luminosity ratio was calculated as follows:
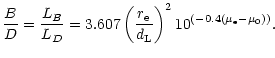 |
(4) |
![\begin{table}
\par\includegraphics[width=16.8cm,clip]{t21.ps}\end{table}](/articles/aa/full/2001/03/aah2366/img71.gif) |
We have calculated for the whole sample three concentration indices in the same way that Vitores et al. (1996a) did for the Gunn r bandpass:
where
![]() is the detection threshold (set to 24.5 magarcsec-2, mean value in our images) and
is the detection threshold (set to 24.5 magarcsec-2, mean value in our images) and
![]() a parameter
a parameter
![]() ,
appropriately chosen (it
was set to 0.3, optimal value as described in Doi et
al. 1993).
,
appropriately chosen (it
was set to 0.3, optimal value as described in Doi et
al. 1993).
All these parameters are listed in Table 3. It was not possible to obtain reliable parameters for two objects, since their images were of very bad quality.
An asymmetry parameter A was computed for each galaxy
according to the definition established by Abraham et
al. (1996). Each image was first smoothed with a
Gaussian kernel of ![]() pixel. After smoothing, it was
rotated 180
pixel. After smoothing, it was
rotated 180![]() around the center of the object (this center
was determined as the average of the inner isophotes of the
galaxy). Finally, the rotated image was subtracted from the
original. The parameter A was calculated as:
around the center of the object (this center
was determined as the average of the inner isophotes of the
galaxy). Finally, the rotated image was subtracted from the
original. The parameter A was calculated as:
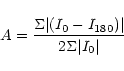 |
(8) |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f1.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg92.gif) |
Figure 1: Bulge-to-disk ratio histogram of the UCM Survey in the Johnson Bband. In this plot and hereafter, the median value and first quartiles of the data will be shown at the top. Black lines correspond to Bband results; dotted lines for the histograms and grey lines for the median and error bars will refer to the Gunn r data from now on |
| Open with DEXTER | |
In Figs. 2-5, we
show the histograms for the bulge and disk parameters
![]() ,
,
![]() ,
,
![]() and
and
![]() ,
respectively. Scales
are in kpc and surface brightnesses in
magarcsec-2. Superindex c denotes correction for
Galactic extinction and inclination (in the disk typical
surface brightness).
,
respectively. Scales
are in kpc and surface brightnesses in
magarcsec-2. Superindex c denotes correction for
Galactic extinction and inclination (in the disk typical
surface brightness).
The averaged
![]() value is
value is
![]() magarcsec-2 (
magarcsec-2 (
![]() magarcsec-2 if we only take into account the galaxies with B/D < 1.7, the
low B/D subsample hereafter), typical for a late-type spiral
(Kent 1985; Simien 1989). The typical scale of
the bulge is in average 2.7 kpc (2.2 kpc for the low-B/D subsample), with a great dispersion (
magarcsec-2 if we only take into account the galaxies with B/D < 1.7, the
low B/D subsample hereafter), typical for a late-type spiral
(Kent 1985; Simien 1989). The typical scale of
the bulge is in average 2.7 kpc (2.2 kpc for the low-B/D subsample), with a great dispersion (
![]() ), but also
common for a Sb-Sc galaxy. These values are very similar to
the ones measured in the Gunn r images, although there seems
to be a lack of small bulges in the red data.
), but also
common for a Sb-Sc galaxy. These values are very similar to
the ones measured in the Gunn r images, although there seems
to be a lack of small bulges in the red data.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f2.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg96.gif) |
Figure 2:
Histogram of the effective bulge surface brightness
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f3.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg97.gif) |
Figure 3: Histogram of the effective radius of the bulge component in kpc |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f4.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg98.gif) |
Figure 4:
Histogram of the characteristic surface brightness of the disk
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f5.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg99.gif) |
Figure 5:
Histogram of the exponential scale length of the disk
|
| Open with DEXTER | |
The histogram of the characteristic surface brightness of the
disk (Fig. 4) is dominated by galaxies with
![]() magarcsec-2, with the average in
magarcsec-2, with the average in
![]() magarcsec-2 (
magarcsec-2 (
![]() magarcsec-2 for the low-B/D subsample). The narrow
range of
magarcsec-2 for the low-B/D subsample). The narrow
range of
![]() seems to support the existence of a
universal central surface brightness for the disk, as proposed
for normal spirals by Freeman (1970) and confirmed by
other authors (i.e., Boroson 1981; Simien & de
Vaucouleurs 1986), although other works in the
literature present samples of galaxies with a wider spread in
seems to support the existence of a
universal central surface brightness for the disk, as proposed
for normal spirals by Freeman (1970) and confirmed by
other authors (i.e., Boroson 1981; Simien & de
Vaucouleurs 1986), although other works in the
literature present samples of galaxies with a wider spread in
![]() (see, for example, McGaugh et al. 1995 or
Beijersbergen et al. 1999). Our
(see, for example, McGaugh et al. 1995 or
Beijersbergen et al. 1999). Our
![]() value is
value is
![]() 0.5
0.5![]() brighter than the Freeman central surface
brightness. Therefore, the UCM sample of star-forming galaxies
appears to have brighter disks than those of normal spirals;
this fact is probably related to the higher star-formation
activity. Scale lengths are dominated by disks smaller than 4
kpc (68% of the total number of galaxies fitted), with mean
brighter than the Freeman central surface
brightness. Therefore, the UCM sample of star-forming galaxies
appears to have brighter disks than those of normal spirals;
this fact is probably related to the higher star-formation
activity. Scale lengths are dominated by disks smaller than 4
kpc (68% of the total number of galaxies fitted), with mean
![]() kpc (the same for the low-B/D subsample). This
value is higher than that found by Chitre et
al. (1999) for a sample of starburst galaxies in the
Markarian sample (
kpc (the same for the low-B/D subsample). This
value is higher than that found by Chitre et
al. (1999) for a sample of starburst galaxies in the
Markarian sample (
![]() kpc), very similar to the averaged
value found by Vennik et al. (2000) for a sample of
emission-line galaxies (
kpc), very similar to the averaged
value found by Vennik et al. (2000) for a sample of
emission-line galaxies (
![]() kpc), although they
only fit an exponential to the outer parts of the
profiles. Our value is lower than the one found by de Jong
(1996a) for normal edge-on spirals (
kpc), although they
only fit an exponential to the outer parts of the
profiles. Our value is lower than the one found by de Jong
(1996a) for normal edge-on spirals (
![]() kpc) - they argue that their selection biases against galaxies
with low surface brightness and short scale lengths are
large -. Other works (for example, Boroson 1981; Kent
1985; Bothun et al. 1989; Andredakis & Sanders
1994) agree in placing our galaxies in the zone of
short disk spirals, though one should be cautious against
comparing scale lengths from different authors due to the
subjective nature of disk parameters (Knapen & van der Kruit
1991 find discrepancies up to a factor of two in the
scale lengths calculated from several authors).
kpc) - they argue that their selection biases against galaxies
with low surface brightness and short scale lengths are
large -. Other works (for example, Boroson 1981; Kent
1985; Bothun et al. 1989; Andredakis & Sanders
1994) agree in placing our galaxies in the zone of
short disk spirals, though one should be cautious against
comparing scale lengths from different authors due to the
subjective nature of disk parameters (Knapen & van der Kruit
1991 find discrepancies up to a factor of two in the
scale lengths calculated from several authors).
All of the above values are very similar to those found by
Vitores et al. (1996b) and place the UCM sample of
galaxies in the zone of the late-type spirals, with small
bulges and not very extended disks (Freeman
1970). Three remarks are interesting when comparing
both sets of data. First, in the Gunn r decomposition a
lower bulge scale cut-off was observed (at
![]() kpc);
this is not present in the B band study. A possible
explanation is the different handling performed with the
seeing that allows the B bulges to be smaller but brighter
(seeing correction smoothes the profile; this was not the case
with the Gunn r bulge-disk decomposition, where the seeing
effect was not taken into account directly), but this does not
seem to cope with the whole difference. Second, both bands
present a preference for disk scales around 2-3 kpc (larger
disks in the blue band); very short disk scales and large ones
are less frequent. Third, the difference between the surface
brightness levels of the bulge and disk are of the order of
the mean colour, around
kpc);
this is not present in the B band study. A possible
explanation is the different handling performed with the
seeing that allows the B bulges to be smaller but brighter
(seeing correction smoothes the profile; this was not the case
with the Gunn r bulge-disk decomposition, where the seeing
effect was not taken into account directly), but this does not
seem to cope with the whole difference. Second, both bands
present a preference for disk scales around 2-3 kpc (larger
disks in the blue band); very short disk scales and large ones
are less frequent. Third, the difference between the surface
brightness levels of the bulge and disk are of the order of
the mean colour, around
![]() ,
as expected according to the
averaged B-r colour found in Fukugita et al. (1995).
,
as expected according to the
averaged B-r colour found in Fukugita et al. (1995).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f6.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg109.gif) |
Figure 6: Histogram of the diameter of the 24.5 magarcsec-2 isophote D24.5 in kpc |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f7.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg110.gif) |
Figure 7:
Histogram of effective radius |
| Open with DEXTER | |
In order to typify the size of the UCM galaxies, the
histograms representing the diameter of the 24.5 magarcsec-2 isophote D24.5 and the effective
radius ![]() (both in kpc) have been plotted in
Figs. 6 and 7. The averaged diameter of the
UCM objects is
(both in kpc) have been plotted in
Figs. 6 and 7. The averaged diameter of the
UCM objects is ![]() kpc. Comparison with the red data has
been established through the plot of the diameter of the 24 magarcsec-2 Gunn r isophote (that will be nearer
to the 24.5 blue isophote than the corresponding red one,
assuming a mean colour
kpc. Comparison with the red data has
been established through the plot of the diameter of the 24 magarcsec-2 Gunn r isophote (that will be nearer
to the 24.5 blue isophote than the corresponding red one,
assuming a mean colour
![]() ). The mean effective
radius
). The mean effective
radius ![]() is
is
![]() kpc; this reflects the high degree
of spatial luminosity concentration of our objects, most of
them being starburst nuclei with a large emission arising from
the center of the galaxy. Tentatively, UCM galaxies seem to be
more extended in the blue band than in the red one (they show
larger effective radius and diameters in B).
kpc; this reflects the high degree
of spatial luminosity concentration of our objects, most of
them being starburst nuclei with a large emission arising from
the center of the galaxy. Tentatively, UCM galaxies seem to be
more extended in the blue band than in the red one (they show
larger effective radius and diameters in B).
Finally, we plot in Figs. 8 and 9 the mean
effective and isophote 24.5 surface brightnesses in order to
characterize the whole galaxy luminosity distribution. UCM
objects show
![]() and
and
![]() (both in
magarcsec-2), common value for normal galaxies
(Doi et al. 1993). The difference between the Gunn r and the Johnson B values (
(both in
magarcsec-2), common value for normal galaxies
(Doi et al. 1993). The difference between the Gunn r and the Johnson B values (![]() 0.5
0.5![]() )
is a common B-r colour for spirals (Fukugita et al. 1995).
)
is a common B-r colour for spirals (Fukugita et al. 1995).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f8.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg116.gif) |
Figure 8:
Histogram of the mean surface brightness inside the effective aperture
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f9.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg117.gif) |
Figure 9:
Histogram of the mean surface brightness inside the 24.5 isophote
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f10.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg118.gif) |
Figure 10:
Histogram of the concentration index
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f11.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg119.gif) |
Figure 11: Histogram of the concentration index c31 of the UCM sample |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f12.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg120.gif) |
Figure 12: Histogram of the concentration index c42 of the UCM sample |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f13.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg121.gif) |
Figure 13: Histogram of the asymmetry coefficient A of the UCM sample calculated after Abraham et al. (1996) |
| Open with DEXTER | |
In the next 3 figures, labelled 10, 11 and
12, histograms of the concentration indices are
shown. Mean values are
![]() ,
,
![]() and
and
![]() .
All of them are
common values for spiral galaxies, corresponding approximately
to a Hubble type of Sb (Doi et al. 1993; Gavazzi et
al. 1990; Kent 1985; respectively for each
concentration index). These values are higher than those
measured in the Gunn r images. The B luminosity seems to
be more concentrated in the inner parts than the r one,
although galaxies are more extended.
.
All of them are
common values for spiral galaxies, corresponding approximately
to a Hubble type of Sb (Doi et al. 1993; Gavazzi et
al. 1990; Kent 1985; respectively for each
concentration index). These values are higher than those
measured in the Gunn r images. The B luminosity seems to
be more concentrated in the inner parts than the r one,
although galaxies are more extended.
Figure 13 depicts the histogram of the asymmetry
coefficient for the UCM sample. The UCM sample is dominated
by intermediately asymmetrical galaxies with mean
![]() ,
lower than the value found by Bershady et al.
(2000) for a sample of normal local galaxies; this
could be due to a difference in the calculation of A or
because their sample is composed by bright, large objects
which probably have many asymmetrical features. This is what
we should expect for spirals which have a certain axis
symmetry although they present arms, bars or HII regions that
enlarge the asymmetry coefficient. There is a lack of highly
symmetrical objects, which correspond to elliptical galaxies,
not present in our sample as it is composed by star-forming
systems.
,
lower than the value found by Bershady et al.
(2000) for a sample of normal local galaxies; this
could be due to a difference in the calculation of A or
because their sample is composed by bright, large objects
which probably have many asymmetrical features. This is what
we should expect for spirals which have a certain axis
symmetry although they present arms, bars or HII regions that
enlarge the asymmetry coefficient. There is a lack of highly
symmetrical objects, which correspond to elliptical galaxies,
not present in our sample as it is composed by star-forming
systems.
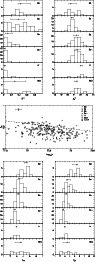 |
Figure 14:
Plots of the 5 criteria used to morphologically classify the UCM galaxies. Top panels show on the left the distribution of the B/T ratio and on the right the mean effective surface brightness (corrected for Galactic extinction) according to the final Hubble type established for each galaxy. The middle panel shows the plot found in Doi et al. (1993) of concentration index
|
| Open with DEXTER | |
All the previous results have been summarized in Table 4 for a quick look, jointly with the Gunn r statistics.
| Magnitudes | symbol | mean | st. dev. | median |
| Magnitudes | ||||
| apparent magnitude | mB | 16.1 (15.5) | 1.1 (1.0) | 16.1 (15.5) |
| absolute magnitude | MB | -19.9 (-20.5) | 1.1 (1.1) | -20.0 (-20.6) |
| B+D parameters | ||||
| bulge-to-disk ratio | B/D | 0.40 (0.82) | 0.65 (0.98) | 0.12 (0.48) |
| effective bulge surface brightness |
|
22.8 (22.6) | 2.3 (1.7) | 22.5 (22.6) |
| effective radius of the bulge | 2.7 (2.1) | 4.8 (3.3) | 1.0 (2.1) | |
| disk face-on central surface brightness |
|
21.1 (20.3) | 1.1 (1.1) | 21.2 (20.3) |
| exponential scale length of the disk |
|
3.6 (1.8) | 2.6 (1.6) | 3.0 (1.8) |
| Geometric parameters | ||||
| diameter of the 24.5 magarcsec-2 isophote | D24.5 | 22 (18) | 12 (9) | 19 (16) |
| Mean photometric parameters | ||||
| effective radius | 3.8 (3.3) | 2.3 (1.9) | 3.2 (2.7) | |
| mean effective surface brightness |
|
21.2 (20.4) | 0.9 (0.7) | 21.2 (20.4) |
| isophote 24.5 magarcsec-2 mean surface brightness |
|
22.5 (22.1) | 0.4 (0.4) | 22.5 (22.1) |
| Concentration indices | ||||
| concentration index (
|
c |
0.41 (0.48) | 0.12 (0.10) | 0.40 (0.48) |
| concentration index | c31 | 3.4 (3.2) | 1.0 (0.9) | 3.2 (3.0) |
| concentration index | c42 | 3.3 (3.1) | 0.6 (0.6) | 3.2 (3.0) |
| Asymmetry coefficient | ||||
| asymmetry coefficient | A | 0.10 (-) | 0.08 (-) | 0.09 (-) |
A morphological classification of the UCM galaxies has been carried out using 5 different criteria. These criteria were already used by Vitores et al. (1996a) with the Gunn r images, and are now applied to the Johnson B data in order to compare the results obtained with different bandpasses. Besides, some galaxies not studied in Vitores et al. (1996a) have now been classified for the first time (15% of the sample). We outline the main features of the classification criteria:
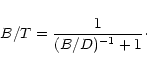 |
(9) |
In this work we utilized all these five criteria to classify the UCM galaxies in S0, Sa, Sb, Sc+ (Sc type or later) and Irr galaxies plus the BCD type (these galaxies were classified using spectroscopic confirmation available in Gallego et al. 1996); some galaxies were very distorted due to interactions and are marked in the result table as an independent class. The final Hubble type was established as that in which most criteria agree. This method is not completely objective and constitutes the main reason for the discrepancy between the classification using the Gunn r data and that performed in this paper with the Johnson B images. Table 5 presents the final classification in both bands. Figure 14 shows the histograms and plots of the 5 criteria used in the classification; in these plots the general trend of each parameter with the Hubble type can be seen, although great scatter and overlap between the different types are also present. Mean values will be shown in Table 7.
Table 6 presents the number of UCM galaxies of each type in the Gunn r and Johnson B filters. A total number of 35 galaxies have been classified differently in the two bands, although the differences are always from one type to the contiguous (except in UCM 2316+2028). Based on the Johnson B data, 65% of the whole sample is classified as Sb or later (61% based on Gunn r images). The percentage of barred galaxies is very similar in both bands (Johnson B 9%, Gunn r 8%); most of them are late-type spirals (47% are Sb galaxies and 35% Sc+). We have marked 6 clear interactions among the UCM galaxies (3%), although there are more objects with tails or structures that could have been formed during an interaction. Seyfert 1 galaxies (6 objects) are all classified as S0, except one (UCM 0003+1955) that is very bright and could not be classified; Sy 2 galaxies have been classified as Sa (1 object), Sb (3 objects) and Sc+ (3 objects). These results are consistent with the ones found in the literature (see, for example, Hunt & Malkan 1999).
| UCM name | MpT(B) | MpT (r) | UCM name | MpT(B) | MpT (r) | UCM name | MpT(B) | MpT (r) |
| (1) | (2) | (3) | (1) | (2) | (3) | (1) | (2) | (3) |
| 0000+2140 | INTER | -- | 0141+2220 | Sa | Sb | 1314+2827 | Sa | Sa |
| 0003+2200 | Sc+ | Sc+ | 0142+2137 | SBb | SBb | 1320+2727 | Sb | Sb |
| 0003+2215 | Sc+ | -- | 0144+2519 | SBc+ | SBc+(r) | 1324+2926 | BCD | BCD |
| 0003+1955 | -- | -- | 0147+2309 | Sa | Sa | 1324+2651 | INTER | -- |
| 0005+1802 | Sb | -- | 0148+2124 | BCD | BCD | 1331+2900 | BCD | BCD |
| 0006+2332 | Sb | -- | 0150+2032 | Sc+ | Sc+ | 1428+2727 | Irr | Sc+ |
| 0013+1942 | Sc+ | Sc+ | 0156+2410 | Sb | Sc+ | 1429+2645 | Sb | Sc+ |
| 0014+1829 | Sa | Sa | 0157+2413 | Sc+ | Sc+ | 1430+2947 | S0 | S0 |
| 0014+1748 | SBb | SBb | 0157+2102 | Sb | Sb | 1431+2854 | Sb | Sb |
| 0015+2212 | Sa | Sa | 0159+2354 | Sb | Sa | 1431+2702 | Sa | Sb |
| 0017+1942 | Sc+ | Sc+ | 0159+2326 | Sc+ | Sc+ | 1431+2947 | BCD | BCD |
| 0017+2148 | Sa | -- | 1246+2727 | Irr | -- | 1431+2814 | Sb | Sa |
| 0018+2216 | Sb | Sb | 1247+2701 | Sc+ | Sc+ | 1432+2645 | SBb | SBb |
| 0018+2218 | Sb | -- | 1248+2912 | SBb | -- | 1440+2521S | Sb | Sb |
| 0019+2201 | Sb | Sc+ | 1253+2756 | Sa | Sa | 1440+2511 | Sb | Sb |
| 0022+2049 | Sb | Sb | 1254+2741 | Sb | Sb | 1440+2521N | Sb | Sa |
| 0023+1908 | Sc+ | -- | 1254+2802 | Sc+ | Sc+ | 1442+2845 | Sb | Sb |
| 0034+2119 | SBc+ | -- | 1255+2819 | Sb | Sb | 1443+2714 | Sa | Sa |
| 0037+2226 | SBc+ | -- | 1255+3125 | Sa | Sa | 1443+2844 | SBc+ | SBc+ |
| 0038+2259 | Sb | Sa | 1255+2734 | Sc+ | Irr | 1443+2548 | Sc+ | Sc+ |
| 0039+0054 | Sc+ | -- | 1256+2717 | S0 | -- | 1444+2923 | S0 | S0 |
| 0040+0257 | Sb | Sc+ | 1256+2732 | INTER | -- | 1452+2754 | Sb | Sb |
| 0040+2312 | Sc+ | -- | 1256+2701 | Sc+ | Irr | 1506+1922 | Sb | Sb |
| 0040+0220 | Sc+ | Sb | 1256+2910 | Sb | Sb | 1513+2012 | Sa | S0 |
| 0040-0023 | Sc+ | -- | 1256+2823 | Sb | Sb | 1537+2506N | SBb | SBb |
| 0041+0134 | Sc+ | -- | 1256+2754 | Sa | Sa | 1537+2506S | SBa | SBa |
| 0043+0245 | Sc+ | -- | 1256+2722 | Sc+ | Sc+ | 1557+1423 | Sb | Sb |
| 0043-0159 | Sc+ | -- | 1257+2808 | Sb | Sa | 1612+1308 | BCD | BCD |
| 0044+2246 | Sb | Sb | 1258+2754 | Sb | Sb | 1646+2725 | Sc+ | Sc+ |
| 0045+2206 | INTER | 1259+2934 | Sb | Sb | 1647+2950 | Sc+ | Sc+ | |
| 0047+2051 | Sc+ | Sc+ | 1259+3011 | Sa | Sa | 1647+2729 | Sb | Sb |
| 0047-0213 | S0 | Sa | 1259+2755 | Sa | Sa | 1647+2727 | Sb | Sa |
| 0047+2413 | Sa | Sa | 1300+2907 | Sa | Sb | 1648+2855 | Sa | Sa |
| 0047+2414 | Sc+ | -- | 1301+2904 | Sb | Sb | 1653+2644 | INTER | -- |
| 0049-0006 | BCD | BCD | 1302+2853 | Sb | Sa | 1654+2812 | Sc+ | Sc+ |
| 0049+0017 | Sb | Sc+ | 1302+3032 | Sa | -- | 1655+2755 | Sc+ | Sb |
| 0049-0045 | Sb | -- | 1303+2908 | Irr | Irr | 1656+2744 | Sa | Sa |
| 0050+0005 | Sa | Sa | 1304+2808 | Sb | Sa | 1657+2901 | Sb | Sc+ |
| 0050+2114 | Sa | Sa | 1304+2830 | BCD | BCD | 1659+2928 | SB0 | SB0 |
| 0051+2430 | Sa | -- | 1304+2907 | Irr | Irr | 1701+3131 | S0 | S0 |
| 0054-0133 | Sb | -- | 1304+2818 | Sc+ | Sc+ | 2238+2308 | Sa(r) | Sa |
| 0054+2337 | Sc+ | -- | 1306+2938 | SBb | Sb | 2239+1959 | S0 | S0 |
| 0056+0044 | Irr | Irr | 1306+3111 | Sc+ | Sc+ | 2249+2149 | Sb | Sa |
| 0056+0043 | Sb | Sc+ | 1307+2910 | SBb | SBb | 2250+2427 | Sa | Sa |
| 0119+2156 | Sb | Sc+ | 1308+2958 | Sc+ | Sc+ | 2251+2352 | Sc+ | Sc+ |
| 0121+2137 | Sc+ | Sc+ | 1308+2950 | SBb | SBb | 2253+2219 | Sa | Sa |
| 0129+2109 | SBc+ | -- | 1310+3027 | Sb | Sa | 2255+1930S | Sb | Sb |
| 0134+2257 | Sb | -- | 1312+3040 | Sa | Sa | 2255+1930N | Sb | Sb |
| 0135+2242 | S0 | S0 | 1312+2954 | Sc+ | Sc+ | 2255+1926 | Sb | Sc+ |
| 0138+2216 | Sc+ | -- | 1313+2938 | Sa | Sa | 2255+1654 | Sc+ | Sc+ |
| UCM name | MpT(B) | MpT (r) | UCM name | MpT(B) | MpT (r) | UCM name | MpT(B) | MpT (r) |
| (1) | (2) | (3) | (1) | (2) | (3) | (1) | (2) | (3) |
| 2256+2001 | Sc+ | Sc+ | 2313+1841 | Sb | Sb | 2325+2318 | INTER | -- |
| 2257+2438 | S0 | S0 | 2313+2517 | Sa | -- | 2325+2208 | SBc+ | SBc+ |
| 2257+1606 | S0 | -- | 2315+1923 | Sb | Sa | 2326+2435 | Sb | Sa |
| 2258+1920 | Sc+ | Sc+ | 2316+2457 | SBa | SBa | 2327+2515N | Sb | Sb |
| 2300+2015 | Sb | Sb | 2316+2459 | Sc+ | Sc+ | 2327+2515S | S0 | S0 |
| 2302+2053W | Sb | Sb | 2316+2028 | Sa | Sc+ | 2329+2427 | Sb | Sb |
| 2302+2053E | Sb | Sb | 2317+2356 | Sa | Sa | 2329+2500 | S0(r) | S0(r) |
| 2303+1856 | Sa | Sa | 2319+2234 | Sb | Sc+ | 2329+2512 | Sa | Sa |
| 2303+1702 | Sc+ | Sc+ | 2319+2243 | S0 | S0 | 2331+2214 | Sb | Sb |
| 2304+1640 | BCD | BCD | 2320+2428 | Sa | Sa | 2333+2248 | Sc+ | Sc+ |
| 2304+1621 | Sa | Sa | 2321+2149 | Sc+ | Sc+ | 2333+2359 | S0a | S0 |
| 2307+1947 | Sb | Sb | 2321+2506 | Sc+ | Sc+ | 2348+2407 | Sa | Sa |
| 2310+1800 | Sb | Sc+ | 2322+2218 | Sc+ | Sc+ | 2351+2321 | Sb | Sb |
| 2312+2204 | Sa | -- | 2324+2448 | Sb | Sc+ |
| (1) UCM name. (2) Morphological type established using 5 different criteria based on luminosity concentration and bulge-disk decomposition applied to the Johnson B images. (3) Morphological type established using 5 different criteria based on luminosity concentration and bulge-disk decomposition applied to the Gunn r images. |
There is a tight correlation between MB and D24.5. A
least-square fit to our data leads to:
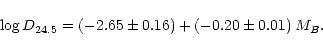 |
(10) |
In Fig. 16 a general trend between the concentration index c31, the absolute B magnitude MB and the morphological type is apparent. Early-type galaxies show medium-high magnitudes and high concentration indices. If we move downwards to the zone of low concentration index we find spirals, from Sa to late-type. Finally, BCDs have c31 values typical for spirals but are fainter than normal galaxies.
Figure 17 shows the segregation in morphological type
in a
![]() versus A diagram. In this plot and the next,
median values for the different morphological types are
plotted with a black dot; ellipse semi-axes are the
versus A diagram. In this plot and the next,
median values for the different morphological types are
plotted with a black dot; ellipse semi-axes are the ![]() of each parameter. There is a clear trend from left to right
in decreasing Hubble type. S0 galaxies are placed in the high
symmetry-high
of each parameter. There is a clear trend from left to right
in decreasing Hubble type. S0 galaxies are placed in the high
symmetry-high
![]() zone. BCDs also appear as highly
symmetrical objects. On the other hand, irregulars are shown
as highly asymmetrical objects in the top-left zone of the
plot and interactive systems are located among the most
asymmetrical galaxies. A trend can be also remarked in the
spiral sequence: early-type galaxies are more symmetrical than
late-type ones (due to the presence of more HII regions, for
example).
zone. BCDs also appear as highly
symmetrical objects. On the other hand, irregulars are shown
as highly asymmetrical objects in the top-left zone of the
plot and interactive systems are located among the most
asymmetrical galaxies. A trend can be also remarked in the
spiral sequence: early-type galaxies are more symmetrical than
late-type ones (due to the presence of more HII regions, for
example).
Figure 14 showed that there is a clear correlation between the concentration indices and Hubble type. This trend is also observed with the asymmetry coefficient. Table 7 presents the mean values of the bulge-to-disk ratio, mean effective surface brightness, concentration indices and asymmetry coefficient of each Hubble type. The statistics of A have been split into barred and non-barred objects; barred galaxies are more asymmetrical than non-barred ones.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f15.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg134.gif) |
Figure 15: Relationship between the size of the UCM galaxies represented by the diameter of the 24.5 isophote D24.5 and the total B luminosity of the object MB. A least-square fit to the data is also plotted |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f16.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg135.gif) |
Figure 16: Concentration index c31 versus absolute magnitude MB. Different symbols stand for distinct morphological types |
| Open with DEXTER | |
Figure 18 depicts the absolute B magnitude of the UCM
objects versus the mean effective surface
brightness. Early-type galaxies appear as bright, high surface
brightness objects. Late-type spirals have lower
![]() ,
although no significant difference in MB is present. BCDs
are clearly segregated due to their faintness. Irregulars and
interactive systems show also a distinctive surface
brightness.
,
although no significant difference in MB is present. BCDs
are clearly segregated due to their faintness. Irregulars and
interactive systems show also a distinctive surface
brightness.
We have carried out a morphological study of the UCM Survey galaxies based on Johnson B imaging. This paper, jointly with Paper I (Pérez-González et al. 2000), have analyzed the main features of the UCM sample concerning integrated and surface photometry in the B bandpass.
Paper I presented integrated apparent and absolute B luminosities as well as isophote 24 magarcsec-2 magnitudes. Effective radii and B-r colours were also calculated in this first release. In the present paper we have outlined the main results concerning bulge-disk decomposition values, ellipticities, position angles, concentration indices, mean photometric radii and surface brightnesses and asymmetry coefficients.
| Filter | S0 | Sa | Sb | Sc+ | Irr | BCD | Int | Total |
| B | 14 | 38 | 69 | 50 | 5 | 8 | 6 | 190 |
| 7% | 20% | 36% | 26% | 3% | 4% | 3% | ||
| r | 12 | 41 | 43 | 46 | 5 | 8 | - | 155 |
| 7% | 27% | 28% | 30% | 3% | 5% |
Number of galaxies and percentage of the UCM galaxies according to their Hubble type in the Johnson B and the Gunn r bandpasses.
| Parameter | S0 | Sa | Sb | Sc+ | Irr | BCD | Int |
| B/T | 0.53 | 0.39 | 0.16 | 0.04 | 0.07 | 0.41 | 0.30 |
|
|
20.6 | 20.7 | 21.3 | 21.5 | 21.8 | 21.5 | 20.1 |
| c31 | 5.3 | 3.8 | 3.3 | 2.7 | 2.9 | 3.5 | 5.0 |
| c42 | 4.3 | 3.5 | 3.2 | 2.7 | 2.8 | 3.4 | 4.0 |
|
|
0.58 | 0.50 | 0.40 | 0.29 | 0.33 | 0.35 | 0.57 |
| A | 0.09 | 0.10 | 0.10 | 0.11 | 0.21 | 0.06 | 0.20 |
| (barred) | 0.06 | 0.15 | 0.11 | 0.12 | - | - | - |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f17.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg136.gif) |
Figure 17:
Concentration index
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{H2366f18.ps}\end{figure}](/articles/aa/full/2001/03/aah2366/Timg137.gif) |
Figure 18: Mean effective surface brightness versus absolute magnitude. Ellipses show the median and standard deviation of each parameter for the different morphological types |
| Open with DEXTER | |
All the above information has been used to perform the morphological classification of the UCM galaxies. The sample is dominated by late Hubble type objects (65% being Sb or later). We have not found a great difference between this classification and the results achieved with the Gunn r data (Vitores et al. 1996a, 1996b). Our galaxies are characterized by shorter disks than those of normal spirals. Besides, they seem to be objects with a high luminosity concentration. A preliminary comparison between the characteristics of the sample in the red and blue bandpasses, yields to the result that emission-line galaxies have a higher concentration of blue light than red light in the inner parts of the objects; on the contrary, they also seem to be more extended in B than in r.
Finally, a size-luminosity correlation has been outlined. We have also presented several plots where a morphological segregation is patent. These plots involve information about luminosity, concentration of light and asymmetry.
In next papers we will face a most exhaustive comparison between bands, including colour gradients and a stellar population study. Likewise, we will likened our sample to high-redshifts surveys searching for clues to their nature and galaxy evolution.
Acknowledgements
This paper is based on observations obtained at the German-Spanish Astronomical Centre, Calar Alto, Spain, operated by the Max-Planck Institute für Astronomie (MPIE), Heidelberg, jointly with the Spanish Commission for Astronomy. It is also partly based on observations made with the Jacobus Kapteyn Telescope operated on the island of La Palma by the Royal Greenwich Observatory in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias and the 1.52 m telescope of the EOCA/OAN Observatory. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. We have also use of the LEDA database, http://www-obs.univ-lyon1.fr. This research was also supported by the Spanish Programa Sectorial de Promoción General del Conocimiento under grants PB96-0610 and PB96-0645. P. G. Pérez-González acknowledges the receipt of a "Formación de Profesorado Universitario'' fellowship from the Spanish "Ministerio de Educación y Cultura''.We would like to thank C. E. García-Dabó and S. Pascual for their help during part of the observing runs and stimulating conversations. We thank M. N. Estévez for carefully reading the manuscript and making some useful remarks. We are also grateful to Dr. E. Emsellem for his helpful comments and suggestions.