A&A 365, 588-597 (2001)
DOI: 10.1051/0004-6361:20000478
Speckle spectro-polarimetry of solar magnetic structures
M. Koschinsky1 - F. Kneer1 - J. Hirzberger1,2
Send offprint request: M. Koschinsky,
1 - Universitäts-Sternwarte Göttingen, Geismarlandstr. 11, 37083 Göttingen, Germany
2 - Institut für Geophysik, Astrophysik und Meteorologie, Universtät Graz, Universitätsplatz 5, 8010 Graz, Austria
Received 19 July 2000 / Accepted 23 October 2000
Abstract
We present speckle observations of small-scale magnetic structures on the Sun. They were obtained with the "Göttingen'' Fabry-Perot interferometer (FPI) in the Vacuum Tower Telescope at the Observatorio del Teide, Tenerife, from quiet and active regions close to disc center. A Stokes V polarimeter was added to the FPI to measure V profiles in the FeI 6302.5 Å line. The setup allows image reconstruction with speckle methods. The achieved spatial resolution in the magnetograms is
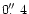 -
-
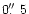 .
We describe the observational technique and the data reduction. The results from small-scale magnetic flux elements in a very quiet region, in an active region with pores and abnormal granulation, and in a sunspot with its surroundings are discussed. In the quiet Sun, granular dynamics dominate the time evolution of the magnetic elements. Flux occurs in both bright intergranular points and in dark intergranular spaces. Likewise, with the present spatial resolution, no preference of magnetic flux in abnormal granulation in an active region can be found. Flux occurs in both bright (abnormal) small-scale granules and in the darker spaces in between them. The small sunspot studied has very little magnetic flux in its ambient quiet regions, especially no strong, conspicuous concentrations of returned flux, i.e. of flux with polarity opposite to that in the sunspot.
.
We describe the observational technique and the data reduction. The results from small-scale magnetic flux elements in a very quiet region, in an active region with pores and abnormal granulation, and in a sunspot with its surroundings are discussed. In the quiet Sun, granular dynamics dominate the time evolution of the magnetic elements. Flux occurs in both bright intergranular points and in dark intergranular spaces. Likewise, with the present spatial resolution, no preference of magnetic flux in abnormal granulation in an active region can be found. Flux occurs in both bright (abnormal) small-scale granules and in the darker spaces in between them. The small sunspot studied has very little magnetic flux in its ambient quiet regions, especially no strong, conspicuous concentrations of returned flux, i.e. of flux with polarity opposite to that in the sunspot.
Key words: Sun: faculae, plages - Sun: magnetic fields - techniques: image processing - techniques: polarimetric
Author for correspondance: mkosch@uni-sw.gwdg.de
Magnetic fields are important constituents of the solar atmosphere on all scales. Their interaction with the solar plasma causes the magnetic heating of the chromosphere and the corona and is responsible for all processes of activity from the low photosphere to the solar wind. The investigation of magnetic fields on the Sun is thus a main topic of solar research. Here, we shall concentrate on small-scale structures.
The existence of small-scale magnetic flux tubes is known since more
than three decades. E.g. Beckers & Schröter (1968) have
found "magnetic knots'' in the neighbourhood of sunspots as well as in quiet
regions of the Sun. From the line ratio method, i.e. the use of two
spectral lines which differ in their properties only by their Landé factor,
Stenflo (1973) could conclude on the existence of kilo-Gauss
fields with a small fill factor in the observed area. The size of the
magnetic structures should be at the lower spatial resolution limit of
today's telescopes or even smaller (see also the monograph by Stenflo 1994). Keller & von der Lühe (1992) could show from speckle
polarimetry that small magnetic structures of
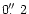 size, or smaller,
do indeed exist. A study on weak, small flux structures in quiet regions
was undertaken by Stolpe & Kneer (2000) with
spectro-polarimetry and with an image scanner of the Gregory Coudé
Telescope at the Observatorio del Teide/Tenerife. Likewise, Sigwarth et al. (1999) used an image scanning device and polarimeter, the
Advanced Stokes Polarimeter at Sacramento Peak Observatory/New Mexico/USA, to
study the properties of small magnetic elements. (The reader is
referred to this work of Sigwarth et al. for much recent literature.) We also mention the efforts by, among others, Steiner et al. (1998) and Grossmann-Doerth et al. (1998) to model with numerical simulations the
temporal evolution of small-scale magnetic elements.
size, or smaller,
do indeed exist. A study on weak, small flux structures in quiet regions
was undertaken by Stolpe & Kneer (2000) with
spectro-polarimetry and with an image scanner of the Gregory Coudé
Telescope at the Observatorio del Teide/Tenerife. Likewise, Sigwarth et al. (1999) used an image scanning device and polarimeter, the
Advanced Stokes Polarimeter at Sacramento Peak Observatory/New Mexico/USA, to
study the properties of small magnetic elements. (The reader is
referred to this work of Sigwarth et al. for much recent literature.) We also mention the efforts by, among others, Steiner et al. (1998) and Grossmann-Doerth et al. (1998) to model with numerical simulations the
temporal evolution of small-scale magnetic elements.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{h2334_f1.eps}\end{figure}](/articles/aa/full/2001/03/aah2334/Timg15.gif) |
Figure 1:
Optical scheme of the two-dimensional spectrometer. F:
primary focus of the VTT; F :
secondary focus where the field
stop is located;
BS: beam splitter cube; VP: Stokes V polarimeter; L: lenses; IF:
interference filters; NF: neutral filter; CCD1 and CCD2: slow-scan CCDs at
the foci of the broad-band and the narrow-band channels, respectively;
FPI1 and FPI2: Fabry-Perot interferometers :
secondary focus where the field
stop is located;
BS: beam splitter cube; VP: Stokes V polarimeter; L: lenses; IF:
interference filters; NF: neutral filter; CCD1 and CCD2: slow-scan CCDs at
the foci of the broad-band and the narrow-band channels, respectively;
FPI1 and FPI2: Fabry-Perot interferometers |
| Open with DEXTER |
Ground-based observations of solar finestructure suffer unavoidably
from seeing effects. Recently, many efforts are undertaken
worldwide to implement Adaptive Optics in solar telescopes to correct
for seeing effects directly during the observations, and recent
successes demonstrate its future feasibility. Meanwhile, image
restoration techniques, to be applied after the observations,
are well established. As
mentioned, Keller & von der Lühe (1992) have used broad-band speckle
polarimetry to measure the circularly polarized light components
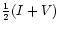 and
and
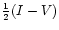 at one spectral position
in a magnetically
sensitive line. This method cannot study the wavelength dependence of
the Stokes vector across a spectral line and draw conclusions on the underlying physical processes from profile parameters such as, e.g., asymmetries,
Doppler shifts, intensities, and saturation of the Stokes V profiles.
at one spectral position
in a magnetically
sensitive line. This method cannot study the wavelength dependence of
the Stokes vector across a spectral line and draw conclusions on the underlying physical processes from profile parameters such as, e.g., asymmetries,
Doppler shifts, intensities, and saturation of the Stokes V profiles.
To exploit the information contained in the profiles of magnetically sensitive spectral lines, we used our "Göttingen''
two-dimensional Fabry-Perot spectrometer with a Stokes V polarimeter.
The spectrometer
scans along wavelength and gives narrow-band images
across spectral
lines. This allows to apply image reconstruction techniques and to
substantially reduce the deteriorations by seeing (see e.g. Krieg et al. 1998, 1999).
The following Sect. 2 describes the observational technique, Sect. 3 the observations for this contribution. Section 4 outlines the data
analysis. In Sect. 5 we present and discuss several results from quiet
and active regions. In this work, we wish to describe, along specific results, the progress in small-scale polarimetry. A detailed discussion of the rich information must be deferred to a forthcoming contribution. Section 6 concludes the paper.
The "Göttingen'' Fabry-Perot interferometer (FPI) device is described
in Bendlin et al. (1992), Bendlin (1993), and Bendlin & Volkmer
(1995). It is mounted in the Vacuum Tower Telescope (VTT) at the
Observatorio del Teide/Tenerife. Here, we outline shortly the principle
and the improvements which have been applied in the last years. A throughout
description is given by Koschinsky (2001).
Figure 1 shows the scheme of the spectrometer, without the rather complex
computer control and data aquisition systems. The Sun is imaged in the
prime focus F of the VTT. From there the image is transferred to a field
stop at the secondary focus F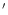 at the entrance of the
spectrometer. In front of F
at the entrance of the
spectrometer. In front of F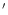 a beam splitter cube BS takes out
approximately 5% of the light to a further focus corresponding to
F
a beam splitter cube BS takes out
approximately 5% of the light to a further focus corresponding to
F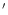 .
There broad-band images are taken with a CCD (CCD1) through
an interference filter IF1 of 50-100 Å FWHM, centered at the appropriate
wavelength, and a neutral filter NF. Directly after the field stop in the
spectrometer a Stokes V polarimeter VP was mounted for the present
purposes. It was already used in earlier investigations by Volkmer
(1995) and Volkmer et al. (1995). It consists of a
.
There broad-band images are taken with a CCD (CCD1) through
an interference filter IF1 of 50-100 Å FWHM, centered at the appropriate
wavelength, and a neutral filter NF. Directly after the field stop in the
spectrometer a Stokes V polarimeter VP was mounted for the present
purposes. It was already used in earlier investigations by Volkmer
(1995) and Volkmer et al. (1995). It consists of a
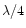 retarder plate and
two crossed calcites giving a separation of the left and right circularly
polarized beams
retarder plate and
two crossed calcites giving a separation of the left and right circularly
polarized beams
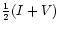 and
and
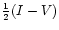 of 4.1 mm, adapted
to the size of the CCDs. The polarimeter is followed by an
appropriate interference filter IF2 of 3-10 Å FWHM for order
sorting of the transmission peaks of the FPIs. F
of 4.1 mm, adapted
to the size of the CCDs. The polarimeter is followed by an
appropriate interference filter IF2 of 3-10 Å FWHM for order
sorting of the transmission peaks of the FPIs. F is re-imaged 1:1 onto CCD2 which takes the narrow-band images. Both
(slow-scan) CCDs have Thompson TH 7863 FT chips with
is re-imaged 1:1 onto CCD2 which takes the narrow-band images. Both
(slow-scan) CCDs have Thompson TH 7863 FT chips with
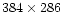 pixels. The image scale is
pixels. The image scale is
 /pixel and the field of view - with
the polarimeter - is
/pixel and the field of view - with
the polarimeter - is
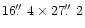 .
.
The two FPIs are mounted in the
parallel beam near the image of the telescope's entrance pupil. This
mounting is different from the telecentric mounting used in TESOS,
another FPI spectrometer at the VTT (Kentischer et al. 1998) and in the
IPM at THEMIS (Cavallini 1998). It has certain advantages such as
no "orange peel'' pattern in the image which arises from tiny flatness
errors of the etalons. FPI1 is a Queensgate etalon ET 100 with 50 mm
aperture, 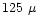 spacing (
spacing (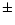 few
few 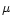 for wavelength
scanning), and a finesse
for wavelength
scanning), and a finesse
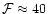 .
FPI1 has replaced the
originally mounted universal birefringent filter (UBF) for further order
sorting. This replacement has increased the transmission of the
spectrometer by a factor of 5, at least. The narrow-band FPI2 is from
Burleigh Instruments Ltd. and has an aperture of 35 mm, variable spacing
from few
.
FPI1 has replaced the
originally mounted universal birefringent filter (UBF) for further order
sorting. This replacement has increased the transmission of the
spectrometer by a factor of 5, at least. The narrow-band FPI2 is from
Burleigh Instruments Ltd. and has an aperture of 35 mm, variable spacing
from few 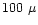 to several mm, and a finesse
to several mm, and a finesse
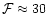 .
To
avoid reflexes on CCD2 arising from reflections between the two FPIs,
FPI1 is slightly inclined against the optical axis. This reduces
somewhat its finesse to
.
To
avoid reflexes on CCD2 arising from reflections between the two FPIs,
FPI1 is slightly inclined against the optical axis. This reduces
somewhat its finesse to
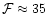 .
The wavelength scanning
is done by computer controlled changes of the spacings of the etalons
by means of Piezo elements.
.
The wavelength scanning
is done by computer controlled changes of the spacings of the etalons
by means of Piezo elements.
The broad- and narrow-band images are taken strictly simultaneously,
which is important for image restoration (see below). The increase of the
overall transmission of the spectrometer in replacing the UBF by FPI1
was a substantial improvement: (1) it allowed to dismount the formerly
installed image amplifier in front of CCD2 and thus to increase the
detective quantum efficiency; (2) the exposure times for the narrow-band
images could be decreased and are now approximately 10-20 ms for observation without polarimeter and
20-30 ms with the V polarimeter. This allows the application of speckle
interferometry for image reconstruction.
Further equipment (not shown in Fig. 1, but see Koschinsky 2001)
concerns a laser beam for finesse adjustment and a beam with continuum
light from a halogen lamp.
The observations for the present investigation were obtained in October
1999 under very good seeing conditions (Fried parameter
r0 = 13-14 cm) with the above "Göttingen'' two-dimensional spectrometer,
including the V polarimeter, in the VTT. Several regions were
selected. On October 22, 1999, a short time series of wavelength scans of the FeI 6302.5 Å line (Landé factor g = 2.5) were taken from a very quiet region
close to disc center for purposes of calibration and tests of the
software for data analysis. Yet
these observations show some interesting features on small-scale
magnetic elements and on the limitations of the present setup (Sect. 5.1).
On the same October 22 a bipolar active region (NOAA 8738) at
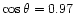 was observed with several wavelength scans, also in
FeI 6302.5 Å. It contained some pores and abnormal granulation
as well as a small sunspot. A
FWHM of 66 mÅ of the spectrometer was chosen in order to reduce
noise by collecting "many'' photons. The exposure time was 20 ms. We
thus, by using a rather broad spectral profile compared to high
resolution spectrographs and by applying short exposure times, sacrifice
on spectral purity, on purpose. We aim at high spatial resolution
via image restoration. For this one has to make compromises between
exposure time, spectral resolution, and noise.
was observed with several wavelength scans, also in
FeI 6302.5 Å. It contained some pores and abnormal granulation
as well as a small sunspot. A
FWHM of 66 mÅ of the spectrometer was chosen in order to reduce
noise by collecting "many'' photons. The exposure time was 20 ms. We
thus, by using a rather broad spectral profile compared to high
resolution spectrographs and by applying short exposure times, sacrifice
on spectral purity, on purpose. We aim at high spatial resolution
via image restoration. For this one has to make compromises between
exposure time, spectral resolution, and noise.
A spacing of 27 mÅ between adjacent wavelength positions was chosen
for the spectral scans. With the narrow-band channel 5 images
at each of 28 wavelength positions were taken
which gives a wavelength coverage of approximately 730 mÅ.
One wavelength scan takes 39 s, and further 35 s are
needed for the storage of the image data onto hard discs. Thus, the
separation of two scans amounts to 74 s. These time scales are of
concern for fast small-scale processes on the Sun. We will improve the
apparatus with substantially faster CCDs and computers.
Further scans had to be taken for the data reduction: dark frames, flat
field scans with defocussed telescope, and scans with the continuum source. The defocussing of the telescope for the flat fields causes a change of illumination of the spectrometer and of the detectors. We found this effect always negligible, e.g. by comparing average line profiles from the quiet Sun and from the flat fields. The defocussed images contain also the information on the noise, which is needed for the data analysis. For many other observations, flat fields are taken with moving pointing of the telescope during exposure. The difficulty and the drawback with this method are that in a rapid sequence with exposure times of 20-30 ms the image motion (from the varying pointing) must be fast such that structures on the Sun are fully smoothed.
Figure 2 demonstrates the
change of Stokes I and V profiles when an Airy FPI transmission
function of 66 mÅ FWHM is applied. The solar FeI 6302.5 Å line
was taken from the Fourier Transform Spectrometer Atlas by Brault & Neckel
(1987). In Fig. 2b, a magnetic flux density of 0.1 T (
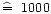 Gauss), parallel to the line of
sight and independent of height was assumed to separate the observed
Gauss), parallel to the line of
sight and independent of height was assumed to separate the observed 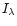 profile into the circularly polarized components
profile into the circularly polarized components
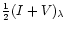 and
and
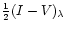 .
This procedure assumes also that the
magnetic and non-magnetic atmospheres possess equal thermal structure. Various fill factors for the magnetic relative to the non-magnetic area were applied.
.
This procedure assumes also that the
magnetic and non-magnetic atmospheres possess equal thermal structure. Various fill factors for the magnetic relative to the non-magnetic area were applied.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{h2334_f2.eps}\end{figure}](/articles/aa/full/2001/03/aah2334/Timg32.gif) |
Figure 2:
Effects of broadening on Stokes I and V profiles of FeI 6302.5 Å by
convolution with a FPI Airy function of 66 mÅ FWHM. a) Stokes I profiles after convolution (solid) and the original profile (dashed) taken from the FTS atlas by Brault & Neckel (1987); dotted: Airy's FPI function. b) Stokes V profiles after convolution (solid) and without convolution (dashed). A constant
magnetic field of 0.1 T along the line of sight and various area fill
factors are adopted. The fill factors are, with decreasing amplitude of V: 1.0, 0.5, 0.2, 0.1, 0.05 (see text). c) Upper two lines: dependence of the V amplitude on the fill factor for the convolved V (solid) and original (dashed) profiles; lower lines: dependence of the separation of the centers of gravity of the
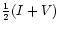 and
and
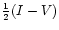 profiles on the area fill factor for the convolved (solid) and original (dashed) profiles. The dotted line gives the expected separation of the centers of gravity
profiles on the area fill factor for the convolved (solid) and original (dashed) profiles. The dotted line gives the expected separation of the centers of gravity |
| Open with DEXTER |
It is seen that the I and V profiles change
noticeably. Comparison with magnetic flux tube models or with numerical
simulations of flux tube dynamics should apply the same convolution with
Airy's function to the predicted profiles. In Fig. 2c we show the dependence of the Stokes V amplitude (left ordinate, upper straight lines) and of the separation of the circularly polarized line profiles (right ordinate, lower curves) on the area fill factor. The amplitudes and line separations are directly proportional to the magnetic flux (or fill factor) in the resolution element (weak field limit). While the amplitudes depend on the spectral resolution, the line separations do not. At low area fill factors, in the range of 0.01-0.02, the separations amount to 1-2 mÅ (
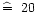 Gauss average field strength) and their determination becomes inaccurate. In these cases, the errors compared to the expected values amount to 30%.
Gauss average field strength) and their determination becomes inaccurate. In these cases, the errors compared to the expected values amount to 30%.
First, certain data processings were applied, some of which are of special
need for FPI spectro-polarimetric data.
Average dark frames were
subtracted. Fluctuations of the sky transparency are obtained from the broad-band images. The gain tables of the CCDs were obtained from the flat field
scans. They depend, for the narrow-band channel, somewhat on the
wavelength position of the FPI transmission curves. Thus each wavelength
setting needs its own gain table for CCD2. Yet, this dependence on the wavelength setting is small,
such that flat field frames from two adjacent wavelength positions could be averaged. This reduces (photon) noise introduced by the flat fielding. To keep the wavelength
dependence of the solar spectrum during the correction processes,
each gain table of CCD2 was normalized
to an average value of 1.
Since FPI1 is inclined against the optical axis
the transmission of the spectrometer varies across the field of view. In
addition, the two FPIs do not scan the wavelength exactly in parallel
which changes slightly this dependence of transmission with wavelength.
Both the
dependence of transmission over the field of view and its variation with
wavelength are retrieved from the flat field scans.
Next, one must be aware that the wavelengths with the highest spectrometer transmission vary also across the field of view, due to the mounting of the FPIs in the parallel beam.
Image motion was taken out by correlating the broad-band images. This
reduces the fields of view by few arcseconds, depending on seeing. The
same corrections as determined from the broad-band images apply to the
narrow-band images. Small displacements of the narrow-band against
broad-band images due to not exact alignment and thermal drifts are
measured again from correlations between narrow-band images in the
continuum spectral range and the broad-band images.
Furthermore, for image reconstruction with speckle methods, i.e. removal
of seeing effects within isoplanatic patches, the frames were divided
into partly overlapping sub-fields of
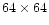 pixel each
(
pixel each
(
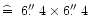 ). At the end, these sub-fields were
recombined again to full images.
). At the end, these sub-fields were
recombined again to full images.
Broad-band images. While the two-dimensional spectrometer scans
over a Fraunhofer line, CCD1
takes 140 images in integrated light. These are used for image
restoration with well established speckle methods (e.g. de Boer et al. 1992; de Boer 1996; Wilken et al. 1997). The spectral ratio method
(von der Lühe 1984) gives estimates of the amplitude correction factors
(in Fourier space). During this processing, the seeing parameter
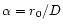 (
(
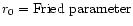 ,
,
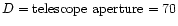 cm) is calculated. The (Fourier) phases are
reliably obtained with the speckle masking method (Weigelt 1977; Weigelt
& Wirnitzer 1983; Lohmann et al. 1983).
cm) is calculated. The (Fourier) phases are
reliably obtained with the speckle masking method (Weigelt 1977; Weigelt
& Wirnitzer 1983; Lohmann et al. 1983).
Narrow-band images. The spectrometric images, i.e. sub-images, are
reconstructed following Keller & von der Lühe (1992) and as
described by Krieg et al. (1999). In principle, given the reconstructed,
"true'' broad-band object
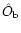 (in Fourier space, with
(in Fourier space, with
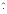 denoting estimates) and the broad-band images
denoting estimates) and the broad-band images
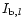 observed at time l, one can retrieve the instantaneous
optical transfer functions Sl, which hold also for the simultaneously
taken narrow-band images
observed at time l, one can retrieve the instantaneous
optical transfer functions Sl, which hold also for the simultaneously
taken narrow-band images
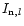 .
After re-ordering and
summation over the 5 images taken at each wavelength position (see Krieg
et al. 1999) one obtains an estimate of the narrow-band object
.
After re-ordering and
summation over the 5 images taken at each wavelength position (see Krieg
et al. 1999) one obtains an estimate of the narrow-band object
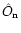
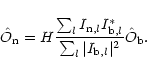 |
(1) |
Here, a (real) noise filter H is introduced. We have tested optimum
filters (Brault & White 1971; Löfdahl 1996; Krieg et al. 1999). With
some experience we found it easier and without noticeable change
of the results to implement filters which are equal to 1 up to a certain
horizontal
wavenumber (independent of azimuth) and then drop quickly to 0. In the
results of the small-scale polarimetry presented below, this cutoff
wavenumber corresponds to typically
 ,
which is thus the spatial
resolution limit of our reconstructed small-band images near line
center.
,
which is thus the spatial
resolution limit of our reconstructed small-band images near line
center.
Certainly, the quality of the reconstructed images, i.e. the spatial
resolution, depends on the instantaneous seeing conditions prevailing
during the exposures at each wavelength position.
To eliminate such effects one could apply the filters from the
worst seeing conditions to all spectral positions. This, however would
suppress the information obtained from the observations with the best
seeing. A better choice is to smooth the 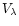 profiles along
wavelength if needed.
profiles along
wavelength if needed.
For polarimetry one has to consider instrumental
polarization. We are mainly interested in the Stokes V component.
After passing through the telescope and the spectro-polarimeter it is
changed to
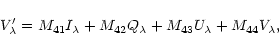 |
(2) |
where M41 ... M44 are the elements in the last row of the
Mueller matrix.
For small-scale magnetic elements the Stokes Q and U components are
small, at the 10-3 level of the continuum intensity 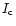 ,
even close to the solar limb. This is due to the partly cancellation of linearly polarized signals from expanding flux tubes and to the squared dependence of the Q and U profiles on the magnetic flux density (cf. Landi degl'Innocenti 1992; Sigwarth et al. 1999). We thus can
neglect the
,
even close to the solar limb. This is due to the partly cancellation of linearly polarized signals from expanding flux tubes and to the squared dependence of the Q and U profiles on the magnetic flux density (cf. Landi degl'Innocenti 1992; Sigwarth et al. 1999). We thus can
neglect the
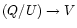 cross talk. (This is no longer correct,
of course, when performing polarimetry of regions with strong magnetic
fields perpendicular to the line of sight and with large fill factors
as for instance in sunspot penumbrae.)
cross talk. (This is no longer correct,
of course, when performing polarimetry of regions with strong magnetic
fields perpendicular to the line of sight and with large fill factors
as for instance in sunspot penumbrae.)
After Capitani et al. (1989)
the element M44 is typically of the order 0.9 for coelostat
systems as the VTT. We do not correct for it, since we have no better measure.
It remains to determine the
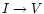 crosstalk, i.e. the element
M41. There should be no true solar V component from non-magnetic areas on the Sun. Then, Eq. (2) reads
crosstalk, i.e. the element
M41. There should be no true solar V component from non-magnetic areas on the Sun. Then, Eq. (2) reads
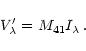 |
(3) |
M41 can be determined from the flat field and the quiet Sun observations. Taking averages over
sub-areas of
 we obtained offsets in the range
we obtained offsets in the range
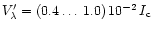 and a "noise'' amplitude of
and a "noise'' amplitude of
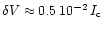 (peak to peak). Both the offsets and the noise pattern persisted
from scan to scan but varied from area to area within the field of view. Presumably, they result
from the difference of the optical path, including the different detector areas, of the two
circularly polarized beams in the apparatus and from interferences. We can reduce these effects by
subtracting the offsets and the fixed pattern noise, similarly as in the second-order flat fielding
introduced by Sánchez Almeida & Martínez Pillet (1994). We then arrive at a lower
detection limit, dominated by photon noise, for the V amplitude of
(peak to peak). Both the offsets and the noise pattern persisted
from scan to scan but varied from area to area within the field of view. Presumably, they result
from the difference of the optical path, including the different detector areas, of the two
circularly polarized beams in the apparatus and from interferences. We can reduce these effects by
subtracting the offsets and the fixed pattern noise, similarly as in the second-order flat fielding
introduced by Sánchez Almeida & Martínez Pillet (1994). We then arrive at a lower
detection limit, dominated by photon noise, for the V amplitude of
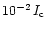 in a
in a
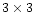 pixel area (
pixel area (
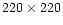 km2). This smoothing over
km2). This smoothing over 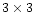 pixels lowers the noise, but still preserves the spatial resolution. The Stokes V profiles presented below have been treated with such an area averaging.
pixels lowers the noise, but still preserves the spatial resolution. The Stokes V profiles presented below have been treated with such an area averaging.
On the other hand, we found no wavelength dependent
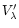 ,
expected from Eq. (3), above the detection limit of approximately 210
,
expected from Eq. (3), above the detection limit of approximately 210
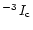 in the spatially averaged quiet Sun observations (outside obvious magnetic structures). We conclude that the
in the spatially averaged quiet Sun observations (outside obvious magnetic structures). We conclude that the
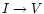 cross talk M41 is below this value in the present observations.
cross talk M41 is below this value in the present observations.
The
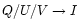 cross talk can be of concern again when dealing with
strong magnetic fields and large filling factors as in sunspots. The
spectral lines
cross talk can be of concern again when dealing with
strong magnetic fields and large filling factors as in sunspots. The
spectral lines 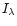 can then become contaminated with asymmetry caused by the crosstalk. Below, we shall therefore refrain from discussing such
asymmetries observed in sunspots.
can then become contaminated with asymmetry caused by the crosstalk. Below, we shall therefore refrain from discussing such
asymmetries observed in sunspots.
As mentioned, the mounting of the FPIs in the parallel beams has the
following effect: the wavelength for which the FPIs have highest transmittance depends on
the position within the field of view. This means that
the solar spectrum is shifted
from one point to the other. Since our V polarimeter
separates the beams for
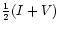 and
and
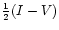 they can be considered as stemming from two separated
fields of view. In consequence, the spectra of corresponding
image points in
they can be considered as stemming from two separated
fields of view. In consequence, the spectra of corresponding
image points in
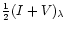 and
and
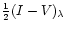 are shifted against each other. This has been
corrected for by carefully re-shifting the spectra by means of the profiles in the flat field and quiet Sun observations.
are shifted against each other. This has been
corrected for by carefully re-shifting the spectra by means of the profiles in the flat field and quiet Sun observations.
Observed Stokes I and V profiles can be used for comparison with model
predictions, i.e. from numerical simulations of flux tube structure and
dynamics. And one may apply inversion techniques to obtain physical
parameters such as the runs of temperature, velocity, and magnetic field
strength with height in the atmosphere (e.g. Bellot Rubio et al. 1997). We shall present
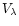 measurements which may be used for such purposes in cases where the
signal to noise ratio is sufficiently large. (The corresponding
measurements which may be used for such purposes in cases where the
signal to noise ratio is sufficiently large. (The corresponding
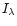 profiles will not be shown.)
profiles will not be shown.)
A fast method to obtain maps of magnetic flux, that is of its component
along the line of sight, is the center of gravity (COG) method by Semel (1967)
and Rees & Semel (1979). This measures simply the wavelength
separation of the COGs of the
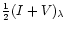 and
and
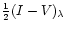 profiles. Obviously and as seen from Fig. 2c, the separation is not dependent on the spectral resolution. In addition, the COG method gives fluxes in each pixel for the average performance of image reconstruction, i.e. for the average seeing conditions during a spectral scan. The best images from one scan bring the wavelength separation toward the direction of best spatial resolution. There is thus no need to reduce, by filtering, all images to the lowest resolution.
profiles. Obviously and as seen from Fig. 2c, the separation is not dependent on the spectral resolution. In addition, the COG method gives fluxes in each pixel for the average performance of image reconstruction, i.e. for the average seeing conditions during a spectral scan. The best images from one scan bring the wavelength separation toward the direction of best spatial resolution. There is thus no need to reduce, by filtering, all images to the lowest resolution.
The data analysis has given us a wealth of information on small-scale magnetic structures of the Sun. Here, we can present only part of the results. A broader discussion of, e.g., profile asymmetries and relationships between intensity, velocity, and magnetic fields at high spatial resolution is prepared for a forthcoming contribution.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2334_f3.eps}\end{figure}](/articles/aa/full/2001/03/aah2334/Timg63.gif) |
Figure 3:
Maps of a quiet Sun disc center area: speckle reconstructed integrated light image (upper left), magnetic flux along the line of sight from COG (upper right), continuum image from the narrow-band channel (lower left), and line center intensity (lower right). The tickmarks are at 1
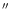 distance, the field of view is
distance, the field of view is
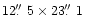 .
The bar at the bottom gives the scaling of the magnetic flux per pixel ( .
The bar at the bottom gives the scaling of the magnetic flux per pixel (
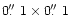 )
in 108 Wb for the magnetic field map )
in 108 Wb for the magnetic field map |
| Open with DEXTER |
Figure 3 shows four maps obtained from the quiet Sun observations: the speckle reconstructed integrated light image, the line of sight component of the magnetic flux in the
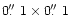 pixels, the continuum intensity, and the line center intensity. The rms fluctuation of the magnetic flux is at approximately
pixels, the continuum intensity, and the line center intensity. The rms fluctuation of the magnetic flux is at approximately
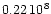 Wb. We thus adopt a detection limit of
Wb. We thus adopt a detection limit of
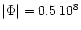 Wb (
Wb (
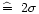 ).
).
The areas marked by rectangles in Fig. 3 contain the most significant magnetic flux. We notice a bow of magnetic features from the area close to the right border towards upper left. It is also seen in the line center image and remained visible during the 5 min of this short time series. Presumably, it represents weak network. Apart from that, the field of view appears very non-active, as is also seen in the magnetogram of this day from NSO at Kitt Peak. The strongest flux in the field of view corresponds to a magnetic fieldstrength, averaged over one pixel, of
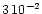 T.
T.
The maximum of the flux (per pixel) of the magnetic element at the lower left corner in Fig. 3 strengthened during the 5 min sequence by a factor of 1.5. Its counterpart in the integrated light image is a photospheric bright point which was "compressed'' by nearby growing granules.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2334_f4.eps}\end{figure}](/articles/aa/full/2001/03/aah2334/Timg68.gif) |
Figure 4:
Magnetic map (left), speckle reconstructed integrated light image (middle), and velocity from the COG method (right) of the magnetic flux region at the lower left corner of Fig. 3; bar at bottom: velocity in kms-1 with bright indicating upward flow. Tickmarks are at
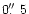 distance
distance |
| Open with DEXTER |
We present in Fig. 4 again the magnetogram and the speckle reconstructed image of this sub-area and in addition its velocity map. The latter was obtained from the COG of the Stokes I profile. We adopted the COG position averaged over the total field of view as zero velocity. The velocities contain both granular and oscillatory motions. Future analysis should disentangle the two contributions via filtering of time sequences longer than the one used here (cf. Espagnet et al. 1995). The magnetic structure is elongated and consists possibly of two flux tubes, or two bundles of flux tubes. It is located at a strong intergranular downdraft. In fact, the fastest downflow of 1.2 kms-1 in this sub-field occured close to the magnetic structure, but not exactly in it. From the position of the zero crossing of the V profile, which gives the velocity of the magnetized plasma, one obtains a downflow of 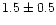 kms-1. Possibly, one witnesses here in a snapshot a convective intensification of flux tubes as, e.g., demonstrated with numerical simulations by Steiner et al. (1998) and Grossmann-Doerth et al. (1998).
kms-1. Possibly, one witnesses here in a snapshot a convective intensification of flux tubes as, e.g., demonstrated with numerical simulations by Steiner et al. (1998) and Grossmann-Doerth et al. (1998).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2334_f5.eps}\end{figure}](/articles/aa/full/2001/03/aah2334/Timg70.gif) |
Figure 5:
Time series (top to bottom, separation of 74 s) of magnetic flux evolution (region at right border of Fig. 3). Left column: speckle reconstructed images; right column: flux maps; bar at bottom: magnetic flux (in one pixel), unit 108 Wb. The images are overlaid with the Stokes V profiles centered at the pixels from which they were obtained. The length of the vertical bar at the lower right corner indicates a V amplitude of
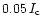 .
Tickmarks are at .
Tickmarks are at
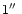 distance. See the text for the rectangles
distance. See the text for the rectangles |
| Open with DEXTER |
The flux region at the right border of Fig. 3 shows substructure, and we use this area for
the discussion of temporal evolution. Figure 5 shows a short time sequence of it together
with its "non-magnetic'' surroundings. The maps are separated in time by 74 s, start is at the top.
The left images are the speckle reconstructions from integrated light, the right images represent the magnetic flux. The images are overlaid with Stokes V profiles centered at the pixels from which they were obtained.
The maximum V amplitudes amount to
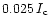 .
By means of Fig. 2, we can approximately correct for the limited spectral resolution of the FPI setup and estimate maximum amplitudes of
.
By means of Fig. 2, we can approximately correct for the limited spectral resolution of the FPI setup and estimate maximum amplitudes of
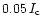 .
.
We must interpret Fig. 5 with caution, since the spatial resolution of the magnetograms is
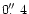 ,
at best, and their noise poses a lower detection limit for the flux. The positive magnetic flux (magnetic field towards observer) is mostly located above small-scale "white light'' features. These are the three bright "points'' to the right of the exploding granule and evolving from the second time step on. However, positive flux is also detected above areas which are inconspicuous in white light or even clearly darker than average. This is seen e.g. from the V profiles marked by rectangles in the third time step. Just to the left of these two positions, at the border of the exploding granule and just at the detection limit, negative flux becomes visible. Possibly, convective re-shuffling of magnetic flux is at work. The whole evolution appears dominated by the dynamics of the exploding granule. A sort of bow of the magnetic structure develops by the intrusion of the granular material. The latter itself does not carry detectable flux. Roudier et al. (1994) have drawn similar conclusions from the temporal evolution of photospheric bright points.
,
at best, and their noise poses a lower detection limit for the flux. The positive magnetic flux (magnetic field towards observer) is mostly located above small-scale "white light'' features. These are the three bright "points'' to the right of the exploding granule and evolving from the second time step on. However, positive flux is also detected above areas which are inconspicuous in white light or even clearly darker than average. This is seen e.g. from the V profiles marked by rectangles in the third time step. Just to the left of these two positions, at the border of the exploding granule and just at the detection limit, negative flux becomes visible. Possibly, convective re-shuffling of magnetic flux is at work. The whole evolution appears dominated by the dynamics of the exploding granule. A sort of bow of the magnetic structure develops by the intrusion of the granular material. The latter itself does not carry detectable flux. Roudier et al. (1994) have drawn similar conclusions from the temporal evolution of photospheric bright points.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2334_f6.eps}\end{figure}](/articles/aa/full/2001/03/aah2334/Timg72.gif) |
Figure 6:
Speckle reconstructed image (left) and magnetic flux map (right, from COG) of active region near disc center. The images are overlaid with the Stokes V profiles centered at the pixels from which they were obtained. The length of the vertical bar at the lower right corner indicates a V amplitude of
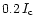 .
Tickmarks are at .
Tickmarks are at
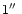 distance. Bar at bottom: scaling of magnetic flux in 108 Wb
distance. Bar at bottom: scaling of magnetic flux in 108 Wb |
| Open with DEXTER |
We present in Fig. 6 a speckle reconstructed, integrated light image (left) together with its magnetogram of an active region with small, not fully developed pores. The images are again overlaid with V profiles, which are well defined this time. The maximum measured V amplitudes outside pores amount to
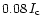 .
We may again correct this value for the limited spectral resolution by means of Fig. 2. One thus obtains V amplitudes of
.
We may again correct this value for the limited spectral resolution by means of Fig. 2. One thus obtains V amplitudes of
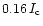 .
.
Most of the magnetic flux in this area is negative, i.e. the field is directed away from the
observer. The maximum field strength from the COG method is found in the pore located in the central
upper part of the field of view and amounts to 0.08 T. This is substantially smaller than the value
of approximately 0.2 T given by e.g. Sütterlin (1996, Fig. 23, 1998). The reason
for the low value found here comes likely from the scattered light produced in the Earth's
atmosphere and in the telescope. We took not special care of it for these observations. False light
from outside the pores introduces an unshifted profile and thus can largely reduce the field strength measured with the COG method. We tentatively adopt that, with a fill factor of 1 and for strong fields of 0.2T the amplitude of the Stokes V profile of the Fe I 6302 line is saturated and that therefore the separation of the V extrema gives the field strength. (A Zeeman splitting of the I profile is hardly detectable and not reliable in view of the spectral resolution of 66 mÅ.) We then arrive at a maximum of 0.21 T in the largest pore in the upper part of Fig. 6. We have tested such a magnetic field measurement using 0.2 T, instead of 0.1 T, in the model for Fig. 2. The separation of the V extrema returns the field strength within 2.5% accuracy. The convolution of the V profiles with the profile of the spectrometer (Airy's function) adds an error of only 3%. A further justification for this measurement of field strength comes from model calculations by Amer & Kneer (1993) of the FeI 6173.3 Å line which has the same Landé factor g=2.5 as the 6302.5 Å line, although it is somewhat weaker than the latter. At magnetic field strengths 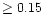 T the extrema of the V profile do not increase any more with field strength, but separate.
T the extrema of the V profile do not increase any more with field strength, but separate.
Much of the field of view of Fig. 6 is covered with abnormal granulation which contains magnetic flux. It is now important to know whether the flux is located in the bright abnormal granulation features or in the darker spaces in between them. Likewise, the relation between magnetic flux and line center intensity, i.e. essentially the temperature structure in medium to high photospheric layers, is of interest. Figure 7, then, gives scatter plots of magnetic flux vs. granulation intensity and vs. line center intensity. For these, only areas of abnormal granulation were selected, data from pores are not included.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2334_f7.eps}\par\end{figure}](/articles/aa/full/2001/03/aah2334/Timg76.gif) |
Figure 7:
a) Magnetic flux (in each pixel) vs. white light intensity in selected areas with anomalous granulation (SP on the abscissa indicates speckle reconstructed image). b) Magnetic flux vs. line center intensity (LC on the abscissa). The intensities are relative to the mean intensities of the selected areas. The lower detection limit for flux is 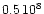 Wb Wb |
| Open with DEXTER |
Firstly, we notice that there exists no detectable correlation between magnetic flux and abnormal granular intensity, although the magnetogram in Fig. 6 does show structure. There may be several reasons for this negative finding:
(1) The magnetic field is located in both bright "granules'' and darker spaces in between the granules and is essentially equally strong in both features;
(2) The magnetic field is located preferentially in either bright or dark features but has merged at atmospheric heights from which the signal for the magnetic flux is obtained;
(3) Close inspection of some areas with small bright points shows that they contain substantially less magnetic flux than expected for abnormal granulation. Thus, small-scale bright features, or conglomorates of them, in white light pictures do often, but not necessarily indicate magnetic flux. It was already noted by Keller & von der Lühe (1992) that small-scale magnetic flux elements do not correlate with small-scale brightenings in integrated light;
(4) The spatial resolution is not yet sufficient to find exactly the locations of magnetic flux.
Observations with still higher spatial resolution and with magnetically sensitive lines formed at low atmospheric heights are needed to come to a clearer conclusion.
Secondly, the line center intensities are well correlated with the magnetic flux, as known from many investigations. The stronger the flux the higher is the temperature in high atmospheric layers.
A word on the V asymmetry appears appropriate. Close inspection of the V profiles in Fig. 6 shows that these are sometimes strongly asymmetric and occasionally exhibit two lobes on one side of the wavelength axis. This is already seen in the magnetic flux features of the quiet Sun, Fig. 5.
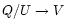 cross talk is unlikely to produce such abnormal V profiles, although we cannot fully exclude it. The amplitudes of the Q and U profiles are usually found to be an order of magnitude smaller than those of the V profiles, especially near disc center (e.g. Sigwarth et al. 1999; Sánchez Almeida & Lites 2000).
cross talk is unlikely to produce such abnormal V profiles, although we cannot fully exclude it. The amplitudes of the Q and U profiles are usually found to be an order of magnitude smaller than those of the V profiles, especially near disc center (e.g. Sigwarth et al. 1999; Sánchez Almeida & Lites 2000).
Sánchez Almeida (1997) and Sánchez Almeida & Lites (2000) have interpreted the abnormal V profiles with the MISMA hypothesis (MIcro-Structured Magnetic Atmosphere). MISMAs contain flows and bundles of optically thin flux tubes with 10 km diameter, or less, and with both polarities. Their substructure cannot be resolved, in principle. Grossmann-Doerth et al. (2000) can explain the anomalies by special flow situations in magnetic canopies. However, the V amplitudes observed in these latter works are well below
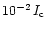 ,
below our detection limit. Possibly, the high spatial resolution achieved here allows to isolate such dynamic flux tubes, or bundles of flux tubes, with large fill factors. Yet further work on the analysis of the present data (classification, smoothing, averaging, determination of cross talk) is needed. This will be pursued in a further investigation.
,
below our detection limit. Possibly, the high spatial resolution achieved here allows to isolate such dynamic flux tubes, or bundles of flux tubes, with large fill factors. Yet further work on the analysis of the present data (classification, smoothing, averaging, determination of cross talk) is needed. This will be pursued in a further investigation.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2334_f8.eps}\end{figure}](/articles/aa/full/2001/03/aah2334/Timg78.gif) |
Figure 8:
Speckle reconstructed image (upper left), magnetic flux map (upper right, from COG), continuum intensity (lower left), and line center intensity (lower right) of small sunspot near disc center. Tickmarks are at
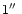 distance. Bar at bottom: scaling of magnetic flux in 108 Wb. The intensities of the sunspot were enhanced to show its internal small-scale structure
distance. Bar at bottom: scaling of magnetic flux in 108 Wb. The intensities of the sunspot were enhanced to show its internal small-scale structure |
| Open with DEXTER |
Figure 8, finally, gives images from the small sunspot in the same active region as the pores and the abnormal granulation above. We show the speckle reconstruction of the integrated light observations, the magnetogram, the continuum image and the line center image. The maximum magnetic field strength in the umbra was 0.09 T, again a very low value for sunspots. And again, the reason for this low value is in the false light which reduces the field strength as measured with the COG method. As above, for the field strength in the pores, we obtain from the separation of the extrema of the V profile a maximum field strength of 0.233 T.
It is noteworthy that the surrounding of the sunspot contains flux only at very few places, with preferentially the same polarity. Most of the ambient quiet area does not posses detectable flux. The granular pattern is normal, and the line center image does not exhibit brightenings, in most parts, to be related with magnetic fields. Returned magnetic flux elements, i.e. with polarity opposite to that of the sunspot, are not conspicuous.
Most of the outer penumbral magnetic filaments in the magnetogram are related to dark filaments. There, the flux component towards the observer seems to be larger than in the bright penumbral points. But, upon close inspection, one can also find few bright filaments with enhanced flux.
However, as mentioned above (4.3, instrumental polarization), the measurements of polarized light from a penumbra have to be interpreted with caution due to the possible
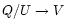 instrumental cross talk. A further discussion of the sunspot results has thus to await measurements of this cross talk. Also, the velocities in the penumbral filaments will be of interest. Such an investigation of the penumbra dynamics at small scales, as in our data, is beyond the scope of this paper, and we refer to the review by Wiehr (1999, see also many references therein).
instrumental cross talk. A further discussion of the sunspot results has thus to await measurements of this cross talk. Also, the velocities in the penumbral filaments will be of interest. Such an investigation of the penumbra dynamics at small scales, as in our data, is beyond the scope of this paper, and we refer to the review by Wiehr (1999, see also many references therein).
We have demonstrated the high potential of two-dimensional
spectro-polarimetry in combination with methods of speckle
reconstruction. The computational load for image reduction is large, however not unsurmountable with today's and future computer facilities. With these methods of observation and data treatment, it was possible to arrive at high spatial resolution and to enter the realms of small-scale magnetic field dynamics by direct observation. The results presented above can be compared with polarized radiation expected from numerical models, of course only after adequate smoothing of the simulated data to the spatial and spectral resolution of the observations.
The work and the results above represent a further step towards the physics of solar finestructure. The next steps will be to observe longer time sequences with higher spatial and spectral resolution. The instrumental improvements for this purpose (faster computers, narrower bandwidths) are underway. Modern detector technology will also allow faster cadences of exposures during wavelength scans, thus will allow to take more images per wavelength scan and to reduce the photon noise.
To arrive at substantially higher spatial and spectral
resolution than achieved here telescopes with larger aperture than the VTT are
needed. There exist well developed plans for a 1.5 m Gregorian solar telescope at the Observatorio del Teide. This will possibly give, at higher spatial resolution than the VTT, larger fill factors, thus stronger signals at small scales. A Gregorian telescope is also much less sensitive to instrumental cross talk of the components of the Stokes vector than a coelostat system as the VTT. Further improvement could come from a polarimetric device like the Zurich Imaging Polarimeter (ZIMPOL, Keller et al. 1992). This has the advantage of using exactly the same optical paths and detector areas for the various polarized light beams, which leads to high polarimetric accuracy. Finally, in the near future, one will take profit from Adaptive Optics. Even then, image reconstruction will still be necessary since Adaptive Optics should not be expected to fully correct for the seeing effects in large fields of view. But the reconstruction process will certainly be much eased with high quality input data.
Acknowledgements
Financial support by the Deutsche Forschungsgemeinschaft through grants KN 152/19-1,2 is gratefully acknowledged. J. H. acknowledges the financial support of the Austrian Fonds zur Förderung der wissenschafltlichen Forschung (Erwin-Schrödinger-Stipendium J-1802PHY)
and thanks for the hospitality and the support of the Universitäts-Sternwarte Göttingen.
The Vacuum Tower Telescope at the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias/Tenerife is operated by the Kiepenheuer-Institut für Sonnenphysik in Freiburg, Germany.
-
Amer, M. A., & Kneer, F. 1993, A&A, 273, 304
In the text
NASA ADS
-
Beckers, J. M., & Schröter, E. H. 1968, Solar Phys., 4, 142
In the text
NASA ADS
-
Bellot Rubio, L. R., Ruiz Cobo, B., & Collados, M. 1997, ApJ, 478, L45
In the text
NASA ADS
-
Bendlin, C. 1993, Ph.D. Thesis, Göttingen University
In the text
-
Bendlin, C., & Volkmer, R. 1995, A&AS, 112, 371
In the text
NASA ADS
-
Bendlin, C., Volkmer, R., & Kneer, F. 1992, A&A, 257, 817
In the text
NASA ADS
-
Brault, J. W., & Neckel, H. 1987, Spectral Atlas of Solar Absolute
Disk-averaged and Disk-center Intensities from 3290 to 12510 Å, unpublished
In the text
-
Brault, J. W., & White, R. O. 1971, A&A, 13, 169
In the text
NASA ADS
-
Capitani, C., Cavallini, F., Ceppatelli, G., et al. 1989, Solar Phys., 120, 173
In the text
NASA ADS
-
Cavallini, F. 1998, A&AS, 128, 589
In the text
NASA ADS
-
de Boer, C. R. 1996, A&AS, 120, 195
In the text
NASA ADS
-
de Boer, C. R., Kneer, F., & Nesis, A. 1992, A&A, 257, L4
In the text
NASA ADS
-
Espagnet, O., Muller, R., Roudier, Th., Mein, N., & Mein, P. 1995, A&AS, 109, 79
In the text
NASA ADS
-
Grossmann-Doerth, U., Schüssler, M., & Steiner, O. 1998, A&A, 337, 928
In the text
NASA ADS
-
Grossmann-Doerth, U., Schüssler, M., Sigwarth, M., & Steiner, O. 2000, A&A, 357, 351
In the text
NASA ADS
-
Keller, C. U., & von der Lühe, O. 1992, A&A, 261, 321
In the text
NASA ADS
-
Keller, C. U., Aebersold, F., Egger, U., et al. 1992, Zürich Imaging Stokes Polarimeter ZIMPOL I - Design Review, LEST Technical Report Series No. 53, ed. O. Engvold, & Ø. Hauge, Oslo University
In the text
-
Kentischer, T., Schmidt, W., Sigwarth, M., & von Uexküll, M. 1998, A&A, 340, 569
In the text
NASA ADS
-
Koschinsky, M. 2001, Ph.D. Thesis, Göttingen University
In the text
-
Krieg, J., Kneer, F., Koschinsky, M., Ritter, C., & Starck, J.-L. 1998, Ground-based observation
with high spatial and spectral resolution, in A Crossroads for European Solar and Heliospheric
Physics, ed. R. H. Harris, F. Moreno Insertis, & E. Priest, ESA SP-417, 317
In the text
-
Krieg, J., Wunnenberg, M., Kneer, F., Koschinsky, M., & Ritter, C. 1999, A&A,
343, 983
In the text
NASA ADS
-
Landi degl'Innocenti, E. 1992, in Magnetic Field Measurements, ed. F. Sánchez, M. Collados, & M. Vázquez, Solar observations: Techniques and interpretation (Cambridge: Cambridge University Press), 73
In the text
-
Löfdahl, M. G. 1996, Ph.D. Thesis, Stockholm University
In the text
-
Lohmann, A. W., Weigelt, G. P., & Wirnitzer, B. 1983, Appl. Opt., 22, 4028
In the text
NASA ADS
-
Rees, D. E., & Semel, M. D. 1979, A&A, 74, 1
In the text
NASA ADS
-
Roudier, T., Espagnet, O., Muller, R., & Vigneaux, J. 1994, A&A, 287, 982
In the text
NASA ADS
-
Sánchez Almeida, J. 1997, ApJ, 491, 993
In the text
NASA ADS
-
Sánchez Almeida, J., & Lites, B. W. 2000, ApJ, 532, 1215
In the text
NASA ADS
-
Sánchez Almeida, J., & Martínez Pillet, V. 1994, ApJ, 424, 1014
In the text
NASA ADS
-
Semel, M. D. 1967, Ann. Astrophys., 30, 513
In the text
NASA ADS
-
Sigwarth, M., Balasubramaniam, K. S., Knölker, M., & Schmidt, W. 1999, ApJ,
349, 941
In the text
-
Steiner, O., Grossmann-Doerth, U., Knölker, M., & Schüssler, M. 1998, ApJ, 495, 468
In the text
NASA ADS
-
Stenflo, J. O. 1973, Solar Phys., 32, 41
In the text
NASA ADS
-
Stenflo, J. O. 1994, Solar Magnetic Fields - Polarized Radiation Diagnostics (Kluwer Academic Publ.), 273
In the text
-
Stolpe, F., & Kneer, F. 2000, A&A, 353, 1094
In the text
NASA ADS
-
Sütterlin, P. 1996, Ph.D. Thesis, Freiburg University
In the text
-
Sütterlin, P. 1998, A&A, 333, 305
In the text
NASA ADS
-
Volkmer, R. 1995, Ph.D. Thesis, Göttingen University
In the text
-
Volkmer, R., Kneer, F., & Bendlin, C. 1995, A&A, 304, L1
In the text
NASA ADS
-
von der Lühe, O. 1984, J. Opt. Soc. Am., A1, 510
In the text
-
Weigelt, G. P. 1977, Opt. Comm., 21, 55
In the text
NASA ADS
-
Weigelt, G. P., & Wirnitzer, B. 1983, Opt. Lett., 8, 389
In the text
NASA ADS
-
Wiehr, E. 1999, Mass Motions and Magnetic Fields in Penumbrae, in Third Advances in Solar Physics
Euroconference: Magnetic Fields and Oscillations, ed. B. Schmieder, A. Hofmann, & J. Staude,
Astron. Soc. Pac. Conf. Ser., 184, 86
In the text
-
Wilken, V., de Boer, C. R. Denker, C., & Kneer, F. 1997, A&A, 325, 819
In the text
NASA ADS
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=15cm,clip]{h2334_f1.eps}\end{figure}](/articles/aa/full/2001/03/aah2334/Timg15.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{h2334_f2.eps}\end{figure}](/articles/aa/full/2001/03/aah2334/Timg32.gif)
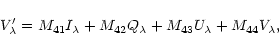
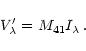
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2334_f3.eps}\end{figure}](/articles/aa/full/2001/03/aah2334/Timg63.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2334_f5.eps}\end{figure}](/articles/aa/full/2001/03/aah2334/Timg70.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2334_f6.eps}\end{figure}](/articles/aa/full/2001/03/aah2334/Timg72.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2334_f7.eps}\par\end{figure}](/articles/aa/full/2001/03/aah2334/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2334_f8.eps}\end{figure}](/articles/aa/full/2001/03/aah2334/Timg78.gif)