A&A 365, 656-659 (2001)
DOI: 10.1051/0004-6361:20000013

The electron-impact broadening effect in hot star atmospheres: The case of singly- and doubly-ionized zirconium[*]

L. C. Popovic - N. Milovanovic - M. S. Dimitrijevic

Send offprint request: L. C. Popovic,

Astronomical Observatory, Volgina 7, 11160 Belgrade 74, Serbia, Yugoslavia

Received 14 December 1999 / Accepted 31 August 2000

Abstract
The electron-impact widths for 30 Zr III lines were calculated using the modified semi-empirical (MSE) method. For two Zr II and four Zr III astrophysically important UV lines, only electron-impact widths are given, since for their calculation the experimental oscillator strengths were used and consequently the accuracy of the parameters is lower than in the case of other lines. The influence of the electron-impact mechanism on line shapes and equivalent widths in hot star atmospheres was also considered. The impact of the electron-impact broadening effect on abundance determination, particularly its effect on "zirconium conflict'' is discussed as well.

Key words: atomic data - plasma - stars: atmospheres

Author for correspondance: lpopovic@aob.bg.ac.yu


1 Introduction

Electron-impact broadening is the main broadening mechanism in A and B type star atmospheres (see e.g. Popovic et al. 1999). Electron-impact broadening data are needed to solve various problems in astrophysics and physics, for example, diagnosis and modeling of laboratory and stellar plasma, investigation of its physical properties and for abundance determination. These investigations provide information useful for the modeling of stellar evolution, e.g. abundance studies in stellar atmospheres provide evidence of the chemical composition of the stellar primordial cloud, of processes occurring within the stellar interior, and the dynamic processes occuring in the stellar atmosphere.

Present abundance analyses for early-type stars show that 10%-20% of A and B stars have abundance anomalies, including anomalies in isotopic composition (Leckrone et al. 1993). The abundance anomalies in these stars, called CP stars, could be caused by diffusion occurring in the presence of selective radiative acceleration. The chemical species that absorb more of the outgoing photons are dragged by the photons to the stellar surface (see e.g. Michaud & Richter 1997). In order to investigate these processes, atomic data for multiple lines of numerous emitters are needed. Here, we have considered electron-impact broadening parameters for Zr III spectral lines. Also, we present the electron-broadening widths for two astrophysically important UV Zr II lines. For six Zr II multiplets the electron-broadening widths and shifts were published in Popovic & Dimitrijevic (1996a). The zirconium lines are present in spectra of HgMn stars (Cowley & Aikman 1975; Heacox 1979; Leckrone et al. 1993; Sikström et al. 1999). It is interesting that the zirconium abundance determination from weak Zr II optical lines and from strong Zr III lines (detected in UV) is quite different (see Leckrone et al. 1993; Sikström et al. 1999) in the HgMn star $\chi$ Lupi. This so-called "zirconium conflict'' was supposed by Sikström et al. (1999) to be due to inadequate use of stellar models, e.g. if the influence of non-LTE effects or diffusion are not taken into account. Zirconium, often overabundant in HgMn stars (see Heacox 1979), is one member of Sr-Y-Zr triad, which is vital for the study of s-process nucleosynthesis and has been suggested to represent a non-nuclear abundance pattern in HgMn stars. The most obvious interpretation of this anomaly involves diffusion theory or the inclusion of non-LTE effects.

Due to poor knowledge of the energy levels as well as the transition probabilities for singly- and doubly-ionized zirconium, the approximate methods are suitable for Stark broadening calculations. Here, we present the results of electron-impact broadening parameter calculations of two astrophysically important Zr II and 34 Zr III lines. Also, we tested the influence of electron-impact broadening on the determination of equivalent widths and have discussed the possible influence of electron-impact broadening on zirconium abundance determination.

2 Method of calculation

We have applied the modified semiempirical approach - MSE (Dimitrijevic & Konjevic 1980; Dimitrijevic & Krsljanin 1986), tested several times for complex spectra (see e.g. Popovic & Dimitrijevic 1996b,c, 1997). This method, applicable only for the Stark broadening of isolated, nonhydrogenic ion lines, has been described several times (Dimitrijevic & Konjevic 1980; Dimitrijevic & Krsljanin 1986; Popovic & Dimitrijevic 1996b; Popovic & Dimitrijevic 1997)

Compared to the semiclassical perturbation approach, the modified semiempirical approach needs less atomic data. In fact, if there are no perturbing levels strongly violating the assumed approximation, we need only the energy levels with $\Delta n=0\ {\rm and}\ \ell_{\rm if}'=\ell_{\rm if}\pm 1$, for e.g. the line width calculations, since all perturbing levels with $\Delta n\neq 0$, needed for a full semiclassical investigation, are lumped together and approximately estimated. E.g. for transition $5{\rm s}^1{\rm D}-5{\rm p}^1{\rm D}^0$, the atomic energy levels needed explicitly as perturbing levels within the MSE formalism for the final energy level $5{\rm s}^1{\rm D}$ are the atomic energy levels $5{\rm p}^1{\rm D}^0$( $E=53\,648.88$ cm-1), $5{\rm p}^1{\rm P}^0$ ( $E=62\,117.41$ cm-1) and $5{\rm p}^1{\rm F}^0$( $E=62\,590.70$ cm-1), while for the initial energy level $5{\rm p}^1{\rm D}^0$ we need the energy values for atomic energy levels $5{\rm s}^1{\rm D}$ ( $E=25\,068.35$ cm-1), $5{\rm d}^1{\rm F}$ ( $E=103\,585.01$ cm-1), $5{\rm d}^1{\rm P}$( $E=105\,554.66$ cm-1) and $5{\rm d}^1{\rm D}$ ( $E=109\,272.70$ cm-1). The perturbations by the other levels (with $\Delta n\neq 0$) are lumped together and estimated.

In the case of 30 Zr III transitions, it was possible to adequately use the MSE approach (Dimitrijevic & Konjevic 1980; Dimitrijevic & Krsljanin 1986) and to calculate Stark widths (W - full width at half maximum) for the multiplet as a whole. For other transitions it was not possible to apply the MSE approach because of the lack of atomic data. In order to apply the MSE method (Dimitrijevic & Konjevic 1980), we must have reliable atomic energy data for the initial and final level of the transition forming the considered line. In addition, for each of the considered levels, we should have reliable data for the energy of levels with the same principal quantum number n and the orbital quantum numbers $\ell-1$ and $\ell+1$. Moreover, we should have good information concerning the levels with the principal quantum number different from that of the initial or final level, but which are close to the initial or final levels. These are required to check the validity of the assumed approximations and, if they are not satisfied, to take such levels into account separately. For the simple spectrum, the Stark broadening parameters of different lines are nearly the same within a multiplet (Wiese & Konjevic 1982, 1992). Consequently, one may take the averaged atomic data for a multiplet as a whole and calculate the corresponding Stark widths. If the wavelength of a particular line within the multiplet differs significantly from the averaged wavelength $<\lambda >$ of the multiplet, one may obtain more accurate values for each line by scaling multiplet values for widths:

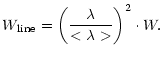$\displaystyle W_{\rm line}=\left({\lambda \over{<\lambda>}}\right)^2\cdot W.$     (1)

In the above expression, W and $<\lambda >$ are values for the multiplet, and $W_{\rm line}$ and $\lambda$ refer to a particular line within the multiplet.

It is not always possible to apply this approximation to complex spectra. If irregularities of atomic energy level structure are present, forbidden and inter-combination transitions can influence different lines of the multiplet in different ways, and we have to calculate Stark broadening data for each line separately (Dimitrijevic 1982; Popovic & Dimitrijevic 1997; Dimitrijevic & Tankosic 2000). Such a situation occurred for two Zr II and four Zr III astrophysically important UV lines considered in our paper.

Atomic energy levels needed for the calculations have been taken from Reader & Acquista (1997) and oscillator strengths when available from Charro et al. (1999) and Sikström et al. (1999). In the paper of Reader & Acquista (1997) the spectrum of Zr III obtained with sliding spark discharges was observed from 630 Å to 4610 Å using the 10.7 m normal-incidence vacuum spectrograph. A total of 482 lines were classified as transitions between 139 energy levels. In their work, from the optimized energy level values, a system of Ritz-type wavelengths with uncertainties varying from about $\pm$0.005 Å to $\pm$0.003 Å was determined. From this paper, we obtained the determined energy level configurations and the values of the energy levels. In Charro et al. (1999) the oscillator strengths for the dipole-allowed transition in Zr III between the levels belonging to $4{\rm d}^2$ and $4{\rm d}n\ell$ configuration have been calculated using the relativistic quantum-defect orbital method. From this paper we obtained the oscillator strengths for matrix element calculations for $4{\rm d}^2$- $4{\rm d}5{\rm p}$ transitions. In Sikström et al. (1999), the lifetimes for the levels $v^2{\rm D}_{3/2}$, $v^2{\rm F}_{3/2}$ and $v^2{\rm F}_{5/2}$ in the $4{\rm d}5{\rm s}5{\rm p}$ configuration in Zr II have been measured, using the method of laser-induced fluorescence. Combined with branching fractions obtained with the Lund Ultraviolet Fourier Transform Spectrometer, experimental oscillator strengths also were derived. The estimated uncertainty in the obtained oscillator strengths is $\pm 25$% in lines with high observed intensities and no more than $\pm 40$% in the weakest line observed. From this paper we obtained the oscillator strengths for matrix element calculations for two Zr II lines considered. For other transitions, the matrix elements were calculated by the method of Bates & Damgaard (1949). The line and multiplet factors required were taken from Shore & Menzel (1968).

The accuracy of the MSE approximation is assumed to be about $\pm50\%$(Dimitrijevic & Konjevic 1980). In order to test the MSE method, Dimitrijevic & Konjevic (1980) selected experimental data for 36 multiplets (7 different ion species) of doubly-charged ions and 7 multiplets (4 different ion species) of triply-charged ions and compared them with theoretical results. The averaged values of the ratios of measured to calculated widths are as follows: for doubly-charged ions $1.06\pm 0.32$ and for triply-charged ions $0.91\pm 0.42$. It was shown in Popovic & Dimitrijevic (1996c, 1998) that the MSE approach, even in the case of the emitters with very complex spectra (e.g. Xe II and Kr II), gives very good agreement with experimental measurements (in the interval $\pm 30\%$). For example, for Xe II $6{\rm s}{-}6{\rm p}$ transitions, the averaged ratio between experimental and theoretical widths is $1.15\pm0.5$ (Popovic & Dimitrijevic 1996c). In Krsljanin & Dimitrijevic (1989) Stark shifts for 47 Ar II multiplets have been calculated within the framework of the MSE method and compared to selected (Konjevic & Wiese 1976; Konjevic et al. 1984) experimental data. Mean experimental-to-theoretical shift ratio of $1.26\pm 0.34$ has been obtained. Generally, if the width and absolute shift values are comparable, the principal contributions to the shift will have the same sign and their accuracy will be similar. If the absolute shift values are considerably smaller (due to the mutual cancelations of important contributions with different signs), we assume that the error bars remain $\pm50\%$ of the width value. The Stark shift data for Zr III are available upon request.


  
Table 3: The Stark widths (W) in rad s-1 per electron for $T=10\,000$ K, and constants A0,1 as described in the text
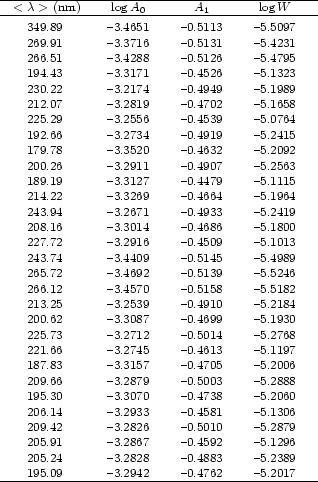\begin{table} {\halign to 8cm{\strut ...

3 Results and discussion

The results of our calculations are presented in Tables 1 and 2 (accessible only in electronic form). In Table 1, the Stark widths calculated for a multiplet as a whole, and in Table 2 for particular lines within a multiplet, are given. The data are given for an electron density of $10^{23}~\rm m^{-3}$ and temperatures from 5000 to 50000 K. The electron-broadening data are a linear function of electron density. However, for higher densities, it is advisable to check whether the considered line is still isolated (Sahal-Bréchot 1969; Dimitrijevic & Sahal-Bréchot 1984), as well as to verify the influence of Debye shielding (Griem 1974) and non-ideal plasma effects (Konjevic & Uzelac 1990).

For the spectrum synthesis, it is convenient to use small numbers for the input parameters. We therefore have fitted each data set from Tables 1 and 2 with the expression (Popovic et al. 1999):

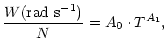$\displaystyle {W({\rm rad \ s^{-1}})\over N}=A_0\cdot T^{A_1},$     (2)

where

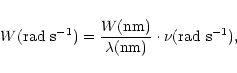
\begin{eqnarray*}W({\rm rad\ s^{-1}})={W({\rm nm})\over{\lambda({\rm nm})}}\cdot\nu({\rm rad\ s^{-1}}), \end{eqnarray*}


and $\nu$ is the transition frequency. The parameters A0 and A1 as well as the Stark width $W({\rm rad \ s^{-1}})$ per electron for $T=10\,000$ K are shown in Tables 3 and 4. In Eq. (2) W is a full width at half maximum (FWHM) expressed in rad s-1 per electron, and constants A0,1 are determined numerically from the best fit. Equation (2) may be used to extrapolate toward higher temperatures. It is not advisable to extrapolate toward temperatures lower than those given in Tables 1 and 2 without checking the validity of the impact approximation. Moreover, at lower temperatures, the importance of quantum effects increases and the application of the MSE method (as well as the other semiclassical, classical or semiempirical methods which neglect quantum effects) becomes questionable.


  
Table 4: Same as in the Table 3, but for two Zr II and four Zr III astrophysically important UV lines
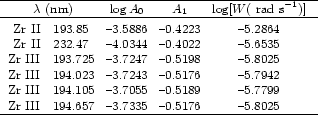\begin{table} {\halign to 8cm{\strut ...

We also have analyzed the influence of the electron-impact broadening mechanism on the equivalent width and consequently on the determination of zirconium abundance. We investigated the effect of the electron-impact broadening in the so-called "zirconium conflict'' in the HgMn star $\chi$ Lupi. In order to test the importance of the electron-impact broadening effect in determinations of zirconium abundance, we synthesized the line profiles of Zr II ( $\lambda=193.8$ nm and $\lambda = 232.5$ nm) and Zr III ( $\lambda = 194.02$ nm and $\lambda = 194.10$ nm) using SYNTH code (Piskunov 1992) where the LTE conditions are assumed and the Kurucz's ATLAS9 code for a model of stellar atmosphere (Kurucz 1993) ( $T_{\rm eff}=$ 10000 K and $ \log g=4.0$), i.e. with the stellar models with similar characteristics as those of $\chi$ Lupi ( $T_{\rm eff}=10\,650$ K and $ \log g=3.8$, see e.g. Leckrone et al. 1999). We have modified the SYNTH code, which uses $\log W$(rads-1) per electron for $T=10\,000$ K as an input parameter, replacing it with the two parameters: A0 and A1 from Eq. (2) (see Popovic et al. 1999). We chose these lines because they have been commonly used for abundance determination, as they have a small wavelength displacement and are well resolved (Leckrone et al. 1993).

We have calculated the equivalent widths with and without the electron-impact broadening effect for different abundances of zirconium. The ratio of equivalent widths for the Zr II and Zr III lines considered here, calculated with and without the electron-impact broadening effect is presented in Fig. 1. As one can see from Fig. 1, the electron-broadening effect is more important in the case of higher abundances of zirconium. The equivalent width increases with abundances for both lines, but the equivalent widths for Zr III lines are more sensitive than Zr II lines. This may cause an error in abundance determination in cases where the electron-impact broadening effect is not taken into account. In any case, synthesizing of these two lines in order to measure the zirconium abundance without taking into account the electron-impact widths will result in Zr III lines suggesting an abundance of zirconium higher than that obtained with the Zr II lines. However, this effect is less than one order of magnitude of the abundance.


  \begin{figure} \par\includegraphics[width=5.2cm,clip]{ds1828f1.ps} \end{figure} Figure 1: The ratio of equivalent widths of: a) Zr II [232.5 nm], b) Zr II [193.85 nm], c) Zr III [194.1 nm] and d) Zr III [194.0 nm] lines calculated with Stark broadening effect ( $EW_{\rm St}$) and without (EW) as a function of zirconium abundance
Open with DEXTER

Although the "zirconium conflict'' in the HgMn star $\chi$ Lupi cannot be explained only by this effect, one should be aware that the electron-impact broadening effect may cause errors in abundance determination.

In the case of Zr II and Zr III there are no measured Stark broadening data. Moreover, for Zr III there are no previously published theoretical electron-impact broadening parameters. We hope that the Stark broadening data presented here, as well as consideration of the influence of the electron-impact broadening mechanism on abundance determination will be of interest not only for consideration of "zirconium conflict'' but also for different problems in astrophysical and physical plasma investigation and modeling.

Acknowledgements
This work was supported by the Ministry of Science and Technology of Serbia through the project "Astrometrical, Astrodynamical and Astrophysical Researches'' and by the Federal Ministry of Development, Sciences and Environment Protection of Yugoslavia.

References

 

Copyright ESO 2001