A&A 365, 347-359 (2001)
DOI: 10.1051/0004-6361:20000045
Evolution of photoionization and star formation in starbursts and H II galaxies
E. Moy1 - B. Rocca-Volmerange1,2 - M. Fioc1,3
Send offprint request: E. Moy,
1 - Institut d'Astrophysique de Paris, 98bis
boulevard Arago, 75014 Paris, France
2 -
Institut d'Astrophysique Spatiale, Bât. 121, Université Paris XI,
91405 Orsay Cedex, France
3 -
NASA/Goddard Space Flight Center, code 685, Greenbelt, MD 20771, USA
Received 17 January 2000 / Accepted 4 September 2000
Abstract
We analyze coherently the stellar and nebular energy
distributions of starbursts and H II galaxies, using our
evolutionary synthesis model, PÉGASE (Fioc & Rocca-Volmerange 1997,
2000), coupled to the photoionization code CLOUDY (Ferland
1996). The originality of this study is to relate the evolution and
the metallicity of the starburst to the past star formation history of
the host galaxy. Extinction and geometrical effects on emission lines
and continua are computed in coherency with metallicity.
We compare our model predictions to an observed sample of  750
H II regions and starbursts.
When fitting [O III]
750
H II regions and starbursts.
When fitting [O III]
 /[O III]
/[O III]
 ,
[O I]
,
[O I]
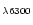 /H
/H ,
[S II]
,
[S II]
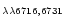 /H
/H ,
[N II]
,
[N II]
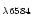 /H
/H and [O III]
and [O III]
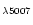 /H
/H ,
the most striking feature
is the decreasing spread in U with
increasing metallicity Z. High-U objects systematically have a
low metallicity while low levels
of excitation happen at any Z. The best fits of emission line
ratios
are obtained with a combination of a high- and a low-ionization
components. No additional source of ionizing photons -
shocks or hidden AGN - is needed.
The high level of excitation observed in metal-poor H II galaxies
requires a very
young population (
,
the most striking feature
is the decreasing spread in U with
increasing metallicity Z. High-U objects systematically have a
low metallicity while low levels
of excitation happen at any Z. The best fits of emission line
ratios
are obtained with a combination of a high- and a low-ionization
components. No additional source of ionizing photons -
shocks or hidden AGN - is needed.
The high level of excitation observed in metal-poor H II galaxies
requires a very
young population (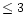 Myr), while starburst nuclear galaxies (SBNGs) are
consistent with a wider range of age (
Myr), while starburst nuclear galaxies (SBNGs) are
consistent with a wider range of age (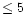 Myr).
Colors (B-V, V-R) and equivalent widths are fitted
in coherency with emission line ratios. An underlying
population is needed, even for small-aperture observations. This underlying
population not only reddens the
continuum and dilutes the equivalent width of the emission lines, but also
participates
in the ionization process. Its main effect
on line ratios is to maintain a high level of excitation
when the burst stops. Models combining underlying populations typical
of Hubble sequence galaxies and instantaneous starbursts
with ages between 0 and 8Myr agree satisfactorily
with all the data.
Myr).
Colors (B-V, V-R) and equivalent widths are fitted
in coherency with emission line ratios. An underlying
population is needed, even for small-aperture observations. This underlying
population not only reddens the
continuum and dilutes the equivalent width of the emission lines, but also
participates
in the ionization process. Its main effect
on line ratios is to maintain a high level of excitation
when the burst stops. Models combining underlying populations typical
of Hubble sequence galaxies and instantaneous starbursts
with ages between 0 and 8Myr agree satisfactorily
with all the data.
Key words: galaxies: starburst - galaxies: evolution -
galaxies: stellar content - ISM: H II regions
Author for correspondance: moy@iap.fr
Table 1:
Data sources. SBNG: starburst
nucleus galaxies; H IIG: H II galaxies;
H II: H II regions
| References |
Starburst type |
Balmer absorption |
Reddening |
| |
|
correction |
correction |
| Terlevich et al. 1991 |
H IIG,
SBNG |
no |
no |
| Veilleux & Osterbrock 1987 |
SBNG |
no |
no |
| Veilleux et al. 1995 |
IRAS SBNG |
yes |
no |
| French 1980 |
H IIG |
no |
no |
| Leech et al. 1989 |
IRAS SBG |
yes |
yes |
| Storchi-Bergmann et al.
1995 |
H IIG, SBNG |
no |
no |
| Contini et al. 1998 |
IRAS SBNG, H II |
yes |
no |
The "starburst'' phenomenon calls to mind a class of objects
dominated by the radiation of massive stars (Gallego et al. 1995)
embedded in a dusty H II region. Modelling starbursts consistently
is the key to interpret the
properties of the actively star-forming galaxies detected at a redshift
z>2 (Giavalisco
et al. 1996; Madau et al. 1996; Steidel et al. 1996;
Lowenthal et al. 1997). To this purpose, the extensive study of local samples
is a requisite step.
Local starbursts span a wide range of types, from individual H II
regions
in spiral arms to blue compact H II galaxies and huge kpc-scale
nuclear starbursts (Coziol et al. 1998). Types differ from one another
in their main characteristics (line ratios, equivalent widths,
colors), and presumably have different stellar populations and physical
conditions. So, is it possible to find correlations between the basic properties:
age, initial mass function, metallicity, relative distributions
of stars, gas and dust? Among these, which
one dominates spectral properties? In which range do parameters vary?
Answering these questions requires
a consistent model of starbursts coupling the evolution of stars, dust and gas.
The first studies dealing with emission lines of H II regions (Shields
1974, 1978; Stasinska 1978, 1980;
McCall et al. 1985)
relied on single-star photoionization models. Average physical
properties of large starburst samples were deduced from these
pioneering works. As an example, a relation between the metallicity Zand the ionization parameter U was derived by Dopita & Evans
(1986) by fitting the emission line ratios from large samples of
extragalactic H II regions.
More realistic stellar populations of star clusters were computed by McGaugh (1991) with
the Salpeter (1955) initial mass function (IMF), to calibrate metallicity dependant line ratios.
Further improvements were the implementation of theoretical
tracks of massive stars, allowing to follow the evolution in time of a starburst (e.g.
García-Vargas & Díaz 1994). Thanks to the computation of
evolutionary tracks for various metal abundances, the
influence of the metallicity could also be studied (Cid-Fernandes et al. 1992;
Cerviño &
Mas-Hesse 1994; Olofsson 1997;
García-Vargas et al. 1995a,b; Stasinska &
Leitherer 1996). Evans (1991) emphasized the importance
of using up-to-date stellar atmosphere models to calibrate nebular diagnostics. The most
recent models take into account modern, updated stellar physics
(Leitherer &
Heckman 1995; Leitherer et al. 1999), in particular
the impact on stellar spectra of line blanketing and of departures
from local thermodynamic equilibrium (Stasinska & Schaerer 1997).
Till now, only a few large datasets
covering a wide range of physical conditions
have been analyzed with state-of-the-art models, coupling evolving
stellar populations and
photoionization. Stasinska & Leitherer (1996), for example,
restricted their analysis to metal-poor (
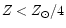 )
objects. As a matter of fact, statistical properties of starbursts
are not definitely established. A
metal-dependent IMF was early proposed as an explanation for the
[O III]
)
objects. As a matter of fact, statistical properties of starbursts
are not definitely established. A
metal-dependent IMF was early proposed as an explanation for the
[O III]
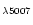 /H
/H decrease at high Z (Terlevich 1985;
Shields & Tinsley 1976). Although a standard IMF seems in agreement
with the bulk of observations (Leitherer 1998), the IMF slope (see e.g.
Eisenhauer et al. 1998; Greggio et al. 1998) and mass cut-offs (Goldader
et al. 1997) are still under debate.
decrease at high Z (Terlevich 1985;
Shields & Tinsley 1976). Although a standard IMF seems in agreement
with the bulk of observations (Leitherer 1998), the IMF slope (see e.g.
Eisenhauer et al. 1998; Greggio et al. 1998) and mass cut-offs (Goldader
et al. 1997) are still under debate.
Our aim is hereafter to study the evolution of the spectral properties of
aging starbursts with the help of models taking into account the effects
of metallicity, geometry, dust and the excitation level of the gas.
To avoid normalization problems, we
selected relative properties independent of
distance (colors, equivalent widths and line ratios). We focused on emission
line ratios at
close wavelengths - thus reducing reddening effects -
to study the ionizing
spectrum and the excitation of the gas. Equivalent widths and colors are used
preferentially to study age effects, as well as the impact of the spatial
distribution of stars, gas and dust.
The observational sample is presented in Sect. 2. The
coupling of the codes PÉGASE, to model the evolution of star formation
and stellar emission, and CLOUDY, for a consequent photoionization of the gas by
massive stars in a given geometry,
is described in Sect. 3. The relation between the metallicity Z and the
ionization parameter U is analyzed in Sect. 4, while equivalent widths and
colors are considered in Sect. 5.
The contribution of an underlying population is analyzed in Sect. 6.
Discussion and conclusion are respectively in Sects. 7 and 8.
Our data set (Table 1) is a selection of 754 objects from observational
samples of galaxies having properties characteristic of starbursts:
intense emission lines (French 1980; Veilleux &
Osterbrock 1987; Terlevich et al. 1991), strong far-infrared emission
(Leech et al. 1989; Veilleux et al. 1995), or excess of blue or
ultraviolet emission (Storchi-Bergmann et al. 1995); in addition,
Contini et al. (1998) require galaxies to have a bar. Objects
dominated by an active galactic nucleus (AGN) are excluded from our
sample, though some of them may be faintly contaminated by nuclear activity.
Effects of aperture and differences in data reduction processes are considered
in Sect. 2.2.
Objects listed in the source papers are classified in two
families. The first one includes metal-poor H II galaxies
(H IIGs) and extra-nuclear H II regions, both likely devoid of active
nucleus. The second one gathers galactic central regions where the ionized-gas
emission
could be partly due to shocks (Kim et al. 1998)
or AGNs (see Heckman 1991 and references therein). To select only
starburst nucleus galaxies (SBNGs) in this last class, we
keep the classification of the authors, which is based
on the pioneering works of Baldwin et al.
(1981, hereafter BPT) and Veilleux & Osterbrock (1987, hereafter VO).
The Terlevich et al. (1991) sample is mainly composed of H IIGs
with some possible SBNGs. The
authors used two of the BPT criteria based on the [O III]
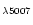 /H
/H and
[O II]
and
[O II]
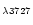 /[O III]
/[O III]
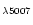 ratios. We
also analyzed their sample with the VO method and obtained the same
classification.
ratios. We
also analyzed their sample with the VO method and obtained the same
classification.
Contini et al. (1998) adopted the VO criteria. Their sample includes
SBNGs and giant H II regions located in IRAS barred spiral galaxies,
selected from Mazzarella & Balzano (1986) and listed in the
Lyon-Meudon Extragalactic Database (LEDA).
Two samples contain only SBNGs located inside IRAS galaxies. Veilleux
et al. (1995) followed both BPT and VO criteria, while
Leech et al. (1989) used only some of the criteria of BPT. Actually, an
important part of their sample lies far beyond the limit reported by VO
between
H II-like regions and AGNs in the [O III]/H vs. [O I]/H
vs. [O I]/H and [O III]/H
and [O III]/H vs. [N II]/H
vs. [N II]/H diagrams. These objects are clearly misclassified and have been
excluded from our selection. Storchi-Bergmann et al.
(1995) reported observations of emission line galaxies of various
types. Following Coziol et al. (1998), all compact galaxies are hereafter
classified as H II galaxies, whether dwarf or not.
Finally, we include in our
selection the observations of five starbursts from the sample of
Balzano (1983) reported by VO, and the data of French (1980) on 14
H IIGs.
diagrams. These objects are clearly misclassified and have been
excluded from our selection. Storchi-Bergmann et al.
(1995) reported observations of emission line galaxies of various
types. Following Coziol et al. (1998), all compact galaxies are hereafter
classified as H II galaxies, whether dwarf or not.
Finally, we include in our
selection the observations of five starbursts from the sample of
Balzano (1983) reported by VO, and the data of French (1980) on 14
H IIGs.
Most line ratios considered here are computed from close lines; so, reddening
effects should be small and will be neglected in the following.
In most samples, the
contamination, through large apertures, of the starburst light by the host
galaxy population is likely to increase the continuum emission and to
dilute the equivalent width of emission
lines. To avoid this problem, we will restrict the analysis of colors and
equivalent widths to the sample of Contini et al.
(1998). These data were acquired with a long-slit spectrograph, but the spectra presented by the authors correspond to H emitting regions exclusively. Hence, the
contamination of the starburst continuum by the environment of the host galaxy
should be very
weak.
emitting regions exclusively. Hence, the
contamination of the starburst continuum by the environment of the host galaxy
should be very
weak.
The host galaxy can also modify the apparent line ratios involving Balmer lines
through the presence of stellar absorption lines.
Emission line fluxes are corrected for this effect as follows:
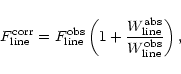 |
(1) |
where
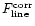 and
and
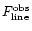 are respectively the
absorption-corrected and the apparent emission line fluxes, and
are respectively the
absorption-corrected and the apparent emission line fluxes, and
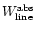 and
and
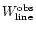 are the absorption and measured emission
equivalent widths.
Not all the samples were corrected (Table 1). The correction should be
negligible for the H
are the absorption and measured emission
equivalent widths.
Not all the samples were corrected (Table 1). The correction should be
negligible for the H line because
line because
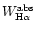
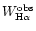 .
It is stronger for H
.
It is stronger for H (up to 100% in Leech et al. 1989) and
the ratio [O III]/H
(up to 100% in Leech et al. 1989) and
the ratio [O III]/H may be affected. This ratio is systematically higher in the samples of
French (1980)
and Terlevich et al. (1991), mainly composed of H IIGs, than in the other ones, which include mainly SBNGs. Is this trend real, or is it due to the fact that these two data sets are not corrected for underlying stellar lines? Note that
Storchi-Bergmann et al.
(1995) already noticed that [O III]/H
may be affected. This ratio is systematically higher in the samples of
French (1980)
and Terlevich et al. (1991), mainly composed of H IIGs, than in the other ones, which include mainly SBNGs. Is this trend real, or is it due to the fact that these two data sets are not corrected for underlying stellar lines? Note that
Storchi-Bergmann et al.
(1995) already noticed that [O III]/H is higher in H II
galaxies than in SBNGs. Moreover, the correction for absorption lines should be very small in H IIGs, since these
objects have simultaneously large
is higher in H II
galaxies than in SBNGs. Moreover, the correction for absorption lines should be very small in H IIGs, since these
objects have simultaneously large
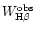 (67Å in
Terlevich et al. 1991) and low
(67Å in
Terlevich et al. 1991) and low
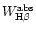 .
Hence, we conclude that the trend we observe is real and not due to the discrepancies between the reduction procedures.
.
Hence, we conclude that the trend we observe is real and not due to the discrepancies between the reduction procedures.
The evolutionary synthesis code we use, PÉGASE,
takes into account metallicity and dust
effects. PÉGASE computes the stellar spectral energy distributions (SEDs) and
the metallicities of
starbursts and galaxies of the Hubble sequence at any stage
of evolution, within the metallicity range Z=10-4to 10-1.
Typical parameters of PÉGASE are the star
formation rate (SFR) and the initial mass function. The new
version![[*]](/icons/foot_motif.gif) used
hereafter, PÉGASE.2, is based on the evolutionary tracks of Girardi et al.
(1996), Fagotto et al. (1994a-c) and Bressan et al. (1993).
The AGB to
post-AGB phases are computed following the prescriptions of
Groenewegen & de Jong (1993) models.
The synthetic stellar spectral library is
from Kurucz (1992), modified by Lejeune et al. (1997) to fit observed colors.
For details, see Fioc & Rocca-Volmerange (1999, 2000, in preparation).
used
hereafter, PÉGASE.2, is based on the evolutionary tracks of Girardi et al.
(1996), Fagotto et al. (1994a-c) and Bressan et al. (1993).
The AGB to
post-AGB phases are computed following the prescriptions of
Groenewegen & de Jong (1993) models.
The synthetic stellar spectral library is
from Kurucz (1992), modified by Lejeune et al. (1997) to fit observed colors.
For details, see Fioc & Rocca-Volmerange (1999, 2000, in preparation).
The photoionization code CLOUDY (version 90.04, Ferland 1996) predicts the
spectra of
low- to high-density astrophysical plasmas in the
most extreme astrophysical sites, such as starbursts and quasar environments.
It takes into account recent changes in
atomic databases and new numerical methods. In addition to its physical
performances, the code was chosen for its easy Web access, its
documentation and its friendly on-line help. CLOUDY proposes options to
explore the influence of geometrical factors: type of geometry -
spherical or plane parallel -, covering factor
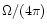 ,
filling factor f, and the distance R from the source to
the plasma.
,
filling factor f, and the distance R from the source to
the plasma.
The coupling of PÉGASE.2 with CLOUDY allows to compute coherently the
stellar and nebular emission, and to fit simultaneously
the continuum and lines from
stellar populations embedded in a gas cloud. The metallicity Z(t),
and the stellar SED - in particular the energy distribution of the ionizing
photons - provided by PÉGASE are used as inputs by CLOUDY.
Hereafter, we call
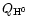 the emission rate of
ionizing photons. This quantity is used to normalize the SEDs computed by PÉGASE.
the emission rate of
ionizing photons. This quantity is used to normalize the SEDs computed by PÉGASE.
The results of the current version of the code have been compared to those
obtained by similar "coupled models''. They are presented in Table 2
for two sets of predictions: the model 16 from
García-Vargas et al. (1995b),
and the 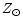 -model computed by Stasinska & Leitherer
(1996) for a
-model computed by Stasinska & Leitherer
(1996) for a
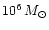 -cluster. In both cases, we used
inputs matching the reference model (IMF, age, geometrical parameters
and chemical abundances). For the first comparison test, the agreement is very
good (Table 2, top). Our results also agree relatively well with those of
Stasinska & Leitherer (1996), given that the evolutionary tracks, the
spectral libraries and the photoionization codes are different in the two
models.
-cluster. In both cases, we used
inputs matching the reference model (IMF, age, geometrical parameters
and chemical abundances). For the first comparison test, the agreement is very
good (Table 2, top). Our results also agree relatively well with those of
Stasinska & Leitherer (1996), given that the evolutionary tracks, the
spectral libraries and the photoionization codes are different in the two
models.
An instantaneous star formation episode
("pure starburst'') is assumed for starbursts - a scenario
well suited to study emission line properties.
In Sect. 6, we will also consider an underlying stellar population
formed either during a previous burst or continuously.
We tentatively tested several IMFs
of the form dN/d
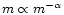 ,
,
![$m\in[M_{\rm low},
M_{\rm up}]$](/articles/aa/full/2001/03/aa9567/img56.gif) :
:
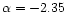 ,
,
![$m\in[0.1, 120]\,M_{\odot}$](/articles/aa/full/2001/03/aa9567/img57.gif) (Salpeter 1955);
(Salpeter 1955);
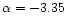 ,
,
![$m\in[0.1, 120]\,M_{\odot}$](/articles/aa/full/2001/03/aa9567/img57.gif) ;
and
;
and
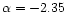 ,
,
![$m\in[3, 30]\,M_{\odot}$](/articles/aa/full/2001/03/aa9567/img58.gif) .
The last one is truncated, as suggested by various infrared studies
(Rieke et al. 1993; Lançon &
Rocca-Volmerange 1996). The initial metallicity
is left as a free parameter.
.
The last one is truncated, as suggested by various infrared studies
(Rieke et al. 1993; Lançon &
Rocca-Volmerange 1996). The initial metallicity
is left as a free parameter.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9567f1a.eps}\hspace*{3mm}
...
....eps}\hspace*{3mm}
\includegraphics[width=7.5cm,clip]{9567f1d.eps}
\end{figure}](/articles/aa/full/2001/03/aa9567/Timg59.gif) |
Figure 1:
Models of pure instantaneous starbursts for
various filling factors (f) and metallicities (Z). The data are from
Terlevich et al. ("plus'' signs), Veilleux & Osterbrock (asterisks), French
(filled circles), Veilleux et al. (diamonds), Contini et al. (triangles),
Storchi-Bergmann et al. (squares) and Leech et al. (crosses) |
| Open with DEXTER |
The emission line spectrum of an ionized nebula depends on the combination
of the ionizing spectrum, the chemical composition of the gas and the so-called
ionization parameter U.
The elemental abundances of the gas have been made consistent with the metallicity
of the ionizing stars. The solar abundances used here are given
in Table 3. All the
abundances were scaled linearly according to the metallicity, except
for nitrogen and helium. For the likely secondary
element N, we adopted the law proposed
by Coziol et al. (1999), multiplied by a factor 1.5 to account for the excess
of nitrogen observed in starbursts. For He, we followed a prescription proposed
by Dopita & Kewley (private communication; see Table 3 for details).
The ionization parameter U is defined as:
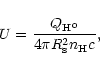 |
(2) |
where 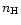 is the hydrogen density, c the speed of light, and
is the hydrogen density, c the speed of light, and
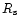 the Strömgren radius (i.e. the radius of the ionization front).
Taking into account the inner radius R (e.g. Evans & Dopita 1985),
the Strömgren radius (i.e. the radius of the ionization front).
Taking into account the inner radius R (e.g. Evans & Dopita 1985),
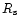 is roughly equal to:
is roughly equal to:
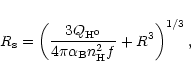 |
(3) |
where
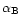 is the case B temperature-dependent recombination
coefficient and f is the filling factor. This formula highlights
the impact of each parameter on U, but is only approximate, since it assumes a
constant temperature through all the nebula. The effective Strömgren radius
is obtained only at the end of a CLOUDY calculation.
is the case B temperature-dependent recombination
coefficient and f is the filling factor. This formula highlights
the impact of each parameter on U, but is only approximate, since it assumes a
constant temperature through all the nebula. The effective Strömgren radius
is obtained only at the end of a CLOUDY calculation.
The spherical geometry (Stasinska & Leitherer
1996; González-Delgado et al. 1999)
and plane-parallel geometry
(García-Vargas & Díaz 1994;
García-Vargas et al. 1997)
are
extreme situations for which the right-hand side of Eq. (3) is
respectively dominated by the first and the second term. The adopted geometry
was spherical. The hydrogen density 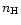 was 100 cm-3 in most models, but we also computed a few cases for
was 100 cm-3 in most models, but we also computed a few cases for
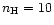 and
and
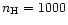 cm-3, to assess the specific
impact of density on emission line ratios. We set the number of ionizing
photons to
cm-3, to assess the specific
impact of density on emission line ratios. We set the number of ionizing
photons to
 photonss-1, corresponding to a maximum
luminosity of
photonss-1, corresponding to a maximum
luminosity of 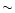 1040ergs-1 in the H
1040ergs-1 in the H emission line
- a value characteristic of intense star formation sites (Shields
1990). For emission lines, the exact value of
emission line
- a value characteristic of intense star formation sites (Shields
1990). For emission lines, the exact value of
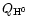 is not
important as long as the density does not exceed the critical limit of
collisional de-excitation, below which models with the same U, ionizing
spectrum and metallicity predict the same line ratios.
To obtain reasonable values for U, we varied the volume filling factor
between 10-5 and 1 and set R to 4pc.
is not
important as long as the density does not exceed the critical limit of
collisional de-excitation, below which models with the same U, ionizing
spectrum and metallicity predict the same line ratios.
To obtain reasonable values for U, we varied the volume filling factor
between 10-5 and 1 and set R to 4pc.
We assume that
the gas is distributed in a spherical shell covering a solid angle 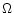 around the star cluster. The covering factor
around the star cluster. The covering factor
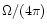 was allowed to
vary in the interval [0.1, 1]. The continuum
luminosity from the starburst
was allowed to
vary in the interval [0.1, 1]. The continuum
luminosity from the starburst
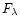 (ergs-1 Å-1) at any
wavelength
(ergs-1 Å-1) at any
wavelength 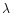 is:
is:
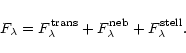 |
(4) |
The transmitted stellar continuum
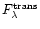 and the
nebular continuum
and the
nebular continuum
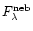 both scale with
both scale with
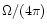 .
.
 ,
scaling as
,
scaling as
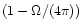 ,
refers to the part of the
stellar spectrum not crossing the gas (and thus not contributing to the
ionization process).
,
refers to the part of the
stellar spectrum not crossing the gas (and thus not contributing to the
ionization process).
Assuming a dust screen at the outer edge of the H II region,
the continuum flux is reddened as follows:
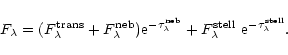 |
(5) |
Emission line fluxes are also multiplied by
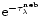 .
The optical depth
.
The optical depth
 was a free
parameter, as well as the
was a free
parameter, as well as the
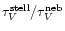 ratio (
ratio (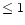 ). This option
takes
into account a possible dust concentration outside the
nebula rather than on the line-of-sight not covered by the gas.
The variation of the optical depth with wavelength is derived from
the metallicity-dependent extinction laws of the Magellanic Clouds and
our Galaxy.
). This option
takes
into account a possible dust concentration outside the
nebula rather than on the line-of-sight not covered by the gas.
The variation of the optical depth with wavelength is derived from
the metallicity-dependent extinction laws of the Magellanic Clouds and
our Galaxy.
We have explored the impact of the IMF, the age of the starburst, the metallicity and the ionization parameter on the following optical line ratios: [O III]
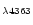 /[O III]
/[O III]
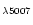 ,
[O I]
,
[O I]
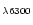 /H
/H ,
[S II]
,
[S II]
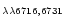 /H
/H ,
[N II]
,
[N II]
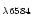 /H
/H and [O III]
and [O III]
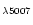 /H
/H .
The value of f was varied between
10-5 and 1.
The corresponding
.
The value of f was varied between
10-5 and 1.
The corresponding 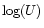 (as
defined in Sect. 3.2) belongs to
[-5.5, -1.5]. Note that similar results could
also be derived by varying the inner radius R (in a plane-parallel
geometry), the density
(as
defined in Sect. 3.2) belongs to
[-5.5, -1.5]. Note that similar results could
also be derived by varying the inner radius R (in a plane-parallel
geometry), the density 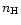 or a combination of both.
or a combination of both.
In the following, if not specified, the IMF is Salpeter (1955).
Emission line ratios are sensitive to the metallicity through two competing
effects.
On the one hand, the opacity increases with Z, lowering
the stellar effective temperatures and thus
the hardness of the ionizing spectrum. A trend towards lower excitation levels
is therefore expected in high-Zstarbursts, even if there is no dependence of the
IMF or the geometry on the metallicity. This effect is reinforced at high Z by the
efficient cooling by metals and thus the low electronic temperature
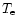 .
.
On the other hand, the energy in metal emission lines tends
naturally to increase
with higher elemental abundances. For oxygen lines, this
process dominates at
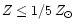 ,
while the opposite happens at higher metallicity
(e.g. McGaugh 1991). As a consequence,
two models with metallicities respectively below and above this limit
can predict comparable emission lines. For this reason, we present hereafter
our predictions for Z in the range
,
while the opposite happens at higher metallicity
(e.g. McGaugh 1991). As a consequence,
two models with metallicities respectively below and above this limit
can predict comparable emission lines. For this reason, we present hereafter
our predictions for Z in the range
![$[1/50, 3/2]\, Z_{\odot}$](/articles/aa/full/2001/03/aa9567/img85.gif) if no degeneracy
happens in the considered diagram, but in
if no degeneracy
happens in the considered diagram, but in
![$[1/5, 3/2]\, Z_{\odot}$](/articles/aa/full/2001/03/aa9567/img86.gif) otherwise.
otherwise.
For a given density 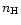 ,
varying the filling factor f changes
the optical depth per unit length and the ionization structure: the smaller
f, the smaller the mean ionization level, and the
lower the luminosities of high excitation lines such as
[O III]
,
varying the filling factor f changes
the optical depth per unit length and the ionization structure: the smaller
f, the smaller the mean ionization level, and the
lower the luminosities of high excitation lines such as
[O III]
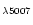 .
Low-excitation lines behave inversely.
.
Low-excitation lines behave inversely.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9567f3a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{9567f3b.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg87.gif) |
Figure 3:
Comparison of the data with five sequences obtained by
varying the relative weights of the high (f=1) and low (f=10-5)
excitation components. Solid diamonds are the points for which the low
excitation component contributes to 0, 1, 10, 50, 90, 99 and 100% of the
H flux (from right to left)
flux (from right to left) |
| Open with DEXTER |
Models of pure instantaneous starbursts, with metallicities in the range
![$[1/5, 3/2]\, Z_{\odot}$](/articles/aa/full/2001/03/aa9567/img86.gif) ,
are compared to the data in Fig. 1 for six
values of the filling
factor f: 10-5, 10-4, 10-3, 10-2, 10-1, and 1.
The data are largely covered by the models when at least two parameters vary - here
chemical and geometrical.
Interestingly, different types of objects seem to occupy
different zones in the Z-U plane:
H II galaxies are in better agreement with low-Z (1/50
,
are compared to the data in Fig. 1 for six
values of the filling
factor f: 10-5, 10-4, 10-3, 10-2, 10-1, and 1.
The data are largely covered by the models when at least two parameters vary - here
chemical and geometrical.
Interestingly, different types of objects seem to occupy
different zones in the Z-U plane:
H II galaxies are in better agreement with low-Z (1/50 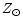 to
3/4
to
3/4 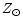 ), high-U models (
), high-U models (
![$f\in[10^{-3},1]$](/articles/aa/full/2001/03/aa9567/img88.gif) ); SBNGs are
compatible with low values of f (10-5 to 10-2), but encompass
a wide range of metallicities.
); SBNGs are
compatible with low values of f (10-5 to 10-2), but encompass
a wide range of metallicities.
We also report in Fig. 2 the comparison of predictions with
observations in following diagrams: [O II]
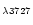 /H
/H vs.
[O III]
vs.
[O III]
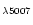 /H
/H and [O II]
and [O II]
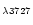 /[O III]
/[O III]
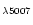 vs. [S III]
vs. [S III]
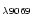 /[S II]
/[S II]
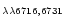 .
Note that the
[O II]/H
.
Note that the
[O II]/H ,
[O II]/[O III] and [S III]/[S II] ratios are
sensitive to reddening and, for this reason, we do not include them in the
discussion. We can only notice that, given the uncertain
impact of dust on these ratios, our results are compatible with the
observations.
,
[O II]/[O III] and [S III]/[S II] ratios are
sensitive to reddening and, for this reason, we do not include them in the
discussion. We can only notice that, given the uncertain
impact of dust on these ratios, our results are compatible with the
observations.
A mean U-Z relation fitting the data could easily be derived
from Fig. 1, as in Dopita & Evans (1986).
However, this relation would suffer from too many uncertainties: first,
it would
not take into account the high Z-low Z degeneracy; second, age effects are
very similar to those induced by the metallicity. This is illustrated in
Fig. 4, where [O I]/H and
[S II]/H
and
[S II]/H vs. [O III]
vs. [O III]
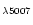 /H
/H are
plotted for
are
plotted for
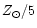 at t=0, 4, 5 and 6Myr.
Variations of the IMF give rise to similar uncertainties, as
shown in Fig. 6: the lower number of massive stars for a steeper or
truncated
IMF causes a strong decrease of both [O III]/H
at t=0, 4, 5 and 6Myr.
Variations of the IMF give rise to similar uncertainties, as
shown in Fig. 6: the lower number of massive stars for a steeper or
truncated
IMF causes a strong decrease of both [O III]/H and [O I]/H
and [O I]/H ,
just as if the metallicity was higher.
,
just as if the metallicity was higher.
Due to this age-metallicity-IMF degeneracy, a meaningful Z-U analytical
relation cannot be established on the basis of line ratio diagrams.
Moreover, Fig. 1 clearly shows that the dispersion of U,
rather than the mean value of this parameter, is linked to the metallicity:
while starbursts exist at any U at low Z, only low-U starbursts
are observed at high metallicity. We consider a possible cause of
this trend in the next paragraph.
In the [O I]/H vs. [O III]/H
vs. [O III]/H and [S II]/H
and [S II]/H vs. [O III]/H
vs. [O III]/H diagrams, many data points lie above
predictions, even when the misclassified objects of Leech et al. (1989) are
excluded from the sample. To check whether this discrepancy can be
solved by varying the density, we have performed two series of
calculations at
diagrams, many data points lie above
predictions, even when the misclassified objects of Leech et al. (1989) are
excluded from the sample. To check whether this discrepancy can be
solved by varying the density, we have performed two series of
calculations at
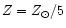 with
with
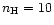 and 1000 cm-3. We chose
this metallicity because the corresponding sequence defines the upper envelope of
our model grid in these diagrams. The results are shown in Table 4. The main one is that model sequences with different densities
largely overlap: clearly, the outliers
cannot be explained by a variation of
and 1000 cm-3. We chose
this metallicity because the corresponding sequence defines the upper envelope of
our model grid in these diagrams. The results are shown in Table 4. The main one is that model sequences with different densities
largely overlap: clearly, the outliers
cannot be explained by a variation of 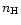 .
.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9567f4a.eps}\hspace*{3mm}
\includegraphics[width=7.5cm,clip]{9567f4b.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg90.gif) |
Figure 4:
Evolution with the starburst age of the
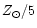 -model sequence plotted in Fig. 1 -model sequence plotted in Fig. 1 |
| Open with DEXTER |
Many authors have
proposed that a faint contribution from shocks or AGNs could explain the
intensity of the [O I] line in starbursts (see e.g. Stasinska & Leitherer 1996).
We consider here an alternative possibility where there are, inside the
starburst, both high- and low-excitation zones, due for example to a distribution
of gas and stars more complex than the classical geometry adopted in our
calculations. To test this hypothesis, we computed a series of sequences
obtained by varying the relative weight of high- and
low-excitation models (f=1 and f=10-5, respectively) for
five metallicities. The results (Fig. 3) are in much better agreement with the data than pure U
sequences, as they explain both the trend and the dispersion of the
observations. Another advantage of this explanation is that no other source of ionization, such as AGNs or shocks, is required.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{9567f5.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg91.gif) |
Figure 5:
Time evolution of the [O III]
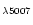 /H /H ratio for instantaneous starbursts. The decrease of the ratio after
5Myr is very rapid and puts severe constraints on the age of starbursts (see
text for details)
ratio for instantaneous starbursts. The decrease of the ratio after
5Myr is very rapid and puts severe constraints on the age of starbursts (see
text for details) |
| Open with DEXTER |
If this hypothesis is correct, the evolution of the apparent
U with Z in fact corresponds to the presence in
low-metallicity objects of a high-U component,
which is absent in high-Z starbursts. We come
back to this point in the discussion.
Figure 5 shows the evolution, up to 6 Myr, of the [O III]
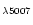 /H
/H ratio for the models plotted in Figs. 1
and 2. The constraints on age shown by this plot are
very strong, though noticeably different for H II
galaxies and SBNGs: H II galaxies, of high-excitation level, need the high
energy photons emitted by massive stars, so that only young (
ratio for the models plotted in Figs. 1
and 2. The constraints on age shown by this plot are
very strong, though noticeably different for H II
galaxies and SBNGs: H II galaxies, of high-excitation level, need the high
energy photons emitted by massive stars, so that only young (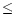 3Myr)
models are compatible with observations (see Sect. 7); SBNGs, requiring a
lower excitation level, span a wider range of ages. In any case, the
rapid drop of the [O III]/H
3Myr)
models are compatible with observations (see Sect. 7); SBNGs, requiring a
lower excitation level, span a wider range of ages. In any case, the
rapid drop of the [O III]/H ratio after 5Myr requires the presence of stars younger than 6Myr.
ratio after 5Myr requires the presence of stars younger than 6Myr.
Line ratios depend on the hardness of the spectrum, and so on the IMF.
The [O I] line, emitted
from the partly ionized zone, requires high-energy photons and is thus
particularly sensitive to the high-mass end of the IMF. Figure 6
presents the sensitivity of [O I]
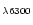 /H
/H and [O III]/H
and [O III]/H to the initial mass function.
A Salpeter IMF is favored by our
results, in good agreement with recent studies (e.g. Stasinska &
Leitherer 1996; García-Vargas et al. 1995). An interesting point
is that the steeper and truncated
IMFs, while clearly excluded by the data for high-U H IIGs,
are acceptable for metal-rich starbursts.
to the initial mass function.
A Salpeter IMF is favored by our
results, in good agreement with recent studies (e.g. Stasinska &
Leitherer 1996; García-Vargas et al. 1995). An interesting point
is that the steeper and truncated
IMFs, while clearly excluded by the data for high-U H IIGs,
are acceptable for metal-rich starbursts.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9567f6.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg93.gif) |
Figure 6:
Impact of the IMF on [O I]/H vs. [O III]/H
vs. [O III]/H for two metallicities (
for two metallicities (
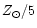 and
and 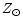 ). In each
case, three f sequences are plotted: A ( ). In each
case, three f sequences are plotted: A (
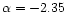 , ,
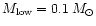 and
and
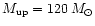 ), B ( ), B (
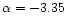 , ,
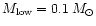 and
and
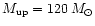 )
and C ( )
and C (
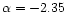 , ,
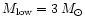 and
and
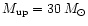 ) ) |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9567f7a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{9567f7b.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg94.gif) |
Figure 7:
Pure starburst models
for various ages (0 to 6Myr) and 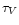 between 0 to 6. The ratio
between 0 to 6. The ratio
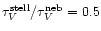 is equal to 1. The covering
factor is
0.1. Data (triangles) are from Contini et al. (1998). The solid lines
indicate the predictions of the
is equal to 1. The covering
factor is
0.1. Data (triangles) are from Contini et al. (1998). The solid lines
indicate the predictions of the
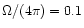 model grid. The two dashed
lines show the t=0Myr (upper line) and t=6Myr (lower line) model results
for
model grid. The two dashed
lines show the t=0Myr (upper line) and t=6Myr (lower line) model results
for
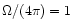 |
| Open with DEXTER |
In the
following, we aim to keep our previous fits of emission line ratios and,
simultaneously, to reproduce
 and B-V and V-R colors from the
sample of Contini et al. (1998). The models plotted in Figs. 1 and 2 predict
H
and B-V and V-R colors from the
sample of Contini et al. (1998). The models plotted in Figs. 1 and 2 predict
H equivalent widths above 500Å, while the observed
equivalent widths above 500Å, while the observed
 seldom exceed 300Å.
Predicted equivalent widths in excess to the observations
are a well-known problem (Bresolin et al. 1999 and references therein).
The hypothesis of a "density bounded'' nebula (Leitherer et al. 1996) is ruled out by the observed intensities of the low-ionization lines; the reduction of the thickness of the partly-ionized zone would lead to
lower [S II]/H
seldom exceed 300Å.
Predicted equivalent widths in excess to the observations
are a well-known problem (Bresolin et al. 1999 and references therein).
The hypothesis of a "density bounded'' nebula (Leitherer et al. 1996) is ruled out by the observed intensities of the low-ionization lines; the reduction of the thickness of the partly-ionized zone would lead to
lower [S II]/H and [O I]/H
and [O I]/H than
in Fig. 1, and the models would not fit any more these line ratios.
than
in Fig. 1, and the models would not fit any more these line ratios.
A low covering factor
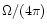 reduces the
equivalent widths by increasing
the stellar emission relative to the nebular one, without changing
line ratios.
A similar explanation of the
faint
reduces the
equivalent widths by increasing
the stellar emission relative to the nebular one, without changing
line ratios.
A similar explanation of the
faint
 of blue compact and irregular
galaxies was suggested by Mas-Hesse & Kunth (1999).
of blue compact and irregular
galaxies was suggested by Mas-Hesse & Kunth (1999).
Figure 7 shows the influence of
dust and age in the
 vs. B-V and
vs. B-V and
 vs. V-R
planes, for
vs. V-R
planes, for
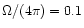 .
For comparison, we also show
t=0 and t=6Myr sequences
for
.
For comparison, we also show
t=0 and t=6Myr sequences
for
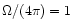 .
We plot only
.
We plot only
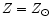 models, since the metallicity has
only weak effects on B-V, V-R and
models, since the metallicity has
only weak effects on B-V, V-R and
 .
Similarly, for such a low value of
.
Similarly, for such a low value of
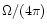 ,
f hardly affects the
colors
and the only models in Fig. 7 are for f=1.
Ages between 0 and 6Myr,
,
f hardly affects the
colors
and the only models in Fig. 7 are for f=1.
Ages between 0 and 6Myr,
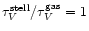 and
and
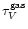 in the range [0,6] are
suggested by the
in the range [0,6] are
suggested by the
 vs. B-V diagram.
However,
vs. B-V diagram.
However,
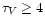 is excluded by the V-R data, and
ages
is excluded by the V-R data, and
ages
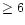 Myr are incompatible with line ratios (see also Sect. 7.2).
Myr are incompatible with line ratios (see also Sect. 7.2).
A ratio
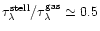 (following Calzetti et al. 1997; see also Fanelli
et al. 1988; Keel 1993; Mas-Hesse & Kunth 1999) can simultaneously fit
B-V and V-R, but requires very high extinctions, up to
(following Calzetti et al. 1997; see also Fanelli
et al. 1988; Keel 1993; Mas-Hesse & Kunth 1999) can simultaneously fit
B-V and V-R, but requires very high extinctions, up to
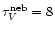 (Fig. 8), while Contini et al.
(1998) derived
a maximum value of
(Fig. 8), while Contini et al.
(1998) derived
a maximum value of 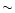 4 from the Balmer decrement. The B-V of
the reddest objects are considered as anomalous
(Contini, private communication) and are not reproduced by
any model.
4 from the Balmer decrement. The B-V of
the reddest objects are considered as anomalous
(Contini, private communication) and are not reproduced by
any model.
The distribution of the data in the
 vs. B-V or V-R diagrams is very
difficult to explain with pure instantaneous starburst models. The main problem
is the very low covering factor required.
An alternative hypothesis, able to explain the
equivalent widths and colors of the Contini et al. (1998) sample
with the much more reasonable value
vs. B-V or V-R diagrams is very
difficult to explain with pure instantaneous starburst models. The main problem
is the very low covering factor required.
An alternative hypothesis, able to explain the
equivalent widths and colors of the Contini et al. (1998) sample
with the much more reasonable value
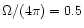 ,
is the presence
of evolved stars inside the starburst.
Such a population, created during past formation episodes, can account for
the observed weakness of equivalent
widths by increasing the continuum (e.g. McCall et al. 1985; Díaz et al.
1991). It may also explain the red colors of the sample without requiring huge
amounts of dust.
,
is the presence
of evolved stars inside the starburst.
Such a population, created during past formation episodes, can account for
the observed weakness of equivalent
widths by increasing the continuum (e.g. McCall et al. 1985; Díaz et al.
1991). It may also explain the red colors of the sample without requiring huge
amounts of dust.
We considered two possible underlying populations. The first one consists of
an instantaneous burst which occured 100Myr ago. This old burst
is assumed to have been ten times more intense than the current one.
The predictions of these
models are plotted in Fig. 9. As in Fig. 8,
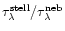 is set to
0.5. However, these models face two problems: first, it is still necessary
to extend the age of the young burst to t=6Myr, unless the covering factor
is much lower than the value adopted in Fig. 9 (0.5); second, the
sum of the evolved and the young population does not reproduce the colors. To
reconcile this type of models with the data, it would be necessary to assume
that the old burst was systematically
is set to
0.5. However, these models face two problems: first, it is still necessary
to extend the age of the young burst to t=6Myr, unless the covering factor
is much lower than the value adopted in Fig. 9 (0.5); second, the
sum of the evolved and the young population does not reproduce the colors. To
reconcile this type of models with the data, it would be necessary to assume
that the old burst was systematically 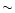 100 times more intense than the
current one.
100 times more intense than the
current one.
The second type of underlying population is assumed to have formed continuously.
We computed a series of scenarios matching the observations of standard
Hubble sequence galaxies at z=0, and added a starburst. For the sake of
consistency, the
initial metallicity of the burst is
the current metallicity Z(t) of the host galaxy and is provided by PÉGASE.
The input parameters are chosen so that the starburst metallicities belong to
the range
![$[1/5\, Z_{\odot}, 3/2\, Z_{\odot}]$](/articles/aa/full/2001/03/aa9567/img110.gif) derived from line ratios. Each scenario is defined by three parameters:
the age
derived from line ratios. Each scenario is defined by three parameters:
the age
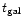 of the host galaxy when the starburst occurs; the
infall timescale
of the host galaxy when the starburst occurs; the
infall timescale 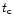 used to parameterize
the accretion rate of the galaxy; the gas-to-star conversion
efficiency,
used to parameterize
the accretion rate of the galaxy; the gas-to-star conversion
efficiency, 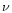 ,
relating the star formation rate
,
relating the star formation rate 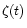 to the gas
density
to the gas
density 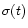 by the Schmidt law
by the Schmidt law
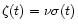 .
.
Five models (A, B, C, D, E) were computed for each scenario,
corresponding to five different contributions of the evolved
population to the total emission: A is the pure host galaxy,
E is the pure starburst
and B, C and D are intermediate cases. Note that the
star formation does not stop after the burst, but returns to the quiescent
regime. The fraction of ionizing photons due to the underlying population
immediately after the burst is given in Table 5, as well as the values of
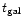 ,
,
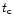 ,
and
,
and 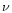 for the considered scenario.
for the considered scenario.
Figure 10 presents the impact of the parameters on colors and equivalent widths.
We compare the results of
model D at
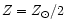 to the sample
of Contini et al. (1998). We also show the results of model C for
to the sample
of Contini et al. (1998). We also show the results of model C for
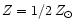 ,
and the predictions of model D for
,
and the predictions of model D for
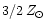 .
The filling factors are
10-2 at
.
The filling factors are
10-2 at
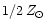 and 5 10-4at
and 5 10-4at
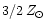 .
As in Fig. 8,
.
As in Fig. 8,
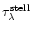 /
/
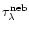 is set to 0.5. However, the covering factor (0.5) is
significantly higher, and the
is set to 0.5. However, the covering factor (0.5) is
significantly higher, and the
 range (0 to 4) is much more
reasonable.
range (0 to 4) is much more
reasonable.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9567f9a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{9567f9b.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg120.gif) |
Figure 9:
H equivalent widths and colors for
instantaneous + 100Myr-old starbursts. The metallicity of the young starburst
is solar. The old burst is assumed to have been ten times more intense
than the current one. The model sequences are labeled in
terms of the age of the present starburst and of the value of
equivalent widths and colors for
instantaneous + 100Myr-old starbursts. The metallicity of the young starburst
is solar. The old burst is assumed to have been ten times more intense
than the current one. The model sequences are labeled in
terms of the age of the present starburst and of the value of

|
| Open with DEXTER |
Another important point is that, contrary to the pure starburst case, ages of 6Myr and more are compatible with emission line ratios. This is due to the
presence of massive stars, formed after the burst in the underlying population. The presence of such stars ensures that the line ratios are virtually unchanged compared to their values during the
burst. Contrary to the case of a burst that occured 100 Myr ago, these scenarios are able to explain simultaneously the colors, the equivalent widths and the line ratios in our sample. They do not require very high levels of extinction, and, maybe more important, do not imply a covering factor lower than 0.5. For all these reasons,
the hypothesis of an underlying population formed continuously is our preferred one.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9567f10a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{9567f10b.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg121.gif) |
Figure 10:
H equivalent widths and colors for
instantaneous burst + continuous star formation scenarios. The thick solid
lines show the predictions of model D for different ages and extinction levels
of the burst. The metallicity of the burst is 1/2
equivalent widths and colors for
instantaneous burst + continuous star formation scenarios. The thick solid
lines show the predictions of model D for different ages and extinction levels
of the burst. The metallicity of the burst is 1/2 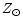 .
The dashed lines
indicate the shift of the right part of the grid when the contribution of the
underlying population is increased (model C). The thin solid lines show the
shift of the low part of the grid when the metallicity is equal to 3/2 .
The dashed lines
indicate the shift of the right part of the grid when the contribution of the
underlying population is increased (model C). The thin solid lines show the
shift of the low part of the grid when the metallicity is equal to 3/2
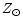 |
| Open with DEXTER |
Dopita & Evans (1986) proposed an analytical relation between the metallicity
and the ionization parameter to describe the observational
distribution of line ratios in their sample of extragalactic H II regions. In
Sect. 4.3, we saw that such a relation suffers from many degeneracies due
to age, IMF and metallicity. Moreover, it seems that the quantities which are
really related are the dispersion of U and the metallicity.
What could be the physical link between Z and U? According to one
hypothesis, this is a link through geometrical effects.
Following Castor et al. (1975) and assuming their equations are valid also for a
star cluster, the inner radius R of
a gaseous shell surrounding a massive star or cluster is:
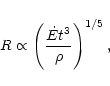 |
(6) |
where 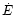 is the energy deposition rate of a star (or cluster) of age t
in the interstellar medium (ISM) of
density
is the energy deposition rate of a star (or cluster) of age t
in the interstellar medium (ISM) of
density 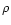 .
Leitherer et al. (1992) found that
.
Leitherer et al. (1992) found that
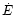 is constant for an instantaneous burst until
is constant for an instantaneous burst until 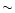 6 Myr
and scales linearly with Z,
regardless of the age. Hence, high-Z H II regions expand faster.
6 Myr
and scales linearly with Z,
regardless of the age. Hence, high-Z H II regions expand faster.
We therefore propose the following scenario to explain the distribution
of starbursts in the line ratio diagrams. For some reason, a site of intense
star formation appears in a galaxy with a metal-poor interstellar medium. This
starburst can be composed of many individual H II regions surrounding star
clusters. As these sub-components evolve with age, the H II regions expand
because of stellar winds. At the same time, the enrichment
of the ISM by massive-star ejecta begins. If star formation goes on,
very young components will coexist inside the starburst with more evolved
components. The former will dominate the nebular emission during the first
few Myr,
and the latter after.
Two additional effects can explain the lack of high-Z and high-U objects:
first, at high metallicity, individual H II regions expand faster, leading
to a lower ionization parameter; second, according to this scenario, the bulk
of nebular emission in high-Z starbursts is produced by evolved,
low-excitation H II regions. Checking the validity of this hypothesis
requires to model also the expansion of nebulae. This is
the subject of a forthcoming paper.
The problems encountered by pure starburst scenarios to account for the
weakness of the H equivalent widths from the sample of Contini et al.
(1998) are several. The main one is that a very low covering factor is required.
From Figs. 7 and 8, we deduce that a value
equivalent widths from the sample of Contini et al.
(1998) are several. The main one is that a very low covering factor is required.
From Figs. 7 and 8, we deduce that a value
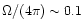 is necessary to reproduce both
is necessary to reproduce both
 and the line ratios in the case of a pure starburst. This means that 90% of the Lyman continuum
photons do not contribute to ionization, but are directly absorbed by dust or
escape from the starburst. This is in contradiction with many previous studies
using H
and the line ratios in the case of a pure starburst. This means that 90% of the Lyman continuum
photons do not contribute to ionization, but are directly absorbed by dust or
escape from the starburst. This is in contradiction with many previous studies
using H or H
or H luminosities to estimate the mass of stellar
clusters inside starbursts. In many cases, the agreement between such
estimations and those based on ultraviolet continuum luminosities is excellent
(González-Delgado et al. 1999). Some discrepancies appear frequently
(Leitherer et al. 1996; Vacca et al. 1995), but they are however weak enough
to exclude an absorption fraction of the ionizing photons by the gas as low as
10%. Moreover, observations of diffuse H
luminosities to estimate the mass of stellar
clusters inside starbursts. In many cases, the agreement between such
estimations and those based on ultraviolet continuum luminosities is excellent
(González-Delgado et al. 1999). Some discrepancies appear frequently
(Leitherer et al. 1996; Vacca et al. 1995), but they are however weak enough
to exclude an absorption fraction of the ionizing photons by the gas as low as
10%. Moreover, observations of diffuse H emission in nearby
galaxies lead to an estimation of 15-50% for the fraction
of ionizing photons escaping from individual H II regions
(Kennicutt 1998 and references therein).
emission in nearby
galaxies lead to an estimation of 15-50% for the fraction
of ionizing photons escaping from individual H II regions
(Kennicutt 1998 and references therein).
Such a systematic low value of the covering factor is therefore clearly ruled
out by the observations. Note also that pure starbursts models, even with
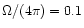 ,
cannot reproduce simultaneously the emission line
ratios and the equivalent widths (see
Sect. 5). Hence, the presence of an evolved stellar
population coexisting with a starburst, as analysed in Sect. 6, seems mandatory to explain
equivalent widths and colors, even for the data of Contini et al. (1998),
who strictly limitated their apertures to H
,
cannot reproduce simultaneously the emission line
ratios and the equivalent widths (see
Sect. 5). Hence, the presence of an evolved stellar
population coexisting with a starburst, as analysed in Sect. 6, seems mandatory to explain
equivalent widths and colors, even for the data of Contini et al. (1998),
who strictly limitated their apertures to H -emitting
areas. A similar conclusion for galaxies
observed through 5-arcsec apertures was drawn
by Lançon & Rocca-Volmerange (1996)
from the near-infrared spectral synthesis of starbursts.
-emitting
areas. A similar conclusion for galaxies
observed through 5-arcsec apertures was drawn
by Lançon & Rocca-Volmerange (1996)
from the near-infrared spectral synthesis of starbursts.
Including underlying populations in the models allows to fit the
data in a satisfactory way in the
 vs. B-V
and V-R diagrams with
vs. B-V
and V-R diagrams with
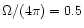 ,
which means that
,
which means that 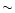
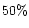 of the ionizing photons escape
from the gaseous nebula. This value is close to the 60% fraction suggested by
Mas-Hesse & Kunth (1999). The nature of this population remains however
elusive.
of the ionizing photons escape
from the gaseous nebula. This value is close to the 60% fraction suggested by
Mas-Hesse & Kunth (1999). The nature of this population remains however
elusive.
We have tested an old (100 Myr old) instantaneous burst as a possible
underlying population. The agreement with the data, at first sight, is
relatively good (Fig. 9). In this case, however, the age of the
youngest burst has to extend up to 8Myr to explain the faint end of the
W(H )
observational distribution. At this age, our models are
incompatible with line ratio data. Note that there is no Wolf-Rayet(W-R)
star SED in our spectral library; instead, the spectra of the
hottest stars available in the library are used during W-R stages.
The implementation of W-R SEDs in the library could in principle extend
the range of ages compatible with line ratios up to 6Myr or more. As an
example, González-Delgado et al. (1998)
obtained an age between 6 and 9Myr for
IRAS 0833+6517. However, this conclusion is based on models with
an IMF truncated at
)
observational distribution. At this age, our models are
incompatible with line ratio data. Note that there is no Wolf-Rayet(W-R)
star SED in our spectral library; instead, the spectra of the
hottest stars available in the library are used during W-R stages.
The implementation of W-R SEDs in the library could in principle extend
the range of ages compatible with line ratios up to 6Myr or more. As an
example, González-Delgado et al. (1998)
obtained an age between 6 and 9Myr for
IRAS 0833+6517. However, this conclusion is based on models with
an IMF truncated at
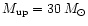 .
Such a low value is
clearly excluded for the bulk of our sample (Fig. 6). Moreover, the
role of W-R stars in
starburst nebular emission is still under
debate. According to the most recent studies, the bulk of nebular emission
is due to stellar populations younger than 3Myr (Bresolin et al. 1999).
.
Such a low value is
clearly excluded for the bulk of our sample (Fig. 6). Moreover, the
role of W-R stars in
starburst nebular emission is still under
debate. According to the most recent studies, the bulk of nebular emission
is due to stellar populations younger than 3Myr (Bresolin et al. 1999).
We have assumed that the old burst was only ten times more intense
than the current one. Changing this value to one hundred, for example, would
move the predictions in Fig. 9 toward the bottom-right
and might explain
the bulk of the data with ages lower than, or equal to, 4Myr. In this case,
however, such a difference between past and present star formation remains
to be explained.
In this context, the models plotted in Fig. 10 appear as the most
attractive ones. Scenarios with an underlying population providing from
2.5 up to 20% of the number of
ionizing photons are in acceptable agreement with the data and
explain naturally all the observables
(emission lines, colors
and equivalent widths). The range of 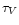 is consistent with the Balmer
decrement measurements of Contini et al. (1998). Moreover, the age
and metallicity of the underlying population are typically those
of normal spirals, suggesting that starbursts are normal events in galaxy
evolution. These scenarios draw a coherent picture of the starburst phenomenon,
and for this reason, remain the most plausible ones.
is consistent with the Balmer
decrement measurements of Contini et al. (1998). Moreover, the age
and metallicity of the underlying population are typically those
of normal spirals, suggesting that starbursts are normal events in galaxy
evolution. These scenarios draw a coherent picture of the starburst phenomenon,
and for this reason, remain the most plausible ones.
We have analyzed the emission line and continuum properties of a large sample of
starbursts and put new constraints on their stellar populations,
metallicity, photoionization state and dust content. Our tool was the
spectral evolution code PÉGASE coupled to the photoionization
code CLOUDY.
From the comparison of a dataset of emission lines with pure instantaneous
starburst scenarios, we have been able to constrain the evolution of the
ionization parameter U with the metallicity Z. At high abundance, the
high-excitation component clearly detected at low Z is absent or very weak. A
preliminary analysis based on energy deposition rate considerations is
unsufficient to explain this trend, and a more refined analysis
of the dependency of the H II region expansion with Z is needed.
The second important result concerns underlying populations
inside starbursts; they are detected even through small-aperture
observations. This contribution is needed to reproduce simultaneously all
the observables of our sample
(line ratios, colors and equivalent widths). The underlying populations are
simulated through the whole computation of the past star formation history of
the galaxy hosting the starburst. In the scenarios favored by our analysis,
the
burst itself is supposed to be a brief, intense episode, preceded and followed
by a quiescent regime. After the burst, this quiescent formation rate is
sufficient to keep the line ratios compatible with the data.
Future prospects should consider the problem of metal depletion on dust grains,
since depletion changes the composition of nebular gas. However, the question
of the presence of dust inside
H II regions will be solved only with more constraining data,
e.g. those of the ISO satellite.
Finally, the large grids computed with the help of
a coupled photoionization and stellar evolutionary synthesis
model will be also used to study other samples with better
statistics.
Acknowledgements
We are pleased to thank Gary Ferland for his multiple consultation
and help for the interface with CLOUDY. M. F. acknowledges support from the
National Research Council through the Resident Research Associateship Program.
-
Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP,
93, 5 (BPT)
In the text
NASA ADS
-
Balzano, V. A. 1983, ApJ, 268, 602
In the text
NASA ADS
-
Bresolin, F., Kennicutt, R. C., & Garnett, D. R. 1999, ApJ,
510, 104
In the text
NASA ADS
-
Bressan, A., Fagotto, F, Bertelli, G., & Chiosi, C. 1993, A&AS, 100, 647
In the text
NASA ADS
-
Calzetti, D., Meurer, G. R., Bohlin, R. C., et al.
1997, AJ, 114, 1834
In the text
NASA ADS
-
Castor, J., McCray, R., & Weaver, R. 1975, ApJ, 200,
L107
In the text
NASA ADS
-
Cerviño, M., & Mas-Hesse, J. M. 1994, A&A, 284, 749
In the text
NASA ADS
-
Cid-Fernandes, R., Dottori, H. A., Gruenwald, R. B., & Viegas, S. M. 1992,
MNRAS, 255, 165
In the text
NASA ADS
-
Contini, T., Considère, S., & Davoust, E. 1998, A&AS,
130, 285
In the text
NASA ADS
-
Coziol, R., Carlos Reyes, R.E., Considère, S., Davoust, E., & Contini,
T.
1999, A&A, 345, 733
In the text
NASA ADS
-
Coziol, R., Torres, C. A. O., Quast, G. R., Contini, T.,
& Davoust, E. 1998, ApJS, 119, 239
In the text
NASA ADS
-
Díaz, A. I., Terlevich, E., Vílchez, J. M., Pagel, B. E. J., &
Edmunds, M. G. 1991, MNRAS, 253, 245
In the text
NASA ADS
-
Dopita, M. A., & Evans, I. N. 1986, ApJ, 307, 431
In the text
NASA ADS
-
Eisenhauer, F., Quirrenbach, A., Zinnecker, H., & Genzel, R.
1998, ApJ, 498, 278
In the text
NASA ADS
-
Evans, I. N. 1991, ApJS, 76, 985
In the text
NASA ADS
-
Evans, I. N., & Dopita, M. A. 1985, ApJS, 58, 125
In the text
NASA ADS
-
Fanelli, M. N., O'Connell, R. W., & Thuan, T. X. 1988, ApJ,
334, 665
In the text
NASA ADS
-
Fagotto, F., Bressan, A., Bertelli, G., & Chiosi, C. 1994a, A&AS, 104,
365
In the text
NASA ADS
-
Fagotto, F., Bressan, A., Bertelli, G., & Chiosi, C. 1994b, A&AS, 105, 29
NASA ADS
-
Fagotto, F., Bressan, A., Bertelli, G., & Chiosi, C. 1994c, A&AS, 105, 39
NASA ADS
-
Ferland, G. J. 1996, HAZY, a brief introduction to
Cloudy, University of Kentucky, Department of Physics and Astronomy
Internal Report
In the text
-
Fioc, M., & Rocca-Volmerange, B. 1997, A&A, 326, 950
In the text
NASA ADS
-
Fioc, M., & Rocca-Volmerange, B. 2000 [astro-ph/9912179]
In the text
-
French, H. B. 1980, ApJ, 240, 41
In the text
NASA ADS
-
Gallego, J., Zamorano, J., Aragón-Salamanca, A., & Rego, M.
1995, ApJ, 445, L1
In the text
NASA ADS
-
García-Vargas, M. L., Bressan, A., & Díaz, A. I.
1995a, A&AS, 112, 13
In the text
NASA ADS
-
García-Vargas, M. L., Bressan, A., & Díaz, A. I.
1995b, A&AS, 112, 35
In the text
NASA ADS
-
García-Vargas, M. L., & Díaz, A. I. 1994, ApJS, 91,
553
In the text
NASA ADS
-
García-Vargas, M. L. González-Delgado, R. M., Pérez, E., et al.
1997, ApJ, 478, 112
In the text
NASA ADS
-
Giavalisco, M., Steidel, C. C., & Maccheto, F. D. 1996, ApJ,
470, 189
In the text
NASA ADS
-
Girardi, L., Bressan, A., Chiosi, C., Bertelli, G., & Nasi, E. 1996, A&AS,
117, 113
In the text
NASA ADS
-
Goldader, J. D., Joseph, R. D., Doyon, R., & Sanders, D. B.
1997, ApJ, 474, 104
In the text
NASA ADS
-
González-Delgado, R. M., García-Vargas, M. L., Goldader, J.,
Leitherer, C., & Pasquali, A. 1999, ApJ, 513, 707
In the text
NASA ADS
-
González-Delgado, R. M., Leitherer, C., Heckman, T., et al.
1998, ApJ, 495,
698
In the text
NASA ADS
-
Greggio, L., Tosi, M., Clampin, M., et al.
1998, ApJ, 504, 725
In the text
NASA ADS
-
Groenewegen, M., & De Jong, T. 1993, A&A, 267, 410
In the text
NASA ADS
-
Heckman, T. M. 1991, in Massive Stars in Starbursts,
ed. C. Leitherer, T. M. Heckman, & C. A. Norman (Cambridge University Press),
289
In the text
-
Keel, W. C. 1993, AJ, 106, 1771
In the text
NASA ADS
-
Kennicutt, R. C. 1998, ARA&A,
36, 189
In the text
NASA ADS
-
Kim, D. C., Veilleux, S., & Sanders, D. B. 1998, ApJ, 508,
627
In the text
NASA ADS
-
Kurucz, R. L. 1992, Model Atmospheres for Population
Synthesis,
ed. B. Barbuy, & A. Renzini, The stellar populations of Galaxies, IAU Symp. 149 (Reidel, Dordrecht), 225
In the text
-
Lançon, A., & Rocca-Volmerange, B. 1996, New Astron.
1, 215
In the text
NASA ADS
-
Leech, K. J., Penston, M. V., Terlevich, R., et al.
1989, MNRAS, 240, 349
In the text
NASA ADS
-
Leitherer, C. 1998, in 38th
Herstmonceux Conference, The Stellar Initial Mass function,
ed. G. Gilmore, I. Parry, & S. Ryan (ASP, San Francisco),
61
In the text
-
Leitherer, C., Ferguson, H. C., Heckman, T. M., & Lowenthal,
J. D. 1995, ApJ, 454, L19
NASA ADS
-
Leitherer, C., & Heckman, T. M. 1995, ApJS, 96, 9
In the text
NASA ADS
-
Leitherer, C., Robert, C., & Drissen, L. 1992, ApJ,
401, 596
In the text
NASA ADS
-
Leitherer, C., Schaerer, D., Goldader, J. D., et al.
1999, ApJS,
123, 3
In the text
NASA ADS
-
Leitherer, C., Vacca, W. D., Conti, P. S., et al.
1996, ApJ, 465, 717
In the text
NASA ADS
-
Lejeune, T., Cuisinier, F., & Buser, R. 1997, A&AS, 125, 229
In the text
NASA ADS
-
Lowenthal, J., Koo, D., Guzmán, R., et al.
1997, ApJ, 481, 673
In the text
NASA ADS
-
Madau, P., Ferguson, H. C., Dickinson, M. E., et al.
1996, MNRAS, 283, 1388
In the text
NASA ADS
-
Mas-Hesse, J. M., & Kunth, D. 1999, A&A, 349, 765
In the text
NASA ADS
-
Mazzarella, J. M., & Balzano, V. 1986, ApJS, 85, 27
In the text
NASA ADS
-
McCall, M. L., Rybski, P. M., & Shields, G. A. 1985, ApJS, 57, 1
In the text
NASA ADS
-
McGaugh, S. 1991, ApJ, 380, 140
In the text
NASA ADS
-
Olofsson, K. 1997, A&A, 321, 29
In the text
NASA ADS
-
Rieke, G. H., Loken, K., Rieke, M. J., & Tamblyn, P. 1995, ApJ, 412, 99
NASA ADS
-
Salpeter, E. E. 1955, ApJ, 121, 161
In the text
NASA ADS
-
Schaerer, D. 1996, A&A, 309, 129
NASA ADS
-
Shields, G. A. 1974, ApJ, 193, 335
In the text
NASA ADS
-
Shields, G. A. 1978, ApJ, 219, 565
In the text
NASA ADS
-
Shields, G. A. 1990, ARA&A, 28, 525
In the text
NASA ADS
-
Shields, G. A., & Tinsley, B. M. 1976, ApJ, 203, 66
In the text
NASA ADS
-
Stasinska, G. 1978, A&A, 66, 257
In the text
NASA ADS
-
Stasinska, G. 1980, A&A, 84, 320
In the text
NASA ADS
-
Stasinska, G., & Leitherer, C. 1996, ApJS, 107, 661
In the text
NASA ADS
-
Stasinska, G., & Schaerer, D. 1997, A&A, 322, 615
In the text
NASA ADS
-
Steidel, C. C., Giavalisco, M., Pettini, M., Dickinson, M.,
& Adelberger, K. L. 1996, ApJ, 462, L17
In the text
NASA ADS
-
Storchi-Bergmann, T., Kinney, A. L., & Challis, P. 1995,
ApJS, 98, 103
In the text
NASA ADS
-
Terlevich, R. J. 1985, in Star Forming Dwarf Galaxies and Related Objects,
ed. D. Kunth, T. X. Thuan, & J. T. Thanh Van (Éditions Frontières,
Paris), 395
In the text
-
Terlevich, R., Melnick, J., Masegosa, J., Moles, M., & Copetti,
M. V. F. 1991, A&AS, 91, 285
In the text
NASA ADS
-
Vacca, W. D., Robert, C., Leitherer, C., & Conti, P. S. 1995, ApJ, 444,
647
In the text
NASA ADS
-
Veilleux, S., Kim, D.-C., Sanders, D. B., Mazzarella, J. M.,
& Soifer, B. T. 1995, ApJS, 98, 171
In the text
NASA ADS
-
Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295
In the text
NASA ADS
Copyright ESO 2001
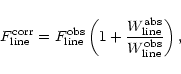
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9567f1a.eps}\hspace*{3mm}
...
....eps}\hspace*{3mm}
\includegraphics[width=7.5cm,clip]{9567f1d.eps}
\end{figure}](/articles/aa/full/2001/03/aa9567/Timg59.gif)
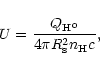
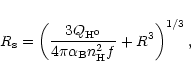
![\begin{figure}\par\includegraphics[width=7.5cm,clip]{9567f2a.eps}\hspace*{3mm}
\includegraphics[width=7.5cm,clip]{9567f2b.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg69.gif)
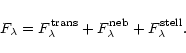
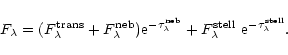
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9567f3a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{9567f3b.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg87.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9567f4a.eps}\hspace*{3mm}
\includegraphics[width=7.5cm,clip]{9567f4b.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg90.gif)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{9567f5.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg91.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9567f6.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg93.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9567f7a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{9567f7b.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg94.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9567f8a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{9567f8b.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg95.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9567f9a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{9567f9b.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg120.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9567f10a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{9567f10b.eps}
\par\end{figure}](/articles/aa/full/2001/03/aa9567/Timg121.gif)