A&A 365, 409-416 (2001)
DOI: 10.1051/0004-6361:20000508

ISO continuum observations of quasars at z=1-4[*]

I. Spectral energy distributions of quasars from the UV to far-infrared

S. Oyabu1 - K. Kawara1 - Y. Tsuzuki1 - Y. Sofue1 - Y. Sato1 - H. Okuda2,3 - Y. Taniguchi4 - H. Shibai5 - C. Gabriel6 - T. Hasegawa3 - E. Nishihara3

Send offprint request: S. Oyabu,


1 - Institute of Astronomy, The University of Tokyo, 2-21-1 Osawa Mitaka, Tokyo 181-0015, Japan
2 - Institute of Space and Astronautical Science (ISAS), 3-1-1 Yoshinodai, Sagamihara, Kanagawa 229-8510, Japan
3 - Gunma Astronomical Observatory, 6860-86 Nakayama, Takayama, Agatsuma, Gunma 371-0702, Japan
4 - Astronomical Institute, Tohoku University, Aoba, Sendai 980-8578, Japan
5 - Department of Astrophysics, School of Science, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8602, Japan
6 - ISO Data Centre, Astrophysics Division of ESA, Villafranca, 28080 Madrid, Spain

Received 10 August 2000 / Accepted 24 October 2000

Abstract
Eight luminous quasars with -30 < MB < -27 at z = 1.4-3.7 have been observed in the mid- and far-infrared using ISO. All the quasars have been detected in the mid-infrared bands of ISOCAM, while no far-infrared detections have been made with ISOPHOT. SEDs (Spectral Energy Distributions) from the UV to far-infrared have been obtained while supplementing ISO observations with photometry in the optical and near-infrared made from the ground within 17 months. The SEDs are compared with the MED (Mean spectral Energy Distributions) of low-redshift quasars with -27 < MB < -22. It is shown that our far-infrared observations were limited by confusion noise due to crowded sources.

Key words: infrared: galaxies - infrared: ISM: continuum - quasars: general - galaxies: photometry

Author for correspondance: shinki@mtk.ioa.s.u-tokyo.ac.jp


1 Introduction

The IRAS sky survey was the first observation in which many quasars in the far-infrared were detected, and Neugebauer et al. (1986) presented IRAS measurements of 179 quasars from 12 to 100 $\mu $m. Combining IRAS observations with data taken in other wavelengths, Sanders et al. (1989) have given SEDs from $\sim$0.3 nm to 6 cm of 109 quasars in the Palomar-Green (PG) survey (Green et al. 1986). Compiling Einstein, IUE, and IRAS data with a supplement of ground-based observations, Elvis et al. (1994) have presented SEDs for a sample of 47 normal quasars, and derived the SEDs for radio-quiet and radio-loud quasars. Recently, Andreani et al. (1999) have presented SEDs for 120 optically selected quasars at low- and high-redshift, combining sub-mm and mm observations with optical, near-infrared, IRAS, and radio observations.

The gross shape of quasars SEDs is characterized by two major features; the big blue bump shortward of 0.3 $\mu $m and the infrared bump between 2 and 200 $\mu $m (Sanders et al. 1989; Elvis et al. 1994). It is generally considered that the blue bump is dominated by thermal emission from an accretion disk. The infrared bump is ubiquitous in both radio-quiet and radio-loud quasars. The infrared emission in radio-loud quasars has generally been taken to be dominated by non-thermal emission (e.g., Impey & Neugebauer 1988; Bloom et al. 1994; Neugebauer & Matthews 1999).

The origin of the infrared emission in radio quiet quasars is generally attributed to thermal emission from heated dust. The rise from 1 $\mu $m minimum toward 3 $\mu $m, which is universally present in quasars, is naturally explained by the sublimation of dust grains at $\sim$1500 K (e.g., Kobayashi et al. 1993). This is expected from the current unified models of active galactic nuclei, which have a dusty obscuring torus around a central source. Pier & Krolik (1993) computed the infrared properties predicted for the dust obscuring tori surrounding central sources by modeling free parameters of the inner radius of the torus to its thickness, the Thomson depths constraining the outer radius of the torus, and the flux of the nuclear radiation. The infrared emission in 1-10 $\mu $m of PG quasars is well explained by their models, while the emission in the far-infrared is much greater than that predicted. Several models were proposed to account for the far-infrared emission of quasars; these are (1) warm dust in a distorted disk extending from 0.1 kpc to more than 1 kpc, which is heated directly by radiation from central source (Sanders et al. 1989), (2) dust clouds in the narrow line region heated by the radiation from the central sources and star-forming regions (Rowan-Robinson 1995), and (3) dust in the obscuring tori extending to 200-3 kpc (Andreani et al. 1999). However, it should be noted that temporal variations of 10 $\mu $m brightness of radio-quiet quasar PG 1535+547 found by Neugebauer & Matthews (1999) casts doubt on the thermal origin of the infrared emission in radio-quiet quasars.

High-redshift quasars have been widely recognized to provide unique probes of high-redshift star formation and galaxy evolution. Metallic abundance in high-redshift quasars is solar or higher metallicities out to z > 4. Comparing the UV-to-optical spectra of 186 quasars with 0 < z < 3.8, Osmer et al. (1994) concluded that there was no evidence for redshift-dependent spectral changes. Hamann & Ferland (1993) analyzed N $_{{\rm V}}$/C $_{{\rm IV}}$ and N $_{{\rm V}}$/He $_{{\rm II}}$ broad emission ratios, and found that metallicities in the broad line gas at high redshift are 1-10 times solar. The ratio of UV Fe $_{{\rm II}}$/Mg $_{{\rm II}}$ of B 1422+231 at z = 3.6 shows that the host galaxy was already in the late-evolutionary phase of the Fe enrichment by SNe Ia at z = 3.6 (Kawara et al. 1996; Yoshii et al. 1998). These all suggest that the central part of host galaxies formed rapidly at very high-redshift $z \geq 10$, and metallicity enrichment in the central part was already completed at z = 4-5.

Dust emission from high-redshift quasars provide another probe to study star formation and evolution of host galaxies, especially in outer regions. Up to date, many quasars at z > 3 have been detected in the region from 350 $\mu $m to 1.3 mm (e.g., Andreani et al. 1993; Chini & Krügel 1994; Dunlop et al. 1994; Isaak et al. 1994; McMahon et al. 1994; Ivison 1995; Omont et al. 1996a; Hughes et al. 1997; Benford et al. 1999; Carilli et al. 2000). An extensive 240 GHz survey by Chini et al. (1989) revealed that the majority of z < 1 quasars have dust masses about a few times 10 $^7~M_{\odot}$, comparable to normal spiral galaxies, thus suggesting that dust is heated by radiation from the central sources. On the other hand, dust masses $\geq$ 10 $^8~M_{\odot}$ have been found in six of 16 quasars at z > 4 (Omont et al. 1996a), and CO emission was found in three of these (Ohta et al. 1996; Omont et al. 1996b; Guilloteau et al. 1997, 1999; Carilli et al. 1999). This may imply that dust emission in these host galaxies may be dominated by radiation from star-forming regions at high-redshift.

To study the distribution of dust in high-redshift quasars, mid- and far-infrared observations are indispensable. The emission from sublimated dust could be observed in the mid-infrared, thus probing that the innermost part of the obscuring tori, and the distribution of dust from obscuring tori to disks (or outer star-forming regions) could be obtained from far-infrared observations. The IRAS sky survey has only detected several quasars at z > 3 with exceptionally high luminosity in the far-infrared (Neugebauer et al. 1986; Bechtold et al. 1994; Irwin et al. 1998); F08279+5255 (APM 08279+5255) at z = 3.87, 2126-158 (PKS 2126-15) at z = 3.275, and 0320-388 at z = 3.12. In hoping to detect more quasars, several groups have carried out mid- and far-infrared photometry using the Infrared Space Observatory (ISO; Kessler et al. 1996). The first report of the ISO European Central Quasar Programme which observed 70 quasars between 4.8 and 200 $\mu $m including high-redshift quasars has been published by Haas et al. (1998), and the ISO/NASA AGN Key Project has also observed 72 quasars and AGNs covering a range of redshift up to 4.7 (Wilkes et al. 1999). As an ISO open time program, we have executed mid- and far-infrared observations of eight quasars at 1.4 < z < 3.7 using the raster mapping mode. This paper presents the results of the photometry of these quasars supplemented with optical and near-infrared data taken on the ground. In the course of this work, mid- and far-infrared sources have serendipitously been discovered. These sources will be described in the forthcoming paper (Oyabu & Kawara 2000). Throughout this paper, H0 = 75 km s-1 Mpc-1 with q0 = 0 is assumed.

2 Observations and results

Eight quasars have been observed with ISO in revolution 169-781 (1996 March - 1998 January). Optical and near-infrared imaging observations have followed within 24 months (mostly within 17 months).

2.1 The sample


 

 
Table 1: Quasars' sample
Object RA (J2000) Dec. z MBa Radiob Rev (UT)c Other name and Notes
PC 1548+4637 15:50:07.6 +46:28:55 3.544 -27.0 Quiet 169 (960504)  
PC 1640+4628 16:42:05.1 +46:22:27 3.700 -26.8 Quiet 185 (960520)  
H 0055-2659 00:57:58.1 -26:43:14 3.662 -29.2 Optical 380 (961130)  
UM 669 01:05:16.8 -18:46:42 3.037 -28.4 Optical 415 (970104) Q 0102-190
B 1422+231 14:24:38.1 +22:56:01 3.62 -29.8d Loud 424 (970113) Lensed quasar
PG 1630+377 16:32:01.1 +37:37:49 1.478 -28.2 Quiet 424 (970113) Also observed on rev. 778 (980101)
PG 1715+535 17:16:35.4 +53:28:15 1.940 -28.5 Quiet 712 (971027)  
UM 678 02:51:40.4 -22:00:27 3.205 -29.4 Optical 781 (980104) Q 0249-222

a The absolute B magnitude for H0 = 75 km s-1 Mpc-1 with q0 = 0.0.
b Radio property; Quiet = radio quiet, Loud = radio loud, and Optical = optically selected.
c UT is given in the yymmdd format where yy = year, mm = month, and dd = day.
d $M_{B}\sim -26$ after demagnification (Kormann et al. 1994).

Table 1 lists the sample of the eight quasars in the sequence of ISO revolutions for execution. The sample consists of luminous quasars with MB < -28 except PC 1548+4637 and PC 1640+4628; these two quasars which were observed at the beginning of this work, turned out to be too faint to be detected in the far-infrared, and thus the sample selection criterion was changed to include very luminous quasars in low far-infrared background of infrared cirrus emission. Figure 1 presents the eight quasars (large filled diamonds) on the z - MB plane together with those (small filled circles) in the sample by Elvis et al. (1994) and those (faint gray points) complied by Véron-Cetty & Véron (1998). All the sample quasars are radio-quiet or optically selected except B 1422+231 which is a core-dominant flat-spectrum radio source.

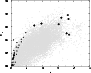  \begin{figure} \par\resizebox{80mm}{!}{\includegraphics{MS9157f1.eps}}\hfill \end{figure} Figure 1: Sample quasars (large filled diamonds) compared with other samples of quasars on the z - MB plane. Small filled circles show quasars studied by Elvis et al. (1994). Quasars cataloged by Véron-Cetty & Véron (1998) were plotted by dots, which appears as a gray background on this plane

2.2 Mid-infrared observations with ISOCAM

The mid-infrared observations were performed with ISOCAM (Cesarsky et al. 1996). Three broad band filters, namely, LW2 (reference wavelength 6.7 $\mu $m), LW3 (14.3 $\mu $m), and LW10 (12.0 $\mu $m) were used. All the quasars were observed in LW2 with additional measurements in LW3 or LW10. To detect faint sources against the intense background dominated by zodiacal light, the AOT (Astronomical Observation Template) CAM01 which is the microscan raster mapping mode was used to achieve accurate flat-fielding (e.g., Taniguchi et al. 1997; Altieri et al. 1999). Table 2 lists the details of CAM01 parameters as well as the characteristics of the broad band filters.

The standard ISOCAM reduction software CIA 3.0[*] was used to produce ISOCAM images from ERD (Edited Raw Data). This process includes dark subtraction, deglitching, correction for the transient behavior of ISOCAM pixel signals, and flat fielding (Delaney 1998). The inversion transient correction model of Starck et al. (1999) was applied. The factor of the correction for the transient behavior is 0.58-0.77 in LW2, 0.79-1.0 in LW10, and 0.87 in LW10. Figure 2 shows LW2 and LW3 maps for the two brightest quasars B 1422+231 and PG 1715+535. All the quasars were clearly detected at the expected positions. Aperture photometry was performed using IDL. Two apertures centered on the object were used; the small one has a diameter of $2d_{\rm airy}$, two times the Airy diameter as given in Table 2 and the other has a diameter of $4d_{\rm airy}$. The photometry was corrected for loss of flux in the PSF (Point Spread Function) wings by computing the PSF based on the model having a two mirror f/15 telescope with radii for the primary and secondary mirror of 30 and 10 cm, respectively (Müller 1999). The factor of the PSF correction is 0.75-0.90 (i.e., loss of flux is 0.1-0.25), depending on the raster step and the pixel field of view.


 

 
 
Table 2: Filters and settings for raster mapping

Filtera		 LW2 LW3 LW10 C_90 C_160
$\lambda_{\rm ref}$ 6.7 $\mu $m 14.3 $\mu $m 12.0 $\mu $m 90 $\mu $m 170 $\mu $m
$\Delta\lambda$ 3.5 $\mu $m 6.0 $\mu $m 7.0 $\mu $m 51 $\mu $m 89 $\mu $m
Airy diameterb 5.6 $^{\prime \prime }$ 12.0 $^{\prime \prime }$ 10.1 $^{\prime \prime }$ 76 $^{\prime \prime }$ 143 $^{\prime \prime }$
  Raster points M $\times$ N, Raster step, Exposure time per raster pointc, Pixel field of view
QSO field LW2 LW3 LW10 C_90 C_160

PC 1548+4637		 $5 \times 2$, 6 $^{\prime \prime }$, 60 s, 6 $^{\prime \prime }$ ... $4 \times 1$, 6 $^{\prime \prime }$, 25 s, 6 $^{\prime \prime }$ $4 \times 4$, 44 $^{\prime \prime }$, 64 s, 44 $^{\prime \prime }$ $3 \times 3$, 90 $^{\prime \prime }$, 64 s, 89 $^{\prime \prime }$
PC 1640+4628 $5 \times 2$, 6 $^{\prime \prime }$, 60 s, 6 $^{\prime \prime }$ ... $4 \times 1$, 6 $^{\prime \prime }$, 25 s, 6 $^{\prime \prime }$ $4 \times 4$, 44 $^{\prime \prime }$, 64 s, 44 $^{\prime \prime }$ $3 \times 3$, 90 $^{\prime \prime }$, 64 s, 89 $^{\prime \prime }$
H 0055-2659 $5 \times 2$, 6 $^{\prime \prime }$, 60 s, 6 $^{\prime \prime }$ ... ... $5 \times 3$, 44 $^{\prime \prime }$, 69 s, 44 $^{\prime \prime }$ $4 \times 2$, 90 $^{\prime \prime }$, 73 s, 89 $^{\prime \prime }$
UM 669 $ 6 \times 6$, 7 $^{\prime \prime }$, 90 s, 3 $^{\prime \prime }$ ... ... ... $10 \times 10$, 46 $^{\prime \prime }$, 16 s, 89 $^{\prime \prime }$
B 1422+231 $4 \times 4$, 7 $^{\prime \prime }$, 90 s, 3 $^{\prime \prime }$ $4 \times 4$, 7 $^{\prime \prime }$, 90 s, 3 $^{\prime \prime }$ ... ... $10 \times 10$, 46 $^{\prime \prime }$, 16 s, 89 $^{\prime \prime }$
PG 1630+377d $4 \times 4$, 7 $^{\prime \prime }$, 38 s, 3 $^{\prime \prime }$ $4 \times 4$, 7 $^{\prime \prime }$, 38 s, 3 $^{\prime \prime }$ ... ... $10 \times 10$, 46 $^{\prime \prime }$, 16 s, 89 $^{\prime \prime }$
PG 1715+535 $4 \times 4$, 7 $^{\prime \prime }$, 38 s, 3 $^{\prime \prime }$ $4 \times 4$, 7 $^{\prime \prime }$, 38 s, 3 $^{\prime \prime }$ ... ... $10 \times 10$, 46 $^{\prime \prime }$, 16 s, 89 $^{\prime \prime }$
UM 678 $4 \times 4$, 7 $^{\prime \prime }$, 90 s, 3 $^{\prime \prime }$ $4 \times 4$, 7 $^{\prime \prime }$, 90 s, 3 $^{\prime \prime }$ ... ... $6 \times 5$, 92 $^{\prime \prime }$, 64 s, 89 $^{\prime \prime }$

a Cited from $ISO\ Handbook\ Volume\ III\ (CAM)$ (Siebenmorgen et al. 1999) and $Volume\ V\ (PHT)$.
b The aperture photometry was performed by using the apertures with a diameter of $2\times d_{\rm airy}$ for ISOCAM and of $d_{\rm airy}$ for ISOPHOT. The diameter of the Airy disk $d_{\rm airy}$ is $2.44(\lambda/60~{\rm cm})$ in radian or $0.84\lambda~(\mu$m) in arcsec. Note that the FWHM of the Airy disk is $0.422 \times d_{\rm airy}$.
c ISOCAM exposure time per raster point is given as $T_{\rm int}\times N_{\exp}$ where $T_{\rm int}$ is an integration time of a single exposure and $N_{\exp}$ is the number of exposures. $T_{\rm int}= 5$ s was used for all LW2 and LW3 observations except for PG 1630+377 and PG 1715+535 for which $T_{\rm int}=2$ s was used. $T_{\rm int}=2$ s was used for LW10 observations.
d The second observation was executed on revolution 778 in C_160 with a parameter set of ( $ 6 \times 6$, 92 $^{\prime \prime }$, 64 s, 89 $^{\prime \prime }$).

 

 
Table 3: ISO mid/far-infrared flux density and UV to IR luminosity. This table is also available in electronic form at the CDS
via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5)
or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/365/409
  ISOCAM (mJy)   ISOPHOT (mJy)   Luminosity $~(10^{13}L_{\odot})^a$
Object LW2 LW3 LW10   C_90 C_160   $L_{\rm UVO}$ $L_{\rm ir}$ $L_{1.25~\mu{\rm m}}$
PC 1548+4637 $0.16\pm0.04$ ... $0.67\pm0.17$   $8.2\pm28$ $32\pm80$   11 <130 1.7
PC 1640+4628 $0.15\pm0.04$ ... $0.29\pm0.11$   $-8.3\pm20$ $83\pm121$   8.1 <240 1.8
H 0055-2659 $0.29\pm0.06$ ... ...   $16\pm19$ $-2.7\pm60$   24 <160 3.3
UM 669 $0.50\pm0.01$ ... ...   ... $-9.9\pm18$   27 <39 3.5
B 1422+231 $5.8\pm0.06 $ $15.1\pm0.07 $ ...   ... $83\pm56$   410 <320 64
PG 1630+377 $4.3\pm0.04 $ $7.3\pm0.07$ ...   ... $5.6\pm14$b   28 <16 4.3
PG 1715+535 $4.7\pm0.06 $ $10.3\pm0.06$ ...   ... $-13\pm16$   81 <26 9.4
UM 678 $0.73\pm0.01$ $1.9\pm0.03$ ...   ... $-15\pm58$   30 <116 5.9

a The UVO ($0.1~\mu$m to $1~\mu$m) luminosity $L_{\rm UVO}$ = $4\pi D_{\rm L}^{2} \times 2.3\int_{14.5}^{15.5}\nu f_\nu {\rm d}\log_{10}\nu$, the IR ($1.5~\mu$m to $100~\mu$m) luminosity $L_{\rm ir}$ = $4\pi D_{\rm L}^{2} \times 2.3 \int_{12.5}^{14.3}\nu f_\nu {\rm d}\log_{10}\nu$, and the $1.25~\mu$m luminosity $L_{1.25~\mu{\rm m}}$ = $4\pi D_{\rm L}^{2}\nu f_\nu$, where $D_{\rm L}$ and $f_{\nu}$ denote the luminosity distance and observed flux density, respectively. Where no observations exist such as $1~\mu$m flux densities, interpolated flux densities were used. $L_{\rm UVO}$ is based on the optical and near-infrared flux densities given in Table 4.
b $f_\nu(170~\mu{\rm m}) = 89\pm78$ mJy was obtained in the second observation.


  \begin{figure} \par\resizebox{80mm}{!}{\includegraphics{MS9157f2.eps}} \hfill \end{figure} Figure 2: ISOCAM LW2 (6.7 $\mu $m) and LW3 (14.3 $\mu $m) and ISOPHOT C_160 (170 $\mu $m) maps are shown on the top, middle, and bottom panels, respectively. B 1422+231 shown on the left was observed on revolution 424 and PG 1715+535 on revolution 712. The ISOCAM and ISOPHOT maps are 90 $^{\prime \prime }$ and 598 $^{\prime \prime }$(10$^\prime $), respectively, with North and East as indicated by the arrows. Quasars should be at the center of the gray circles

The results after these corrections are given in Table 3 with statistical errors. The errors in the absolute photometric calibration are not included in Table 3; these errors are estimated to be 15% (Siebenmorgen et al. 1999).


2.3 Far-infrared observations with ISOPHOT


The far-infrared observations were made with ISOPHOT (Lemke et al. 1996). All the quasars were observed in the broad C_160 (170 $\mu $m) band with additional measurement in C_90 (90 $\mu $m). ISO far-infrared surveys (Kawara et al. 1998; Puget et al. 1999) clearly indicate that the sky seen in the far-infrared has a clumpy structure which is made up of IR cirrus and extragalactic sources. This structure rotates with time relative to the ISO coordinate system due to the field rotation, increasing the probability of fault detection if the chopping mode is used. We thus selected the PHT22 staring raster map mode to make small maps around the quasar. Table 2 presents the characteristics of the photometric filters and the details of observational parameters for raster mapping.

ISOPHOT images were produced by using the standard ISOPHOT reduction software PIA V7.3 and V8.1[*] (Gabriel et al. 1997), starting at the edited raw data (ERD) created via the off-line processing version 7.0. The AOT/Batch processing mode of PIA is used with the default parameters to reduce ERD to the Astronomical Analysis Processing (AAP) level. This standard reduction includes linearization and deglitching of integration ramps on the ERD level, signal deglitching and drift recognition on the SRD (Signal per Ramp Data) level, reset interval normalization, signal deglitching, dark current subtraction, signal linearization, and vignetting correction[*] on the SCP (Signal per Chopper Plateau data) level. The responsivity calibration was made on the SPD (Standard Processed Data) level by using the second measurement of the internal Fine Calibration Source 1 (FCS1) which is calibrated against celestial standards. The correction for the transient behavior of the detectors was applied to point sources (quasars) on this level. Images were produced on the AAP (Astronomical Analysis Processing) in the mapping mode with median brightness values.

The correction for drift in the responsivity is not important to our observations, and so this correction was not made. To check the importance of the drift, the MEDIAN filter technique was applied to the results from AAP (hereafter called AAP map). Applying this technique to large AAP maps in the Lockman hole, Kawara et al. (1998) show that this is a powerful tool to correct for drift in the detector responsivity. However, unlike large AAP maps in the Lockman hole, the MEDIAN filter technique does not improve our AAP maps. This is attributed to the size of our AAP maps; the observing time of these small maps is shorter than the timescale of drift in the detector responsivity, and so impact by the drift is small. In fact, every detector pixel of the C100 and C200 detector arrays has been checked for signal, and neither spike noise nor drift in the responsivity was found. Maps with all the detector pixels always give better results than those obtained by masking some of the detector pixels. In addition, it was confirmed that there were no significant differences between two AAP maps produced by two different algorithms on the AAP level, namely, the full coverage and distance weighting algorithms. Figure 2 shows AAP maps of C_160 for the brightest quasars B 1422+231 and PG 1715+535.

Aperture photometry was then performed using IRAF[*] and Skyview[*] in the manner similar to ISOCAM. The original pixel sizes of AAP maps are equal to the raster steps. Because these are too large to center the aperture on the quasar with sufficient accuracy, AAP maps were rebinned in such a way that each original pixel is converted into $10 \times 10$ sub-pixels. Two apertures centered on the object were used; the small one has a diameter of $d_{\rm airy}$, the Airy diameter as given in Table 2, and the other has a diameter of $2d_{\rm airy}$. The photometry was corrected for loss of flux in the PSF (Point Spread Function) wings by computing the same PSF model as used for ISOCAM. The factor of the PSF correction is 0.63 except for PC 1548+4632 and PC 1640+4628. These two quasars were centered between four pixels in such a way that quasars illuminate the four pixels equally. Consequently the loss of flux measured with the two apertures is large, and the factor of the PSF correction is 0.27 for C_90 and 0.23 for C_160.

The results after these corrections are given in Table 3 with statistical errors. The errors in the absolute photometric calibration are not included in Table 3; these errors are estimated to be 30% (Klaas et al. 2000). It is noted that PG 1630+377 was observed twice at $170~\mu$m to check variability.


 

 
Table 4: Optical to near-infrared magnitudes. This table is also available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/365/409
This work
Object V R I J H $K^{\prime a}$ UTb Obs.c
PC 1640+4628 $20.13\pm0.12$ $19.38\pm0.16$ $18.80\pm0.15$ ... ... ... 970828 Kiso
PC 1640+4628 ... ... ... ... $17.8\pm 0.2$ ... 980606 OAO
H 0055-2659 $18.17\pm0.02$ $17.79\pm0.02$ $17.69\pm0.03$ ... ... ... 971018 CTIO
UM 669 $17.65\pm0.01$ $17.47\pm0.01$ $17.23\pm0.02$ ... ... ... 971018 CTIO
PG 1630+377 $16.13\pm0.01$ $15.76\pm0.16$ $15.51\pm0.15$ ... ... ... 970824 Kiso
PG 1630+377 ... ... ... $14.92\pm0.03$ $14.38\pm0.01$ $14.12\pm0.04$ 980603 OAO
UM 678 $17.63\pm0.02$ $17.62\pm0.02$ $17.30\pm0.03$ ... ... ... 971018 CTIO
Data from others
Objectd $u^\prime$ $g^\prime$ $r^\prime$ $i^\prime$ $z^\prime$ UT Obs.e
PG 1715+535 16.53 15.89 15.47 15.25 15.24 July 1995 R
PG 1630+377 16.27 16.13 15.94 15.83 15.70 July 1995 R
B 1422+231 ... 16.33 15.18 15.07 ... July 1995 R
PC 1548+4637 ... ... 19.27f ... ... April 1987 S

a The $K^\prime$ bandpass filter ( $2.15\pm0.15~\mu$m) is slightly narrower and bluer than the standard K filter ( $2.20\pm0.20~\mu$m).
b Universal time when observed in the yymmdd format.
c At the Kiso Observatory, the 20482 CCD with 1.5 $^{\prime \prime }$ per pixel was used on the 105 cm Schmidt telescope.
At CTIO, the 20482 CCD with 0.4 $^{\prime \prime }$ per pixel was used on the 90 cm telescope.
At OAO (Okayama Astrophysical Observatory), the infrared imager spectrometer which has a HgCdTe 2562 detector array with 0.97 $^{\prime \prime }$ per pixel was used on the 188 cm telescope.
d All but PG 1548+4637 were observed within 27 months before the ISO observations.
e R = Richards et al. (1997); S = Schneider et al. (1994).
f The r4 bandpass was used.

2.4 Optical and near-infrared data from ground-based observations

Optical images were taken on the 0.9 m telescopes at CTIO and the Schmidt 1.05 m telescope at Kiso Observatory. Near-infrared imaging was made in the standard dithering mode on the 1.88 m telescope at the Okayama Astrophysical Observatory, NAOJ. SExtractor (Bertin & Arnouts 1996) was applied to the optical and near-infrared images to perform photometry. Flux calibration was made using the standards given by Landolt (1992) in the optical and the UKIRT faint standards (Casali et al. 1992) in the near-infrared. A typical photometric error is 0.05 mag.

Table 4 presents magnitudes of the quasars together with statistical errors. As shown in the table, all the ground-based observations were performed within 24 months (mostly 17 months) from the ISO observations so as to reduce the chance of having flux variations between ISO and ground-based observations. Table 4 also supplements optical magnitudes taken by Richards et al. (1997) and Schneider et al. (1994). All the supplementary quasars but PG 1548+4637 were observed within 27 months before the ISO observations.

3 Discussion


  \begin{figure} \par\resizebox{17.8cm}{!}{\includegraphics{MS9157f3.eps}} \hfill \parbox[b]{18cm}{} \end{figure} Figure 3: Restframe SEDs compared with the MED of low-redshift quasars compiled by Elvis et al. (1994). Dashed lines show the $1\sigma $ deviation (actually 68 Kaplan-Meier percentile) envelopes. Asterisks denote data taken by Richards et al. (1997) and Schneider et al. (1994). The dot-dashed and dot lines for B 1422+231 shows the MED of radio-loud quasars from Elvis et al. (1994) and the SED of 3C 273 from Lichti et al. (1995), respectively. Note that $3\sigma $ upper limits correspond three times uncertainties listed in Table 3

All the quasars have been detected in the ISOCAM LW2 and LW3 or LW10 band. Combining optical and near-infrared observations, SEDs from the UV to mid-infrared have been obtained for eight quasars at z = 1.4-3.7. Figure 3 shows the restframe SEDs ($L_{\nu}$[*]). The down arrows indicate the $3\sigma $ upper limits obtained with the ISOPHOT observations. Note that $3\sigma $ upper limits in Fig. 3 correspond to three times uncertainties listed in Table 3. The mean spectral distributions (MEDs) of low redshift quasars by Elvis et al. (1994) are also shown by fitting to the ISO $6.7~\mu$m flux density. Note that $6.7~\mu$m in the observing frame is approximately $1.25~\mu$m in the restframe. The dash lines indicate the $1\sigma $ deviation (strictly speaking 68 Kaplan-Meier percentile) envelopes. The rise from the 1 $\mu $m minimum toward 3 $\mu $m is evident at least in z = 3.5 quasar PC 1548+4637. This rise is naturally explained by the sublimation of dust grains at $\sim$$1\,500$ K (e.g., Kobayashi et al. 1993) as expected from the current unified models of active galactic nuclei. Hence, our data suggest that the obscuring torus model could be applied to high-redshift quasars.

The original objective of this work was to study whether there was any evidence for redshift-dependent changes in SEDs from the UV to far-infrared. As shown in Fig. 3, the data from the UV to mid-infrared do not deviate significantly from the MED of the low-redshift sample. However, this cannot be taken as evidence for no SED evolution in the UV to mid-infrared, because our sample is too small in number and too narrow in spectral coverage. Our far-infrared observations only provide $3\sigma $ upper limits, and are not very helpful to check SED evolution in the far-infrared.

The far-infrared detection with ISO have been severely limited by the confusion due to galaxies and local peaks of the IR cirrus (Kawara et al. 1998; Herbstmeier et al. 1998; Matsuhara et al. 2000). Simulating the 90 and 170 $\mu $m source counts in the Lockman Hole, Kawara et al. (2000a, 2000b) concluded that the effect of confusion due to crowded sources (presumably extragalactic) was significant in the flux range below 200 mJy, and 50% of 140 mJy sources at 170 $\mu $m were left undetected due to confusion noise. The expected fluxes of our sample quasars ranges from 7-170 mJy at 170 $\mu $m. Such confusion is clearly seen in Fig. 2. There are a few sources scattering around the quasar, which hampers detection in the far-infrared. It should be noted that the brightest source in the PG 1630+377 field has 106 mJy and the one in PG 1715+535 has 190 mJy (Oyabu & Kawara 2000).

It is clear that larger aperture telescopes like FIRST, which provide spatial resolution finer than ISO, are required for far-infrared studies of high-redshift quasars. In cases where similar aperture telescopes such as IRIS(ASTRO-F) and SIRTF are used, data sampling, namely a step size of raster mapping, should be carefully designed so that far-infrared images can be improved by deconvolution without violating the sampling theorem (Magain et al. 2000).

Acknowledgements
We wish to thank the staff of Vilspa, CTIO, OAO, and the Kiso observatory for their assistance and hospitality. We are grateful to T. Tsuji for his continuous support to this work. We thank the referee, P. Andreani, for valuable suggestions on how to improve this work.

References

 
Copyright ESO 2001