A&A 365, 545-561 (2001)
DOI: 10.1051/0004-6361:20000075

Incidence and survival of remnant disks around
main-sequence stars[*][*]

H. J. Habing1 - C. Dominik1 - M. Jourdain de Muizon2,3 - R. J. Laureijs4 - M. F. Kessler4 - K. Leech4 -
L. Metcalfe4 - A. Salama4 - R. Siebenmorgen4 - N. Trams4 - P. Bouchet5

Send offprint request: H. J. Habing,


1 - Sterrewacht, Leiden, PO Box 9513, 2300 RA Leiden, The Netherlands
2 - DESPA, Observatoire de Paris, 92190 Meudon, France
3 - LAEFF-INTA, ESA Vilspa, PO Box 50727, 28080 Madrid, Spain
4 - ISO Data Center, Astrophysics Division of ESA, Vilspa, PO Box 50727, 28080 Madrid, Spain
5 - Cerro Tololo Inter-American Observatory, NOAO, Casilla 603, La Serena, Chile 1353

Received 8 August 2000 / Accepted 26 October 2000

Abstract
We present photometric ISO 60 and 170 um measurements, complemented by some IRAS data at 60  \ensuremath {\mu \textrm {m}}, of a sample of 84 nearby main-sequence stars of spectral class A, F, G and K in order to determine the incidence of dust disks around such main-sequence stars. Fifty stars were detected at 60  \ensuremath {\mu \textrm {m}}; 36 of these emit a flux expected from their photosphere while 14 emit significantly more. The excess emission we attribute to a circumstellar disk like the ones around Vega and $\beta$ Pictoris. Thirty four stars were not detected at all; the expected photospheric flux, however, is so close to the detection limit that the stars cannot have an excess stronger than the photospheric flux density at 60  \ensuremath {\mu \textrm {m}}. Of the stars younger than 400 Myr one in two has a disk; for the older stars this is true for only one in ten. We conclude that most stars arrive on the main sequence surrounded by a disk; this disk then decays in about 400 Myr. Because (i) the dust particles disappear and must be replenished on a much shorter time scale and (ii) the collision of planetesimals is a good source of new dust, we suggest that the rapid decay of the disks is caused by the destruction and escape of planetesimals. We suggest that the dissipation of the disk is related to the heavy bombardment phase in our Solar System. Whether all stars arrive on the main sequence surrounded by a disk cannot be established: some very young stars do not have a disk. And not all stars destroy their disk in a similar way: some stars as old as the Sun still have significant disks.

Key words: stars: planetary systems - infrared: stars

Author for correspondance: habing@strw.leidenuniv.nl


1 Introduction

In 1983, while using standard stars to calibrate the IRAS photometry, Aumann et al. (1984) discovered that Vega ($\alpha$ Lyr), one of the best calibrated and most used photometric standards in the visual wavelength range, emits much more energy at mid- and far-infrared wavelengths than its photosphere produces. Because the star is not reddened Aumann et al. proposed that the excess IR radiation is emitted by small, interplanetary-dust particles in a disk rather than in a spherical envelope. This proposal was confirmed by Smith & Terrile (1984) who detected a flat source of scattered light around $\beta$ Pic, one of the other Vega-like stars detected in the IRAS data (Gillett 1986), and the one with the strongest excess. The disk around Vega and other main-sequence stars is the remnant of a much stronger disk built up during the formation of the stars. Aumann et al. (1984) pointed out that such disks have a lifetime much shorter than the stellar age and therefore need to be rebuilt continuously; collisions between asteroids are a probable source of new dust (Weissman 1984). Except for the somewhat exceptional case of $\beta$ Pic (Hobbs et al. 1985) and in spite of several deep searches no trace of any gas has ever been found in the disks around main-sequence stars; see e.g. Liseau (1999).

Since 1984 the search for and the study of remnant disks has made substantial progress by the discovery of numerous "fatter'' disks around pre-main sequence stars that contain dust and gas; for overviews see Beckwith & Sargent (1996), Sargent & Welch (1993), van Dishoeck & Blake (1998). The IRAS data base also contains detections of Vega-like disks around red giant stars that have developed from A and F-type main-sequence stars (Plets et al. 1997).

The discovery of Aumann et al. has prompted deeper searches in the IRAS data base with different strategies (Aumann 1985; Walker & Wolstencroft 1988; Mannings & Barlow 1998). For a review see Backman & Paresce (1993). Recently Plets & Vynckier (1999) have discussed these earlier results and concluded that a significant excess at $60~\mu$m is found in $13\pm 10\%$ of all main sequence stars with spectral type A, F, G and K. Unfortunately all these studies based on IRAS data only were affected by severe selection effects and did not answer important questions such as: will a star loose its disk when it grows older? On what time-scale? Does the presence of planets depend on the stellar main-sequence mass? Do multiple stars have disks more, or less frequently? Do stars that formed in clusters have disks less often? With such questions unanswered we clearly do not understand the systematics of the formation of solar systems.

Here we present results of a continuation with ISO (Kessler et al. 1996) of the succesful search of IRAS. Our aim has been to obtain a better defined sample of stars. The major step forward in this paper is not in the detection of more remnant disks, but in reliable information about the presence or absence of a disk. Earlier reports on results from our program have been given in Habing et al. (1996), Dominik et al. (1998), Jourdain de Muizon et al. (1999) and Habing et al. (1999).

2 Selecting and preparing the sample

Stars were selected so that their photospheric flux was within our sensitivity limit. Any excess would then appear immediately. We also wanted to make certain that any excess flux should be attributed to a circumstellar disk and not to some other property of the star, such as circumstellar matter ejected during the stellar evolution or to the presence of a red companion.

In selecting our stars we used the following criteria:

To illustrate what stars are bright enough to be included we use an equation that gives the stellar colour, ( $V-[60~\mu {\rm m}]$), as a function of (B-V). The equation has been derived empirically from IRAS data by Waters et al. (1987); we use a slightly different version given by H. Plets (private communication):

 
$\displaystyle V-[60~\mu {\rm m}]$ = 0.01+2.99(B-V)  
    -1.06(B-V)2+0.47(B-V)3. (1)

The zero point in this equation has a formal error of 0.01. Intrinsic, reddening-free (B-V) values must be used, but all our stars are nearby and we assume that the measured values are reddening-free. A posteriori we checked that we may safely ignore the reddening produced by the disks that we detected; only in the case of $\beta$ Pic is a small effect expected. Adopting a flux density of 1.19 Jy for $[60~\mu {\rm m}]=0$ we find apparent-magnitude limits and distance limits of suitable main-sequence stars as summarized in Table 1. The distance limit varies strongly with spectral type.


 

 
Table 1: Apparent magnitude and distance from the Sun (in parsec) of main-sequence stars with a 60  \ensuremath {\mu \textrm {m}} flux density of 30 mJy
Sp. Type A0 A5 F0 F5 G0 G5 K0 K5
V(mag) 4.0 4.4 4.8 5.2 5.7 6.0 6.8 7.4
d(pc) 45 31 25 19 15 13 10 7.5



   
Table 2: The stars of the sample
HD HIP Name V B-V d Spect. age $T_{{\rm eff}}$
      mag mag pc   Gyrs K
(1) (2) (3) (4) (5) (6) (7) (8) (9)
693 910 6 Cet 4.89 0.49 18.9 F5V 5.13 6210
1581 1599 $\zeta$ Tuc 4.23 0.58 8.6 F9V 6.46 5990
2151 2021 $\beta$ Hyi 2.82 0.62 7.5 G2IV 5.37 5850
4628 3765   5.74 0.89 7.5 K2V 7.94 5050
4813 3909 $\phi^2$ Cet 5.17 0.51 15.5 F7IV-V 1.38 6250
7570 5862 $\nu$ Phe 4.97 0.57 15.1 F8V 3.16 6080
9826 7513 50 And 4.10 0.54 13.5 F8V 2.88 6210
10700 8102 $\tau $ Cet 3.49 0.73 3.6 G8V 7.24 5480
10780 8362   5.63 0.80 10.0 K0V 2.82 5420
12311 9236 $\alpha$ Hyi 2.86 0.29 21.9 F0V 0.81 7080
13445 10138   6.12 0.81 10.9 K0V 5.37 5400
14412 10798   6.33 0.72 12.7 G8V 7.24 5420
14802 11072 $\kappa$ For 5.19 0.61 21.9 G2V 5.37 5850
15008 11001 $\delta$ Hyi 4.08 0.03 41.5 A3V 0.45 8920
17051 12653 $\iota$ Hor 5.40 0.56 17.2 G3IV 3.09 6080
17925 13402   6.05 0.86 10.4 K1V 0.08 5000
19373 14632 $\iota$ Per 4.05 0.60 10.5 G0V 3.39 6040
20630 15457 $\kappa^1$ Cet 4.84 0.68 9.2 G5Vv 0.30 5750
20766 15330 $\zeta^1$ Ret 5.53 0.64 12.1 G2V 4.79 5750
20807 15371 $\zeta^2$ Ret 5.24 0.60 12.1 G1V 7.24 5890
22001 16245 $\kappa$ Ret 4.71 0.41 21.4 F5IV-V 2.04 6620
22049 16537 $\epsilon$ Eri 3.72 0.88 3.2 K2V 0.33 5000
22484 16852 10 Tau 4.29 0.58 13.7 F9V 5.25 5980
23249 17378 $\delta$ Eri 3.52 0.92 9.0 K2V 7.59 5000
26965 19849 o2 Eri 4.43 0.82 5.0 K1V 7.24 5100
30495 22263 58 Eri 5.49 0.63 13.3 G3V 0.21 5820
33262 23693 $\zeta$ Dor 4.71 0.53 11.7 F7V 2.95 6160
34411 24813 $\lambda$ Aur 4.69 0.63 12.7 G0V 6.76 5890
37394 26779   6.21 0.84 12.2 K1V 0.34 5100
38392     6.15 0.94 9.0 K2V 0.87 4950
38393 27072 $\gamma$ Lep 3.59 0.48 9.0 F7V 1.66 6400
38678 27288 $\zeta$ Lep 3.55 0.10 21.5 A2Vann 0.37 8550
39060 27321 $\beta$ Pic 3.85 0.17 19.3 A3V 0.28 8040
43834 29271 $\alpha$ Men 5.08 0.71 10.2 G5V 7.24 5630
48915 32349 $\alpha$ CMa -1.44 0.01 2.6 A0m   9920
50281 32984   6.58 1.07 8.7 K3V 2.63 5000
61421 37279 $\alpha$ CMi 0.40 0.43 3.5 F5IV-V 1.70 6700
74956 42913 $\delta$ Vel 1.93 0.04 25.0 A1V 0.35 9200
75732 43587 $\rho^1$ Cnc 5.96 0.87 12.5 G8V 5.01 5300
80007 45238 $\beta$ Car 1.67 0.07 34.1 A2IV   8600
95418 53910 $\beta$ UMa 2.34 0.03 24.4 A1V 0.36 9530
102647 57632 $\beta$ Leo 2.14 0.09 11.1 A3Vvar 0.24 8580
102870 57757 $\beta$ Vir 3.59 0.52 10.9 F8V 2.63 6180
103287 58001 $\gamma$ UMa 2.41 0.04 25.7 A0V SB 0.38 9440
106591 59774 $\delta$ UMa 3.32 0.08 25.0 A3Vvar 0.48 8630
110833 62145   7.01 0.94 15.1 K3V 12.60 5000
112185 62956 $\epsilon$ UMa 1.76 -0.02 24.8 A0p 0.30 9780
114710 64394 $\beta$ Com 4.23 0.57 9.2 G0V 3.63 6030
116842 65477 80 UMa 3.99 0.17 24.9 A5V 0.32 8000
126660 70497 $\theta$ Boo 4.04 0.50 14.6 F7V 2.95 6280
128167 71284 $\sigma$ Boo 4.46 0.36 15.5 F3Vwvar 1.70 6770
134083 73996 45 Boo 4.93 0.43 19.7 F5V 1.82 6500
139664 76829 g Lup 4.64 0.41 17.5 F5IV-V 1.12 6680
142373 77760 $\chi$ Her 4.60 0.56 15.9 F9V 8.51 5840
142860 78072 $\gamma$ Ser 3.85 0.48 11.1 F6V 3.24 6330
149661 81300 12 Oph 5.77 0.83 9.8 K2V 2.09 5200
154088 83541   6.59 0.81 18.1 K1V 7.24 5000
156026 84478   6.33 1.14 6.0 K5V 0.63 4350
157214 84862 72 Her 5.38 0.62 14.4 G0V 7.24 5790
157881 85295   7.54 1.36 7.7 K7V 5.25 3950
160691 86796 $\mu $ Ara 5.12 0.69 15.3 G5V 6.17 5750
161797 86974 $\mu $ Her 3.42 0.75 8.4 G5IV 4.79 5670


 
Table 2: continued
HD HIP Name V B-V d Spect. age $T_{{\rm eff}}$
      mag mag pc   Gyrs K
(1) (2) (3) (4) (5) (6) (7) (8) (9)
166620 88972   6.38 0.88 11.1 K2V 7.24 4970
172167 91262 $\alpha$ Lyr 0.03 0.00 7.8 A0Vvar 0.35 9620
173667 92043 110 Her 4.19 0.48 19.1 F6V 2.40 6370
185144 96100 $\sigma$ Dra 4.67 0.79 5.8 K0V 5.50 5330
185395 96441 $\theta$ Cyg 4.49 0.40 18.6 F4V 1.29 6750
187642 97649 $\alpha$ Aql 0.76 0.22 5.1 A7IV-V 1.23 7550
188512 98036 $\beta$ Aql 3.71 0.86 13.7 G8IV 4.27 5500
190248 99240 $\delta$ Pav 3.55 0.75 6.1 G5IV-Vvar 5.25 5650
191408 99461   5.32 0.87 6.0 K2V 7.24 4700
192310 99825   5.73 0.88 8.8 K3V   5000
197692 102485 $\psi$ Cap 4.13 0.43 14.7 F5V 2.00 6540
198149 102422 $\eta$ Cep 3.41 0.91 14.3 K0IV 7.94 5000
203280 105199 $\alpha$ Cep 2.45 0.26 15.0 A7IV-V 0.89 7570
203608 105858 $\gamma$ Pav 4.21 0.49 9.2 F6V 10.50 6150
207129 107649   5.57 0.60 15.6 G2V 6.03 5930
209100 108870 $\zeta$ Ind 4.69 1.06 3.6 K5V 1.29 4600
215789 112623 $\epsilon$ Gru 3.49 0.08 39.8 A3V 0.54 8420
216956 113368 $\alpha$ Psa 1.17 0.15 7.7 A3V 0.22 8680
217014 113357 51 Peg 5.45 0.67 15.4 G5V 5.13 5810
219134 114622   5.57 1.00 6.5 K3Vvar 12.60 4800
222368 116771 $\iota$ Psc 4.13 0.51 13.8 F7V 3.80 6190
222404 116727 $\gamma$ Cep 3.21 1.03 13.8 K1IV 8.91 5000

Table 2 contains basic data on all stars from the sample for which we present ISO data. Columns 1 and 2 contain the number of the star in the HD and in the Hipparcos Catalogue (Perryman et al. 1997) and Col. 3 the name. V and B-V have been taken from the Geneva photometric catalogue (Kunzli et al. 1997). Columns 6 and 7 contain the distance and the spectral type as given in the Hipparcos Catalog (Perryman et al. 1997). The age given in Col. 8 is from Lachaume et al. (1999), where errors in the age determinations are discussed. The effective temperature in Col. 11 has been derived by fitting Kurucz' model atmospheres to the Geneva photometry; we will need this temperature to calculate the dust mass from the flux-density excess at 60  \ensuremath {\mu \textrm {m}}.

3 Measurements, data reduction, checks

3.1 Measurements

Pre-launch recommendations made us start with chopped measurements (observing mode PHT03; see Laureijs et al. 2000) at 60, 90, 135 and 170 $\mu $m. After a few months of operation of the satellite it appeared that at 60 and 90 $\mu $m the on-off signal was strongly distorted by transients in the responsitivity of the detectors. Similarly, chopping appeared to be an inadequate observing mode at 135 and at 170 $\mu $m because of confusion with structure in the background from infrared cirrus. We therefore switched to the observing mode PHT22 and made minimaps. Minimaps consumed more observing time and we therefore dropped the observations at 90 and 135 $\mu $m. We tried to reobserve in minimap mode those targets that had already been observed in chopped mode (using extra time allocated when ISO lived longer than expected) but succeeded only partially: several targets had left the observing window. In total we used 65 hrs of observations. In this article we discuss only the stellar flux densities derived from the 60 and 170 $\mu $m minimaps. Appendix A contains a detailed description of our measurement procedure.

Instrumental problems (mainly detector memory effects) made us postpone the reduction of the chopped measurements until a later date; this applies also to the many (all chopped) measurements at 25  \ensuremath {\mu \textrm {m}}.

We added published (Ábrahám et al. 1998) ISOPHOT measurements of five A-type stars ($\beta$ UMa, $\gamma$ UMa, $\delta$ UMa, $\epsilon$ UMa and 80 UMa). The measurements have been obtained in a different mode from our observations, but we treat all measurements equally. These five stars are all at about 25 pc (Perryman et al. 1997), sufficiently nearby to allow detection of the photospheric flux. These stars are spectroscopic doubles and they do not fulfill all of our selection criteria; below we argue why we included them anyhow. Ábrahám et al. (1998) present ISOPHOT measurements of four more stars, which they assume to be at the same distance because all nine stars are supposed to be members of an equidistant group called the "Ursa Major stream''. The Hipparcos measurements (Perryman et al. 1997), however, show that four of the nine stars are at a distance of 66 pc and thus too far away to be useful for our purposes.

3.2 Data reduction

All our data have been reduced using standard calibration tables and the processing steps of OLP6/PIA7. These steps include the instrumental corrections and photometric calibration of the data. At the time when we reduced our data there did not yet exist a standard procedure to extract the flux. We therefore developed and used our own method - see Appendix B.

Later versions of the software which contain upgrades of the photometric calibration do not significantly alter our photometric results and the conclusions of this paper remain unchanged. For each filter the observing mode gave two internal calibration measurements which were closely tuned to the actual sky brightness. This makes the absolute calibration insensitive to instrumental effects as filter-to-filter calibrations and signal non-linearities which were among others the main photometric calibration improvements for the upgrades. In addition, it is standard procedure to ensure that each upgrade does not degrade the photometric calibration of the validated modes of the previous processing version.

   
Table 3: 60 \ensuremath {\mu \textrm {m}} data: see text for an explanation of the various columns
HD ISO_id $F_{\nu}$ $\sigma_{\nu}$ $F_{\nu}^{{\rm pred}}$ $F_{\nu}^{{\rm exc}}$ $F_{\nu}^{{\rm exc}}$/ $\sigma_{\nu}$ $F_{\nu}^{{\rm disk}}$ $\log\, \tau^{{\rm disk}}_{60}$ Reference
    mJy mJy mJy mJy   mJy    
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
693 74900501 33 34 43 -10 <1   <-4.6 ISO minimap
1581 69700102 94 19 94 0 <1   <-5.0 ISO minimap
2151   351 100 376 -25 <1     IFSC
4628 61901104 41 24 44 -4 <1   <-4.1 ISO minimap
4813 61901705 55 37 34 20 <1   <-4.3 ISO minimap
7570 72002506 85 25 47 38 1.6   <-4.4 ISO minimap
9826 61503786 100 22 98 2 <1   <-5.0 ISO minimap
10700 75701121 433 37 253 180 4.9 190 -4.6 ISO minimap
10780 61503507 43 30 41 3 <1   <-4.1 ISO minimap
12311 69100108 189 18 178 10 <1   <-5.6 ISO minimap
13445 73100771 25 24 26 -2 <1   <-4.1 ISO minimap
14412 76301673 -12 14 18 -30 <1   <-4.4 ISO minimap
14802 80201174 56 19 41 14 <1   <-4.5 ISO minimap
15008 71801511 41 9 30 10 1.1   <-5.4 ISO minimap
17051 76500413 45 15 31 14 <1   <-4.5 ISO minimap
17925 78100314 104 24 31 73 3.1 80 -3.9 ISO minimap
19373 81001847 122 13 116 6 <1   <-5.2 ISO minimap
20630 79201553 9 33 66 -57 <1   <-4.9 ISO minimap
20766 69100715 34 24 32 2 <1   <-4.4 ISO minimap
20807 57801756 30 13 39 -9 <1   <-4.9 ISO minimap
22001 69100659 52 9 42 9 1.0   <-5.1 ISO minimap
22049   1250 100 278 967 9.7 1260   IFSC
22484 79501562 141 27 89 51 1.9   <-4.6 ISO minimap
23249   270 100 363 -92 <1     IFSC
26965 84801865 121 21 128 -7 <1   <-4.7 ISO minimap
30495 83901668 174 31 33 141 4.5 150 -4.1 ISO minimap
33262 58900871 81 21 55 26 1.3   <-4.7 ISO minimap
34411 83801474 63 13 69 -5 <1   <-5.0 ISO minimap
37394 83801977 40 13 26 14 1.0   <-4.0 ISO minimap
38392 70201402 31 24 34 -2 <1   <-3.9 ISO minimap
38393 70201305 160 25 138 22 <1   <-5.1 ISO minimap
38678 69202308 349 22 60 289 13.3 310 -4.7 ISO minimap
39060 70201080 14700 346 54 14650 42.4 15500 -2.8 ISO minimap
43834 62003217 48 16 56 -8 <1   <-4.8 ISO minimap
48915 72301711 4230 155 4650 -420 <1   <-7.5 ISO minimap
50281 71802114 -4 16 30 -33 <1   <-4.3 ISO minimap
61421   2290 100 2350 -59 <1   <-6.0 IFSC
74956   399 100 226 173 1.7     IPSC
75732 17800102 160 28 35 126 4.4 130 -3.8 Dominik et al. 1998
80007   284 100 311 -27 <1     IFSC
95418 19700563 539 135 152 387 2.9 410 -5.0 Ábrahám et al. 1998
102647   784 100 213 571 5.7 750 -4.8 IFSC
102870   137 100 150 -14 <1   <-4.6 IFSC
103287 19500468 164 41 147 17 <1   <-5.5 Ábrahám et al. 1998
106591 19700973 94 59 69 25 <1   <-4.9 Ábrahám et al. 1998
110833 60000526 -7 14 15 -22 <1     ISO minimap
112185 34600578 322 81 223 99 1.2   <-5.4 Ábrahám et al. 1998
114710 61000119 106 34 93 13 <1   <-4.7 ISO minimap
116842 19500983 40 34 47 -7 <1     Ábrahám et al. 1998
126660 61000834 93 21 95 -2 <1   <-5.1 ISO minimap
128167 61001236 100 19 48 52 2.8 55 -5.0 ISO minimap
134083 61001337 70 26 36 34 1.3   <-4.5 ISO minimap
139664 64700880 488 48 45 442 9.2 470 -4.0 ISO minimap
142373 61001139 71 21 64 6 <1   <-4.8 ISO minimap
142860 63102981 113 24 109 4 <1   <-5.1 ISO minimap
149661 80700365 56 22 38 18 <1   <-4.1 ISO minimap
154088 64702041 40 55 17 22 <1   <-3.3 ISO minimap
156026 64702142 30 34 43 -13 <1   <-3.4 ISO minimap
157214 71000144 27 26 36 -8 <1   <-4.4 ISO minimap
157881 65000845 41 22 24 17 <1   <-2.6 ISO minimap
160691 64402347 73 18 52 21 1.2   <-4.5 ISO minimap
161797   222 100 281 -59 <1   <-4.6 IFSC


 
Table 3: continued
HD ISO_id $F_{\nu}$ $\sigma_{\nu}$ $F_{\nu}^{{\rm pred}}$ $F_{\nu}^{{\rm exc}}$ $F_{\nu}^{{\rm exc}}$/ $\sigma_{\nu}$ $F_{\nu}^{{\rm disk}}$ $\log\, \tau^{{\rm disk}}_{60}$ Reference
    mJy mJy mJy mJy   mJy    
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
166620 71500648 41 21 24 17 <1   <-3.8 ISO minimap
172167 71500582 6530 217 1170 5360 24.7 5700 -4.8 ISO minimap
173667 71500883 78 12 80 -1 <1   <-5.3 ISO minimap
185144 69500449 92 21 96 -5 <1   <-4.7 ISO minimap
185395 69301251 63 34 51 12 <1   <-4.7 ISO minimap
187642 72400584 1010 66 1050 -41 <1   <-6.1 ISO minimap
188512   257 100 269 -12 <1     IFSC
190248   174 100 250 -76 <1   <-4.6 IFSC
191408 72501252 43 37 62 -19 <1   <-4.0 ISO minimap
192310 70603454 73 13 44 29 2.2   <-4.1 ISO minimap
197692 70603356 68 18 76 -8 <1   <-5.2 ISO minimap
198149   552 100 393 159 1.6     IFSC
203280 61002158 253 49 243 10 <1   <-5.4 ISO minimap
203608 72300260 109 21 80 30 1.4   <-4.9 ISO minimap
207129 13500820 275 55 29 246 4.5 260 -3.8 Jourdain de Muizon et al. 1999
209100 70800865 146 24 166 -19 <1   <-4.4 ISO minimap
215789 71801167 74 16 60 14 <1   <-5.4 ISO minimap
216956 71800269 6930 204 605 6320 31.0 6700 -4.3 ISO minimap
217014 73601191 1 24 37 -36 <1   <-4.7 ISO minimap
219134 75100962 17 15 65 -48 <1     ISO minimap
222368 74702964 83 18 90 -7 <1   <-5.2 ISO minimap
222404   537 100 607 -70 <1     IFSC


   
Table 4: Flux densities measured at 170 \ensuremath {\mu \textrm {m}}. The various columns have the same meaning as in the previous table
HD ISO_id $F_{\nu}$ $\sigma_{\nu}$ $F_{\nu}^{{\rm pred}}$ $F_{\nu}^{{\rm exc}}$ $F_{\nu}^{{\rm exc}}$/ $\sigma_{\nu}$ $F_{\nu}^{{\rm disk}}$ $\log\, \tau^{{\rm disk}}_{170}$
    mJy mJy mJy mJy   mJy  
(1) (2) (3) (4) (5) (6) (7) (8) (9)
693 37500903 12 13 5 7 <1    
4628 39502509 -10 9 5 -15 <1    
4813 38701512 12 10 4 8 <1    
7570 38603615 14 36 5 9 <1    
9826 42301521 -22 82 10 -32 <1    
10700 39301218 125 21 28 97 4.7 120 -5.4
10780 45701321 180 626 4 176 <1    
12311 69100209 98 52 19 79 1.5    
14412 40101733 -20 12 2 -22 <1    
14802 40301536 1 16 5 -4 <1    
15008 75000612 23 49 3 20 <1    
17051 41102842 4 9 3 1 <1    
19373 81001848 -163 182 11 -174 <1    
20630 79201554 -122 85 6 -128 <1    
20807 57801757 73 17 4 69 4.1 80 -4.8
22001 69100660 -49 25 5 -54 <1    
22484 79501563 7 21 9 -2 <1    
26965 84801866 60 38 16 44 1.2    
30495 83901669 51 25 4 47 1.9    
33262 58900872 -33 33 6 -39 <1    
34411 83801475 -59 98 7 -66 <1    
37394 83801978 61 57 3 58 1.0    
38392 70201403 25 20 4 21 1.1    
38393 70201306 68 8 14 54 6.9 65 -5.4
38678 69202309 22 48 6 16 <1    
39060 70201081 3807 143 6 3801 26.5 4600 -3.2
48915 72301712 184 401 456 -272 <1    
50281 71802115 -826 268 2 -828 <1    
95418 19700564 133 73 13 120 1.6    
103287 19500469 95 117 12 83 <1    
106591 33700130 -5 17 7 -12 <1    
110833 60000527 -31 23   -31 <1    
112185 34600579 -35 65 21 -56 <1    
126660 61000935 -39 20 10 -49 <1    
128167 39400840 56 12 6 50 4.3 60 -5.0
139664 29101241 122 207 5 117 <1    
142373 62600340 -12 31 8 -20 <1    
142860 30300242 31 73 12 19 <1    
149661 30400943 113 69 4 109 1.6    
154088 45801569 -138 137 2 -140 <1    
156026 83400343 -383 318 6 -389 <1    
157214 33600844 -31 34 4 -35 <1    
160691 29101345 -171 65 5 -176 <1    
166620 36901487 -9 21 3 -12 <1    
172167 44300846 2621 142 123 2498 17.6 3000 -4.8
173667 31902147 -53 91 8 -61 <1    
185395 35102048 -35 26 5 -40 <1    
197692 70603857 27 34 8 19 <1    
203608 72300361 -52 9 10 -62 <1    
207129 34402149 293 23 3 290 12.4 350 -4.0
217014 37401642 -57 23 4 -61 <1    
222368 37800836 -30 59 10 -40 <1    
Note: Fluxes in Cols. 3, 4, 6, 7 are corrected for point spread function and Rayleigh-Jeans colour-correction, i.e. the inband flux has been divided by 0.64 (psf) and by 1.2 (cc). The ``Excess'' in Col. 8 is ``de-colour-corrected'' from Col. 6.

4 Results

4.1 Flux densities at 60 $\mu $m

The flux densities at 60  \ensuremath {\mu \textrm {m}} are presented in Table 3. The content of each column is as follows: Col. (1): the HD number; Col. (2): the TDT number as used in the ISO archive; Col. (3) the flux density corrected for bandwidth effects (assuming that the spectrum is characterized by the Rayleigh-Jeans equation) and for the fact that the stellar flux extended over more than 1 pixel; Col. (4) the error estimate assigned by the ISOPHOT software to the flux measurement in Col. (3); for the IRAS measurements the error has been put at 100 mJy; Col. (5) the flux expected from the stellar photosphere, $F^{{\rm pred}}_{\nu}$ as derived from Eq. (1) using the V and (B-V) values in Table 2; Col. (6): the difference between Cols. (3) and (5); we call it the "excess flux'', $F_{\nu}^{{\rm exc}}$; (7): the ratio of the excess flux compared to the measurement error given in Col. (4); when we concluded that the excess is real and not a measurement error we recalculated the monochromatic flux density by assuming a flat spectrum within the ISOPHOT 60 $\mu $m bandwidth; the result is in Col. (8) and is called $F_{\nu}^{{\rm disk}}$. Column (9) shows an estimate of $\tau_{60}^{{\rm disk}}$, the optical depth of the disk at visual wavelengths, but estimated from the flux density at $60~\mu$m; see below for a definition and see Appendix D for more details. Flux densities in Cols. (3), (4), (6) and (7) have been corrected for the point spread function being larger than the pixel size of the detector and for Rayleigh-Jeans colour-correction (cc); for ISO fluxes, the inband flux has been divided by 0.69 (the correction for the point spread function $(={\rm psf})$, see Appendix B) and by 1.06 (cc) and for IRAS fluxes, the IFSC or IPSC flux have been divided by 1.31 (cc). The "disk emission'' in Col. (8) is "de-colour-corrected'' from Col. (6).

We have checked the quality of our results at 60  \ensuremath {\mu \textrm {m}} in two ways: (i) by comparing ISO with IRAS flux densities; (ii) by comparing fluxes measured by ISO with predictions based on the (B-V)photometric index. The second approach allows us to assess the quality of ISO flux densities below the IRAS sensitivity limit.


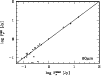  \begin{figure} \par\psfig{figure=isoiras.eps,width=8.8cm,clip=} \end{figure} Figure 1: Correlation of fluxes measured by IRAS and by ISO, respectively. The line marks the relation $F_{\nu }^{{\rm IRAS}}=F_{\nu }^{{\rm ISO}}$
Open with DEXTER


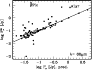  \begin{figure} \par\psfig{figure=meas_pred60.eps,width=8cm,clip=} \end{figure} Figure 2: Diagram of predicted and measured fluxes at 60  \ensuremath {\mu \textrm {m}}. The predicted fluxes were derived mainly from Eq. (1) except in a few cases where Kurucz model atmospherese were fitted to photometric points at optical wavelengths. See text. The line marks the relation $F_{\nu }= F_{\nu }^{{\rm pred}}$
Open with DEXTER


  \begin{figure} \par\psfig{figure=histex60.eps,width=7.5cm,clip=,angle=270} \end{figure} Figure 3: Histogram of the differences between the measured flux density and the one predicted at 60  \ensuremath {\mu \textrm {m}}. Top: distribution of the flux densities measured by ISO; there are three stars with an excess higher than 500 mJy; the drawn curve is a Gauss curve with average $\mu = 4~$mJy and dispersion $\sigma = 21~$mJy. Bottom: the same for stars where only IRAS data are available; two stars have an excess higher than 500 mJy
Open with DEXTER

4.2 The correlation between IRAS and ISO measurements at 60$~\mu$m

Figure 1 shows the strong correlation between IRAS and ISO 60  \ensuremath {\mu \textrm {m}} flux densities down to about the 60 mJy level of ISO. For three of the fainter stars the IRAS fluxes are considerably higher than those of ISO. For one of these three, HD 142860, the ISO measurements show the presence of two nearby 60 $\mu $m sources; the larger IRAS beam has merged the three sources; see Fig. 4. For the two remaining sources in Fig. 1 with different IRAS and ISO flux densities we assume that the IRAS measurement is too high because noise lifted the measured flux density above the detection limit, a well-known effect for measurements close to the sensitivity limit of a telescope.


  \begin{figure} \par\psfig{figure=HD142860r.eps,height=5.0cm,width=8.8cm,clip=} \par\end{figure} Figure 4: The 60 $\mu $m image in spacecraft orientation of the region around HD 142860 as obtained from the ISOPHOT minimap. There are three point sources in the field, the position of the source in the centre corresponds to the position of HD 142860. The upper source has $F_{\nu }=$ $140\pm 40$  mJy and coordinates (J2000) RA ${\rm 15^h 56^m 25^s}$, Dec $15^\circ 40' 43''$; the lower source has $F_{\nu }= 250\pm 40$ mJy and coordinates (J2000) RA ${\rm 15^h 56^m 33^s}$, Dec. $15^\circ 39' 15''$
Open with DEXTER

4.3 The correlation between predicted and measured flux densities at 60 $\mu $m

A strong correlation exists between predicted and measured flux density, Cols. (8) and (3) in Table 3, as seen in Fig. 2. Figure 3 shows that the distribution of the excess fluxes can be split into two components: a very narrow distribution around zero plus a strong wing of positive excesses, i.e. cases where we measure more flux than is produced by the stellar photosphere. In these cases a disk is very probably present. A Gauss curve has been drawn in the figure with parameters $\mu=4$ mJy and $\sigma=21$ mJy, where $\mu $ is the average and $\sigma$ the dispersion. The value of $\sigma$ agrees with the magnitude of individual error measurements as given in Col. 8 in Table 3. The one case in Fig. 3 with a strong negative excess, i.e. where we measured less than is predicted, concerns Sirius, $\alpha$ CMa; we interpret this negative excess as a consequence of the poor correction for transient effects of the detector for this strong infrared source.

We have concluded that a disk is present when $F_{\nu}^{{\rm exc}} >\mu+3\sigma= 65$ mJy. A summary of data on all stars with disks is in Table 6. HD 128167 has also been labelled as a "detection'' although $F_{\nu}^{{\rm exc}}$ is only $2.8\,\sigma_\nu$. The star is one of the few with a detection at 170  \ensuremath {\mu \textrm {m}} and this removed our doubts about the detection at 60  \ensuremath {\mu \textrm {m}}.

4.4 Results at 170 $\mu $m

The results are shown in Table 4 which has the same structure as Table 3. IRAS did not measure beyond 100  \ensuremath {\mu \textrm {m}} and we have no existing data to compare with our ISO data. Neither can we make a useful comparison between measured and predicted flux densities because the photospheric flux is expected to be roughly 1/8 of the 60  \ensuremath {\mu \textrm {m}} flux density and for most stars this is below the sensitivity limit of ISO.

We accepted fluxes as real when $F^{{\rm exc}}_{\nu}> 3\sigma_{\nu}$ and the minimap showed flux only in the pixel illuminated by the star. This leads to seven detections at 170  \ensuremath {\mu \textrm {m}} in Table 4. All seven stars have excess emission also at 60  \ensuremath {\mu \textrm {m}} except HD 20807 and HD 38393. Very probably these last two stars have accidentally been misidentified with unrelated background sources, as we will show now.

4.5 Should some detections be identified
with unrelated field sources?

We need to consider the possible influence of the field-source population upon our results.

Dole et al. (2000), Matsuhara et al. (2000), Oliver et al. (2000) and Elbaz et al. (2000) quote source counts at respectively 170, 90 and 15  \ensuremath {\mu \textrm {m}} from which the surface density of sources on the sky can be read down to the sensitivity limits of our measurements. In the 170 and 90  \ensuremath {\mu \textrm {m}} cases this involves the authors' extrapolations, via models, of their source counts from the roughly 100-200 mJy flux limits of their respective datasets. At 60  \ensuremath {\mu \textrm {m}} source counts can be approximated, with sufficient accuracy for present purposes, by interpolation from the other wavelengths. Using these source densities we now estimate the probability that our samples of detections contain one or two field sources unrelated to the star in question.

Since we know, for all of our targets, into exactly which pixel of the PHT map they should fall, we need to consider the probability that a field source with flux down to our sensitivity limit falls into the relevant PHT pixel. This effective "beam'' area is $45''\times 45''$ and $100''\times 100''$, at 60 and 170$~\mu$m respectively.

At 60  \ensuremath {\mu \textrm {m}} we have explored 84 beams (targets) and at 170  \ensuremath {\mu \textrm {m}} 52 beams (targets). We apply the binomial distribution to determine the probability P(q,r) that at least r spurious detections occur in q trials when the probability per observation equals p.

Table 5 lists the following parameters: Col. (1) shows the wavelength that we consider; Col. (3) contains the probability p to find a source in any randomly chosen pixel with a flux density above the limit $F_{\nu}^{{\rm lim}}$ given in Col. (2). Column (4) lists the number q of targets (i.e. trials) in the 60 and 170  \ensuremath {\mu \textrm {m}}  samples. Columns (5)-(7) give the probability P(q,r) of finding at least 1, 2 and 3 spurious detections with $F_{\nu} >F_{\nu}^{{\rm lim}}$ within a sample of size q.


 

 
Table 5: Probability of spurious detections
$\lambda$ $F_{\nu}^{{\rm lim}}$ p q P(q,1) P(q,2) P(q,3)
\ensuremath {\mu \textrm {m}} mJy          
60 100 0.006 84 0.397 0.091  
60 150 0.0015 84 0.117 0.007  
60 200 0.001 84 0.079 0.003  
170 50 0.15 52 1.000 0.997 0.988
170 100 0.07 52 0.975 0.881 0.702
170 200 0.04 52 0.875 0.61 0.334
170 300 0.005 52 0.226 0.027  
170 1000 0.00025 52 0.013    


4.5.1 Probability of spurious detections at 60 $\mu $m

It follows from Table 5 that there is a 40% chance that at least one of the two detections at 60$~\mu$m below 100 mJy is due to a field source, and there is a 9% chance that both are.

If we ignore field sources and consider the likelihood of spurious excesses occurring above a $3\,\sigma$ detection-limit due purely to statistical fluctuations in the measurements, we find that random noise contributes (coincidentally) a further 0.006 spurious detections per beam, on average, for the faintest detections (near $3\,\sigma$).

The cumulative probability, therefore, is 0.64 that at least 1 of the two detections at 60$~\mu$m below 100 mJy is not related to a disk; the probability is 0.17 that they are both spurious.

4.5.2 Probability of spurious detections at 170 $\mu $m

Table 4 lists 3 detections below 100 mJy. Two (HD 20630 and 38393) have not been detected at 60  \ensuremath {\mu \textrm {m}}. Table 5 shows that the probability is high that both are background sources unrelated to the two stars in question. In the further discussion these two stars have been considered to be without a disk. The third source with a 170  \ensuremath {\mu \textrm {m}} flux density below 100 mJy, HD 128167, has been detected also at 60  \ensuremath {\mu \textrm {m}}. We assume that this detection is genuine and that the source coincides with the star. The remaining four detections at 170  \ensuremath {\mu \textrm {m}} with $F_{\nu}> 100$ mJy are also correctly identified with the appropriate star.

   
Table 6: The 60$~\mu$m excess stars
        60$\mu $m 170$\mu $m  
HD Name Spect. age $F_{\nu}$ $\sigma_{\nu}$ $F_{\nu}^{{\rm disk}}$ $^{10}{{\rm\log}}\tau_{60}^{{\rm disk}}$ $F_{\nu}$ $\sigma_{\nu}$ $F_{\nu}^{{\rm disk}}$ $M_{\rm d}$
      Gyrs mJy mJy mJy   mJy mJy mJy $10^{-5}M_{\oplus}$
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12)
10700 $\tau $ Cet G8V 7.24 433 37 190 -4.6 125 21 120 20
17925   K1V 0.08 104 24 80 -3.9       108
22049 $\epsilon$ Eri K2V 0.33 1250 100 1260          
30495 58 Eri G3V 0.21 174 31 150 -4.1 51 25   73
38678 $\zeta$ Lep A2Vann 0.37 349 22 310 -4.7 22 48   18
39060 $\beta$ Pic A3V 0.28 14700 346 15500 -2.8 3810 143 4600 1200
75732 $\rho^1$ Cnc G8V 5.01 160 28 130 -3.8       130
95418 $\beta$ UMa A1V 0.36 539 135 410 -5.0 133 290   8
102647 $\beta$ Leo A3V 0.24 784 100 750 -4.8       13
128167 $\sigma$ Boo F3Vwvar 1.70 100 19 55 -5.0 56 12 60 8
139664 g Lup F5IV-V 1.12 488 48 470 -4.0 122 830   84
172167 $\alpha$ Lyr A0Vvar 0.35 6530 217 5700 -4.8 2620 142 3000 13
207129   G2V 6.03 275 55 260 -3.8 293 23 350 132
216956 $\alpha$ PsA A3V 0.22 6930 204 6700 -4.3       44
Note: Fluxes in Cols. 5, 6, 9, 10 are corrected for point spread function and Rayleigh-Jeans colour-correction. Excesses in Col. 7 and 11 are ``de-colour-corrected'' from Cols. 5 and 9 respectively (see text).

5 Discussion

Data for the stars with a disk are summarized in Table 6. Each column contains quantities defined and used in earlier tables with the exception of the last column that contains an estimate of the mass of the disk, $M_{\rm d}$.

5.1 Comparison with the IRAS heritage

The overall good agreement between the IRAS and ISO measurements has already been discussed. The IRAS data base has been explored by several different groups in search of more Vega-like stars. Backman & Paresce (1993) have reviewed most of these searches. Their Table X contains all stars with disks. For nine of those in Table X we have ISO measurements, and in eight cases these show the presence of a disk. The one exception is $\delta$ Vel, HD 74956. We find excess emission but the excess is insignificant (only $1.7\sigma$) and we did not include the star in Table 6. Thus our data agree well with those discussed by Backman & Paresce (1993). Although ISO was more sensitive than IRAS at 60  \ensuremath {\mu \textrm {m}} by about a factor of 5 we have only one new detection of a disk: HD 17925, with an excess of 82 mJy at 60  \ensuremath {\mu \textrm {m}}.

Plets & Vynckier (1999) have analysed IRAS data in search of "Vega-like'' stars and paid special attention to our list of candidate stars. In general there is good agreement between their conclusions and ours. Nine of the disk stars they find in IRAS we confirm with our ISO data. Four of the stars for which they find evidence of a disk at 60  \ensuremath {\mu \textrm {m}} are without excess emission in our sample. In two cases (HD 142860 and HD 215789) the difference IRAS/ISO is large: IRAS: 413 and 220 mJy; ISO: 113 and 78 mJy). In both cases we are of the opinion that at such low flux levels the ISO data are to be preferred over the IRAS data.

5.2 Differences with disks around pre-main-sequence stars

Disks have been found around many pre-main-sequence (= PMS) stars; here we discuss disks around main-sequence ($={\rm MS}$) stars. Disks around PMS stars are always detected by their molecular line emission; they contain dust and gas. The search for molecular emission lines in MS disks, however, has been fruitless so far (Liseau 1999). This is in line with model calculations by Kamp & Bertoldi (2000) who show that CO in disks around MS-stars will be dissociated by the interstellar radiation field. Recent observations with ISO indicate the presence of H2 in the disk around $\beta$ Pic and HST spectra show the presence of CO absorption lines (van Dishoeck, private communication), but the disk around $\beta$ Pic is probably much "fatter'' than those around our MS-stars; it is not even certain that $\beta$ Pic is a PMS or MS-star. We will henceforth assume that disks detected around MS-stars contain only dust and no gas.

5.3 A simple quantitative model

We have very little information on the disks: in most cases only the photometric flux at 60  \ensuremath {\mu \textrm {m}}. For the quantitative discussion of our measurements we will therefore use a very simple model. We assume a main-sequence star with an effective temperature $T_{{\rm eff}}$ and a luminosity \ensuremath{L_{\star}}. The star is surrounded by a disk of N dust particles. For simplicity, and to allow an easy comparison between different stars, we use a unique distance of the circumstellar dust of r=50 AU. This value is consistent with the measurements of spatially resolved disks like Vega and $\epsilon$ Eri and also with the size of the Kuiper Belt in our own solar system. The particles are spherical, have all the same diameter and are made of the same material. The important parameter of the disk that varies from star to star is N. The temperature, \ensuremath{T_{{\rm d}}}, of each dust particle is determined by the equilibrium between absorption of stellar photons and by emission of infrared photons; thus \ensuremath{T_{{\rm d}}} depends on  $T_{{\rm eff}}$.

Each dust particle absorbs photons with an effective cross section equal to $Q_\nu \pi a^2$; $Q_\nu$ is the absorption efficiency of the dust and a the radius of a dust particle. The average of $Q_\nu$over the Planck function will be written as $Q_{{\rm ave}}$. The dust particles absorb a fraction $\tau\equiv N Q_{{\rm ave}} (T_{{\rm eff}})\, a^2/(4\, r^2)$ of the stellar energy and reemit this amount of energy in the infrared; in all cases the value of $\tau $ is very small. We will call $\tau $ the "optical depth of the disk''; it represents the extinction by the disk at visual wavelengths:

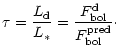$\displaystyle \tau=\frac{L_{{\rm d}}}{L_{*}}= \frac{F^{{\rm d}}_ {{\rm bol}}}{F^{{\rm pred}}_{{\rm bol}}}\cdot$     (2)

The mass of the disk, $M_{\rm d}$, is proportional to $\tau $:
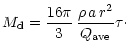$\displaystyle M_{{\rm d}}= \frac{16\pi}{3}\,\frac{\rho\, a\, r^2}{Q_{{\rm ave}}} \tau\cdot$     (3)

We will use spheres with a radius a of 1  \ensuremath {\mu \textrm {m}} and with material density $\rho$ and optical constants of interstellar silicate (Draine & Lee 1984); we use $Q_{{\rm ave}}= 0.8$ and derive $M_{\rm d}$ $= 0.5\,\tau\,$M$_\oplus$. It is known that the grains in Vega-like systems are much larger than interstellar grains. For A stars, the emission is probably dominated by grains larger than 10  \ensuremath {\mu \textrm {m}} (Aumann et al. 1984; Zuckerman & Becklin 1993; Chini et al. 1991), because smaller grains are blown out by radiation pressure. However, for F, G, and K stars, the blowout sizes are 1  \ensuremath {\mu \textrm {m}} or smaller and it must be assumed that the emission from these stars is dominated by smaller grains. We calculate mass estimates using the grain size of 1 \ensuremath {\mu \textrm {m}}. Since the mass estimates depend linearly upon the grain size, the true masses of systems with bigger grains can easily be calculated by scaling the value. The mean absorption efficiency factor $Q_{{\rm ave}}$ is only weakly dependent upon the grain size for sizes between 1 and 100 \ensuremath {\mu \textrm {m}}.

Numerical simulations made us discover a simple property of this model that is significant because it makes the detection probability constant for disks of stars of different spectral type . Define a variable called "contrast'': $ C_{60}\equiv (L_{\nu,{\rm d}} /L_{\nu,*})_{60~\mu {\rm m}}$, and assume black body radiation by the star and by the dust particles, then C60 is constant for $T_{{\rm eff}}$ in the range of A, F, and G-stars. The reason for this constancy is that when $T_{{\rm eff}}$ drops the grains get colder and emit less in total, but because 60  \ensuremath {\mu \textrm {m}} is at the Wien side of the Planck curve, their emission rate at 60  \ensuremath {\mu \textrm {m}} goes up. For a more elaborate discussion see Appendix C. Let us then make a two-dimensional diagram of the values of $\tau $ (or of $M_{\rm d}$) as a function of $T_{{\rm eff}}$ and C60: see Fig. 5. Constant values of $\tau $appear as horizontal contours for $T_{{\rm eff}}$> 5000 K. The triangles in the diagram represent the disks that we detected; small squares represent upper limits. The distribution of detections and upper limits makes clear that we detected all disks with $\tau>2~10^{-5}$ or $M_{{\rm d}}\,1.0~10^{-5}$ M$_\oplus$ around the A, F, G-type stars in our sample of 84 stars; we may, however, have missed a few disks around our K stars and we may have missed truncated and thus hot disks.


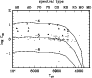  \begin{figure} \par { \psfig{figure=TeffC60.eps,width=8cm,clip=} }\end{figure} Figure 5: The 10logarithm of the fraction of stellar energy emitted by the disk is shown as a function of $T_{{\rm eff}}$ and C60. The labels to the curves indicate the 10logarithm of $\tau $. The triangles represent stars with a disk, and the small squares indicate the upper limit of non-detections. Using our standard dust particle model the mass of each disk is given by $M_{\rm d}=0.5\tau M_\oplus $ (see text)
Open with DEXTER

5.4 The incidence and survival of remnant dust disks

The results discussed here have also been presented in Habing et al. (1999).

Stellar ages have been derived in an accompanying paper (Lachaume et al. 1999). Errors in the determination of the ages have been given in that paper; occasionally they may be as large as a factor of 2 to 3; errors that large will not detract from our main conclusions.

5.4.1 The question of completeness and statistical bias

Our sample has been selected from the catalogue of stars within 25 pc from the Sun by Woolley et al. (1970); this catalogue is definitely incomplete and so must be our sample. Even within the distance limits given in Table 1 stars will exist that we could have included but did not. This incompleteness does not, however, introduce a statistical bias: we have checked that for a given spectral type the distribution of the stellar distances is the same for stars with a disk as for stars without a disk; this is illustrated by the average distances in Table 7.


 

 
Table 7: Average distances of stars with and without a disk
  # without disk # with disk
    (pc)   (pc)
A** 9 $22.6\pm 11.0$ 6 $16.8\pm 7.1$
F** 21 $14.6\pm 4.6$ 2 $14.0\pm ...$
G** 17 $12.3\pm 3.9$ 4 $11.3\pm 5.3$
K** 20 $9.5\pm 3.8$ 2 $6.6\pm ...$


5.4.2 Detection statistics and stellar age


  \begin{figure} \par { \psfig{figure=tauofage.eps,width=8cm,clip=} }\end{figure} Figure 6: $\tau $, the fraction of the stellar light reemitted at infrared wavelengths, is shown as a function of stellar age
Open with DEXTER


 

 
Table 8: Detection statistics
  <400 400-1000 1.0-5.0 >5.00
  Myr Myr Gyr Gyr
  tot disk tot disk tot disk tot disk
A** 10 6 4 0 1 0 0 0
F** 0 0 1 0 17 2 5 0
G** 2 1 0 0 7 0 12 3
K** 3 2 2 0 5 0 12 0
                 
total 15 9 7 0 30 2 29 3


Figure 6 presents graphically the fraction of the (visual) stellar light reemitted in the infrared by the disk as a function of the stellar age. Similar diagrams based mainly on IRAS results, have been published before- see, for example, Holland et al. (1998). A general, continuous correlation appears: disks around PMS-stars (e.g. Herbig AeBe) are more massive than disks around stars like $\beta$ Pic and Vega, and the disk around the Sun is still less massive. These earlier diagrams have almost no data on the age range shown in Fig. 6 and the new ISO data fill in an important hole.

Table 8 summarizes the detections at 60  \ensuremath {\mu \textrm {m}} separately for stars of different age and of different spectral type together with the same numbers for stars with a disk; in the column marked "tot'' the total number of stars (disks plus no-disks) is shown and under the heading "disk'' the number of stars with a disk. The total count is 81 instead of 84 because for three of our target stars (two A-stars and one K-star) the age could not be estimated in a satisfying manner. Table 8 shows that the stars with a detected disk are systematically younger than the stars without disk: out of the 15 stars younger than 400 Myr nine (60%) have a disk; out of the 66 older stars only five have a disk (8%). Furthermore, there exists a more or less sharply defined age above which a star has no longer a disk. This is best demonstrated by the A-stars. Six A-stars have a disk; the stellar ages are 220, 240, 280, 350, 360, 380 Myr. For the A-stars without disk the corresponding ages are 300, 320, 350, 380, 420, 480, 540, 890, 1230 Myr: 350 to 400 Myr is a well-defined transition region. We conclude that the A stars in general arrive on the main-sequence with a disk, but that they loose the disk within 50 Myr when they are about 350 Myr old.

Is what is true for the A-stars also valid for the stars of other spectral types? Our answer is "probably yes'': of the five F, G, and K stars younger than 400 Myr three (60%) have a disk. Of the 61 F, G, and K stars older than 400 Myr five have a disk (one in twelve or 8%). The percentages are the same as for the A-stars but the 60% for young G- and K-stars is based on only three detections. It seems that the disks around F, G, and K stars decay in a similarly short time after arrival on the main sequence.


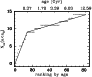  \begin{figure} \par { \psfig{figure=cumul_just_model.eps,width=8cm,clip=,angle=-90} }\end{figure} Figure 7: Cumulative distribution of excess stars, as a function of the index after sorting by age. The two segments of a continuous straight line are predicted by assuming that in the first 400 Myr the rate of disappearance of disks is much higher than afterwards (see text)
Open with DEXTER

An immediate question is: do all stars arrive at the main sequence with a disk? Studies of pre-main-sequence stars show that disks are common, but whether they always exist is unknown. The sequence of ages of the A-stars shows that the three youngest A-stars have a disk. This suggests that all stars arrive on the main sequence with a disk, but the suggestion is based on small-number statistics. We therefore leave the question without an answer but add two relevant remarks without further comment: some very young stars have no detectable disk, for example HD 116842 (A5V, 320 Myr), HD 20630 (G5V, 300 Myr), HD 37394 (K1V, 320 Myr) and some old stars have retained their disk; examples: HD 10700 (G8V, 7.2 Gyr), HD 75732 (G5V, 5.0 Gyr) and HD 207129 (G0V, 6.0 Gyr); the last case has been studied in detail (Jourdain de Muizon et al. 1999).

The age effect is shown graphically in Fig. 7; it displays the cumulative distribution of stars with a disk. The x-axis is the index of a star after all stars have been sorted by age. At a given age the local slope of the curve in this diagram gives the probability that stars of that age have a disk. The two line segments shows how the cumulative number increases when 70% of the disks disappear gradually in the first 0.4 Gyr and the remaining 30% gradually in the 12 Gyr thereafter.

In Sect. 5.6 we will review the evidence that at about 400 Myr after the formation of the Sun a related phenomenon took place in the solar system.

5.5 The need to continuously replenish the dust particles

In "Vega-like'' circumstellar disks the dust particles have a life-time much shorter than the age of the star. Within 1 Myr they will disappear via radiation pressure and the Poynting-Robertson effect (Aumann et al. 1984). An upper limit of 106 year is given for dust around A-type stars by Poynting-Robertson drag (Burns et al. 1979; Backman & Paresce 1993); the actual life time will be smaller: for $\beta$ Pic, Artymowicz & Clampin (1997) find only 4000 years. Continuously new grains have to replace those that disappear. A plausible mechanism that can supply these new grains at a high enough rate and for a sufficient long time are the collisions between asteroids and planetesimals. Direct detection of such larger bodies is not yet possible although the existence of comets around $\beta$ Pic is suggested by the rapidly appearing and disappearing components of the CaII K-absorption line (Ferlet et al. 1987). The total mass of the dust that ISO detected is about that of the Moon. To produce the dust for 400 Myr much more mass must be present in invisible form, that of asteroids or "planetesimals''. Thus the disappearance of the infrared excess on a timescale of 400 Myr does not trace the removal of the dust grains, but the lifetime of the disk or planetesimals that replenishes the dust. In the solar system the same may have happened; see below.

5.6 Disks in the presence of a companion star
or a planet

When a star has a companion or a planet the gravitational field will have a time-variable component. Will this component destroy the disk? Not necessarily so: the planets Jupiter and Saturn have both a dust disk and many satellites.

On purpose we did not select narrow binaries: we rejected stars within 1 arcmin from a target star, unless this other star was at least 5 magnitudes fainter in the V-band. This criterium accepts wide multiple-stars and indeed these occur. We used the Hipparcos Catalogue to check all 84 stars from Table 2 for multiplicity. Forty-eight stars have an entry in the "Catalogue of companions of double and multiple stars'' $(={\rm CCDM})$, see Dommanget & Nys (1994). Among the 14 stars with a disk there are seven wide multiple-stars. In one case (HD 22049) the star is part of an astrometric double; we ignore the object. That leaves us with six stars that have both a disk and stellar companions. The conclusion is therefore that companions do not necessarily destroy a disk.

Table 9 contains information on these six stars with both a disk and (at least) one companion. In Col. (1) the name appears, in Col. (2) the HD-number and in Col. (3) the entry-number in the CCDM; Col. (4) gives the total number of companions given in the CCDM, Col. (5) gives the distance, r, between A and B in astronomical units and Col. (6) the magnitude difference in the V-band between the first and the second component ("A'' and "B'', respectively).

There are at least two remarkable cases in Table 9. One is Vega (HD 172167) with four companions; its brightest companion is at 490 AU, but its closest companion at only 200 AU, just outside of Vega's disk. The other is $\rho^1$ Cnc that has a disk (Dominik et al. 1998; Trilling & Brown 1998; Jayawardhana et al. 2000), a planet (Butler et al. 1997) and a stellar companion.


 

 
Table 9: Multiple systems with a dust disk
Name HD CCDM $N_{{\rm tot}}$ r $\Delta m$
        AU  
$\tau $ Cet 10700 01441-1557 1 328 9.5
$\rho^1$ Cnc 75732 08526+2820 1 1100 7.2
$\beta$ Leo 102647 11490+1433 3 440 13.5
$\sigma$ Boo 128167 14347+2945 2 3700 5.3
$\alpha$ Lyr 172167 18369+3847 4 490 9.4
  207129 21483-4718 1 860 3.0


The data in Table 9 thus show that disks are found in wide multiple-systems: multiplicity does not necessarily destroy a disk.

5.7 The connection to the solar system

The solar system shows evidence for a fast removal of a disk of planetesimals a few hundred Myr after the Sun formed a disk. The best case is given by the surface of the Moon, where accurate crater counting from high resolution imaging can be combined with accurate age determinations of different parts of the Moon's surface. The age of the lunar surface is known from the rocks brought back to earth by the Apollo missions; the early history of the Moon was marked by a much higher cratering rate than observed today; see for a discussion Shoemaker & Shoemaker (1999). This so-called "heavy bombardment'' lasted until some 600 Myr after the formation of the Sun. Thereafter the impact rate decreased exponentially with time constants between 107 and a few times 108 years (Chyba 1990).

Other planets and satellites with little erosion on their surface confirm this evidence: Mercury (Strom & Neukum 1988), Mars (Ash et al. 1996; Soderblom et al. 1974) Ganymede and Callisto (Shoemaker & Wolfe 1982; Neukum et al. 1997; Zahnle et al. 1998). The exact timescales are a matter of debate. Thus there are indications of a cleanup phase of a few hundred Myr throughout the solar system; these cleanup processes may be dynamically connected.

6 Conclusions on the incidence of remnant disks

The photometers on ISO have been used to measure the 60 and 170 $\mu {\rm m}$ flux densities of a sample of 84 main-sequence stars with spectral types from A to K.

On the basis of the evidence presented we draw the following conclusions:

Acknowledgements
The ISOPHOT data presented in this paper were reduced using PIA, which is a joint development by the ESA Astrophysics Division and the ISOPHOT consortium. In particular, we would like to thank Carlos Gabriel for his help with PIA. We also thank J. Dommanget for helpful information on the multiplicity of our stars and the referee, R. Liseau for his careful comments. This research has made use of the Simbad database, operated at CDS, Strasbourg, France, and of NASA's Astrophysics Data System Abstract Service. CD was supported by the Stichting Astronomisch Onderzoek in Nederland, Astron project 781-76-015.

Appendix A Observing strategy for minimaps

The observations at 60  \ensuremath {\mu \textrm {m}} and 170  \ensuremath {\mu \textrm {m}} have been taken as minimaps with the C100 and C200 detector arrays using $3\times 3$ rastersteps; see Fig. A.1. In this figure the upper half shows the labeling, "p'', of the 9, respectively 4 pixels (detectors) for the C100 and C200 arrays. The lower diagram gives the numbering, "r'', of the successive array positions as it moves over the sky; the raster step is 46 arcsec for both arrays. Consider first a measurement with the C100 array. At raster step r=1 the source illuminates pixel p=7; at the next step, r=2, the source illuminates p=4, at r=3 the source is on p=1, etc. For the C200 measurements r=1has the source on p=1; at r=2 the source is half on p=1 and half on p=2; at r=3 the source is on p=2, etc.


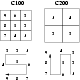  \begin{figure} \par {\psfig{figure=rasterr.eps,width=7cm,clip=} }\end{figure} Figure A.1: The upper half labels the different pixels of the C100 and C200 detectors seen in projection on the sky. The lower half describes the stepping directions: see text

B Data reduction

We used the following procedure to extract the flux. The result of a minimap measurement is a flux per pixel for each pixel and each raster position. Let f(p,r) be the measured flux in pixel p at raster position r. There are np pixels and nr raster positions. We first calculate a flat field correction $f_{{\rm flat}}(p)$ for each pixel by assuming that at one raster position the flux averaged over all pixels is the same


 

 
Table B.1: Weight factors for minimap flux determination
  Raster position
Pix 1 2 3 4 5 6 7 8 9
C100                  
1 0 0 1 0 0 ( $-\frac{1}{3}$) $-\frac{1}{3}$ $-\frac{1}{3}$ 0
2 $-\frac{1}{3}$ 0 0 1 0 ( $-\frac{1}{3}$) $-\frac{1}{3}$ 0 0
3 $-\frac{1}{3}$ $-\frac{1}{3}$ 0 0 0 ( $-\frac{1}{3}$) 0 0 1
4 0 1 0 0 0 (0) $-\frac{1}{3}$ $-\frac{1}{3}$ $-\frac{1}{3}$
5 $-\frac{1}{4}$ 0 $-\frac{1}{4}$ 0 1 (0) $-\frac{1}{4}$ 0 $-\frac{1}{4}$
6 $-\frac{1}{3}$ $-\frac{1}{3}$ $-\frac{1}{3}$ 0 0 (0) 0 1 0
7 1 0 0 $-\frac{1}{3}$ 0 (0) 0 $-\frac{1}{3}$ $-\frac{1}{3}$
8 0 0 $-\frac{1}{3}$ $-\frac{1}{3}$ 0 (1) 0 0 $-\frac{1}{3}$
9 0 $-\frac{1}{3}$ $-\frac{1}{3}$ $-\frac{1}{3}$ 0 (0) 1 0 0
C200                  
1 1 0 0 0 0 0 0 0 -1
2 0 0 1 0 0 0 -1 0 0
3 -1 0 0 0 0 0 0 0 1
4 0 0 -1 0 0 0 1 0 0



 
$\displaystyle f_{{\rm flat}}(p) = \frac{\frac{1}{n_p}\sum\limits_{p'=1}^{n_p}\sum\limits_{r'=1}^{n_r} f(p',r')}{\sum\limits_{r'=1}^{n_r}f(p,r')}\cdot$     (B.1)

Since the individual pixels in the C100/C200 cameras have different properties, we use the measurements of each pixel to derive a separate measurement of the source flux. In order to compute the background-subtracted source flux, we assign to each raster position a weight factor g(p,r). Since the exact point spread function is not known well enough, we use as on-source measurement the raster position where the pixel was centered on the source (weight factor 1). The background measurement is derived by averaging over the raster postions where the same pixel p was far away from the source (weight -1/3 or -1/4). Raster positions in which the pixel was partially on the source are ignored (weight 0). The resulting weight factors are given in Table B.1. The source flux measured by pixel p is given by
 
$\displaystyle F(p) = \frac{f_{{\rm flat}}}{f_{{\rm psf}}} \sum\limits_{r'=1}^{n_r} g(p,r') f(p,r')$     (B.2)

$f_{{\rm psf}}$ is the point spread function correction factor as given by Laureijs et al. (2000). We then derive the flux F and the error $\sigma$ by treating the different F(p) as independent measurements.
 
F = $\displaystyle \frac{1}{n_p} F(p)$ (B.3)


 
$\displaystyle \sigma$ = $\displaystyle \frac{1}{\sqrt{n_p-1}} \sqrt{\sum\limits_{p'=1}^{n_p} (F(p')-F)^{2}}.$ (B.4)

The point spread function is broader than a pixel. We have corrected for this, using the parameter $f_{{\rm psf}}$ given above. The correction factor may be too low: Dent et al. (2000) show that the disk around Fomalhaut ($\alpha$ PsA) is extended compared to our point-spread function. This means that all our 60  \ensuremath {\mu \textrm {m}} and 170  \ensuremath {\mu \textrm {m}} detections are probably somewhat underestimated.

We have ignored pixel 6 of the C100 camera entirely, because its characteristics differ significantly from those of the other pixels: it has a much higher dark signal and anomalous transient behaviour.

In the future the characteristics of each pixel will be determined with increasing accuracy. It may prove worthwhile to redetermine the fluxes again.

Appendix C Optical depth of the disk, detection limit and illumination bias

We discuss how the contrast factor, C60, depends on the spectral type of the star, $T_{{\rm eff}}$, and on the optical depth, $\tau $, of the disk. The dust grains in the remnant disk are relatively large, at least in cases where a determination of the grain size has been possible (Bliek et al. 1994; Artymowicz et al. 1989) and the absorption efficiency for stellar radiation will be high for stars of all spectral types. The efficiency for emission is low: the dust particles emit beyond 30  \ensuremath {\mu \textrm {m}} and these wavelengths are larger than that of the particles. We assume that the dust grains are all of a single size, a, and located at a single distance, r, from the star. We will introduce various constants that we will call Ai, i=0-6.

 
$\displaystyle C_{60}\equiv \frac{L_{\nu,{\rm d}}}{L_{\nu,*}}= \frac{L_{\nu,{\rm d}}}{L_{d}}\cdot \frac{L_{\rm d}}{L_{*}}\cdot \frac{L_{*}}{L_{\nu,*}}\cdot$     (C.1)

First we determine $L_{\nu,{{\rm d}}}$, the luminosity of the disk at the frequency $\nu$, and $L_{{\rm d}}$, the total luminosity of the disk:
 
$\displaystyle L_{\nu,{{\rm d}}}=N 4\pi^2 a^2 Q_\nu B_\nu(T_{{\rm d}})$     (C.2)

and
 
$\displaystyle L_{{\rm d}}= N 4\pi^2 a^2\int_0^\infty Q_\nu B_\nu(T_{{\rm d}}) {\rm d}\nu.$     (C.3)

We consider dust emission at 60  \ensuremath {\mu \textrm {m}}; $B_\nu(T)$ can be approximated by the Wien-equation. We thus write:
 
$\displaystyle L_{\nu,{\rm d}}= A_0 \exp\left (-\frac{240~{\rm K}}{T_{{\rm d}}}\right )$     (C.4)

Define the average absorption efficiency:
 
$\displaystyle Q_{{\rm ave}}(T_{{\rm d}})\equiv\pi{\int_{0}^{\infty}}{Q_\nu B_\nu} (T_{{\rm d}}) {\rm d}\nu /(\sigma T_{{\rm d}}^4).$     (C.5)

For low dust-temperatures $Q_{{\rm ave}}$can be approximated by $Q_{{\rm ave}}=A_1 \ensuremath{T_{{\rm d}}} ^{\alpha}$ with $\alpha\approx 2$ (Natta & Panagia 1976) and thus
 
$\displaystyle L_{{\rm d}}= A_2 T_{{\rm d}}^6.$     (C.6)

Second, we determine the stellar luminosity, $L_{\nu,*}$, at frequency $\nu$ and the total stellar luminosity, L*, both by ignoring the effects of dust, that is the luminosity at the photospheric level. The photospheric emission is approximated by the Rayleigh-Jeans equation:
 
$\displaystyle L_{\nu,*}=\frac{\pi B_\nu(T_{{\rm eff}})} {\sigma T_{{\rm eff}}^4} L_*= \frac{A_3 L_*}{T_{{\rm eff}}^{3}}\cdot$     (C.7)

The stellar luminosity for main sequence stars of spectral type A0-K5 can be approximated within 30% by:
 
$\displaystyle L_*=A_4 \, T_{{\rm eff}}^{8.2}.$     (C.8)

Third, we determine the relation between $T_{{\rm d}}$ and $T_{{\rm eff}}$. For photospheric temperatures $Q_{{\rm ave}}$is independent of $T_{{\rm eff}}$. The energy absorbed by a grain is thus $\propto L_*\propto T_{{\rm eff}}^{8.2}$. The energy emitted is $\propto T_{{\rm d}}^6$. Because the energy emitted equals the energy absorbed we conclude that $T_{{\rm eff}}= A_5 T_{{\rm d}}^{6/8.2}$.

Combining these results we find

 
$\displaystyle C_{60}= {A_6}\cdot\frac{1}{T_{{\rm d}}^{3.8}}\cdot \exp\left (-\frac{240}{T_{{\rm d}}}\right ).$     (C.9)

We have calculated C60 without making the various approximations in Eqs. (C.1) through (C.7): Fig. C.1 shows the results. The results are valid if the distance dustring/star is the same (50 AU) for all stars irrespective of the spectral type.

In the figure we assume that for an A0-star C60 has the value 1 and $T_{{\rm d}}= 80$ or 120 K. For a star of later spectral type, the dust will be cooler and will emit less energy (see Eq. (C.6)), but since $\lambda= 60~\mu$m is at the Wien-side of the black body curve, the emission at 60  \ensuremath {\mu \textrm {m}} will increase- see Eq. (C.4). The consequence is that C60 remains constant for A-, F- and early G-type stars. For late G- and for K- and M-type stars the dust becomes too cold to be detected at 60  \ensuremath {\mu \textrm {m}}. Only photometry at longer wavelengths will ultimately be able to detect such very cold disks.


  \begin{figure} \par { \psfig{figure=analytically.eps,width=8cm,clip=} }\end{figure} Figure C.1: The contrast factor $C_{60} \equiv F_\nu ^{{\rm d}}/F_\nu ^{{\rm pred}}$ for a ring of dust at a distance of 50 AU from the star and for stars of different effective temperature. We assumed $T_{{\rm d}}$ to be 80 or 120 K for an A0 star

Appendix D Determination of $\mathsf{\tau}$ from observed fluxes

For most of our stars we have only a detection of the disk at 60  \ensuremath {\mu \textrm {m}}. To calculate the optical depth and the mass of the disk we need an estimate of the disk emission integrated over all wavelengths. If the dust around an A star has a temperature of $\hbox{$T_{\rm d}\kern -8.7pt\raise 7.5pt\hbox{\tiny$\circ$ }$ ~}$, the stars of later types will have lower dust temperatures. Numerical evaluation shows that, assuming constant distance between the star and the dust, the following relation is a good approximation

 
$\displaystyle \ensuremath{T_{{\rm d}}} = \hbox{$T_{\rm d}\kern -8.7pt\raise 7.5... ...\star}\kern -8.3pt\raise 7.5pt\hbox{\tiny$\circ$ }$ }-\ensuremath{T_{\star}} ).$     (D.1)

With this estimate of the dust temperature, a single flux determination is sufficient to determine the the fractional luminosity. We have used this method to determine estimates of $\tau $independently from all wavelength where we have determined an excess. We used $\hbox{$T_{\star}\kern -8.3pt\raise 7.5pt\hbox{\tiny$\circ$ }$ }= 9600$ K and $\hbox{$T_{\rm d}\kern -8.7pt\raise 7.5pt\hbox{\tiny$\circ$ }$ ~}= 80$ K, values that agree with those measured for Vega.

References

 
Copyright ESO 2001