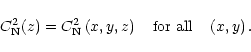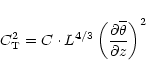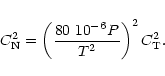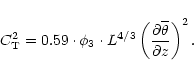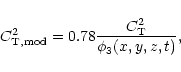A&A 365, 699-708 (2001)
DOI: 10.1051/0004-6361:20000050
3D numerical simulations of optical turbulence at the Roque
de Los Muchachos Observatory using the atmospherical model Meso-Nh
E. Masciadri1 - J. Vernin2 - P. Bougeault3
Send offprint request: E. Masciadri
1 - Instituto de Astronomía Universidad de Mexico, Apartado
Postal 70-264, CP 04510 Mexico D.F., Mexico
2 - UMR 6525 Astrophysique, Université de Nice-Sophia Antipolis - Centre
National de la Recherche Scientifique, Parc Valrose, 06108 Nice Cedex 2,
France
3 - Centre National de Recherches Météorologiques Météo France, 42 Av. G. Coriolis, 31057 Toulouse, France
Received 15 June 2000 / Accepted 24 October 2000
Abstract
We show results obtained from simulations of the optical turbulence (OT), provided by the atmospheric non-hydrostatic Meso-Nh model applied to the astronomical site of Roque de Los Muchachos (RLM) in the Canary Islands. The validation of the numerical technique is done comparing simulated and measured
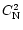 profiles obtained by different instruments operating during the same observation campaign of 11 nights. The results of this study show, for each night, a good average estimation of the OT obtained with Meso-Nh, compared to the dispersion of measurements from the different instruments. For the first time, the contribution to the optical turbulence of the radiation of the ground was studied. Quantitative estimations are given of the ability of the model to simulate the temperature near the ground around the telescope. Moreover, a set of 3D simulations shows that the horizontal distribution of the optical turbulence is not necessarily uniform, especially in the first 10 km above the ground. Finally, a study of the optimization of the optical turbulence parameterization in the model code is presented.
profiles obtained by different instruments operating during the same observation campaign of 11 nights. The results of this study show, for each night, a good average estimation of the OT obtained with Meso-Nh, compared to the dispersion of measurements from the different instruments. For the first time, the contribution to the optical turbulence of the radiation of the ground was studied. Quantitative estimations are given of the ability of the model to simulate the temperature near the ground around the telescope. Moreover, a set of 3D simulations shows that the horizontal distribution of the optical turbulence is not necessarily uniform, especially in the first 10 km above the ground. Finally, a study of the optimization of the optical turbulence parameterization in the model code is presented.
Key words: atmospheric turbulence - numerical model - seeing - site testing - flexible scheduling
1 Introduction
In a precedent article (Masciadri et al. 1999a) we presented the atmospheric non-hydrostatic model Meso-Nh (Lafore et al. 1998), conceived to provide 3D maps of the classic meteorological parameters p, T and
 and modified to provide 3D maps of
and modified to provide 3D maps of
 optical turbulence profiles as well. We refer to the precedent paper (Masciadri et al. 1999b) for the principal results obtained comparing
optical turbulence profiles as well. We refer to the precedent paper (Masciadri et al. 1999b) for the principal results obtained comparing
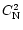 profiles simulated by the model and measured by a Scidar at the Paranal site (Chile) during the VLT (Very Large Telescope) site testing campaign.
profiles simulated by the model and measured by a Scidar at the Paranal site (Chile) during the VLT (Very Large Telescope) site testing campaign.
Here we present the results obtained for the validation of the same model using measurements provided from an observing campaign done at Roque de Los Muchachos in the Canary Islands (1-9 and 10-13 November 1995). The larger number of instruments employed during this campaign and the better performance of some of these instruments allow us to test the model in a more precise way than was possible in the previous campaign (Masciadri et al. 1999b).
The importance of the present study can be summarized as follows:
(a) In the Paranal study we analyzed the effect of friction of the flow over the ground and we studied the optical turbulence 3D distribution produced by gravity waves, but we neglected the contribution of the ground and atmosphere radiation to the energy budget. This latter aspect will be analyzed in the present paper;
(b) We study the ability of the model to simulate the temperature near the ground around the telescope (
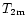 );
(c) We characterize, using 3D maps, the typical
);
(c) We characterize, using 3D maps, the typical
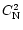 horizontal distribution at different altitudes in order to estimate its level of uniformity. This information could be fundamental for adaptive optics applications.
horizontal distribution at different altitudes in order to estimate its level of uniformity. This information could be fundamental for adaptive optics applications.
In Sect. 2, we describe the observation campaign. In Sect. 3, we analyze the radiation contribution to the optical turbulence simulation. In Sect. 4, we study the ability of Meso-Nh to simulate the temperature near the ground. In Sect. 5, we compare the model simulation with the dispersion of the measurements computed for each night. In Sect. 6, we discuss the results of model simulations showing that the
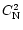 spatial distribution in horizontal planes is not necessarily uniform.
Finally, in Sect. 7, we demonstrate that the particular optical turbulence
parameterization introduced in the Meso-Nh code improves the model sensitivity especially in the interfaces between stable and unstable regions in the atmosphere, i.e. the regions where the turbulence production is greater.
spatial distribution in horizontal planes is not necessarily uniform.
Finally, in Sect. 7, we demonstrate that the particular optical turbulence
parameterization introduced in the Meso-Nh code improves the model sensitivity especially in the interfaces between stable and unstable regions in the atmosphere, i.e. the regions where the turbulence production is greater.
2 Canaries 1995 campaign
The goal of the campaign was, on the one hand, to characterize the optical turbulence in an
exhaustive way using different instruments and techniques in order to intercalibrate the
instruments. On the other hand, we wanted to give an estimation of the turbulence during a
reasonable number of nights to calculate the statistical reliability of the characterization. Three
different teams participated in the campaign of November 1995, on the site of Roque de Los Muchachos
(28.45 N, 17.52 W) in La Palma (Canary Islands): the DAUNSA (Département d'Astrophysique de
Nice-Sophia Antipolis), the ONERA (Office National d'Études et de Recherches Aérospastiales) and the IAC (Instituto de Astrofísica de Canarias). The instruments used during the campaign were: the Generalized Scidar (DAUNSA), three DIMM (two IAC-DIMM and an ONERA-DIMM), a Shack-Hartmann sensor (ONERA) and some free-fly balloons (DAUNSA). The Generalized Scidar and the Shack-Hartmann sensor shared the observation time at the focus of NOT telescope (D = 2.5 m) during 8 nights (1-9 November). Moreover, the Generalized Scidar worked at the focus of WHT telescope (D = 4.2 m) during 3 nights (10-13 November). Measurements of different parameters characterizing the atmosphere near the ground were obtained by two masts (IAC) placed in the GTC1 and GTC2 positions reported in Fig. 1. Only measurements issued from the GCT1 position are used in the present study because it is nearer to the NOT telescope.
We refer to Avila et al. (1997) for the analysis of the measurements and the intercalibration of the instruments.
A feasibility study of the optical turbulence forecasting was made using an orographic model of La Palma Island and the radiosoundings of the Tenerife meteorological station (28.35 N, 16.25 W); both provided by the IAC. The former is responsible for the gravity waves generated in the atmospheric flow and the latter were used to initialize the atmospheric model.
 |
Figure 1:
Roque de Los Muchachos Observatory map. The positions of WHT, the NOT and the TNG telescopes are aligned in a North-East/South-West direction. The two masts were placed in the GCT1 and GCT2 positions. The square in the top part of the figure indicates the position from which the balloons were launched. The natural Caldera crater is seen in the South-East part of the figure |
| Open with DEXTER |
 |
Figure 2:
Absolute temperature profile measured by a radiosounding at (dots) Antofagasta meteorological station (23.43 S, 70.43 W) and (line) Tenerife meteorological station (28.35 N, 16.25 W) |
| Open with DEXTER |
The principal differences from the previous Paranal feasibility study are the following:
- We analyzed measurements from a Generalized Scidar (Fuchs et al.
1998; Avila et al. 1997) that is sensitive to the
scintillation provided by turbulence shears of the whole atmosphere down to
the ground. The simulations could thus be compared to a more realistic
estimation of
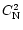 low-level profiles. During the Paranal campaign, measurements
from a Classical Scidar which is only sensitive to the free-atmosphere turbulence,
were used;
low-level profiles. During the Paranal campaign, measurements
from a Classical Scidar which is only sensitive to the free-atmosphere turbulence,
were used;
- We had at our disposal
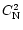 measurements provided by balloons launched from the Roque de Los Muchachos peak during each night. These balloons measure the meteorological parameters (p, T and
measurements provided by balloons launched from the Roque de Los Muchachos peak during each night. These balloons measure the meteorological parameters (p, T and
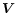 )
and the
)
and the
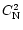 profiles. The vertical resolution of the balloons is about 6 m while the one of the Scidar is of about 1000 m.
We could not use measurements from these balloons to initialize the model because their measurements are affected by the mountain waves. However we compared the balloons measurements to the simulations results in order to validate the model. Having two different kinds of measurements (Scidar and balloons) we could compare, for the first time, the simulation profiles with the dispersion of measured profiles obtained the same night;
profiles. The vertical resolution of the balloons is about 6 m while the one of the Scidar is of about 1000 m.
We could not use measurements from these balloons to initialize the model because their measurements are affected by the mountain waves. However we compared the balloons measurements to the simulations results in order to validate the model. Having two different kinds of measurements (Scidar and balloons) we could compare, for the first time, the simulation profiles with the dispersion of measured profiles obtained the same night;
- The Tenerife radiosoundings that we used to initialize the model have a better vertical resolution than the Antofagasta ones, used for the Paranal study. As an example of the different resolution, in Fig. 2 we show vertical profiles of absolute temperature measured in the Antofagasta (dots) and Tenerife (line) meteorological stations. Beside this, we should remember that in the high troposphere (about 10 km) the wind flows principally from the direction West/North-West over La Palma Island and at low altitudes, it flows from the North-West/North-East. The Tenerife station is placed at the East of La Palma Island, downstream of the principal wind direction. This means that the initialization data are not completely adapted to this analysis;
- We have a more precise description of the ground. The Instituto Meteorológico Español provided us a vegetation map (data base: Corine Land Cover) of La Palma Island. The vegetation model was implemented in the Meso-Nh atmospheric model;
- The IAC mast provided the measurements of temperature above and under the ground.
 |
Figure 3:
Orographic model of La Palma Island. A domain of
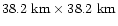 corresponding to
corresponding to
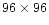 grid points is shown. Horizontal resolution: 400 m. The island extends over 26 km (in the
West-East direction) and 43 km (in the North-South direction). The black square marks the
Observatory position. The semi-circular crater of the volcano ( Caldera) is visible in the
center of the figure. (This figure is available in color in electronic form)
grid points is shown. Horizontal resolution: 400 m. The island extends over 26 km (in the
West-East direction) and 43 km (in the North-South direction). The black square marks the
Observatory position. The semi-circular crater of the volcano ( Caldera) is visible in the
center of the figure. (This figure is available in color in electronic form) |
| Open with DEXTER |
In Fig. 3 we show the orographic model (
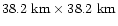 - horizontal resolution 400 m) installed in the atmospheric Meso-Nh model. One can observe that the geographic characteristics are completely different from the Paranal ones. The Roque de los Muchachos Observatory is placed near (500 m) the regions of maximum mountain slope (the crater of the extinct volcano the Caldera), which is the main cause of turbulence production. The Paranal site is placed at about 10 km from the region of maximum slope, which is the Chilean coast.
- horizontal resolution 400 m) installed in the atmospheric Meso-Nh model. One can observe that the geographic characteristics are completely different from the Paranal ones. The Roque de los Muchachos Observatory is placed near (500 m) the regions of maximum mountain slope (the crater of the extinct volcano the Caldera), which is the main cause of turbulence production. The Paranal site is placed at about 10 km from the region of maximum slope, which is the Chilean coast.
3 Influence of radiation from the ground on the optical turbulence (OT) simulation
The origin of the turbulence during the night time (which is characterized by a strong thermal stability) is not yet well understood (André et al. 1978; Mahart 1985). The principal difficulty is the identification of the turbulence sources. The most reliable hypothesis (Coulman et al. 1995) is that small wind instabilities could create a dynamic turbulence that mixes air particles with different temperatures in such a way as to reduce the temperature gradient in an extended region of some ten kilometers bounded in the upper and lower side by thin stable shears. In the energy budget considered in the precedent feasibility study we always omitted the contribution of the radiation transfer. This is a good approximation to the real state of the atmosphere but we think that a quantitative analysis of this contribution could be interesting because the nightly phenomenon of inversion could modify the thermodynamic evolution of the flow. In fact, the radiative cooling of the ground during the night can modify the thermal air-ground gradient and the thermal stability of the air near the ground. The seeing related to the surface shear is obviously affected by this phenomenon. The question is to know whether the radiation can affect quantitatively the seeing produced by the whole atmosphere.
Because of not very good weather conditions, we were able to obtain
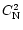 profile measurements for only 4 nights so that, in this study, we could not provide statistical information such as we have done for the Paranal study.
profile measurements for only 4 nights so that, in this study, we could not provide statistical information such as we have done for the Paranal study.
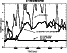 |
Figure 4:
Temporal evolution of the seeing simulated above the Roque de Los Muchachos (a), one grid point to the North of RLM (b) and above the Caldera (c) |
| Open with DEXTER |
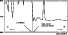 |
Figure 5:
Vertical section of simulated seeing above a North-South axis passing over the RLM site. The vertical line marks the RLM position. The most stable grid point is indicated by the arrow in the right part of the figure |
| Open with DEXTER |
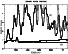 |
Figure 6:
Temporal evolution of the seeing simulated above the Caldera (a) and above
the RLM site (b). The thin lines are obtained including the radiative scheme and the
bold lineswithout it |
| Open with DEXTER |
We tested the model sensitivity to the radiation comparing, for each night, a 4-hour simulation with and without radiative transfer. In the first case, the temperature of the ground surface 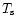 is constant during the simulation and in the second case,
is constant during the simulation and in the second case, 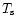 changes during the night.
In this latter case one has to initialize in the model (p, T and
changes during the night.
In this latter case one has to initialize in the model (p, T and
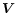 )
and also the ground surface temperature
)
and also the ground surface temperature 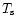 and the underground temperature
and the underground temperature
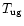 (about 1 m below the surface). The IAC mast provides
(about 1 m below the surface). The IAC mast provides 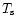 ,
the temperature above the ground
,
the temperature above the ground
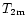 (about 2 m above the ground) but not
(about 2 m above the ground) but not
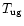 .
This last temperature is characterized by low amplitude and frequency modulations because of the large thermal inertia of the earth and its value is not too different from the climatological average. So we put
.
This last temperature is characterized by low amplitude and frequency modulations because of the large thermal inertia of the earth and its value is not too different from the climatological average. So we put
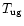 =
=
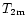 .
.
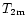 is likely to be almost equal to the climatological average because its daily modulation is not too high.
is likely to be almost equal to the climatological average because its daily modulation is not too high.
Moreover, we observe that the proximity of Roque de los Muchachos to the
Caldera causes some strong horizontal thermal gradients.
This fact motivated us to carry out a more precise study to estimate the best
representative grid point of the position of the peak. So, for each simulation, we
analyzed the temporal evolution of the seeing over three grid points along a North-South axis: (a)
the point best correlated to the geographic RLM position, (b) one grid point to the North of the
RLM position and (c) a grid point directly above the Caldera. In order to show the model
sensitivity near the steep slope, in Fig. 4 we show (as an example) the simulated
temporal evolution of the seeing over the 3 points (a, b and c) during the 3-4 November night. The position (b) revealed to be the most stable (as for all of the other nights) so we select this one as the most representative of the measured optical turbulence over the RLM site. In Fig. 5 we show a North-South section of the seeing simulated over the site. A rapid seeing augmentation, reconstructed with 1 grid point precision, is evident near the Caldera. The comparisons between the simulations and the measurements for all of the nights was done for the grid point (b). In the following we shall call it the optimal point.
The systematic analysis of all of the campaign nights proved that, over regions characterized by a
strong turbulent state, the radiative transfer modifies the seeing locally but the average amplitude
remains unmodified. As an example, in Fig. 6 (b) we show the evolution of the seeing
over the Caldera during the 3-4 November night with (bold line) and without (thin line) the
radiative transfer computation. In proximity of regions characterized by a low turbulent activity,
the results do not show any clear trend. Also, in Fig. 6 (a), we show the temporal
evolution of the seeing over the optimal point with (bold line) and without (thin line) the
radiative transfer scheme, obtained during the 3-4 November night. In this case the radiative contribution gives a systematically higher seeing. Finally, we estimated that, from a quantitative point of view, the radiation transport only has a weak influence on the turbulent energy. The analysis of all of the nights showed an average seeing difference 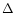
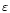 = 0.09 arcsec between the 2 kinds of simulation (with and without radiation). In
Table 1 we give the seeing values measured and simulated over the RLM site in different
atmospheric regions: the boundary layer
= 0.09 arcsec between the 2 kinds of simulation (with and without radiation). In
Table 1 we give the seeing values measured and simulated over the RLM site in different
atmospheric regions: the boundary layer
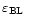 ,
the free atmosphere
,
the free atmosphere
 and the sum of the
two precedent contributions
and the sum of the
two precedent contributions
 .
Considering that the balloons were launched from about
200 m below the telescope level, in our computation we considered only half of the contribution of
the seeing for this low atmospheric region. One can observe that, when the model is initialized with
meteorological parameters representative of the flow above the site (as is the case in the 3-4 November night), the simulated seeing correlates well with both Scidar and balloon measurements in each region of the atmosphere.
.
Considering that the balloons were launched from about
200 m below the telescope level, in our computation we considered only half of the contribution of
the seeing for this low atmospheric region. One can observe that, when the model is initialized with
meteorological parameters representative of the flow above the site (as is the case in the 3-4 November night), the simulated seeing correlates well with both Scidar and balloon measurements in each region of the atmosphere.
A cornerstone in the validation of the radiative computation was the study of the model sensitivity to the estimation of surface temperature 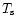 during the night.
The ability of the model to provide a correct
during the night.
The ability of the model to provide a correct 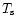 guarantees
a good estimation of the heat flux from the ground. As an example, Fig. 7 shows horizontal
maps of
guarantees
a good estimation of the heat flux from the ground. As an example, Fig. 7 shows horizontal
maps of 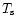 simulated on the lowestmodel level of the computational grid and obtained (a) at the simulation time t=0
(i.e. the 22:00 U.T.) and (b) after 3-hour simulations (i.e. 00:00 U.T.) over a
12.8 km
simulated on the lowestmodel level of the computational grid and obtained (a) at the simulation time t=0
(i.e. the 22:00 U.T.) and (b) after 3-hour simulations (i.e. 00:00 U.T.) over a
12.8 km
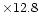 km surface the 8-9 November night. One can see that
km surface the 8-9 November night. One can see that 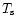 decreases during this time period. This same trend is observed for the
decreases during this time period. This same trend is observed for the 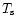 measurements (Fig. 8) obtained during the same night.
measurements (Fig. 8) obtained during the same night.
4 Simulation of the temperature near the ground
Beside this, for flexible-scheduling applications, the
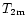 temperature is a more interesting parameter. Indeed, the image perturbations at the telescope focus depend on many contributions: the seeing related to free atmosphere turbulence (h > 1 km from the ground)
temperature is a more interesting parameter. Indeed, the image perturbations at the telescope focus depend on many contributions: the seeing related to free atmosphere turbulence (h > 1 km from the ground)
 ,
the seeing related to the boundary layer turbulence (0 < h < 1 km)
,
the seeing related to the boundary layer turbulence (0 < h < 1 km)
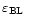 ,
the seeing
,
the seeing
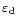 caused by local temperature inhomogeneities between the inside (T0) and outside (
caused by local temperature inhomogeneities between the inside (T0) and outside (
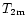 )
temperatures and the seeing due to the primary mirror
)
temperatures and the seeing due to the primary mirror
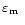 caused by temperature differences between the primary mirror (
caused by temperature differences between the primary mirror (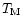 )
and the outdoors (
)
and the outdoors (
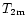 ). Recent studies (Racine et al. 1991; Zago 1995) showed that the dome seeing
). Recent studies (Racine et al. 1991; Zago 1995) showed that the dome seeing
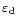 is related to the temperature difference
is related to the temperature difference
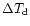 =
=
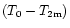 as:
as:
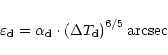 |
(1) |
and the primary mirror seeing
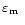 is related to the
temperature difference
is related to the
temperature difference
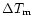 =
=
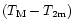 as:
as:
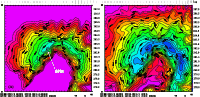 |
Figure 7:
Maps of the surface temperature 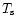 simulated at the lowest model level during the
8-9 November night after a) t = 0 hours and b) t = 3 hours. The temperature
simulated at the lowest model level during the
8-9 November night after a) t = 0 hours and b) t = 3 hours. The temperature
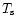 above the RLM site is a)
above the RLM site is a) 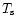
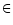 [280.5 - 281] degrees and b)
[280.5 - 281] degrees and b)
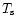
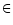 [278. - 278.5] degrees. (This figure is available in color in electronic form)
[278. - 278.5] degrees. (This figure is available in color in electronic form) |
| Open with DEXTER |
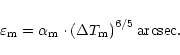 |
(2) |
Table 2:
Simulated and measured temperature near the ground. The first column lists the measured temperature at 22:00 U.T., the second column gives the initialization temperature at the same hour, the third column the measured temperature at 01:00 U.T. and the fourth column the temperature after 3 simulation hours. The last two columns show the temperature difference (simulated and measured) at 22:00 U.T. and 01:00 U.T.
|
Night |
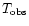 [22:00]
[22:00] |
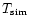 [22:00]
[22:00] |
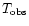 [01:00]
[01:00] |
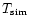 [01:00]
[01:00] |
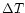 [22:00]
[22:00] |
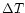 [01:00]
[01:00] |
| |
(K) |
(K) |
(K) |
(K) |
(K) |
(K) |
|
3-4 |
283.1 |
283.6 |
282.8 |
282.5 |
0.5 |
0.3 |
| 8-9 |
277.1 |
277.9 |
276.6 |
277.3 |
0.8 |
0.7 |
| 11-12 |
277.5 |
280.4 |
277.7 |
278.8 |
2.9 |
1.1 |
| 12-13 |
279.9 |
282.0 |
280.2 |
282.9 |
2.1 |
2.7 |
The values
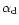 and
and
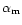 were
obtained from a mean square adjustment to experimental
measurements. For the CFHT telescope (Hawaii)
were
obtained from a mean square adjustment to experimental
measurements. For the CFHT telescope (Hawaii)
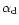 = 0.1 and
= 0.1 and
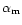 = 0.4 (Racine et al. 1991). This means that
the temperature difference
= 0.4 (Racine et al. 1991). This means that
the temperature difference
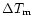 is a very critical parameter.
A
is a very critical parameter.
A
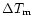 = 2 degrees temperature difference corresponds to
a
= 2 degrees temperature difference corresponds to
a
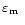
 0.9 arcsec seeing. The contribution to the seeing of
0.9 arcsec seeing. The contribution to the seeing of
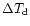 is lower and it can be neglected for
is lower and it can be neglected for
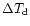
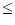 3 degrees. This corresponds to the seeing limit of the optical aberrations (
3 degrees. This corresponds to the seeing limit of the optical aberrations (
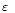
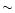 0.38 arcsec) for the CFHT telescope. So, in order to adjust the primary
mirror temperature, the outdoor temperature
0.38 arcsec) for the CFHT telescope. So, in order to adjust the primary
mirror temperature, the outdoor temperature
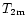 should be estimated by the
model with a precision of about 1 degree. Table 2 lists the
should be estimated by the
model with a precision of about 1 degree. Table 2 lists the
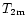 values obtained at t=0 hours and t=3 hours of simulation time. We also list the
corresponding temperatures measured by the IAC masts at 22:00 hours U.T and 01:00 U.T.
One can observe that the difference between the simulations and the measurements (the
last two columns) is always
values obtained at t=0 hours and t=3 hours of simulation time. We also list the
corresponding temperatures measured by the IAC masts at 22:00 hours U.T and 01:00 U.T.
One can observe that the difference between the simulations and the measurements (the
last two columns) is always 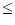 3 degrees. Moreover, the temperature differences
are in general lower at the end of the simulations than at the beginning. This shows a
good atmospheric flow adaptation to the general boundary Meso-Nh conditions. We therefore
find encouraging results for simulating the temperature near the ground with the Meso-Nh
code, although it would be good, in the future, to analyze a richer statistical
sample.
3 degrees. Moreover, the temperature differences
are in general lower at the end of the simulations than at the beginning. This shows a
good atmospheric flow adaptation to the general boundary Meso-Nh conditions. We therefore
find encouraging results for simulating the temperature near the ground with the Meso-Nh
code, although it would be good, in the future, to analyze a richer statistical
sample.
5 Comparison between measurements and simulations
Knowing different measurements (M) of a parameter P, we can access its natural variability. We can compare the dispersion of measurements obtained between different instruments with the dispersion between the average of all measurements and the simulations. We define:
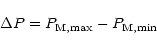 |
(3) |
where 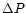 is the dispersion between all measurements of the parameter P.
is the dispersion between all measurements of the parameter P.
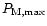 and
and
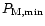 are, respectively, the maximum and the minimum measured values of P. We also define:
are, respectively, the maximum and the minimum measured values of P. We also define:
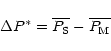 |
(4) |
where
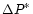 is the dispersion between simulations and measurements for each parameter P.
is the dispersion between simulations and measurements for each parameter P.
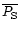 is the time average of the simulations and
is the time average of the simulations and
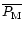 is the average of the measurements.
Table 3 gives, for each night, the values of the isoplanatic angle
is the average of the measurements.
Table 3 gives, for each night, the values of the isoplanatic angle
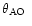 ,
the wavefront coherence time
,
the wavefront coherence time
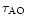 and the equivalent velocity
and the equivalent velocity
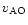 ,
which is defined
as:
,
which is defined
as:
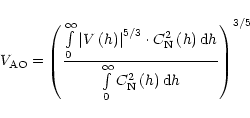 |
(5) |
and can be computed both from the measurements and from the simulations.
Table 4 gives, for each integrated parameter studied
(
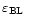 ,
,
 ,
,
 ,
,
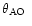 ,
,
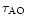 and
and
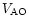 ),
the dispersion
),
the dispersion
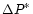 and
and 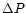 .
One can observe that in 8 cases out of 12,
.
One can observe that in 8 cases out of 12,
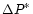 and
and 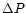 are comparable. This means that the model estimation is not worse than the natural fluctuations of the measurements. We note that the accuracy of the measurements, which is fundamental to this analysis, was proven in a previous paper (Avila et al. 1997).
are comparable. This means that the model estimation is not worse than the natural fluctuations of the measurements. We note that the accuracy of the measurements, which is fundamental to this analysis, was proven in a previous paper (Avila et al. 1997).
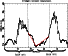 |
Figure 8:
Temporal evolution of the surface temperature
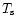 measured by the IAC masts during the 8-9 night.
The dashed lines indicate the boundaries of the night time.
The straight lines show the temperature trend during the night
measured by the IAC masts during the 8-9 night.
The dashed lines indicate the boundaries of the night time.
The straight lines show the temperature trend during the night |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10007f9.eps}
\end{figure}](/articles/aa/full/2001/03/aa10007/Timg82.gif) |
Figure 9:
Vertical section above the Roque de los Muchachos Observatory - Canary Islands (South is to
the left) of
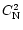 isolines of a simulation. The level of turbulence with respect to the zenith above
the peak (point (a)) of the mountain is relatively low but at
isolines of a simulation. The level of turbulence with respect to the zenith above
the peak (point (a)) of the mountain is relatively low but at 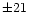 degrees (point (b)) the
intensity of
degrees (point (b)) the
intensity of
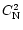 is higher. (This figure is available in color in electronic form)
is higher. (This figure is available in color in electronic form) |
| Open with DEXTER |
 |
Figure 10:
Vertical
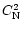 profiles simulated above the points (a) and (b) marked in Fig. 9
profiles simulated above the points (a) and (b) marked in Fig. 9 |
| Open with DEXTER |
6 Usefulness of Meso-Nh for instrument calibration
All of the astronomical parameters simulated by the model are usually computed
by integration of the optical turbulence with respect to the zenith. In this way, one can compare
directly the simulations with the measurements provided by the optical instruments such as the
Scidar. Of course, in the use of these instruments, a correction has to be introduced in the
computation of different integrated parameters depending on the star position with respect to the
zenith. The z coordinate is replaced by z 
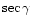 and the integral is carried
out following the line of sight.
and the integral is carried
out following the line of sight. 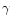 is the angle between the line of sight and the zenith.
This operation is based on the hypothesis that the horizontal
is the angle between the line of sight and the zenith.
This operation is based on the hypothesis that the horizontal
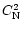 distribution is uniform. This means that:
distribution is uniform. This means that:
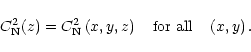 |
(6) |
This is a strong hypothesis and we can show that it is not necessarily true, especially in the lower 10 km where the orographic effects are more important. Figure 9 shows a
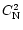 vertical section (South/North) of a simulation obtained over the RLM site. It is evident that if we integrate along the zenithal direction we have low intensity of
vertical section (South/North) of a simulation obtained over the RLM site. It is evident that if we integrate along the zenithal direction we have low intensity of
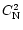 but, at
but, at 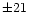 degrees with respect to the zenith the optical turbulence intensity is higher at an altitude of about 8 km. The high
degrees with respect to the zenith the optical turbulence intensity is higher at an altitude of about 8 km. The high
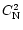 generated at 8 km gives an equivalent seeing of 0.55 arcsec (as shown in Fig. 10) where the two
generated at 8 km gives an equivalent seeing of 0.55 arcsec (as shown in Fig. 10) where the two
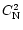 profiles simulated above the points (a) and (b) of Fig. 9 are given.
profiles simulated above the points (a) and (b) of Fig. 9 are given.
From this we conclude that large errors could be introduced into the calibration of the optical instruments that can not measure, at the same time, many different lines of sight. We recently modified the Meso-Nh code in order to integrate the optical turbulence along a path which is not necessarily towards the zenith. Some preliminary results were presented in Masciadri et al. (2000), and in a forthcoming article we will present a more exhaustive analysis of the results obtained from such simulations. We note that, from a numerical point of view, the problem is not trivial because the model levels are not horizontal. These levels are like sheets following the orographic model.
7 Optimization of the OT parameterization:
The thermo dynamic stability function
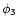
In the literature one can find many different ways to parameterize the optical turbulence
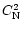 .
The general assumption is the definition of the structure constant of the temperature
.
The general assumption is the definition of the structure constant of the temperature
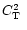 as depending on macroscopic parameters:
as depending on macroscopic parameters:
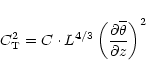 |
(7) |
where L is the outer scale of the turbulence, 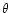 the potential temperature and C is a constant. The refraction index structure constant
the potential temperature and C is a constant. The refraction index structure constant
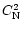 is related to the
is related to the
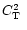 by the Gladstone law:
by the Gladstone law:
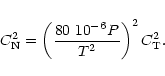 |
(8) |
There are basically two different philosophies in the adimensional turbulence theory. The first one defines a parameterization
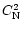 in a limited region of the atmosphere where there are uniform and homogeneous turbulence characteristics. The constant C is defined, in this case, in an experimental way. Following this philosophy one could define different constants Ci for different regions in the atmosphere such as the surface layer, the boundary layer and the free atmosphere. The second philosophy is to use an universal constant C and to change the parameterization depending on the resolution used to analyze the system.
in a limited region of the atmosphere where there are uniform and homogeneous turbulence characteristics. The constant C is defined, in this case, in an experimental way. Following this philosophy one could define different constants Ci for different regions in the atmosphere such as the surface layer, the boundary layer and the free atmosphere. The second philosophy is to use an universal constant C and to change the parameterization depending on the resolution used to analyze the system.
Many authors measured the constant C in the surface shear layers. Its values differ, with C = 3.2 (Wyngaard & Coté 1971), C = 1.6 (Hill 1978), C = 2.8 (Tatarski 1961). In astronomical applications, the constant value found by Tatarski is generally extended to the whole atmosphere.
The Meso-Nh model was conceived following the second methodology in order to have a model which is useful in many different applications. The constant C is universal and one can select the turbulence parameterization that one needs. Following this methodology, the
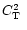 coded in Meso-Nh is:
coded in Meso-Nh is:
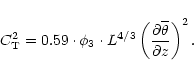 |
(9) |
where 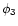 is a dimensionless function depending on the thermal and dynamical stability of the atmosphere (Masciadri et al. 1999a) which takes into account the 3D spatial temperature and humidity variations in the atmosphere. This would improve the turbulence parameterization in the Meso-Nh model. In this section we study the sensitivity of the
is a dimensionless function depending on the thermal and dynamical stability of the atmosphere (Masciadri et al. 1999a) which takes into account the 3D spatial temperature and humidity variations in the atmosphere. This would improve the turbulence parameterization in the Meso-Nh model. In this section we study the sensitivity of the
 to this parameter. Is the
to this parameter. Is the  quantitatively important for the seeing estimation?
quantitatively important for the seeing estimation?
One can observe that Eqs. (7) and (9) with C = 2.8 differ by a factor 0.35
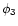 .
We note that the
.
We note that the
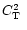 in the model depends on a scale free parameter, related to the minimum kinetic energy
in the model depends on a scale free parameter, related to the minimum kinetic energy
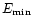 .
One can fix the value of
.
One can fix the value of
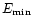 only with a calibration done a posteriori (i.e. adjusting simulations with measurements). So, to characterize the influence of
only with a calibration done a posteriori (i.e. adjusting simulations with measurements). So, to characterize the influence of 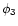 on the seeing simulation we compare two different equations. The first one is
Eq. (9). The second one, which we will call
on the seeing simulation we compare two different equations. The first one is
Eq. (9). The second one, which we will call
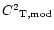 ,
is:
,
is:
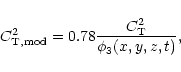 |
(10) |
where 0.78 is the value of 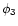 in a stable thermo dynamic conditions
(Masciadri et al. 1999a). Thus, the comparison of the two
equations will give us the contribution of
in a stable thermo dynamic conditions
(Masciadri et al. 1999a). Thus, the comparison of the two
equations will give us the contribution of 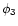 in the unstable region
and at the stable-unstable interfaces, where the optical turbulence is
principally developed. Finally, the different seeing
in the unstable region
and at the stable-unstable interfaces, where the optical turbulence is
principally developed. Finally, the different seeing
 ,
,
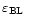 and
and
 were retrieved from the two different
were retrieved from the two different
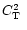 parameterizations.
Table 5 lists the seeing estimations with and without radiation contribution simulated for all of the campaign nights.
parameterizations.
Table 5 lists the seeing estimations with and without radiation contribution simulated for all of the campaign nights.
One can see that, independent of the radiation contribution, the
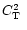 parameterization gives a worse seeing than the
parameterization gives a worse seeing than the
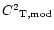 one. The average error between the two parameterizations is equal to
one. The average error between the two parameterizations is equal to
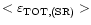 = 0.14 arcsec (with radiation) and
= 0.14 arcsec (with radiation) and
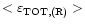 = 0.13 arcsec (without radiation). So we conclude that the contribution of
= 0.13 arcsec (without radiation). So we conclude that the contribution of 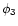 to the calculated seeing is not negligible.
to the calculated seeing is not negligible.
8 Conclusions
In this paper we present the results of a feasibility study for seeing forecasting on the Roque de Los Muchachos site in the Canary Islands. For the first time we have compared simulations with measurements obtained with different instruments. We show that the dispersion between the measurements 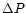 and the dispersion between the average of the measurements and the simulations
and the dispersion between the average of the measurements and the simulations
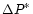 are comparable. Moreover we see a high level of model sensitivity to the orographic characteristics: the optical turbulence is reconstructed with a precision of about 1 grid point (500 m) near the maximum mountain slope, which is at the edge the crater of the extinct volcano the Caldera. We think that, with a larger statistical sampling, it would be possible to put into evidence the Caldera effect. This phenomenon is related with generally bad seeing, occuring when the wind is blowing from the Caldera, as has been noticed by astronomers. We have studied, for the first time, the radiation contribution to the optical turbulence simulation. The results show that this contribution is quantitatively insignificant for the integration of the turbulence over the whole atmosphere. The average difference between the simulated seeing with and without radiation is
are comparable. Moreover we see a high level of model sensitivity to the orographic characteristics: the optical turbulence is reconstructed with a precision of about 1 grid point (500 m) near the maximum mountain slope, which is at the edge the crater of the extinct volcano the Caldera. We think that, with a larger statistical sampling, it would be possible to put into evidence the Caldera effect. This phenomenon is related with generally bad seeing, occuring when the wind is blowing from the Caldera, as has been noticed by astronomers. We have studied, for the first time, the radiation contribution to the optical turbulence simulation. The results show that this contribution is quantitatively insignificant for the integration of the turbulence over the whole atmosphere. The average difference between the simulated seeing with and without radiation is 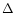
 = 0.09 arcsec. Also we study the ability of the Meso-Nh model to simulate the temperature near the ground around the telescope. The results show that the difference between the measured and simulated temperatures is
= 0.09 arcsec. Also we study the ability of the Meso-Nh model to simulate the temperature near the ground around the telescope. The results show that the difference between the measured and simulated temperatures is 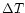
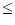 3 degrees, which is, comparable to the results obtained with other techniques, such as multiregression (Buffa & Porceddu 1997). This is a very promising result considering that it was proven (Racine
et al. 1991) that to prevent seeing caused by outside temperature
3 degrees, which is, comparable to the results obtained with other techniques, such as multiregression (Buffa & Porceddu 1997). This is a very promising result considering that it was proven (Racine
et al. 1991) that to prevent seeing caused by outside temperature
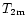 and the primary mirror temperature
and the primary mirror temperature 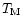 differences, the
differences, the
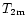 should be known with a precision of about 1 degree.
should be known with a precision of about 1 degree.
In this paper, we prove that the
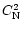 horizontal distribution is not necessarily uniform especially in the first 10 km from the ground where the effects of the orographic waves are more important. Because of this, errors can be introduced in the calibrations of optical instruments (such as the Scidar) that measure the optical turbulence along directions that can be different from the zenithal one.
horizontal distribution is not necessarily uniform especially in the first 10 km from the ground where the effects of the orographic waves are more important. Because of this, errors can be introduced in the calibrations of optical instruments (such as the Scidar) that measure the optical turbulence along directions that can be different from the zenithal one.
Finally we show that the particular parameterization of the optical turbulence used in Meso-Nh permits to better estimate the
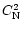 at the interfaces of stable-unstable regions, which are the regions in which one can expect the turbulence to be greater.
This means that the parameterization of
Eq. (9) is better than the classical one used in the astronomical context (Tatarski 1961).
at the interfaces of stable-unstable regions, which are the regions in which one can expect the turbulence to be greater.
This means that the parameterization of
Eq. (9) is better than the classical one used in the astronomical context (Tatarski 1961).
Acknowledgements
This work was supported by a CNRM/ONERA contract (Convention 22.988/DA.B1/DC).
We are greatful to the ONERA team, the NOT telescope and
IAC staff for their collaboration during the observation
campaign. The balloon measurements were kindly provided by M. Azouit and
J. F. Manigault. We acknowledge E. Gizard and the Centre
National des Recherches Météorologiques (CNRM) for their complementary
operation and the loan of their balloon tracking system. We would like
to thank B. Fleury, C. Dainty, C. Muñoz-Tuñón and M. Anderson
for their help in the successful completion of this campaign and to
J. Stein, P. Jabouille and J. L. Redelsperger for their useful
comments about the Meso-Nh model and A. Raga for a revision of the text.
-
André, J. C., et al. 1978,
J. Atm. Sci., 35, 1861
In the text
NASA ADS
-
Avila, R., et al. 1997,
Appl. Opt., 36, 7898
In the text
NASA ADS
-
Buffa, F., & Porceddu, I. 1997,
A&AS, 126, 547
In the text
NASA ADS
-
Coulman, C., et al. 1995,
Appl. Opt., 34, 5461
In the text
NASA ADS
-
Fuchs, A., et al. 1998,
PASP, 110, 86
In the text
NASA ADS
-
Hill, R. J. 1978,
J. Fluid. Mech., 88, 541
In the text
NASA ADS
-
Lafore, J. P., et al. 1998,
Ann. Geophys., 16, 90
In the text
-
Mahart, L. 1985,
J. Atm. Sci., 42, 2333
In the text
-
Masciadri, E., et al. 1999a,
A&AS, 137, 185
In the text
NASA ADS
-
Masciadri, E., et al. 1999b,
A&AS, 137, 203
In the text
NASA ADS
-
Masciadri, E., et al. 2000,
Astronomical Telescopes and Instrumentation - SPIE Congress,
to be published
In the text
-
Racine, R., et al. 1991,
PASP, 103, 1020
In the text
NASA ADS
-
Tatarski, V. I. 1961,
Wave Propagation in a Turbulent Medium (Dover Editions)
In the text
-
Zago, L. 1995,
Ph.D. Thesis, Département de Génie Civil, Institut d'Hydraulique
et d'Énergie, LASEN Laboratoire de systèmes énergétiques
In the text
-
Wyngaard, J. C., & Coté, O. R. 1971,
J. Atmos. Sci., 28, 190
In the text
Copyright ESO 2001




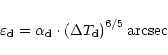

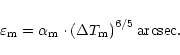
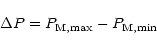
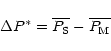
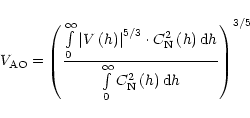

![\begin{figure}
\par\includegraphics[width=8cm,clip]{10007f9.eps}
\end{figure}](/articles/aa/full/2001/03/aa10007/Timg82.gif)