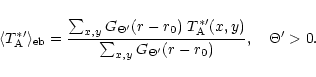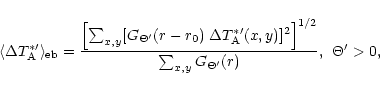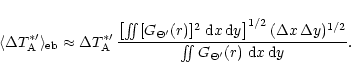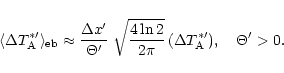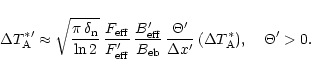A&A 365, 285-293 (2001)
DOI: 10.1051/0004-6361:20000485
Methods and constraints for the correction of the error
beam pick-up in single dish radio observations
F. Bensch1 - J. Stutzki1 - A. Heithausen1,2
Send offprint request: F. Bensch,
1 - I. Physikalisches Institut der Universität zu Köln,
Zülpicher Straße 77, 50937 Köln, Germany
2 -
Radioastronomisches Institut der Universität Bonn, Auf
dem Hügel 71, 53121 Bonn, Germany
Received 27 January 2000 / Accepted 1 August 2000
Abstract
The beam pattern of a single dish radio telescope is given by the
main beam and additional components at
larger angles, usually called error beam or
stray pattern.
The latter have relatively small peak amplitudes
(typ. below -25 dB), depending on the rms surface error
of the primary reflector. However, because of their large angular
extent, they are sensitive to extended sources, and a significant fraction
of the observed intensity can result from error beam pick-up.
For (sub-)mm observations suffering from error beam pick-up
we introduce a new temperature scale for the corrected data,
the corrected main beam brightness temperature
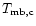 ,
which provides a better
approximation to the intensity detected by the main
beam than the commonly used antenna temperature and
main beam brightness temperature.
We consider two different correction methods. The first method uses
complementary observations obtained with a smaller telescope.
Smeared to the angular resolution
of the error beam pattern they provide an estimate of the
error beam pick-up in the observations of the large telescope.
For the second method, the error beam pick-up is de-convolved from the
observed map in Fourier space.
The requirements for both correction
methods and their advantages and limitations are discussed in detail.
Both correction methods require additional observations, unless
the full spatial extent of the emission is observed.
We find that the de-convolution
method is attractive for the correction of fully sampled maps
with an angular extent much larger than the error beam pattern. For smaller
maps and more sparsely sampled observations, the subtraction method
is favorable, because the additional observations with a small
telescope are less time consuming.
,
which provides a better
approximation to the intensity detected by the main
beam than the commonly used antenna temperature and
main beam brightness temperature.
We consider two different correction methods. The first method uses
complementary observations obtained with a smaller telescope.
Smeared to the angular resolution
of the error beam pattern they provide an estimate of the
error beam pick-up in the observations of the large telescope.
For the second method, the error beam pick-up is de-convolved from the
observed map in Fourier space.
The requirements for both correction
methods and their advantages and limitations are discussed in detail.
Both correction methods require additional observations, unless
the full spatial extent of the emission is observed.
We find that the de-convolution
method is attractive for the correction of fully sampled maps
with an angular extent much larger than the error beam pattern. For smaller
maps and more sparsely sampled observations, the subtraction method
is favorable, because the additional observations with a small
telescope are less time consuming.
Key words:
methods: data analysis - techniques: miscellaneous - telescopes
- radio lines: ISM
Author for correspondance: bensch@ph1.uni-koeln.de
1 Introduction
The presence of a significant error beam pick-up was noted for HI
observations more than three decades ago (cf. van Woerden et al. 1962;
Westerhout et al. 1973).
The error or stray pattern
responsible for the additional pick-up mainly
resulted from surface irregularities in the
primary reflector (cf. Harten 1973; Heiles & Hoffman 1968).
The improved reflector surface of
present day cm wave telescopes greatly reduced the amplitude of
these components and the residual error beam is
often found to be dominated by spillover and scattering.
Typically, these components are not axially-symmetric
with amplitudes below -30 dB (cf. Kalberla et al. 1980).
With the increasing number of large telescopes and sensitive
receivers for the (sub-)mm range, the importance of an error beam
correction was recognized for observations at shorter wavelengths
(cf. Schneider et al. 1998). Essential pre-requisite for a
correction is an accurately measured beam pattern.
For the IRAM 30m telescope, this was done by
Garcia-Burillo et al. (1993) and Greve et al. (1998).
Based on these studies, Bensch et al. (2001) determined
the influence of the error beam pick-up in the data set of the
IRAM key-project, and estimated the accuracy of the
applied correction method. They demonstrate
that the error beam pick-up of the IRAM 30m at wavelengths of
1.3mm can account for 20-50% of the
observed intensity (map average), and locally for up to
100%.
The error beam problem is well known to HI observers
and large surveys are routinely corrected for the
additional pick-up (cf. Hartmann et al. 1996).
For observations at (sub-)mm wavelengths, however,
only very few quantitative studies exist (cf. Garcia-Burillo et al. 1993;
Dame & Thaddeus 1994; Schneider et al. 1998),
despite the fact
the error beam problem is expected to be quite common also to large
(sub-)mm telescopes. In addition, the ratio of the error beam pattern to
the spatial extent of the source can be very different for cm and (sub-)mm
wavelengths. The correction methods and results found for HI
observations therefore do not necessarily apply to the observations made at
shorter wavelengths, and a more detailed study of the influence
of error beam pick-up and the correction methods is needed.
This paper supplements
Paper III in the series presenting the results of the
IRAM key-project "Small-scale structure of pre-star forming regions''.
The data set of the key-project and first results are published by
Falgarone et al. (1998, Paper I) and Heithausen et al. (1998).
The data reduction is presented by Panis et al. (in preparation;
Paper II) and the influence and correction of the error beam pick-up
is discussed by Bensch et al. (2001, Paper III).
The present paper puts the error beam
correction of (sub-)mm observations on firmer grounds.
The relevant definitions are provided and the possible correction
methods are reviewed, discussing their advantages and limitations.
In addition,
a guideline is provided for observers who wish to correct their own data.
In Sect. 2, we introduce the notation and give the
definition of the corrected main beam brightness temperature.
The error beam pattern of (sub-)mm telescopes is discussed in
Sect. 3, and the error beam correction methods
are presented in Sects. 4 and 5.
The requirements of both correction
methods are discussed and compared, their advantages and limitations
are outlined (Sect. 6).
A summary is given in Sect. 7.
2 Definitions
In the following, we review some of the definitions and basic relations which
are relevant for the intensity calibration of radio astronomical
single dish observations. For a more detailed presentation we refer to
the publications of e.g. Baars (1973) and
Rohlfs & Wilson (1996). The
calibration of observations at (sub-)mm wavelengths is covered by
e.g. Kutner & Ulich (1981), Downes (1989) and
Kramer (1997).
Consider a radio telescope pointing toward a source of brightness
distribution
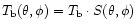 ,
where
,
where  is the peak brightness temperature, and
is the peak brightness temperature, and
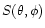 varies between 0 and 1. The observed antenna
temperature, corrected for atmospheric and rear-ward losses, then reads
varies between 0 and 1. The observed antenna
temperature, corrected for atmospheric and rear-ward losses, then reads
where
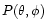 is the antenna pattern of the telescope
(normalization P(0,0)=1). Here, we have used the "
is the antenna pattern of the telescope
(normalization P(0,0)=1). Here, we have used the "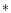 '' symbol
as shorthand notation for convolution. Note, that all quantities such
as efficiencies, source brightness distribution, etc. depend on the
observed frequency, although not further indicated in the following.
'' symbol
as shorthand notation for convolution. Note, that all quantities such
as efficiencies, source brightness distribution, etc. depend on the
observed frequency, although not further indicated in the following.
The main beam brightness temperature (cf. Downes 1989) is
defined by
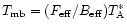 ,
where
,
where
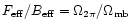 and
and
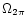 (
(
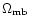 )
is the integral of the beam
pattern
)
is the integral of the beam
pattern
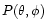 over the forward hemisphere (main beam) of
the telescope. The main beam is defined e.g. as the beam pattern enclosed
by the -20 dB threshold, or the equivalent Gaussian with a
half power beam width (HPBW) determined from cross-scans on
calibration sources (e.g. planets).
Here, we accept the former
definition:
over the forward hemisphere (main beam) of
the telescope. The main beam is defined e.g. as the beam pattern enclosed
by the -20 dB threshold, or the equivalent Gaussian with a
half power beam width (HPBW) determined from cross-scans on
calibration sources (e.g. planets).
Here, we accept the former
definition:
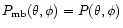 for
for
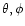 inside the -20 dB level, and
inside the -20 dB level, and
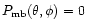 elsewhere.
The forward beam pattern outside the main beam,
elsewhere.
The forward beam pattern outside the main beam,
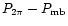 ,
is
then denoted as error beam.
Note, that this definition of the main beam
is not identical to the diffraction beam of a telescope with a
perfect reflector surface, because components resulting from
surface irregularities partly contribute to
,
is
then denoted as error beam.
Note, that this definition of the main beam
is not identical to the diffraction beam of a telescope with a
perfect reflector surface, because components resulting from
surface irregularities partly contribute to
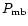 .
However, this contribution is small in most cases (Sect. 3).
.
However, this contribution is small in most cases (Sect. 3).
For telescopes with a negligible error beam, the
main beam brightness temperature gives the
intensity detected by the main beam, averaged over the solid angle of
the main beam,
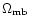 .
For telescopes where a
significant error beam is present, the main beam brightness
temperature potentially overestimates the intensity detected by the
main beam, whereas the antenna temperature underestimates it.
Both, Kutner & Ulich (1981) and
Downes (1989), discuss the consequences of a
non-negligible error beam pick-up.
Kutner & Ulich (1981) a priori define a temperature scale
.
For telescopes where a
significant error beam is present, the main beam brightness
temperature potentially overestimates the intensity detected by the
main beam, whereas the antenna temperature underestimates it.
Both, Kutner & Ulich (1981) and
Downes (1989), discuss the consequences of a
non-negligible error beam pick-up.
Kutner & Ulich (1981) a priori define a temperature scale
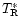 which gives the intensity averaged over
the "diffraction pattern of the telescope'', with the
components of the error beam pattern (resulting from surface
irregularities) being included.
Pick-up from larger angles (due to e.g. spillover past the secondary) are
included in the a priori unknown source coupling efficiency
which gives the intensity averaged over
the "diffraction pattern of the telescope'', with the
components of the error beam pattern (resulting from surface
irregularities) being included.
Pick-up from larger angles (due to e.g. spillover past the secondary) are
included in the a priori unknown source coupling efficiency
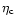 .
Downes (1989) points out that in case of a significant
error beam,
the main beam efficiency
.
Downes (1989) points out that in case of a significant
error beam,
the main beam efficiency
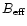 has to be replaced by the larger
full
beam efficiency, encompassing the main lobe and the error beam pattern.
The resulting quantity is then denoted as beam averaged brightness
temperature.
has to be replaced by the larger
full
beam efficiency, encompassing the main lobe and the error beam pattern.
The resulting quantity is then denoted as beam averaged brightness
temperature.
These definitions avoid the problem that the main beam-averaged intensity is
exceedingly overestimated because of the additional error beam pick-up.
The main draw back is, however, that the thus defined quantities
depend on the details of the error beam pattern. In addition, the error beam
pick-up might give rise to "fake'' velocity and spatial features, depending on
the angular extent and the velocity structure of the
source. Therefore, a simple scaling
of the efficiencies cannot properly correct for the error beam
pick-up. This motivates us to introduce a new quantity, the
corrected main beam brightness temperature,
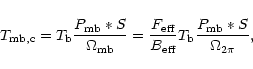 |
(2) |
where we use the above definition of the main beam,
and the convolution integral extends over the forward hemisphere of the
telescope. The crucial point is, however, not the definition of a
new temperature scale, but to find a correction method which is not
too time consuming and which can be applied to observed data with the
limited observing time, limited signal-to-noise ratio, and the data
reduction resources available.
For cm wave telescopes, an equivalent
quantity is introduced by Kalberla et al. (1980) with the
corrected brightness temperature 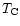 .
In fact, both (
.
In fact, both (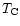 and
and
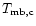 )
are identical
if the same main beam definition is used.
However, the main beam definition for cm and (sub-)mm
telescopes often differ because of practical reasons.
Due to the limited signal-to-noise ratio of the observations at
(sub-)mm wavelengths, the dynamical range in intensity often is not
sufficient to accurately
measure the side-lobes of the beam pattern. Therefore,
the main beam definition commonly used for cm telescopes
(beam pattern between first nulls, cf. Hartmann et al. 1996)
often cannot
be applied to (sub-)mm observations. This motivates us to introduce
)
are identical
if the same main beam definition is used.
However, the main beam definition for cm and (sub-)mm
telescopes often differ because of practical reasons.
Due to the limited signal-to-noise ratio of the observations at
(sub-)mm wavelengths, the dynamical range in intensity often is not
sufficient to accurately
measure the side-lobes of the beam pattern. Therefore,
the main beam definition commonly used for cm telescopes
(beam pattern between first nulls, cf. Hartmann et al. 1996)
often cannot
be applied to (sub-)mm observations. This motivates us to introduce
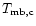 as a new quantity for the (sub-)mm range.
as a new quantity for the (sub-)mm range.
With the observed intensity given in terms of antenna
temperature
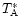 (Eq. (1)), the
corrected main beam brightness temperature can be written as
(Eq. (1)), the
corrected main beam brightness temperature can be written as
where the convolution integral extends over the forward hemisphere,
and
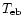 is denoted as error beam pick-up.
The error beam correction according to Eq. (3)
involves a far more complicated procedure than the calibration of the
observations using the main beam efficiency. It requires a detailed
knowledge of the beam pattern and information on the spatial distribution of
the emission at larger angular scales, and thus additional
observations in many cases.
is denoted as error beam pick-up.
The error beam correction according to Eq. (3)
involves a far more complicated procedure than the calibration of the
observations using the main beam efficiency. It requires a detailed
knowledge of the beam pattern and information on the spatial distribution of
the emission at larger angular scales, and thus additional
observations in many cases.
3 The error beam pattern of single dish radio telescopes
The error beam pattern arises from imperfections in
the primary reflector, spillover past the secondary mirror
and scattering from support legs and the secondary mirror. The latter
results in a not axially-symmetric error beam and is
expected to play a role for telescopes with a primary reflector surface
of high accuracy where the surface errors are negligible compared to
the wavelength of the observations. Their correction
requires information on the actual orientation of the error beam
on the sky (cf. Kalberla et al. 1980; Dame & Thaddeus 1994;
Hartmann et al. 1996).
For larger (sub-)mm wave telescopes, the error beam pattern often is
dominated by surface errors arising from
the limited alignment accuracy of the panels in the primary
reflector. The resulting error beam pattern has an approximately
Gaussian profile, centered on the main beam, with a HPBW corresponding to
the correlation length of the surface error distribution
(antenna tolerance theory,
see Scheffler 1962; Ruze 1952, 1966;
Shifrin 1971; Baars 1973).
Detailed studies of the beam pattern for several large (sub-)mm wave
telescopes have shown that the error beam can be represented
by a combination of several Gaussian error beams, arising
from independent surface error distributions. Examples are
the Itatepinga 14 m telescope (Kaufmann et al. 1987), the JCMT
15 m (Hills & Richter 1992; Prestage 1993),
and the IRAM 30 m (Garcia-Burillo et al. 1993; Greve et al. 1998).
The correlation length of the error distributions is given
by the linear dimension of the panels, panel frames, and the mounting
of the panels on the back-structure of the telescope (e.g. the array of
adjustment screws). The similar design of large telescopes, and
because the root mean square (rms) of the surface error is not
negligible compared to the wavelength for (sub-)mm
observations (as opposite to most of the present day cm-wave
telescopes), it is reasonable to assume that the error beam pattern
is dominated by one (or several) Gaussian components,
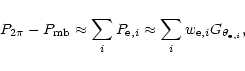 |
(4) |
where
![$G_{\theta_{{\rm e},i}}=4\,\ln
2/(\theta_{{\rm e},i}^2\pi)\exp[-4\,\ln2(\theta/\theta_{{\rm e},i})^2]$](/articles/aa/full/2001/02/aah1989/img37.gif) and
and
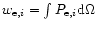 .
The panels (panel frames) of e.g. the IRAM 30 m
have a linear dimension of typically
.
The panels (panel frames) of e.g. the IRAM 30 m
have a linear dimension of typically
 to
to
 the diameter of the primary
reflector, and thus the error beam HPBW
the diameter of the primary
reflector, and thus the error beam HPBW
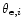 is 15-80 times the main
beam HPBW. The amplitude of the Gaussian error beam depends on
the ratio of the rms surface error to the wavelength.
is 15-80 times the main
beam HPBW. The amplitude of the Gaussian error beam depends on
the ratio of the rms surface error to the wavelength.
Equation (4) is only an approximation to
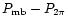 and includes two assumptions. Firstly, the
Gaussian error beams do not significantly contribute to the integral of the
beam pattern on the solid angle covered by the main beam,
and includes two assumptions. Firstly, the
Gaussian error beams do not significantly contribute to the integral of the
beam pattern on the solid angle covered by the main beam,
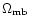 .
Secondly, the contribution of the tapered Airy
pattern
.
Secondly, the contribution of the tapered Airy
pattern
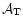 outside the main beam is small
(
outside the main beam is small
(
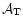 is the beam pattern of a telescope with a
perfect reflector surface, with no blockage and spillover).
The error introduced with both approximations is
negligible in most cases. We choose the IRAM 30m to give an example.
For wavelengths of
is the beam pattern of a telescope with a
perfect reflector surface, with no blockage and spillover).
The error introduced with both approximations is
negligible in most cases. We choose the IRAM 30m to give an example.
For wavelengths of
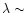 1.3mm, the ratio
1.3mm, the ratio
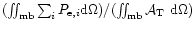 is
is 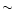 5%, while the contribution of the tapered Airy
pattern to the integrated beam pattern outside the -20 dB
contour is less than one percent, assuming a primary reflector
illumination with a -13 dB edge taper.
5%, while the contribution of the tapered Airy
pattern to the integrated beam pattern outside the -20 dB
contour is less than one percent, assuming a primary reflector
illumination with a -13 dB edge taper.
4 Error beam correction by using observations at lower
angular resolution
With an error beam pattern given by a combination of several Gaussians, the
pick-up therein is approximated by
![\begin{displaymath}
T_{\rm eb} \approx T_{\rm b} \sum_i \frac{P_{{\rm e},i} \ast...
...m_i p_{{\rm e},i}
\left[G_{\theta_{{\rm e},i}} \ast S\right],
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img47.gif) |
(5) |
where
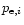 is the normalized, integrated power in the ith
Gaussian,
is the normalized, integrated power in the ith
Gaussian,
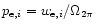 .
.
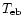 can be
determined using observations made with a smaller telescope,
provided that the main beam HPBW of the small telescope
(
can be
determined using observations made with a smaller telescope,
provided that the main beam HPBW of the small telescope
(
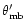 )
is smaller than
the HPBW of the error beam,
)
is smaller than
the HPBW of the error beam,
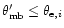 (in the following, the
"prime'' denotes quantities of the smaller telescope).
With
(in the following, the
"prime'' denotes quantities of the smaller telescope).
With
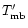 being the main beam brightness temperature
observed with the smaller telescope we have
being the main beam brightness temperature
observed with the smaller telescope we have
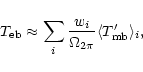 |
(6) |
where
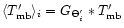 denotes the
smoothing of the spatial intensity distribution to the angular
resolution of the
ith error beam (
denotes the
smoothing of the spatial intensity distribution to the angular
resolution of the
ith error beam (
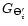 is a Gaussian of HPBW
is a Gaussian of HPBW
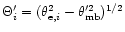 ).
We refer to this method as the (error beam) subtraction method.
).
We refer to this method as the (error beam) subtraction method.
The accuracy of the error beam correction depends on the accuracy of
the beam pattern parameters (
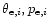 ).
For a reliable correction, additional
requirements apply to the signal to noise ratio and the spatial
extent of the additional observations.
For a quantification, we consider a rectangular map
).
For a reliable correction, additional
requirements apply to the signal to noise ratio and the spatial
extent of the additional observations.
For a quantification, we consider a rectangular map
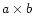 ,
observed with a large telescope. The main beam HPBW of
the large large telescope is
,
observed with a large telescope. The main beam HPBW of
the large large telescope is
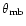 ,
and the main beam (forward)
efficiency is
,
and the main beam (forward)
efficiency is
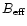 (
(
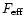 ,
respectively).
The observed spectra are contaminated by the pick-up in one Gaussian error
beam of HPBW
,
respectively).
The observed spectra are contaminated by the pick-up in one Gaussian error
beam of HPBW
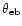 and "error beam efficiency''
and "error beam efficiency''
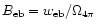 .
The signal to noise ratio of the observations is
.
The signal to noise ratio of the observations is
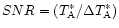 .
.
For an error beam correction, additional observations are made with a
smaller telescope (main
beam and forward efficiency of
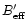 and
and
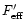 ). These observations have to cover a larger area
). These observations have to cover a larger area
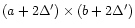 because a part of the
pick-up originates from outside the map observed with the
larger telescope. An estimate for
because a part of the
pick-up originates from outside the map observed with the
larger telescope. An estimate for
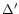 is given
in Appendix A with Eq. (A.4),
is given
in Appendix A with Eq. (A.4),
![\begin{displaymath}
\Delta^{\prime} \mathrel{\mathchoice {\vcenter{\offinterline...
... B_{\rm eb} }{ B_{\rm eff}^{\prime} } \right)
\right]^{1/2} ,
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img65.gif) |
(7) |
where
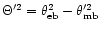 .
Here,
.
Here,
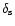 denotes the fraction of the error beam pick-up
which is missed due to the finite angular extent of the map, typically
accepted to be of the order of a few percent. Note,
that this estimate applies to a uniform intensity distribution of the
source. A
spatially more extended map (larger
denotes the fraction of the error beam pick-up
which is missed due to the finite angular extent of the map, typically
accepted to be of the order of a few percent. Note,
that this estimate applies to a uniform intensity distribution of the
source. A
spatially more extended map (larger
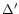 )
is required if
strong emission is found nearby, and a smaller
)
is required if
strong emission is found nearby, and a smaller
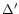 is
sufficient for a more compact source distribution.
is
sufficient for a more compact source distribution.
The error beam subtraction will increase the rms noise of the
corrected spectra because of the noise in the
observations made with the smaller telescope. Therefore, the
rms noise of the latter observations has
to be sufficiently small in order to not
significantly influence the corrected spectra.
With
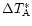 being the rms
noise of the original (uncorrected) observations, we define
the rms noise of the corrected spectra as
being the rms
noise of the original (uncorrected) observations, we define
the rms noise of the corrected spectra as
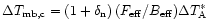 (Appendix A) and require
(Appendix A) and require
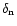 to be small (of the order of a few percent). An upper limit
to the required rms noise level of the observations with the
small telescope is given by Eq. (A.2),
to be small (of the order of a few percent). An upper limit
to the required rms noise level of the observations with the
small telescope is given by Eq. (A.2),
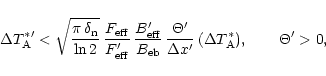 |
(8) |
where
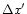 is the sampling in the observed map.
is the sampling in the observed map.
In the case of matching HPBWs (of the small telescope's main and the
larger telescope's error beam, i.e.
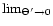 )
we find
)
we find
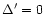 and
and
Note, that the 2-dimensional Gaussian
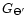 with
with
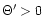 is used to
deduce Eq. (8), whereas
in the limiting case of
is used to
deduce Eq. (8), whereas
in the limiting case of
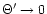 we have to
consider that
we have to
consider that
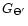 approaches the
approaches the
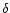 -function (see Appendix A).
-function (see Appendix A).
4.2 Time estimate for the additional observations
The time needed to obtain the observations with the smaller telescope is
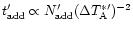 ,
where
,
where
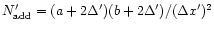 is the number of positions in the map.
In the following we assume fully sampled observations, usually accepted
to be fulfilled with a sampling of
is the number of positions in the map.
In the following we assume fully sampled observations, usually accepted
to be fulfilled with a sampling of
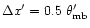 .
We then have
.
We then have
![\begin{displaymath}
t_{\rm add}^{\prime}
\propto \left[ \frac{ (a+2\Delta^{\pr...
...rime} /2)^2 }
(\Delta T_{\rm A}^{\ast \prime})^{-2} \right],
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img84.gif) |
(9) |
where
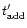 not only depends on
not only depends on
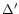 and
and
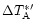 ,
but also on the geometry of the
map to be corrected.
,
but also on the geometry of the
map to be corrected.
For an illustration, we assume that the N positions in the
map observed with the large telescope cover a square (a=b).
In addition, we assume equal forward efficiencies for both telescopes,
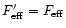 ,
and the
same equipment and atmospheric conditions for all observations.
Dividing Eq. (9) by
the time needed to complete the
observations in the original map,
,
and the
same equipment and atmospheric conditions for all observations.
Dividing Eq. (9) by
the time needed to complete the
observations in the original map,
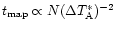 ,
gives
,
gives
where we have used Eqs. (7) and
(8)
for
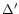 and
and
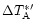 .
.
For an order of magnitude estimate we choose
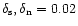 and a signal-to-noise ratio of
SNR=10. In addition, we choose
and a signal-to-noise ratio of
SNR=10. In addition, we choose
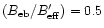 ,
which is appropriate e.g. for
the IRAM 30 m at 230 GHz.
In addition, we assume fully sampled observations for the large telescope,
,
which is appropriate e.g. for
the IRAM 30 m at 230 GHz.
In addition, we assume fully sampled observations for the large telescope,
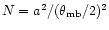 .
This gives
.
This gives
which is illustrated in Fig. 1 for
different ratios
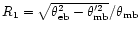 .
.
In order to give a numerical example and to compare the results
obtained here to those obtained for a de-convolution
of the error beam pattern in Fourier space
(Sect. 5), we consider two extreme cases.
For case A, we assume that the
map to be corrected is small, containing up to a few 10
positions, and that the HPBW of the error beam is substantially
larger than the main
beam HPBW of the small telescope (
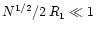 ).
For case B we consider large maps with more than 1000 positions,
and the case that the small telescope's main and the
large telescope's error beam closely match, both giving
).
For case B we consider large maps with more than 1000 positions,
and the case that the small telescope's main and the
large telescope's error beam closely match, both giving
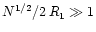 .
.
For case A, we obtain
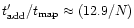 .
Thus, the time needed for the additional observations is of the same
order than the time needed to complete the high resolution observations to
be corrected.
For case B, the additional time needed is
.
Thus, the time needed for the additional observations is of the same
order than the time needed to complete the high resolution observations to
be corrected.
For case B, the additional time needed is
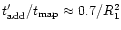 .
This is much smaller than unity, unless
.
This is much smaller than unity, unless
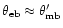 .
In most cases, however, the HPBW of the error beam
is larger and the time needed for the additional observations
is only a small fraction of the time needed to complete
the original map.
.
In most cases, however, the HPBW of the error beam
is larger and the time needed for the additional observations
is only a small fraction of the time needed to complete
the original map.
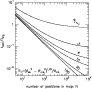 |
Figure 1:
Time needed for the additional observations
( error beam subtraction method):
the ratio
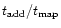 (total integration time needed for
the additional observations to the integration time of
original map) is shown for typical
ratios
(total integration time needed for
the additional observations to the integration time of
original map) is shown for typical
ratios
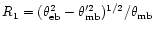 = 1, 3, 6, 10, 30, 100, where = 1, 3, 6, 10, 30, 100, where
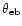 and
and
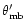 denote the error
beam HPBW of the large telescope and main beam HPBW of the small
telescope. We choose square geometry for the original map,
denote the error
beam HPBW of the large telescope and main beam HPBW of the small
telescope. We choose square geometry for the original map,
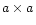 (see text for the additional assumptions made)
(see text for the additional assumptions made) |
| Open with DEXTER |
5 Error beam correction by de-convolution
An alternative correction
is the de-convolution of the error beam pattern in Fourier
space (de-convolution method). This is motivated by the convolution
theorem which links the convolution in the spatial domain to a multiplication
of the Fourier transform quantities.
The Fourier transform of Eq. (2) reads
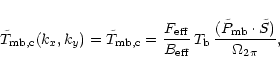 |
(10) |
where kx, ky are wave numbers. We use the "tilde''
symbol to denote the Fourier transform.
With the Fourier transform of Eq. (1),
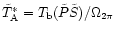 ,
we obtain
,
we obtain
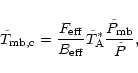 |
(11) |
where
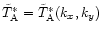 is
the Fourier transform of the observed map.
Back transform of
Eq. (11) gives the corrected map.
is
the Fourier transform of the observed map.
Back transform of
Eq. (11) gives the corrected map.
The de-convolution method requires the observations to be
fully sampled, covering a rectangular area.
Padding with zeros in order to fill a rectangular map is
allowed, provided that the full spatial extent of the emission is
observed for the given noise limit. Often, this is not the case,
and the error beam de-convolution requires additional, fully
sampled observations of the intensity distribution outside the
considered map with the same, large telescope (note, that it is
the intrinsic property of the error beam to smear the emission to a
larger area). For these observations, a larger rms noise
and thus a smaller integration time per position is sufficient,
because only the integral intensity on the angular scale of the error beam
is of interest.
For a quantification we use the same notation and assumptions as
above. The original map contains N spectra (rms noise
 )
and covers an area of
)
and covers an area of
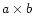 .
Additional observations are made with the same
telescope to extend the existing map:
(
.
Additional observations are made with the same
telescope to extend the existing map:
(
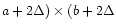 ). Here,
). Here, 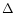 is given by the same
equation as
is given by the same
equation as
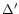 above (Eq. 7) with
above (Eq. 7) with
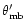 being replaced by
being replaced by
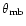 ,
,
![\begin{displaymath}
\Delta \mathrel{\mathchoice {\vcenter{\offinterlineskip\hali...
...\,
\frac{ B_{\rm eb} }{ B_{\rm eff}} \right)
\right]^{1/2} ,
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img108.gif) |
(12) |
and where
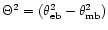 is the difference of the squared HPBW of the large telescope's
main and error beam. Because of
is the difference of the squared HPBW of the large telescope's
main and error beam. Because of
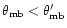 ,
,
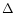 is larger than
is larger than
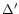 .
.
Compared to the spectra in the original map, a larger rms noise
(
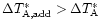 )
and thus a shorter integration time is sufficient for the spectra
in the extended map. In the following, we give an estimate for
)
and thus a shorter integration time is sufficient for the spectra
in the extended map. In the following, we give an estimate for
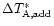 .
Using
.
Using
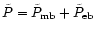 in
Eq. (11) we obtain
in
Eq. (11) we obtain
where
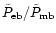 is given by
is given by
with
k2 = kx2 + ky2.
Using
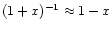 for
small
for
small
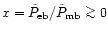 gives a lower
limit to
gives a lower
limit to
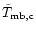 ,
,
![\begin{displaymath}
\tilde{T}_{\rm mb,c} \mathrel{\mathchoice {\vcenter{\offinte...
...\left[-\frac{\pi^2\,\Theta^2\,k^2}
{4\ln 2}
\right] \right).
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img120.gif) |
(13) |
The back Fourier transform of Eq. (13) then reads
where
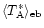 denotes the map observed with the large telescope, smoothed to the
angular resolution of error beam. For the spectra in the
smoothed map,
observations of the original map (rms noise
denotes the map observed with the large telescope, smoothed to the
angular resolution of error beam. For the spectra in the
smoothed map,
observations of the original map (rms noise
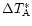 )
and the observations in the extended map (rms noise
)
and the observations in the extended map (rms noise
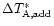 )
are averaged. Because of
)
are averaged. Because of
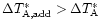 ,
an upper limit
to the rms noise of the corrected spectra is given by
,
an upper limit
to the rms noise of the corrected spectra is given by
This is identical to Eq. (A.1) where
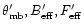 are replaced by the quantities of the large telescope,
are replaced by the quantities of the large telescope,
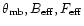 .
Therefore, we can use Eq.
(A.6) to obtain
.
Therefore, we can use Eq.
(A.6) to obtain
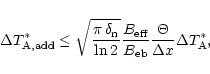 |
(14) |
where 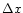 is the sampling of the observations.
is the sampling of the observations.
5.2 Time estimate for the additional observations
The time needed to obtain the additional observations with the large
telescope is given by
![\begin{displaymath}
t_{\rm add}^{\prime}
\propto \frac{N_{\rm add}}{(\Delta T_...
...a_{\rm mb}/2)^2}
(\Delta T_{\rm A,add}^{\ast})^{-2} \right],
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img128.gif) |
(15) |
assuming a sampling of
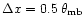 for
all observations.
for
all observations.
For an evaluation of Eq. (15), we
use Eqs. (12, 14)
and the assumptions made in the
previous section (a=b,
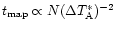 ,
same atmospheric conditions for
all observations). This gives
,
same atmospheric conditions for
all observations). This gives
For a numerical example
we adopt
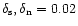 ,
a signal-to-noise
ratio of SNR=10, and
,
a signal-to-noise
ratio of SNR=10, and
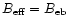 .
With
.
With
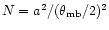 ,
this gives
,
this gives
where
![$R_2= [(\theta_{\rm eb}/\theta_{\rm mb})^2 - 1]^{1/2}
\approx \theta_{\rm eb}/\theta_{\rm mb}$](/articles/aa/full/2001/02/aah1989/img136.gif) .
The latter approximation
can be done because
of the angular size of the error beam pattern, typically being
.
The latter approximation
can be done because
of the angular size of the error beam pattern, typically being
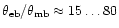 .
In
Fig. 2, the ratio
.
In
Fig. 2, the ratio
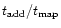 is
shown as a function of N and ratios
is
shown as a function of N and ratios
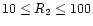 .
.
If we consider the limit of small maps with up to a few 10 positions
(
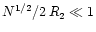 ,
case A introduced in Sect. 4.2) we obtain
,
case A introduced in Sect. 4.2) we obtain
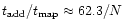 .
Here, the time needed for the
additional observations is comparable to and may even exceed the time
needed to complete the observations for
the original map. In the limit of large
maps (
.
Here, the time needed for the
additional observations is comparable to and may even exceed the time
needed to complete the observations for
the original map. In the limit of large
maps (
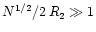 ,
case B) we get
,
case B) we get
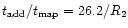 ,
which is much smaller than 1% in most cases, because
,
which is much smaller than 1% in most cases, because
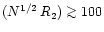 .
.
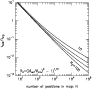 |
Figure 2:
Time needed for the additional observations
( error beam de-convolution method):
the ratio
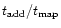 is shown for ratios
is shown for ratios
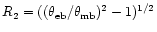 =10, 20,
40, 100. =10, 20,
40, 100.
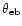 and
and
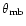 denote the error beam
and main beam HPBW of the large telescope
denote the error beam
and main beam HPBW of the large telescope |
| Open with DEXTER |
6 Comparison of both correction methods
For the subtraction method, an area of
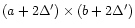 has to be covered with
fully sampled observations made with a small telescope, whereas the de-convolution method requires the existing map to be spatially extended
to cover the (larger) area
has to be covered with
fully sampled observations made with a small telescope, whereas the de-convolution method requires the existing map to be spatially extended
to cover the (larger) area
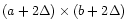 ,
provided that the observations of the original map are fully sampled.
Assuming the same equipment and atmospheric conditions at both
telescopes, the time required for the additional observations,
,
provided that the observations of the original map are fully sampled.
Assuming the same equipment and atmospheric conditions at both
telescopes, the time required for the additional observations,
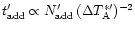 (subtraction
method) and
(subtraction
method) and
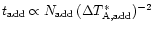 (de-convolution method), compare as
(de-convolution method), compare as
where we have used Eqs. (8) and
(14)
for
 and
and
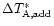 .
Recall that
.
Recall that
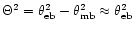 and
and
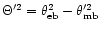 are the
differences between the squared HPBW of the Gaussian error beam
(
are the
differences between the squared HPBW of the Gaussian error beam
(
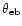 )
and the
main beam of the large (small) telescope
)
and the
main beam of the large (small) telescope
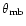 (
(
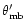 ).
).
For small maps (
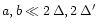 ,
discussed in
Sect. 4.2 as case A) we obtain
,
discussed in
Sect. 4.2 as case A) we obtain
and thus that the subtraction method is more efficient.
The additional observations with the smaller
telescope are less
time consuming (
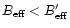 ,
while
,
while
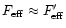 ).
For spatially extended maps (
).
For spatially extended maps (
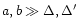 ;
case B) we get
;
case B) we get
Typically, we have
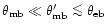 ,
and hence
,
and hence
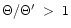 .
With
.
With
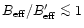 ,
this gives
,
this gives
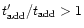 ,
and that
the additional observations with the large telescope
are less time consuming.
For large maps and the de-convolution method, the
disadvantage of the smaller main beam efficiency (
,
and that
the additional observations with the large telescope
are less time consuming.
For large maps and the de-convolution method, the
disadvantage of the smaller main beam efficiency (
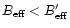 )
is outweighed by the smaller
area which has to be covered with the additional observations.
)
is outweighed by the smaller
area which has to be covered with the additional observations.
Limitations of the error beam subtraction method
are given by the accuracy of the intensity calibration of the
observations made with the smaller telescope. For instance,
they potentially suffer from a significant error beam pick-up, too.
However, this is a second order effect in most cases, and the subtraction
method still gives a better estimate for the intensity detected by
the main beam than the commonly used antenna temperature and
main beam brightness temperature. For the KOSMA observations
(used to correct the IRAM key-project CO J = 2
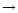 1 data)
we estimate the error beam pick-up to be smaller than 18%.
This is to be compared to an error beam pick-up in the key-project
maps of 31-50% (Paper III).
1 data)
we estimate the error beam pick-up to be smaller than 18%.
This is to be compared to an error beam pick-up in the key-project
maps of 31-50% (Paper III).
An additional limitation is given by the finite angular resolution of
observations made with the small telescope.
This might be a problem for the correction of observations made with
large (sub-)mm telescopes (diameter
of several ten meters). Here, large-scale deformations
in the reflector surface potentially result in an error beam with a
small HPBW, such as the first error beam of
the IRAM 30m (
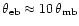 ,
see Greve et al. 1998). A correspondingly
large telescope with a clean beam pattern is then needed for a correction,
which may be difficult to find.
,
see Greve et al. 1998). A correspondingly
large telescope with a clean beam pattern is then needed for a correction,
which may be difficult to find.
For the de-convolution method,
additional observations have to be made for a large number of
positions with an extremely short integration time per position
(only the intensity integrated on the angular extent of the error
beam pattern is of interest).
This possibly results in an huge overhead in dead time
due to telescope motion, data acquisition, etc. In addition,
the large number of spectra in the extended map creates a
comparably large amount of raw
data to be handled in a relatively short time. The application
of de-convolution method therefore may be
impracticable or even impossible to apply.
For an illustration, we give the example of the
12CO 2
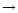 1 map of MCLD 123.5+24.9, observed
in the framework of the IRAM key-project. The correction for the
pick-up in the second error beam requires additional
observations with the IRAM 30m at
1 map of MCLD 123.5+24.9, observed
in the framework of the IRAM key-project. The correction for the
pick-up in the second error beam requires additional
observations with the IRAM 30m at
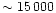 positions
and an integration time of less than 0.1s per position.
Even more extreme numbers are obtained for the correction of
the third error beam. This is currently not feasible and
we apply the subtraction method to correct the key-project
data.
positions
and an integration time of less than 0.1s per position.
Even more extreme numbers are obtained for the correction of
the third error beam. This is currently not feasible and
we apply the subtraction method to correct the key-project
data.
7 Summary
The presence of a significant error beam pattern potentially gives
rise to additional pick-up of intensity from outside the main beam,
in particular for observations of spatially extended sources.
For
(sub-)mm observations suffering from a significant
error beam pick-up we introduce the corrected main beam
brightness temperature,
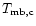 as new intensity scale.
It provides a better estimate for the intensity detected by the main
beam than the commonly used main beam brightness temperature and
antenna temperature. In the limit of a negligible error beam pick-up,
the corrected main beam brightness temperature is equal to the
main beam brightness temperature.
as new intensity scale.
It provides a better estimate for the intensity detected by the main
beam than the commonly used main beam brightness temperature and
antenna temperature. In the limit of a negligible error beam pick-up,
the corrected main beam brightness temperature is equal to the
main beam brightness temperature.
We discuss and compare two different correction methods in detail. The
subtraction method, which uses additional observations made with
a smaller telescope, and the de-convolution method, where the
error beam pick-up is de-convolved from the observed map in the
Fourier space.
Both methods have been described and successfully applied to observed
spectral line maps (cf. Kalberla et al. 1980;
Dame & Thaddeus 1994; Hartmann et al. 1996; Schneider et al. 1998).
The de-convolution method is attractive for the correction of
fully sampled maps which cover the full spatial extent of the emission
for the given noise limit. Here, the observed map contains all
information required to correct for the error beam pick-up. For maps which
cover only a fraction of a more extended intensity distribution, both correction
methods require additional observations. Observations with a smaller
telescope are required for the subtraction method, while the
existing (fully sampled) map has to be extended for the
de-convolution method. Typically, the additional
observations require less time than was
needed to complete the original observations to be corrected (in terms of total
integration time), except for small maps with a few ten positions.
For large maps (
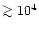 positions), such as those typically observed
with large surveys, the time needed is only a few percent of
the time spent for the original map. Though this a minor fraction,
it should be taken into account when planning large mapping
projects and a corresponding fraction of the time should be
allocated for the additional observations required.
positions), such as those typically observed
with large surveys, the time needed is only a few percent of
the time spent for the original map. Though this a minor fraction,
it should be taken into account when planning large mapping
projects and a corresponding fraction of the time should be
allocated for the additional observations required.
For the correction of a small map or single spectra, the subtraction
method is favorable because the additional
observations can be done more efficiently with a smaller telescope
(in this context, "small'' means that the angular extent of the original
map is smaller than a few times
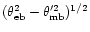 ,
where
,
where
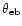 is the HPBW of the error beam and
is the HPBW of the error beam and
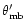 is the HPBW of the small telescope).
The subtraction method is limited by a potentially significant
error beam pick-up in the observations made with the smaller telescope
and the lower angular resolution. In particular,
one has to consider that
smaller telescopes tend to have cleaner beams allowing for a
more accurate correction of the error beam pick-up, but
possibly do not have the required angular resolution.
is the HPBW of the small telescope).
The subtraction method is limited by a potentially significant
error beam pick-up in the observations made with the smaller telescope
and the lower angular resolution. In particular,
one has to consider that
smaller telescopes tend to have cleaner beams allowing for a
more accurate correction of the error beam pick-up, but
possibly do not have the required angular resolution.
For the correction of large maps (angular extent 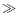 error beam),
the de-convolution method is attractive because the integration
time for the additional observations is
smaller than for the subtraction method. In practice, however,
these observations are often limited by the data handling capacity
and dead time (as a large amount of data
has to be collected in a relatively short time) and by the limited
availability of large (sub-)mm telescope for such (additional)
observations.
error beam),
the de-convolution method is attractive because the integration
time for the additional observations is
smaller than for the subtraction method. In practice, however,
these observations are often limited by the data handling capacity
and dead time (as a large amount of data
has to be collected in a relatively short time) and by the limited
availability of large (sub-)mm telescope for such (additional)
observations.
Acknowledgements
The KOSMA 3m radio telescope at Gornergrat-Süd Observatory is operated by
the University of Cologne and supported by the Deutsche
Forschungsgemeinschaft through grant SFB-301, as well as special
funding from the Land Nordrhein-Westfalen. The receiver development was partly
funded by the Bundesminister für Forschung and Technologie. The Observatory
is administered by the Internationale Stiftung Hochalpine
Forschungsstationen Jungfraujoch und Gornergrat, Bern.
The authors have benefitted from a joint European grant (Procope, grant#
312-pro-bmbw-gg) during the years 1995 and 1996. This research made
use of NASA's Astrophysics Data System Abstract Service.
Appendix A: Error beam correction by using observations of a smaller telescope:
Influence of edge effects and of the noise in the observations obtained with
the smaller telescope
Consider a large telescope with the beam pattern denoted by
P and the normalization P(0,0)=1.
We assume that the beam pattern consists of
a tapered Airy pattern
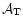 ,
approximated by a Gaussian
of half power
beam width (HPBW)
,
approximated by a Gaussian
of half power
beam width (HPBW)
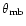 ,
and a Gaussian error beam
,
and a Gaussian error beam
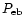 of HPBW
of HPBW
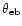 :
:
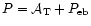 .
Forward and main beam efficiency of the telescope are
denoted by
.
Forward and main beam efficiency of the telescope are
denoted by
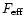 and
and
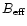 ,
and the "efficiency'' of the
Gaussian error beam is defined according
,
and the "efficiency'' of the
Gaussian error beam is defined according
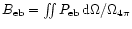 .
.
A spatially extended source is observed and the
resulting map covers a rectangular area 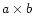 .
The error beam correction is done using the subtraction method.
Additional observations are made with a small telescope
(main beam HPBW and efficiency of
.
The error beam correction is done using the subtraction method.
Additional observations are made with a small telescope
(main beam HPBW and efficiency of
 ,
forward efficiency
,
forward efficiency
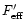 ). They cover a larger area
). They cover a larger area
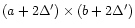 because of the
angular extent of the error beam,
because of the
angular extent of the error beam,
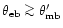 .
.
The error beam pick-up is estimated using Eq. (6), with the summation being done over
only one Gaussian error beam. The corrected main beam brightness
temperature is then approximated by
The accuracy of the corrected main beam brightness temperature
(
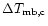 )
is given by the rms noise in the original observations
(
)
is given by the rms noise in the original observations
(
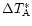 )
and the noise in the additional
observations made with the
smaller telescope. An additional, systematic error might be due
to the limited spatial extent of the map observed
with the smaller telescope, missing a fraction of the error beam.
Although being a systematic error, we
include the latter as a Gaussian average in our error
calculations, as if it is an independent, statistical error.
)
and the noise in the additional
observations made with the
smaller telescope. An additional, systematic error might be due
to the limited spatial extent of the map observed
with the smaller telescope, missing a fraction of the error beam.
Although being a systematic error, we
include the latter as a Gaussian average in our error
calculations, as if it is an independent, statistical error.
With the accuracy of the estimated error beam pick-up denoted by
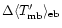 ,
we deduce
the accuracy of the corrected main beam brightness temperature scale
to be
,
we deduce
the accuracy of the corrected main beam brightness temperature scale
to be
![\begin{displaymath}
\Delta T_{\rm mb,c} = \frac{F_{\rm eff}}{B_{\rm eff}} (\Delt...
...{\rm eb}}{\Delta T_{\rm A}^{\ast}}
\right)^2
\right]^{1/2} ,
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img174.gif) |
(A.1) |
where we neglect a possible error beam pick-up in the observations of
the smaller telescope.
For a reliable error beam correction, the additional error
introduced by the rms noise and the finite size of the observations
made with the small telescope
should be small compared to the rms noise in the original
observations,
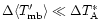 .
Therefore, we can assume
.
Therefore, we can assume
 which allows us to use the approximation
which allows us to use the approximation
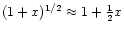 to obtain
to obtain
Specifying the relative error introduced by the error beam correction
as
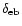 ,
we can write
,
we can write
which gives an upper limit
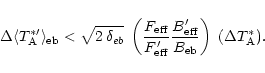 |
(A.2) |
We now determine the systematic
error introduced due to the finite spatial extent
of the map observed with the smaller telescope,
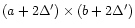 ,
and require that it is small compared
to the rms noise in the original spectra,
,
and require that it is small compared
to the rms noise in the original spectra,
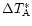 .
For an estimate, we assume an uniform source distribution of an angular
extent much larger than the error beam pattern.
Dividing Eq. (A.2) by
.
For an estimate, we assume an uniform source distribution of an angular
extent much larger than the error beam pattern.
Dividing Eq. (A.2) by
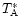 gives
gives
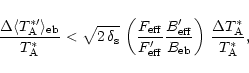 |
(A.3) |
where we have used that
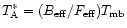 .
Typically,
.
Typically,
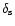 is of the order of a few percent. The assumption of a uniform source
distribution of angular extent larger than the error beam pattern
gives
is of the order of a few percent. The assumption of a uniform source
distribution of angular extent larger than the error beam pattern
gives
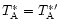 .
Thus,
.
Thus,
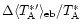 can be re-written to
can be re-written to
where
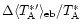 is the fraction of the error beam
pick-up which is missed.
is the fraction of the error beam
pick-up which is missed.
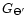 is
the normalized, 2-dimensional Gaussian of HPBW
is
the normalized, 2-dimensional Gaussian of HPBW
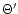 ,
,
![$G_{\Theta^{\prime} }(r) =
(4 \ln2/\Theta^{\prime 2} \pi)\,\exp[-4\ln 2 (r/\Theta^{\prime})^2]$](/articles/aa/full/2001/02/aah1989/img188.gif) ,
with
,
with
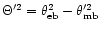 and
r=(x2 + y2)1/2. Evaluation of the integrals gives
and
r=(x2 + y2)1/2. Evaluation of the integrals gives
which provides an upper limit to
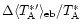 .
This finally gives
.
This finally gives
![\begin{displaymath}
\Delta^{\prime} < \left[ \frac{\Theta^{\prime 2} }{4 \ln 2} ...
...]^{1/2},
\quad \theta_{\rm eb} \ge \theta_{\rm mb}^{\prime} ,
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img190.gif) |
(A.4) |
where
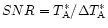 is the signal-to-noise
ratio of the observations
made with the large telescope. For typical values
(
is the signal-to-noise
ratio of the observations
made with the large telescope. For typical values
(
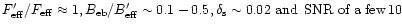 )
we obtain
)
we obtain
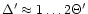 .
In the limit of equal HPBW for the small telescope's main and
the large telescope's error beam (
.
In the limit of equal HPBW for the small telescope's main and
the large telescope's error beam (
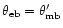 )
we have
)
we have
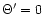 and
and
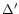 vanishes.
vanishes.
A.2 Contribution of the noise in the observations of the smaller
telescope to the noise in the corrected spectra
To estimate the additional noise introduced with the error beam correction,
we assume that the additional observations
are made on a regular grid, and that
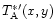 gives the observed intensity
as function of the offset position x,y. The spectrum at position
(x0,y0), smoothed to the resolution of the error beam,
is then given by
gives the observed intensity
as function of the offset position x,y. The spectrum at position
(x0,y0), smoothed to the resolution of the error beam,
is then given by
Here,
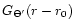 is the 2-dimensional Gaussian defined
above with
r-r0=((x-x0)2-(y-y0)2)1/2. The summation is done
over all positions (x,y) of the grid.
For
is the 2-dimensional Gaussian defined
above with
r-r0=((x-x0)2-(y-y0)2)1/2. The summation is done
over all positions (x,y) of the grid.
For
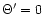 (the main beam HPBW of the small
telescope matches the HPBW of the error beam) we have
(the main beam HPBW of the small
telescope matches the HPBW of the error beam) we have
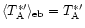 .
The rms noise of the smoothed spectra is given by
.
The rms noise of the smoothed spectra is given by
and
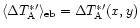 for
for
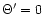 .
We assume a constant rms noise level,
.
We assume a constant rms noise level,
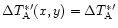 for the observations made with the small telescope.
Multiplication of the numerator and denominator by the
sampling
for the observations made with the small telescope.
Multiplication of the numerator and denominator by the
sampling
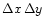 and replacing the summation by an
integration gives
and replacing the summation by an
integration gives
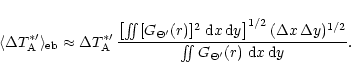 |
(A.5) |
This includes the limiting case of
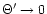 where the Gaussian approaches the
where the Gaussian approaches the
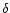 -function,
-function,
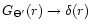 .
Evaluation of the integrals for
.
Evaluation of the integrals for
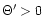 gives
gives
Thus, the rms noise required for the observations of the small telescope is
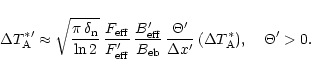 |
(A.6) |
Typical values (
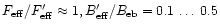 ,
,
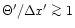 and
and
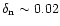 )
give
a ratio (
)
give
a ratio (
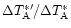 )
of
the order of a few tenths.
)
of
the order of a few tenths.
-
Baars, J. W. M. 1973, IEEE Trans. Ant. Propag., AP-21, 461
In the text
-
Bensch, F., Panis, J.-F., Stutzki, J., Heithausen, A.,
& Falgarone, E. 2001,
A&A, 365, 275 (Paper III)
In the text
-
Dame, T., & Thaddeus, P. 1994, ApJ, 436, L173
In the text
NASA ADS
-
Downes, D. 1989, Introductory courses in Galaxies (Springer)
In the text
-
Falgarone, E., Panis, J.-F., Heithausen, A.,
et al. 1998, A&A, 331, 669 (Paper I)
In the text
NASA ADS
-
Garcia-Burillo, S., Guélin, M., & Cernicharo, J.
1993, A&A, 274, 123
In the text
NASA ADS
-
Greve, A., Kramer, C., & Wild, W. 1998, A&AS, 133, 271
In the text
NASA ADS
-
Harten, R. H. 1973, AJ, 78, 565
In the text
NASA ADS
-
Hartmann, D., Kalberla, P. M. W., Burton, W. B., & Mebold, U.
1996, A&AS, 119, 115
In the text
NASA ADS
-
Heiles, C., & Hoffman, W. 1968, AJ, 73, 412
In the text
NASA ADS
-
Heithausen, A., Bensch, F., Stutzki, J., Falgarone, E., & Panis, J.-F.
1998, A&A, 331, L65
In the text
NASA ADS
-
Hills, R. E., & Richter, J. 1992, The JCMT Newsletter, Aug. 24
In the text
-
Kalberla, P. M. W., Mebold, U., & Reich, W. 1980, A&A, 82, 275
In the text
NASA ADS
-
Kaufmann, P., Abraham, Z., Scalise, E., et al. 1987, IEEE Trans. Ant.
Propag., AP-35, 996
In the text
NASA ADS
-
Kramer, C. 1997, Calibration of spectral line data at the IRAM 30 m
ratio telescope (v2.1), IRAM report
In the text
-
Kutner, M. L., & Ulich, B. L. 1981, ApJ, 250, 341
In the text
NASA ADS
-
Prestage, R. 1993, The JCMT Newsletter, July 27
In the text
-
Rohlfs, K., & Wilson, T. L. 1996, Tools of Radio Astronomy, 2nd edition
(Springer-Verlag Berlin)
In the text
-
Ruze, J. 1952, Suppl. al Nuovo Cimento, 9, 364
In the text
-
Ruze, J. 1966, Proc. IEEE, 54, 633
-
Scheffler, H. 1962, Z. f. Astrophys., 55, 1
In the text
NASA ADS
-
Schneider, N., Stutzki, J., Winnewisser, G., & Block, D.
1998, A&A, 335, 1049
In the text
NASA ADS
-
Shifrin, Y. S. 1971, Statistical Antenna Theory
(The Golem Press,
Boulder, Colorado, USA)
In the text
-
van Woerden, H., Takakkubo, K., & Braes, L. L. E. 1962, Bulletin of the
Astronomical Institutes of the Netherlands, Vol. 16, No. 524, 321
In the text
-
Westerhout, G., Wendlandt, & Harten, R. H. 1973, AJ, 78, 569
In the text
NASA ADS
© ESO 2001
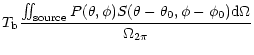
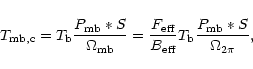
![$\displaystyle \frac{F_{\rm eff}}{B_{\rm eff}}
\left[ T_{\rm A}^{\ast} - T_{\rm b} \frac{(P_{\rm 2\pi}-P_{\rm mb})
\ast S}{\Omega_{2\pi}} \right]$](/articles/aa/full/2001/02/aah1989/img33.gif)
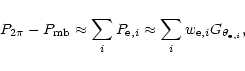
![\begin{displaymath}
T_{\rm eb} \approx T_{\rm b} \sum_i \frac{P_{{\rm e},i} \ast...
...m_i p_{{\rm e},i}
\left[G_{\theta_{{\rm e},i}} \ast S\right],
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img47.gif)
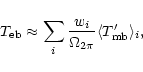
![\begin{displaymath}
\Delta^{\prime} \mathrel{\mathchoice {\vcenter{\offinterline...
... B_{\rm eb} }{ B_{\rm eff}^{\prime} } \right)
\right]^{1/2} ,
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img65.gif)
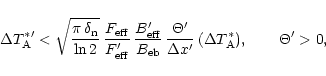
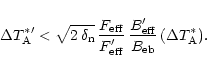
![\begin{displaymath}
t_{\rm add}^{\prime}
\propto \left[ \frac{ (a+2\Delta^{\pr...
...rime} /2)^2 }
(\Delta T_{\rm A}^{\ast \prime})^{-2} \right],
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img84.gif)
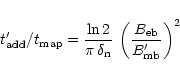
![\begin{displaymath}\qquad\qquad \times N^{-1} \left[ \frac{a}{\Theta^{\prime}}\,...
...rm eb}}{B_{\rm mb}^{\prime}}
\right)\right)^{1/2}
\right]^2,
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img90.gif)
![\begin{displaymath}t_{\rm add}^{\prime}/t_{\rm map} =
2.76\,N^{-1}\, \left[\frac{N^{1/2}}{2\,R_1} + 2.16\right]^2,
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img94.gif)

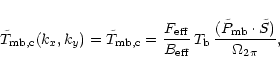
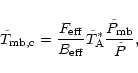
![\begin{displaymath}
\Delta \mathrel{\mathchoice {\vcenter{\offinterlineskip\hali...
...\,
\frac{ B_{\rm eb} }{ B_{\rm eff}} \right)
\right]^{1/2} ,
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img108.gif)
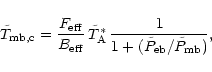
![\begin{displaymath}\frac{\tilde{P}_{\rm eb}}{\tilde{P}_{\rm mb}} = \frac{B_{\rm ...
... (\theta_{\rm eb}^2 -
\theta_{\rm mb}^2)}{4\ln 2}k^2\right],
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img116.gif)
![\begin{displaymath}
\tilde{T}_{\rm mb,c} \mathrel{\mathchoice {\vcenter{\offinte...
...\left[-\frac{\pi^2\,\Theta^2\,k^2}
{4\ln 2}
\right] \right).
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img120.gif)
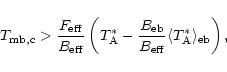
![\begin{displaymath}\Delta T_{\rm mb,c}^{\ast} < \frac{F_{\rm eff}}{B_{\rm eff}}
...
...\Delta T_{\rm A,add}^{\ast}
\rangle_{\rm eb}^2 \right]^{1/2}.
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img123.gif)
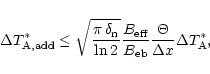
![\begin{displaymath}
t_{\rm add}^{\prime}
\propto \frac{N_{\rm add}}{(\Delta T_...
...a_{\rm mb}/2)^2}
(\Delta T_{\rm A,add}^{\ast})^{-2} \right],
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img128.gif)
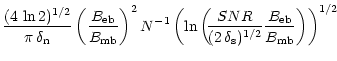
![$\displaystyle \left[ \frac{a}{\Theta}
+ \left(\frac{1}{4\,\ln2}\,
\ln\left(\fra...
...ta_{\rm s})^{1/2}}
\frac{B_{\rm eb}}{B_{\rm mb}}
\right) \right)^{1/2} \right].$](/articles/aa/full/2001/02/aah1989/img133.gif)
![\begin{displaymath}t_{\rm add}/t_{\rm map} = 52.42\,N^{-1}\,
\left[\frac{N^{1/2}}{2\,R_2} + 1.19\right],
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img135.gif)

![\begin{displaymath}\frac{t_{\rm add}^{\prime}}{t_{\rm add}} =
\frac{(a+2\Delta...
...\rm eff}^{\prime}} \frac{\Theta}{\Theta^{\prime}}
\right]^2,
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img148.gif)
![\begin{displaymath}\frac{t_{\rm add}^{\prime}}{t_{\rm add}} \approx
\left[ \fr...
... eff}}
\frac{B_{\rm eff}}{B_{\rm eff}^{\prime}} \right]^2 ,
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img151.gif)
![\begin{displaymath}\frac{t_{\rm add}^{\prime}}{t_{\rm add}} \approx
\frac{a\;b...
... eff}^{\prime}}
\frac{\Theta}{\Theta^{\prime}}
\right]^2 .
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img155.gif)
![\begin{displaymath}T_{\rm mb,c} \approx \frac{F_{\rm eff}}{B_{\rm eff}} \left[ T...
... eff}}
\langle T_{\rm mb}^{\prime} \rangle_{\rm eb} \right].
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img171.gif)
![\begin{displaymath}
\Delta T_{\rm mb,c} = \frac{F_{\rm eff}}{B_{\rm eff}} (\Delt...
...{\rm eb}}{\Delta T_{\rm A}^{\ast}}
\right)^2
\right]^{1/2} ,
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img174.gif)
![\begin{displaymath}\Delta T_{\rm mb,c} \approx \frac{F_{\rm eff}}{B_{\rm eff}}
(\Delta T_{\rm A}^{\ast})
\left[ 1 + \frac{1}{2} x \right].
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img178.gif)
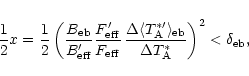
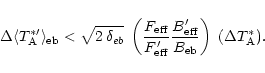
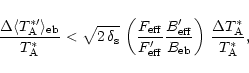
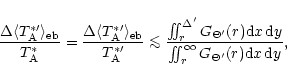
![\begin{displaymath}\frac{\Delta \langle T_{\rm A}^{\ast \prime} \rangle_{\rm eb}...
...
\approx
\exp [-4\ln 2 (\Delta^{\prime}/\Theta^{\prime})^2],
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img189.gif)
![\begin{displaymath}
\Delta^{\prime} < \left[ \frac{\Theta^{\prime 2} }{4 \ln 2} ...
...]^{1/2},
\quad \theta_{\rm eb} \ge \theta_{\rm mb}^{\prime} ,
\end{displaymath}](/articles/aa/full/2001/02/aah1989/img190.gif)