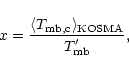 |
(3) |
The comparison of the error beam corrected key-project data, smoothed
to the KOSMA resolution, with the KOSMA observations provides a check
for the correction method and the intensity calibration of both data
sets. For a quantification we define
For perfectly corrected IRAM 30m data
and KOSMA observations with a negligible error beam pick-up, a
narrow distribution, centered on 1, is expected. An average value
smaller than unity suggests that the IRAM 30 m
error beam pick-up is overestimated, and hence that the
corrected main beam brightness temperature is underestimated.
For the corrected key-project maps, the x-distributions are given
in Fig. 11, together with the average (![]() ), median,
and width
), median,
and width ![]() (standard deviation) of the distribution.
(standard deviation) of the distribution.
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{h1988f11.eps}\end{figure}](/articles/aa/full/2001/02/aah1988/Timg67.gif) |
Figure 11:
Distribution of x, determined as the ratio of the
corrected key-project data (smoothed to angular
resolution of the KOSMA telescope) and the KOSMA observations
(Eq. 3). The ratio x was determined
for each velocity channel with an
intensity larger than three times the rms in the spectrum.
Positions which are located closer than 1 arcmin to the edge of
the map are excluded.
For each distribution, the average |
For the 12CO
![]() 1 maps,
1 maps, ![]() is found to be
equal or smaller than unity (0.82, 1.02 and 0.88 for
MCLD 123.5+24.9, L1512 and L134A, respectively),
while for the 13CO
is found to be
equal or smaller than unity (0.82, 1.02 and 0.88 for
MCLD 123.5+24.9, L1512 and L134A, respectively),
while for the 13CO
![]() 1 maps,
1 maps, ![]() is larger than
unity (1.15, 1.26 and 1.06). For the 12CO
is larger than
unity (1.15, 1.26 and 1.06). For the 12CO
![]() 0 map
of MCLD 123.5+24.9 we find
0 map
of MCLD 123.5+24.9 we find ![]() 1.02.
The width
1.02.
The width ![]() of the distributions is between
0.10 and 0.18, except for the 13CO
of the distributions is between
0.10 and 0.18, except for the 13CO
![]() 1 map of
MCLD 123.5+24.9, where
1 map of
MCLD 123.5+24.9, where ![]() is significantly larger
(0.22). In general,
we find larger
is significantly larger
(0.22). In general,
we find larger ![]() for the 13CO
for the 13CO
![]() 1 maps,
except for L134A where both maps have
1 maps,
except for L134A where both maps have
![]() .
The influence of the finite signal-to-noise in the spectra on the
.
The influence of the finite signal-to-noise in the spectra on the
![]() and
and ![]() is negligible.
We obtain the same results for distributions deduced with spectra
binned to a lower velocity resolution, and hence with a lower
rms noise per velocity channel. Thus, the
is negligible.
We obtain the same results for distributions deduced with spectra
binned to a lower velocity resolution, and hence with a lower
rms noise per velocity channel. Thus, the ![]() and
and ![]() can be used to determine the
accuracy of the error beam correction method
and to examine the limiting factors.
can be used to determine the
accuracy of the error beam correction method
and to examine the limiting factors.
We estimate the total uncertainty in the
![]() scale using
the self-consistency check (
scale using
the self-consistency check (![]() and
and ![]() )
and by comparing the observed line profiles to the
estimated error beam pick-up.
)
and by comparing the observed line profiles to the
estimated error beam pick-up.
An average value ![]() offset from unity indicates systematic
errors, which may result from
offset from unity indicates systematic
errors, which may result from
The width of the distribution (![]() )
depends on statistical
variations from position to position. These uncertainties may
arise from
)
depends on statistical
variations from position to position. These uncertainties may
arise from
The exact amount of error beam pick-up in the KOSMA observations
is unknown because it depends on the large-scale structure
of the emission and the (unknown) details of the KOSMA error beam
pattern. If present, the KOSMA error beam pick-up is expected to play
a role for the observations of the spatially extended
12CO
![]() 1 emission only.
An estimate of the KOSMA error beam pick-up
at 230GHz is obtained by comparing
the main beam efficiency determined for bright planets
(
1 emission only.
An estimate of the KOSMA error beam pick-up
at 230GHz is obtained by comparing
the main beam efficiency determined for bright planets
(
![]() )
and measured on the Moon (
)
and measured on the Moon (
![]() =
0.72). This shows that a KOSMA error beam of angular extent
=
0.72). This shows that a KOSMA error beam of angular extent
![]() is present, and that the power radiated into this error beam is
is present, and that the power radiated into this error beam is ![]() 13% of the power in the main beam. Thus, for extended sources,
an error beam pick-up of
13% of the power in the main beam. Thus, for extended sources,
an error beam pick-up of ![]() 13% is expected for KOSMA
observations at 230 GHz (assuming an uniform intensity distribution).
13% is expected for KOSMA
observations at 230 GHz (assuming an uniform intensity distribution).
Indeed, for the maps with the spatially most extended emission
(the 12CO
![]() 1 maps observed toward
MCLD123.5+24.9 and L134A) we find
1 maps observed toward
MCLD123.5+24.9 and L134A) we find ![]() which are
significantly smaller than unity, suggesting that the
KOSMA error beam is not negligible. The
which are
significantly smaller than unity, suggesting that the
KOSMA error beam is not negligible. The
![]() (0.88,
respectively) suggest that the KOSMA error beam pick-up is
12 - 18% for the 12CO
(0.88,
respectively) suggest that the KOSMA error beam pick-up is
12 - 18% for the 12CO
![]() 1 maps, and this
only if we fully attribute the
1 maps, and this
only if we fully attribute the ![]() to a KOSMA error beam.
For the 13CO
to a KOSMA error beam.
For the 13CO
![]() 1 maps we find that the
1 maps we find that the
![]() are larger than unity. This is consistent with a negligible
KOSMA error beam pick-up for the not very extended emission
of the rarer isotopomer, and that other
systematic errors limit the accuracy of the intensity
calibration. The same applies to
the 12CO
are larger than unity. This is consistent with a negligible
KOSMA error beam pick-up for the not very extended emission
of the rarer isotopomer, and that other
systematic errors limit the accuracy of the intensity
calibration. The same applies to
the 12CO
![]() 0 map of MCLD123.5+24.9,
because of the smaller amplitude of the error beam pattern at lower
frequencies.
0 map of MCLD123.5+24.9,
because of the smaller amplitude of the error beam pattern at lower
frequencies.
The correction for the first (smaller) error beam of the IRAM 30m is not possible
because of the large temporal variations of the amplitude and the
insufficient angular resolution of the KOSMA observations. Thus, an
additional error in the intensity calibration of the corrected data set
arises from the uncorrected first error beam.
This error is expected to play a significant role for maps which show
strong intensity variations
on the angular scale of the error beam (![]() 1.9' at 230GHz).
Here, the x-distribution is expected to be significantly wider
(lager
1.9' at 230GHz).
Here, the x-distribution is expected to be significantly wider
(lager ![]() )
with an average
)
with an average ![]() larger than unity,
because the pick-up in the small error beam strongly varies with the
position.
This is observed for the 13CO
larger than unity,
because the pick-up in the small error beam strongly varies with the
position.
This is observed for the 13CO
![]() map
of MCLD 123.5+24.9 and L1512. Both contain cores and/or
steep gradients extending over
map
of MCLD 123.5+24.9 and L1512. Both contain cores and/or
steep gradients extending over ![]() 1 arcmin (Figs. 1
and 2) and, at the same time, have the
largest
1 arcmin (Figs. 1
and 2) and, at the same time, have the
largest ![]() (1.15 and 1.26) and
(1.15 and 1.26) and ![]() (0.22 and 0.18). We therefore conclude that the
accuracy of the intensity calibration for these maps is limited by the
uncorrected first error beam, and that the
thus introduced error is up to 26%. For the other maps, the first error
beam accounts for less than 12% of the observed intensity, judged from the
(0.22 and 0.18). We therefore conclude that the
accuracy of the intensity calibration for these maps is limited by the
uncorrected first error beam, and that the
thus introduced error is up to 26%. For the other maps, the first error
beam accounts for less than 12% of the observed intensity, judged from the
![]() in Fig. 11
and taking into account that the accuracy of the relative intensity
calibration in the maps is 9% (Panis 1995),
assuming that both errors add in quadrature.
in Fig. 11
and taking into account that the accuracy of the relative intensity
calibration in the maps is 9% (Panis 1995),
assuming that both errors add in quadrature.
In the 12CO
![]() 1 map of
L134A the estimated error beam pick-up
systematically exceeds the observed line profile for a few positions
at
1 map of
L134A the estimated error beam pick-up
systematically exceeds the observed line profile for a few positions
at ![]() (
(
![]() ,
,
![]() ), while both profiles appear velocity-shifted
in respect to each other for positions
), while both profiles appear velocity-shifted
in respect to each other for positions
![]() .
This cannot be reconciled unless we modify the amplitude of the
error beam pattern by much more than
.
This cannot be reconciled unless we modify the amplitude of the
error beam pattern by much more than ![]() ,
which is excluded by the
accuracy of the beam pattern parameters (GKW).
Similarly, the possible contribution of a KOSMA error beam
cannot fully account for the discrepancy because it would
imply an additional pick-up in the KOSMA observations
of far more than 20%, and thus
extended areas with strong emission outside the
maps, which is not observed (Bensch 1998).
,
which is excluded by the
accuracy of the beam pattern parameters (GKW).
Similarly, the possible contribution of a KOSMA error beam
cannot fully account for the discrepancy because it would
imply an additional pick-up in the KOSMA observations
of far more than 20%, and thus
extended areas with strong emission outside the
maps, which is not observed (Bensch 1998).
One plausible explanation is provided by a possible deviation of the
IRAM error beam pattern from the assumed axial symmetry.
In the L134A maps, a velocity gradient is
present South of
![]() ,
extending over several arcmins.
A slight deviation from the assumed axial symmetry can mimic a velocity shift in the line
profile of the error beam pick-up. This is not excluded by the
measurements of GKW, because they used cross-scans in
,
extending over several arcmins.
A slight deviation from the assumed axial symmetry can mimic a velocity shift in the line
profile of the error beam pick-up. This is not excluded by the
measurements of GKW, because they used cross-scans in
![]() East-West direction and explicitly assume axial symmetry.
Moreover, a not axially-symmetric error
beam pattern is not entirely unrealistic, given the shape of the panels/panel
frames of the IRAM 30m.
East-West direction and explicitly assume axial symmetry.
Moreover, a not axially-symmetric error
beam pattern is not entirely unrealistic, given the shape of the panels/panel
frames of the IRAM 30m.
© ESO 2001