A&A 365, 275-284 (2001)
DOI: 10.1051/0004-6361:20000475

The IRAM key-project: Small-scale structure of pre-star forming regions[*]

III. Influence of and correction for the error beam pick-up

F. Bensch1 - J.-F. Panis2,3 - J. Stutzki1 - A. Heithausen1,4 - E. Falgarone3

Send offprint request: F. Bensch,


1 - I. Physikalisches Institut der Universität zu Köln, Zülpicher Straße 77, 50937 Köln, Germany
2 - ASIAA, Academica Sinica, PO Box 1-87, Nankang, Taipei 115, Taiwan, PR China
3 - Radioastronomie, CNRS URA 336, École Normale Supérieure, 24 rue Lhomond, 75005 Paris, France
4 - Radioastronomisches Institut der Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany

Received 27 January 2000 / Accepted 1 August 2000

Abstract
The goal of the IRAM key-project "Small-scale structure of pre-star forming regions'' is to map three nearby ( $d\sim 150~{\rm pc}$), quiescent molecular clouds with a high angular and spectral resolution to study the molecular cloud structure down to the smallest linear scales currently accessible by single dish radio telescopes. Here, we give a detailed discussion of the influence and the correction of the error beam pick-up. A new set of corrected data is presented using the beam pattern parameters of the IRAM 30m telescope recently published by Greve et al. (1998). For the correction we use observations made at lower angular resolution with the KOSMA 3m telescope. Smeared to the resolution of the error beam, they provide an estimate of the pick-up therein. The error beam pick-up accounts for a significant fraction of the observed intensity in the key-project maps: on average 31% to 50% for the 12CO $J=2\rightarrow $ 1 maps, 10% to 35% for the 13CO $J=2\rightarrow $ 1 maps, and 16.5% in the 12CO $J=1\rightarrow $ 0 map of MCLD 123.5+24.9. In addition, the line profiles are significantly modified by the error beam pick-up. The large data set available with the IRAM key-project allows us to investigate the accuracy of the correction method and its limitations in detail. For the corrected maps, we determine the overall accuracy of the temperature scale to be better than 15%, except for the 13CO $J=2\rightarrow $ 1 map of MCLD123.5+24.9 and L1512 where we estimate an accuracy of 22% and 18%. The key-project maps presented here and the released maps published by Falgarone et al. (1998) (with the correction done using the previous beam pattern parameters determined by Garcia-Burillo et al. 1993) differ by no more than 10% and only in localized regions. Both data sets and the supplementary observations made with the KOSMA telescope are available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/Abstract.html The "error beam problem'' is not limited to observations obtained with the IRAM 30m. Similar beam pattern are found for other large single dish (sub-)mm telescopes, although few quantitative studies exist. In particular, for observations of spatially extended sources, the error beam contribution has to be considered and corrected for if necessary.

Key words: methods: data analysis - techniques: miscellaneous - radio lines: ISM - line: profiles - interstellar medium (ISM): clouds - ISM: structure

Author for correspondance: bensch@ph1.uni-koeln.de


   
1 Introduction

The present paper is the third in a series presenting the observations and the results of the first IRAM key-project "small-scale structure of pre-star-forming regions''. Fully sampled maps had been obtained for three nearby ($d\sim 150$pc) quiescent molecular clouds (MCLD 123.5+24.9, L1512 and L134A) with high spatial and spectral resolution with the IRAM 30m telescope. The data set covers observations in both lowest rotational transitions of 12CO and 13CO, and in C18O $J=1\rightarrow $ 0. A detailed description of the key-project, the presentation of the data and first results are published by Falgarone et al. (1998), hereafter Paper I. The discussion of the data reduction procedure will be given by Panis et al. (in preparation; Paper II). Here, we present a detailed study of the influence and the correction of the error beam pick-up and discuss the factors limiting the accuracy of the intensity calibration for the corrected data. An independently reduced data set is presented with the error beam correction based on the beam pattern measurements by Greve et al. (1998, GKW). This data set is compared to the released data from Paper I, where the correction was done using the earlier beam pattern measurements by Garcia-Burillo et al. (1993, GGC).

With the increasing number of surveys covering spatially extended emission, such as those needed to study the structure of the interstellar medium (ISM), it has become clear that a significant fraction of the detected intensity can be due to pick-up in beam pattern components outside the main beam. Early studies of the influence of the stray radiation pick-up and methods for its correction have been done for HI observations (cf. Heiles & Hoffman 1968; Westerhout et al. 1973; Hartmann et al. 1996), based on accurate beam pattern measurements (cf. Baars & Mezger 1964; Hartsuijker et al. 1972; Harten 1973). Kalberla et al. (1980) have shown, that the pick-up in a relatively weak but spatially constrained stray pattern can significantly contribute to the observed intensity. For (sub-)mm wave telescopes, studies of the error beam pick-up were done by e.g. Schneider et al. (1998) for IRAM 30m observations, and Dame & Thaddeus (1994) for observations made with CfA 1.2m telescope.

Measurements of the IRAM 30 m beam pattern show that the error beam accounts for a substantial fraction of the beam pattern (GGC and GKW), more than 50% for observations at wavelengths $\le1.3$mm (frequencies $\nu \ge 230$GHz). This demonstrates that an error beam correction is essential, in particular for observations of spatially extended sources, such as those of the key-project.

For the correction of the key-project data set we use observations made with the KOSMA telescope. Smeared to the spatial resolution of the error beam (appropriately scaled to account for the relative contribution of the error beam to the full beam pattern), they provide an estimate of the error beam pick-up. In Sect. 2 we summarize the beam pattern parameters of the IRAM 30 m and the correction method applied. In Sect. 3 the original and corrected maps are compared. The accuracy of the correction method and of the corrected data set is discussed in Sect. 4. In Sect. 5 we describe the self-consistent error beam correction, which is applied to the released data set (Paper I) and the data set presented here. Both independently reduced data sets are compared. A summary of our results is given in Sect. 6.

For the error beam corrected data we use the corrected main beam temperature scale $T_{\rm mb,c}$. The rigorous definition of $T_{\rm mb,c}$ is given in a supplementary paper (Bensch et al. 2001) where we compare two correction methods and provide a guideline for observers wishing to correct their own data.

   
2 Error beam correction of the IRAM key-project data

   
2.1 Beam pattern of the IRAM 30m telescope

The beam pattern of the IRAM 30m was determined by GGC, and more recently by GKW. GKW combined a larger data set (measurements on Moon, planets and holographic data) obtained at four different wavelengths ranging from $\lambda=3.4$ mm to 0.75 mm to deduce a consistent beam pattern model. They find that the beam pattern is given by a tapered Airy pattern ( ${\cal A}_{\rm T}$) of HPBW $\theta_{\tiny\! \mbox{{${\cal A}_{\rm T}$ }}}= \theta_{\rm mb}$, and three Gaussian error beams $P_{{\rm e},i}$ of HPBW $\theta _i$ ( $i=1\dots 3$). The latter result from three independent surface error distributions in the primary reflector. Both more extended (second and third) error beams result from surface errors attributed to the panel frames and the mounting of each panel with a $3 \times 5$ array of adjustment screws. The first error beam ( $\theta_{1}\sim 10\theta_{\rm mb}$) is due to temporally variable, large-scale deformations of the reflector surface, suspected to result from residual thermal deformations (see GKW and references therein).


 

 
Table 1: Beam pattern of the IRAM 30 m at $\lambda =2.6$ mm (115 GHz) and 1.3 mm (230 GHz) before a re-adjustment of the panel frames in July 1997. The HPBW $\theta _i$ and the amplitudes ai of the three error beams are taken from the fit shown in Fig. 5 of GKW. The pi are determined according $p_i \propto a_i\,\theta _i^2$, using the normalization of $\sum _i p_i = 1$ (summed over main beam and the Gaussian error beams)
  $\lambda=$ 2.6mm (115 GHz) $\lambda=$ 1.3mm (230 GHz)
component   HPBW [arcsec] pi HPBW [arcsec] pi
tapered Airy patt. ${\cal A}_{\rm T}$ 21 0.71 10.5 0.41
$1^{\rm st}$ error beam $P_{\rm e,1}$ 228 0.08 114 0.16
$2^{\rm nd}$ error beam $P_{\rm e,2}$ 317 0.08 158 0.16
$3^{\rm rd}$ error beam $P_{\rm e,3}$ 1900 0.13 950 0.27


In the following, we use

 \begin{displaymath}% P(\phi,\theta) = \mbox{{${\cal A}_{\rm T}$ }}(\theta) + \su... ... \ln2}{\theta_{i}^2\pi} \exp[-4\ln2\,(\theta/\theta_{i})^2], \end{displaymath} (1)

for the beam pattern of the IRAM 30m, where $w_i \propto \int\!\!\!\int_{2\pi} P_{{\rm e},i} {\rm d}\Omega$. With the normalization of P(0,0)=1, the wi are given by $w_i = p_i\,F_{\rm eff}$, where $F_{\rm eff}=\Omega_{2\pi}/\Omega_{4\pi}$ and $\Omega_{2\pi} (\Omega_{4\pi})$ is the integral of the beam pattern over the forward hemisphere ($4\pi$). Table 1 gives $\theta _i$ and pi for the wavelengths of both lowest CO rotational transitions, applicable to the observations of the key-project[*].

The accuracy of the HPBW and the power in the Gaussian error beams is estimated by GKW to be $\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...% and $\sim$5%, respectively. This applies to the individual components, determined from observations at one frequency, whereas the numbers given in Table 1 are results from a consistent beam pattern model, fitted to a larger number of observations at different wavelengths. We therefore expect a higher accuracy for the latter. The exception is the integral over the first error beam, showing temporal variations of some $\pm50$% with a time constant of 1 h or more (Table 1 gives the average p1). Therefore, a large uncertainty applies to the pick-up by the first error beam.

   
2.2 Error beam correction

The correction of the pick-up in the second and third error beam is done using KOSMA observations. Because it is not possible to trace back the contribution of the temporally variable first error beam, we count the latter as part of the main beam and use the approximation
 
$\displaystyle % T_{\rm mb,c} \approx \frac{F_{\rm eff}}{B_{\rm eff} + p_1\,F_{\... ...{\ast} - \sum_{i={\rm 2,3}} p_i \langle T_{\rm mb}' \rangle_{{\rm e},i} \right]$     (2)

for the corrected main beam brightness temperature. Here, $\langle T_{\rm mb}' \rangle_{{\rm e},i}$ denotes the KOSMA observations, smoothed to the angular resolution of the ith error beam. KOSMA observations were made in the 12CO and 13CO $J=2\rightarrow $ 1 transition towards all three sources (Bensch 1998), and a 12CO $J=1\rightarrow $ 0 map of MCLD 123.5+24.9 is available from Großmann et al. (1990).

The correction by de-convolution of the error beam pattern in Fourier space turned out to be not possible (Bensch et al. 2001). For each map in the data set, this correction method requires additional, fully sampled observations with the IRAM 30 m of several 104 positions, and an integration time of less than 1 s per position. Currently, this is not feasible without an excessive overhead in dead-time (due to moving of the telescope, etc.) and because of the huge amount of data to be handled in a relatively short time.

   
3 Comparison of the original data to the error beam corrected data

3.1 Velocity integrated maps

Figures 1 to 4 compare the velocity integrated maps of the original (uncorrected) and the corrected observations[*]. For the uncorrected maps we use the observed spectra scaled to $T_{\rm A}^{\ast }$. This corresponds to a "0th order error beam correction'' where the forward efficiency $F_{\rm eff}$ is used as "full beam efficiency'' (cf. Downes 1989). Note that the signal to noise ratio is lower in the corrected maps because the correction subtracts signal and adds noise.


  \begin{figure} \par\includegraphics[width=15.5cm]{h1988f1.eps}\end{figure} Figure 1: Integrated spectral line maps of MCLD 123.5+24.9, 12CO $J=2\rightarrow $ 1 (top) and 13CO $J=2\rightarrow $ 1 (bottom). The KOSMA observations are given in the left panels, the uncorrected and corrected key-project maps are shown in the middle and right panels. The latter two are smoothed to 22'', the angular resolution of the IRAM $J=1\rightarrow $ 0 observations. For each map, the grey scale covers the range from the minimum to the maximum of the line integrated intensity (units of [Kkms-1]) to better show the enhanced intensity contrast for the corrected map as larger (local) intensity variations. Note that for most of the positions the intensity in the corrected map (scaled to $T_{\rm mb,c}$) is larger than in the original, uncorrected map (scaled to the antenna temperature $T_{\rm A}^{\ast }$). However, if the uncorrected map is scaled to main beam brightness temperature ( $T_{\rm mb,c}$), the intensity in the corrected map will be smaller
Open with DEXTER

3.1.1 CO $\mathsfsl{J}\ \mathsf{= 2 \rightarrow 1}$ maps
The pick-up by the second and third error beam accounts for a substantial fraction of the observed intensity. The map-averaged value of the additional pick-up is 50% (31%, 44%) of the intensity in the 12CO $J=2\rightarrow $ 1 maps of MCLD 123.5+24.9 (L1512 and L134A). For the 13CO $J=2\rightarrow $ 1 maps, the corresponding figures are 10%, 23% and 35%. The larger error beam pick-up is found for the 12CO maps because of the spatially more extended emission of the more abundant isotopomer, coupling more efficiently to the error beam pattern. For the same reason, the relative contribution of the error beam pick-up is larger in the 12CO $J=2\rightarrow $ 1 map of MCLD 123.5+24.9 than for L134A and L1512.

The corrected spectral line maps show an enhanced contrast. More details are visible at small angular scales which are (partially) obscured in the uncorrected maps due to the smearing with the error beam. The actual percentage of the observed intensity attributed to the error beam pick-up significantly varies with position and velocity. For positions where strong emission is found nearby, the relative contribution of the error beam is much larger than average, accounting for up to 100% of the observed emission. Examples are found in the North-West corner of MCLD 123.5+24.9, 13CO $J=2\rightarrow $ 1 map (right panel of Fig. 5) and the South-East corner of the L1512, 13CO $J=2\rightarrow $ 1 map (right panel of Fig. 6).

3.1.2 $\mathsf{^{12}}$CO $\mathsfsl{J}\ \mathsf{=1 \rightarrow 0}$map of MCLD 123.5+24.9

In the 12CO $J=1\rightarrow $ 0 map of MCLD 123.5+24.9, the error beam pick-up accounts (on average) for 16.5% of the observed intensity. The line profile of the error beam pick-up does not vary much across the observed area, in contrast to the CO $J=2\rightarrow $ 1 observations. This is because of the larger angular extent of the error beams for lower frequencies ( $\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...GHz), which are comparable or larger than the observed map. The correction therefore modifies the morphology of the intensity distribution only to a minor degree. Comparing the corrected ( $T_{\rm mb,c}$) and the uncorrected (scaled to $T_{\rm mb}$) spectra, we find that the latter are larger by $\sim$30%. This can be considered as an upper limit to the systematic error for CO $J=1\rightarrow $ 0 data, if no correction is done, scaling them to $T_{\rm mb}$ instead. Scaling the spectra to the antenna temperature $T_{\rm A}^{\ast }$ gives intensities which are (on average) smaller by $\sim$8%, and thus a better approximation to the corrected main beam brightness temperature if no further correction is applied.

3.2 Line profiles

Figures 5 to 8 compare the line profiles of the observed spectra ( $T_{\rm A}^{\ast }$) and the estimated pick-up in the second and third error beam[*]. This is a crucial test for the correction method and the beam model used for the IRAM 30 m. Additionally, it provides information on the accuracy of the error beam correction method and the corrected data. An estimated error beam pick-up which systematically exceeds the observed line profile points to a systematic error in either the beam pattern model or the intensity calibration of the observations made with the smaller telescope.


  \begin{figure} \par\includegraphics[width=15.5cm,clip]{h1988f5.eps}\end{figure} Figure 5: MCLD 123.5+24.9: The observed (uncorrected) spectra (scaled to $T_{\rm A}^{\ast }$) is compared to the pick-up in the 2nd and 3rd Gaussian error beam ( $T_{\rm 2eb}+T_{\rm 3eb}$), as determined with KOSMA observations. The 12CO $J=2\rightarrow $ 1 observations are shown in the left panel, 13CO $J=2\rightarrow $ 1 observations are shown on the right. Each spectrum represents the average of $8 \times 8$ individual spectra, covering an area of 1 square arcmin
Open with DEXTER

Inspection of Figs. 5 to 8 shows that this is not the case, except for a few of the 12CO $J=2\rightarrow $ 1 spectra observed towards L134A (left panel of Fig. 7). Here, the estimated error beam pick-up slightly exceeds the observed line profile in the red line wing (between 3 and 4 km s-1) for positions at ( $\Delta \alpha,\Delta \delta$) $\sim$ ( $-74^{\prime \prime}$, $50^{\prime \prime}$). In addition, the estimated error beam pick-up appears to be red-shifted with respect to the observed line profile for $\Delta\delta > 600^{\prime \prime}$. Two possible explanations remain for the discrepancy. Firstly, the KOSMA observations potentially suffer from a significant error beam pick-up, which results in the error beam pick-up of the IRAM 30 m being overestimated. Secondly, the actual (error) beam pattern of the IRAM 30 m significantly differs from the model used. In either case, the thus introduced systematic error can mimic a velocity offset between the observed line profile and the estimated error beam pick-up, because of the velocity gradient observed for the line profiles south of $\Delta\delta \sim 700^{\prime \prime}$. A further, more quantitative discussion is given in Sect. 4.

The line profiles shown in Figs. 5 to 7 demonstrate that the error beam pick-up not only adds intensity, but modifies the line profile. On average, the relative contribution is larger in the line wings than in the line core. This is documented in Fig. 9, where the systematic variation of the error beam pick-up with velocity channel is shown for the map-averaged spectra. Only for the 12CO J= $1\rightarrow$ 0 observations made towards MCLD 123.5+24.9, the percentage of the observed intensity attributed to the error beam pick-up roughly is constant across the line profile.


  \begin{figure} \par\includegraphics[width=15.5cm,clip]{h1988f9.eps}\end{figure} Figure 9: Map-averaged line profiles of the 12CO $J=2\rightarrow $ 1 observations (first row), 13CO $J=2\rightarrow $ 1 observations (second row), and the MCLD 123.5+24.9, 12CO $J=1\rightarrow $ 0 map (lower left panel). The uncorrected spectra (dotted) are given in antenna temperature, $T_{\rm A}^{\ast }$. The pick-up by the 2nd and 3rd error beam is shown by the solid line. The fraction of the intensity attributed to the error beam pick-up is indicated by the dashed line (labels given on the right of the boxes). The bar on the velocity axis indicates the line wing region, defined in Paper I as the velocity range where significant 12CO emission is seen, but little orno 13CO
Open with DEXTER

The modification of the individual line profiles by the error beam pick-up is more complex than suggested by the map-averaged profiles. It depends on the position and the velocity structure of the emission on angular scales of the error beam pattern. An inspection of individual line profiles shows that for some positions, the intensity in the line wing is effectively lowered with the error beam correction (e.g. in the South-Eastern part of the MCLD 123.5+24.9, 12CO $J=2\rightarrow $ 1 map), while for other positions, the line wings are found to be more pronounced in the corrected spectra. The same result is suggested by maps showing the spatial variation of the second moment, determined from the line profiles. An example is given with Fig. 10, where the intensity contrast is substantially higher for the corrected spectra, consistent with a larger spatial variation of the line profile.


  \begin{figure} \par\includegraphics[width=15.5cm,clip]{h1988f10.eps}\end{figure} Figure 10: Maps of the second moments, determined for the 12CO $J=2\rightarrow $ 1 line profiles observed toward MCLD 123.5+24.9, and smoothed to a resolution of $22^{\prime \prime }$. The second moment are determined according $(\sum _i T(v_i)\,v_i^2)/(\sum _i T(v_i))$, where T(vi) is the intensity detected in channel i (velocity vi) of the spectrum. The left panel shows the result for the original line profiles, the right panel for the corrected data
Open with DEXTER

   
4 Self-consistency check and accuracy of the corrected data

   
4.1 Self-consistency check

The comparison of the error beam corrected key-project data, smoothed to the KOSMA resolution, with the KOSMA observations provides a check for the correction method and the intensity calibration of both data sets. For a quantification we define

 \begin{displaymath}% x = \frac{\langle T_{\rm mb,c} \rangle_{\rm KOSMA}}{T_{\rm mb}'}, \end{displaymath} (3)

where $T_{\rm mb}^{\prime}$ is the main beam brightness temperature of the KOSMA observations and $\langle T_{\rm mb,c} \rangle_{\rm KOSMA}$ denotes the corrected, smoothed IRAM data. For a quantitative analysis we determine the ratio x for positions within an area where KOSMA and IRAM observations are available, and for those velocity channels where the intensity exceeds a threshold of three times the rms noise level. Positions lying closer than 1arcmin to the edge of the map are excluded, because it is not possible to obtain a reliable estimate for the smoothed spectra, $\langle T_{\rm mb,c} \rangle_{\rm KOSMA}$.

For perfectly corrected IRAM 30m data and KOSMA observations with a negligible error beam pick-up, a narrow distribution, centered on 1, is expected. An average value smaller than unity suggests that the IRAM 30 m error beam pick-up is overestimated, and hence that the corrected main beam brightness temperature is underestimated. For the corrected key-project maps, the x-distributions are given in Fig. 11, together with the average ($\mu _x$), median, and width $\sigma _x$ (standard deviation) of the distribution.


  \begin{figure} \par\includegraphics[width=15.5cm,clip]{h1988f11.eps}\end{figure} Figure 11: Distribution of x, determined as the ratio of the corrected key-project data (smoothed to angular resolution of the KOSMA telescope) and the KOSMA observations (Eq. 3). The ratio x was determined for each velocity channel with an intensity larger than three times the rms in the spectrum. Positions which are located closer than 1 arcmin to the edge of the map are excluded. For each distribution, the average $\mu _x$, standard deviation $\sigma _x$, and the median (med.) is given
Open with DEXTER

For the 12CO $J=2\rightarrow $ 1 maps, $\mu _x$ is found to be equal or smaller than unity (0.82, 1.02 and 0.88 for MCLD 123.5+24.9, L1512 and L134A, respectively), while for the 13CO $J=2\rightarrow $ 1 maps, $\mu _x$ is larger than unity (1.15, 1.26 and 1.06). For the 12CO $J=1\rightarrow $ 0 map of MCLD 123.5+24.9 we find $\mu_x=$1.02. The width $\sigma _x$ of the distributions is between 0.10 and 0.18, except for the 13CO $J=2\rightarrow $ 1 map of MCLD 123.5+24.9, where $\sigma _x$ is significantly larger (0.22). In general, we find larger $\sigma _x$ for the 13CO $J=2\rightarrow $ 1 maps, except for L134A where both maps have $\sigma_x\sim 0.13$. The influence of the finite signal-to-noise in the spectra on the $\mu _x$ and $\sigma _x$ is negligible. We obtain the same results for distributions deduced with spectra binned to a lower velocity resolution, and hence with a lower rms noise per velocity channel. Thus, the $\mu _x$and $\sigma _x$ can be used to determine the accuracy of the error beam correction method and to examine the limiting factors.

   
4.2 Accuracy of the correction method and the corrected data set

We estimate the total uncertainty in the $T_{\rm mb,c}$ scale using the self-consistency check ($\mu _x$ and $\sigma _x$) and by comparing the observed line profiles to the estimated error beam pick-up.

An average value $\mu _x$ offset from unity indicates systematic errors, which may result from

The width of the distribution ($\sigma _x$) depends on statistical variations from position to position. These uncertainties may arise from

It is not possible to fully disentangle the contribution of the different effects which result in a broader $\sigma _x$ or an average $\mu _x$ offset from unity. However, a systematic analysis of the results obtained for the different sources and transitions provides an upper limit to the magnitude of the different sources of error, and allow us to estimate the accuracy of the final data set.

4.2.1 Error beam pick-up of the KOSMA telescope

The exact amount of error beam pick-up in the KOSMA observations is unknown because it depends on the large-scale structure of the emission and the (unknown) details of the KOSMA error beam pattern. If present, the KOSMA error beam pick-up is expected to play a role for the observations of the spatially extended 12CO $J=2\rightarrow $1 emission only. An estimate of the KOSMA error beam pick-up at 230GHz is obtained by comparing the main beam efficiency determined for bright planets ( $B_{\rm eff}\,=\,0.64$) and measured on the Moon ( $B_{\rm Moon}$ = 0.72). This shows that a KOSMA error beam of angular extent $\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...is present, and that the power radiated into this error beam is $\sim$13% of the power in the main beam. Thus, for extended sources, an error beam pick-up of $\sim$13% is expected for KOSMA observations at 230 GHz (assuming an uniform intensity distribution).

Indeed, for the maps with the spatially most extended emission (the 12CO $J=2\rightarrow $ 1 maps observed toward MCLD123.5+24.9 and L134A) we find $\mu _x$ which are significantly smaller than unity, suggesting that the KOSMA error beam is not negligible. The $\mu_x=0.82$ (0.88, respectively) suggest that the KOSMA error beam pick-up is 12 - 18% for the 12CO $J=2\rightarrow $ 1 maps, and this only if we fully attribute the $\mu_x<1$ to a KOSMA error beam. For the 13CO $J=2\rightarrow $ 1 maps we find that the $\mu _x$ are larger than unity. This is consistent with a negligible KOSMA error beam pick-up for the not very extended emission of the rarer isotopomer, and that other systematic errors limit the accuracy of the intensity calibration. The same applies to the 12CO $J=1\rightarrow $ 0 map of MCLD123.5+24.9, because of the smaller amplitude of the error beam pattern at lower frequencies.

4.2.2 Influence of the uncorrected first error beam

The correction for the first (smaller) error beam of the IRAM 30m is not possible because of the large temporal variations of the amplitude and the insufficient angular resolution of the KOSMA observations. Thus, an additional error in the intensity calibration of the corrected data set arises from the uncorrected first error beam. This error is expected to play a significant role for maps which show strong intensity variations on the angular scale of the error beam ($\sim\,$1.9' at 230GHz). Here, the x-distribution is expected to be significantly wider (lager $\sigma _x$) with an average $\mu _x$ larger than unity, because the pick-up in the small error beam strongly varies with the position. This is observed for the 13CO $J= 2\rightarrow 1$ map of MCLD 123.5+24.9 and L1512. Both contain cores and/or steep gradients extending over $\sim\,$1 arcmin (Figs. 1 and 2) and, at the same time, have the largest $\mu _x$ (1.15 and 1.26) and $\sigma _x$ (0.22 and 0.18). We therefore conclude that the accuracy of the intensity calibration for these maps is limited by the uncorrected first error beam, and that the thus introduced error is up to 26%. For the other maps, the first error beam accounts for less than 12% of the observed intensity, judged from the $\sigma _x$ in Fig. 11 and taking into account that the accuracy of the relative intensity calibration in the maps is 9% (Panis 1995), assuming that both errors add in quadrature.

4.2.3 Accuracy of the error beam model

In the 12CO $J=2\rightarrow $ 1 map of L134A the estimated error beam pick-up systematically exceeds the observed line profile for a few positions at $\sim$( $-74^{\prime \prime}$, $50^{\prime \prime}$), while both profiles appear velocity-shifted in respect to each other for positions $\Delta\delta \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\di... ...p\halign{\hfil$\scriptscriptstyle .... This cannot be reconciled unless we modify the amplitude of the error beam pattern by much more than $20\%$, which is excluded by the accuracy of the beam pattern parameters (GKW). Similarly, the possible contribution of a KOSMA error beam cannot fully account for the discrepancy because it would imply an additional pick-up in the KOSMA observations of far more than 20%, and thus extended areas with strong emission outside the maps, which is not observed (Bensch 1998).

One plausible explanation is provided by a possible deviation of the IRAM error beam pattern from the assumed axial symmetry. In the L134A maps, a velocity gradient is present South of $\delta\sim 700^{\prime \prime}$, extending over several arcmins. A slight deviation from the assumed axial symmetry can mimic a velocity shift in the line profile of the error beam pick-up. This is not excluded by the measurements of GKW, because they used cross-scans in $\sim\,$East-West direction and explicitly assume axial symmetry. Moreover, a not axially-symmetric error beam pattern is not entirely unrealistic, given the shape of the panels/panel frames of the IRAM 30m.

   
5 The released data set and comparison to the independently reduced data set presented here

   
5.1 Self-consistent error beam correction

Irrespective of the possible reasons which result in a systematically under-(or over-) estimated error beam pick-up, we now assume that the $\mu_x\ne1$ is due to systematic errors in the intensity calibration of the KOSMA data. In this case a correction can be done by scaling the KOSMA spectra by $(\mu_x)^{-1}$. This is reasonable because the distributions in Fig. 11 are narrow with a distinct maximum (except for the 13CO $J=2\rightarrow $ 1 map of MCLD 123.5+24.9). The thus corrected key-project spectra give a better estimate for the corrected main beam brightness temperature scale.

This procedure was applied to the released data set of the key-project (Paper I) and the data set presented here. However, one has to keep in mind that this is an ad hoc correction. The residual difference between the KOSMA and the corrected, smoothed IRAM spectra is not solely due to the KOSMA error beam pick-up, as shown above.

5.2 Correction of the CO $\mathsfsl{J}\ \mathsf{=1 \rightarrow 0}$ observations

No observations from a smaller telescope are available to correct the CO $J=1\rightarrow $ 0 maps of the key-project, except for the 12CO $J=1\rightarrow $ 0 map of MCLD 123.5+24.9. An alternative correction method is therefore applied, based on the assumption that the intensity ratio CO $J=2\rightarrow $ 1 to CO $J=1\rightarrow $ 0 (hereafter ${{\cal R}_{21}}$) is constant on the angular scale of the error beam pattern. We can then use the KOSMA CO $J=2\rightarrow $ 1 observations, scaled by ${{\cal R}_{21}}^{-1}$, to estimate the error beam pick-up in the CO $J=1\rightarrow $ 0 maps. A constant ratio ${{\cal R}_{21}}$ has been noted for a large number of cold molecular clouds (e.g. Falgarone & Phillips 1996).

For an application to the key-project maps we merge the ratio ${{\cal R}_{21}}$ and the ad hoc scaling factor for the KOSMA data to a single scaling factor, which is determined for each map with the x-distribution. This is done for the 12CO $J=1\rightarrow $ 0 map of L1512 and L134A, and for the 13CO $J=1\rightarrow $ 0 map of MCLD 123.5+24.9 and L134A. The signal-to-noise ratio of the remaining maps (C18O $J=1\rightarrow $ 0 maps, and the 13CO $J=1\rightarrow $ 0 map of L1512) is too small to reliably determine the scaling factor. For these maps the correction is done using the KOSMA CO $J=2\rightarrow $ 1 data, assuming a constant ratio of ${{\cal R}_{21}}=0.65$ (Paper I).

The accuracy of this correction method is estimated by using the 12CO $J=1\rightarrow $ 0 map of MCLD 123.5+24.9, where KOSMA observations of both lower CO transitions are available. The key-project map, corrected with the KOSMA 12CO $J=1\rightarrow $ 0 data, and the same map, corrected with the KOSMA 12CO $J=2\rightarrow $ 1 observations scaled by ${{\cal R}_{21}}^{-1}=1/0.65$, differ by no more than 15% if the correction is done according to Eq. (2), and 7% if the correction is done self-consistently.

   
5.3 Accuracy of the final data set

For the 12CO and 13CO $J=2\rightarrow $ 1 key-project maps we estimate an overall accuracy of the intensity calibration of 10-15%, judged from the $\sigma _x$ in Fig. 11. Only for two data sets (the 13CO $J=2\rightarrow $ 1 map of MCLD 123.5+24.9 and L1512) we determine larger uncertainties of 22% and 18%, respectively. For these maps the accuracy is limited by the uncorrected first error beam. For the CO J= $1\rightarrow$ 0 data we deduce an overall accuracy of 11%, using the 7% accuracy estimated in the previous section with the 9% accuracy of the relative intensity calibration (Panis 1995) being added in quadrature.

The data reduction of key-project maps was done independently in Paris and Cologne. For the released data set (Paper I), the correction was done using the beam pattern parameters determined by GGC. The correction of the independently reduced data set presented here is done using the more recent beam measurements by GKW. The comparison of both data sets show that the integrated spectral line maps differ by no more than 10%, consistent with the estimated accuracy.

The released maps of the key-project, the data set presented with this paper and the complementary observations made with the KOSMA telescope are available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/Abstract.html

   
6 Summary and discussion

We use complementary data observed at lower angular resolution with the KOSMA telescope to estimate the error beam pick-up in the maps of the IRAM key-project. The pick-up in the second and third Gaussian error beam of the IRAM 30m telescope accounts for a substantial fraction of the observed intensity, on average 31%$-50\%$ for the 12CO $J=2\rightarrow $ 1 maps and 10%$-35\%$ for the 13CO $J=2\rightarrow $ 1 maps. The error beam pick-up significantly modifies the spatial intensity distribution and the line profile, with the corrected maps showing a considerably enhanced contrast. For the map-averaged line profile, the fraction of the observed intensity attributed to the error beam pick-up is larger in the line wings than in the line core. For the individual spectra, however, the degree of modification strongly varies with position. While for some positions the line wing is essentially removed with the correction, they are found to be even more pronounced for other positions. These results demonstrate that a careful correction is important and that a correction by application of a simple scaling factor ("effective'' or "full beam efficiency'') is insufficient here.

For the 12CO $J=1\rightarrow $ 0 map of MCLD 123.5+24.9, the error beam pick-up is determined to be 16.5% (map average). The intensity distribution as well as the line profiles are modified only to a minor degree.

We apply a self-consistent error beam correction to the released data set, where we match the KOSMA observations to the corrected IRAM observations, smoothed to the angular resolution of the KOSMA observations. The accuracy of the thus corrected spectral line maps is 11% (CO $J=1\rightarrow $ 0) and 15% (CO $J=2\rightarrow $ 1), except for the 13CO $J=2\rightarrow $ 1 map of L1512 and MCLD 123.5+24.9, where we assign larger uncertainties (18% and 22%, respectively). The systematic errors in the intensity calibration of the key-project data set are dominated by the error beam pick-up of the KOSMA telescope (accounting for $\le$18% in the 12CO $J=2\rightarrow $ 1 maps) and the uncorrected first error beam of the IRAM 30 m (resulting in the larger uncertainties for the 13CO $J=2\rightarrow $ 1 map of L1512 and MCLD 123.5+24.9). Taking both effects into account, we find that the residual errors are in accordance with the accuracy estimated by GKW for the beam pattern parameters of the IRAM 30 m. Only for the 12CO $J=2\rightarrow $ 1 map of L134A, we find indications that the actual error beam pattern slightly deviates from the assumed axial symmetry.

This study focuses on the observations made in the framework of the key-project with the IRAM 30m telescope. However, we expect that the error beam pick-up potentially plays a significant role for observations made with other (sub-)mm telescopes, too. An error beam pattern similar to the pattern of the IRAM 30m has been found for a number of (sub-)mm telescopes (cf. Kaufmann et al. 1987; Hills & Richter 1992; Prestage 1993). The correction methods (cf. Bensch et al. 2001) and the conclusions presented in this paper are therefore not limited to observations made with the IRAM 30 m. This should be taken into account when planning large mapping projects, where a fraction of the time should be allocated for the additional observations required to correct for the error beam pick-up.

Acknowledgements

The authors wish to thank A. Greve and C. Kramer for discussions and providing the detailed numerical results of their error beam measurements of the IRAM 30m telescope. The KOSMA 3m radio telescope at Gornergrat-Süd Observatory is operated by the University of Cologne and supported by the Deutsche Forschungsgemeinschaft through grant SFB-301, as well as special funding from the Land Nordrhein-Westfalen. The receiver development was partly funded by the Bundesminister für Forschung and Technologie. The Observatory is administered by the Internationale Stiftung Hochalpine Forschungsstationen Jungfraujoch und Gornergrat, Bern. The authors have benefitted from a joint European grant (Procope, grant# 312-pro-bmbw-gg) during the years 1995 and 1996. This research made use of NASA's Astrophysics Data System Abstract Service.

References

 

Online Material


  \begin{figure}\par\resizebox{16cm}{!}{\includegraphics{h1988f2.eps}}\par\end{figure} Figure 2: Same as Fig. 1 for L1512. The 12CO J=2 $\rightarrow $1 maps are given in the top panels, the 13CO J=2 $\rightarrow $1 maps in the bottom panels.
Open with DEXTER


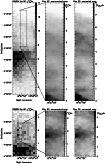  \begin{figure}\par\resizebox{12cm}{!}{\includegraphics{h1988f3.eps}}\par\end{figure} Figure 3: Same as Fig. 1 for L134A. Because of the elongated geometry of the KOSMA maps (see Bensch et al. 2000), only a sub-set of them is shown in the panels on the left.
Open with DEXTER


  \begin{figure}\par\resizebox{16cm}{!}{\includegraphics{h1988f4.eps}}\par\end{figure} Figure 4: Same as Fig. 1 for MCLD 123.5+24.9, 12CO J=1 $\rightarrow $0.
Open with DEXTER


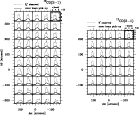  \begin{figure}\par\resizebox{16cm}{!}{\includegraphics{h1988f6.eps}}\end{figure} Figure 6: Same as Fig. 5 for L1512.
Open with DEXTER


  \begin{figure}\resizebox{12cm}{!}{\includegraphics{h1988f7.eps}}\end{figure} Figure 7: Same as Fig. 5 for L134A.
Open with DEXTER


  \begin{figure}\resizebox{8cm}{!}{\includegraphics{h1988f8.eps}}\end{figure} Figure 8: Same as Fig. 5 for the 12CO J=1 $\rightarrow $0 map of MCLD 123.5+24.9
Open with DEXTER

© ESO 2001