A&A 365, 314-323 (2001)
DOI: 10.1051/0004-6361:20000185

Piston control with adaptive optics in stellar interferometry

Application to the GI2T interferometer and bimorph mirrors

C. Vérinaud1 - F. Cassaing2

Send offprint request: C. Vérinaud


1 - Observatoire de la Côte d'Azur (OCA), Département Fresnel, 2130, route de l'Observatoire,
06460 Saint-Vallier-de-Thiey, France

2 - Office National d'Études et de Recherches Aérospatiales (ONERA), DOTA, BP 72,
92322 Châtillon Cedex, France

Received 29 August 2000 / Accepted 18 October 2000

Abstract
The general purpose of an adaptive optics system is to correct for the wavefront corrugations due to atmospheric turbulence. When applied to a stellar interferometer, care must be taken in the control of the mean optical path length, commonly called differential piston. This paper defines a general formalism for the piston control of a deformable mirror in the linear regime. It is shown that the usual filtering of the piston mode in the command space is not sufficient, mostly in the case of a bimorph mirror. Another algorithm is proposed to cancel in the command space the piston produced in the pupil space. This analysis is confirmed by simulations in the case of the GI2T interferometer located on Plateau de Calern, France. The contrast of the interference fringes is severely reduced in the case of a classical wavefront correction, even in short exposures, but is negligible with our algorithm, assuming a realistic calibration of the mirror. For this purpose, a simple concept for the calibration of the piston induced by a deformable mirror is proposed.

Key words: instrumentation: interferometers - instrumentation: adaptive optics - atmospheric effects - methods: numerical - techniques: interferometric

Author for correspondance: cassaing@onera.fr


1 Introduction

Adaptive Optics (AO) in astronomy (Rousset et al. 1990) is now a well established technique to correct the severe starlight wavefront disturbances induced by atmospheric turbulence and to restore the diffraction limit of single telescopes. An AO system comprises a wavefront sensor (WFS) and a deformable mirror (DM) in a conjugated pupil plane, which can be either a bimorph deformable mirror (BDM), generally associated to a curvature WFS (Roddier 1988), or a piezo-stack DM (PDM) with a Shack-Hartmann WFS (Rigaut 1992). The quality of AO correction is directly linked to the spatial variance of the corrected phase over the pupil. The spatial average of the phase, the piston, has no effect on imaging and is not seen by the WFS.

For very high spatial resolution, the beams of two or more telescopes can be combined in a stellar interferometer (SI) (Labeyrie 1975). Performance of SIs is limited by the optical path difference (OPD) between the telescopes, induced mainly by atmospheric turbulence. As in AO, this can be corrected using a Fringe Sensing Unit (Cassaing et al. 2000) and a delay line.

Up to now, SIs were limited to the very bright stars because of the severe atmospheric limitations. The main challenge of very high angular resolution is to drastically improve the limiting magnitude. Several SIs under construction plan to use large telescopes corrected by AO techniques, such as the VLTI (Donaldson et al. 2000), the Keck Interferometer (Colavita et al. 1998), and the GI2T (Mourard et al. 1994), for which an AO system based on a curvature WFS and a BDM is under construction (Vérinaud et al. 2000).

When using AO in a stellar interferometer, the control of the DM piston mode is a critical issue since a piston induced by each DM creates an additional OPD, shifting the interference fringes. A solution is to consider all the sensors (WFSs and fringe sensor) and the DM actuators as a whole (dashed line in Fig. 1), driven by a global control system (Roddier 1999).

  \begin{figure} \par\leavevmode \includegraphics[width=\linewidth]{MS10230f1.eps}\par\end{figure} Figure 1: General layout of a stellar interferometer equipped with AO
Open with DEXTER

In this paper, we investigate further the interaction between AO correction and OPD. In Sect. 2, we explain the origin of the DM piston effect and describe a correction method. In Sect. 3, a simulation of the piston effect for the GI2T is presented. In Sect. 4 we propose an experiment to calibrate the piston contribution of each DM mode and evaluate its precision in terms of error propagation on the sky.

   
2 Piston control in Adaptive Optics

2.1 Basics of AO control

For the good understanding of the piston effect, it can be useful to consider the general control algorithms of an AO system and the behavior of the DM. In the weak deformations regime, a DM can be characterized by the vectorial basis of its influence functions $F_i(\vec{r})$, defined as the DM phase response at a point $\vec{r}$ in the pupil, to a unit voltage applied to each actuator i. The components $\phi_i$ of a given DM phase response $ \arrowvert \Phi \rangle$ on the influence functions form the command vector $\vec{\phi}$ applied to the mirror. This can be written:

$\displaystyle % \arrowvert \Phi \rangle =\sum_i\ \phi_i \arrowvert F_i \rangle.$     (1)

The mirror phase can also be decomposed on a more convenient basis such as Zernike-like DM modes $\arrowvert Z'_i\rangle $ that fit the better, at the least-square sense, the real Zernike polynomials $\arrowvert Z_i\rangle$(Noll 1976). We define $\vec{z'_i}$ as the normalized command-vector producing $\arrowvert Z'_i\rangle $ on the DM. The two vectorial spaces (respectively DM commands and DM phases) are provided with the scalar products defined as:
$\displaystyle % \vec{\phi} \cdot \vec{\phi}'= \sum_i \phi_i \phi'_i,$     (2)


 
$\displaystyle % \langle \Phi \arrowvert \Phi' \rangle = \frac{1}{S} \int \int_{{\rm I\!R}^{2}}\Phi(\vec{r}) \Phi'(\vec{r}) \gamma(\vec{r}) {\rm d}\vec{r},$     (3)

where $\gamma(\vec{r})$ is a weighting function describing the pupil apodization due to a possible spatial filtering (Ruilier & Cassaing 2000) and Sis the weighted pupil surface. In the non-filtered case $\gamma(\vec{r})$ is simply the pupil function.

For a BDM, the influence functions can easily be computed in the case of an infinite plate by solving a Poisson equation in the Fourier space (Kokorowski 1970):

 
$\displaystyle % F_i(\vec{r})=FFT^{-1} \left( W_i(\vec{k}) (\alpha \Arrowvert \vec{k} \Arrowvert ^{2}-\beta) \right ),$     (4)

where $W_i(\vec{k})$ is the 2D Fourier transform of the function of the voltage distribution over the DM when electrode i is driven (equal to a constant on the surface of the actuator and to 0 outside) and $\alpha$ and $\beta$ are constants depending on the piezoelectric material. This model can be applied to a DM of finite size since the useful aperture is only half the whole plate diameter. A final 3D rotation is applied to take into account the DM mount (3 fixed points giving the boundary conditions). Two influence functions computed with this method are displayed in Fig. 2.
  \begin{figure} \par\includegraphics[width=.99\linewidth,clip]{aa10230f2a.eps}\par\includegraphics[width=.99\linewidth,clip]{aa10230f2b.eps}\end{figure} Figure 2: Simulated deformations of a BDM. Influence functions of the central electrode (top) and of an electrode of the outer ring (bottom); the dashed line represents the outline of the useful pupil and the spikes denote the position of the 3 fixed points of the DM mount
Open with DEXTER


  \begin{figure} \par\includegraphics[width=.99\linewidth,height=2.8cm,clip]{MS102... ...ar\includegraphics[width=.99\linewidth,height=3.5cm]{MS10230f3f.eps}\end{figure} Figure 3: 3D view and plot of a mirror section for the piston and defocus modes of a BDM. Top: the piston mode $\arrowvert Z'_1\rangle$. Center: the defocus mode $\arrowvert {Z'_4}^{\perp} \rangle $ orthogonal to the $\arrowvert Z'_1\rangle$ mode in the command space. Bottom: the defocus mode after piston correction
Open with DEXTER

The commands applied to the DM can be linked to the analyzed phase by a linear model of the WFS (Rousset 1993). To compute the command matrix Clinking the command $\vec{\phi}$ to apply to the actuators with the wavefront measurements $\vec{s}$, ( $\vec{\phi}=C \vec{s}$), one must first determine the interaction matrix D whose column-vectors are the WFS measurements when each actuator is driven individually. The response of the WFS to a given command writes:
$\displaystyle % \vec{s}=D \vec{\phi}.$     (5)

As some DM modes are not detected by the WFS, D is singular and the command matrix must be computed by inverting D after a singular value decomposition (SVD). The command matrix C is given by:
 
C=X E(-1) Ut,     (6)

where E(-1) is the pseudo-inverse of E the diagonal matrix containing the eigen-values $\lambda_i$, and U and X are the matrices of the orthogonal eigen-vectors (usually called the system modes) of respectively D Dt and Dt D. In practice the eigen-vectors of X corresponding to the lowest eigen-values $\lambda_k$ are mirror modes whose detection by the WFS is very noisy. Such undetected modes are at least the piston mode $\arrowvert Z'_1\rangle$ (Fig. 3) and also the waffle mode for a PDM coupled with a Shack-Hartmann WFS.

To compute a command matrix allowing to close the loop without saturation, the undetected modes are discarded in the command space by setting their huge gains $\lambda_k^{-1}$ in E(-1) to zero and leaving the other $\lambda_i^{-1}$ unchanged. The DM piston mode $\arrowvert Z'_1\rangle$ is thus never commanded. We may call this approach classical control.

To close the loop and to ensure stability, the command is usually temporally filtered by a simple integrator with a given gain g. The command vector at the time ti is given by:

 
$\displaystyle % \vec{\phi}_{t_i} = \vec{\phi}_{t_{i-1}}-g C \vec{s}_{t_i}.$     (7)

Another approach is modal control, based on a filtering in a relevant basis (Gendron & Lena 1994). This basis can be the Zernike-like modes $\arrowvert {Z'_i}^{\perp} \rangle$, orthogonalized to $\arrowvert Z'_1\rangle$ in the command space (Rigaut et al. 1994). Let O be the change of base matrix from the $\arrowvert F_i \rangle$ to the $\arrowvert {Z'_i}^{\perp} \rangle$. The modal control command matrix $C_{\rm mod}$ can be derived from the zonal control command matrix C by:
 
$\displaystyle % C_{{\rm mod}}=O^{-1} G_{{\rm mod}} O C,$     (8)

where $G_{{\rm mod}}$ is the diagonal matrix containing the gains, that can be optimized according to the SNR of each mode.

2.2 Origin of the piston effect

To describe how piston can be introduced, we suppose the mirror is able to produce a perfect piston mode so that $\arrowvert Z'_1\rangle = \arrowvert Z_1\rangle $. The piston in the pupil is then given by:


 
$\displaystyle % \langle \Phi \arrowvert Z'_1 \rangle= \sum_{i,j} \phi_i {z_1'}_j. \langle F_i \arrowvert F_j \rangle\cdot$     (9)

Therefore, when the influence functions are orthonormal, i.e. $\langle F_i \arrowvert F_j \rangle = \delta_{ij}$, orthogonality to $\vec{z'_1}$ in the command space (i.e. $\vec{\phi} \cdot \vec{z'_1}=0$) automatically implies orthogonality to the piston in the pupil ( $\langle \Phi \arrowvert Z'_1 \rangle=0$). This is nearly the case of a PDM for which the matrix $\langle F_i \arrowvert F_j \rangle$ is almost diagonal (Fig. 4): filtering the piston in the command space may also filter it efficiently in the pupil. But for a BDM, the matrix $\langle F_i \arrowvert F_j \rangle$ is rather uniform (Fig. 4): the condition $\vec{\phi} \cdot \vec{z'_1}=0$ is not sufficient to produce a zero-mean deformation. For example, if the Zernike-like defocus $\arrowvert Z'_4 \rangle$ is filtered in the command space by
 
$\displaystyle % \vec{{z'_4}^{\perp}} = \vec{{z'_4}} - (\vec{{z'_4}} \cdot \vec{z'_1}) \vec{z'_1},$     (10)

the mean of the resulting phase $\arrowvert {Z'_4}^{\perp} \rangle $ is far from zero as shown by Fig. 3.


  \begin{figure} \par\leavevmode \includegraphics[width=0.45\linewidth]{aa10230f4a.eps}\hfil \includegraphics[width=0.45\linewidth]{aa10230f4b.eps}\par\end{figure} Figure 4: Matrix $\langle F_i \arrowvert F_j \rangle$ simulated for a PDM (left) and for a BDM (right)
Open with DEXTER

2.3 Correction of the piston effect

The simplest strategy for correcting the piston effect is to completely discard the DM piston induced in the pupil at the command level. Each influence function contributes to the piston mode in the pupil plane by a quantity $\eta^{\rm F}_i$ given by:

 
$\displaystyle % \eta^{{\rm F}}_{i}=\langle F_i \arrowvert Z_1 \rangle\cdot$     (11)

We assume for the following that the $\eta^{\rm F}_i$values are known. A method to determine them experimentally is described in Sect. 4.

The piston correction in the control loop can be obtained by subtracting from the command vector $C \vec{s}$ the piston command weighted by a coefficient representing the overall contribution of $C \vec{s}$ to the pupil piston. This coefficient is simply the scalar product between $C \vec{s}$ and the $\vec{\eta}^{\rm F} $ vector of components $\eta^{\rm F}_i$. The command giving a zero-mean deformation may be written:

 
$\displaystyle % \vec{\phi}=C \vec{s}- \left[(C \vec{s}) \cdot \vec{\eta}^{\rm F} \right] \frac{\vec{z'_1}}{\eta^{Z'}_1},$     (12)

where $\eta^{Z'}_1=\langle Z'_1 \arrowvert Z_1 \rangle$. Although this correction term could be merely added at each iteration of the control loop, we show below that Eq. (12) can be rewritten as a single matrix multiplication. By developing Eq. (12) for the actuator i we obtain:
 
$\displaystyle % \phi_{i} =$ $\textstyle \sum_{j} C_{ij} s_{j} - \left[ \sum_{k} \left( \sum_{j}C_{kj} s_{j} \right) \eta^{\rm F}_{k} \right] \displaystyle{\frac{{z'_1}_{i}}{\eta^{Z'}_1}}$ =$\textstyle \sum_{j} \left[ C_{ij} - \displaystyle{\frac{{z'_1}_i}{\eta^{Z'}_1}} \left( \sum_{k} C_{kj} \eta^{\rm F}_{k} \right) \right] s_{j}.$         (13)

This can be condensed in:
 
$\displaystyle % \vec{\phi} = K \vec{s} \quad {\rm with} \quad K_{ij} = C_{ij} - \frac{{z'_1}_i}{\eta^{Z'}_1} \left( C^{\rm t} \vec{\eta}^{\rm F} \right)_{j}.$     (14)

Therefore the piston effect can be corrected by using a single command matrix K given by Eq. (14), so that $K \vec{s}$ gives a zero-mean mirror deformation. For example, the result of piston correction for the application of a defocus on a BDM is shown in Fig. 3.

The main feature of this algorithm is that no extra computation time is needed for the piston effect correction.

2.4 Limitations

The first limitation of the piston correction algorithm is saturation. The absolute values of the voltages applied to the actuators are limited in practice to a given maximum $V_{\rm max}$. Thus, the erratic saturations of the commands occurring during atmospheric compensation induce phase correction errors, and also jumps in the average of the DM phase over the pupil (i.e. of the piston $\arrowvert Z_1 \rangle$), because of a mis-correction of the piston mode. The piston mis-correction $\Delta$ can be written:

 
$\displaystyle % \Delta = \frac{\vec{\eta^{\rm F}}}{\eta^{Z'}_1} \cdot (\vec{\phi_T} - \vec{\phi}) ,$     (15)

where $\vec{\phi}$ is the ideal command computed by the matrix multiplication $K \vec{s}$ and by the loop integration (Eq. 7), and $\vec{\phi}_T$ is the real command limited to the thresholds $\pm V_{{\rm max}}$.

Piston residuals due to saturation can be corrected by subtracting $\Delta \vec{z'_1}$ from the applied command when saturation is present. Furthermore this correction needs to be applied only during the loop iterations where the command saturates, which occurs only in a sporadic way. Accordingly, the saturation correction doesn't add any significant temporal delay in the loop. The saturation issue is illustrated by simulations in Sect. 3.

Another limitation is hysteresis of the piezoelectric materials inducing departure from the linear hypothesis. For most of the materials used for BDMs, the amplitude of the hysteresis cycle curve is comprised between 5 and $10 \%$. The complete study of the hysteresis effect is a difficult task because of the complexity of the behavior of the mirror as every deformation depends on the entire trajectory of the commands applied to the mirror. However an analytical study of the hysteresis effect on the piston mode (Tordo et al. 2000) shows that the maximum error remains negligible at least for short time-scales.

  
3 Simulations of the piston induced
by a bimorph mirror

To evaluate the bimorph piston effect during atmospheric compensation, the GI2T with two curvature-based AO systems and their close-loop temporal control have been simulated. The turbulence spatial and temporal characteristics are obtained by shifting three phase-screens based on von Karman statistics in front of the pupils, with an average wind speed of $15~{\rm m\;s^{-1}}$. At each iteration, the DM phase is recorded and projected on the Zernike-like modes $\arrowvert {Z'_i}^{\perp} \rangle$ and on $\arrowvert Z_1 \rangle$ giving the piston in the pupil.

3.1 Piston filtering in the command space

We first show the effect of classical AO control when the DM piston command $\vec{z'_1}$ is filtered.


  \begin{figure} \par\leavevmode \includegraphics[width=\linewidth]{MS10230f5.eps}\par\end{figure} Figure 5: Piston contribution of Zernike-like modes for one BDM ( $D~=1.5~ {\rm m}$, $r_0(0.5~{\rm \mu m})=8~{\rm cm}$). The total standard deviation of the piston is $0.9~\lambda$ (at $0.7~{\rm \mu m}$). Some relevant modes: 2-3: tip-tilt, 4: defocus, 11: spherical aberration
Open with DEXTER

In order to determine the contribution to the piston of each correction mode we compute the covariance matrix $\Gamma$ of the components $\zeta_i$ of the DM phase $ \arrowvert \Phi \rangle$ on the Zernike-like modes.

 
$\displaystyle % \Gamma_{ij} = \langle \zeta_i \zeta_j \rangle - \langle \zeta_i... ...uad \arrowvert \Phi \rangle =\sum_i\ \zeta_i \arrowvert {Z'_i}^{\perp} \rangle,$     (16)

where $\langle \rangle$ denotes temporal average. The piston contribution of a mode is then computed from $\Gamma$ and from the mean value $\eta^{Z'}_i$of each mode over the pupil which is defined by:
 
$\displaystyle % \eta^{Z'}_{i} = \langle {Z'_i}^{\perp} \arrowvert Z_1 \rangle\cdot$     (17)

The piston variance induced by mode k is:
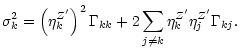$\displaystyle % \sigma_k^2= \left(\eta^{Z'}_k \right)^2 \Gamma_{kk} + 2 \sum_{j\neq k} \eta^{Z'}_k \eta^{Z'}_j \Gamma_{kj}.$     (18)

The results for the GI2T configuration and for $r_0=8~{\rm cm}$ are displayed in Fig. 5. The amplitude of the induced piston is obviously not negligible since the standard deviation of the total piston in one pupil is $0.9\lambda$ at $0.7~{\rm \mu m}$ and is proportional to (D/r0)5/6. We can notice that defocus is the mode that carries most of the piston and tip and tilt have different contributions because of the three-point mount.

To evaluate the piston effect on fringe contrast measurements for a given exposure time, we assume that the pistons induced by the two DMs are uncorrelated. The OPD induced by the two DMs, as shown in Fig. 6, is rather fast compared to the atmospheric OPD based on the model of Conan (Conan et al. 1995). Indeed the bimorph OPD cut-off frequency $\nu_2=30~{\rm Hz}$ is greater than the atmospheric OPD cut-off frequency $\nu_1$ due to aperture filtering.


  \begin{figure} \par\leavevmode \includegraphics[width=\linewidth]{MS10230f6.eps}\par\end{figure} Figure 6: Temporal power spectrum of the OPD induced by two bimorph mirrors in classical control and with the K matrix, compared with the atmospheric OPD. The conditions are: $r_{0}(0.5)=8~{\rm cm}$, outer-scale: $L_{0}=50~{\rm m}$, Diameter: $D=1.5~{\rm m}$, baseline $=40~{\rm m}$, wind speed $v=15~{\rm m\;s^{-1}}$, $\lambda=0.7~{\rm \mu m}$. ( $\nu_1=0.3v/D=3~{\rm Hz}$)
Open with DEXTER

Such a strong high frequency additional OPD leads to a significant fringe contrast loss, even in short exposures. The variance $\sigma^2_{{\rm p},\tau}$ of the OPD during the exposure time $\tau$ can be computed from classical spectral theory (Tango & Twiss 1980):

 
$\displaystyle % \sigma^2_{{\rm p},\tau}=\int_0^\infty\left[1-\left(\frac{\sin(\pi f\tau)}{\pi f\tau}\right)^2\right] W_{{\rm p}}(f)\,{\rm d}f,$     (19)

where $W_{{\rm p}}(f)$ is the temporal power spectrum of the OPD variations. The fringe visibility of a point-source can be approximated by (Conan 1994):
 
$\displaystyle % V \simeq \exp(-\sigma_{{\rm p},\tau}^2/2).$     (20)

Figure 7 plots the fringe visibility attenuation due to the atmospheric and bimorph OPD versus the exposure time. These fringe visibilities are computed with Eqs. (19) and (20), using the spectra given in Fig. 6. It clearly shows that, even on short exposures, the OPD induced by AO in the classical zonal command must be attenuated to limit the loss and wandering of fringe contrast during the observation. For example, according to Fig. 7, the fringe visibility would be $48\%$ for the $7~{\rm ms}$ exposure time of the Next Generation Photon-Counting camera under construction for the GI2T (Abe et al. 2000).
  \begin{figure} \par\leavevmode \includegraphics[width=\linewidth]{MS10230f7.ps}\par\end{figure} Figure 7: Fringe visibility attenuation versus exposure time due to bimorph piston (solid line) and atmospheric piston (dashed line) in the conditions of Fig. 6
Open with DEXTER

3.2 Piston filtering in the pupil space

The induced piston can be considerably reduced using the command matrix Kwith saturation effect correction. Assuming a perfectly known $\vec{\eta}^{\rm F} $ vector the residual OPD becomes negligible as shown in Fig. 6.

To illustrate the need of saturation effect correction, we analyze the DM piston residual under strong turbulence. The standard deviation of the residual piston due to saturation, by using the command matrix K alone, can be very large. For $r_0=6~{\rm cm}$ it is about $0.6~ {\rm\mu m}$ as shown in Fig. 8. We plotted in the same figure the BDM piston residuals by using the algorithm of the saturation effect correction defined by Eq. (15). The standard deviation of these residuals are less than ten nanometers.

These simulation results show that the piston effect can be very well corrected if the contribution to the piston of each actuator is known. In Sect. 4 we propose a method to calibrate experimentally the $\vec{\eta}^{\rm F} $ vector, which is the key parameter for piston correction.


  \begin{figure} \includegraphics[width=\linewidth]{MS10230f8a.eps}\par\includegraphics[width=\linewidth]{MS10230f8b.eps}\end{figure} Figure 8: Piston residuals due to saturation (with command matrix K) under strong turbulence (top) and residuals for saturation effect correction (bottom). $r_0=6~{\rm cm}$, wind speed = $\,15~{\rm m\;s}^{-1}$
Open with DEXTER

   
4 Proposition of an interferometric experiment for the DM piston characterization

The contribution to the piston for each actuator ( $\vec{\eta}^{\rm F} $ vector) is not easy to evaluate. The usual influence functions measured with a Zygo interferometer are not sufficient as the pure piston component may be sensed with difficulty. Simulations including the positions of the three fixed points confronted to real influence functions would probably permit to obtain a good estimate of the piston term. Yet simulations usually show discrepancies with the real influence functions, and the position of the three fixed points may be somewhat fuzzy. Furthermore, if the behavior of the DM is changing for some reason (temperature mostly), the precise responses of the actuators should be taken into account with a built-in instrument, like it is done by measuring an interaction matrix. Thereby, we propose an interferometric experiment intended to characterize the piston effect and we evaluate the precision expected from the calibration and the error propagation through the AO reconstruction process.

4.1 Optical layout


  \begin{figure} \par\leavevmode \includegraphics[width=\linewidth]{MS10230f9.eps}\par\end{figure} Figure 9: Optical scheme for measuring the piston contribution of the DM correction modes. (DM: deformable mirror, RL: Relay Lenses for pupil transfer)
Open with DEXTER

Figure 9 schematically describes an optical setup that can be included in an AO bench to measure the piston induced by the DM. For good spatial and temporal coherence, the source is a laser filtered by a pinhole and collimated. Two beam-splitters are used to split the beam in two arms and then to recombine them in a flat tint mode. One arm includes the DM and the other is used as a reference. The pupil is defined before splitting by a diaphragm matching the telescope obstruction, then re-imaged by relay lenses on the second beam-splitter and last on a single-pixel detector, with an intermediate image on the DM. For fine alignment, one can use a pupil camera and the WFS to close the loop on the low order modes with a low temporal bandwidth.

4.2 Principle of the measurement

Before starting the calibration, one must first determine the piston command-vector $\vec{z'_1}$ of the DM. This vector can be obtained by the SVD of an interaction matrix recorded with the WFS. It is usually the eigen-vector of matrix X, resulting from the SVD (Sect. 2.1), corresponding to the lowest eigen-value. If the influence functions of the DM are known, from a Zygo interferometer for example, the piston command can also be determined by least-square techniques. In this latter case, the user can also build a more convenient set of mirror modes like for example Zernike-like modes.

The calibration procedure can be performed either in a zonal or in a modal way. In the first case, each actuator is calibrated individually in order to determine directly the $\vec{\eta}^{\rm F} $ vector. In the second case, a set of new modes orthogonal to the piston in the pupil can be built and injected in the modal command matrix computation.

We show here how to calibrate the piston contribution of Zernike-like $\arrowvert {Z'_i}^{\perp} \rangle$ modes of the DM, represented by the change of base matrix Odefined in Sect. 2. If a zonal method is used, the $\arrowvert {Z'_i}^{\perp} \rangle$ modes are merely to be replaced in this description by the influence functions $\arrowvert F_i \rangle$.

The intensity at a given point $\vec{r}$ in the recombined pupil is given by:

 
$\displaystyle % I(\vec{r})=I_1+I_2+2 \sqrt{I_1I_2} \sin \left [ \left ( \phi_0- \frac{\pi}{2} \right) +\Phi(\vec{r}) \right],$     (21)

where I1 and I2 are the intensities of the two beams after splitting, $\phi_0$ is the phase between the two arms and $\Phi(\vec{r})$ is the mirror phase displacement. The OPD between the two arms is adjusted in order to get a grey tint in the pupil, whose intensity is midway between the maximum and the minimum of the fringe intensity ( $\phi_0=(2k+1) \pi/2$). In this region and for weak amplitudes of the deformation, the intensity is linear with respect to $\Phi(\vec{r})$. Accordingly, the overall intensity for a zero-mean mirror deformation remains unchanged. Conversely, if the deformation is not zero-mean, which is a priori the case for the Zernike-like modes $\arrowvert {Z'_i}^{\perp} \rangle$, the change in intensity reveals the presence of piston in the pupil (Fig. 10). This property is used to calibrate the piston contribution of each actuator.

The general process of piston calibration consists in modulating the mirror mode to characterize at a given temporal frequency $f_{{\rm0}}$, with a deformation amplitude less than $\lambda /4$. The overall intensity fluctuations measured on the single-pixel detector are recorded and can be processed by synchronous detection.

  \begin{figure} \includegraphics[width=\linewidth]{MS10230f10.eps}\end{figure} Figure 10: Simulation of interferograms in the recombined pupil of the coma Zernike-like DM mode $\arrowvert {Z'_7}^{\perp} \rangle$ driven with a $\pm \lambda /4$ amplitude. The overall intensities for two opposite coma commands are different, revealing the presence of piston in the pupil
Open with DEXTER

When a non zero-mean mode Zernike-like mode is driven with a sine signal for example, the overall intensity at the output is characterized by fluctuations (Fig. 11) with a significant contribution at f0. Now this mode has to be modified by adding the DM piston command $\vec{z'_1}$ weighted by a coefficient $\kappa$ to the command producing the $\arrowvert {Z'_i}^{\perp} \rangle$ in order to cancel the piston in the pupil. The new deformation to modulate writes:

$\displaystyle % \arrowvert Z''_i \rangle = \arrowvert {Z'_i}^{\perp} \rangle + \kappa \arrowvert Z'_1 \rangle.$     (22)

By adjusting the coefficient $\kappa$ during the temporal modulation of $\arrowvert Z''_i \rangle$ on the DM, it is possible to cancel the contribution of intensity fluctuations at $f_{{\rm0}}$. When this is realized the mode $\arrowvert Z''_i \rangle$ is orthogonal to $\arrowvert Z_1 \rangle$ in the pupil space. The corresponding command vector $\vec{z''_i}$contains now the DM piston command $\vec{z'_1}$ and is related to the contribution $\eta^{Z'}_i$ of the uncalibrated Zernike-like mode $\arrowvert {Z'_i}^{\perp} \rangle$:
 
$\displaystyle % \vec{z''_i} \cdot \vec{z'_1} = \frac { \eta^{Z'}_i}{ \eta^{Z'}_... ...{\rm where} \quad \eta^{Z'}_{i}= \langle {Z'_i}^{\perp} \arrowvert Z_1 \rangle.$     (23)

If the actuators are calibrated (zonal method) instead of modes, the vector $\vec{\eta}^{Z'}$ in Eq. (23) is to be replaced by $\vec{\eta}^{\rm F} $ and can thus be injected in Eq. (14) for computing the searched command matrix K. In the modal method we described, the $\vec{\eta}^{\rm F} $ vector is related to $\vec{\eta}^{Z'}$ by:
$\displaystyle \vec{\eta}^{\rm F} = O^{-1} \vec{\eta}^{Z'}.$     (24)

As the new modes represented by a change of base matrix O' obtained by the piston adjustment are zero-mean modes, they can also be directly used in the computation of a modal optimized command matrix by replacing O by O' in Eq. (8). The resulting command matrix produces zero-mean deformations like the matrix K.

For sensitivity purposes we wish to apply a modulation with the largest possible amplitude. With a maximum deformation amplitude of $\lambda /4$, the response already reached the non-linear region, so that some intensity fluctuation remains even when the driven mode is zero-mean as shown in Fig. 12. However these results show that calibrating Zernike-like modes, which have a more symmetric shape than single influence functions, may induce negligible errors except for a few modes.


  \begin{figure} \par\leavevmode \includegraphics[width=\linewidth,height=5cm]{MS1... ...ar\includegraphics[width=\linewidth,height=5cm]{MS10230f11c.eps}\par\end{figure} Figure 11: Simulated power spectrum of intensity fluctuations for the coma mode driven with an amplitude of $\lambda /4$ at $f_{0}=30~{\rm Hz}$. Top: $\arrowvert {Z'_7}^{\perp} \rangle$, middle: $\arrowvert Z''_7 \rangle$ with a $\lambda /500$ piston error, bottom: $\arrowvert Z''_7 \rangle$ calibrated
Open with DEXTER


  \begin{figure} \par\leavevmode \includegraphics[width=\linewidth]{MS10230f12.eps}\par\end{figure} Figure 12: Simulation of piston errors due to non-linear effects: intensity fluctuation transposed to piston error in nm for piston-free modes driven with a $\pm \, \lambda /4$ amplitude (at 0.7 $\mu $m). (Cross: calibration for single actuators, stars: calibrated Zernike-like modes)
Open with DEXTER

4.3 Simulation results

We simulated this interferometric experiment by computing the pupil interferograms at the single-pixel detector considering our 31 element BDM model. We took into account photon noise, $8\;10^5$ photons per second, and chose rather pessimistic parasite vibrations in the bench including a slow drift of $\lambda/16$ and an arbitrary white piston noise of $\lambda/200$standard deviation. The slow drift is corrected with a low bandwidth with the mirror itself by using the mean intensity as feed-back. In a real experiment, the modulation frequency could be adjusted taking into account the real vibrations spectrum. The power spectrum analysis of the simulation results displayed in Fig. 11, shows that it should be easy to extract the contribution of intensity fluctuations due to a small piston in the driven mode, even in presence of photon noise, parasite vibrations and possible source instability.

4.4 Error propagation


  \begin{figure} \par\leavevmode \includegraphics[width=\linewidth]{MS10230f13.eps}\hfill \par\end{figure} Figure 13: Residual piston error of bimorph mirror during atmospheric compensation versus mode number for a $\lambda /500$ accuracy of mode calibration with a $\lambda /4$ amplitude. $r_0=8~{\rm cm}$, wind speed = $15~{\rm m\;s^{-1}}$
Open with DEXTER

Assuming our DM model is right, it is possible to evaluate the precision we can reach for the piston calibration. From Fig. 11, we can assume that an accuracy of $\lambda /500$ for the piston adjustment of each correction modes may be easily reached. From this precision, it is possible to compute as for Fig. 5 the residual contribution of each mode to the pupil piston when it is propagated by the AO correction of atmospheric turbulence. The results displayed in Fig. 13 take into account the non-linear effects. The overall residual piston standard deviation for one DM is less than $\lambda/48$ and thus the final error in OPD due to the two DMs would be $\lambda/33$. This is sufficient to make the fringe contrast loss due to AO negligible in short exposures. In long exposures the loss would be of about $2\%$ for these mean turbulence conditions.

4.5 Effect of spatial filtering

For calibration purposes the science beam of an interferometer is sometimes spatially filtered by single-mode optical devices (Coudé du Foresto et al. 1998) (Malbet et al. 1999). This leads to an apodization of the intensity in the pupil, defined by the function $\gamma(\vec{r})$ of Eq. (3) close to a truncated Gaussian (Ruilier & Cassaing 2000). Thus the method presented in Sect. 4 can not be used just as it is. Indeed the same spatial filtering as in the science beam must be applied in a focal plane of the calibration bench. In this case the calibration can be done only with a square signal modulation because the intensity after spatial filtering depends on the wavefront shape. If a sinusoidal modulation is used one should use the free interferometric output of the calibration bench (output 2 of Fig. 9). The signal to be recorded is then the normalized difference of the overall intensity between the two arms.

A second order effect of single-mode filtering could be the difference between the shapes of the fundamental mode for different bandwidths. The correction modes should then be optimized to minimize the piston induced by the bimorph mirrors in the spectral bands of observation.

As instrumental characteristics may significantly affect the fringe contrast measurements of an astrophysical object, the AO piston calibration processes we considered could greatly benefit from direct measurements through the science instrument (Fig. 1) in order to include all the effects.

5 Conclusions

The effect of AO correction on the fringe contrast measured with a Michelson Stellar Interferometer has been analyzed. Control of the deformable mirror piston mode is critical since it is not seen by the WFS, but can induce contrast losses. Our analysis shows that filtering the piston mode in the command space for a bimorph mirror is not applicable, since this leads to severe contrast losses in typical conditions, even for short exposures. By deriving the general formalism of piston control in AO, we demonstrate that the fast piston motions can be corrected without any significant additional computation time. However, this requires a prior knowledge of the absolute influence functions of the deformable mirror, including the piston term.

In this goal, we propose a calibration bench able to measure the piston contributions; this set-up could be used to qualify the performances of piston control and could also be upgraded to a built-in facility for on-site calibrations.

Acknowledgements
The simulations of the GI2T AO system presented in this paper are based on F. Rigaut's AO simulation package. The authors are very grateful to him. We also wish to thank P.-Y. Madec (ONERA) and A. Blazit (OCA) for very fruitful discussions and we acknowledge heartily the anonymous referee for very constructive suggestions. This work is supported by the Technology and Research department of the region Provence-Alpes-Côte d'Azur and by the CNRS (France).

References

 

© ESO 2001