A&A 365, 241-247 (2001)
DOI: 10.1051/0004-6361:20000026

Rate coefficients for the reactions of C(3PJ) atoms with C2H2, C2H4, CH3C$\equiv$CH and H2C=C=CH2 at temperatures down to 15 K

D. Chastaing - S. D. Le Picard - I. R. Sims - I. W. M. Smith

Send offprint request: I. W. M. Smith,

School of Chemistry, The University of Birmingham, Edgbaston, Birmingham B15 2TT, UK

Received 29 August 2000 / Accepted 11 October 2000

Abstract
Rate coefficients for the reactions of ground state carbon atoms, C(3PJ), with the four unsaturated hydrocarbons C2H2, C2H4, ${\rm CH_3C\equiv CH}$ and ${\rm H_2C=C=CH_2}$ have been measured at temperatures down to 15 K. The experiments have been performed in a continuous flow CRESU (Cinétique de Réaction en Écoulement Supersonique Uniforme) apparatus using pulsed laser photolysis of C3O2 to generate C(3PJ) atoms and laser-induced fluorescence in the vacuum ultraviolet to observe the kinetic decays of the atoms and hence determine the rate coefficients. All four reactions are found to occur at rates close to the collision-determined limit and the rates show at most a very mild dependence on temperature. It is argued that normally these reactions proceed along a reaction path with no barrier to form a strongly bound energised adduct, which subsequently eliminates an H atom to form the reaction products. The rates of the reactions of C(3PJ) atoms with larger unsaturated hydrocarbons are discussed. Finally, the relevance of the results for the chemistry of dense interstellar clouds is considered.

Key words: molecular data - molecular processes - methods: laboratory - ISM: clouds

Author for correspondance: i.w.m.smith@bham.ac.uk


1 Introduction

Carbon is the fourth commonest element in the universe with an abundance of ca. 3 10-4 relative to that of hydrogen (Anders & Grevesse 1989; Cardelli et al. 1996). Ground state carbon atoms, C(3PJ), have been detected in a wide variety of astronomical environments. They are particularly abundant in dense interstellar clouds (ISCs) (Phillips & Huggins 1981; Schilke et al. 1995; Zmuidzinas et al. 1988), where their abundance is comparable to that of CO, the second commonest molecule in ISCs. The typical column density of carbon atoms is $N_{\rm C} = 2.5 \, 10^{16}~{\rm cm}^{-2} \approx 0.1~N_{\rm CO}$ (Phillips & Huggins 1981; Schilke et al. 1995; Zmuidzinas et al. 1988; Petitpas & Wilson 1998). C(3PJ) atoms have also been detected in the circumstellar envelopes of evolved stars, such as the outer shell of IRC $+ 10^{\circ}216$ and the inner envelope of $\alpha$ Ori (Van der Veen et al. 1998). Of the approximately 120 molecules that have been definitely identified in ISCs (Herbst 1996), over two-thirds contain carbon and most of these are "carbon-rich'', despite the overwhelmingly high abundance of hydrogen in such clouds.

One of the aims of astrophysical chemists is to understand the chemistry that leads to the observed abundances of molecules in dense ISCs. To this end, reaction networks have been constructed and computer simulations of the molecular evolution in dense ISCs have been carried out. In recent years, the importance of reactions between electrically neutral species has been recognised (Herbst et al. 1994; Sims & Smith 1996), even though the temperatures in dense ISCs are typically between 10 and 50 K. One problem is how larger molecules are assembled and, in particular, how molecules containing chains of several carbon atoms are created.

Experiments from our laboratory, including many in collaboration with Rowe's group from Rennes, have demonstrated that the radicals CH (Canosa et al. 1997) and C2H (Chastaing et al. 1998) react rapidly with unsaturated hydrocarbons at low temperatures. It has been argued that the reaction mechanism probably involves the incorporation of one (with CH) or two (with C2H) more carbon atoms into the molecule and the elimination of a hydrogen atom; i.e.

\begin{displaymath}% {\rm CH, C_2H} + {\rm C}_n{\rm H}_m \to {\rm C}_{n+1}{\rm H}_m, {\rm C}_{n+2}{\rm H}_m + {\rm H}. \end{displaymath} (1)

Thereby forming molecules containing a larger number of carbon atoms.

Neutral-neutral reactions of atomic carbon with unsaturated hydrocarbons have been identified by Herbst and co-workers (Herbst et al. 1994; Bettens et al. 1995; Bettens & Herbst 1997) as potentially of great importance in the synthesis of larger carbon-containing species, if successive addition-elimination reactions occur, similar to those represented by Eq. (1); i.e.

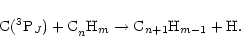\begin{displaymath}% {\rm C(^3P_{\it J}) + C}_n{\rm H}_m \to {\rm C}_{n+1}{\rm H}_{m-1} + {\rm H}. \end{displaymath} (2)

The proposition that these reactions will be very fast even at very low temperatures was supported by the extensive room temperature measurements of Husain and co-workers (Haider & Husain 1992; Haider & Husain 1993a; Haider & Husain 1993b; Husain & Ioannou 1997). They showed that the rate coefficients for the reactions of C(3PJ) atoms with a wide range of alkenes and alkynes are close to the collision-determined limits, suggesting the lack of a barrier on the potential energy surface leading from reagents to products in all of these systems. The theoretical work of Clary et al. (1994) confirmed that these reactions were likely to remain rapid down to the temperatures prevailing in dense ISCs.

The only kinetic data for reactions of C(3PJ) atoms with unsaturated hydrocarbons at temperatures below room temperature are the earlier measurements from our laboratory (Chastaing et al. 1999). Those experiments, like the present ones, employed the CRESU technique (CRESU is a French acronym for Reaction Kinetics in Uniform Supersonic Flow). This technique relies on the cooling that occurs when gas is expanded through a convergent-divergent Laval nozzle to generate a supersonic flow of relatively dense gas at a defined temperature. Kinetic measurements on reactions involving neutral radicals, including radical atoms, are then normally made by: (i) generating the radicals by pulsed laser photolysis of a suitable precursor, and (ii) observing subsequent changes in the concentration of the radicals, using an appropriate spectroscopic technique (Sims & Smith 1996). In the present experiments, as in our earlier ones, C(3PJ) atoms were generated by photolysis of C3O2 using the output of an ArF excimer laser at 193 nm. In the earlier experiments, the subsequent kinetic behaviour of these atoms was inferred by observing chemiluminescence from NO formed in the reaction between the C(3PJ) atoms and a small concentration of NO2 that was included in the reaction mixture. In the present experiments, we have observed decays in the concentration of C(3PJ) atoms directly by applying the technique of time-resolved laser-induced fluorescence (LIF) in the vacuum ultraviolet (VUV). Further details of this method are given in the next section.

2 Experimental

The rate constants for the reactions of C(3PJ) atoms with unsaturated hydrocarbons have been measured in the Birmingham CRESU apparatus (James et al. 1998) at temperatures down to 15 K. In a CRESU apparatus, low temperatures are achieved by isentropic expansion of a gas mixture, consisting predominantly (typically $> 99\%$) of a carrier gas (He, Ar or N2) through an axisymmetric, convergent-divergent, Laval nozzle. A supersonic flow of gas is generated in which the Mach number, the temperature, the total pressure of the gas, and the mole fractions of the components of the mixture are uniform along the flow. In all the experiments referred to here, a small concentration of C3O2 was included in the flow and C(3PJ) atoms were generated by pulsed laser photolysis of this precursor at 193 nm, using an excimer laser operating on ArF. The output from this laser was directed through the gas reservoir and Laval nozzle and along the axis of the gas flow.

In the present CRESU experiments, data for the reactions of C(3PJ) atoms have been obtained by directly monitoring the kinetic decays of the C(3PJ) atomic concentration using resonant vacuum-ultraviolet laser-induced fluorescence (VUV-LIF); that is, with both excitation and observation of the fluorescence on the (2s22p3s 3PJ - 2s22p2 3PJ) transition in atomic carbon. Pulses of VUV laser radiation were generated using four-wave mixing in Xe (Hilbig & Wallenstein 1983a). The method is described in some detail elsewhere (Chastaing et al. 2000a). Briefly, dye laser radiation was tuned to 255.94 nm in order to excite Xe in a two-photon transition to its 5p56p[21/2, 2] state. A second pulsed dye laser could be tuned through the wavelength range between 560 and 565 nm to generate VUV radiation between 165.9 and 165.4 nm. This radiation propagated horizontally and was directed perpendicular to the gas flow at a fixed point in the apparatus. LIF spectra of the (2s22p3s 3PJ - 2s22p2 3PJ) transition were recorded and confirmed that spin-orbit relaxation within the electronic ground state was achieved on a time-scale that was short relative to that for reaction (Chastaing et al. 2000a; Canosa et al. 2000).

For kinetic measurements, the VUV probe laser was set at the wavelength of the (2s22p3s 3P J=1 - 2s22p2 3PJ=0) transition at 165.69 nm and LIF signals, observed by a photomultiplier mounted above the gas flow, were recorded as the time delay between the pulses from the photolysis and probe lasers was systematically varied. The recorded traces of LIF signal versus time accurately fitted single exponential decays yielding pseudo-first-order rate constants ( $k_{\rm 1st}$), as long as sufficient delay (ca. 10 $\mu$s) was allowed before starting the fitting to allow for complete relaxation among the spin-orbit components of the C(3PJ) ground state. Second-order rate constants for reaction at a particular temperature were obtained by measuring values of $k_{\rm 1st}$, with different concentrations of the co-reagent (CnHm) added to the flowing gas mixture, and plotting $k_{\rm 1st}$ versus [CnHm].

C3O2 was synthesised by the dehydration of bis(trimethylsilyl) malonate as described by Chastaing et al. (1999). C2H2, C2H4, and the carrier gases (He, Ar and N2) were provided by Air Products. Methyl acetylene (or propyne; i.e. CH $_3 {\rm C\equiv CH}$) and allene (or propadiene; i.e. ${\rm H_2C=C=CH_2}$) were supplied by Intergas. All gases were used directly from their cylinders without further purification.

3 Results

The rate coefficients for the reactions of C(3PJ) atoms with the unsaturated hydrocarbons, C2H2, C2H4, ${\rm CH_3C\equiv CH}$ and ${\rm H_2C=C=CH_2}$, which have been determined in the present work are listed in Table 1, along with the main flow conditions for each measurement.

 

 
Table 1: Rate coefficients for the reactions of C(3PJ) atoms with C2H2, C2H4, ${\rm CH_3C\equiv CH}$ and ${\rm H_2C=C=CH_2}$
Temperature (K) 15 27 54 83 207 295
Carrier gas He He Ar N2 N2 Ar
Total density            
(1016 mol cm-3) 5.05 4.65 5.36 4.88 5.83 19-20
Range of reagent gas            
(1013 mol cm-3)            
C2H2 0-5.9 0-5.7 0-7.7 0-10 0-7.0 0-57
C2H4 0-5.8 0-5.5 0-7.4 0-14 0-6.7 0-60
CH3C $\equiv$ CH 0-0.82 0-3.5 0-4.2 0-3.7 0-4.8 0-50.8
${\rm H_2C=C=CH_2}$ 0-1.9 0-4.0 0-4.9 0-3.8.9 0-4.9 0-23.6
Rate coefficient            
(10-10 cm3 mol-1 s-1)            
C2H2 $4.76 \pm 0.56^1$ $3.23 \pm 0.47$ $3.33 \pm 0.35$ $3.90 \pm 0.29$ $2.87 \pm 0.43$ $3.09 \pm 0.12$
C2H4 $4.79 \pm 0.79$ $4.12 \pm 0.46$ $4.38 \pm 0.42$ $3.52 \pm 0.31$ $3.67 \pm 0.44$ $2.66 \pm 0.09$
${\rm CH_3C\equiv CH}$ $3.9 \pm 1.6$ $3.59 \pm 0.32$ $2.43 \pm 0.33$ $3.62 \pm 0.45$ $3.10 \pm 0.16$ $2.49 \pm 0.20$
${\rm H_2C=C=CH_2}$ $ 2.91 \pm 0.58$ $4.10 \pm 0.55$ $3.42 \pm 0.39$ $4.67 \pm 0.60$ $3.63 \pm 0.36$ $3.22 \pm 0.32$
1 Estimated errors are quoted $\pm t \sigma$ where $\sigma$ is the standard error and t is the appropriate value of Student's
t-distribution for 95% confidence.


Only statistical errors are quoted. Some systematic errors may have arisen from, for example, inaccuracies in the calibration of flow controllers or in the determination of the total gas density, but we estimate these additional errors to be $< 10\%$.

In Figs. 1 and 2, the rate coefficients, k(T), that we have determined for the reactions of C(3PJ) atoms with C2H2 and C2H4 are displayed as a function of temperature (T) on log-log plots.

  \begin{figure} \par\includegraphics[width=7.7cm,clip]{aa10229f1.eps} \end{figure} Figure 1: Rate coefficients for the reaction of C(3PJ) atoms with C2H2 as a function of temperature plotted on a log-log scale. The filled circles ($\bullet $) show the results from the present work and the open circles ($\circ $) the results of previous experiments in the CRESU apparatus using the chemiluminescent marker technique (Chastaing et al. 1999). Results of other workers at room temperature are shown as an open square ($\square $) (Haider & Husain 1993a) and an open triangle ($\triangle $) (Loison et al. 2000). The continuous line is a fit to all the CRESU data yielding: $k(T) = 2.9 \,\, 10^{-10} (T / 298)^{-0.12}$ cm3 mol-1 s-1
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{aa10229f2.eps} \end{figure} Figure 2: Rate coefficients for the reaction of C(3PJ) atoms with C2H4 as a function of temperature plotted on a log-log scale. The symbols have the same meaning as in Fig. 1. The line is a fit to all the CRESU data yielding: $k(T) = 3.0 \,\, 10^{-10} (T / 298)^{- 0.11}$ cm3mol-1 s-1
Open with DEXTER

The quality of the data for the reactions of C(3PJ) with ${\rm CH_3C\equiv CH}$ and ${\rm H_2C=C=CH_2}$ is similar. In every case, the variation of k(T) with T is slight, and the rate coefficients at all temperatures are close to the collision-determined limit. The data are fitted to the form k(T) = A (T / 298)n, and the resulting values of A and n are given in Table 2.
 

 
Table 2: Values of the parameters A and n obtained by non-linear least-squares fitting of the rate coefficients k(T) to the form k(T) = A (T / 298)n. For ${\rm C}(^3{\rm P}_J) + {\rm C_2H_2}$ and ${\rm C(^3P}_J) + {\rm C_2H_4}$, the upper entries are from fits to the data obtained in the present work by time-resolved VUV- LIF observation of C(3PJ) atom decays, and the lower entries are from fitting the data from both the present work and the previous data obtained by Chastaing et al. (1999) using a chemiluminescent marker technique
Reaction A / 10-10 cm3 mol-1 s$^{-1\,a}$ na
${\rm C(^3P}_J) +{\rm C_2H_2}$ $2.9 \pm 0.7$ $- 0.12 \pm 0.10$
  $2.9 \pm 0.3$ $- 0.12 \pm 0.10$
${\rm C(^3P}_J) + {\rm C_2H_4}$ $3.1 \pm 0.5$ $- 0.14 \pm 0.08$
  $3.0 \pm 0.4$ $- 0.11 \pm 0.07$
${\rm C(^3P}_J) + {\rm CH_3C \equiv CH}$ $2.7 \pm 0.6$ $- 0.11 \pm 0.07$
${\rm C(^3P}_J) + {\rm H_2C=C=CH_2}$ $3.5 \pm 0.8$ $- 0.01 \pm 0.12$
a Errors are quoted as $\pm 2 \sigma$, where $\sigma$ is the standard error.


In Figs. 1 to 2, we have also plotted the rate constants obtained in previous studies of the reactions of C(3PJ) atoms with C2H2 and C2H4. Except for the earlier results which we obtained for these reactions using the chemiluminescent marker technique, the previous data are limited to room temperature. The present results are in excellent agreement with those obtained using the chemiluminescent technique. The parameters A and n found by fitting both sets of data for each reaction, according each set equal weighting, are also listed in Table 2. Our results at room temperature are in fair agreement with those of Haider & Husain (1993). For ${\rm C(^3P}_J) + {\rm CH}_3{\rm C\equiv CH}$ and ${\rm C(^3P}_J) + {\rm H_2C=C=CH_2}$, the only previous kinetic data are the room temperature rate constants of Haider & Husain (1993). The rate coefficients that they reported are 60% larger than ours in the case of ${\rm C(^3P}_J) + {\rm CH_3C \equiv CH}$ and 2.3 times larger for ${\rm C(^3P}_J) + {\rm H_2C=C=CH_2}$.

For all four reactions that we have studied here, there is no apparent dependence on the nature of the carrier gas confirming that the experiments determine rate coefficients for bimolecular reactions between the unsaturated hydrocarbon and the C(3PJ) atoms.

4 Discussion

4.1 Reaction mechanisms

The present measurements confirm our earlier conclusion (Chastaing et al. 1999) that C(3PJ) atoms react rapidly with simple unsaturated hydrocarbons at very low temperatures. The rapidity of these reactions, and the fact that their rate coefficients are almost independent of temperature leads to two important fundamental conclusions. First, there must be no barrier on the potential energy surfaces leading from reagents to products for these reactions. This conclusion is confirmed by very recent crossed molecular beam experiments performed at low collision energies on the reactions of C(3PJ) atoms with C2H2, C2H4, ${\rm CH_3CH\equiv CH}$ and ${\rm H_2C=C=CCH_2}$ (Chastaing et al. 2000b; Costes 2000). The cross-sections for all four of these reactions were shown to increase monotonically as the relative translational energy was reduced from ca. 120 meV to ca. 4 meV.

In addition, it appears that the rate coefficients of these reactions of C(3PJ) atoms must be essentially independent of the spin-orbit state of the atom, i.e. of J. The spin-orbit states in C(3PJ) are closely spaced with J = 1 only 16.4 cm-1 (corresponding to 23.6 K) above the lowest J = 0 component, and J = 2 lying 43.4 cm-1 (corresponding to 62.4 K) above J = 0. There is a dramatic change in the relative spin-orbit populations as the temperature is reduced between 295 K (where NJ=0 : NJ=1 : NJ=2 = 1.0 : 2.77 : 4.05) and 15 K (where NJ=0 : NJ=1 : NJ=2 = 1.0 : 0.62 : 0.08). Consequently, if the rate coefficient for reactions of C(3PJ) atoms depended appreciably on the J level, then we should expect to have observed a similarly strong dependence of the thermally-averaged rate coefficients on temperature.

Our experimental results provide no information about the products of the reactions of C(3PJ) atoms with C2H2, C2H4, ${\rm CH_3C\equiv CH}$ and ${\rm H_2C=C=CH_2}$ at low temperatures. Of course, for modelling purposes, as well as for a full fundamental understanding of these reactions, it is desirable to know the product branching ratios, as well as rate coefficients for the overall reactions. Extensive quantum chemical calculations performed by Kaiser and co-workers (Kaiser et al. 1996a; Kaiser et al. 1996b; Oschenfeld et al. 1997; Kaiser et al. 1997a; Kaiser et al. 1997b; Kaiser et al. 1999; Mebel et al. 2000) indicate that each of these reactions proceeds via the initial formation of an adduct across an attractive potential energy surface with no barrier on the path leading from reagents to the deep potential well associated with the adduct. In molecular beam experiments, and at the low total pressures in interstellar clouds and in our experiments, the energised adduct will not be collisionally stabilised but must fragment to yield two products. In some cases, fragmentation may occur at competitive rates to more than one final set of products. However, in most cases the dominant process is likely to be loss of an H atom, which is usually highly exothermic and requires the cleavage of just one C-H bond.

Table 3 lists the changes in enthalpy associated with (a) formation of the adduct between C(3PJ) and the unsaturated hydrocarbon reagent, and (b) some of the more likely exothermic channels identified in the theoretical work of Kaiser et al.

 

 
Table 3: Pathways and thermochemistry for the reactions of C(3PJ) atoms with unsaturated hydrocarbons
Reagents Products $\Delta_r H^{\circ}_0$ / kJ mol-1
${\rm C(^3P}_J) +{\rm C_2H_2}$ (HCCCH) $- 390^{\rm a}$
  l- ${\rm C_3H}(X^2\Pi_{\Omega}) + {\rm H}(^2{\rm S}_{1/2})$ $- 1.5^{\rm a, b, c}$
  c- ${\rm C_3H}(X^2B_2) + {\rm H}(^2{\rm S}_{1/2})$ $- 8.6^{\rm a, b, c}$
  ${\rm c^3}(X^1\Sigma_{\rm g}^+) + {\rm H_2}(X^1\Sigma_{\rm g}^+)$ $- 127.0^{\rm b}$
${\rm C(^3P}_J) + {\rm C_2H_4}$ ${\rm (H_2CCCH_2)}$ $- 367^{\rm a}$
  ${\rm HCCCH_2}(X^2B_2) + {\rm H(^2S_{1/2})}$ $- 215^{\rm a, d}$
  c- ${\rm C_3H_3}(X^2E^{\prime \prime}) + {\rm H(^2S_{1/2})}$ $- 115^{\rm d}$
  c- ${\rm C_3H_2}(X^2A_1) + {\rm H_2}(X^1\Sigma_{\rm g}^+)$ $- 284^{\rm d}$
${\rm C(^3P}_J) + {\rm CH_3C \equiv CH}$ ${\rm (HCCCCH_3)}$ $- 391^{\rm a, e}$
  n- ${\rm CH_2CCCH}(X^2A^{\prime}) + {\rm H(^2S_{1/2})}$ $- 194^{\rm f}$
  ${\rm HCCCCH}(X^1\Sigma_{\rm g}^+) + {\rm 2 H(^2S_{1/2})}$ $- 12^{\rm f}$
  ${\rm HCCCCH}(X^1 \Sigma_{\rm g}^+) + {\rm H_2}(X^1\Sigma_{\rm g}^+)$ $- 444^{\rm f}$
${\rm C(^3P}_J) +{\rm CH_2C=CH_2}$ ${\rm (H_2CCCCH_2)}$ $- 406^{\rm e}$
  n- ${\rm CH_2CCCH}(X^2A^{\prime}) + {\rm H(^2S_{1/2})}$ $- 180^{\rm g}$
  ${\rm HCCCCH}(X^1\Sigma_{\rm g}^+) + {\rm 2 H(^2S_{1/2})}$ $- 18^{\rm g}$
  ${\rm HCCCCH}(X^1 \Sigma_{\rm g}^+) + {\rm H_2}(X^1\Sigma_{\rm g}^+)$ $- 450^{\rm g}$
$^{\rm a}$ Kaiser et al. (1997b), $^{\rm b}$ Kaiser et al. (1997a), $^{\rm c}$ Ochsenfeld et al. (1997),
$^{\rm d}$ Kaiser et al. (1996a), $^{\rm e}$ Mebel et al. (2000), $^{\rm f}$Kaiser et al. (1996b), $^{\rm g}$ Kaiser et al. (1999).


In addition, Kaiser et al. (1995, 1996a, 1996b, 1997a, 1999) have examined the dynamics of several reactions of C(3PJ) atoms with unsaturated hydrocarbons in a series of crossed molecular beam experiments, usually observing the scattered reaction product with a mass spectrometer set to the m/e value corresponding to replacement of one H-atom in the molecular reagent by one C atom.

The ${\rm C(^3P}_J) +{\rm C_2H_2}$ reaction was studied at three collision energies, 8.8, 28.0 and 45.0 kJ mol-1. They observed the angular distribution of products with m/e = 37, corresponding to C3H, and were unable to detect any other reaction products (Kaiser et al. 1995; Kaiser et al. 1997a). From changes in the angular scattering with collision energy, they inferred that both l- ${\rm C_3H}(X^2\Pi_{\Omega})$ and c- ${\rm C_3H}(X^2B_2)$ were formed under the conditions of their experiments, with the contribution of the latter, more exothermic channel decreasing at higher collision energies. Of course, the collision energies in Kaiser's experiments were appreciably larger than the average energy of thermal collisions between 10 and 50 K, that is at the temperatures typical of dense interstellar clouds, and the collision energies were also larger than the exoergicities of the reactions to l- ${\rm C_3H + H}$ and c- ${\rm C_3H + H}$. As the temperature is lowered, one might expect the more exothermic channel producing c- ${\rm C_3H}$ to be increasingly favoured, so the branching ratio between these two sets of products may change appreciably with temperature. However, very recent calculations by Buonomo and Clary (Buonomo & Clary 2000) performed on a new ab-initio surface have indicated that c- ${\rm C_3H}$ is disfavoured at low temperatures: indeed, they predict negligible formation of the cyclic isomer at temperatures below ca. 500 K.

The production of both ${\rm H(^2S_{1/2})} + l$- ${\rm C}_3{\rm H}(X^2 \Pi_{\Omega})$ and ${\rm H(^2S_{1/2})} +$c- ${\rm C_3H}(X^2{\rm B_2})$ from ${\rm C}(^3{\rm P}_j) + {\rm C_2H_2}(X^1\Sigma_{\rm g}^+)$ is spin-allowed. On the other hand, the production of ${\rm C_3}(X^1\Sigma_{\rm g}^+) + {\rm H}_2(X^1\Sigma_{\rm g}^+)$ which is much more exothermic does not conserve spin. In their experiments, Kaiser et al. (1995, 1997b) detected no reaction products other than ${\rm H + C_3H}$. On the other hand, very recent flow-tube experiments by Loison et al. (2000) at room temperature suggest that the yield of H atoms per C atom consumed in the reaction between C(3PJ) atoms and C2H2 is no more than $0.53 \pm 0.08$. It may be that, in this particular reaction, as the loss of an H atom from the adduct is only slightly exothermic, the adduct is quite long-lived, allowing time for intersystem crossing to a singlet surface, and subsequent production of C3( $X^1\Sigma_{\rm g}^+) + {\rm H}_2(X^1\Sigma_{\rm g}^+)$, to take place.

For ${\rm C(^3P}_J) + {\rm C_2H_4}$, the addition-elimination reaction to produce ${\rm C_3H_3 + H}$ is more exothermic ( $\Delta_r H^{\circ}_0 = - 215$ kJ mol-1) than the corresponding channel in the reaction of C(3PJ) atoms with C2H2. Therefore the energised adduct is likely to eliminate an H atom rapidly and thereby suppress the contribution of any competing channels. In their crossed beam study of the ${\rm C(^3P}_J) + {\rm C_2H_4}$ reaction, Kaiser et al. (1996) observed mass 39, consistent with the pathway to ${\rm C_3H_3 + H}$, and Loison et al. (2000) estimate the yield of H atoms from ${\rm C(^3P}_J) + {\rm C_2H_4}$ to be $0.92 \pm 0.08$ at room temperature; that is, unity within their error limits. For the reactions of C(3PJ) with both ${\rm CH_3C\equiv CH}$ and ${\rm H_2C=C=CH_2}$, observation of products with mass 51 in crossed beam experiments (Kaiser et al. 1996b; Kaiser et al. 1999), confirms the formation of C4H3 species. Again the substitution of C for H, is strongly exothermic (see Table 3) and the fragmentation of the initial adduct will probably be sufficiently rapid to suppress any other pathways.

In summary, at temperatures down as low as 15 K, C(3PJ) atoms react very rapidly with the simple alkynes and alkenes, C2H2, C2H4, ${\rm CH_3C\equiv CH}$ and ${\rm H_2C=C=CH_2}$. With the possible exception of the ${\rm C(^3P}_J) +{\rm C_2H_2}$ reaction, the products are very probably an H atom plus a species derived by replacement of one H atom in the molecular reagent by a C atom.

4.2 Astrochemical implications

Of the alkynes and alkenes whose reactions with C(3PJ) atoms have been studied in the present work, C2H2, C2H4 and ${\rm CH_3C\equiv CH}$ have been positively identified in interstellar clouds. Other such molecules that have been seen in ISCs include C4H2 and C6H2, i.e. di- and tri- acetylene. Our measurements demonstrate that the first three of these molecules react at essentially the collision-determined limit with C(3PJ) atoms at the temperatures found in dense ISCs. At 25 K, a median temperature in such environments, the rate coefficients for all four of the reactions studied in the present work, and the rate coefficient for ${\rm C(^3P}_J) + {\rm C_3H_6}$ determined earlier by Chastaing et al. (1999) are the same within experimental uncertainty, having values in the range 3.6-4.0 $\,\,\, 10^{-10}$ cm3 mol-1 s-1.

The rate coefficients for reactions of radicals with alkenes and alkynes are sometimes correlated with properties of the reactants. For example, in the case of H atoms reacting with a series of alkenes, the activation energies associated with the reactions fall as the ionisation energies of the unsaturated hydrocarbons become smaller (Clarke et al. 2000 and references therein). Because the ionisation energies fall and the van der Waals attraction increases as the size of unsaturated hydrocarbons increases, there is every reason to suppose that the reactions of C(3PJ) atoms with larger alkenes and alkynes will be no smaller than those which we have determined directly for the simplest alkenes and alkynes.

Our measurements indicate that the reactions of C(3PJ) atoms with alkenes and alkynes are rapid at low temperatures and should be included in chemical models of ISCs. It is argued above that it is likely that, as with the reaction of CH and C2H with alkenes and alkynes, reaction generally involves the addition of the atom or radical to the molecule and the loss of an H atom. In this context, it is interesting to note that the radicals C3H, C5H and C7H have all been observed in dense ISCs. These species could all be formed from reaction of C(3PJ) atoms with the appropriate alkyne according to Eq. (2), i.e.

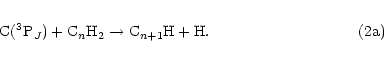
\begin{eqnarray*}{\rm C}(^3{\rm P}_J) + {\rm C}_n{\rm H}_2 \to {\rm C}_{n+1}{\rm H + H}.\hspace*{3.4cm}{\rm (2a)} \end{eqnarray*}


In addition, we note that the Cn+1H radicals are themselves likely to react rapidly with C(3PJ) atoms, with CH radicals, and with C2H radicals through formation of an energised adduct and subsequent loss of an H atom.

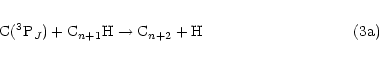
\begin{eqnarray*}{\rm C}(^3{\rm P}_J) + {\rm C}_{n+1}{\rm H} \to {\rm C}_{n+2} + {\rm H}\hspace*{3.45cm}{\rm (3a)} \end{eqnarray*}



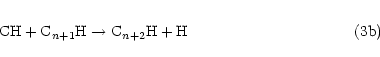
\begin{eqnarray*}{\rm CH + C}_{n+1}{\rm H} \to {\rm C}_{n+2}{\rm H + H}\hspace{3.8cm}{\rm (3b)} \end{eqnarray*}



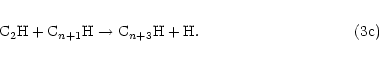
\begin{eqnarray*}{\rm C_2H + C}_{n+1}{\rm H \to C}_{n+3}{\rm H + H }.\hspace{3.55cm}{\rm (3c)} \end{eqnarray*}


The present, low temperature, measurements on reactions of C(3PJ) atoms, together with those made earlier in our laboratory on the low temperature reactivity of CH, CN and C2H radicals, demonstrate that all these species react with unsaturated hydrocarbons at, or close to, the collision-determined limit. For example, for the reactions of C2H2 with C(3PJ) atoms, CH, CN and C2H, the rate constants at 25 K are 3.9 10-10, 4.0 10-10, 4.5 10-10 and 2.0 10-10 cm3 mol-1 s-1, respectively. Given the similarity of these rate constants, it is clear that the relative rates of these reactions of C2H2 in dense ISCs, and presumably those of other alkynes and alkenes, will depend on the relative abundances of C(3PJ) atoms, CH, CN and C2H. In TMC-1, for example, the fractional abundances of CH, CN and C2H, relative to that of H2 are 2 10-8, 3 10-8 and 5 10-8 (Terzieva & Herbst 1998), so the reaction of these species with C2H2 will occur at rather similar rates. On the other hand, C atoms may be much more abundant (Phillips & Huggins 1981; Schilke et al. 1995; Zmuidzinas et al. 1988) and, if so, they will be the predominant mechanism for destruction of unsaturated hydrocarbons.

Acknowledgements
We thank the EPSRC for a substantial research grant to construct the CRESU apparatus, and for the loan of lasers through the Laser Loan Pool at the Rutherford-Appleton laboratory. We are grateful to the European Community for a TMR Research Network grant, contract FMRX-CT97-0132 (DG12-MIHT), for research on Astrophysical Chemistry under whose programme these experiments were performed and which provided a research Fellowship for S.D.L.P. We are also grateful to the TMR programme of the European Community for a research studentship for D. C. (contract ERBFMBICT961858). We thank Dr. Astrid Bergeat and Prof. David Clary for permission to cite their results (Loison et al. 2000; Buonomo & Clary 2000) prior to publication.

References

 

© ESO 2001