A&A 365, 174-185 (2001)
DOI: 10.1051/0004-6361:20000020

Warm H2 in the Galactic center region[*]

N. J. Rodríguez-Fernández1 - J. Martín-Pintado1 - A. Fuente1 - P. de Vicente1 -
T. L. Wilson2,3 - S. Hüttemeister4

Send offprint request: N. J. Rodríguez-Fernández,


1 - Observatorio Astronómico Nacional, IGN, Apartado 1143, 28800 Alcalá de Henares, Spain
2 - Max-Planck-Institut für Radioastronomie, Postfach 2024, 53010 Bonn, Germany
3 - Sub-mm Telescope Observatory, Steward Observatory, The University of Arizona, Tucson, AZ 85728, USA
4 - Radioastronomisches Institute der Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany

Received 10 August 2000 / Accepted 6 October 2000

Abstract
We present ISO observations of several \ensuremath {\rm H_2} pure-rotational lines (from S(0) to S(5)) towards a sample of 16 molecular clouds distributed along the central $\sim \,$500 pc of the Galaxy. We also present \ensuremath {\rm C^{18} \rm O} and \ensuremath {^{13}{\rm CO}} $J=1\rightarrow 0$ and $J=2 \rightarrow 1$ observations of these sources made with the IRAM-30 m telescope. With the CO data we derive \ensuremath {\rm H_2} densities of 10 3.5-4.0 cm-3 and \ensuremath {\rm H_2} column densities of a few 1022 cm-2. We have corrected the \ensuremath {\rm H_2} data for $\sim \,$30 magnitudes of visual extinction using a self-consistent method. In every source, we find that the \ensuremath {\rm H_2} emission exhibits a large temperature gradient. The S(0) and S(1) lines trace temperatures (T) of $\sim \,$150 K while the S(4) and S(5) lines indicate temperatures of $\sim \,$600 K. The warm \ensuremath {\rm H_2} column density is typically $\sim \,$1-2 1022 cm-2, and is predominantly gas with T=150 K. This is the first direct estimate of the total column density of the warm molecular gas in the Galactic center region. These warm \ensuremath {\rm H_2} column densities represent a fraction of $\sim \,$30% of the gas traced by the CO isotopes emission. The cooling by \ensuremath {\rm H_2}  in the warm component is comparable to that by CO. Comparing our \ensuremath {\rm H_2} and CO data with available ammonia (NH3) observations from literature one obtains relatively high NH3 abundances of a few 10-7 in both the warm and the cold gas. A single shock or Photo-Dissociation Region (PDR) cannot explain all the observed \ensuremath {\rm H_2} lines. Alternatives for the heating mechanisms are discussed.

Key words: ISM: clouds - ISM: molecules - ISM: dust, extinction - galaxy: center - infrared: ISM: continuum - infrared: ISM: lines and bands

Author for correspondance: nemesio@oan.es


1 Introduction

The interstellar matter in the inner few hundreds parsecs of the Galaxy (hereafter GC) is mainly molecular. In this region there are molecular clouds and huge cloud complexes like Sgr B2 which can be as large as 70 pc, with masses of 106 solar masses. The physical conditions in the GC clouds differ appreciably to those of the clouds of the disk of the Galaxy. The GC clouds have average densities of $\sim \,$104 cm-3 instead of 102 cm-3 typical of the clouds of the disk. In addition, with widespread high temperatures (up to 200 K), GC clouds are hotter than disk clouds.

The temperatures of the warm gas are known mainly by observations of ammonia (NH3) metastable lines. Güsten et al. (1981, 1985) derived rotational temperatures ( $T_{\rm rot}$) of 60-120 K in several GC clouds, most of them in the Sgr A complex. Morris et al. (1983) showed that $T_{\rm rot} \sim 30$-60 K are common in the region $\vert l\vert<2^\circ$. The most complete study of the temperature structure of the molecular gas in the GC, was carried out by Hüttemeister et al. (1993). They presented a multilevel study of NH3 metastable lines of 36 molecular clouds distributed all along the "Central Molecular Zone" (CMZ, in notation of Morris & Serabyn 1996) and the "Clump 2" complex, which, although not belonging to the actual CMZ, exhibits similar properties. They detected warm gas at all galactic longitudes and showed that the NH3 emission can be characterized by two temperature components since the $T_{\rm rot}$ derived from the (1,1) and (2,2) levels is $\sim \,$20-30 K and that derived from the (4,4) and (5,5) levels is $\sim \,$70-200 K. Unfortunately, the a priori unknown abundance of the NH3 molecule has made it difficult to estimate the total column density of warm gas in the GC clouds.

The heating of the molecular gas over large regions ($\sim \,$10 pc) where the dust temperature is lower than 30 K (Odenwald & Fazio 1984; Cox & Laureijs 1989; Martín-Pintado et al. 1999a; Rodríguez-Fernández et al. 2000) is a puzzle. Indirect arguments such as the large widths of molecular lines or large abundances in gas phase of molecules such as SiO (Martín-Pintado et al. 1997; Hüttemeister et al. 1998) or NH3 points towards a mechanical heating. Wilson et al. (1982) proposed the dissipation of turbulence induced by differential Galactic rotation as a possible heating source.

For the first time, we have measured the total column densities of warm gas in the GC clouds by observing the lowest \ensuremath {\rm H_2} pure-rotational transitions with the Infrared Space Observatory (ISO; Kessler et al. 1996). The \ensuremath {\rm H_2} pure-rotational lines trace gas with temperatures of a few hundred K (see Shull & Beckwith 1982 for a review on the properties and the notation of the \ensuremath {\rm H_2} molecule). ISO has detected \ensuremath {\rm H_2} pure-rotational lines in a variety of sources such as: Young Stellar Objects (van den Ancker 1999); galactic nuclei (see e.g. Kunze et al. 1999); Photo Dissociation Regions (PDRs) like NGC 7023 (Fuente et al. 1999, 2000) or S140 (Timmermann et al. 1996); shock-excited sources such as Orion Peak 1 (Rosenthal et al. 2000); and proposed X-ray excited regions (XDRs) like RCW 103 (see Wright 2000).

Our sample consists of 18 molecular clouds from the surveys of Hüttemeister et al. (1993) and Martín-Pintado et al. (1997). Two of these show a non-equilibrium \ensuremath {\rm H_2} ortho-to-para ratio and have been studied in detail by Rodríguez-Fernández et al. (2000). In this paper we present the other 16 clouds of the sample. The clouds are distributed along the CMZ, from the Sgr E region to the vicinity of Sgr D and the "Clump 2" complex. Four clouds are located in the Sgr C complex, three in the vicinity of Sgr A (two are in the radio Arc). Two clouds are situated in the cold dust ridge reported by Lis & Carlstrom (1994) that seems to connect the radio Arc and Sgr B. Other three clouds belong to the Sgr B complex.

This paper is organized as follows. In Sect. 2 we present \ensuremath {\rm C^{18} \rm O} and \ensuremath {^{13}{\rm CO}} IRAM-30 m observations and \ensuremath {\rm H_2} ISO observations. The analysis of the CO isotopes and \ensuremath {\rm H_2}, is presented in Sects. 3 and 4, respectively. The results and the possible heating mechanism of the warm gas are discussed in Sect. 5.

2 Observations

2.1 IRAM 30-m observations and results

We have observed the $J=1\rightarrow 0$ and $J=2 \rightarrow 1$ lines of \ensuremath {^{13}{\rm CO}} and \ensuremath {\rm C^{18} \rm O} with the IRAM 30-m telescope (Pico de Veleta, Spain) towards the GC molecular clouds given in Table 1.

   
Table 1: J2000 coordinates of the sources
Source RA DEC Complex
  h m s $^\circ$ ' ''  
M -0.96+0.13 17:42:48.3 -29:41:09.1 Sgr E
M -0.55-0.05 17:44:31.3 -29:25:44.6 Sgr C
M -0.50-0.03 17:44:32.4 -29:22:41.5 Sgr C
M -0.42+0.01 17:44:35.2 -29:17:05.4 Sgr C
M -0.32-0.19 17:45:35.8 -29:18:29.9 Sgr C
M -0.15-0.07 17:45:32.0 -29:06:02.2 Sgr A
M +0.16-0.10 17:46:24.9 -28:51:00.0 Arc
M +0.21-0.12 17:46:34.9 -28:49:00.0 Arc
M +0.24+0.02 17:46:07.9 -28:43:21.5 Dust Ridge
M +0.35-0.06 17:46:40.0 -28:40:00.0  
M +0.48+0.03 17:46:39.9 -28:30:29.2 Dust Ridge
M +0.58-0.13 17:47:29.9 -28:30:30.0 Sgr B
M +0.76-0.05 17:47:36.8 -28:18:31.1 Sgr B
M +0.83-0.10 17:47:57.9 -28:16:48.5 Sgr B
M +0.94-0.36 17:49:13.2 -28:19:13.0 Sgr D
M +2.99-0.06 17:52:47.6 -26:24:25.3 Clump 2

This table also gives the pointing positions and the complexes where the clouds belong. Figure 1 shows the position of the sources overlayed on the large scale \ensuremath {\rm C^{18} \rm O}( $1\rightarrow 0$) map of Dahmen et al. (1997).
  \begin{figure} { \psfig{figure=ms10191f1.eps,width=11cm} } \end{figure} Figure 1: The positions of all the sources of our sample (including the two clouds presented in Rodríguez-Fernández et al. 2000) overlayed in the \ensuremath {\rm C^{18} \rm O}(1-0) map by Dahmen et al. (1997)
Open with DEXTER

The observations were carried out in May 1997, May 1998 and June 2000. The $J=1\rightarrow 0$ and $J=2 \rightarrow 1$ lines were observed simultaneously, with two $512\times 1$ MHz channel filter banks connected to two SIS receivers at 3 and 1.3 mm. The receivers were tuned to single side band mode. The image rejection, checked against standard calibration sources, was always larger than 10 dB. Typical system temperatures were $\sim \,$250 K for the $J=1\rightarrow 0$ lines and $\sim \,$400 K for the $J=2 \rightarrow 1$ lines. The velocity resolution obtained with this configuration was 2.7 and 1.4 kms-1 at 3 and 1.3 mm respectively. The beam size of the telescope was 22'' for the $J=1\rightarrow 0$ lines and 11'' for the $J=2 \rightarrow 1$ line. Pointing and focus were monitored regularly. The pointing corrections were never larger than 3''. The spectra were taken in position switching with a fixed reference position at $(l,b)=(0\hbox{$.\!\!^\circ$ }65,~0\hbox{$.\!\!^\circ$ }2)$, which was selected from the \ensuremath {^{13}{\rm CO}} map of Bally et al. (1987). Calibration of the data was made by observing hot and cold loads with known temperatures, and the line intensities were converted to main beam brightness temperatures, $T_{\rm MB}$, using main beam efficiencies of 0.68 and 0.41 for 3 and 1.3 mm respectively. The main beam efficiencies for the observations of June 2000 are 0.80 and 0.53 for 3 and 1.3 mm respectively.

A sample of spectra is shown in Fig. 2. Most of the sources show CO emission in several velocity components with Gaussian profiles.

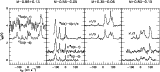  \begin{figure} { \psfig{figure=ms10191f2.eps,width=14cm} } \end{figure} Figure 2: \ensuremath {^{13}{\rm CO}}  and \ensuremath {\rm C^{18} \rm O}  spectra of four sources
Open with DEXTER

However, in some clouds the different components are blended, giving rise to more complex profiles. The observed parameters derived from Gaussian fits are listed in Table 2.
  
Table 2: Observational parameters and LVG results for the CO data: Integrated intensities of the $J=1\rightarrow 0$ transitions of \ensuremath {\rm C^{18} \rm O} and \ensuremath {^{13}{\rm CO}} and \ensuremath {\rm C^{18} \rm O} $J=2 \rightarrow 1$ to $J=1\rightarrow 0$ line intensity ratio. Column densities and $n_{\ensuremath {\rm H_2} }$ derived from the LVG calculations. $N_{\ensuremath {\rm H_2} }$ derived from $N_{\ensuremath {^{13}{\rm CO}} }$ assuming a \ensuremath {^{13}{\rm CO}} abundance relative to \ensuremath {\rm H_2} of 5 10-6. Numbers in parentheses are 1$\sigma $ errors of the last significant digit
\begin{table} \smallskip { \psfig{figure=ms10191f7.eps,width=17cm} } \smallskip... ...} \rm O} }/ I_{(1-0)}^{\ensuremath{\rm C^{18} \rm O} }$ . \end{list}\end{table}

2.2 ISO observations and results

Several \ensuremath {\rm H_2} pure-rotational lines (from S(0) to S(5)) have also been observed towards the molecular clouds given in Table 1. The observations were carried out with the Short Wavelength Spectrometer (SWS; de Graauw et al. 1996) on board ISO. The sizes of the SWS apertures at each wavelength are listed in Table 3. The orientation of the apertures on the sky varies from source to source, but it is within position angle 89.34$^\circ$ and 93.58$^\circ$ for all the observations (measuring the angles anti-clockwise between north and the short sides of the apertures).

   
Table 3: Fluxes of the \ensuremath {\rm H_2} lines as derived from Gaussian fits in units of 10-20 Wcm-2. Upper limits are 3$\sigma $ values at the instrumental spectral resolution for point sources. Numbers in parentheses are 1$\sigma $ errors of the last significant digit as derived from the Gaussian fits. The radial velocities and the widths of the lines with better signal-to-noise ratio (the S(1) lines) are also shown. The errors in the radial velocities are dominated by the wavelength calibration uncertainties (15-30 kms-1  for the S(1) line). Typical 1$\sigma $ error of the line widths derived from the Gaussian fits is less than 5 kms-1
Line S(0) S(1) S(3) S(4) S(5) $v_{\rm S(1)}$ $\Delta v_{\rm S(1)}$
Aper. ( $~{''}\times ~{''}$) $ 20\times 27$ $14\times 27$ $14\times 20$ $14\times 20$ $14\times 20$  kms-1  kms-1
$\lambda (\mu$m) 28.2188 17.03483 9.66491 8.02505 6.9095    
M -0.96+0.13 7.8(9) 18.4(8) 2.2(5) - - -70 270
M -0.55-0.05 9.5(14) 9.7(6) $\leq$0.80 $\leq$0.78 $\leq$2.0 -80 230
M -0.50-0.03 8.2(10) 8.4(4) $\leq$0.64 - - -60 230
M -0.42+0.01 6.2(6) 13.1(7) $\leq$0.70 - - -57 230
M -0.32-0.19 7.8(6) 23.0(6) 2.1(2) 3.5(7) 5.7(8) -59 230
M -0.15-0.07 9.4(13) 9.9(12) $\leq$1.1 $\leq$1.4 $\leq$2.8 -35 220
M +0.16-0.10 6.1(9) 10.5(7) $\leq$0.9 2.7(6) 6.5(10) 40 180
M +0.21-0.12 4.7(9) 13.3(8) $\leq$1.2 2.8(4)$^{\rm a}$ 4.8(11)$^{\rm a}$ 16 260
M +0.24+0.02 9.8(5) 18.9(4) $\leq$0.92 - - -6 170
M +0.35-0.06 5.3(8) 17.2(6) $\leq$1.0 2.0(7) 3.5 (8) 27 200
M +0.48+0.03 6.7(8) 15.9(8) 1.6(3)$^{\rm a}$ 2.4(10)$^{\rm a}$ $\leq$3.4 17 170
M +0.58-0.13 6.0(6) 8.7(7) $\leq$0.96 $\leq$0.97 $\leq$2.1 4 210
M +0.76-0.05 12.4(9) 32.8(8) 2.0(5) - - -18 180
M +0.83-0.10 10.8(9) 27.1(4) 2.2(3) 5.6(10) 6.7(8) 16 170
M +0.94-0.36 5.7(9) 10.6(5) $\leq$1.2 $\leq$1.1 $\leq$2.7 -30 190
M +2.99-0.06 9.2(6) 19.4(8) $\leq$0.79 - - 28 190
$^{\rm a}$ Detections with low signal-to-noise ratio ($\sim \,$2.5).

The observations presented in this paper are the result of two different observing proposals. In one of them only the S(0), S(1) and S(3) lines were observed, in the second one all the lines from the S(0) to the S(5) but the S(2) were observed. The wavelength bands were scanned in the SWS02 mode with a typical on-target time of 100 s. Three sources were also observed in the SWS01 mode but the signal-to-noise ratio of these observations is rather poor and will not be discussed in this paper. Data were processed interactively at the MPE from the Standard Processed Data (SPD) to the Auto Analysis Results (AAR) stage using calibration files of September 1997 and were reprocessed automatically through version 7.0 of the standard Off-Line Processing (OLP) routines to the AAR stage. The two reductions give similar results. In this paper we present the results of the reduction with OLP7.0. The analysis has been made using the ISAP2.0[*] software package. With ISAP we have zapped the bad data points and averaged the two scan directions for each of the 12 detectors. Then, we have shifted (flatfielded) the different detectors to a common level using the medium value as reference and finally, we have averaged the 12 detectors and rebinned to one fifth of the instrumental resolution. No defringing was necessary since the continuum flux at these wavelengths ( $\lambda <30~\mu$m) is lower than 30 Jy for all the clouds.

Baseline (order 1) and Gaussian fitting to the lines have also been carried out with ISAP. The spectra are shown in Fig. 3 and the observed fluxes as derived from the fits are listed in Table 3.

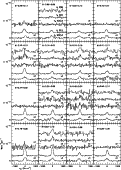  \begin{figure} { \psfig{figure=ms10191f3.eps,width=14cm} } \end{figure} Figure 3: H2 spectra. They have been rebinned to one fifth of the instrumental resolution for point sources
Open with DEXTER

The absolute flux calibration errors are less than 30, 20, 25, 25, and 15% for the S(0), S(1), S(3), S(4), and S(5) lines, respectively (Salama et al. 1997). Because of the medium spectral resolution of the SWS02 mode ( $ \lambda/ \Delta\lambda \sim1000$-2000) and the wavelength calibration uncertainties ($\sim \,$15-50 kms-1 depending on the wavelength, see Valentijn et al. 1996), it is difficult to undertake a detailed comparison between the kinematics of the \ensuremath {\rm H_2} lines and those of the \ensuremath {^{13}{\rm CO}} and \ensuremath {\rm C^{18} \rm O} lines. Table 3 lists the radial velocities of the S(1) lines, which have the higher signal-to-noise ratio. Within the calibration uncertainties, the radial velocity of the \ensuremath {\rm H_2} lines agrees with at least one of the \ensuremath {^{13}{\rm CO}} components listed in Table 2.

Unfortunately, the lack of resolution does not allow us to establish if the \ensuremath {\rm H_2} emission is indeed arising from just one or several of the CO velocity components since, in general, all of them are within the velocity range of the unresolved \ensuremath {\rm H_2} emission. M -0.96+0.13 is the only cloud for which we can say that the warm \ensuremath {\rm H_2} is not likely to arise in all the velocity components seen in CO. The CO components are centered at -110, 11, and 133 kms-1, while the \ensuremath {\rm H_2} S(1) line is centered at -70 kms-1. Even with the spectral resolution of the SWS02 mode, one can see that the CO component with forbidden velocities (133 kms-1) is not likely to contribute to the \ensuremath {\rm H_2} emission.

Table 3 also lists the widths of the \ensuremath {\rm H_2} S(1) lines. The \ensuremath {\rm H_2}  line widths of the GC clouds tend to be larger than the instrumental resolution for extended sources ($\sim \,$170 kms-1 for the S(1) line, see Lutz et al. 2000). This is due to the large intrinsic line widths typical of the GC clouds and mainly, to the presence of several velocity components along the line of sight that contribute to the \ensuremath {\rm H_2} emission. However, not all the sources that show CO emission in several velocity components have line widths larger than $\sim \,$170 kms-1 (for instance M +0.83-0.10 or M +0.16-0.10). This implies that not all the CO velocity components detected in these sources are contributing to the \ensuremath {\rm H_2} emission, although it is difficult to discriminate which ones are emitting in \ensuremath {\rm H_2}.

3 C $^\mathsf{18}$O and ${}^\mathsf{13}$CO column densities

The excitation analysis of the three lowest \ensuremath {\rm C^{18} \rm O} rotational lines by Hüttemeister et al. (1998) shows that the CO emission could arise in cold (20-30 K) and dense (104 cm-3) gas or warmer ( $\stackrel{>}{\scriptstyle \sim}$100 K) and less dense gas (103 cm-3). However, the large column densities of cold ($\sim \,$25 K) dust (Martín-Pintado et al. 1999a; Rodríguez-Fernández et al. 2000) suggest that most of the $J=1\rightarrow 0$ and $J=2 \rightarrow 1$ CO emission should arise from cold and dense gas coupled to the dust.

We have derived physical conditions and gas column densities from the \ensuremath {\rm C^{18} \rm O} and \ensuremath {^{13}{\rm CO}} data using the Large Velocity Gradient (LVG) approximation (see e.g. Hüttemeister et al. 1998). Assuming a kinetic temperature ($T_{\rm K}$) of 20 K, we have constrained the \ensuremath {\rm H_2} densities ( $n_{\ensuremath {\rm H_2} }$) from the $J=2 \rightarrow 1$ to $J=1\rightarrow 0$ \ensuremath {\rm C^{18} \rm O} ratio (or the same ratio of \ensuremath {^{13}{\rm CO}} for a few sources, see Table 2). Then, we have derived the \ensuremath {\rm C^{18} \rm O} and \ensuremath {^{13}{\rm CO}} column densities ( $N_{\ensuremath{\rm C^{18} \rm O} }$ and $N_{\ensuremath {^{13}{\rm CO}} }$) for corresponding $n_{\ensuremath {\rm H_2} }$, using the $J=1\rightarrow 0$ lines intensities. The results of the analysis are listed in Table 2. Typical \ensuremath {\rm C^{18} \rm O} $J=2 \rightarrow 1$ to $J=1\rightarrow 0$ line ratios are $\sim \,$1.0-1.5 which give $n_{\ensuremath {\rm H_2} }$ of $\sim \,$ 103.5-4.0 cm-3 for $T_{\rm K}=20$ K. The typical integrated intensities of the \ensuremath {\rm C^{18} \rm O}( $J=1\rightarrow 0$) lines ($\sim \,$3-9 Kkms-1) imply $N_{\ensuremath{\rm C^{18} \rm O} }$ of $\sim \,$2-8 1015 cm-2. $N_{\ensuremath {^{13}{\rm CO}} }$ is approximately a factor of 10 larger than $N_{\ensuremath{\rm C^{18} \rm O} }$. Since the expected abundance ratio of the two species in the GC is 12.5 (Wilson & Matteucci 1992), the observed ratio indicates that both lines are optically thin. We can also explain the observed CO lines ratios and intensities with higher kinetic temperatures (see above). For instance, for $T_{\rm K}=100$ K one would obtain \ensuremath {\rm H_2} densities which are lower by a factor of $\sim \,$2.5. However, even in the unrealistic case that all the $J=1\rightarrow 0$ and $J=2 \rightarrow 1$ CO arise in warm gas with $T_{\rm K}=100$ K, the column densities do not change more than 10% with respect to those at low temperature. Thus, in general, if one considers a mixture of warm and cool gas the total column densities traced by CO will be similar to those derived with $T_{\rm K}=20$ K.

Table 2 also gives the estimated \ensuremath {\rm H_2} column densities as derived from $N_{\ensuremath {^{13}{\rm CO}} }$ assuming that the abundance of \ensuremath {^{13}{\rm CO}} relative to \ensuremath {\rm H_2} is 5 10-6. This ratio is based on the 13C/12C isotopic ratio in the Galactic center of 1/20 (Wilson & Matteucci 1992) and a CO/ \ensuremath {\rm H_2} ratio of 10-4(see e.g. Hüttemeister et al. 1998 and references therein). The typical \ensuremath {\rm H_2} column densities derived for the main velocity components in all the sources are of a few 1022 cm-2.

4 Warm H $_\mathsf{2}$

Table 3 lists the observed fluxes of the \ensuremath {\rm H_2} lines. The most intense lines are the S(0) ( $J=2 \rightarrow 0$) and S(1) ( $J=3 \rightarrow 1$) lines, with typical fluxes of 0.5-1 10-19 and 1-2 10-19 W cm-2, respectively. Unfortunately, the S(2) line was only observed in the two clouds already discussed in detail by Rodríguez-Fernández et al. (2000). The S(3) line is very weak and it has only been detected in the sources with more intense S(1) emission. Even in some sources which show emission in the S(4) and S(5) lines, the S(3) line has not been detected. This is due to strong dust absorption produced by the solid state band of the silicates at $9.7~\mu$m (Martín-Pintado et al. 1999a).

The pure rotational lines of \ensuremath {\rm H_2}  arise due to electric quadrupole transitions. The quadrupole transition probabilities are small (Turner et al. 1977) and thus the rotational lines remain optically thin. In this case, the column density of the upper level involved in a transition from level i to level j can be obtained from the line fluxes Fij of Table 3 using the following expression:

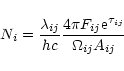
\begin{displaymath}N_i=\displaystyle{\frac{\lambda_{ij}}{hc} \frac{4\pi F_{ij} {\rm e}^{\tau_{ij}}}{\Omega_{ij}A_{ij}}}\end{displaymath}

where $\lambda_{ij}$ and Aij are the wavelength and the quadrupole probability of the transition, and $\tau_{ij}$ and $\Omega_{ij}$ are the dust opacity and the aperture at $\lambda_{ij}$, respectively. Since the column densities are averaged on the ISO apertures, in the case of extended sources (assumed homogeneous), it is not necessary to apply any additional correction to account for the different ISO apertures (see also Rodríguez-Fernández et al. 2000).

4.1 Extinction and ortho-to-para ratio

Figure 4 shows the population diagrams for one of the sources for which more than four lines were detected: M -0.32-0.19.

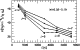  \begin{figure} { \psfig{figure=ms10191f4.eps,width=7cm} } \end{figure} Figure 4: Population diagrams for M -0.32-0.19 without any extinction correction (circles) and corrected for 15 (squares), 30 (triangles), and 45 mag (stars) of visual extinction ( $A_{\rm V}$). We have assumed the relative extinctions derived toward the Galactic center by Lutz (1999). Note that a smooth curve is obtained with $A_{\rm V}\sim 30$ mag
Open with DEXTER

It shows, for each observed line, the logarithm of the upper level population divided by both the rotational and nuclear spin degeneracy, i.e. 3(2J+1) for the ortho levels (odd J) and (2J+1) for the para levels (even J). The filled circles show the populations without any extinction correction. One can see that the population in the J=5 level is lower than expected from the interpolation from the other levels. As discussed in Rodríguez-Fernández et al. (2000), this fact can be used to estimate the total extinction caused by the dust located between the observer and the \ensuremath {\rm H_2} emitting region. Once an extinction law is assumed, we can correct the \ensuremath {\rm H_2} line intensities by increasing the visual extinction until the column density in any level (in particular that in the J=5 level) is consistent with the column densities derived for the other levels, i.e. until the population diagrams are smooth curves.

We have used the extinction law derived by Lutz (1999) towards the Galactic center using hydrogen recombination lines. This extinction law differs from that of Draine (1989) for silicate-graphite mixtures of grains in that there is no deep minimum at $\sim \,$$7~\mu$m and there is a slightly higher value for the $A_{9.7\mu{\rm m}}/A_{\rm V}$ ratio, where $A_{\rm V}$ the visual extinction (at 0.55  $\mu{\rm m}$) and $A_{9.7\mu{\rm m}}$ is the extinction at 9.7  $\mu{\rm m}$. For instance, in the case of M -0.32-0.19 one sees that 15 mag of visual extinction (squares in Fig. 4) is a lower limit to the extinction while 45 mag (stars in Fig. 4) is an upper limit. The best result is obtained for a visual extinction of around 30 mag (triangles). Using this method for the other sources with more than four lines detected, we also derive a visual extinction of $\sim \,$30. This value should be considered as a lower limit to the actual extinction for the sources where the S(3) line was not detected. It is not possible to know how much of this extinction is caused by material in the line-of-sight towards the GC (foreground extinction) and how much is intrinsic to the GC clouds. Nevertheless, a visual extinction of $\sim \,$30 mag is in agreement with the average foreground extinction as measured by Catchpole et al. (1990) using stars counts and suggests that the \ensuremath {\rm H_2} emission can arise from the clouds surfaces (see also Pak et al. 1996). In the other sources where we cannot estimate the extinction from our \ensuremath {\rm H_2} data we have applied a correction of $A_{\rm V}=30$ mag. For those clouds located farther from the center of the Galaxy and/or the Galactic plane, we have corrected the observed fluxes by 15 mag (see Table 4). This value was derived by Rodríguez-Fernández et al. (2000) by analyzing the far infrared dust emission toward two sources in the "Clump 2" and the $l=1.5^{\circ}$ complexes. In any case, the extinction correction has a minor impact in the main results of this paper (see below). Figure 5 shows the extinction corrected population diagrams for all the sources presented in this paper.

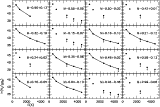  \begin{figure} { \psfig{figure=ms10191f5.eps,width=14cm} } \end{figure} Figure 5: Population diagrams for all the sources corrected for the extinctions listed in Table 4. The filled circles are connected when more than three lines are detected. Arrows indicate upper limits. The error-bars are smaller than the circles (even taking into account both calibration and Gaussian fitting errors)
Open with DEXTER

The values of extinction required to give a smooth population diagram would be somewhat smaller if the \ensuremath {\rm H_2} ortho-to-para (OTP) ratio were lower than the local thermodynamic equilibrium (LTE) ratio. This is obvious since the method to derive the extinction depends mainly on the extinction at the wavelength of an ortho level (J=5). Non-equilibrium OTP ratios measured with the lowest rotational lines has been found in two clouds of our sample (Rodríguez-Fernández et al. 2000). Unfortunately, for the clouds presented in this paper, it is difficult to estimate the OTP ratio since the S(2) line has not been observed and the S(3) line is completely extincted in most of them. Current data do not show any evidence for a non-equilibrium OTP ratio, but we cannot rule it out a priori. For instance, assuming OTP ratios of $\sim \,$2 we still can find a smooth population diagrams, i.e. without the typical zig-zag shape characteristic of non-equilibrium OTP ratios (see e.g. Fuente et al. 1999). In this case, the extinction would be of $\sim \,$20-25 mag instead of 30 mag. On the contrary, assuming OTP ratios of $\sim \,$1 one finds, in general, rather artificial diagrams, which suggests that OTP ratios as low as $\sim \,$1 are not compatible with the data. Although one must bear in mind these considerations, in the following we assume that the OTP ratios are LTE.

4.2 H $_\mathsf{2}$ column densities and excitation temperatures

Table 4 lists the results derived from the \ensuremath {\rm H_2} lines after applying the extinction corrections.

 

 
Table 4: Total \ensuremath {\rm H_2} column densities and rotational temperatures between the J=3 and the J=2 levels (T32) and between the J=7 and the J=6 levels (T76) after correcting for extinction. Numbers in parentheses are $1\sigma $ errors of the last significant digits as derived from the fluxes errors in the Gaussian fits of the lines
Source $A_{\rm V}$ T32 T76 $N_{\ensuremath {\rm H_2} }$(T32)
    K K 1022 cm-2
M -0.96+0.13 15 157(6) - 1.10(9)
M -0.55-0.05 30 135(5) - 2.7(3)
M -0.50-0.03 30 135(4) - 2.3(2)
M -0.42+0.01 30 167(6) - 1.03(8)
M -0.32-0.19 30 188(5) 650(90) 1.03(5)
M -0.15-0.07 30 136(6) - 2.6(4)
M +0.16-0.10 30 157(7) 900(200) 1.17(13)
M +0.21-0.12 30 186(13) 670(110) 0.64(7)
M +0.24+0.02 30 163(2) - 1.73(6)
M +0.35-0.06 30 195(11) 700(200) 0.66(5)
M +0.48+0.03 30 174(7) $\leq$600 1.03(9)
M +0.58-0.13 30 149(5) - 1.3(2)
M +0.76-0.05 30 181(4) - 1.77(8)
M +0.83-0.10 30 178(5) 550(60) 1.59(6)
M +0.94-0.36 15 146(7) - 0.95(10)
M +2.99-0.06 15 152(3) - 1.40(9)


The excitation temperature derived from the J=3 and J=2 levels (T32) is between 130 and 200 K while the excitation temperature derived from the J=7and J=6 levels (T76) is $\sim \,$500-700 K. The temperatures are only 15-20% larger than those one obtains without any extinction correction. For the four clouds in which the S(4) and S(5) lines were undetected, we derive T32 of $\sim \,$135-150 K, clearly lower than the temperature derived for the sources where the S(4) and S(5) lines were detected. There is no clear dependence of T32 on the distance to the Galactic center. However, it is noteworthy that the two clouds with lower T32 are located in the Sgr C complex, one of them in the non-thermal filament.

Obviously, T32 lacks of physical sense if the ortho- \ensuremath {\rm H_2} and para- \ensuremath {\rm H_2} abundances are not in equilibrium. As mentioned, we can obtain smooth population diagrams assuming OTP ratios lower than the LTE ratio. The temperature T32 derived in this case ( $T_{32}^{\rm corr}$) is higher than the one derived directly from the observations (T32). For instance, assuming OTP ratios $\sim \,$2 one obtains a $T_{32}^{\rm corr}$ which is $\sim \,$10% larger than T32.

It is possible to estimate the total warm \ensuremath {\rm H_2} column densities ( $N_{\ensuremath {\rm H_2} }$) by extrapolating the populations in the J=2 level to the J=1 and J=0 levels at the temperature T32. The derived warm $N_{\ensuremath {\rm H_2} }$ are listed in Table 4 and should be considered lower limits to the actual amount of warm molecular gas since the lowest levels can be populated with colder, although still warm, gas. The total column density of warm \ensuremath {\rm H_2} varies from source to source but it is typically of 1-2 1022 cm-2. These column densities are only a factor of 1.2 higher than those one would obtain without any extinction correction. Thus, in regard to the derived gas temperatures and total column densities, the extinction correction is not critical. On the other hand, extrapolating the column densities in the J=6 and J=7 to lower levels at the temperature T76, one finds that the amount of gas at $\sim \,$600 K is less than 1% of the column densities measured at $\sim \,$150 K. The \ensuremath {\rm H_2} total column densities at temperatures $T_{32}^{\rm corr}$assuming an OTP ratio of $\sim \,$2 are lower than those of Table 4 by a factor of 1.8. Note, that in this case the total column density should be derived extrapolating the observed population in the J=3 to the J=1 level and the population in the J=2 to the J=0 levels, as two different species at temperature $T_{32}^{\rm corr}$. Of course, these column densities are still lower limits to the actual warm \ensuremath {\rm H_2} column densities.

These results are the first direct estimation of the \ensuremath {\rm H_2} column densities and the structure of the warm gas in the GC clouds. They show the presence of large column densities of warm molecular gas with large temperature gradients (150-700 K), extending the results derived by Hüttemeister et al. (1993) from their NH3 data.

5 Discussion

5.1 Warm H $_\mathsf{2}$ to CO and NH3 ratios

As mentioned in Sect. 2.2, we cannot identify which velocity components seen in CO are associated to the warm \ensuremath {\rm H_2}. Furthermore, the bulk of the CO seen in the $J=1\rightarrow 0$ and $J=2 \rightarrow 1$ lines do not show the characteristics of warm CO associated to the warm \ensuremath {\rm H_2} (see Sect. 3). In the following, we will estimate the ratio of the warm \ensuremath {\rm H_2} column densities observed with ISO to the \ensuremath {\rm H_2} column densities derived from the CO using LVG calculations. We have added the column densities of each velocity component in every source. These total \ensuremath {\rm H_2} column densities are listed in Table 5.

 

 
Table 5: Total column densities of \ensuremath {\rm H_2} derived from \ensuremath {^{13}{\rm CO}}. Fraction of warm $N_{\ensuremath {\rm H_2} }$ as measured with ISO to the total $N_{\ensuremath {\rm H_2} }$ derived from \ensuremath {^{13}{\rm CO}}. Abundances of NH3 in the warm and cold components (see text)
Source $N_{\ensuremath {\rm H_2} }$$^{\rm CO}$ $N_{\ensuremath {\rm H_2} }$ $^{\rm warm}$/ $N_{\ensuremath {\rm H_2} }$$^{\rm CO}$ X(NH3) $_{\rm warm}$ X(NH3) $_{\rm cold}$
  1022 cm-2      
M -0.96+0.13 0.6-1.1 1 3.7 10-7 4.9 10-6
M -0.55-0.05 4.3-6.0 0.45    
M -0.50-0.03 2.4-3.0 0.77 2.6 10-8 1.6 10-7
M -0.42+0.01 2.1-3.4 0.29 8.3 10-8 2.9 10-8
M -0.32-0.19 1.1-2.2 0.45 1.8 10-8 3.1 10-7
M -0.15-0.07 6.6-8.4 0.31 2.4 10-7 2.7 10-7
M +0.16-0.10 3.7-4.9 0.24    
M +0.21-0.12 0.8-1.5 0.41    
M +0.24+0.02 4.8-7.1 0.24 1.3 10-7 8.9 10-7
M +0.35-0.06 1.7-2.7 0.25    
M +0.48+0.03 3.2-3.6 0.28    
M +0.58-0.13 3.1-3.9 0.33    
M +0.76-0.05 6.6-8.6 0.21    
M +0.83-0.10 4.8-6.5 0.25   3.4 10-8
M +0.94-0.36 1.3-2.9 0.33   6.7 10-7
M +2.99-0.06 1.0-2.1 0.65   9.0 10-7


One can compare the maximum column densities derived from CO to the \ensuremath {\rm H_2} column densities listed in Table 4 to derive a lower limit to the fraction of warm molecular gas with respect to the gas emitting in CO. These ratios are given in Table 5 for all the molecular clouds. We find that the warm \ensuremath {\rm H_2} is about $\sim \,$30% of the \ensuremath {\rm H_2} column densities measured from CO. For a few clouds the fraction of warm gas is as high as 77% (M -0.50-0.03) or even $\sim \,$100% for M -0.96+0.13. This implies that, for two clouds all the CO emission should arise from warm gas.

Table 5 also lists the NH3 abundances in the warm (X(NH3) $_{\rm warm}$) and cold components (X(NH3) $_{\rm cold}$). The X(NH3) $_{\rm warm}$has been derived from the column densities of warm ammonia (Hüttemeister et al. 1993) and our warm \ensuremath {\rm H_2} column densities. We find that, X(NH3) $_{\rm warm}$ is within a range of 3 10-8 to 4 10-7. On the other hand, X(NH3) $_{\rm cold}$ has been derived from the cold ammonia column densities of Hüttemeister et al. and the \ensuremath {\rm H_2} column densities derived from the \ensuremath {^{13}{\rm CO}} data. In this case, we have taken into account only the \ensuremath {^{13}{\rm CO}} velocity components with NH3 emission and we have assumed that, in average, $\sim \,$70% of the gas traced by CO is cold gas. With these assumptions, X(NH3) $_{\rm cold}$ varies between 4 10-8 and 6 10-6, being the average value $\sim \,$5 10-7. This is similar to the abundance in the warm component, and approximately 10 times higher than the "typical" interstellar ammonia abundance (Irvine et al. 1987). The high NH3 abundances in the cold gas point to the existence of a cold post-shocked gas component as suggested by Hüttemeister et al. (1998) to explain the SiO emission in the GC clouds.

5.2 Heating mechanism

What is the heating mechanism that produces such a large amount of warm molecular gas in the GC? Shocks have been invoked to explain the widespread distribution and the large abundances of refractory molecules like SiO (Martín-Pintado et al. 1997; Hüttemeister et al. 1998), the high temperatures observed in NH3 (Wilson et al. 1982; Güsten et al. 1985) and the non-equilibrium \ensuremath {\rm H_2} ortho-to-para ratio of two sources in our sample (Rodríguez-Fernández et al. 2000). The high NH3 abundance derived in the previous section points to a mechanical heating mechanism since the ammonia molecule is easily photo-dissociated by ultraviolet radiation. The small column densities of warm dust in these clouds also points to a mechanical heating mechanism (Martín-Pintado et al. 1999a).

On the other hand, in some of the clouds we have detected line emission from ionized species like Neii, Neiii or Oiii, that should arise in an Hii region ionized by ultraviolet (UV) photons (Martín-Pintado et al. 1999a, 2000). This implies that, at least in those clouds, there must be a PDR in the interface between the Hii region and the molecular material. Large scale emission of the \ensuremath {\rm H_2} v=1-0 S(1) line has also been interpreted as arising from PDRs of density $n \sim10^4$ cm-3 and incident far-UV flux of $G_0 \sim10^3$ (in units of 1.6 10-3 ergscm-2s-1) in the clouds surfaces (Pak et al. 1996). The total visual extinction of $\sim \,$30 mag derived for the clouds of our sample matches the expected foreground extinction and suggest that the pure-rotational \ensuremath {\rm H_2} emission could also arise in the surfaces of the clouds as the ro-vibrational lines.

We have compared the population diagrams obtained for the GC clouds with the same type of diagrams predicted by models of C-shocks, J-Shocks and PDRs. Figure 6a shows the comparison between the predictions of a C-Shock from Draine et al. (1983), a J-Shock from Hollenbach & McKee (1989), and the data for M -0.32-0.19.

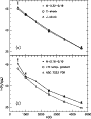  \begin{figure} { \psfig{figure=ms10191f6.eps,width=8cm} } \end{figure} Figure 6: a) Population diagram for M -0.32-0.19 (open squares) corrected for 30 mag of visual extinction. The errorbars represent upper limits to the flux calibration uncertainties (see text). For comparison, it also displays the population diagrams derived from the model of Draine et al. (1983) of a shock with velocity $\sim \,$12 kms-1 and preshock density 106 cm-3 (circles and dashed lines). Triangles and long-dashed lines are used to plot the population diagram derived from the J-shock model of Hollenbach & McKee (1989) for a velocity of 50 kms-1 and a preshock density of 106 cm-3. b) Comparison of the population diagram derived for M +0.16-0.10 (open squares) with the results of Fuente et al. (1999) for the NGC 7023 PDR (triangles and dashed line) and the population diagram one obtains integrating the H2 emission along the temperature and H2 abundance gradient derived by Burton et al. (1990) for a PDR with density of 106 cm-3 and G0=104 (open circles)
Open with DEXTER

The S(1) to S(5) lines (squares) can be explained with both a C-Shock with velocity of $\sim \,$12 kms-1 acting on gas with preshock density of 106 cm-3 (circles) or a J-Shock of 50 kms-1 and preshock density of 106 cm-3 (triangles). However, the observed emission in the S(0) line is $\sim \,$3 times larger than the predicted by both models.

Figure 6b shows the population diagram for M +0.16-0.10 (squares) versus the prototypical reflection nebula NGC 7023 (triangles). As discussed by Fuente et al. (1999), the \ensuremath {\rm H_2} emission from this source is well fitted by the PDR model of Burton et al. (1990, 1992) with G0=104 and n=106 cm-3 although with an OTP ratio of 1.5-2. Comparing the NGC 7023 population diagram with M +0.16-0.10, one finds that the agreement is excellent for the S(4) and S(5) lines but it is not so good for the lowest lines, even taking into account the non-equilibrium OTP ratio found in NGC 7023. In particular, the GC clouds exhibit more emission in the lowest lines than expected from the PDR model for G0=104 and n=106 cm-3. In contrast, the \ensuremath {\rm H_2} v=1-0 S(1) intensity predicted by this PDR model is a factor of $\sim \,$10 larger than observed by Pak et al. (1996). This fact would imply that the vibrational line emission is more diluted in a 3' beam than the pure-rotational lines in the SWS beam or that the PDR models do not apply.

In any case, the observed curvature of the population diagrams seems to be in good agreement with the predicted temperature gradient in a PDR. In Fig. 6b, we also show the population diagram one obtains integrating the \ensuremath {\rm H_2} emission in LTE with the temperature and \ensuremath {\rm H_2} abundance profiles along the G0=104 and n=106 cm-3 PDR model of Burton et al. (1990). The result differs from that of Burton et al. in that we do not take into account any radiative pumping, which affects mainly to higher levels than those involved in the S(0) and S(1) lines. Although the GC emission is $\sim \,$3 times larger, it is evident that the shape of the population diagram is very similar to that observed.

With regard to those sources where the S(4) and S(5) were not detected, the upper limits imply that if they are PDR-excited the density must be somewhat lower than n=106 cm-3, or if shock-excited, the shock velocity should be slightly lower than those of the models ploted in Fig. 6.

Both shock and PDR models suggest densities as high as 106 cm-3 and fail to explain the observed intensity of the S(0) emission and to less extend the S(1) line. The densities implied by the models seem somewhat large, but it looks like the \ensuremath {\rm H_2}  traces two components: a hot ($\sim \,$500 K) and dense ( $\stackrel{<}{\scriptstyle \sim}$106 cm-3) component necessary to explain the observed S(4) and S(5) lines, and a warm component ($\sim \,$150 K) traced by the S(0) and S(1) lines. To match the measured $J=2 \rightarrow 1$/ $J=1\rightarrow 0$ \ensuremath {^{13}{\rm CO}} and \ensuremath {\rm C^{18} \rm O}  ratios the warm \ensuremath {\rm H_2}  component should have densities of $\sim \,$103 cm-3  (see Sect. 3). The hot and dense gas would have $J=2 \rightarrow 1$/ $J=1\rightarrow 0$ \ensuremath {^{13}{\rm CO}} ratios of $\sim \,$4-5 but it would emit mainly in the high-J CO lines. In any case, the column density of hot and dense gas is very small to make it detectable in the low-J CO lines when mixed with the colder and less dense gas that dominates the emission of these lines.

To explain the derived $T_{32}\sim150$ K is necessary to invoke PDRs with $G_0 \sim10^3$ and $n \sim10^3$ cm-3, but to obtain the observed intensities $\sim \,$20 of such PDRs are needed. J-shock models do not predict temperatures as low as 150 K. Moreover, the high velocities required to explain our data are difficult to reconcile with the observations. C-shocks could explain the observed S(0) and S(1) emission with, at least, 10 shocks with velocities as low as $\sim \,$7 kms-1 and n=106 cm-3 (even more shock fronts are needed for lower gas densities). In addition, dissipation of supersonic turbulence could heat the gas to temperatures of $\sim \,$150 K (Wilson et al. 1982; Güsten et al. 1985) and thus, could contribute to the emission in the two lowest \ensuremath {\rm H_2} lines. The origin of the turbulence would be the movement of dense clumps in a less dense interclump medium due to the differential Galactic rotation and the tidal disruption of the clumps.

The heating rate by dissipation of supersonic turbulence can be estimated as

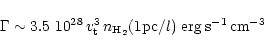
\begin{displaymath}{\Gamma \sim3.5~10^{28}\,v_{\rm t}^3 \,n_{\ensuremath{\rm H_2} } (1 {\rm pc}/ l)~{\rm erg}\,{\rm s}^{-1}\,{\rm cm}^{-3}} \end{displaymath}

(Black 1987), where l and $v_{\rm t}$ are the spatial scale and the velocity of the turbulence, respectively. Taking $v_{\rm t}\sim15$ kms-1 (the typical linewidths of GC clouds), l=5 pc, and $n_{\ensuremath{\rm H_2} }=10^3$ cm-3, one obtains $\Gamma \sim5\,10^{-22}$ ergs-1cm-3. For the conditions of the warm gas, $T\sim150$ K and $n_{\ensuremath{\rm H_2} }\sim10^3$ cm-3, the cooling is expected to be dominated by \ensuremath {\rm H_2}  and CO. Le Bourlot et al. (1999) has recently estimated the cooling rate by \ensuremath {\rm H_2}  ( $\Lambda_{\ensuremath{\rm H_2} }$) for a wide range of parameters. For the warm gas component of the GC clouds we obtain $\Lambda_{\ensuremath{\rm H_2} } \sim3~10^{-22}$ ergs-1cm-3, which is comparable to the CO cooling rate (see e.g. Goldsmith & Langer 1978) Thus, comparing heating and cooling rates, one finds that the dissipation of supersonic turbulence could account for the heating of the warm component.

In summary, several agents could heat the warm component, while the hot component should trace the densest gas in the GC clouds heated by a PDR or a shock. For instance, if the inhomogeneous structure revealed in the Sgr B2 envelope by interferometric NH3 observations (Martín-Pintado et al. 1999b) is common in the GC, and due to evolved massive stars as they propose, both C-shocks of $\sim \,$10 kms-1 (shell expansion) and PDRs (stellar radiation) would be present. However, it is not possible to rule out mechanical heating by large scale shocks. In fact, the high fraction of warm \ensuremath {\rm H_2} derived for M -0.96+0.13 and the fact that the CO component with positive velocities apparently does not contribute to the \ensuremath {\rm H_2} emission suggests this kind of heating since, at this galactic longitude, shocks are expected at negative velocities due to the intersection of x1 and x2 orbits in the context of a barred potential (Binney et al. 1991).

6 Summary and conclusions

We have observed the S(0) to S(5) \ensuremath {\rm H_2} pure-rotational lines with the SWS spectrometer on-board ISO toward a sample of 18 molecular clouds of the Galactic center region. The S(3) line is strongly affected by dust extinction due to the 9.7 $\mu$m band of the silicates. After correcting the \ensuremath {\rm H_2} data for extinction using a self-consistent method, and assuming that the ortho- and para- \ensuremath {\rm H_2} populations are in equilibrium one finds that the S(0) and S(1) lines indicate temperatures of $\sim \,$150 K. Extrapolating to the lowest levels at that temperature, a total \ensuremath {\rm H_2} column density of $\sim \,$1-2 1022 cm-2 is derived. This is the first direct estimate of the column density of warm gas in the GC clouds. In addition, it shows a complex temperature structure of the warm gas.

The temperature derived from the S(5) and S(4) levels is $\sim \,$600 K for the sources in which it can be derived. However the column density of gas at this temperature is less than 1% of the column density at T=150 K. Assuming an OTP ratio of $\sim \,$2 the temperatures would be 10% larger than those derived assuming a LTE OTP ratio, while the total \ensuremath {\rm H_2} column densities at those temperatures would be a factor of $\sim \,$1.8 lower than the column densities derived assuming the ortho- and para- \ensuremath {\rm H_2} populations in equilibrium. Comparing the \ensuremath {\rm H_2} warm column densities with the column densities derived from our CO data by LVG calculations one finds that the average fraction of warm \ensuremath {\rm H_2} to the gas observed in CO is $\sim \,$30%. With our data and the NH3 observations of Hüttemeister et al. (1993) we derive relatively high NH3 abundances of a few 10-7 in both the warm and the cold components.

Several indirect arguments point to shocks as the heating mechanism of the warm gas but PDRs may also play a role. Direct comparison of the \ensuremath {\rm H_2} data with PDRs and shocks models indicate that the S(4) and S(5) trace the densest gas in the GC clouds ( $\stackrel{<}{\scriptstyle \sim}$106 cm-3) heated in PDRs or shocks. Nevertheless, such dense PDRs or shocks fail to explain the S(0) and S(1) lines: several low density PDRs, low velocity shocks (< 10 kms-1) or both, along the line of sight would be needed to explain the observed emission.

The cooling by H2 in the warm component of GC clouds is comparable to the cooling by CO. Equating the \ensuremath {\rm H_2}  cooling rate with the heating rate by dissipation of supersonic turbulence, one finds that this mechanism could also contribute to the emission in the two lowest \ensuremath {\rm H_2}  lines. In one source (M -0.96+0.13), we have also found some evidence of large scale shocks that should be checked with higher spectral resolution \ensuremath {\rm H_2} observations.

Acknowledgements
We thank the referee, Rolf Güsten, for his useful comments. We acknowledge support from the ISO Spectrometer Data Center at MPE, funded by DARA under grant 50 QI 9402 3. NJR-F, JM-P, PdV, and AF have been partially supported by the CYCIT and the PNIE under grants PB96-104, 1FD97-1442 and ESP99-1291-E. NJR-F acknowledges Consejería de Educación y Cultura de la Comunidad de Madrid for a pre-doctoral fellowship.

References

 

© ESO 2001