The Nançay decimentric radio
telescope is a meridian transit-type instrument of the
Kraus/Ohio State
design, consisting of a fixed spherical mirror (300 m long and 35 m high),
a tiltable flat mirror (
![]() m), and a focal carriage moving along a
curved rail track. Due to an ongoing major renovation of the focal system, the
length of the focal track was reduced to
m), and a focal carriage moving along a
curved rail track. Due to an ongoing major renovation of the focal system, the
length of the focal track was reduced to ![]() 60 m during the period
of our observations, thus allowing
tracking of a source on the
celestial equator for about 45 min. The effective collecting
area of the Nançay telescope
is roughly 7000 m2 (equivalent to a 94-m diameter parabolic dish).
Due to the elongated geometry of the mirrors, at 21-cm wavelength the Nançay telescope has a
half-power beam width of
60 m during the period
of our observations, thus allowing
tracking of a source on the
celestial equator for about 45 min. The effective collecting
area of the Nançay telescope
is roughly 7000 m2 (equivalent to a 94-m diameter parabolic dish).
Due to the elongated geometry of the mirrors, at 21-cm wavelength the Nançay telescope has a
half-power beam width of
![]() E-W
E-W![]() 22' N-S for the range of
declinations covered in this work (E. Gérard, private comm.; see also
Matthews & van Driel 2000). Typical system temperatures were
22' N-S for the range of
declinations covered in this work (E. Gérard, private comm.; see also
Matthews & van Driel 2000). Typical system temperatures were ![]() 40 K for
our project.
40 K for
our project.
The observations at Nançay were made in the period June 1998 - October 1999,
using a total of about 300 hours of telescope time.
We obtained our observations in total
power (position-switching) mode using consecutive pairs
of two-minute on- and two-minute
off-source integrations. Off-source integrations were taken at
approximately 20' E of the target position.
The autocorrelator was divided into two pairs
of cross-polarized receiver banks, each with 512 channels and a 6.4 MHz
bandpass. This yielded a channel spacing of 2.64 kms-1, for an effective
velocity resolution of ![]() 3.3 kms-1 at 21-cm. The center
frequencies of the two banks were tuned to the expected redshifted H I
frequency of the target based on values from the literature
(Table 1). Depending on the
signal strength, the spectra were smoothed
to a channel separation of
3.3 kms-1 at 21-cm. The center
frequencies of the two banks were tuned to the expected redshifted H I
frequency of the target based on values from the literature
(Table 1). Depending on the
signal strength, the spectra were smoothed
to a channel separation of ![]() 7.9 or
7.9 or ![]() 13.2 kms-1 during the data reduction in order to increase signal-to-noise.
Total integration times were up to
12 hours per galaxy, depending on the strength of the source and
scheduling constraints.
13.2 kms-1 during the data reduction in order to increase signal-to-noise.
Total integration times were up to
12 hours per galaxy, depending on the strength of the source and
scheduling constraints.
In all cases, data were initially obtained with
the telescope pointed at the published
optical center of the galaxy. However, as shown by van der Hulst et al. (1993),
the H I disks of large LSB spirals may frequently
extend to up to ![]() 2.5
2.5![]() their optical diameter.
We therefore observed several of the targets, including the 8 galaxies
with
their optical diameter.
We therefore observed several of the targets, including the 8 galaxies
with
![]() (i.e. one-third the Nançay FWHP E-W beamwidth) at three
or more spatial positions: one at the target's optical center, plus
additional pointings offset to the east or west by multiples of one-half
beamwidth (see Table 3, discussed below).
Because of
the large N-S diameter of the Nançay beam (
(i.e. one-third the Nançay FWHP E-W beamwidth) at three
or more spatial positions: one at the target's optical center, plus
additional pointings offset to the east or west by multiples of one-half
beamwidth (see Table 3, discussed below).
Because of
the large N-S diameter of the Nançay beam (![]() 22'), these mapping observations were limited to pointings
along an E-W line.
22'), these mapping observations were limited to pointings
along an E-W line.
Flux calibration (i.e.,
![]() -to-mJy conversion)
at Nançay is determined via regular measurements of a cold load
calibrator and periodic monitoring of strong continuum sources by
the Nancay staff. Standard calibration procedures
include correction for declination-dependent gain variations of the telescope (e.g., Fouqué
et al. 1990). These techniques
typically yield an internal calibration accuracy of
-to-mJy conversion)
at Nançay is determined via regular measurements of a cold load
calibrator and periodic monitoring of strong continuum sources by
the Nancay staff. Standard calibration procedures
include correction for declination-dependent gain variations of the telescope (e.g., Fouqué
et al. 1990). These techniques
typically yield an internal calibration accuracy of ![]() 15% at frequencies
near 1420 MHz.
15% at frequencies
near 1420 MHz.
In our present program several of our targets have recessional velocities
![]() 12000 kms-1 and hence were observed at frequencies where
calibration reliability and consistency at Nançay and other radio
telescopes are less well established.
To estimate the comparative accuracy of our flux
density calibration
at these lower frequencies as well as recheck frequency dependent changes in
the noise diode temperature,
we examined continuum calibration data obtained at
1400, 1425, and 1280 MHz,
from several periods over the course of the months during which
our spectral line data were acquired (L. Alsac, private
comm.; see also Thuan et al. 2000). Over this frequency range we found
the noise diode temperature to vary by less than 10%. Our data were
corrected for this effect based on a linear correction curve derived from
the continuum data. These calibration data also
confirm the expected internal calibration accuracy of our data
is
12000 kms-1 and hence were observed at frequencies where
calibration reliability and consistency at Nançay and other radio
telescopes are less well established.
To estimate the comparative accuracy of our flux
density calibration
at these lower frequencies as well as recheck frequency dependent changes in
the noise diode temperature,
we examined continuum calibration data obtained at
1400, 1425, and 1280 MHz,
from several periods over the course of the months during which
our spectral line data were acquired (L. Alsac, private
comm.; see also Thuan et al. 2000). Over this frequency range we found
the noise diode temperature to vary by less than 10%. Our data were
corrected for this effect based on a linear correction curve derived from
the continuum data. These calibration data also
confirm the expected internal calibration accuracy of our data
is ![]() 15% near 1420-1425 MHz, but only
15% near 1420-1425 MHz, but only ![]() 25% near 1280 MHz.
25% near 1280 MHz.
An additional step was required for accurate flux calibration of our Nançay data, as it has been found that changes have occurred in the output power of the calibration diode used at Nançay since the early 1990's (see Fig. 4 of Theureau et al. 1998; see also Thuan et al. 2000), resulting in an overall shift of the absolute calibration scale. This makes it necessary to appropriately renormalize the fluxes determined via the standard calibration techniques described above (e.g., Theureau et al. 1998; Matthews et al. 1998; Thuan et al. 2000).
Matthews et al. (1998) showed via a statistical comparison
of integrated fluxes measured for ![]() 30 galaxies
at Nançay and elsewhere that applying a
scaling factor of 1.26 to the Nançay flux densities very effectively corrects
for the above effect, and restores the correct normalization of the Nançay flux scale. Matthews & van Driel (2000) subsequently found that the
application of this same factor minimized scatter between fluxes determined
for a second sample of galaxies observed at both Nançay and at
Arecibo. Theureau et al. (1998 and priv. comm.) also derived similar
corrections via independent observations of line calibration
sources. As a final calibration step
we therefore apply a renormalization factor of 1.26 to all fluxes
reported in the present work.
30 galaxies
at Nançay and elsewhere that applying a
scaling factor of 1.26 to the Nançay flux densities very effectively corrects
for the above effect, and restores the correct normalization of the Nançay flux scale. Matthews & van Driel (2000) subsequently found that the
application of this same factor minimized scatter between fluxes determined
for a second sample of galaxies observed at both Nançay and at
Arecibo. Theureau et al. (1998 and priv. comm.) also derived similar
corrections via independent observations of line calibration
sources. As a final calibration step
we therefore apply a renormalization factor of 1.26 to all fluxes
reported in the present work.
To construct the global H I profiles for each of the mapped galaxies, we employed the procedure of Matthews et al. (1998). A Gaussian model with appropriate sidelobes for the Nançay beam was assumed (see Guibert 1973). We treated the beam as infinite in the N-S direction, thus reducing the analysis to a one-dimensional problem. With our model beam, the model galaxy flux distributions were then iteratively integrated numerically until the best-fit model that reproduced the observed flux distribution in each of the telescope pointings was found.
In all cases an asymmetric Gaussian H I distribution (i.e., a
lopsided Gaussian with a different ![]() on the E and W sides, but
uniform height) was assumed for the H I distribution of
the galaxy.
Because all of our sample galaxies were
only coarsely resolved by the Nançay beam in the E-W direction,
use of models for the H I distribution more complex than a Gaussian
(e.g., containing central H I depressions,
etc.) was not attempted (see also Fouqué 1984). Moreover, we found
the simple Gaussian models produced a good match to the data in all
but two cases (F568-6 & F533-3; see Sect. 4).
on the E and W sides, but
uniform height) was assumed for the H I distribution of
the galaxy.
Because all of our sample galaxies were
only coarsely resolved by the Nançay beam in the E-W direction,
use of models for the H I distribution more complex than a Gaussian
(e.g., containing central H I depressions,
etc.) was not attempted (see also Fouqué 1984). Moreover, we found
the simple Gaussian models produced a good match to the data in all
but two cases (F568-6 & F533-3; see Sect. 4).
Our reduced Nançay global H I spectra for all of our target
galaxies are shown in Fig. 1. For the
mapped galaxies, the spectra at each individual pointing are
shown in Fig. 2.
Parameters for the final global spectra for all of our targets, including the mapped galaxies, are given in Table 2. The columns in Table 2 are defined as follows:
(1) Galaxy name;
(2) Spectrum rms, in millijanskys;
(3) Peak flux density of the line profile, in millijanskys;
(4) & (5) Raw, measured full width at 20% and 50%
of the maximum profile height, respectively, in kms-1.
No correction has been applied to the raw linewidths for cosmological
stretching, instrumental resolution, or for the
errors arising from describing equal frequency-width channels by a constant velocity
width across the entire bandwidth of the spectrum (but see Table 4).
The latter effect
is inherent in the Nançay software, but is negligible
![]() 1.5 kms-1)
compared with our measurement uncertainties;
1.5 kms-1)
compared with our measurement uncertainties;
(6) Heliocentric radial velocity, in kms-1,
quoted using the optical convention,
![]() ;
;
(8) Raw, integrated H I line flux, in Jykm s-1. No corrections have been applied for beam attenuation;
(9) Uncertainty in the integrated line flux, in Jykm s-1, computed following Fouqué et al. (1990);
(10) Signal-to-noise ratio of the detected line, defined as the ratio of the peak flux density to the spectrum rms;
(11) Comments. For more detailed comments on individual spectra, see Sect. 4.
Table 3 summarizes the raw, integrated line profile fluxes (
![]() )
and velocity
centroids (
)
and velocity
centroids (![]() )
for each pointing in our mapping observations.
In cases where no flux was detected at a
particular pointing, a
)
for each pointing in our mapping observations.
In cases where no flux was detected at a
particular pointing, a ![]() upper limit to the integrated flux
was estimated simply by multiplying the rms
noise of the spectrum by the linewidth at 50% peak maximum from the
previous pointing.
upper limit to the integrated flux
was estimated simply by multiplying the rms
noise of the spectrum by the linewidth at 50% peak maximum from the
previous pointing.
In Table 4 we tabulate several additional parameters for our target
galaxies. Columns in Table 4 are as follows:
(1) Galaxy name;
(2) & (3) W20 and W50 values
corrected for cosmological stretching and
spectral resolution, using the relation
![\begin{displaymath}W_{\rm w,cor}=\left[W_{\rm w,raw} + \delta_{\rm c}\right]/(1+z)
\end{displaymath}](/articles/aa/full/2001/02/aa10104/img54.gif) |
(1) |
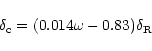 |
(2) |
(4) Radial velocity, in kms-1, corrected to the Local
Standard of Rest, following the prescription of Sandage & Tammann (1981):
| + | |||
| - | (3) |
(5) Galaxy distance in Mpc, computed from
![]() ;
;
(7) Ratio of the
![]() mass to the optical B-band
luminosity LB, in solar units.
LB was derived from the mean of the absolute
B magnitudes for each galaxy given in Table 6 (discussed below) and
assuming a solar absolute magnitude of
mass to the optical B-band
luminosity LB, in solar units.
LB was derived from the mean of the absolute
B magnitudes for each galaxy given in Table 6 (discussed below) and
assuming a solar absolute magnitude of
![]() .
For NGC 7589 a
B-band magnitude was taken from the NED database;
.
For NGC 7589 a
B-band magnitude was taken from the NED database;
(8) Rough estimate of the H I diameter of the source in
arcminutes. Estimates were made only for mapped galaxies where flux
was detected at 2 or more positions (see Table 3).
Following Fouqué (1984), we
define the H I diameter as the isophote enclosing half of the H I mass in a flat H I disk model, which for a Gaussian H I surface density,
is equal to the FWHM of the model (Fouqué 1984). Because of
the elongation of the Nançay beam and the fact that our maps were
obtained along an E-W axis, a correction to the raw H I diameter
for the position angle and
inclination of the source was also applied. Hence,
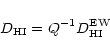 |
(4) |
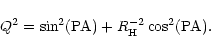 |
(5) |
© ESO 2001