The ESA X-ray Multi Mirror mission, XMM-Newton, carries two identical Reflection Grating Spectrometers (RGS) behind two of its three nested sets of Wolter I type mirrors. The instrument allows high-resolution (
A&A 365, L7-L17 (2001)
J. W. den Herder 1 - A. C. Brinkman 1 - S. M. Kahn 2 - G. Branduardi-Raymont 3 - K. Thomsen 4 - H. Aarts 1 - M. Audard 4 - J. V. Bixler 6 - A. J. den Boggende 1 - J. Cottam 2 - T. Decker 6 - L. Dubbeldam 1 - C. Erd 5 - H. Goulooze 1 - M. Güdel 4 - P. Guttridge 3 - C. J. Hailey 2 - K. Al Janabi 3 - J. S. Kaastra 1 - P. A. J. de Korte 1 - B. J. van Leeuwen 1 - C. Mauche 6 - A. J. McCalden 3 - R. Mewe 1 - A. Naber 1 - F. B. Paerels 2 - J. R. Peterson 2 - A. P. Rasmussen 2 - K. Rees 3 - I. Sakelliou 3 - M. Sako 2 - J. Spodek 2 - M. Stern 2 - T. Tamura 1 - J. Tandy 3 - C. P. de Vries 1 - S. Welch 3 - A. Zehnder 4
Send offprint request: J. W. den Herder
1 - Space Research Organization of The Netherlands,
Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
2 -
Columbia Astrophysics Laboratory, Columbia University, 550 West 120th Street,
New York, NY 10027, USA
3 -
Mullard Space Science Laboratory, University College London, Holmbury St. Mary, Dorking,
Surrey,
RH5 6NT, UK
4 -
Paul Scherrer Institute, 5232 Villigen, Switzerland
5 -
Astrophysics Division, Space Science Department of ESA, ESTeC,
2200 AG Noordwijk, The Netherlands
6 -
Lawrence Livermore National Laboratory, PO Box 808 Livermore, CA 94550, USA
Received 2 October 2000 / Accepted 26 October 2000
Abstract
The ESA X-ray Multi Mirror mission, XMM-Newton, carries two identical Reflection Grating Spectrometers (RGS) behind two of its three nested sets of Wolter I type mirrors.
The instrument allows high-resolution (
![]() to 500) measurements in the soft
X-ray range (6 to 38 Å or 2.1 to 0.3 keV) with a maximum effective area of about 140 cm2at 15 Å. Its design is optimized for the detection of the K-shell transitions of carbon,
nitrogen, oxygen, neon, magnesium, and silicon, as well as
the L shell transitions of iron. The present paper gives a full description of the design of
the RGS and its operational modes. We also review details of the calibrations and in-orbit
performance including the line spread function, the wavelength calibration, the effective
area, and the instrumental background.
to 500) measurements in the soft
X-ray range (6 to 38 Å or 2.1 to 0.3 keV) with a maximum effective area of about 140 cm2at 15 Å. Its design is optimized for the detection of the K-shell transitions of carbon,
nitrogen, oxygen, neon, magnesium, and silicon, as well as
the L shell transitions of iron. The present paper gives a full description of the design of
the RGS and its operational modes. We also review details of the calibrations and in-orbit
performance including the line spread function, the wavelength calibration, the effective
area, and the instrumental background.
Key words: space vehicles: instruments, reflection gratings, XMM-Newton
The 0.2 to 10 keV energy band contains the K-shell transitions of carbon, nitrogen, oxygen, neon, magnesium, silicon, sulphur and calcium, as well as both the L and K shell transitions of iron. Of particular interest, due to their high abundances, are oxygen and iron at temperatures of 106 K and 107-108 K, respectively. Detailed analysis of spectral features from these elements will permit the determination of density, temperature, ionisation state, elemental abundances, mass motions and velocity shifts of the emitting regions and their surrounding environments. The spectral properties of the medium will depend on the excitation process (collisional or photo-ionization and recombination), the state (transient or quiescent) and on whether the plasma is optically thick or thin. With RGS it is possible to measure most of these transitions with the notable exception of those associated with the Fe K-shell. Amongst others, observations with RGS will give new information about the heating of stellar coronae, the propagation of supernova remnant shocks through the interstellar medium, the conditions in the circumsource environments of X-ray binaries and active galactic nuclei, and the hot intracluster medium of clusters of galaxies.
There are two identical RGSs behind two of the three mirror assemblies. The RGS design is illustrated in Fig. 1. Each incorporates an array of reflection gratings
placed in the converging beam of the XMM-Newton telescope. This telescope, of type Wolter I, has a
focal length of 7500 mm and includes 58 nested shells (Jansen et al.2001).
The grating stack consists of 182 precisely aligned reflection gratings and intercepts about half
of the light emanating from the telescope. The undeflected light passes through and is
intercepted by EPIC in the telescope focal plane.
The gratings are actually located on a
toroidal Rowland surface, formed by rotating the Rowland circle about
an axis passing through the telescope and spectroscopic foci, as
illustrated in the left panel of Fig. 1. The gratings are slightly
trapezoidal, since their edges lie along rays converging on the
telescope focus. The field of view in the cross dispersion direction is determined by the width
of the CCDs (
![]() ),
and the spatial resolution in this direction is largely determined by
the imaging properties of the mirror.
In the dispersion direction this
is more complex: the extent
of the source affects the wavelength resolution.
Nine large format back-illuminated CCDs are located on the Rowland circle to detect the
dispersed spectra in single photon counting mode.
The position of the X-ray on the
detector gives the wavelength through the dispersion equation:
),
and the spatial resolution in this direction is largely determined by
the imaging properties of the mirror.
In the dispersion direction this
is more complex: the extent
of the source affects the wavelength resolution.
Nine large format back-illuminated CCDs are located on the Rowland circle to detect the
dispersed spectra in single photon counting mode.
The position of the X-ray on the
detector gives the wavelength through the dispersion equation:
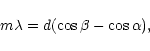 |
(1) |
![\begin{figure}
\includegraphics[angle=0,width=8cm,clip]{XMM19_f1.eps} %
\end{figure}](/articles/aa/full/2001/01/aaxmm19/Timg6.gif) |
Figure 1: Optical design of the RGS (not to scale). X-rays, indicated by red arrows, enter from the top. Numerical values for a few key dimensions and angles are indicated (linear dimensions in mm, angles in degrees) |
| Open with DEXTER | |
| par | value | comment |
|
|
15 Å | first order blaze wavelength |
| 0.6989 |
blaze angle of facets | |
| 2.2751 |
graze angle on facets | |
| 1.5762 |
angle of incidence | |
|
|
2.9739 |
diffraction angle for
|
| 1/d | 645.6 lines/mm | Central groove density |
| CCDs | 9 | back illuminated,
|
| pixels |
|
pixel size; standard |
| CCD size |
|
image area, identical storage area |
| T | -80 -
|
nominally
|
The Reflection Grating Array (RGA) contains 182 identical gratings
(one of the two RGAs contains 181 gratings due to a
fabrication problem encountered during installation).
The gratings are
mounted at grazing incidence in the in-plane, or classical
diffracted X-rays lie in a plane that is perpendicular to the grating
grooves. Because the beam is
converging, the gratings are oriented so that the angle of the
incident X-ray at
the center of the grating, ![]() ,
is the same for all gratings in
the array. In addition, the
gratings all lie on the Rowland circle, which also contains the
telescope focus and the spectroscopic focus for the blaze wavelength.
In this configuration, aberrations, which would otherwise be
introduced by the arraying, are eliminated (Kahn 1990)
(see right side of Fig. 1). The telescope aperture is
filled by rotating the Rowland circle about an axis passing through
the telescope and spectroscopic blaze foci. In all, each RGA contains
six rows of gratings.
,
is the same for all gratings in
the array. In addition, the
gratings all lie on the Rowland circle, which also contains the
telescope focus and the spectroscopic focus for the blaze wavelength.
In this configuration, aberrations, which would otherwise be
introduced by the arraying, are eliminated (Kahn 1990)
(see right side of Fig. 1). The telescope aperture is
filled by rotating the Rowland circle about an axis passing through
the telescope and spectroscopic blaze foci. In all, each RGA contains
six rows of gratings.
![\begin{figure}
\includegraphics[angle=0,width=8cm,clip]{XMM19_f2.eps} %
\end{figure}](/articles/aa/full/2001/01/aaxmm19/Timg20.gif) |
Figure 2: Schematic drawing of a grating, including some of the key dimensions and angles |
| Open with DEXTER | |
Each grating measures about 10 by 20 cm (see Fig. 2).
These large gratings need to be very flat in the long (i.e.
dispersion) direction,
since any non-flatness translates directly into a degradation
of the resolution. At the same time the
grating substrates need to be very thin in order to minimize the
obstruction of the direct beam by the
gratings.
The grating substrates consist of 1 mm SiC face sheets with five
stiffening ribs at the back, running in the direction of the X-ray
beam.
The face sheets are fabricated
to 1 ![]() (634.8 nm) and 10
(634.8 nm) and 10 ![]() flatness in the long
and the short direction, respectively.
The gratings are replicated from a mechanically ruled master
and are covered with a 2000 Å gold coating.
The groove density varies slightly (
flatness in the long
and the short direction, respectively.
The gratings are replicated from a mechanically ruled master
and are covered with a 2000 Å gold coating.
The groove density varies slightly (![]() %) over the length
of the gratings, to correct for aberrations
associated with the converging beam (Hettrick & Bowyer 1983;
Kahn 1990).
The groove density is
%) over the length
of the gratings, to correct for aberrations
associated with the converging beam (Hettrick & Bowyer 1983;
Kahn 1990).
The groove density is ![]() 646 grooves/mm at the center.
646 grooves/mm at the center.
The grating array support structure was machined out of a monolithic
billet of vacuum hot-pressed
beryllium. Beryllium was selected for the grating support structure
for its low specific mass and
good stability over the operational temperature range
(10-30 ![]() C). This structure is mounted with
three flexible kinematic mounts to the mirror support structure
(Wilke et al. 1995).
C). This structure is mounted with
three flexible kinematic mounts to the mirror support structure
(Wilke et al. 1995).
To obtain the desired resolution,
it is essential that all gratings are properly aligned
(with 1 ![]() m tolerance on the position of any grating corner).
This high precision alignment is achieved by positioning the
individual gratings against four, coplanar
bosses, which are precision machined into stainless steel rails.
Half of the rails
have been positioned using a high precision measurement device.
The remaining half (those at the top)
are rough-positioned, and then precision aligned interferometrically
using the inserted gratings themselves as a
reference. For a more detailed description of the RGAs see Kahn et al. (1996).
m tolerance on the position of any grating corner).
This high precision alignment is achieved by positioning the
individual gratings against four, coplanar
bosses, which are precision machined into stainless steel rails.
Half of the rails
have been positioned using a high precision measurement device.
The remaining half (those at the top)
are rough-positioned, and then precision aligned interferometrically
using the inserted gratings themselves as a
reference. For a more detailed description of the RGAs see Kahn et al. (1996).
The spectrum is integrated on nine large format back illuminated CCDs. These nine
CCDs are mounted in a row, following the curvature of
the Rowland circle (see top two panels of
Fig. 3). To reduce the dark current the CCDs are cooled to
![]() C.
The increase in CCD charge transfer inefficiency (CTI)
due to radiation damage can be reduced by
lowering the temperature to
C.
The increase in CCD charge transfer inefficiency (CTI)
due to radiation damage can be reduced by
lowering the temperature to
![]() C.
Cooling is accomplished by a two-stage radiator,
facing deep space, and by three nested thermal shells around the CCD bench (see Thomsen
1991).
The first shield also contains four internal calibration sources.
These consist of the
C.
Cooling is accomplished by a two-stage radiator,
facing deep space, and by three nested thermal shells around the CCD bench (see Thomsen
1991).
The first shield also contains four internal calibration sources.
These consist of the ![]() emitter
244Cm, and an Al target or a Teflon target, which
produces Al K
emitter
244Cm, and an Al target or a Teflon target, which
produces Al K![]() (1487 eV) and F K
(1487 eV) and F K![]() (676.8 eV) fluorescent emission.
These sources each
illuminate a small area of two CCDs, which is offset in the cross dispersion direction from the
source image.
In addition,
the energies of the internal calibration sources are selected to be different from the energies (both orders) of the dispersed astrophysical spectra at
the same position.
At launch, the camera was protected by a door,
which was opened in orbit (it can not be closed).
(676.8 eV) fluorescent emission.
These sources each
illuminate a small area of two CCDs, which is offset in the cross dispersion direction from the
source image.
In addition,
the energies of the internal calibration sources are selected to be different from the energies (both orders) of the dispersed astrophysical spectra at
the same position.
At launch, the camera was protected by a door,
which was opened in orbit (it can not be closed).
![\begin{figure}
\resizebox{\hsize}{!}{\includegraphics[angle=0,clip, bb=75 95 570 650]{XMM19_f3.eps}}\end{figure}](/articles/aa/full/2001/01/aaxmm19/Timg24.gif) |
Figure 3: CCD bench (top two panels) as well an enlarged view of two CCDs (bottom panel). The figure is not to scale |
| Open with DEXTER | |
The nine CCD chips are back-illuminated GEC/EEV devices with an image and storage section of 384 by 1024
pixels each and a pixel size of 27 ![]() 27
27 ![]() m2. The width of the detector is matched to the size of the RGS
spectrum in the cross dispersion direction. The length of the
CCD assembly
(253 mm) covers the first order 6-38 Å wavelength range.
The inter-chip gap between two adjacent CCDs is about 0.5 mm.
For optimum scientific performance, the detector is operated in
frame transfer mode; the image is first accumulated in one half of
the CCD (the image section) and then quickly (20 msec) transferred to the other half (storage section),
where it
is read out through two low noise serial output registers.
This doubles the read out speed and gives redundancy in case of an
amplifier failure. The width of the line spread function
(typically in the order of 250
m2. The width of the detector is matched to the size of the RGS
spectrum in the cross dispersion direction. The length of the
CCD assembly
(253 mm) covers the first order 6-38 Å wavelength range.
The inter-chip gap between two adjacent CCDs is about 0.5 mm.
For optimum scientific performance, the detector is operated in
frame transfer mode; the image is first accumulated in one half of
the CCD (the image section) and then quickly (20 msec) transferred to the other half (storage section),
where it
is read out through two low noise serial output registers.
This doubles the read out speed and gives redundancy in case of an
amplifier failure. The width of the line spread function
(typically in the order of 250 ![]() m) allows for 3
m) allows for 3 ![]() 3
on-chip binning (OCB)
of the pixels. This results in a reduction of the
read-out time and the read-out noise (as most X-rays will be confined to two
3
on-chip binning (OCB)
of the pixels. This results in a reduction of the
read-out time and the read-out noise (as most X-rays will be confined to two
![]() bins). The storage section is shielded from direct illumination by the housing. A thin Al light shield is put on top of each CCD to reduce the sensitivity to optical light. This light shield is isolated from the Si by a
bins). The storage section is shielded from direct illumination by the housing. A thin Al light shield is put on top of each CCD to reduce the sensitivity to optical light. This light shield is isolated from the Si by a
![]() isolation layer (about 26 nm thick).
The Al shield is 75 nm thick for the two CCDs closest to the optical axis (short wavelength end of the bandpass),
68 nm for the next three CCDs,
and 45 nm for the four CCDs furthest away from the optical axis. This gives a reduction
in stray light between 105 and 102, equivalent to 1 e- per
pixel per readout (compared with the electronic noise of 5 e-). The
CCDs, operated in a just depleted mode, have an energy resolution
of
isolation layer (about 26 nm thick).
The Al shield is 75 nm thick for the two CCDs closest to the optical axis (short wavelength end of the bandpass),
68 nm for the next three CCDs,
and 45 nm for the four CCDs furthest away from the optical axis. This gives a reduction
in stray light between 105 and 102, equivalent to 1 e- per
pixel per readout (compared with the electronic noise of 5 e-). The
CCDs, operated in a just depleted mode, have an energy resolution
of ![]() 160 eV (FWHM) at 2 keV. This is sufficient for an efficient
separation of the spectral orders.
160 eV (FWHM) at 2 keV. This is sufficient for an efficient
separation of the spectral orders.
![\begin{figure}
\includegraphics[angle=0,width=8.4cm,clip]{XMM19_f4.eps} %
\end{figure}](/articles/aa/full/2001/01/aaxmm19/Timg27.gif) |
Figure 4: Block diagram of RGS electronics. Cold redundancy is indicated by yellow and dashed lines, the signal chain (which is warm redundant) by red lines |
| Open with DEXTER | |
The electronic block diagram of the focal plane camera and its control electronics is shown in Fig. 4. It consists of the focal plane camera proper (RFC), a unit containing the analog electronics (RAE) and two units (one redundant) with the digital electronics (RDE). The instrument is under control of the Instrument Controller (IC) which is fully programmable. The IC sets all bias settings of the CCDs and also configures the Clock Sequence Generator (CSG) which controls the clock drivers for each CCD. Different clock patterns can be loaded from the ground. The nominal readout of each CCD is through two output nodes resulting in different gains and offsets per read-out node of each CCD. The signals are amplified close to the focal plane camera and digitized in the RAE using a correlated double sampler (CDS). All data are then transferred to the Data Pre-Processor. The temperature of the CCD bench is controlled by the RDE and this unit includes also the power converter (Power Supply Unit). All interfaces with the spacecraft On Board Data Handling bus (OBDH) are channeled via the IC. During periods when RGS is switched off (immediately following launch and during eclipses) the spacecraft provides a fixed power level to the CCD bench to avoid too much cooling.
The control chain is fully cold redundant (hence two RDEs) whereas the signal chain is warm redundant. In case of a failure in one of the two signal chains it is possible to read out the CCDs through one output node. In case of the failure of a single CCD the others will not be affected and the second camera will provide the required redundancy (although the effective area will then be reduced).
Three operating modes are available within the RGS: SPECTROSCOPY, HIGH TIME RESOLUTION and DIAGNOSTIC. The most commonly used mode is
SPECTROSCOPY: the nine CCDs are read out sequentially in frame
transfer mode (with 3 ![]() 3 on chip binning) resulting in an accumulation time of about 5.7 s.
After applying a low signal threshold, hot columns and hot pixels are rejected (defined by a lookup table). The remaining pixels
are treated in a programmable processor (DPP). Pixels exceeding an
upper signal threshold
and pixels with too
complex structures are rejected (these are due to cosmic rays), and
only events which fit in a 2
3 on chip binning) resulting in an accumulation time of about 5.7 s.
After applying a low signal threshold, hot columns and hot pixels are rejected (defined by a lookup table). The remaining pixels
are treated in a programmable processor (DPP). Pixels exceeding an
upper signal threshold
and pixels with too
complex structures are rejected (these are due to cosmic rays), and
only events which fit in a 2 ![]() 2
pattern are transferred to the ground (including information on their
shape).
The HIGH TIME RESOLUTION mode affords the shortest
accumulation time (about 15 msec) if only one CCD is read out. This is
obtained by summing the image in the
cross dispersion direction over 74 pixels,
thus eliminating the possibility to use data cuts in
the cross dispersion direction to reduce the background.
More than one CCD can be used to collect data, but this
increases the accumulation time accordingly. In the DIAGNOSTIC mode
the on-board data processing is bypassed
completely, and the full images are stored on board and transferred
to the ground. These data are used for
dark current and system noise level verification. Using the same
mechanism as in the DIAGNOSTIC mode, full
images
can be transferred to the ground in SPECTROSCOPY mode as well,
but at a low repetition rate.
2
pattern are transferred to the ground (including information on their
shape).
The HIGH TIME RESOLUTION mode affords the shortest
accumulation time (about 15 msec) if only one CCD is read out. This is
obtained by summing the image in the
cross dispersion direction over 74 pixels,
thus eliminating the possibility to use data cuts in
the cross dispersion direction to reduce the background.
More than one CCD can be used to collect data, but this
increases the accumulation time accordingly. In the DIAGNOSTIC mode
the on-board data processing is bypassed
completely, and the full images are stored on board and transferred
to the ground. These data are used for
dark current and system noise level verification. Using the same
mechanism as in the DIAGNOSTIC mode, full
images
can be transferred to the ground in SPECTROSCOPY mode as well,
but at a low repetition rate.
The ground calibrations concentrated on the grating and CCD performance. These measurements were performed in three stages: first the individual gratings and CCDs were characterized; next we performed measurements after assembly of the reflection grating array and focal plane camera. Finally, end-to-end tests were performed with these units in combination with the mirrors. Prior to launch, the two RGS instrument chains went through their environmental tests (vibration, acoustic and thermal).
| parameter | value | comment |
| typical event size | 1.3 to 1.7 | pixels in 1 |
| partial event fraction | P-K |
|
|
|
0.02 to 0.08 |
|
| hot columns RFC1 | 5 | at
|
| hot columns RFC2 | 1 | at
|
| QE | for E=0.35-2 keV, see Fig. 5 | |
| CTI
|
< 10-5 | at
|
| CTI
|
at
|
|
| Si thickness | variation over CCD | |
| read-out noise | 5 to 6 e- |
To select the flight devices from the larger set of available
CCDs several diagnostic tests were performed. CCDs were singly
installed in a dedicated camera which was connected to both a
fluorescent X-ray source and a UV source.
Most measurements were performed at
![]() C. Where
relevant,
measurements were also
performed at other temperatures (between
C. Where
relevant,
measurements were also
performed at other temperatures (between
![]() C and
C and
![]() C).
C).
![\begin{figure}
\includegraphics[width=8cm,clip]{XMM19_f5r.eps}\end{figure}](/articles/aa/full/2001/01/aaxmm19/Timg35.gif) |
Figure 5: Calculated and measured quantum efficiency for three typical devices |
| Open with DEXTER | |
Typical values for the CCDs are given in Table 2 where we
also indicate whether a parameter
is temperature dependent. Although the read-out noise is low, there is some fixed
pattern noise induced by the electronics. This becomes visible if the low signal threshold is close
to the offset, but the effect on the CCD energy resolution is negligible.
To optimize the energy response of the CCDs they
are operated such that the silicon is
just depleted (the electrical field extends to the back side to reduce the
diffusion of the charge over more pixels and thus minimizing the read-out noise for an X-ray which is spread over more pixels). Charge collection and readout is controlled by
14 bias voltages per CCD, and these are optimized
to minimize the number of multiple pixel events.
For 1 ![]() 1 OCB this results in a typical event size of 1.5 pixels depending
on the energy.
Partial events are X-ray events that
are absorbed close to the surface and therefore lose
part of their charge in this surface layer, despite its passivation (van den Berg et al.1996).
This fraction, derived from the measured intensity between
20% and 40% of the energy of the absorbed X-rays, has been measured as function of
position on the device and only devices with a sufficiently
uniform backside and low partial event
fraction have been selected. The Charge Transfer Inefficiency (CTI) is a measure for the charge loss when the pixel content is transfered from one pixel to the next and is caused by traps in the silicon. The CTI is in general very low (see Table 2) except near
the edges of the CCDs where, possibly due to mechanical stress during production (dicing),
the parallel CTI increases to
1 OCB this results in a typical event size of 1.5 pixels depending
on the energy.
Partial events are X-ray events that
are absorbed close to the surface and therefore lose
part of their charge in this surface layer, despite its passivation (van den Berg et al.1996).
This fraction, derived from the measured intensity between
20% and 40% of the energy of the absorbed X-rays, has been measured as function of
position on the device and only devices with a sufficiently
uniform backside and low partial event
fraction have been selected. The Charge Transfer Inefficiency (CTI) is a measure for the charge loss when the pixel content is transfered from one pixel to the next and is caused by traps in the silicon. The CTI is in general very low (see Table 2) except near
the edges of the CCDs where, possibly due to mechanical stress during production (dicing),
the parallel CTI increases to ![]() 10-3.
In Fig. 5 the modeled and measured quantum efficiency of two typical devices are
shown. The data were collected during a long beam test at MPE with a beam that
was normalized
using an accurately calibrated Si drift chamber. Edges due to Si,
Al, Mg, and F are clearly visible. Additional measurements were performed at
the Bessy synchrotron facility, in order
to map the X-ray Absorption Fine Structure (variations up to a few %,
see Bootsma et al. 2000).
10-3.
In Fig. 5 the modeled and measured quantum efficiency of two typical devices are
shown. The data were collected during a long beam test at MPE with a beam that
was normalized
using an accurately calibrated Si drift chamber. Edges due to Si,
Al, Mg, and F are clearly visible. Additional measurements were performed at
the Bessy synchrotron facility, in order
to map the X-ray Absorption Fine Structure (variations up to a few %,
see Bootsma et al. 2000).
After the flight CCD's were selected, a number of additional measurements were performed on a few devices. The long term stability of the devices was verified with repeated UV and X-ray measurements over a period of four months on a single device that was kept continuously cooled and under vacuum. No degradation of the performance was observed. Using the long-term X-ray measurements the uniformity of the Al filter was verified. The X-ray transmission of the filter was found to be uniform within the accuracy of the measurement (1% per pixel). One CCD has also undergone repeated thermal cycles to verify the stability and integrity of the Al filter.
Two devices were exposed to a proton spectrum representative of
the exposure during a 10 year mission (consistent with 109 10 MeV equivalent protons) under a 25 mm thick aluminum
flight-representative housing. The parallel CTI degraded to
![]() 10-3 at
10-3 at
![]() C as expected. It was later verified that
lowering the temperature to
C as expected. It was later verified that
lowering the temperature to
![]() C reduces the effect of this
degradation. Following the launch of Chandra the sensitivity of the
RGS devices to soft protons was studied as this mission experienced a significant
degradation of the CCD response in its early phase due to soft protons reflected off the mirrors. For the
C reduces the effect of this
degradation. Following the launch of Chandra the sensitivity of the
RGS devices to soft protons was studied as this mission experienced a significant
degradation of the CCD response in its early phase due to soft protons reflected off the mirrors. For the
![]() thick back illuminated devices, protons with energies of
1.4 to 1.5 MeV cause maximum damage in the CCD channels.
Additional tests were performed at these energies. It was found that the
CTI degrades to
2 10-3 for a
107 dose of 1.4 to 1.5 MeV protons.
Fortunately,
the in orbit spectrum of protons is steep. Furthermore, protons ``focused'' by the mirrors,
must be reflected off the gratings before they hit the
CCDs, which decreases the flux incident on the cameras further. Based on these
results the risk to the CCDs in the RGS configuration was
considered minimal.
thick back illuminated devices, protons with energies of
1.4 to 1.5 MeV cause maximum damage in the CCD channels.
Additional tests were performed at these energies. It was found that the
CTI degrades to
2 10-3 for a
107 dose of 1.4 to 1.5 MeV protons.
Fortunately,
the in orbit spectrum of protons is steep. Furthermore, protons ``focused'' by the mirrors,
must be reflected off the gratings before they hit the
CCDs, which decreases the flux incident on the cameras further. Based on these
results the risk to the CCDs in the RGS configuration was
considered minimal.
The CCD response has been modeled based on the measurements from
the end-to-end ground calibration tests, where the gratings provided
almost monochromatic illumination.
The model is based on a set of physical parameterizations of the
absorption and charge collection processes. The absorption
probability is calculated in the standard way by using the
Henke atomic constants (Henke et al.
1993). The charge collection efficiency is modeled as
an exponential function of the depth into the device.
We add a noise
component, which includes Fano-noise and electronic readout noise.
Convolving these three components analytically yields a model with
only two adjustable parameters: the electronic noise and the
effective charge collection depth, ![]() .
By using the ratio of
.
By using the ratio of
![]() over the mean absorption length these can be reduced to a
single energy independent parameter. Assuming a heuristic Fano factor of 0.14, the
electronic noise was found to be 5 to 6 electrons
(using
over the mean absorption length these can be reduced to a
single energy independent parameter. Assuming a heuristic Fano factor of 0.14, the
electronic noise was found to be 5 to 6 electrons
(using ![]() OCB), which is consistent with our measurements.
The pulse height distribution of this model is
compared to data in Fig. 6.
The energy resolution of the CCD's is used to separate the orders
of the dispersed spectra. Order selection filters are based on the
modelled CCD reponse, and the accuracy of this model affects the
estimate of the integral of the selected distribution.
This in turn is used for the calculation of the effective area.
The effect of inaccuracies in this model on
the effective area is estimated to be of the order of 2% for filters
that include
OCB), which is consistent with our measurements.
The pulse height distribution of this model is
compared to data in Fig. 6.
The energy resolution of the CCD's is used to separate the orders
of the dispersed spectra. Order selection filters are based on the
modelled CCD reponse, and the accuracy of this model affects the
estimate of the integral of the selected distribution.
This in turn is used for the calculation of the effective area.
The effect of inaccuracies in this model on
the effective area is estimated to be of the order of 2% for filters
that include ![]() of the distribution.
of the distribution.
![\begin{figure}
\includegraphics[width=8cm,clip]{XMM19_f6r.eps}\end{figure}](/articles/aa/full/2001/01/aaxmm19/Timg40.gif) |
Figure 6:
Composite pulse height spectrum for O-K |
| Open with DEXTER | |
The grating replicas were selected based on quantitative measurements of several properties. The following measurements, performed for every grating, were obtained at a dedicated facility at Columbia University Nevis Laboratories (Craig et al. 1988). The results were used to reject and remanufacture parts, and to ultimately define two nearly identical sets that were used to complete the two grating arrays (Rasmussen et al.1998).
![\begin{figure}
\includegraphics[width=8.3cm,clip]{XMM19_f7r.eps}\end{figure}](/articles/aa/full/2001/01/aaxmm19/Timg42.gif) |
Figure 7: Efficiencies for first and second order as measured (solid curve) and as modeled (dashed curve) |
| Open with DEXTER | |
In addition to the measurement list above, the following measurements were performed on a subset of gratings that helped constrain physical modelling of the RGS; in particular the grating reflectivity. These measurements were performed randomly on one grating in every six, unless otherwise noted:
A model of the diffraction efficiency was constructed using the full
vector solution to Maxwell's equations subject to the boundary
conditions
of the grating profile. A scalar theory modification was
implemented to
account for coherent and incoherent modulations on the surface of the
grating (Cottam et al. 2001).
The parameters of the model
were determined by iteratively fitting simultaneously
calibration data from the long-beam and BESSY facilities.
An incoherent
noise component that scatters
light to large angles and out of the standard measurement apertures
was characterized by fitting inter-order scans taken at the Nevis long-beam
facility. The measured efficiency is predicted
by integrating the normalized line profile with both small and large
angle
scattering components over the angular range subtended by the
measurement
aperture. The model is consistent with the measurements to
![]() 5%
for all incident angles, spectral orders, and wavelengths above
5%
for all incident angles, spectral orders, and wavelengths above
![]() .
This is illustrated in Fig. 7, where the results of
the reflectivity measurement for one grating at
Bessy is shown.
.
This is illustrated in Fig. 7, where the results of
the reflectivity measurement for one grating at
Bessy is shown.
![\begin{figure}
\resizebox{\hsize}{!}{\includegraphics[angle=0, clip, bb= 117 428 490 703]{XMM19_f8r.eps}}\end{figure}](/articles/aa/full/2001/01/aaxmm19/Timg45.gif) |
Figure 8: Measured and modelled effective area for RGS1 (corrected for finite source distance) |
| Open with DEXTER | |
The X-ray performance was verified at the MPE long beam ``Panter'' facility (Aschenbach et al. 1979). Due to the finite source distance (120 m) at this facility, the spectrometer does not focus properly if the optical elements and detectors are positioned in the flight configuration. In particular, the focus of the telescope moves outward 500 mm relative to the nominal focus. To maintain the Rowland circle, the RGA must be moved by the same amount. Owing to the finite width of the X-ray lines generated with an electron impact target source, the resolution properties could not be verified directly for the longer wavelength portion of the RGS band. However, using higher order spectra of short wavelength lines, it was still possible to investigate all of the various contributions to the line spread function (Rasmussen et al. 1998). These measurements indicated that the two RGAs have slightly different focussing properties. This explains the different expectations for the resolution as is given in Fig. 11.
The effective area was calibrated at the Panter facility
at 6 energies, on axis. The off-axis response was calibrated at one energy (Al-K![]() ).
Given the finite source distance, the telescope and RGA are under-illuminated, and the
measured effective area had to be corrected for this effect using a detailed raytrace model
of this configuration.
These corrections were verified using segmented illumination of
the mirrors (16 azimuthal sectors
).
Given the finite source distance, the telescope and RGA are under-illuminated, and the
measured effective area had to be corrected for this effect using a detailed raytrace model
of this configuration.
These corrections were verified using segmented illumination of
the mirrors (16 azimuthal sectors ![]() 4 radial selections). The results of the
end-to-end effective area calibration agreed with model calculations to within 5% for both the first and
second spectral orders. This is illustrated in Fig. 8.
4 radial selections). The results of the
end-to-end effective area calibration agreed with model calculations to within 5% for both the first and
second spectral orders. This is illustrated in Fig. 8.
![\begin{figure*}
\includegraphics[angle=-90,width=16cm,clip]{XMM19_f9.eps}\end{figure*}](/articles/aa/full/2001/01/aaxmm19/Timg46.gif) |
Figure 9: Capella observation (id: 0121500201001). The color scale represents a logarithmic intensity scale. The dispersion axis runs horizontally and increases to the right. In the top panel the cross dispersion is along the vertical axis whereas in the bottom panel this is replaced by the CCD energy. In the bottom panel the low and high level thresholds are visible. Standard data selections are indicated by the red curves |
| Open with DEXTER | |
| |
Figure 10: First and second order spectrum for Capella observation. Emission lines are clearly visible (see Audard et al. 2000 for a full analysis) |
| Open with DEXTER | |
The commissioning phase of the XMM-Newton instruments started on January 4, 2000, followed by a calibration and performance verification phase between March 9 and July 4, 2000. During these periods a number of astrophysical targets were observed (see Table 3).
| object | purpose |
| Capella | wavelength scale, bore sight, |
| effective area, CCD response | |
| HR 1099 | wavelength scale, CCD CTI |
| AB Dor | repeated wavelength scale; after June |
| 3C 273 | on- and off-axis effective area |
| GX 13+1 | effective area ( |
| Mkr 421 | on-axis effective area |
| Lockman hole | background estimate |
| PKS 2155-304 | effective area simultaneously with Chandra |
| Sco X-1 | CCD gain and CTI (partially successful) |
| Canopus | stray light |
After the first week of operations, an electronic component in the clock driver of CCD 4 in RGS2 failed. A similar problem showed up in early September, 2000, on CCD 7 of RGS1. The affected wavelength ranges are 20.1-23.9 Å for RGS2 and 10.5-14 Å for RGS1 reducing the effective area by a factor of 2 for these ranges. The operational conditions have been modified to reduce the load of these commonly used components to a minimum.
An example of the data is shown in Fig. 9, where the dispersed image of Capella is shown in the upper panel, while in the lower panel CCD pulse height is plotted against dispersion. In the lower panel the first, second, and even higher orders are visible. The four internal calibration sources (at 1487 eV and at 677 eV) are also discernible. In order to extract a spectrum from these data, the following cuts are applied. In the cross-dispersion direction a filter is applied which includes typically 90% of the total intensity. The spectral order is selected in the CCD pulse height versus dispersion angle space (lower panel of Fig. 9) with a joint pulse height-dispersion filter. The extracted spectra are shown in Fig. 10 and these are discussed in detail by Audard et al. (2001). In addition the exposure time per wavelength bin is calculated taking into account the data selections, rejected columns and pixels (either due to cosmics or to cosmetic blemishes in the CCD) and the dead space between CCDs (see also Erd et al. 2000).
A number of key performance parameters were checked. The gains of the CCDs were calibrated using the internal calibration sources and a few strong astrophysical continuum sources. The gains are slightly different from pre-flight but have been very stable since launch. The CCD energy resolution was verified with a few known emission lines. No changes with respect to the preflight conditions were observed. Position dependent offsets of the CCD energy scale due to straylight were measured and are consistent with the pre-launch expectations. Using DIAGNOSTIC data it was verified that the system peak (a combination of electronic noise, dark current and optical load of the CCDs) is very stable over an orbit (within 1 eV) with the exception of a jump of about 2 eV, which occurred following a very strong solar flare on July 7, 2000. The only component that is slightly variable are the hot pixels and columns.
Special attention was given to a potential increase of the CTI due to soft protons (entering through the mirror) and hard protons (the mission is close to the solar max). This property of the system is monitored continuously. Based on these results (position of the Al and F peak as function of number of orbits) the maximum CTI increase is estimated to be 1 10-7 per transfer per orbit. Accepting a CTI loss of 25%, which still allows for good order separation, this translates into a lifetime of more than 15 years without the need to lower the camera temperatures. Using the intensity of the internal sources it is possible to monitor contamination. Comparison of these intensities with the intensities from the ground calibration indicate an upper limit to any change in quantum efficiency (QE) at the O-K edge of 8%.
The CCDs also exhibit low amplitude, low pulse height Fixed Pattern Noise. This is a minor effect, easily suppressed with an appropriate pulse height filter.
The Line
Spread Function (LSF) is a convolution of the mirror response and the grating response,
and it depends on the proper alignment of these units.
The mirror response includes the figure properties and co-alignment of all 58 nested
mirrors. The
grating response depends on the co-alignment and flatness of the 182 gratings that are integrated per RGA.
In addition there is also a significant (but well calibrated)
component due to scattering on the surfaces of the mirrors
and the gratings (seen as the horizontal distribution of events in the bottom panel of
Fig. 9).
The various components scale differently with wavelength, which
gives rise to a composite line shape which can not easily be characterized in terms of a simple
analytical function. The shape of the core largely determines the ability of the spectrometer
to separate closely spaced emission lines. The telescope blur contributes a constant term to the
spectrometer line width, while misalignments and flatness errors of the gratings
contribute a
term which slowly increases with increasing wavelength. The scattering component is most significant at
the shortest wavelengths and the highest
diffraction orders. This is illustrated in Fig. 11 where the
predicted resolution for the two RGSs is shown (the steep rise below 7 Å is due to the scattering
component of the gratings). Also shown are the measurements, which are deduced from a
few narrow, bright emission lines in HR 1099
(Ly![]() lines of Ne (m=-1,-2), O, N and C). This demonstrates that the instrument
resolving power
is close to the expectations.
The explicit spectrometer line response is close to predictions based on a raytrace model
for the spectrometer.
lines of Ne (m=-1,-2), O, N and C). This demonstrates that the instrument
resolving power
is close to the expectations.
The explicit spectrometer line response is close to predictions based on a raytrace model
for the spectrometer.
![\begin{figure}
\includegraphics[angle=0,width=8.4cm,clip]{XMM19_f11r.eps}\end{figure}](/articles/aa/full/2001/01/aaxmm19/Timg48.gif) |
Figure 11: Comparison of the measured and predicted resolution (FWHM) for RGS1 (red) and for RGS2 (blue). Data for second order are shown as dashed lines and triangular datapoints |
| Open with DEXTER | |
The ability to detect weak emission lines above the background or the continuum is better measured by the
half energy width (HEW)
of the profile. This width, especially at short wavelengths, is more dependent on the amplitude and width
of the scattering wings. Again, the data agree with the predictions and in the HEW sense the resolving power goes to ![]() 800 at the longest wavelengths.
800 at the longest wavelengths.
To measure wavelengths, event locations (pixel coordinates) are mapped into
3-dimensional coordinates using the camera geometry measured at
![]() C
and a thermal-mechanical model for the optical bench.
The dispersion angle
C
and a thermal-mechanical model for the optical bench.
The dispersion angle ![]() ,
and
the polar angle
,
and
the polar angle ![]() subtended from the mirror in the cross-dispersion direction,
are then assigned based on the spacecraft geometry.
The angle of incidence of a photon on the grating
and the dispersion angle determine the measured
wavelength according to the dispersion equation Eq. (1).
The relative misalignment between the RGS instrument axis and the star tracker
axis (the bore-sight described by three Euler angles), the rotation of the grating array relative to the RGS
axis (Ry(RGA)), and the position of the focal plane camera
(Tz(RFC)) are used to calculate
subtended from the mirror in the cross-dispersion direction,
are then assigned based on the spacecraft geometry.
The angle of incidence of a photon on the grating
and the dispersion angle determine the measured
wavelength according to the dispersion equation Eq. (1).
The relative misalignment between the RGS instrument axis and the star tracker
axis (the bore-sight described by three Euler angles), the rotation of the grating array relative to the RGS
axis (Ry(RGA)), and the position of the focal plane camera
(Tz(RFC)) are used to calculate ![]() and
and
![]() .
.
In-flight
calibrations further refined ground-based measurements of these geometric parameters.
There is a inherent degeneracy in the determination of these five parameters,
however, so Ry(RGA) was fixed to its ground alignment value.
Using on-axis and off-axis (up to 10 arcmin)
observations of Capella, HR 1099, and AB Dor, we constrained the
other four parameters using the theoretical wavelengths of Ly![]() lines of Mg,
Ne, O, N, and C.
The geometric parameters were consistent with expected
tolerances for these parameters from the ground measurements.
The measurement of
wavelengths with RGS is currently accurate to 8 mÅ (rms) across the entire
wavelength band, based on the distribution of the wavelength residuals
of the calibration lines.
lines of Mg,
Ne, O, N, and C.
The geometric parameters were consistent with expected
tolerances for these parameters from the ground measurements.
The measurement of
wavelengths with RGS is currently accurate to 8 mÅ (rms) across the entire
wavelength band, based on the distribution of the wavelength residuals
of the calibration lines.
The boresight angles as well as the cross-dispersion position of the focal
plane camera (Ty(RFC))
also give the angle ![]() .
It was found to be consistent
with the cross-dispersion measurements to better than 4
arcsec (rms). This
can be used to predict the measured position of the source and is used in the
calculation of the instrument response.
.
It was found to be consistent
with the cross-dispersion measurements to better than 4
arcsec (rms). This
can be used to predict the measured position of the source and is used in the
calculation of the instrument response.
![\begin{figure}
\includegraphics[angle=0,width=8cm,clip]{XMM19_f12r.eps}\end{figure}](/articles/aa/full/2001/01/aaxmm19/Timg51.gif) |
Figure 12: Effective area for the two RGSs (clearly visible are the gaps between the CCDs and the failing read-out of CCD4 in RGS2, the narrow drops in the curves are due to corrections for cosmetic blemishes) |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[angle=0,width=8.4cm,clip]{XMM19_f13r.eps}\end{figure}](/articles/aa/full/2001/01/aaxmm19/Timg52.gif) |
Figure 13: Typical countrate for standard data selections (m=-1, 90% in CCD pulse height, full range in cross dispersion direction for a quiet part of the Lockman Hole observation |
| Open with DEXTER | |
The effective area model of the RGS has been verified during in-flight calibration. Off-axis observations were performed on the continuum sources 3C 273 and GX 13+1, which sample both the full wavelength band and the short wavelength region, respectively. The ratios of the observed count rates in the off-axis to on-axis measurements were compared to the ratios predicted by the effective area model. This comparison is sensitive to the details of the model components, particularly to the grating efficiency and the geometric intercept and vignetting factors. The measured behavior agrees with the predicted behavior to within the statistical uncertainties for off-axis angles up to 10 arcmin in both first and second order, for all wavelengths above 9 Å. As a further check of the model the second to first order count rate ratio for both sources was compared with the predicted ratio. The prediction agrees across the band with the exception of the 7 to 9 Å region, where the ratio is overpredicted.
There is evidence for a narrow absorption feature at the neutral O K edge. It has a a threshold wavelength of 23.5 Å, and a relative amplitude of about 27%. This feature appears in all bright continuum sources. A comparison of the spectrum of the bright BL Lac object PKS 2155-304 as measured with the RGS, and with the Chandra LETGS suggests that the feature is instrumental. A detailed calibration is in progress.
The absolute effective area of the RGS will be cross-calibrated with the diffraction grating spectrometers on Chandra, as well as with the Chandra ACIS and XMM-Newton EPIC detectors, using suitable bright cosmic sources. This work is currently in progress.
The effective area for the nominal data selections is shown in Fig. 12 for the two RGSs. Due to the data selections the maximum effective area is lower than measured during the end-to-end tests (see Fig. 8 for reference).
The background model for the RGS was cross-checked using a deep observation of the Lockman Hole. Several different components contribute, including:
| parameter | value | comment |
|
|
140 cm2 | peak effective area |
| 6-38 Å | wavelength range first order | |
|
|
100-500 | resolution (line separation) |
|
|
100-800 | resolution (weak line detection) |
|
|
8 m Å | wavelength accuracy |
Following the onboard background rejection, the major constituents of the background are a tail on the CCD response due to readout noise, and the soft proton radiation. Using a model for the behavior of these components, the Lockman Hole data appear to be adequately described. However, as some of the components are clearly time variable, it is not trivial to use the same model for other observations of extended sources. For point sources, however, one can simply select a region on the CCDs in the cross dispersion direction and use the same windows in the CCD pulse height as for the source. For reference we give the first order spectrum for a standard selection (90% window in CCD energy only) of the Lockman Hole data for a quiet period (see Fig. 13). The increase in background below 8 Å is due to a change in the width of the pulse height filter at that wavelength (given as red curves in Fig. 9).
The RGS performs as expected with the exception of the electronics of two CCDs. Several papers in this issue attest to its unique capabilities. Simultaneous measurements together with the three EPIC cameras and the Optical Monitor enhance the scientific return significantly. Although some small refinements in the performance parameters can be expected following analysis of a larger dataset, the key parameters as listed in Table 4 are characteristic.
Acknowledgements
Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and the USA (NASA). We are particular grateful to Mr. Robert Lainé and his team for their support during the development of the hardware. The Laboratory for Space Research Utrecht is supported financially by NWO, The Netherlands Organization for Scientific Research. The Mullard Space Science Laboratory acknowledges financial support form the UK Particle Physics and Astronomy Research Council. The Swiss contribution has been supported by the PRODEX program, the Swiss National Science Foundation (Grant 21-49343.96), and the Swiss Commission for Space Research. The Columbia and Lawrence Livermore groups are supported by the U.S. National Aeronautics and Space Administration.