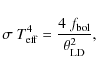| Issue |
A&A
Volume 512, March-April 2010
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200913405 | |
| Published online | 01 April 2010 | |
The radius and effective temperature of
the binary Ap star  CrB from CHARA/FLUOR
and VLT/NACO observations
CrB from CHARA/FLUOR
and VLT/NACO observations![[*]](/icons/foot_motif.png)
H. Bruntt1,2 - P. Kervella1 - A. Mérand3 - I. M. Brandão4,5 - T. R. Bedding2 - T. A. ten Brummelaar6 - V. Coudé du Foresto1 - M. S. Cunha4 - C. Farrington6 - P. J. Goldfinger6 - L. L. Kiss2,7 - H. A. McAlister6 - S. T. Ridgway8 - J. Sturmann6 - L. Sturmann6 - N. Turner6 - P. G. Tuthill2
1 - LESIA, CNRS UMR 8109, Observatoire de Paris-Meudon, 5 place Jules
Janssen, 92195 Meudon Cedex, France
2 - Sydney Institute for Astronomy, School of Physics, The University
of Sydney, NSW 2006, Australia
3 - European Southern Observatory, Alonso de Córdova 3107, Casilla
19001, Santiago 19, Chile
4 - Universidade do Porto, Centro de Astrofísica, Rua das Estrelas,
4150-762 Porto, Portugal
5 - Departamento de Matemática Aplicada, Faculdade de Ciências,
Universidade do Porto, 4169 Porto, Portugal
6 - Center for High Angular Resolution Astronomy, Georgia State
University, PO Box 3965, Atlanta, Georgia 30302-3965, USA
7 - Konkoly Observatory of the Hungarian Academy of Sciences, Budapest,
Hungary
8 - National Optical Astronomy Observatory, PO box 26732, Tucson, AZ
85726, USA
Received 5 October 2009 / Accepted 10 December 2009
Abstract
Context. The prospects for using the
asteroseismology of
rapidly oscillating Ap (roAp) stars are hampered by the large
uncertainty in fundamental stellar parameters. Results in the
literature for the effective temperature (
![]() )
often span a range of 1000 K.
)
often span a range of 1000 K.
Aims. Our goal is to reduce systematic errors and
improve the ![]() calibration of Ap stars based on new interferometric measurements.
calibration of Ap stars based on new interferometric measurements.
Methods. We obtained long-baseline interferometric
observations of ![]() CrB
using the CHARA/FLUOR instrument. To disentangle the flux contributions
of the two components of this binary star, we obtained VLT/NACO
adaptive optics images.
CrB
using the CHARA/FLUOR instrument. To disentangle the flux contributions
of the two components of this binary star, we obtained VLT/NACO
adaptive optics images.
Results. We determined limb-darkened angular
diameters of ![]() mas
for
mas
for ![]() CrB A
(from interferometry) and
CrB A
(from interferometry) and ![]() mas
for
mas
for ![]() CrB B
(from surface brightness-colour relations), corresponding to radii of
CrB B
(from surface brightness-colour relations), corresponding to radii of
![]() (3.4% uncertainty) and
(3.4% uncertainty) and
![]() (4.5%). The combined bolometric flux of the A+B components was
determined from satellite UV data, spectrophotometry in the visible,
and broadband data in the infrared. The flux from the B
component
constitutes
(4.5%). The combined bolometric flux of the A+B components was
determined from satellite UV data, spectrophotometry in the visible,
and broadband data in the infrared. The flux from the B
component
constitutes ![]() %
of the total flux and was determined by fitting an ATLAS9 model
atmosphere to the broad-band NACO J and K
magnitudes. By combining the flux of the A component with its
measured angular diameter, we determined the effective temperature
%
of the total flux and was determined by fitting an ATLAS9 model
atmosphere to the broad-band NACO J and K
magnitudes. By combining the flux of the A component with its
measured angular diameter, we determined the effective temperature
![]() K
(2.3%).
K
(2.3%).
Conclusions. Our new interferometric and imaging
data enable nearly model-independent determination of the effective
temperature of ![]() CrB A.
Including our recent study of
CrB A.
Including our recent study of ![]() Cir, we now have
direct
Cir, we now have
direct ![]() measurements of two of the brightest roAp stars, providing a strong
benchmark for improved calibration of the
measurements of two of the brightest roAp stars, providing a strong
benchmark for improved calibration of the
![]() scale for Ap stars. This will support the use of potentially strong
constraints imposed by asteroseismic studies of roAp stars.
scale for Ap stars. This will support the use of potentially strong
constraints imposed by asteroseismic studies of roAp stars.
Key words: stars: chemically peculiar -
stars: fundamental parameters - stars: individual: ![]() CrB
- stars: individual:
CrB
- stars: individual: ![]() Cir
- stars: individual:
Cir
- stars: individual: ![]() Equ
- stars: individual: 10 Aql
Equ
- stars: individual: 10 Aql
1 Introduction
Photometric and spectroscopic determinations of the effective
temperatures of Ap stars are affected by
systematic errors. This has been corroborated by the asteroseismic data
of rapidly oscillating Ap (roAp) stars in general and, more recently,
by the first interferometric determination of
the angular diameter of the roAp star ![]() Cir (Bruntt et al. 2008).
Unfortunately, the intriguing asteroseismic potential offered by roAp
stars is strongly compromised by these systematic errors. We therefore
seek to directly measurement
of the radii and effective temperatures of a number of Ap stars
using interferometry and spectrophotometry.
We first give a brief summary of the properties of
Cir (Bruntt et al. 2008).
Unfortunately, the intriguing asteroseismic potential offered by roAp
stars is strongly compromised by these systematic errors. We therefore
seek to directly measurement
of the radii and effective temperatures of a number of Ap stars
using interferometry and spectrophotometry.
We first give a brief summary of the properties of
![]() CrB
before describing our observations, data reduction (Sect. 2),
and analysis (Sect. 3).
CrB
before describing our observations, data reduction (Sect. 2),
and analysis (Sect. 3).
![]() CrB (
CrB (![]() CrB,
CrB, ![]() CrB)
is one of the brightest, coolest, and best-studied magnetic Ap stars.
The literature on the star is extensive and we only mention a few of
the most
important results here. It was classified as a type
A9 Sr Eu Cr star by Renson
& Manfroid (2009).
Its binary nature was first suggested by Campbell
& Moore (1907), and recent determinations of its
orbital elements have been obtained by Tokovinin
(1984) and North
et al. (1998). From speckle interferometric
measurements using narrow-band filters,
Horch et al. (2004)
measured the magnitude difference to be 2.37 mag at
551 nm and 1.99 mag at 503 nm.
In the analysis presented in Sect. 3
we retain the orbital elements obtained by Tokovinin
(1984), as they are in significantly better agreement with
our NACO astrometry than those by North
et al. (1998).
CrB)
is one of the brightest, coolest, and best-studied magnetic Ap stars.
The literature on the star is extensive and we only mention a few of
the most
important results here. It was classified as a type
A9 Sr Eu Cr star by Renson
& Manfroid (2009).
Its binary nature was first suggested by Campbell
& Moore (1907), and recent determinations of its
orbital elements have been obtained by Tokovinin
(1984) and North
et al. (1998). From speckle interferometric
measurements using narrow-band filters,
Horch et al. (2004)
measured the magnitude difference to be 2.37 mag at
551 nm and 1.99 mag at 503 nm.
In the analysis presented in Sect. 3
we retain the orbital elements obtained by Tokovinin
(1984), as they are in significantly better agreement with
our NACO astrometry than those by North
et al. (1998).
Neubauer (1944)
suggested that a third body could be present in the system, causing
radial velocity variations with a period of ![]() 321 days, but Oetken & Orwert (1984), Kamper et al. (1990),
and Söderhjelm (1999)
excluded this possibility. Recently, Muterspaugh
et al. (2006) established an upper limit of
321 days, but Oetken & Orwert (1984), Kamper et al. (1990),
and Söderhjelm (1999)
excluded this possibility. Recently, Muterspaugh
et al. (2006) established an upper limit of ![]() 10 to
100 MJ
(depending on the orbital period) for a possible substellar tertiary
from differential interferometric astrometry. Trilling
et al. (2007) searched for 24 and 70
10 to
100 MJ
(depending on the orbital period) for a possible substellar tertiary
from differential interferometric astrometry. Trilling
et al. (2007) searched for 24 and 70 ![]() m infrared
excess around
m infrared
excess around ![]() CrB
using Spitzer but did not find any.
Interestingly, the Spitzer flux they
obtained is significantly below the expected flux at 24
CrB
using Spitzer but did not find any.
Interestingly, the Spitzer flux they
obtained is significantly below the expected flux at 24 ![]() m, and
slightly lower (although compatible)
at 70
m, and
slightly lower (although compatible)
at 70 ![]() m.
This result could come from the chosen physical parameters for their
stellar atmosphere model.
In the following, we will therefore consider that
m.
This result could come from the chosen physical parameters for their
stellar atmosphere model.
In the following, we will therefore consider that ![]() CrB
is a binary system.
CrB
is a binary system.
Early photometric searches for pulsation in ![]() CrB
(e.g. Kreidl
1991; Weiss
& Schneider 1989) gave null results and this
contributed to the discussion of the existence of non-oscillating Ap
stars (``noAp''; Kurtz 1989).
This has changed since the advent of large telescopes and ultra-stable
spectrographs.
Based on spectroscopic time series of a single Fe line, Kochukhov et al. (2002)
claim the first possible detection of a pulsation mode in
CrB
(e.g. Kreidl
1991; Weiss
& Schneider 1989) gave null results and this
contributed to the discussion of the existence of non-oscillating Ap
stars (``noAp''; Kurtz 1989).
This has changed since the advent of large telescopes and ultra-stable
spectrographs.
Based on spectroscopic time series of a single Fe line, Kochukhov et al. (2002)
claim the first possible detection of a pulsation mode in ![]() CrB
with a period of 11.5 min. This result is questioned by Hatzes & Mkrtichian (2004)
and has also not been confirmed by Kurtz
et al. (2007).
However, the good agreement between the independent spectroscopic
studies of
Hatzes & Mkrtichian (2004),
Kurtz et al. (2007),
and Kochukhov et al. (2008)
confirm
that
CrB
with a period of 11.5 min. This result is questioned by Hatzes & Mkrtichian (2004)
and has also not been confirmed by Kurtz
et al. (2007).
However, the good agreement between the independent spectroscopic
studies of
Hatzes & Mkrtichian (2004),
Kurtz et al. (2007),
and Kochukhov et al. (2008)
confirm
that ![]() CrB
is indeed an roAp star with a single known low-amplitude mode with
period 16.2 min.
The most robust result was found by Kurtz
et al. (2007), who used 2 h of high-cadence
time-series spectra obtained with
VLT/UVES. They detected a single oscillation frequency
at 1.031 mHz (P = 16.2 min) with
an amplitude of
CrB
is indeed an roAp star with a single known low-amplitude mode with
period 16.2 min.
The most robust result was found by Kurtz
et al. (2007), who used 2 h of high-cadence
time-series spectra obtained with
VLT/UVES. They detected a single oscillation frequency
at 1.031 mHz (P = 16.2 min) with
an amplitude of
![]() km s-1
in the H
km s-1
in the H ![]() line and
a higher amplitude in the cesium lines.
Unlike most roAp stars, variation was only observed in
singly-ionized rare-earth elements, but not doubly ionized lines. The
abundance analysis done by Kurtz
et al. (2007) on their averaged spectrum confirmed
earlier investigations by Ryabchikova
et al. (2004). These analyses show that
line and
a higher amplitude in the cesium lines.
Unlike most roAp stars, variation was only observed in
singly-ionized rare-earth elements, but not doubly ionized lines. The
abundance analysis done by Kurtz
et al. (2007) on their averaged spectrum confirmed
earlier investigations by Ryabchikova
et al. (2004). These analyses show that ![]() CrB
has an
overabundance of rare-earth elements but only by about 1 dex,
contrary to the 2-3 dex seen in most roAp stars.
CrB
has an
overabundance of rare-earth elements but only by about 1 dex,
contrary to the 2-3 dex seen in most roAp stars.
2 Observations and data reduction
2.1 VLT/NACO adaptive optics imaging
We observed ![]() CrB
on 16 June 2008 using the Nasmyth Adaptive Optics System (NAOS; Rousset et al. 2003) of
the Very Large Telescope (VLT), coupled to the CONICA infrared camera (Lenzen et al. 1998),
abbreviated as NACO. We selected the smallest available pixel scale of
CrB
on 16 June 2008 using the Nasmyth Adaptive Optics System (NAOS; Rousset et al. 2003) of
the Very Large Telescope (VLT), coupled to the CONICA infrared camera (Lenzen et al. 1998),
abbreviated as NACO. We selected the smallest available pixel scale of
![]() mas/pix
(Masciadri et al. 2003),
giving a field of view of 13.6
mas/pix
(Masciadri et al. 2003),
giving a field of view of 13.6
![]()
![]() 13.6
13.6
![]() .
This small scale resulted in good sampling of the point spread function
(PSF).
We employed the J and K filters
of NACO, with respective bandpasses of
.
This small scale resulted in good sampling of the point spread function
(PSF).
We employed the J and K filters
of NACO, with respective bandpasses of
![]() m
and
m
and ![]() m, together
with a neutral density filter (labelled ``ND2_short'',
transmission
m, together
with a neutral density filter (labelled ``ND2_short'',
transmission ![]() 1.5%)
to avoid saturation of the detector. The transmission curves of these
filters are available on the NACO instrument web page
1.5%)
to avoid saturation of the detector. The transmission curves of these
filters are available on the NACO instrument web page![]() .
.
We obtained 20 images in the J band and 40
images in the K band, each with an exposure time of
0.35 s. This is the minimum full-frame integration time of
CONICA. The J band images were collected during ![]() 2 min
around UT01:53:31, and the K images in
2 min
around UT01:53:31, and the K images in ![]() 4 min
around UT01:58:20. During these observations the DIMM seeing at Paranal
in the visible was good (
4 min
around UT01:58:20. During these observations the DIMM seeing at Paranal
in the visible was good (
![]() ),
resulting in a high Strehl ratio (
),
resulting in a high Strehl ratio (![]()
![]() ).
The raw images were dark-subtracted, flat-fielded (using lamp flats),
and corrected for bad pixels using IRAF
).
The raw images were dark-subtracted, flat-fielded (using lamp flats),
and corrected for bad pixels using IRAF![]() .
On the NACO images, we measured both the differential photometry and
the differential astrometry of
.
On the NACO images, we measured both the differential photometry and
the differential astrometry of ![]() CrB B
relatively to
CrB B
relatively to ![]() CrB A
taken as the reference.
CrB A
taken as the reference.
To measure the relative astrometry, we treated each image
separately using the Yorick![]() software package. We used a classical
software package. We used a classical ![]() minimization to fit an extracted subimage of
minimization to fit an extracted subimage of ![]() CrB A (with
a size of
CrB A (with
a size of ![]() pixels)
at the position of the fainter component B. The interpolation of the
shifted image of A was done in Fourier space. The adjusted parameters
were the relative positions
pixels)
at the position of the fainter component B. The interpolation of the
shifted image of A was done in Fourier space. The adjusted parameters
were the relative positions ![]() and
and ![]() ,
the flux ratio, and the background level, although we used only the
relative separations for our astrometric analysis. To estimate the
associated error bars, we used the bootstrapping technique described by
Kervella et al. (2004a).
This technique is also called ``sampling with replacement'' and
consists of constructing a hypothetical, large population derived from
the original measurements and estimate the statistical properties from
this population. The technique allows us to compute meaningful
confidence intervals without any assumption on the properties of the
underlying population (e.g. a Gaussian distribution).
We validated the adopted Fourier interpolation method by comparing the
results with a simple Gaussian fit of the two PSF cores. The two
methods yield exactly the same relative positions (within
,
the flux ratio, and the background level, although we used only the
relative separations for our astrometric analysis. To estimate the
associated error bars, we used the bootstrapping technique described by
Kervella et al. (2004a).
This technique is also called ``sampling with replacement'' and
consists of constructing a hypothetical, large population derived from
the original measurements and estimate the statistical properties from
this population. The technique allows us to compute meaningful
confidence intervals without any assumption on the properties of the
underlying population (e.g. a Gaussian distribution).
We validated the adopted Fourier interpolation method by comparing the
results with a simple Gaussian fit of the two PSF cores. The two
methods yield exactly the same relative positions (within ![]() as),
although the Gaussian fit has a slightly larger dispersion because of
the mismatch of the slightly seeing-distorted PSF and the Gaussian
function. We obtained the following vector separations along the RA and
Dec directions of B relatively to A, for the epoch of the observations
(MJD 54633.08):
as),
although the Gaussian fit has a slightly larger dispersion because of
the mismatch of the slightly seeing-distorted PSF and the Gaussian
function. We obtained the following vector separations along the RA and
Dec directions of B relatively to A, for the epoch of the observations
(MJD 54633.08):
| (1) |
| (2) |
The two stated error bars are the statistical and systematic uncertainties, respectively. The latter includes the pixel scale uncertainty and the detector orientation uncertainty. These values correspond to a separation r and position angle
| (4) |
These measurements were done on the K images since they have the highest Strehl ratio. In the J band, the Strehl ratio was lower and more unstable, resulting in a significantly variable background from A to B. Although its average value is not a concern, its slope tends to slightly shift the average apparent position of B, by -0.2 and -1.4 mas in RA and Dec, respectively (towards the lower left quadrant of Fig. 1). The average NACO image in the K band is presented in Fig. 1, together with the orbit by Tokovinin (1984). Our astrometric measurement falls on the predicted orbit within only 7 mas. We find that the reference epoch of the orbital elements by North et al. (1998) appears to be late by approximately 300 days.
![\begin{figure}
\par\includegraphics[width=9cm, angle=0]{13405fg1-colour.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13405-09/Timg39.png)
|
Figure 1:
Average NACO image of |
| Open with DEXTER | |
The photometry was obtained in two steps: (1) we obtained the combined photometry of the two stars; (2) we then measured the differential flux of B relative to A. We will discuss these steps in the following.
- (1)
- The combined ADU count was computed from the NACO images by
using a large aperture enclosing the full PSFs of the two stars. It was
then converted to magnitude using the zero points obtained routinely by
the observatory on the same night,
 and
and
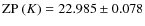 ,
and an attenuation of
,
and an attenuation of 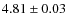 mag
for the neutral density filter. These zero points have not been
corrected for atmospheric absorption, but because they were obtained at
low airmass (
mag
for the neutral density filter. These zero points have not been
corrected for atmospheric absorption, but because they were obtained at
low airmass (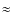 1.15),
we neglect the atmospheric absorption of
1.15),
we neglect the atmospheric absorption of 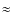 0.01 mag in J
and K. We corrected the atmospheric absorption
using the standard values by Nikolaev
et al. (2000), namely 0.092 mag/AM
(relative to unit airmass) for J and
0.065 mag/AM for K, for our
observation airmass of 1.71. We obtain
0.01 mag in J
and K. We corrected the atmospheric absorption
using the standard values by Nikolaev
et al. (2000), namely 0.092 mag/AM
(relative to unit airmass) for J and
0.065 mag/AM for K, for our
observation airmass of 1.71. We obtain
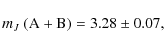
(5)
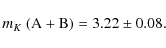
(6)
- (2)
- The differential photometry was obtained slightly
differently, since the diffuse background of
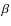 CrB A
tends to contaminate the flux of star B (but the reverse effect is
negligible). We first computed aperture photometry of A on the average J
and K images using very small aperture radii of
3 pixels in the J band and
4 pixels in the K band (contamination is
lower in K).
We calculated the median background value in concentric rings centered
on A. This value was then subtracted from component B's flux.
This allowed us to subtract the diffuse light from the PSF wings of A
at the position of B. We checked that the residual background around B
was negligible. We then integrated the flux of B on the
ring-median-subtracted image using the same aperture radius as for A.
We obtain the following flux ratios of each star relative to the total
of the two, i.e.
CrB A
tends to contaminate the flux of star B (but the reverse effect is
negligible). We first computed aperture photometry of A on the average J
and K images using very small aperture radii of
3 pixels in the J band and
4 pixels in the K band (contamination is
lower in K).
We calculated the median background value in concentric rings centered
on A. This value was then subtracted from component B's flux.
This allowed us to subtract the diffuse light from the PSF wings of A
at the position of B. We checked that the residual background around B
was negligible. We then integrated the flux of B on the
ring-median-subtracted image using the same aperture radius as for A.
We obtain the following flux ratios of each star relative to the total
of the two, i.e.
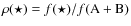 :
:
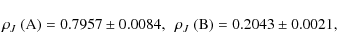
(7)
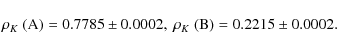
(8)
The quoted uncertainties are statistical errors that do not include possible flat-fielding errors. From the combined magnitudes determined above, we obtain the individual magnitudes of CrB A and
B:
CrB A and
B:
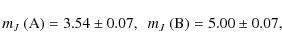
(9)
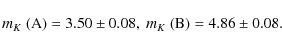
(10)
The individual J,K magnitudes
have large uncertainties,
but we stress that we only use the values of ![]() for the interpretation of our interferometric data (Sect. 2.2), and they
are known with a much higher accuracy.
for the interpretation of our interferometric data (Sect. 2.2), and they
are known with a much higher accuracy.
2.2 CHARA/FLUOR interferometry
Table 1: Interferometric calibrators selected from Mérand et al. (2005).
Our interferometric observations ofFor this reason, we have to correct our measured visibility
for this effect. The monochromatic visibility of the binary is
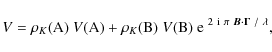
|
(11) |
where
In the case of the observations of B, this multiplicative factor
This leads to the following angular diameters:
| (13) |
| (14) |
The angular diameter of
Table 2: Journal of observations.
2.3 Surface brightness-colour predictions
We can compare the measured angular diameters of ![]() CrB A and B
with the predictions from the surface brightness-colour (hereafter SBC)
relations calibrated by Kervella
et al. (2004b) using their (V, V-K)
relation. The K band magnitudes were obtained in
Sect. 2.1.
We derive the V band magnitudes from the total
magnitude of the system of
CrB A and B
with the predictions from the surface brightness-colour (hereafter SBC)
relations calibrated by Kervella
et al. (2004b) using their (V, V-K)
relation. The K band magnitudes were obtained in
Sect. 2.1.
We derive the V band magnitudes from the total
magnitude of the system of
![]() (Rufener 1988) and the
magnitude difference
(Rufener 1988) and the
magnitude difference
![]() measured by Horch et al.
(2004) by speckle interferometry at 503 nm. We
adopted estimated uncertainties on mV
and
measured by Horch et al.
(2004) by speckle interferometry at 503 nm. We
adopted estimated uncertainties on mV
and ![]() since they are not given explicitly in the references. This gives the
component magnitudes in V,
since they are not given explicitly in the references. This gives the
component magnitudes in V,
and the predicted photospheric angular diameters:
| (16) |
| (17) |
The predicted and measured angular diameters of
![\begin{figure}
\par\includegraphics[width=17cm]{13405fg2.eps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13405-09/Timg97.png)
|
Figure 2:
The solid black line shows the flux distribution for |
| Open with DEXTER | |
2.4 Linear photospheric radii
The original Hipparcos parallax of ![]() CrB
is
CrB
is ![]() mas
(Perryman & ESA 1997),
consistent with the new reduction by van
Leeuwen (2007) of
mas
(Perryman & ESA 1997),
consistent with the new reduction by van
Leeuwen (2007) of
![]() mas.
However, as the new reduction is not corrected for binarity effects, we
adopt the original Hipparcos parallax.
mas.
However, as the new reduction is not corrected for binarity effects, we
adopt the original Hipparcos parallax.
For ![]() CrB A,
the angular diameter measurement presented in Sect. 2.2
represents a significant improvement in accuracy, by a factor of 1.6,
over the surface brightness-colour estimate of Sect. 2.3.
For the B component, this is not the case, as the visibility
measurement is made particularly difficult by the brighter
A component. For the subsequent analysis presented in
Sect. 3,
we therefore choose to adopt our direct interferometric angular
diameter measurement for
CrB A,
the angular diameter measurement presented in Sect. 2.2
represents a significant improvement in accuracy, by a factor of 1.6,
over the surface brightness-colour estimate of Sect. 2.3.
For the B component, this is not the case, as the visibility
measurement is made particularly difficult by the brighter
A component. For the subsequent analysis presented in
Sect. 3,
we therefore choose to adopt our direct interferometric angular
diameter measurement for ![]() CrB A,
while for B we use the SBC estimate computed from our K
band NACO photometry. This gives the following linear radii:
CrB A,
while for B we use the SBC estimate computed from our K
band NACO photometry. This gives the following linear radii:
| (18) |
| (19) |
3 The effective temperatures and masses of 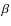 CrB
CrB
In the following we will determine the effective temperatures and
luminosities
of the components of ![]() CrB
using two methods. The first method (Sect. 3.1) relies on
the bolometric correction (model-dependent), while the second method
(Sect. 3.2)
is only weakly model-dependent.
We then compare the radius and
CrB
using two methods. The first method (Sect. 3.1) relies on
the bolometric correction (model-dependent), while the second method
(Sect. 3.2)
is only weakly model-dependent.
We then compare the radius and
![]() of the components with a grid of isochrones
to determine their approximate age and evolutionary masses
(Sect. 3.3).
of the components with a grid of isochrones
to determine their approximate age and evolutionary masses
(Sect. 3.3).
3.1 Luminosity and effective temperature from angular diameter + BC + parallax
We use the bolometric corrections (BCV)
from Bessell et al. (1998).
For the measured V-K values of
![]() and
and ![]() ,
for A and B
we get BC
,
for A and B
we get BC
![]() ,
BC
,
BC
![]() ,
BC
,
BC
![]() ,
and BC
,
and BC
![]() (with
(with
![]() ). We assume
the uncertainties on the BCs are 0.02 mag.
We therefore obtain from the V band photometry:
). We assume
the uncertainties on the BCs are 0.02 mag.
We therefore obtain from the V band photometry:
| (20) |
The same computation with the K band magnitudes gives identical values within 0.01 mag. We thus obtain the following bolometric luminosities, assuming the Hipparcos parallax and
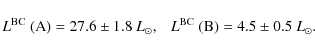
|
(21) |
We can now use the radii determined in Sect. 2.4 to derive the effective temperatures of the two stars through
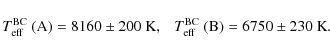
|
(22) |
3.2 Effective temperature from angular diameter + flux
The above method for the determination of
![]() has the caveat that it relies on the bolometric correction being valid
for these stars. The BCs from Bessell
et al. (1998)
are calculated from atmospheric models and do not depend on the
metallicity. As a check, we determine the
has the caveat that it relies on the bolometric correction being valid
for these stars. The BCs from Bessell
et al. (1998)
are calculated from atmospheric models and do not depend on the
metallicity. As a check, we determine the
![]() of the A component by a direct method,
meaning it will only be weakly dependent on the assumed model
atmosphere. This is
done by calculating the integrated bolometric flux of
of the A component by a direct method,
meaning it will only be weakly dependent on the assumed model
atmosphere. This is
done by calculating the integrated bolometric flux of
![]() and subtracting the
flux from the B component using an ATLAS9 model
with the
and subtracting the
flux from the B component using an ATLAS9 model
with the ![]() determined above.
determined above.
The bolometric flux of the combined system, ![]() CrB
A+B, is obtained by combining data from the literature from the UV to
the near IR as shown in Fig. 2.
In the UV range we use five spectrograms from the Sky Survey Telescope (Jamar et al. 1976)
obtained at the IUE ``Newly Extracted Spectra''
data archive
CrB
A+B, is obtained by combining data from the literature from the UV to
the near IR as shown in Fig. 2.
In the UV range we use five spectrograms from the Sky Survey Telescope (Jamar et al. 1976)
obtained at the IUE ``Newly Extracted Spectra''
data archive![]() , covering the
wavelength interval 1150 Å
, covering the
wavelength interval 1150 Å
![]() 3350 Å. We compute
the weighted average of the spectrograms
after removing some spurious data from 1150-1250 Å.
In the optical range we use spectrophotometry
from Alekseeva et al.
(1996) and Breger (1976),
which cover the range 3200 Å
3350 Å. We compute
the weighted average of the spectrograms
after removing some spurious data from 1150-1250 Å.
In the optical range we use spectrophotometry
from Alekseeva et al.
(1996) and Breger (1976),
which cover the range 3200 Å
![]() Å.
In addition, for the near-IR wavelengths we use the broadband
magnitudes VJKLfrom Morel
& Magnenat (1978). We interpolate the points between
the broadband data and make a linear extrapolation at the end points
(UV and IR ranges), although the contribution is negligible in
practice. Finally, we calculate the weighted average flux, which is
shown in Fig. 2.
For the relative flux uncertainties we assume 15% in the UV, 6% in the
optical, and 10% in the near IR. For the ranges where extrapolations
were made, we double these errors.
These adopted uncertainties are larger than the originally published
values.
We have adjusted them based
on the disagreement between different sources of data in the same
wavelength ranges, i.e. the spectrophotometric data
from Breger (1976) and Alekseeva et al. (1996)
in Fig. 2.
Å.
In addition, for the near-IR wavelengths we use the broadband
magnitudes VJKLfrom Morel
& Magnenat (1978). We interpolate the points between
the broadband data and make a linear extrapolation at the end points
(UV and IR ranges), although the contribution is negligible in
practice. Finally, we calculate the weighted average flux, which is
shown in Fig. 2.
For the relative flux uncertainties we assume 15% in the UV, 6% in the
optical, and 10% in the near IR. For the ranges where extrapolations
were made, we double these errors.
These adopted uncertainties are larger than the originally published
values.
We have adjusted them based
on the disagreement between different sources of data in the same
wavelength ranges, i.e. the spectrophotometric data
from Breger (1976) and Alekseeva et al. (1996)
in Fig. 2.
Since ![]() CrB
is a binary system, extra care must be taken
when computing the bolometric flux of the primary star.
The binary has a maximum angular separation of 0.3
CrB
is a binary system, extra care must be taken
when computing the bolometric flux of the primary star.
The binary has a maximum angular separation of 0.3
![]() and all available flux data
contain the combined light of the two
components.
Since our main interest is the A component, we have to estimate and
subtract the flux of the B component.
To accomplish this, we have fitted Kurucz
models to the mJ,
mK and mV
magnitudes of the B component,
taking the statistical errors on the magnitudes into account. For the mJ
and mK
magnitudes we adopt the measurements from NACO, while the mV
magnitude is that derived in Eq. (15). The spectra for
the Kurucz models
are computed with the IDL routine kurget1 (ATLAS9
models) and the corresponding
database of models available in the IUE reduction and data analysis
package IUEDAC
and all available flux data
contain the combined light of the two
components.
Since our main interest is the A component, we have to estimate and
subtract the flux of the B component.
To accomplish this, we have fitted Kurucz
models to the mJ,
mK and mV
magnitudes of the B component,
taking the statistical errors on the magnitudes into account. For the mJ
and mK
magnitudes we adopt the measurements from NACO, while the mV
magnitude is that derived in Eq. (15). The spectra for
the Kurucz models
are computed with the IDL routine kurget1 (ATLAS9
models) and the corresponding
database of models available in the IUE reduction and data analysis
package IUEDAC![]() .
We start by converting the mV
magnitude of
.
We start by converting the mV
magnitude of ![]() CrB B
into flux using
relation (6) of Rufener
& Nicolet (1988) and use this result to
calibrate the models. We then convert the Kurucz fluxes at the NACO J
and K central wavelengths
(12 650 Å and 21 800 Å) into
magnitudes using
CrB B
into flux using
relation (6) of Rufener
& Nicolet (1988) and use this result to
calibrate the models. We then convert the Kurucz fluxes at the NACO J
and K central wavelengths
(12 650 Å and 21 800 Å) into
magnitudes using
![]() .
Here m is the magnitude in a given filter, f
the flux at the central wavelength of
that filter, and f0 the
standard zeroth-magnitude flux for the same filter. The values
of f0 are computed by
integrating the flux of Vega through each of the J
and K filters
of the NACO instrument and assuming that Vega has zero magnitude in all
bands
.
Here m is the magnitude in a given filter, f
the flux at the central wavelength of
that filter, and f0 the
standard zeroth-magnitude flux for the same filter. The values
of f0 are computed by
integrating the flux of Vega through each of the J
and K filters
of the NACO instrument and assuming that Vega has zero magnitude in all
bands![]() .
We then generate 100 values for mJ
and mK of
.
We then generate 100 values for mJ
and mK of
![]() CrB B
by adding random fluctuations consistent with the uncertainties. For
each set we determine the Kurucz model that fit each set of magnitudes
best. The average integrated flux of the 100 fitted Kurucz
models is
CrB B
by adding random fluctuations consistent with the uncertainties. For
each set we determine the Kurucz model that fit each set of magnitudes
best. The average integrated flux of the 100 fitted Kurucz
models is ![]() erg/s/cm2.
We adopt a rather large uncertainty (25%) since we only have three
broadband flux measurements of the B component.
erg/s/cm2.
We adopt a rather large uncertainty (25%) since we only have three
broadband flux measurements of the B component.
The observed flux from the combined system is finally computed
by integrating the
black curve shown in Fig. 2,
from which we obtain
![]() erg/s/cm2and
the bolometric flux of the primary component is thus
erg/s/cm2and
the bolometric flux of the primary component is thus
![]() erg/s/cm-2. We can then obtain the effective
temperature using the relation,
erg/s/cm-2. We can then obtain the effective
temperature using the relation,
where
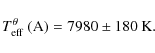
|
(24) |
Combining this with the radius we get the luminosity
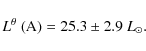
|
(25) |
These values agree with those in Sect. 3.1 where we used the (model dependent) bolometric correction. Since the calculation using Eq. 23 is nearly model-independent (limb-darkening coefficients depend on atmosphere models), we adopt these values as our final estimates of
Several determinations of
![]() are found in the literature, and we mention a few here.
Kochukhov & Bagnulo (2006)
used photometric indices to determine
are found in the literature, and we mention a few here.
Kochukhov & Bagnulo (2006)
used photometric indices to determine
![]() and found
and found ![]() K,
which is significantly lower than our value. Netopil
et al. (2008) have determined the
K,
which is significantly lower than our value. Netopil
et al. (2008) have determined the
![]() of
of ![]() CrB
from three photometric systems
(Strömgren, Geneva, and Johnson) and compared these with values in the
literature. The mean value for the photometric indices is
CrB
from three photometric systems
(Strömgren, Geneva, and Johnson) and compared these with values in the
literature. The mean value for the photometric indices is
![]() K,
and the mean of the literature values is
K,
and the mean of the literature values is
![]() K.
This is a typical example of the large scatter
found for chemically peculiar A stars.
However, since the rms scatter is large, the results summarized by Netopil et al. (2008)
are in acceptable agreement with our new determination. It is worth
stressing that our determination is the first that is not affected by
photometric calibration errors or interstellar reddening
and is only weakly dependent on the adopted limb darkening.
K.
This is a typical example of the large scatter
found for chemically peculiar A stars.
However, since the rms scatter is large, the results summarized by Netopil et al. (2008)
are in acceptable agreement with our new determination. It is worth
stressing that our determination is the first that is not affected by
photometric calibration errors or interstellar reddening
and is only weakly dependent on the adopted limb darkening.
Table 3: Measured quantities and derived fundamental parameters.
3.3 The evolutionary status and mass of 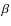 CrB
CrB
To investigate the evolutionary status of the two components of
![]() CrB,
we compare the observed
CrB,
we compare the observed ![]() and radius with isochrones from the BASTI grid (Pietrinferni
et al. 2004) as
shown in Fig. 3.
To transform the mass fraction of heavy elements (Z)
of the isochrones to spectroscopic [Fe/H] values, we use the solar
value
and radius with isochrones from the BASTI grid (Pietrinferni
et al. 2004) as
shown in Fig. 3.
To transform the mass fraction of heavy elements (Z)
of the isochrones to spectroscopic [Fe/H] values, we use the solar
value ![]() (Caffau et al. 2009),
i.e.
(Caffau et al. 2009),
i.e.
![]() .
We assume an uncertainty of
.
We assume an uncertainty of ![]() on
on ![]() ,
which corresponds to
,
which corresponds to ![]() dex
on [Fe/H].
dex
on [Fe/H].
In Fig. 3
we show two sets of isochrones with
![]() and +0.28. The higher metallicity appears to be in better agreement
with the location of the B component. Kurtz
et al. (2007) find [Fe- II/
and +0.28. The higher metallicity appears to be in better agreement
with the location of the B component. Kurtz
et al. (2007) find [Fe- II/
![]() from
11 lines of singly ionized Fe.
This is the metallicity in the photosphere, but we assume it represents
the entire star. Since radial stratification of Fe is known to be
present in roAp stars, our assumed metallicity is an approximation, but
it seems to be supported by the agreement with the location of the
stars in the radius-
from
11 lines of singly ionized Fe.
This is the metallicity in the photosphere, but we assume it represents
the entire star. Since radial stratification of Fe is known to be
present in roAp stars, our assumed metallicity is an approximation, but
it seems to be supported by the agreement with the location of the
stars in the radius-
![]() diagram in Fig. 3.
With this assumption, we determine the age to be
diagram in Fig. 3.
With this assumption, we determine the age to be
![]() Gyr
and the masses of the components to be
Gyr
and the masses of the components to be
![]() and
and ![]() .
These ``evolutionary masses'' are in good agreement with the dynamical
masses determined by North
et al. (1998):
.
These ``evolutionary masses'' are in good agreement with the dynamical
masses determined by North
et al. (1998):
![]() and
and
![]() .
.
![\begin{figure}
\par\includegraphics[width=9cm, angle=0]{13405fg3.eps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13405-09/Timg157.png)
|
Figure 3:
Radius-
|
| Open with DEXTER | |
4 Discussion and conclusion
We have determined the effective temperature of the primary component
of the binary ![]() CrB
using a technique that is
only weakly model-dependent. We used interferometric data to measure
the angular diameter and the fluxes were constrained using NACO J,K
measurements of
each individual component in the binary.
CrB
using a technique that is
only weakly model-dependent. We used interferometric data to measure
the angular diameter and the fluxes were constrained using NACO J,K
measurements of
each individual component in the binary.
We determined the primary component of ![]() CrB to have
CrB to have
![]() K.
In comparison, literature values for the combined star span 7230 to
8700 K (considering 1-
K.
In comparison, literature values for the combined star span 7230 to
8700 K (considering 1-![]() uncertainties).
From a similar analysis of flux data and interferometric data
on the roAp star
uncertainties).
From a similar analysis of flux data and interferometric data
on the roAp star ![]() Cir,
we found
Cir,
we found ![]() K
(Bruntt et al. 2008).
For that star the literature values also span a wide range
from 7470 to 8730 K. It is interesting that, for
K
(Bruntt et al. 2008).
For that star the literature values also span a wide range
from 7470 to 8730 K. It is interesting that, for ![]() CrB A,
our result is in the middle of the
range of previous estimates while the estimate is at the low end of the
range for
CrB A,
our result is in the middle of the
range of previous estimates while the estimate is at the low end of the
range for ![]() Cir.
If we only compare
Cir.
If we only compare ![]() estimates from the same photometric system,
Kochukhov & Bagnulo (2006)
find
estimates from the same photometric system,
Kochukhov & Bagnulo (2006)
find ![]() K for
K for ![]() CrB
and
CrB
and ![]() K for
K for ![]() Cir.
We must remember that the photometric index of
Cir.
We must remember that the photometric index of ![]() CrB includes both
components
and will always give a systematically low temperature. Taking this into
account,
the photometric values from Kochukhov
& Bagnulo (2006) seem to agree with our fundamental
(i.e. model-independent)
CrB includes both
components
and will always give a systematically low temperature. Taking this into
account,
the photometric values from Kochukhov
& Bagnulo (2006) seem to agree with our fundamental
(i.e. model-independent) ![]() values within about
values within about ![]() K.
It will be necessary to make interferometric measurements of several
more of the brightest Ap stars to be able to improve the
K.
It will be necessary to make interferometric measurements of several
more of the brightest Ap stars to be able to improve the
![]() scale of these peculiar stars.
scale of these peculiar stars.
Accurate determinations of
![]() have a strong impact on the
asteroseismic modelling in future work.
The roAp star
have a strong impact on the
asteroseismic modelling in future work.
The roAp star ![]() Cir
was observed for 84 days with the 52 mm
star tracker on the now defunct WIRE satellite.
From the light curves Bruntt
et al. (2009) detected five
frequencies with two that had not been observed before. These two lie
symmetrically around the well-known dominant mode at 2442
Cir
was observed for 84 days with the 52 mm
star tracker on the now defunct WIRE satellite.
From the light curves Bruntt
et al. (2009) detected five
frequencies with two that had not been observed before. These two lie
symmetrically around the well-known dominant mode at 2442 ![]() Hz to form a
triplet. Bruntt et al. (2009)
interpreted the equidistant separation as half the large separation.
Combining this with the new
Hz to form a
triplet. Bruntt et al. (2009)
interpreted the equidistant separation as half the large separation.
Combining this with the new ![]() ,
the properties of the star could be constrained based on preliminary
theoretical modelling of the observed pulsation modes.
To obtain similar results for
,
the properties of the star could be constrained based on preliminary
theoretical modelling of the observed pulsation modes.
To obtain similar results for ![]() CrB would be
worthwhile
now that all ingredients for the modelling of the star are available,
making it the second roAp star with well-established fundamental
atmospheric parameters.
This would require an ambitious asteroseismic campaign (Kurtz et al. 2007)
using a network of telescopes with stable spectrographs
like the Stellar Observations Network Group (SONG; Grundahl et al. 2008).
CrB would be
worthwhile
now that all ingredients for the modelling of the star are available,
making it the second roAp star with well-established fundamental
atmospheric parameters.
This would require an ambitious asteroseismic campaign (Kurtz et al. 2007)
using a network of telescopes with stable spectrographs
like the Stellar Observations Network Group (SONG; Grundahl et al. 2008).
Our understanding of roAp stars would benefit from obtaining
interferometric angular diameters of more targets. However, even with
the
most sensitive beam combiners currently available, only a handful are
bright enough to yield a radius measurement to better than 2%.
Having now measured ![]() Cir
and
Cir
and ![]() CrB,
we next propose to observe
CrB,
we next propose to observe ![]() Equ
and 10 Aql.
Equ
and 10 Aql.
The authors would like to thank all the CHARA Array and Mount Wilson Observatory daytime and nighttime staff for their support. The CHARA Array was constructed with funding from Georgia State University, the National Science Foundation, the W. M. Keck Foundation, and the David and Lucile Packard Foundation. The CHARA Array is operated by Georgia State University with support from the College of Arts and Sciences, from the Research Program Enhancement Fund administered by the Vice President for Research, and from the National Science Foundation under NSF Grant AST 0606958. S.T.R. acknowledges partial support from NASA grant NNH09AK731. M.S.C. acknowledges the support of the Portuguese MCTES and of the FSE, of the European Union, through the programme POPH. I.M.B. would like to acknowledge the support from the Fundação para a Ciência e Tecnologia (Portugal) through the grant SFRH/BD/41213/2007. L.L.K. is supported by the Lendület programme of the Hungarian Academy of Sciences. This research has made use of the Washington Double Star Catalog maintained at the US Naval Observatory. This work received the support of PHASE, the high angular resolution partnership between ONERA, Observatoire de Paris, CNRS, and University Denis Diderot Paris 7. This research took advantage of the SIMBAD and VIZIER databases at the CDS, Strasbourg (France), and NASA's Astrophysics Data System Bibliographic Services.
References
- Alekseeva, G. A., Arkharov, A. A., Galkin, V. D. et al. 1996, Baltic Astron., 5, 603 [Google Scholar]
- Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS] [Google Scholar]
- Bohlin, R. C., & Gilliland, R. L. 2004, AJ, 127, 3508 [NASA ADS] [CrossRef] [Google Scholar]
- Breger, M. 1976, ApJS, 32, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Bruntt, H., North, J. R., Cunha, M. et al. 2008, MNRAS, 386, 2039 [NASA ADS] [CrossRef] [Google Scholar]
- Bruntt, H., Kurtz, D. W., Cunha, M. S. et al. 2009, MNRAS, 396, 1189 [NASA ADS] [CrossRef] [Google Scholar]
- Caffau, E., Maiorca, E., Bonifacio, P. et al. 2009, A&A, 498, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campbell, W. W., & Moore, J. H. 1907, Lick Observatory Bulletin, 4, 162 [NASA ADS] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Coudé du Foresto, V., Borde, P. J., Mérand, A. et al. 2003, in SPIE Conf. Ser. 4838, ed. W. A. Traub, 280 [Google Scholar]
- Coudé Du Foresto, V., Ridgway, S., & Mariotti, J.-M. 1997, A&AS, 121, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, A. N. 2000, Allen's astrophysical quantities (Springer-Verlag) [Google Scholar]
- Grundahl, F., Christensen-Dalsgaard, J., Arentoft, T. et al. 2008, Communications in Asteroseismology, 157, 273 [NASA ADS] [Google Scholar]
- Hatzes, A. P., & Mkrtichian, D. E. 2004, MNRAS, 351, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Horch, E. P., Meyer, R. D., & van Altena, W. F. 2004, AJ, 127, 1727 [NASA ADS] [CrossRef] [Google Scholar]
- Jamar, C., Macau-Hercot, D., Monfils, A. et al. 1976, Ultraviolet bright-star spectrophotometric catalogue. A compilation of absolute spectrophotometric data obtained with the Sky Survey Telescope (S2/68) on the European Astronomical Satellite TD-1 [Google Scholar]
- Kamper, K. W., McAlister, H. A., & Hartkopf, W. I. 1990, AJ, 100, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Ségransan, D., & Coudé du Foresto, V. 2004a, A&A, 425, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004b, A&A, 426, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kochukhov, O., & Bagnulo, S. 2006, A&A, 450, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kochukhov, O., Landstreet, J. D., Ryabchikova, T., Weiss, W. W., & Kupka, F. 2002, MNRAS, 337, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Kochukhov, O., Ryabchikova, T., Bagnulo, S., & Lo Curto, G. 2008, Contributions of the Astronomical Observatory Skalnate Pleso, 38, 423 [NASA ADS] [Google Scholar]
- Kreidl, T. J. 1991, MNRAS, 248, 701 [NASA ADS] [Google Scholar]
- Kurtz, D. W. 1989, MNRAS, 238, 261 [NASA ADS] [Google Scholar]
- Kurtz, D. W., Elkin, V. G., & Mathys, G. 2007, MNRAS, 380, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Lenzen, R., Hofmann, R., Bizenberger, P., & Tusche, A. 1998, in SPIE Conf. Ser. 3354, ed. A. M. Fowler, 606 [Google Scholar]
- Masciadri, E., Brandner, W., Bouy, H. et al. 2003, A&A, 411, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mérand, A., Bordé, P., & Coudé Du Foresto, V. 2005, A&A, 433, 1155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mérand, A., Coudé du Foresto, V., Kellerer, A. et al. 2006, in SPIE Conf. Ser., 6268 [Google Scholar]
- Morel, M., & Magnenat, P. 1978, A&AS, 34, 477 [NASA ADS] [Google Scholar]
- Muterspaugh, M. W., Lane, B. F., Kulkarni, S. R. et al. 2006, ApJ, 653, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- Netopil, M., Paunzen, E., Maitzen, H. M., North, P., & Hubrig, S. 2008, A&A, 491, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neubauer, F. J. 1944, ApJ, 99, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Nikolaev, S., Weinberg, M. D., Skrutskie, M. F. et al. 2000, AJ, 120, 3340 [NASA ADS] [CrossRef] [Google Scholar]
- North, P., Carquillat, J.-M., Ginestet, N., Carrier, F., & Udry, S. 1998, A&AS, 130, 223 [Google Scholar]
- Oetken, L., & Orwert, R. 1984, Astron. Nachr., 305, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., & ESA, eds. 1997, The HIPPARCOS and TYCHO catalogues. Astrometric and photometric star catalogues derived from the ESA HIPPARCOS Space Astrometry Mission, ESA Special Publication, 1200 [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Renson, P., & Manfroid, J. 2009, A&A, 498, 961 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rousset, G., Lacombe, F., Puget, P. et al. 2003, in SPIE Conf. Ser. 4839, ed. P. L. Wizinowich, & D. Bonaccini, 140 [Google Scholar]
- Rufener, F. 1988, Catalogue of stars measured in the Geneva Observatory photometric system : 4 : 1988 (Sauverny: Observatoire de Genève) [Google Scholar]
- Rufener, F., & Nicolet, B. 1988, A&A, 206, 357 [NASA ADS] [Google Scholar]
- Ryabchikova, T., Nesvacil, N., Weiss, W. W., Kochukhov, O., & Stütz, C. 2004, A&A, 423, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Söderhjelm, S. 1999, A&A, 341, 121 [Google Scholar]
- ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T. et al. 2005, ApJ, 628, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A. A. 1984, Pisma Astronomicheskii Zh., 10, 293 [Google Scholar]
- Trilling, D. E., Stansberry, J. A., Stapelfeldt, K. R. et al. 2007, ApJ, 658, 1289 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F., 2007, Astrophysics and Space Science Library, 250, Hipparcos, the New Reduction of the Raw Data [Google Scholar]
- Weiss, W. W., & Schneider, H. 1989, A&A, 224, 101 [NASA ADS] [Google Scholar]
Footnotes
- ... observations
![[*]](/icons/foot_motif.png)
- Based on observations made with ESO telescopes at the La Silla Paranal Observatory, under ESO DDT programme 281.D-5020(A).
- ... page
![[*]](/icons/foot_motif.png)
- http://www.eso.org/instruments/naco/inst/filters.html
- ... IRAF
![[*]](/icons/foot_motif.png)
- IRAF is distributed by the NOAO, which is operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.
- ... Yorick
![[*]](/icons/foot_motif.png)
- http://yorick.sourceforge.net/
- ... archive
![[*]](/icons/foot_motif.png)
- http://sdc.laeff.inta.es/cgi-ines/IUEdbsMY/
- ...
IUEDAC
![[*]](/icons/foot_motif.png)
- http://archive.stsci.edu/iue/iuedac.html
- ... bands
![[*]](/icons/foot_motif.png)
- We note that Bohlin
& Gilliland (2004) recently found
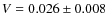 for Vega.
for Vega.
All Tables
Table 1: Interferometric calibrators selected from Mérand et al. (2005).
Table 2: Journal of observations.
Table 3: Measured quantities and derived fundamental parameters.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm, angle=0]{13405fg1-colour.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13405-09/Timg39.png)
|
Figure 1:
Average NACO image of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm]{13405fg2.eps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13405-09/Timg97.png)
|
Figure 2:
The solid black line shows the flux distribution for |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm, angle=0]{13405fg3.eps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13405-09/Timg157.png)
|
Figure 3:
Radius-
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.