| Issue |
A&A
Volume 481, Number 2, April II 2008
|
|
|---|---|---|
| Page(s) | 519 - 527 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361:20078059 | |
| Published online | 17 January 2008 | |
Nebular gas drag and co-orbital system dynamics
1
São Paulo State University – UNESP, Grupo de Dinâmica Orbital & Planetologia, CP 205, Guaratinguetá, CEP 12516-410, SP, Brazil e-mail: madamechanut@terra.com.br; ocwinter@feg.unesp.br
2
São Paulo State University – UNESP, DCCE – IBILCE, São Jose do Rio Preto, SP, Brazil e-mail: tsuchida@ibilce.unesp.br
Received:
11
June
2007
Accepted:
7
December
2007
Aims. We study trajectories of planetesimals whose orbits decay due to gas drag in a primordial solar nebula
and are perturbed by the gravity of the secondary body on an eccentric orbit whose mass ratio takes values from 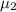 = 10-7 to
= 10-7 to 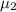 = 10-3 increasing ten times at each step. Each planetesimal ultimately suffers one of the three possible fates: (1) trapping in a mean
motion resonance with the secondary body; (2) collision with the secondary body and consequent increase
of its mass; or (3) diffusion after crossing the orbit of the secondary body.
= 10-3 increasing ten times at each step. Each planetesimal ultimately suffers one of the three possible fates: (1) trapping in a mean
motion resonance with the secondary body; (2) collision with the secondary body and consequent increase
of its mass; or (3) diffusion after crossing the orbit of the secondary body.
Methods. We take the Burlirsh-Stoer numerical algorithm in order to integrate the Newtonian equations of the planar, elliptical restricted three-body problem with the secondary body and the planetesimal orbiting the primary. It is assumed that there is no interaction among planetesimals, and also that the gas does not affect the orbit of the secondary body.
Results. The results show that the optimal value of the gas drag constant k for the 1:1 resonance is between 0.9 and 1.25, representing a meter size planetesimal for each AU of orbital radius. In this study, the conditions of the gas drag are such
that in theory, L4 no longer exists in the circular case for a critical value of k that defines a limit size of the planetesimal, but for a secondary body with an eccentricity
larger than 0.05 when 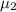 = 10-6, it reappears. The decrease of the cutoff collision radius increase the difusions but does not affect the distribution of trapping. The contribution to the mass accretion of the secondary body is over 40%
with a collision radius
= 10-6, it reappears. The decrease of the cutoff collision radius increase the difusions but does not affect the distribution of trapping. The contribution to the mass accretion of the secondary body is over 40%
with a collision radius  and less than 15% with
and less than 15% with  for
for 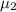 = 10-7. The trappings no longer occur when the drag constant k reachs 30.
That means that the size limit of planetesimal trapping is 0.2 m per AU of orbital radius. In most cases, this accretion occurs for a weak gas drag and small
secondary eccentricity. The diffusions represent most of the simulations showing that gas drag is an efficient process in scattering planetesimals and that the trapping of planetesimals in the 1:1 resonance is a less probable fate.
These results depend on the specific drag force chosen.
= 10-7. The trappings no longer occur when the drag constant k reachs 30.
That means that the size limit of planetesimal trapping is 0.2 m per AU of orbital radius. In most cases, this accretion occurs for a weak gas drag and small
secondary eccentricity. The diffusions represent most of the simulations showing that gas drag is an efficient process in scattering planetesimals and that the trapping of planetesimals in the 1:1 resonance is a less probable fate.
These results depend on the specific drag force chosen.
Key words: planets and satellites: formation / minor planets, asteroids / celestial mechanics
© ESO, 2008
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


