Gravito-turbulent bi-fluid protoplanetary discs - I. An analytical perspective to stratification

Home

All issues

Volume 697 (May 2025)

A&A, 697 (2025) A126

Full HTML

Open Access

Table 1

Definitions.

Name	Symbol + Definition
General
Keplerian frequency	Ω_K
Stopping time	τ_f
Stokes number	St = τ_f Ω_K
Vertical turbulent diffusivity	K_t
Dimensionless in plane α-viscosity	α_s
Dimensionless vertical α-viscosity	$α_{z} = κ_{t} Ω_{K} / c_{g}^{2}$ ${\alpha _z} = {\kappa _t}{\Omega _K}/c_g^2$
Vertical Schmidt number	Sc_z = α_S/α_z

Gas

Gas sound speed	c_g
Effective gas sound speed	${\tilde{c}}_{q} = \sqrt{1 + α_{z}} c_{q}$ ${\tilde c_q} = \sqrt {1 + {\alpha _z}} {c_q}$
Surface density of gas	∑_g
Gas Toomre parameter	$Q_{g} = \frac{{\tilde{c}}_{g} Ω_{K}}{π G Σ_{g}}$ ${Q_g} = \frac{{{{\widetilde c}_g}{\Omega _K}}}{{\pi G{\Sigma _g}}}$
Gas turbulent pressure scale height	$H_{g} = {\tilde{c}}_{g} / Ω_{K}$ ${H_g} = {\rm{ }}{\widetilde c_g}/{\Omega _K}$
Gas gravito-turbulent pressure scale height	$H_{g}^{s g}$ $H_g^{sg}$

Dust

Dust sound speed	$c_{d} = \sqrt{κ_{t} / τ_{f}}$ ${c_d} = \sqrt {{\kappa _t}/{\tau _f}}$ (Eq. (23))
Midplane dust sound speed	$c_{d, mid} = \sqrt{\frac{α_{z}}{S t}} c_{g}$ ${c_{d,{\rm{mid}}}} = \sqrt {\frac{{{\alpha _{\rm{z}}}}}{{{\rm{St}}}}} {c_g}$
Effective dust sound speed	${\tilde{c}}_{d} = \frac{ξ}{\sqrt{1 + ξ^{2}}} c_{d, mid}$ ${\widetilde c_d} = \frac{\xi }{{\sqrt {1 + {\xi ^2}} }}{c_{d,{\rm{mid}}}}$
Surface density of dust	∑_d
Effective dust Toomre parameter	$Q_{d} = \frac{{\tilde{c}}_{d} Ω_{K}}{π G Σ_{d}}$ ${Q_d} = \frac{{{{\widetilde c}_d}{\Omega _K}}}{{\pi G{\Sigma _d}}}$
Dust diffusive scale height	$H_{d} = {\tilde{c}}_{d} / Ω_{K}$ ${H_d} = {\widetilde {\rm{c}}_{\rm{d}}}/{\Omega _K}$
Dust gravito-diffusive scale height	$H_{d}^{s g}$ $H_d^{sg}$ (Eq. (23))

Gas and dust combined

Gas-to-dust temperature	$ξ = \frac{{\tilde{c}}_{g}}{c_{d, mid}} = \sqrt{\frac{(1 + α_{z})}{α_{z}} St}$ $\xi = \frac{{{{\widetilde c}_g}}}{{{c_{d,{\rm{mid}}}}}} = \sqrt {\frac{{(1 + {\alpha _{\rm{z}}})}}{{{\alpha _{\rm{z}}}}}{\rm{ St}}}$
Effective gas-to-dust temperature	$\tilde{ξ} = \frac{{\tilde{c}}_{g}}{{\tilde{c}}_{d, mid}} = \sqrt{1 + ξ^{2}}$ $\widetilde \xi = \frac{{{{\widetilde c}_g}}}{{{{\widetilde c}_{d,{\rm{mid}}}}}} = \sqrt {1 + {\xi ^2}}$
3D Toomre parameter	$Q_{i}^{3 D} = \sqrt{\frac{π}{2}} \frac{Ω_{K}^{2}}{π^{2} G ρ_{i, mid}}$ $Q_i^{3D} = \sqrt {\frac{\pi }{2}} \frac{{\Omega _K^2}}{{{\pi ^2}G{\rho _{i,{\rm{mid}}}}}}$
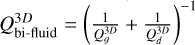General Toomre parameter for a turbulent bi-fluid	$Q_{^{b i - f l u i d}}^{3 D} = {(\frac{1}{Q_{g}^{3 D}} + \frac{1}{Q_{d}^{3 D}})}^{- 1}$ $\[Q_{^{bi - fluid}}^{3D} = {\left( {\frac{1}{{Q_g^{3D}}} + \frac{1}{{Q_d^{3D}}}} \right)^{ - 1}}\$

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.