Fig. 3.
Download original image
In the coronal condition and ![]() ,
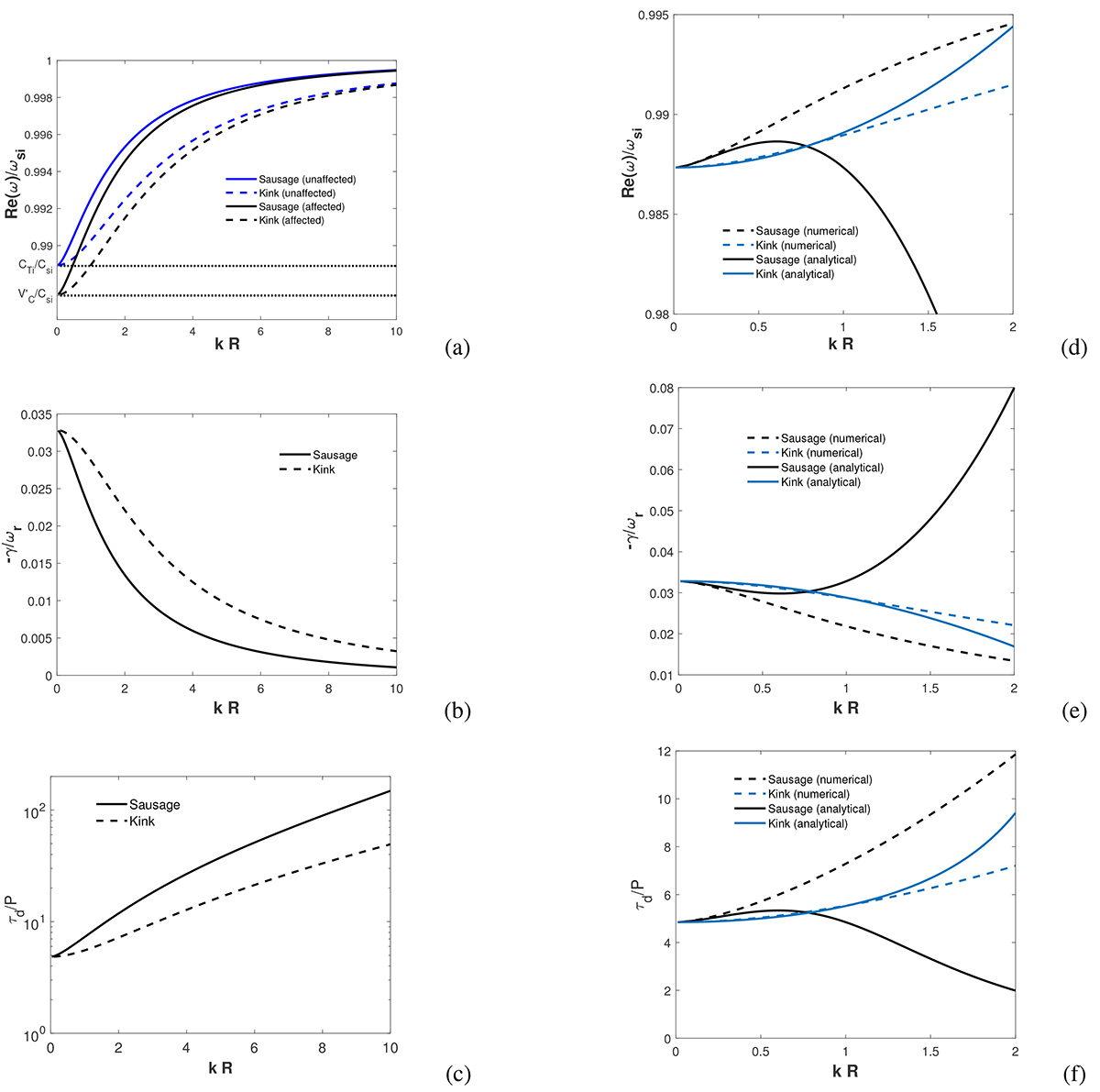
, ![]() : (a) numerical solution of the dispersion relation Eq. (18), computed by MATLAB, for the frequency (phase speed) normalized by the internal acoustic frequency (acoustic speed) (ℜ𝔢(ω)/ωsi ≡ vph/Csi) of the fundamental slow sausage mode without consideration of the thermal misbalance effect (unaffected) (solid blue line) and with consideration of the thermal misbalance effect (affected) (solid black line), as well as the fundamental slow kink mode unaffected (dashed blue line) and affected (dashed black line) by the thermal misbalance versus the normalized longitudinal wavenumber (kR). (b) Damping rate to the frequency ratio (−γ/ωr) of fundamental states of the affected slow sausage (solid line) and kink (dashed line) modes by the thermal misbalance versus the normalized longitudinal wavenumber (kR). (c) Damping time to the wave period ratio (τd/P) of the affected slow sausage (solid line) and kink (dashed line) modes by the thermal misbalance versus the normalized longitudinal wavenumber (kR). For comparison, the analytical results obtained by Eqs. (25, 32) are shown by the black and blue solid curves in panels d, e, f.
: (a) numerical solution of the dispersion relation Eq. (18), computed by MATLAB, for the frequency (phase speed) normalized by the internal acoustic frequency (acoustic speed) (ℜ𝔢(ω)/ωsi ≡ vph/Csi) of the fundamental slow sausage mode without consideration of the thermal misbalance effect (unaffected) (solid blue line) and with consideration of the thermal misbalance effect (affected) (solid black line), as well as the fundamental slow kink mode unaffected (dashed blue line) and affected (dashed black line) by the thermal misbalance versus the normalized longitudinal wavenumber (kR). (b) Damping rate to the frequency ratio (−γ/ωr) of fundamental states of the affected slow sausage (solid line) and kink (dashed line) modes by the thermal misbalance versus the normalized longitudinal wavenumber (kR). (c) Damping time to the wave period ratio (τd/P) of the affected slow sausage (solid line) and kink (dashed line) modes by the thermal misbalance versus the normalized longitudinal wavenumber (kR). For comparison, the analytical results obtained by Eqs. (25, 32) are shown by the black and blue solid curves in panels d, e, f.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


