EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 693 (January 2025) A&A, 693 (2025) A181 Full HTML
Open Access
Issue
A&A
Volume 693, January 2025
Article Number A181
Number of page(s) 9
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/202452977
Published online 15 January 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Hydrogen is the most abundant element in the Universe and is a key factor in our characterization of the physical conditions of the interstellar medium (ISM), star formation, and the chemical evolution of the molecular Universe (Oka 2013). Among its molecular forms (H2, H2+$\[\mathrm{H}_{2}^{+}\]$ and H3+$\[\mathrm{H}_{3}^{+}\]$), H3+$\[\mathrm{H}_{3}^{+}\]$ is an efficient protonator, as the proton affinity of H2 (422.3 kJ/mol) is smaller than that of most stable molecules (Watson 1973; Herbst & Klemperer 1973; Millar et al. 1989; Pagani et al. 1992; Tennyson 1995; McCall & Oka 2000; Oka 2012). For an atom or molecule (generally M), the reaction is M+H3+→MH++H2.$\[\mathrm{M}+\mathrm{H}_{3}^{+} \rightarrow \mathrm{MH}^{+}+\mathrm{H}_{2}.\]$(1)

The resulting ionic hydrides trigger the chemistry cycles of many complex molecules in space (Watson 1973; Herbst & Klemperer 1973).

H3+$\[\mathrm{H}_{3}^{+}\]$ has been the subject of many literature reviews (Tennyson 1995; Herbst 2000; Oka 2012, 2013; Gerlich et al. 2012; Miller et al. 2020) and special issues (Oka 2012; Tennyson & Miller 2019). Its infrared spectrum was first detected in the laboratory by Oka (1980) and was later detected in space (Geballe & Oka 1989; Geballe et al. 1999; McCall et al. 1999; Oka 2013). Since then, H3+$\[\mathrm{H}_{3}^{+}\]$ has been used to probe spatial conditions as a thermometer and a clock of cold molecular clouds (Oka 2006; Pagani et al. 2011) and as a measure of the ionization rate of the ISM (Le Petit et al. 2004; Indriolo & McCall 2012) and in the central molecular zone (CMZ) of our Galaxy (Le Petit et al. 2016). Its infrared spectrum has been theoretically characterized with spectroscopic accuracy (Polyansky et al. 2012; Bachorz et al. 2009; Velilla et al. 2008; Tennyson et al. 2017; Furtenbacher et al. 2013) based on highly accurate potential energy surfaces (PESs) (Jaquet et al. 1998; Tennyson 1995; Cencek et al. 1998; Pavanello et al. 2012; Mizus et al. 2018; Bachorz et al. 2009; Velilla et al. 2010; Röhse et al. 1994; Viegas et al. 2007; Ghosh et al. 2017).

The absence of a permanent dipole moment in the highly symmetric triangular equilibrium geometry in its ground vibrational state makes H3+$\[\mathrm{H}_{3}^{+}\]$ unobservable with pure rotational spectroscopy. H3+$\[\mathrm{H}_{3}^{+}\]$ is thus only observable through its vibrational spectrum. The recent availability of high-sensitivity infrared observations thanks to the James Webb Spatial Telescope (JWST) has even allowed the detection of the infrared emission of H3+$\[\mathrm{H}_{3}^{+}\]$ in ultraluminous infrared galaxies (ULIRGs; Pereira-Santaella et al. 2024). This study demonstrates the feasibility of using H3+$\[\mathrm{H}_{3}^{+}\]$ as a probe of the physical conditions of different objects in the ISM.

The H3+$\[\mathrm{H}_{3}^{+}\]$ + H2 collisional rates, including ortho and para transitions of the two species, have been reported in several theoretical studies (Oka & Epp 2004; Hugo et al. 2009; Park & Light 2007; Gómez-Carrasco et al. 2012). However, the collisional rates with atomic hydrogen remain unavailable despite their potential importance in partially molecular environments, such as diffuse and translucent clouds and in the CMZ of our Galaxy (Miller et al. 2020; Oka 2012).

The deuteration rates in D + H3+$\[\mathrm{H}_{3}^{+}\]$ and isotopic variant reactive collisions have been studied experimentally (Hillenbrand et al. 2019; Bowen et al. 2021). Due to the vibrational excitation during which H3+$\[\mathrm{H}_{3}^{+}\]$ is initially formed, a purely experimental determination of the deuteration rates is not possible. For this reason, a combined experimental and theoretical treatment has been used to determine the reactive deuteration rate constants. In such studies, tunneling through a potential barrier was estimated theoretically, but produced rate constants of lower than 10−12 cm3 s−1 below 100 K. Ring polymer molecular dynamics calculations (Bulut et al. 2019) of these reactions, including quantum effects, are in relatively close agreement with these combined experimental and theoretical results (Hillenbrand et al. 2019; Bowen et al. 2021) above 200 K, but below this temperature there is no consensus on the role of the tunneling rate. Using the tunneling values reported by Bowen et al. (2021) as an upper limit, we can conclude that the reactive exchange rate is lower than 10−12 cm3 s−1 below 100 K and is lower than 10−10 cm3 s−1 below 300 K. Therefore, H+H3+$\[\mathrm{H}_{3}^{+}\]$ rotational inelastic collisions can be considered as the dominant process below 100 K.

As shown in Fig. 1, the exchange barrier is of approximately 1258 cm−1 according to a very accurate potential energy surface (PES) recently developed for studying the H2+H2+→H3++H$\[\mathrm{H}_{2}+\mathrm{H}_{2}^{+} \rightarrow \mathrm{H}_{3}^{+}+\mathrm{H}\]$ reaction (del Mazo-Sevillano et al. 2024). The complete quantum treatment of inelastic and reactive dynamics, especially considering ortho–para permutation symmetry, is prohibitively costly, and new methods are needed to confront this problem. Before addressing this full exact treatment, in this work we study the H+H3+$\[\mathrm{H}_{3}^{+}\]$ rotational inelastic collisions at low temperatures – which mostly correspond to energies below the top of the barrier – to determine their influence on the excitation temperature of H3+$\[\mathrm{H}_{3}^{+}\]$.

In diffuse interstellar clouds, the excitation temperature T12 ( H3+$\[\mathrm{H}_{3}^{+}\]$) derived from the lowest two levels of H3+$\[\mathrm{H}_{3}^{+}\]$ is systematically lower than the gas kinetic temperature as derived from the H2 lowest levels, T01(H2). Le Bourlot et al. (2024, here-after Paper I) provide a thorough discussion of the H3+$\[\mathrm{H}_{3}^{+}\]$ excitation mechanisms and propose an explanation for this observation. T12(H3+$\[\mathrm{H}_{3}^{+}\]$) is defined as T12(H3+)=E12/ ln⁡(g2x1g1x2),$\[T_{12}(\mathrm{H}_{3}^{+})=E_{12} / ~\ln \left(\frac{g_{2} x_{1}}{g_{1} x_{2}}\right),\]$(2)

where E12 = 32.86 K is the energy difference between the two levels, g2/g1 = 2, and x1 and x2 are the populations of levels 1 and 2, respectively. This difference comes as a surprise, as H3+$\[\mathrm{H}_{3}^{+}\]$ is formed in the region where H2 dominates and the lowest levels of both species should be thermalized at the gas kinetic temperature. As in most lines of sight, only these two lowest levels are observed, and all interpretations of H3+$\[\mathrm{H}_{3}^{+}\]$ excitation rely on this single value.

Paper I shows that the difference arises from the fact that state-specific formation and destruction processes of H3+$\[\mathrm{H}_{3}^{+}\]$ must be accounted for when computing the detailed, balanced steady state for this molecule. In essence, a significant fraction of the exothermicity of the formation reaction H2+$\[\mathrm{H}_{2}^{+}\]$ + H2 populates high lying levels of H3+$\[\mathrm{H}_{3}^{+}\]$ (del Mazo-Sevillano et al. 2024), favoring the para form at low temperature due to nuclear spin selection rules (Oka 2004). These levels decay efficiently by radiative transitions to the lowest accessible level, which is either the para-(1, 1, −) level or the ortho-(3, 3, −) level (which is metastable). However, the lower-lying ortho-(1, 0, +) level can only be populated by slow reactive collisions, mainly with H2. This process comes into competition with the destruction of the molecule by dissociative recombination with e−, leading to an underpopulation of the lowest-lying ortho level compared to a Boltzmann population at the gas kinetic temperature.

This mechanism is very sensitive to all the various state-to-state rates used. In the absence of better data, in Paper I, collisions with H are approximated by taking H2 rate coefficients scaled by a mass factor of 2$\[\sqrt{2}\]$. This was done for all transitions, including reactive ones. However, if reactive rate coefficients with H are negligible, this may lead to significant differences in a medium that is not fully molecular. Le Bourlot et al. (2024) also showed that possible small differences in the dissociative recombination rates of ortho and para modifications may have a significant impact on the excitation temperature.

In the following, the inelastic cross sections and rate constants are presented and discussed in Sect. 2 and their impact on two typical examples of diffuse lines of sight is presented in Sect. 3.

thumbnail Fig. 1

Minimum energy path for the H+H3+⟶H3++H$\[\mathrm{H}+\mathrm{H}_{3}^{+} \longrightarrow \mathrm{H}_{3}^{+}+\mathrm{H}\]$ exchange reaction for the PES by del Mazo-Sevillano et al. (2024).

2 Inelastic scattering results

In this work, we use the full-dimensional PES developed by del Mazo-Sevillano et al. (2024), which considers all the degrees of freedom of the four atom systems very accurately using a neural network (NN) method (del Mazo-Sevillano et al. 2024). In addition, this PES very accurately describes the long-range interaction through the use of a triatom-in-molecules (TRIM) formalism (Sanz-Sanz et al. 2013, 2015) originally proposed for the H5+$\[\mathrm{H}_{5}^{+}\]$ system (Aguado et al. 2010).

The H + H3+$\[\mathrm{H}_{3}^{+}\]$ inelastic rotational collisions are studied below 1500 cm−1 of translational energy, considering the rigid-rotor approach and the ortho–para symmetry of H3+$\[\mathrm{H}_{3}^{+}\]$. To this aim, we proceed in two steps. First, the triatomic levels of H3+$\[\mathrm{H}_{3}^{+}\]$ are calculated in full dimension using permutationally invariant basis set functions represented in hyperspherical coordinates (Aguado et al. 2000; Sanz et al. 2001), as described in Appendix A. Second, the inelastic rotational cross sections and rate constants are calculated using a close-coupling approach within a rigid rotor approach, using a symmetric top + atom adapted from the study of NH3 + He (Green 1980) and briefly described in Appendix B.

The close-coupling equations are resolved as follows. A radial grid of 5000 equidistant points is used to describe R, from 1 to 100 bohr. In view of the energy requirements discussed for the basis selection (triatomic basis up to 4100 cm−1), in this study we considered 4000 equispaced total energies from 70 to 2070 cm−1, with a step of 0.5 cm−1, measured from the unphysical ground A1, J = 0, (0, 00) H3+$\[\mathrm{H}_{3}^{+}\]$ level. The calculations are done up to a maximum total angular momentum of J = 30, and separately for Γt = A2 (ortho-H3+$\[\mathrm{H}_{3}^{+}\]$) and E (para-H3+$\[\mathrm{H}_{3}^{+}\]$) representations. The H3+$\[\mathrm{H}_{3}^{+}\]$ states finally considered are shown in Fig. 2 for each irreducible representation Γ, and reducing the quantum numbers to (j, ω, pt, Γt), which are the only ones needed in the scattering calculations presented below (see Appendix A).

Let us recall that the channels α ≡ (β, ℓ) naturally arise from the triatomic levels β ≡ (j, ω, pt, Γt) by introducing in each case all the allowed values for ℓ = |J − j|, . . ., J + j. This implies that the number of channels rapidly increases with increasing total angular momentum J. An additional truncation of channels is imposed. For triatomic levels above j = 6 (1200 cm−1) within the Γt = E representation, the simulated channels are constrained to ℓ ≤ J + j/2. This reduces the computation times, while the net effect on the final rate constants is small – we note that most truncated channels are either predominantly closed or contribute less to the averages.

Transitions involving lower Δj, Δω, and Δpt = 0 are expected to yield larger cross sections, simply because the radial potential coefficients – Vλν, as defined in Eq. (B.5) – connecting them are larger for smaller λ and ν values, as can be seen in Fig. B.2.

It is expected that transitions involving fewer changes in the internal state of the system are more favored – that is, we expect higher σββ′ for lower Δj, Δω, and Δpt = 0. From a mathematical point of view, the transition probability is maximized when the dominant radial coefficients Vλν in that transition are greater. By direct examination of Fig. B.2, it is clear that the coefficients are greater in magnitude for smaller values of λ and ν, with the latter being more critical – for example, Vλ=2,ν=0 is comparable to Vλ=3,ν=3. As long as ν = Δω and λ ≥ Δj, the intuitive rules are perfectly equivalent to the rigorous mathematical criterion.

Apart from this rule, it is important to consider that the channels have an energy threshold. The radial coefficients of the dissociative wave function oscillate with a frequency proportional to 2μ(E−Ejω,pt)$\[\sqrt{2 \mu\left(E-E_{\left.j \omega, p_{t}\right)}\right)}\]$. Having closer thresholds implies similar frequencies, which maximizes the effective radial integrals, yielding larger transition probabilities.

For the Γt = A2 representation (ortho-H3+$\[\mathrm{H}_{3}^{+}\]$), Fig. 3 presents the transitions starting from (1, 0, +), the lowest level in this representation. In this representation, the ω quantum numbers for all the levels are positive integer multiples of three, and the transitions correspond to ν = Δω, which are always multiples of three. In other words, all the transitions in this representation are allowed by symmetry.

Starting from (1,0,+), the most favored transition would be to the (3,0,+) level, as it is energetically close to the entrance level and fulfils Δω = 0, Δj = 2 [Vλ=2,ν=0], and Δpt = 0. In view of Fig. 3, this statement is apparently only true for higher energies, but at lower energies the transitions to (3,3,−) dominate, with Δω = 3, Δj = 2 [Vλ=3,ν=3], and Δpt ≠ 0. The coefficients Vλ=2,ν=0 and Vλ=3,ν=3 are of comparable magnitude, but the (3,3,−) level is closer in energy to the (1,0,+) entrance level. In this situation, it is the energy criterion described above that dominates.

A similar case occurs for the transitions to (5,0,+) [Vλ=4,ν=0]. For energies below its threshold, other less-favored transitions have a higher probability than expected (such as (5,3,−) [Vλ=5,ν=3]). However, once the level opens, its transition probability rapidly increases and finally dominates over the former one.

For the Γt = E representation (para-H3+$\[\mathrm{H}_{3}^{+}\]$), the same propensity rules apply, but some small details must be taken into consideration. This time, for each energy level, there are two degenerate states associated to the ±ω projections. For a generic transition between two levels, β and β′ (each containing two degenerate states ±ω and ±ω′, respectively), four possible sub-transitions may occur. According to the selection rules, two of these subtransitions are always forbidden, while the other two have exactly the same cross section. As a consequence, the final average associated to that transition is in practice equivalent to taking just one of the allowed sub-transitions.

Additionally, as already stated by Bouhafs et al. (2017) for analogous systems, the triatomic levels for this representation have values of ω that are not multiples of three. As a consequence, not all the transitions will have values of ν = Δω that are multiples of three, and so there will be some symmetry-forbidden transitions.

In view of Fig. 4, starting from (1, ±1, −), the most favored transition would be to the (2, ±2, +) level because of its energetic proximity and with Δω = 3, Δj = 1 [Vλ=3,ν=3], Δpt ≠ 0. Then, once the (2, ±1, −) level opens, its transition becomes dominant, as expected: Δω = 0, Δj = 1 [Vλ=1,ν=0], and Δpt = 0.

There is an interesting phenomenon associated to this symmetry representation, which can be exemplified by the transitions to (3, ±2, +) and (4, ±4, +), both of which correspond to the element Vλ=3,ν=3, where Δω = 3, Δpt ≠ 0, with Δj = 2 and Δj = 3, respectively. Therefore, considering their relative energies, one may expect the former level to be more favored; however, as we examine Fig. 4, we see that (4, ±4, +) is indeed the dominant transition. This is because, within Γt = E, there is an extra propensity rule in relation to the sign of ω. Transitions from (1, ±1, −) to (3, ±2, +) imply a change in the sign of ω, while (4, ±4, +) leaves the sign unaltered.

This physically intuitive argument can be algebraically justified if we pay special attention to the expression of the 3-j symbols appearing in the angular elements of the potential; see Eq. (B.6). For the transition to (3, ±2, +), the 3-j element has a value of −0.189, while for (4, ±4, +) this value is 0.333. For this reason, the latter is significantly more favored.

The rate constants share general tendencies in terms of the relative dominance of the transitions, and are shown in Fig. 5 for temperatures between 10 and 300 K, as representative results corresponding to the endothermic transitions starting from (1,0,+) and (1, ±1, −) within the Γt = A2 and Γt = E representations.

The three parameters α, β, and γ obtained from the fit of the results of Fig. 5 to an Arrhenius-type rate constant, k(T)=α(T300)βexp⁡(−γT),$\[k(T)=\alpha\left(\frac{T}{300}\right)^{\beta} \exp \left(\frac{-\gamma}{T}\right),\]$(3)

are listed in Table 1, where k(T) is in cm3 s−1 and the temperatures are in Kelvin.

Additionally, in the Supplementary Information we provide a file containing the calculated state-to-state rate constants at some selected temperatures, that is, for the de-excitation in this case, and in the format required by the Meudon PDR code (Le Petit et al. 2006). This code computes the steady state of a 1D irradiated slab of interstellar gas by solving for chemical, thermal balance, radiative transfer, and statistical equilibrium of many observed species1.

thumbnail Fig. 2

Computed H3+$\[\mathrm{H}_{3}^{+}\]$ rotational levels in the ground vibrational state, conventionally labeled as (j, ω, pt), within each specific irreducible representation, Γ.
thumbnail Fig. 3

Calculated cross sections for the transitions starting from (1,0,+) → (j′,ω′,pt′$\[j^{\prime}, \omega^{\prime}, p_{t}^{\prime}\]$) within the Γt = A2 representation.
thumbnail Fig. 4

Calculated cross sections for the transitions starting from (1,±1,−) within the Γt = E representation.
thumbnail Fig. 5

Calculated state-to-state rate constants for the transitions starting from (1,0,+) within the Γt = A2 (top panel) and E (bottom panel) representations. The fitted curves are represented by the solid black lines, while the computed data are the colored dots.
Table 1

Fitted parameters for the transitions (j, ω, pt) → (j′,ω′,pt′ Γt$\[\mathrm{j}^{\prime}, \omega^{\prime}, \mathrm{p}_{t}^{\prime} ~\Gamma_{t}\]$) within Γt = A2 (1,0,+) and E (1,±,−) representations.

3 Observations and models

In Paper I, the authors discuss the excitation of H3+$\[\mathrm{H}_{3}^{+}\]$ toward nine lines of sight (see their Table 2 and references therein); here, we only consider two of them, HD 110432 and HD 73882. As shown in Table 2, which summarizes the main observational results, the former has a rather low molecular fraction, defined as 2 n(H2)/(2 n(H2) + n(H)) and a warm kinetic temperature, while the latter is colder and has a higher molecular fraction. Here, xObs(H3+$\[\mathrm{H}_{3}^{+}\]$) is the ratio of the column densities of H3+$\[\mathrm{H}_{3}^{+}\]$ and H2, which is believed to be representative of the local fractional ion abundance, and fObs is the molecular fraction towards the line of sight derived from data from Edenhofer et al. (2024), as found in Table 1 of Obolentseva et al. (2024). These values use results from the Gaia DR3 release, which gives the repartition of absorbing matter along the line of sight toward nearby stars. The derived molecular fraction is larger than that obtained from the measured column densities of atomic and molecular hydrogen from ultraviolet observations. This discrepancy is due to the possible presence of atomic hydrogen on the line of sight that does not belong to the considered interstellar translucent cloud. The distances of HD 110432 and HD 73882 are respectively 438 pc and 461 pc (obtained from their measured parallax available on the SIMBAD database), and the sizes of the clouds are approximately a few parsecs, meaning that even a very small atomic hydrogen volumetric density located randomly on the line of sight may contribute a non-negligible amount to the atomic column density.

Using the gas temperature deduced from H2 excitation and the observed molecular fraction, we can use the code ExcitH3+2 to test the impact of various rate coefficients on H3+$\[\mathrm{H}_{3}^{+}\]$ excitation.

We compare the impact of the new rates of collision to the proxy used in Paper I: kH=2kpH2$\[k_{\mathrm{H}}=\sqrt{2} k_{\mathrm{pH}_{2}}\]$, where kpH2$\[k_{\mathrm{pH}_{2}}\]$ are the rate coefficients of H3+$\[\mathrm{H}_{3}^{+}\]$ with para H2, taken from Gómez-Carrasco et al. (2012). Figure 6 shows the rate coefficients for transitions between levels (2, 2, +) and (1, 1, −) (lowest para) and (3, 3, −) and (1, 0, +) (lowest ortho). We see that the new rates are stronger than the proxy, and that the values involving ortho transitions on one hand and para transitions on the other are much closer. Collisions with electrons are included, using the results of Kokoouline et al. (2010).

Paper I emphasizes the important role of the H3+$\[\mathrm{H}_{3}^{+}\]$ destruction rate kDR that is due to dissociative recombination, for which the values pertaining to the para form, kDRp$\[k_{D R}^{p}\]$, and to the ortho form, kDRo$\[k_{D R}^{o}\]$, are introduced. As in Paper I, we adopt a standard electronic recombination rate of H3+$\[\mathrm{H}_{3}^{+}\]$ with electrons of kDRp(T)=5.23 10−8(T300)−0.75 cm3 s−1$\[k_{D R}^{p}(T)= 5.23~10^{-8}\left(\frac{T}{300}\right)^{-0.75} \mathrm{~cm}^{3} \mathrm{~s}^{-1}\]$. However, Paper I stresses that the exact rate is still not well known and, in particular, that ortho and para levels may have different rates. Pagani et al. (2009) suggest a constant rate of kDRo=6 10−8 cm3 s−1$\[k_{D R}^{o}=6~10^{-8} \mathrm{~cm}^{3} \mathrm{~s}^{-1}\]$ below 250 K for ortho-H3+$\[\mathrm{H}_{3}^{+}\]$ (see discussion in Sect. 3.3 of Paper I). Therefore, for each line of sight, we use three values of the ratio kDRo/kDRp$\[k_{D R}^{o} / k_{D R}^{p}\]$ (close to 1/3, 2/3, and 1), corresponding respectively to the rates of Pagani et al. (2009) at 60 K, an intermediate case, and identical rate coefficients.

This leads to six different estimates of T12(H3+$\[\mathrm{H}_{3}^{+}\]$) for each line of sight (three recombination rates for H3+$\[\mathrm{H}_{3}^{+}\]$, multiplied by two sets of collision rate coefficients with H). These are presented in Fig. 7. We see that changing the ratio kDRo/kDRp$\[k_{D R}^{o} / k_{D R}^{p}\]$ has a strong impact on the computed value of T12(H3+$\[\mathrm{H}_{3}^{+}\]$). In addition, using the para-H2 proxy leads to a reduction in the amplitude of the variations of T12(H3+$\[\mathrm{H}_{3}^{+}\]$) with kDRo$\[k_{D R}^{o}\]$. A particularly remarkable result is that, for a given line of sight, the T12(H3+$\[\mathrm{H}_{3}^{+}\]$) curves cross for an intermediate value of kDRo/kDRp$\[k_{D R}^{o} / k_{D R}^{p}\]$, which means that, for that specific value only, there is no difference in the excitation temperature between the two sets of collision rate coefficients. As expected, the impact of the new rates is larger for lower values of the molecular fraction, as in HD 110432 compared to HD 73882.

Studying the origin of the sensitivity of T12(H3+$\[\mathrm{H}_{3}^{+}\]$) to kDRo/kDRp$\[k_{D R}^{o} / k_{D R}^{p}\]$ is out of the scope of this work, and will be done in another paper. However, regardless of the final determination of the recombination rates, it remains essential to use the new collision rate coefficients with H, as they result in significantly different evaluations of T12(H3+$\[\mathrm{H}_{3}^{+}\]$). Depending on the line of sight considered and the choice of other physical parameters, the differences may reach up to 20 % compared to using the proxy.

thumbnail Fig. 6

Comparison of new H collision rate coefficients with the proxy used in Le Bourlot et al. (2024) for the lowest para and ortho transitions. The temperatures of HD 110432 and HD 73882, as derived from the molecular hydrogen J = 1 and J = 0 column density ratio T01(H2), are indicated by a black vertical line.
Table 2

Observational data.

thumbnail Fig. 7

Computed values of T12 for the two lines of sight and three ratios of kDo/kDp$\[k_{D}^{o} / k_{D}^{p}\]$. Two different collections of rate constants are considered: kH=2kpH2$\[k_{\mathrm{H}}=\sqrt{2} k_{\mathrm{pH}_{2}}\]$ is the rescaled proxy values used in paper I; H coll denotes the results using the kH from this work.

4 Conclusions

In this paper, we introduce new accurate computations of collisional cross sections and collisional rate coefficients of H3+$\[\mathrm{H}_{3}^{+}\]$ with H for energies adapted to the physical conditions in the ISM. A time-independent close-coupling method is used to calculate the state-to-state cross sections and rate coefficients using a very accurate and full-dimensional potential energy surface recently developed for this system (del Mazo-Sevillano et al. 2024). H3+$\[\mathrm{H}_{3}^{+}\]$ rovibrational levels are calculated using hyperspherical coordinates, in permutationally symmetry adapted functions up to j = 20 and including the vibrations. From all these levels, only those corresponding to the ground (0,00) vibrational state are selected and included in the close-coupling method in a symmetric top approach, considering frozen H3+$\[\mathrm{H}_{3}^{+}\]$ as an equilateral triangle but with the numerically exact energy levels obtained in full-dimensional H3+$\[\mathrm{H}_{3}^{+}\]$ rovibrational states.

We use these new rate coefficients to evaluate the excitation temperature of H3+$\[\mathrm{H}_{3}^{+}\]$ as determined from its two lowest levels. Compared to using a proxy based on para H2, we find the following:

  • Differences in the estimated excitation temperature may reach 20%.

  • The impact of the new rate coefficients increases as the cloud molecular fraction decreases.

  • Differences between electronic recombination rates of ortho and para H3+$\[\mathrm{H}_{3}^{+}\]$ have a significant impact on the estimated excitation temperature, with larger differences with the new H collision rates.

This last point leads to large difficulties in estimating physical conditions from the observed values of H3+$\[\mathrm{H}_{3}^{+}\]$ abundance and excitation. The reasons for this sensitivity will be explored in a future paper, but its existence stresses the necessity to further improve our understanding of this long-standing question.

In the present work, we do not estimate possible reactive collisions between H and H3+$\[\mathrm{H}_{3}^{+}\]$ that may lead to ortho-to-para transitions. Inspection of the PES shows that these rates must be low (lower than 10−12 cm3 s−1 below 100 K), but even a low value may have an impact in some specific conditions, and this question also merits further examination. As a last point, the present work does not include radiative pumping in the infrared range, which is invoked in Pereira-Santaella et al. (2024) to explain their observations of vibrationally excited H3+$\[\mathrm{H}_{3}^{+}\]$ in (U)LIRGs.

Data availability

The energy levels of H3+$\[\mathrm{H}_{3}^{+}\]$ obtained in this work are listed in file H3p-levels-exomol.dat. The inelastic rates of ortho and para H3+$\[\mathrm{H}_{3}^{+}\]$ are provided in A2-rates.dat and E-rates.dat files.

Acknowledgements

The research leading to these results has received funding from MICIN (Spain), under grant PID2021-122549NB-C21 and PID2021-122549NB-C22, and by the Programme National « Physique et Chimie du Milieu Interstellaire » (PCMI) of the CNRS/INSU with INC/INP co-funded by CEA and CNES. Computational assistance was provided by the Supercomputer facilities of Lusitania founded by the CénitS and Computaex Foundation.

Appendix A H3+$\[\mathrm{H}_{3}^{+}\]$ levels

For the H3+$\[\mathrm{H}_{3}^{+}\]$ we used the PES for H4+$\[\mathrm{H}_{4}^{+}\]$ of del Mazo-Sevillano et al. (2024), placing the fourth hydrogen atom at 100 bohr at a fixed geometry. The rovibrational bound states of H3+$\[\mathrm{H}_{3}^{+}\]$ are calculated in the adiabatically adjusting, Johnson’s principal axis, hyperspherical (denoted APJH) coordinates (Pack & Parker 1989) using a code previously developed (Aguado et al. 2000; Sanz et al. 2001), in which the full wave function is expanded as ΨijmΓ(ρ,θ,ϕτ,α,β,γ)=4ρ−5/2∑v,k,n,ΩCv,k,n,ΩjmΓi×W~Ω,njmΓ(α,β,γ,ϕτ)Fkj,Ω,n(θ)φv(ρ),$\[\begin{aligned}& \Psi_i^{j m \Gamma}\left(\rho, \theta, \phi_\tau, \alpha, \beta, \gamma\right)=4 \rho^{-5 / 2} \sum_{v, k, n, \Omega} C_{v, k, n, \Omega}^{j m \Gamma i} \\\times & \tilde{W}_{\Omega, n}^{j m \Gamma}\left(\alpha, \beta, \gamma, \phi_\tau\right) F_k^{j, \Omega, n}(\theta) \varphi_v(\rho),\end{aligned}\]$(A.1)

where, ϕv(ρ) are numerical functions obtained in a monodimensional radial grid in ρ for the equilibrium configuration (Aguado et al. 2000), Fkj,Ω,n(θ)$\[F_{k}^{j, \Omega, n}(\theta)\]$ are proportional to Jacobi polynomials (Aguado et al. 2000; Abramowitz & Stegun 1972) and W~Ω,njmΓ(α,β,γ,ϕτ)$\[\tilde{W}_{\Omega, n}^{j m \Gamma}\left(\alpha, \beta, \gamma, \phi_{\tau}\right)\]$ are symmetry adapted basis set functions for a given triatomic angular momentum j, with projection m on the space fixed frame and an irreducible representation, Γ, of the D3h point group (isomorphic with the S3 permutation group multiplied by the inversion of spatial symmetry). These symmetry adapted functions are expressed as W~Ω,njmΓ(α,β,γ,ϕτ)=AΩnjΓWΩ,njm(α,β,γ,ϕτ)+BΩnjΓW−Ω,−njm(α,β,γ,ϕτ),$\[\begin{array}{rll}\tilde{W}_{\Omega, n}^{j m \Gamma}\left(\alpha, \beta, \gamma, \phi_\tau\right) & =A_{\Omega n}^{j \Gamma} \quad W_{\Omega, n}^{j m}\left(\alpha, \beta, \gamma, \phi_\tau\right) \\& +B_{\Omega n}^{j \Gamma} \quad W_{-\Omega,-n}^{j m}\left(\alpha, \beta, \gamma, \phi_\tau\right),\end{array}\]$(A.2)

where AΩnjΓ$\[A_{\Omega n}^{j \Gamma}\]$ and BΩnjΓ$\[B_{\Omega n}^{j \Gamma}\]$ coefficients are obtained applying projection operators (Aguado et al. 2000; Sanz et al. 2001), and Wnωjm(α,β,γ,ϕτ)=2j+18π2Dmωj∗(α,β,γ)einϕτ2π,$\[W_{n \omega}^{j m}\left(\alpha, \beta, \gamma, \phi_\tau\right)=\sqrt{\frac{2 j+1}{8 \pi^2}} D_{m \omega}^{j *}(\alpha, \beta, \gamma) \frac{e^{i n \phi_\tau}}{\sqrt{2 \pi}},\]$(A.3)

with Dmωj∗(α,β,γ)$\[D_{m \omega}^{j *}(\alpha, \beta, \gamma)\]$ being Wigner rotation functions (Zare 1988), transforming from the space fixed to the body-fixed frame, with the axes along the principal inertia axes and the z-axis perpendicular to the plane of H3+$\[\mathrm{H}_{3}^{+}\]$, with ω being the projection of the triatomic total angular momentum in the body-fixed z-axis.

The exact triatomic eigenvalues and eigenvectors are obtained for each j, Γ values using a two steps method (Aguado et al. 2000). The eigenvalues are obtained using a nonorthogonal Lanczos method (Cullum & Willoughby 1985) and then the eigenfunctions are obtained using a conjugate gradient method (Fröberg 1985). From the eigenvectors the approximated quantum numbers (v1,v2ℓ$\[v_{1}, v_{2}^{\ell}\]$) (Watson 1984) are obtained together with the ω distribution in Eq. A.1. Bound state calculations have been done up to j = 15 for ortho-H3+$\[\mathrm{H}_{3}^{+}\]$ (nuclear spin I = 3/2 and Γ=A2′,A2′′$\[\Gamma=A_{2}^{\prime}, A_{2}^{\prime \prime}\]$) and para-H3+$\[\mathrm{H}_{3}^{+}\]$ (I = 1/2, Γ = E′, E″), which are listed in the Supplementary Information (S.I.) with the quantum numbers.

A.1 Simplifying to rigid rotor H3+$\[\mathrm{H}_{3}^{+}\]$

The scattering is treated in the rigid rotor approach, and not all the bound states are used. In what follows, we shall consider Γ = Γt × pt, to treat separately the permutation symmetry, Γt which is conserved in inelastic collisions, and the inversion of spacial coordinates, pt, which is not conserved (pt=1 for A2′$\[A_{2}^{\prime}\]$ and E′, pt = -1 for A2′′$\[A_{2}^{\prime \prime}\]$ and E″). To include the “exact” triatomic bound states in the scattering calculations described below, the following approximations have been done:

  1. Only states corresponding to the ground vibrational level, (0, 00), are included, up to an energy of 4100 cm−1 above the ground state.

  2. Triatomic systems are in general asymmetric top. However, for the triangular equilibrium distance, H3+$\[\mathrm{H}_{3}^{+}\]$ is a symmetric top. In the exact bound calculations, the states in general are a linear superposition of several ω values, but for (0, 00) and low triatomic angular momenta j there is a dominant ω value, with a weight larger than 90% (see S.I.). Thus, in the present case we shall consider H3+$\[\mathrm{H}_{3}^{+}\]$ as a symmetric top in the collisions studied below.

  3. Under this symmetric top rigid-rotor approximation, bound states of Eq. A.1 are taken as |jmωptΓt⟩≡2j+18π2Dmωj∗(α,β,γ),$\[\left|j m \omega p_{t} \Gamma_{t}\right\rangle \equiv \sqrt{\frac{2 j+1}{8 \pi^{2}}} D_{m \omega}^{j *}(\alpha, \beta, \gamma),\]$(A.4)

    with the only restriction of adding an intrinsic parity under inversion of spatial coordinates, so that the parity of these functions coincide with the corresponding parity of the exact triatomic state, pt. The functions thus defined have the proper permutation symmetry, A2 or E in the present case.

  4. For Γ = E′ or E″, the functions W~nωjmΓ=f(WnωjmΓ,W−n−ωjmΓ)$\[\tilde{W}_{n \omega}^{j m \Gamma}=f\left(W_{n \omega}^{j m \Gamma}, W_{-n-\omega}^{j m \Gamma}\right)\]$ are decoupled from W~n−ωjmΓ=f(Wn−ωjmΓ,W−nωjmΓ)$\[\tilde{W}_{n-\omega}^{j m \Gamma}=f\left(W_{n-\omega}^{j m \Gamma}, W_{-n \omega}^{j m \Gamma}\right)\]$, with n, ω different from zero. Thus, the two degenerate eigenstates are expressed in the corresponding basis functions separately, and labeled by ω and −ω.

Appendix B Inelastic scattering method

The inelastic scattering calculations have been performed with the code DTICC which has been specifically developed by the authors for this purpose, in which the close coupled equations are solved with a renormalized Numerov algorithm (Gadéa et al. 1997). The system composed by a symmetric top colliding with an atom is described in space fixed (SF) coordinates, using a standard method adapted from NH3 (Green 1980), outlined here for completeness.

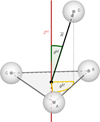thumbnail Fig. B.1

Relative orientation between both fragments, in a body-fixed frame centered in the triatom.
thumbnail Fig. B.2

Radial coefficients corresponding to the expansion of the interaction potential.

A Jacobi vector R ≡ {R, θR, ϕR} is defined in the SF frame joining the ABC (or symmetric top) center-of mass to the colliding atom D, whose associated angular momentum is ℓ. The space-fixed angular basis set functions are defined as |α⟩=∑mmℓ⟨jmℓmℓ||JM⟩|jmωptΓt⟩Yℓmℓ(θR,ϕR),$\[|\alpha\rangle=\sum_{m m_{\ell}}\left\langle j m \ell m_{\ell}\right||J M\rangle\left|j m \omega p_t \Gamma_t\right\rangle Y_{\ell m_{\ell}}\left(\theta_R, \phi_R\right),\]$(B.1)

with |jmωptΓt⟩ being defined in Eq. A.4. The |α⟩=yjωℓptΓtJM p(α,β,γ,θR,ϕR)$\[\mathcal{y}_{j \omega\ell{p}_t\Gamma_{t}}^{J M_{~p}}\left(\alpha, \beta, \gamma, \theta_{R}, \phi_{R}\right)\]$ is introduced to simplify the notation. In this basis, the total scattering wave function is expressed as |ΨEJMα−⟩=∑α′Φα′JMα−(R;E)R|α′⟩$\[\left|\Psi_E^{J M \alpha-}\right\rangle=\sum_{\alpha^{\prime}} \frac{\Phi_{\alpha^{\prime}}^{J M\alpha-}(R; E)}{R}\left|\alpha^{\prime}\right\rangle\]$(B.2)

where the radial coefficients Φα′JMα−(R;E)$\[\Phi_{\alpha^{\prime}}^{J M^{\alpha-}}(R; E)\]$ are obtained numerically by solving the close coupled differential equations obtained by inserting this total wave function, with the Hamiltonian being defined as H^=−ℏ22μ(2R∂∂R+∂2∂R2)+ℓ^22μR2+V(R,θbf,ϕbf)+H^ABC$\[\begin{aligned}\hat{H}= & -\frac{\hbar^2}{2 \mu}\left(\frac{2}{R} \frac{\partial}{\partial R}+\frac{\partial^2}{\partial R^2}\right)+\frac{\hat{\ell}^2}{2 \mu R^2} \\& +V\left(R, \theta^{b f}, \phi^{b f}\right)+\hat{H}_{A B C}\end{aligned}\]$(B.3)

where μ = mDmABC/(mD + mABC) is the reduced mass, H^ABC$\[\hat{H}_{A B C}\]$ is the internal triatomic hamiltonian operator, and V(R, θb f, ϕb f) is the interaction potential which only depends on the relative orientation of the atom D with respect to the triatomic fragment ABC — as shown in Fig. B.1.

The centrifugal term ℓ^2$\[\hat{\ell}^{2}\]$ is diagonal in the SF representation with eigenvalues ℏ2 ℓ(ℓ + 1). The eigenstates and eigenvalues of the ABC system were obtained in the previous section, which in the present treatment are simplified to the symmetry adapted symmetric top functions, |jmωptΓt⟩. The potential matrix elements in the space-fixed representation are then given by ⟨α|V|α′⟩=∑λνVλν(R)⟨α|Yλν|α′⟩,$\[\langle\alpha| V\left|\alpha^{\prime}\right\rangle=\sum_{\lambda \nu} V_{\lambda \nu}(R)\langle\alpha| Y_{\lambda \nu}\left|\alpha^{\prime}\right\rangle,\]$(B.4)

where Vλν(R) are the radial coefficients of the expansion of the potential in spherical harmonics as V(R,θbf,ϕbf)=∑λνVλν(R)Yλν(θbf,ϕbf),$\[V\left(R, \theta^{b f}, \phi^{b f}\right)=\sum_{\lambda \nu} V_{\lambda \nu}(R) Y_{\lambda \nu}\left(\theta^{b f}, \phi^{b f}\right),\]$(B.5)

which are shown in Fig. B.2, and ⟨α|Yλν|α′⟩=[ℓ][λ][ℓ′][j][j′]4π(−1)−J+λ−ω′(ℓλℓ′000){jJℓℓ′λj′}(jλj′ων−ω′),$\[\begin{aligned}& \langle\alpha| Y_{\lambda \nu}\left|\alpha^{\prime}\right\rangle=\sqrt{\frac{[\ell][\lambda]\left[\ell^{\prime}\right][j]\left[j^{\prime}\right]}{4 \pi}}(-1)^{-J+\lambda-\omega^{\prime}} \\& \left(\begin{array}{ccc}\ell & \lambda & \ell^{\prime} \\0 & 0 & 0\end{array}\right)\left\{\begin{array}{ccc}j & J & \ell \\\ell^{\prime} & \lambda & j^{\prime}\end{array}\right\}\left(\begin{array}{ccc}j & \lambda & j^{\prime} \\\omega & \nu & -\omega^{\prime}\end{array}\right),\end{aligned}\]$(B.6)

where the compact notation [j] = 2j + 1 has been used for the angular momenta degeneracies, and the 6-j symbols (Zare 1988) are denoted as {: : :}. The symmetry of the potential ensures that the radial expansion coefficients fulfill the condition Vλν(R) = (−1)νVλ−ν(R), as well as the threefold symmetry for the azimuthal angle V(R, θb f, ϕb f) = V(R, θb f, ϕb f + 2nπ/3) for n ∈ Z$\[\mathbb{Z}\]$. These symmetry constraints are equivalent to say that the only allowed values for ν are multiples of three: ν = 0, ±3, ±6, . . . . The total parity of the four atom system is conserved and equal to p = pt(−1)ℓ, so that pt = ±1 is no longer conserved.

As noted above, the symmetry adapted rigid rotor wave functions of H3+$\[\mathrm{H}_{3}^{+}\]$ used in this work constitute a slight modification, essentially equivalent, of the usual treatment for collisions of symmetric top functions with atoms (Green 1976, 1980). First, the procedure followed allows to exactly determine the symmetry of the triatomic function, which also depends on the hyperspherical angle ϕτ, which is not included in the rigid rotor approach.

The state-to-state cross section are obtained using the usual partial wave summation in the space fixed frame (Arthurs & Dalgarno 1960) as σββ′Γt(E)=π(2j+1)kβ2∑Jℓℓ′p(2J+1)|Sαα′JΓtp(E)−δαα′|2$\[\sigma_{\beta \beta^{\prime}}^{\Gamma_t}(E)=\frac{\pi}{(2 j+1) k_\beta^2} \sum_{J \ell \ell^{\prime} p}(2 J+1)\left|S_{\alpha \alpha^{\prime}}^{J \Gamma_t p}(E)-\delta_{\alpha \alpha^{\prime}}\right|^2\]$(B.7)

where kβ2=2μ(E−Eβ)/ℏ2,E$\[k_{\beta}^{2}=2 \mu\left(E-E_{\beta}\right) / \hbar^{2}, E\]$ is the total energy, and Eβ is the energy of the triatomic level β. Sαα′JΓtp(E)$\[S_{\alpha \alpha^{\prime}}^{J \Gamma_{t} p}(E)\]$ are the elements of the scattering matrices obtained in the resolution of the close coupling equations.

The state-to-state rate constants are obtained by taking Boltzmann averages on the cross sections — i.e. integration over the kinetic energy Eβk=E−Eβ$\[E_{\beta}^{k}=E-E_{\beta}\]$ for a given temperature T, as kββ′(T)=8πμ(kBT)3××∫dEβk Eβk σββ′(Eβk)e−EBkkBT$\[\begin{aligned}& k_{\beta \beta^{\prime}}(T)=\sqrt{\frac{8}{\pi \mu\left(k_B T\right)^3}} \times \\& \times \int d E_\beta^k ~E_\beta^k ~\sigma_{\beta \beta^{\prime}}\left(E_\beta^k\right) e^{-\frac{E_B^k}{k_B T}}\end{aligned}\]$(B.8)

where kB is the Boltzmann constant.

References

  1. Abramowitz, M., & Stegun, I. 1972, Handbook of Mathematical Functions (New York: Dover Publications, Inc.) [Google Scholar]
  2. Aguado, A., Roncero, O., Tablero, C., Sanz, C., & Paniagua, M. 2000, J. Chem. Phys., 112, 1240 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aguado, A., Barragan, P., Prosmiti, R., et al. 2010, J. Chem. Phys., 133, 024306 [NASA ADS] [CrossRef] [Google Scholar]
  4. Arthurs, A. M., & Dalgarno, A. 1960, Proc. R. Soc. Lond. A Math. Phys. Sci., 256, 540 [NASA ADS] [Google Scholar]
  5. Bachorz, R. A., Cencek, W., Jaquet, R., & Komasa, J. 2009, J. Chem. Phys., 131, 024105 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bouhafs, N., Rist, C., Daniel, F., et al. 2017, MNRAS, 470, 2204 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bowen, K. P., Hillenbrand, P.-M., Liévan, J., Savin, D. W., & Urbain, X. 2021, J. Chem. Phys., 154, 084307 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bulut, N., Aguado, A., Sanz-Sanz, C., & Roncero, O. 2019, J. Phys. Chem. A, 123, 8766 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cencek, W., Rychlewski, J., Jaquet, R., & Kutzelnigg, W. 1998, J. Chem. Phys., 108, 2831 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cullum, J., & Willoughby, R. 1985, Lanczos Algorithms for Large Symmetric Eigenvalues Computations (Boston: Birkhäuser) [Google Scholar]
  11. del Mazo-Sevillano, P., Félix-González, D., Aguado, A., et al. 2024, Mol. Phys., 122, e2183071 [CrossRef] [Google Scholar]
  12. Edenhofer, G., Zucker, C., Frank, P., et al. 2024, A&A, 685, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Fröberg, C.-E. 1985, Numerical Mathematics: Theory and Computer Applications (San Francisco: The Benjamin/Cummings Publishing Company) [Google Scholar]
  14. Furtenbacher, T., Szidarovsky, T., Matyus, E., Fabri, C., & Csaszar, A. G. 2013, J. Chem. Theor. Comput., 9, 5471 [CrossRef] [Google Scholar]
  15. Gadéa, F. X., Berriche, H., Roncero, O., Villarreal, P., & Delgado-Barrio, G. 1997, J. Chem. Phys., 107, 10515 [CrossRef] [Google Scholar]
  16. Geballe, T. R., & Oka, T. 1989, ApJ, 342, 855 [NASA ADS] [CrossRef] [Google Scholar]
  17. Geballe, T. R., McCall, B. J., Hinkle, K. H., & Oka, T. 1999, ApJ, 510, 251 [CrossRef] [Google Scholar]
  18. Gerlich, D., Jusko, P., Š. Roučka, et al. 2012, ApJ, 749, 22 [NASA ADS] [CrossRef] [Google Scholar]
  19. Ghosh, S., Mukherjee, S., Mukherjee, B., et al. 2017, J. Chem. Phys., 147, 074105 [NASA ADS] [CrossRef] [Google Scholar]
  20. Gómez-Carrasco, S., González-Sánchez, L., Aguado, A., Zanchet, A., & Roncero, O. 2012, J. Chem. Phys., 137, 094303 [CrossRef] [Google Scholar]
  21. Green, S. 1976, J. Chem. Phys., 64, 3463 [NASA ADS] [CrossRef] [Google Scholar]
  22. Green, S. 1980, J. Chem. Phys., 73, 2740 [NASA ADS] [CrossRef] [Google Scholar]
  23. Herbst, E. 2000, Phil. Trans. R. Soc. Lond. A, 358, 2523 [NASA ADS] [CrossRef] [Google Scholar]
  24. Herbst, E., & Klemperer, W. 1973, ApJ, 185, 505 [Google Scholar]
  25. Hillenbrand, P.-M., Bowen, K. P., Liévin, J., Urbain, X., & Savin, D. W. 2019, ApJ, 877, 38 [NASA ADS] [CrossRef] [Google Scholar]
  26. Hugo, E., Asvany, O., & Schlemmer, S. 2009, J. Chem. Phys., 130, 164302 [Google Scholar]
  27. Indriolo, N., & McCall, B. J. 2012, ApJ, 745, 91 [NASA ADS] [CrossRef] [Google Scholar]
  28. Jaquet, R., Cencek, W., Kutzelnigg, W., & Rychlewski, J. 1998, J. Chem. Phys., 108, 2837 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kokoouline, V., Faure, A., Tennyson, J., Greene, C. H. 2010, MNRAS, 405, 1195 [Google Scholar]
  30. Le Bourlot, J., Roueff, E., Le Petit, F., et al. 2024, Mol. Phys., 122, e2182612 [Google Scholar]
  31. Le Petit, F., Roueff, E., & Herbst, E. 2004, A&A, 417, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [Google Scholar]
  33. Le Petit, F., Ruaud, M., Bron, E., et al. 2016, A&A, 585, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. McCall, B. J., & Oka, T. 2000, Science, 287, 1941 [NASA ADS] [CrossRef] [Google Scholar]
  35. McCall, B. J., Geballe, T. R., Hinkle, K. H., & Oka, T. 1999, ApJ, 522, 338 [NASA ADS] [CrossRef] [Google Scholar]
  36. Millar, T. J., Bernett, A., & Herbst, E. 1989, ApJ, 340, 906 [NASA ADS] [CrossRef] [Google Scholar]
  37. Miller, S., Tennyson, J., Geballe, T. R., & Stallard, T. 2020, Rev. Mod. Phys., 92, 035003 [NASA ADS] [CrossRef] [Google Scholar]
  38. Mizus, I. I., Polyansky, O. L., McKemmish, L. K., et al. 2018, Mol. Phys., 117, 1663 [Google Scholar]
  39. Obolentseva, M., Ivlev, A. V., Silsbee, K., et al. 2024, ApJ, 973, 142 [NASA ADS] [CrossRef] [Google Scholar]
  40. Oka, T. 1980, Phys. Rev. Lett., 45, 531 [CrossRef] [Google Scholar]
  41. Oka, T. 2004, J. Mol. Spectros., 228, 635 [NASA ADS] [CrossRef] [Google Scholar]
  42. Oka, T. 2006, PNAS, 103, 12235 [CrossRef] [Google Scholar]
  43. Oka, T. 2012, Phil. Trans. R. Soc. A, 370, 4991 [CrossRef] [Google Scholar]
  44. Oka, T. 2013, Chem. Rev., 113, 8738 [NASA ADS] [CrossRef] [Google Scholar]
  45. Oka, T., & Epp, E. 2004, ApJ, 613, 349 [NASA ADS] [CrossRef] [Google Scholar]
  46. Pack, R. T., & Parker, G. A. 1989, J. Chem. Phys., 90, 3511 [NASA ADS] [CrossRef] [Google Scholar]
  47. Pagani, L., Salez, M., & Wannier, P. 1992, A&A, 258, 479 [NASA ADS] [Google Scholar]
  48. Pagani, L., Vastel, C., Hugo, E., et al. 2009, A&A, 494, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Pagani, L., Roueff, E., & Lesaffre, P. 2011, ApJ, 739, L35 [NASA ADS] [CrossRef] [Google Scholar]
  50. Park, K., & Light, J. C. 2007, J. Chem. Phys., 126, 044305 [NASA ADS] [CrossRef] [Google Scholar]
  51. Pavanello, M., Adamowicz, L., Alijah, A., et al. 2012, J. Chem. Phys., 136, 184303 [NASA ADS] [CrossRef] [Google Scholar]
  52. Pereira-Santaella, M., González-Alfonso, E., García-Bernete, I., et al. 2024, A&A, 689, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Polyansky, O. L., Alijah, A., Zobov, N. F., et al. 2012, Philos. Trans. A Math. Phys. Eng. Sci., 370, 5014 [NASA ADS] [Google Scholar]
  54. Röhse, R., Kutzelnigg, W., Jaquet, R., & Klopper, W. 1994, J. Chem. Phys., 101, 2231 [CrossRef] [Google Scholar]
  55. Sanz, C., Roncero, O., Tablero, C., Aguado, A., & Paniagua, M. 2001, J. Chem. Phys., 114, 2182 [NASA ADS] [CrossRef] [Google Scholar]
  56. Sanz-Sanz, C., Roncero, O., Paniagua, M., & Aguado, A. 2013, J. Chem. Phys., 139, 184302 [NASA ADS] [CrossRef] [Google Scholar]
  57. Sanz-Sanz, C., Aguado, A., Roncero, O., & Naumkin, F. 2015, J. Chem. Phys., 143, 234303 [NASA ADS] [CrossRef] [Google Scholar]
  58. Tennyson, J. 1995, Rep. Prog. Phys., 58, 412 [Google Scholar]
  59. Tennyson, J., & Miller, S. 2019, Phil. Trans. R. Soc. A, 377, 2154 [Google Scholar]
  60. Tennyson, J., Polyansky, O. L., Zobov, N. F., Alijah, A., & Császár, A. G. 2017, J. Phys. B At. Mol. Opt. Phys., 50, 232001 [NASA ADS] [CrossRef] [Google Scholar]
  61. Velilla, L., Lepetit, B., Aguado, A., Beswick, J. A., & Paniagua, M. 2008, J. Chem. Phys., 129, 084307 [NASA ADS] [CrossRef] [Google Scholar]
  62. Velilla, L., Paniagua, M., & Aguado, A. 2010, Int. J. Quantum Chem., 111, 387 [Google Scholar]
  63. Viegas, L. P., Alijah, A., & Varandas, A. J. C. 2007, J. Chem. Phys., 126, 074309 [NASA ADS] [CrossRef] [Google Scholar]
  64. Watson, W. D. 1973, ApJ, 183, L17 [NASA ADS] [CrossRef] [Google Scholar]
  65. Watson, J. 1984, J. Mol. Spect., 103, 350 [NASA ADS] [CrossRef] [Google Scholar]
  66. Zare, R. 1988, Angular Momentum (Hoboken: John Wiley and Sons, Inc.) [Google Scholar]
1

Available at https://pdr.obspm.fr

All Tables

Table 1

Fitted parameters for the transitions (j, ω, pt) → (j′,ω′,pt′ Γt$\[\mathrm{j}^{\prime}, \omega^{\prime}, \mathrm{p}_{t}^{\prime} ~\Gamma_{t}\]$) within Γt = A2 (1,0,+) and E (1,±,−) representations.

In the text
Table 2

Observational data.

In the text

All Figures

thumbnail Fig. 1

Minimum energy path for the H+H3+⟶H3++H$\[\mathrm{H}+\mathrm{H}_{3}^{+} \longrightarrow \mathrm{H}_{3}^{+}+\mathrm{H}\]$ exchange reaction for the PES by del Mazo-Sevillano et al. (2024).
In the text
thumbnail Fig. 2

Computed H3+$\[\mathrm{H}_{3}^{+}\]$ rotational levels in the ground vibrational state, conventionally labeled as (j, ω, pt), within each specific irreducible representation, Γ.
In the text
thumbnail Fig. 3

Calculated cross sections for the transitions starting from (1,0,+) → (j′,ω′,pt′$\[j^{\prime}, \omega^{\prime}, p_{t}^{\prime}\]$) within the Γt = A2 representation.
In the text
thumbnail Fig. 4

Calculated cross sections for the transitions starting from (1,±1,−) within the Γt = E representation.
In the text
thumbnail Fig. 5

Calculated state-to-state rate constants for the transitions starting from (1,0,+) within the Γt = A2 (top panel) and E (bottom panel) representations. The fitted curves are represented by the solid black lines, while the computed data are the colored dots.
In the text
thumbnail Fig. 6

Comparison of new H collision rate coefficients with the proxy used in Le Bourlot et al. (2024) for the lowest para and ortho transitions. The temperatures of HD 110432 and HD 73882, as derived from the molecular hydrogen J = 1 and J = 0 column density ratio T01(H2), are indicated by a black vertical line.
In the text
thumbnail Fig. 7

Computed values of T12 for the two lines of sight and three ratios of kDo/kDp$\[k_{D}^{o} / k_{D}^{p}\]$. Two different collections of rate constants are considered: kH=2kpH2$\[k_{\mathrm{H}}=\sqrt{2} k_{\mathrm{pH}_{2}}\]$ is the rescaled proxy values used in paper I; H coll denotes the results using the kH from this work.
In the text
thumbnail Fig. B.1

Relative orientation between both fragments, in a body-fixed frame centered in the triatom.
In the text
thumbnail Fig. B.2

Radial coefficients corresponding to the expansion of the interaction potential.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.