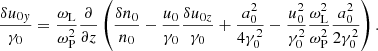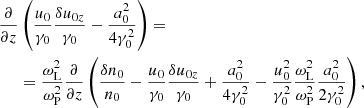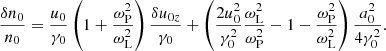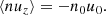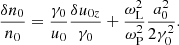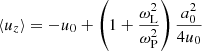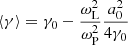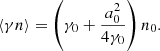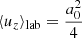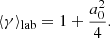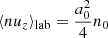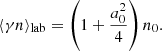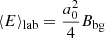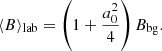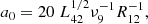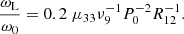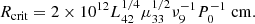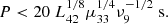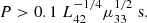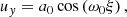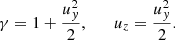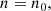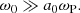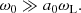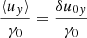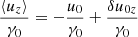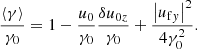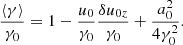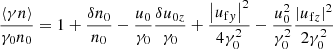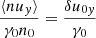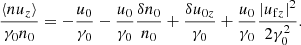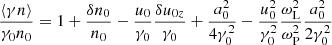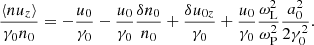| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A332 | |
| Number of page(s) | 6 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202451725 | |
| Published online | 21 October 2024 | |
Escape of fast radio bursts from magnetars
1
Gran Sasso Science Institute, viale F. Crispi 7, L’Aquila, 67100
Italy
2
INFN – Laboratori Nazionali del Gran Sasso, via G. Acitelli 22, Assergi, 67100
Italy
3
Yukawa Institute for Theoretical Physics, Kyoto University, Kitashirakawa-Oiwakecho, Sakyo-Ku, Kyoto, 606-8502
Japan
4
Faculty of Engineering Sciences, Kyushu University, 6-1, Kasuga-koen, Kasuga, Fukuoka, 816-8580
Japan
5
Department of Astronomy and Columbia Astrophysics Laboratory, Columbia University, 550 W 120th St, New York, NY, 10027
USA
6
Center for Computational Astrophysics, Flatiron Institute, 162 5th Avenue, New York, NY, 10010
USA
7
Racah Institute for Physics, The Hebrew University, Jerusalem, 91904
Israel
Received:
30
July
2024
Accepted:
16
September
2024
Fast radio bursts (FRBs) are bright extragalactic transients likely produced by magnetars. We study the propagation of FRBs in magnetar winds, assuming that the wind is strongly magnetized and composed of electron-positron pairs. We focused on the regime where the strength parameter of the radio wave, a0, is larger than unity and the wave frequency, ω0, is larger than the Larmor frequency in the background magnetic field, ωL. We show that strong radio waves with a0 > 1 are able to propagate when ω0 > a0ωL, as the plasma current is a linear function of the wave electric field. The dispersion relation is independent of the wave strength parameter when ω0 > a0ωL. Radio waves could instead be damped when ω0 < a0ωL, as a significant fraction of the wave energy is used to compress the plasma and amplify the background magnetic field. Our results suggest that FRBs should be produced at large distances from the magnetar (i.e., R > 1012 cm, where the condition ω0 > a0ωL is satisfied). Alternatively, the structure of the magnetar wind should be strongly modified during a flare to allow for the escape of FRBs produced at radii R < 1012 cm.
Key words: plasmas / waves / stars: magnetars
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Fast radio bursts (FRBs) are bright extragalactic transients of millisecond duration (Cordes & Chatterjee 2019; Petroff et al. 2019, 2022). Observationally, it is now clear that FRBs can be produced by magnetars (Bochenek et al. 2020; CHIME/FRB Collaboration 2020). However, despite significant theoretical effort, the physical processes powering FRBs have not been conclusively identified (Lyubarsky 2021; Zhang 2023).
Any emission model must satisfy the basic constraint that FRBs can escape from the magnetar. Due to the extraordinary properties of FRBs, this is not a trivial requirement. One can define the FRB strength parameter as
where E0 is the peak electric field of the radio wave, ω0 is the wave frequency, m and −e respectively are the mass and the charge of the electron, and c is the speed of light. When the background magnetic field is smaller than the field of the radio wave, the strength parameter is equal to the peak transverse component of the electron four-velocity in units of the speed of light. Due to the large radio luminosity of FRBs, the strength parameter is a0 > 1 at distances R < 1013 cm from the magnetar (Luan & Goldreich 2014). It is an open question whether strong radio waves with a0 > 1 can escape from the magnetar or whether FRBs should be produced at large radii where a0 < 1.
The magnetosphere and the wind of magnetars are strongly magnetized, and they are composed primarily of electron-positron pairs (Kaspi & Beloborodov 2017). The propagation of strong radio waves with a0 > 1 in magnetized pair plasmas has recently been studied by several authors (Beloborodov 2021, 2022, 2023; Chen et al. 2022; Qu et al. 2022; Golbraikh & Lyubarsky 2023; Lyutikov 2024). These studies focused on the regime where the wave frequency, ω0, is smaller than the Larmor frequency in the background magnetic field, ωL. Two interesting cases have been identified: (i) When ω0 < ωL/a0, the particles oscillate in the field of the wave at nonrelativistic speeds because the background magnetic field is larger than the field of the radio wave. In this case, the plasma current is a linear function of the wave electric field, and radio waves can propagate. (ii) When ωL/a0 < ω0 < ωL, the particle velocity is relativistic, and the plasma current is nonlinear. It has been suggested that in this case, radio waves are damped, which would constrain emission models of FRBs (Beloborodov 2021, 2022, 2023; Chen et al. 2022). However, the latter issue is still debated (Qu et al. 2022; Lyutikov 2024).
In this paper, we study the propagation of strong waves in the regime ω0 > ωL, which has received limited attention so far1. In this regime, the particle velocity is relativistic. We show that (i) when ω0 > a0ωL, the background magnetic field does not affect the particle motion, and the plasma current is a linear function of the wave electric field. Radio waves can then propagate. Interestingly, the dispersion relation is independent of the wave strength parameter. (ii) When ωL < ω0 < a0ωL, the plasma current becomes nonlinear, and radio waves could be damped. The propagation regimes are summarized in Table 1.
Summary of the propagation regimes.
The paper is organized as follows. In Sect. 2, we present the fundamental equations that govern the propagation of strong waves. In Sect. 3, we consider waves that propagate with superluminal phase velocities, as appropriate for ω0 > ωL (in Appendix A, we give an intuitive explanation of the results of Sects. 2 and 3). In Sect. 4, we discuss the implications of our results for the modelling of FRBs and summarize our conclusions.
2. Fundamental equations
We considered a linearly polarized electromagnetic wave that propagates in a cold magnetized pair plasma. In the frame where the plasma ahead of the wave packet is at rest (hereafter, the “lab frame,” or equivalently the proper frame of the magnetar wind), the wave frequency is ω0 and the wave vector is k0. The wave propagates along the z direction. We considered the extraordinary mode, where the electric field of the wave is directed along y and the magnetic field of the wave is directed along x. The background magnetic field is also directed along x. In Sect. 4, we argue that our key results are valid for any direction of propagation with respect to the background magnetic field and for any direction of the wave electric field. We worked in units where the speed of light is c = 1. We assumed that all physical quantities depend only on z and t.
Electrons and positrons move in the yz plane. They have the same number densities, the same velocities in the z direction, and opposite velocities in the y direction. The equation of motion of the positrons is
where u = uyey + uzez and 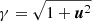 respectively are the four-velocity and the Lorentz factor. The electromagnetic fields, E and B, are the sum of the wave field and the background field. The continuity equation is
respectively are the four-velocity and the Lorentz factor. The electromagnetic fields, E and B, are the sum of the wave field and the background field. The continuity equation is
where n is the proper number density. The evolution of the electromagnetic fields is governed by Faraday’s and Ampère’s laws, which are
We defined the plasma frequency as 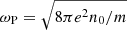 , where n0 is the proper positron number density ahead of the wave packet, and the Larmor frequency as ωL = eBbg/m, where Bbg is the background magnetic field in the lab frame. Since magnetar winds are strongly magnetized, we assumed ωL > ωP.
, where n0 is the proper positron number density ahead of the wave packet, and the Larmor frequency as ωL = eBbg/m, where Bbg is the background magnetic field in the lab frame. Since magnetar winds are strongly magnetized, we assumed ωL > ωP.
It is convenient to apply the operator ∂/∂z to both sides of Eq. (2). Using Eq. (5) to eliminate ∂E/∂z, one finds
At this point, it is convenient to introduce the new variable:
Ahead of the wave packet, one has uy = 0 and n = n0. In the frame where the particles ahead of the wave packet are at rest, one has γ = 1 and (e/m)B = ωL. An arbitrary Lorentz boost along the direction of propagation gives (e/m)B = γωL. Then, one finds Q = 0 in any reference frame. From Eqs. (4) and (7), one can see that the variable Q is governed by
Then, one finds Q = 0 also inside the wave packet. Substituting Q = 0 into Eq. (8), one finds
Substituting Eq. (10) into Eq. (2), one finds
Substituting Eq. (10) into Eq. (3), one finds
or equivalently
Substituting Eqs. (10) and (11) into Eq. (6), one finds
Our final set of equations consists of Eqs. (4), (13), and (14).
3. Superluminal waves
We studied waves that propagate with superluminal phase velocities (i.e., ω0/k0 > 1). We worked in the reference frame that moves with the group velocity, k0/ω0, along the z direction (hereafter, the “wave frame”). As discussed by Clemmow (1974), in this frame the wave vector vanishes, and the wave frequency is
We found an approximate solution for Eqs. (4), (13), and (14) by separating the fast oscillations of the physical quantities, which occur on the temporal scale 1/ω, from their secular evolution, which occurs on a much longer temporal scale.
Particles ahead of the wave packet move along the negative z direction with a large four-velocity, u0 = k0/ω ≫ 1. The four-velocity can be presented as
The proper density can be presented as
We introduced the real functions δu0 = δu0yey + δu0zez and δn0, and the complex functions uf = ufyey + ufzez and nf. For example, δu0(z, t) describes the secular evolution of the four-velocity inside the wave packet, and uf(z, t) describes the amplitude of the fast oscillations of the four-velocity. When the envelope of the wave packet is much longer than a few wavelengths, these functions vary on spatial and temporal scales ≫1/ω. The dots in Eqs. (16)–(18) indicate higher-order harmonics, and c.c. indicates the complex conjugate of the oscillating terms. The expansion in harmonics is justified when the plasma current is a linear function of the wave electric field (i.e., for ω0 ≫ a0ωL, as we show below). Second-order harmonics would be important to calculate nonlinear corrections to the dispersion relation on the order of uf2/u02, which is out of the scope of the paper.
We considered the regime where the four-velocity inside the wave packet is nearly constant and assumed δu0/u0 ∼ uf2/u02 ≪ 1. Below we show that the condition δu0/u0 ∼ uf2/u02 ≪ 1 requires ω0 ≫ a0ωL. In this regime, the plasma current is a linear function of the wave electric field.
Retaining terms of the order of δu0/u0 and uf2/u02, the Lorentz factor can be presented as
where 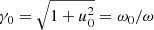 . The number density is
. The number density is
The y component of the current density is
and the z component is
where uf* and nf* respectively indicate the complex conjugates of uf and nf.
3.1. Fast oscillations
When the envelope of the wave packet is much longer than a few wavelengths, the functions δu0, δn0, uf, nf vary on spatial and temporal scales ≫1/ω. The evolution of the physical quantities on the temporal scale 1/ω can be easily determined. Since in the wave frame the wave vector vanishes, one can neglect the spatial derivatives of the physical quantities in Eqs. (4), (13), (14). One can also approximate the time derivatives as ∂/∂t ≃ −iω. From Eq. (4) one sees that γn should be constant on the temporal scale 1/ω. Then, Eq. (20) gives
Substituting Eqs. (17) and (21) into Eq. (13), one finds iωufz = ωLufy, or equivalently
Substituting Eqs. (16), (21), (22) into Eq. (14), one finds
Substituting Eqs. (23) and (24) into Eq. (25), one finds
Taking into account that ω2 = ω02 − k02 and γ02ω2 = ω02, one sees that Eq. (26) is equivalent to the standard dispersion relation in the lab frame, which is (ω02 − k02)(1 − ωL2/ω02) = ωP2. The wave is superluminal for ω0 ≫ ωL.
Next, we discuss the range of validity of our results. We derived the dispersion relation assuming that the particle four-velocity inside the wave packet is nearly constant (i.e., |ufy|≪γ0 and |ufz|≪γ0). For superluminal waves with ω0 ≫ ωL, one has γ0 = ω0/ωP, |ufy|=a0, and |ufz|=(ωL/ωP)|ufy| (the latter two relations follow from Eqs. (11) and (24)). Since the plasma is strongly magnetized, one has |ufz|≫|ufy|. The condition |ufz|≪γ0 requires2
Equation (27) has a simple physical interpretation. As we show in Sect. 3.2, the plasma inside the wave packet is compressed, and consequently the background magnetic field is amplified. In the lab frame, the amplified magnetic field is on the order of a02Bbg. Then, Eq. (27) implies that the amplified magnetic field should be smaller than the wave field. We emphasize that Eq. (27) can be satisfied by strong waves with a0 > 1 when the wave frequency is much larger than the Larmor frequency.
3.2. Secular evolution
In order to study the secular evolution of the physical quantities, one should average Eqs. (4), (13), (14) over the fast oscillations. In this case, the spatial derivatives of the physical quantities should be retained. From Eq. (4), one finds
Eq. (13) gives
Eq. (14) gives
In Appendix B, we present the expressions for the average physical quantities that appear in Eqs. (28)–(30).
We found an approximate solution of Eqs. (28)–(30) by neglecting the time derivatives of the average physical quantities. This “quasi-static” approximation has been extensively used to study laser-plasma interaction (e.g., Sprangle et al. 1990). The approximation is justified because we worked in the frame that moves with the group velocity, where the time derivative of the wave envelope can be neglected. The average physical quantities reach a steady state because (as we show below) they can be expressed as a function of a02. For example, since ∂a02/∂t ≪ ∂a02/∂z and ⟨uy⟩ is a function of a02, one has ∂⟨uy⟩/∂t ≪ ∂⟨uy⟩/∂z.
The average quantities vary on a scale comparable to the length of the wave packet, which in the wave frame is much longer than 1/ωP. Then, for example, one has ∂2⟨uy⟩/∂z2 ≪ ωP2⟨uy⟩. In this case, the third term on the left-hand side of Eq. (30) is much larger than the second term, and Eq. (30) can be approximated as ωP2⟨uy⟩/γ0 = ωL∂(⟨γn⟩/γ0n0)/∂z. Using Eqs. (B.1) and (B.8), the latter equation can be presented as
Equation (29) can be approximated as ∂(⟨γ⟩/γ0)/∂z = −ωL⟨nuy⟩/γ0n0. When substituting Eqs. (B.4) and (B.6) into the latter equation, and using Eq. (31) to eliminate δu0y, one finds
which implies
Eq. (28) can be approximated as ∂⟨nuz⟩/∂z = 0, which implies
Substituting Eq. (34) into Eq. (B.9), one finds
Now one can solve Eqs. (33) and (35), and express δu0z and δn0 as a function of a02. Then, one can substitute δu0z and δn0 into Eqs. (B.2), (B.4), and (B.8), and also express ⟨uz⟩, ⟨γ⟩, and ⟨γn⟩ as a function of a02. This procedure gives
The average Lorentz factor and the average four-velocity in the lab frame can be determined from Eqs. (36) and (37). Taking into account that ω0 ≫ a0ωL, one finds
The background magnetic field does not affect the particle motion in the lab frame, as Eqs. (39) and (40) are identical to the case of a test particle that moves in the field of a vacuum wave (e.g., Gunn & Ostriker 1971).
The average number density and the average current density in the lab frame can be determined from Eqs. (34) and (38). One finds
Substituting Eqs. (41) and (42) into Eqs. (10) and (11), one can determine the average electromagnetic fields in the lab frame, which are given by
In the lab frame, the number density and the background magnetic field inside the wave packet are amplified by a large factor on the order of a02. The amplified magnetic field is smaller than the wave field when ω0 ≫ a0ωL. When the latter condition is violated, particles can be trapped inside the wave packet because ⟨uz⟩ can vanish in the wave frame (see Eq. (36)).
4. Discussion
We have studied the propagation of superluminal electromagnetic waves with strength parameters a0 > 1 in magnetized pair plasmas where ωL > ωP. Our key result is that strong waves are able to propagate when ω0 > a0ωL, where ω0 is the wave frequency and ωL is the Larmor frequency in the background magnetic field. When ω0 > a0ωL, the background magnetic field does not affect the particle motion, and the plasma current is a linear function of the wave electric field. The dispersion relation is independent of the wave strength parameter.
Strong superluminal waves could be damped when ωL < ω0 < a0ωL for the following reasons. (i) The plasma inside the wave packet is compressed, and its density is amplified by a large factor on the order of a02. Although we demonstrated this for the extraordinary mode, we expect that the density is amplified also by the ordinary mode, as the particle motion is not affected by the background field and is nearly identical to the case of a test particle in the field of a vacuum wave. (ii) Since the background magnetic field is frozen into the plasma, its strength is also amplified by a factor on the order of a02. When ω0 < a0ωL, the amplified background field would be larger than the wave field. Then, the wave would be damped, as a significant fraction of its energy would be used to compress the plasma and amplify the background field. The only exception may occur when the wave propagates nearly along the background field, as the background field would not be significantly amplified. This exception does not apply to magnetar winds, where the magnetic field is nearly toroidal and the wave propagates in the radial direction. Fully kinetic simulations can be used to study the damping of strong superluminal waves when ωL < ω0 < a0ωL.
Our results have important implications for the modelling of FRBs. First we summarize the typical parameters of the problem (see, e.g., Sobacchi et al. 2022). The FRB strength parameter is
where L = 1042L42 erg s−1 is the isotropic equivalent FRB luminosity, ν = 1 ν9 GHz is the observed FRB frequency, and R = 1012R12 cm is the distance from the magnetar. The magnetar light cylinder is located at the radius Rlc = cP/2π, where P = 1 P0 s is the magnetar period. In the magnetosphere (i.e., for R < Rlc), the magnetar has a dipole field, Bbg = μ/R3, where μ = 1033μ33 G cm3 is the magnetic moment. In the wind (i.e., for R > Rlc), the magnetic field is Bbg = μ/Rlc2R. In the proper frame of the wind (which we called “lab frame” so far), the ratio of the Larmor frequency and the FRB frequency is
Equations (45) and (46) are independent of the wind Lorentz factor because a0 and ωL/ω0 are Lorentz invariant.
Next, we show that FRBs can propagate through the magnetar wind only at relatively large radii3. The condition ω0 > a0ωL requires R > Rcrit, where
Two consistency checks are needed. Since we considered the propagation of the wave in the wind, Rcrit should be larger than the light cylinder radius. The condition Rcrit > Rlc is satisfied for
Since we assumed that the strength parameter is large, one should have a0 > 1 for R = Rcrit. This condition is satisfied for
Eqs. (48) and (49) are satisfied by most magnetars, which have a typical period of a few seconds (Kaspi & Beloborodov 2017).
Our results suggest that FRBs produced at radii R < Rcrit cannot propagate through the unperturbed magnetar wind, which challenges several magnetospheric models (e.g., Cordes & Wasserman 2016; Dai et al. 2016; Kumar et al. 2017; Yang & Zhang 2018; Lu & Kumar 2018; Kumar & Bošnjak 2020; Lu et al. 2020). There are two alternative possibilities: (i) FRBs could be produced at radii R > Rcrit, as in the shock maser model (Lyubarsky 2014; Beloborodov 2017, 2020; Metzger et al. 2019; Sironi et al. 2021; Iwamoto et al. 2024). (ii) Alternatively, the structure of the wind could be modified during a flare, as in the reconnection model (Lyubarsky 2020; Mahlmann et al. 2022). In this model, FRBs produced at radii R < Rcrit propagate on the top of a large amplitude fast-magnetosonic pulse launched from the magnetosphere, and FRBs can escape because their electromagnetic field is much smaller than the field of the pulse.
Lyutikov (2024) defines an “effective nonlinearity parameter” as 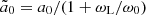 , which is of the order of the transverse component of the particle four-velocity. When ω0 < ωL, one has
, which is of the order of the transverse component of the particle four-velocity. When ω0 < ωL, one has 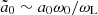 , and when ω0 > ωL, one has
, and when ω0 > ωL, one has 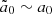 . The parameter
. The parameter 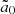 is not the only controlling parameter of the problem because, as we show below, the plasma current can be a linear function of the wave electric field also when the particle velocity is relativistic.
is not the only controlling parameter of the problem because, as we show below, the plasma current can be a linear function of the wave electric field also when the particle velocity is relativistic.
In weakly magnetized pair plasmas where ωL ≪ ωP, one has |ufz|≪|ufy|. The condition |ufy|≪γ0 requires ω0 ≫ a0ωP. As we explain in Appendix A, the latter condition implies that in the lab frame, the particle velocity along the direction of propagation should be smaller than the group velocity of the wave.
Subluminal waves with a0 > 1 can propagate when ω0 < ωL/a0, whereas they could be damped when ωL/a0 < ω0 < ωL (Beloborodov 2021, 2022, 2023; Chen et al. 2022). The condition ω0 < ωL/a0 can be satisfied only well within the magnetar magnetosphere, as it requires 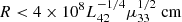 (Beloborodov 2021).
(Beloborodov 2021).
Acknowledgments
This work was supported by the JSPS KAKENHI Grants 20J00280, 20KK0064, and 22H00130 [M.I.], by the Simons Foundation Grant 00001470 to the Simons Collaboration on Extreme Electrodynamics of Compact Sources (SCEECS) [L.S., T.P.], by the DoE Early Career Award DE-SC0023015 [L.S.], by the Multimessenger Plasma Physics Center (MPPC) NSF Grant PHY-2206609 [L.S.], by the NASA Grant 23-ATP23-0074 [L.S.], by the ISF Grant 2126/22 [T.P.], and by the ERC Advanced Grant Multijets [T.P.]. We acknowledge insightful discussions with Andrei Beloborodov and Yuri Lyubarsky.
References
- Beloborodov, A. M. 2017, ApJ, 843, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Beloborodov, A. M. 2020, ApJ, 896, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Beloborodov, A. M. 2021, ApJ, 922, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Beloborodov, A. M. 2022, Phys. Rev. Lett., 128, 255003 [NASA ADS] [CrossRef] [Google Scholar]
- Beloborodov, A. M. 2023, ArXiv e-prints [arXiv:2307.12182] [Google Scholar]
- Bochenek, C. D., Ravi, V., Belov, K. V., et al. 2020, Nature, 587, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, A. Y., Yuan, Y., Li, X., & Mahlmann, J. F. 2022, ArXiv e-prints [arXiv:2210.13506] [Google Scholar]
- CHIME/FRB Collaboration (Andersen, B. C., et al.) 2020, Nature, 587, 54 [Google Scholar]
- Clemmow, P. C. 1974, J. Plasma Phys., 12, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., & Chatterjee, S. 2019, ARA&A, 57, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., & Wasserman, I. 2016, MNRAS, 457, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Z. G., Wang, J. S., Wu, X. F., & Huang, Y. F. 2016, ApJ, 829, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Golbraikh, E., & Lyubarsky, Y. 2023, ApJ, 957, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Ostriker, J. P. 1971, ApJ, 165, 523 [CrossRef] [Google Scholar]
- Iwamoto, M., Matsumoto, Y., Amano, T., Matsukiyo, S., & Hoshino, M. 2024, Phys. Rev. Lett., 132, 035201 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, V. M., & Beloborodov, A. M. 2017, ARA&A, 55, 261 [Google Scholar]
- Kumar, P., & Bošnjak, Ž. 2020, MNRAS, 494, 2385 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., Lu, W., & Bhattacharya, M. 2017, MNRAS, 468, 2726 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, W., & Kumar, P. 2018, MNRAS, 477, 2470 [Google Scholar]
- Lu, W., Kumar, P., & Zhang, B. 2020, MNRAS, 498, 1397 [NASA ADS] [CrossRef] [Google Scholar]
- Luan, J., & Goldreich, P. 2014, ApJ, 785, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubarsky, Y. 2014, MNRAS, 442, L9 [Google Scholar]
- Lyubarsky, Y. 2020, ApJ, 897, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubarsky, Y. 2021, Universe, 7, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M. 2024, MNRAS, 529, 2180 [NASA ADS] [CrossRef] [Google Scholar]
- Mahlmann, J. F., Philippov, A. A., Levinson, A., Spitkovsky, A., & Hakobyan, H. 2022, ApJ, 932, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D., Margalit, B., & Sironi, L. 2019, MNRAS, 485, 4091 [NASA ADS] [CrossRef] [Google Scholar]
- Petroff, E., Hessels, J. W. T., & Lorimer, D. R. 2019, A&ARv, 27, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Petroff, E., Hessels, J. W. T., & Lorimer, D. R. 2022, A&ARv, 30, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Qu, Y., Kumar, P., & Zhang, B. 2022, MNRAS, 515, 2020 [NASA ADS] [CrossRef] [Google Scholar]
- Sironi, L., Plotnikov, I., Nättilä, J., & Beloborodov, A. M. 2021, Phys. Rev. Lett., 127, 035101 [NASA ADS] [CrossRef] [Google Scholar]
- Sobacchi, E., Lyubarsky, Y., Beloborodov, A. M., & Sironi, L. 2022, MNRAS, 511, 4766 [NASA ADS] [CrossRef] [Google Scholar]
- Sprangle, P., Esarey, E., & Ting, A. 1990, Phys. Rev. Lett., 64, 2011 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y.-P., & Zhang, B. 2018, ApJ, 868, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B. 2023, Rev. Mod. Phys., 95, 035005 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Test particles in a vacuum wave
The motion of test particles in the electromagnetic fields of a strong vacuum wave has been studied for a long time. Here we summarize the main results of previous studies (e.g., Gunn & Ostriker 1971). We work in the lab frame where the particles ahead of the wave packet are at rest. We set ωL = 0 in Eqs. (4), (13), (14). We also neglect the feedback of plasma current onto the wave and set ωP = 0 in Eq. (14). In this case, the y component of the four-velocity can be presented as
where ξ = z − t, and a0 > 1 is the wave strength parameter.
Eq. (13) can be presented as d(γ − uz)/dξ = 0. In the lab frame where the particles ahead of the wave packet are at rest, the latter equation has the solution γ − uz = 1, which gives
Taking into account that ⟨uy2⟩=a02/2, one recovers Eqs. (39)-(40). Eq. (4) can be presented as d[(γ − uz)n]/dξ = 0, where n is the proper number density. Taking into account that γ − uz = 1, one finds
where n0 is the proper number density ahead of the wave packet. Eqs. (A.1) and (A.3) show that in the test particle approximation the plasma current, nuy, is a linear function of the wave field.
Now we discuss the validity of the test particle approximation. We focus on pair plasmas, where an electrostatic field is not generated. As we demonstrate formally in Sect. 3, two key conditions should be satisfied. First, the particle velocity along the direction of propagation in the lab frame, vz = 1 − 2/(2 + uy2), should be smaller than the group velocity of the wave, vg ≃ 1 − ωP2/2ω02, otherwise particles would be trapped inside the wave packet. This condition is satisfied for
Second, the average magnetic field inside the wave packet in the lab frame, ⟨B⟩, should be smaller than the peak electric field of the wave, E0 = (m/e)a0ω0. The particles number density inside the wave packet is equal to γn0, whereas the particles number density ahead of it is equal to n0. Since the average magnetic field is frozen into the plasma, one has ⟨B⟩=⟨γ⟩Bbg = (1 + a02/4)Bbg, where Bbg is the strength of the background magnetic field ahead of the wave packet. The average electric field is ⟨E⟩=⟨vzB⟩=(a02/4)Bbg (where vz = uz/γ). The condition ⟨B⟩≪E0 is satisfied for
In strongly magnetized plasmas where ωL ≫ ωP, the current is a linear function of the wave field when Eq. (A.5) is satisfied.
Appendix B: Average physical quantities
The average four-velocity and the average Lorentz factor can be calculated from Eqs. (16), (17), (19), which respectively give
Taking into account that |ufy|=a0, which follows from Eq. (11), one finds
The average number density and the average current density can be calculated from Eqs. (20)-(22). Taking into account that nfufy* + nf*ufy = 0 and nfufz* + nf*ufz = 2n0u0|ufz|2/γ02, which follow from Eqs. (23)-(24), one finds
Taking into account that |ufy|=a0 and |ufz|=(ωL/ωP)|ufy|=a0ωL/ωP, which follow from Eqs. (11) and (24), one finds
All Tables
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



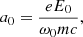
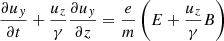
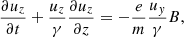
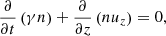
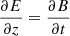
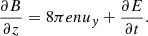
![$$ \begin{aligned} \frac{\partial }{\partial t}\left(\frac{\partial u_y}{\partial z}-\frac{e}{m}B\right) + \frac{\partial }{\partial z}\left[\frac{u_z}{\gamma }\left(\frac{\partial u_y}{\partial z}-\frac{e}{m}B\right)\right] = 0 . \end{aligned} $$](/articles/aa/full_html/2024/10/aa51725-24/aa51725-24-eq9.gif)
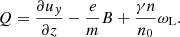
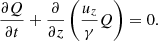
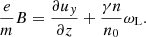
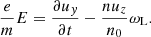
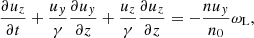
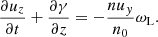
![$$ \begin{aligned} \frac{\partial ^2 u_y}{\partial t^2} - \frac{\partial ^2 u_y}{\partial z^2} +\omega _{\rm P}^2\frac{n}{n_0}u_y = \omega _{\rm L}\left[\frac{\partial }{\partial t}\left(\frac{nu_z}{n_0}\right) + \frac{\partial }{\partial z}\left(\frac{\gamma n}{n_0}\right)\right] . \end{aligned} $$](/articles/aa/full_html/2024/10/aa51725-24/aa51725-24-eq16.gif)
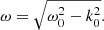
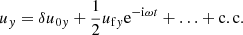
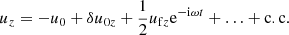
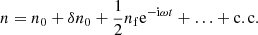
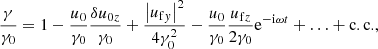
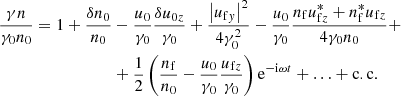
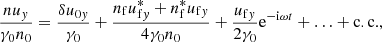
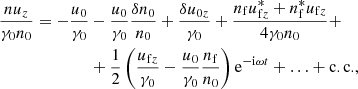
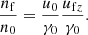
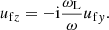
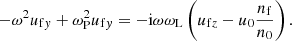
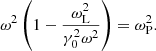
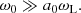
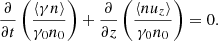
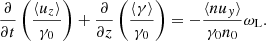
![$$ \begin{aligned} \nonumber \frac{\partial ^2}{\partial t^2}\left(\frac{\langle u_y \rangle }{\gamma _0}\right)&- \frac{\partial ^2}{\partial z^2}\left(\frac{\langle u_y\rangle }{\gamma _0}\right) +\omega _{\rm P}^2\frac{\langle u_y \rangle }{\gamma _0} = \\&= \omega _{\rm L} \left[ \frac{\partial }{\partial t}\left( \frac{\langle nu_z\rangle }{\gamma _0n_0}\right) + \frac{\partial }{\partial z}\left( \frac{\langle \gamma n\rangle }{\gamma _0n_0}\right) \right] . \end{aligned} $$](/articles/aa/full_html/2024/10/aa51725-24/aa51725-24-eq33.gif)