| Issue |
A&A
Volume 647, March 2021
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202038366 | |
| Published online | 23 March 2021 | |
The survey of planetary nebulae in Andromeda (M 31)
III. Constraints from deep planetary nebula luminosity functions on the origin of the inner halo substructures in M 31
1
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
e-mail: sbhattac@eso.org; marnabol@eso.org
2
Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
3
NRC Herzberg Institute of Astrophysics, 5071 West Saanich Road, Victoria, BC V9E 2E7, Canada
4
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
5
European Southern Observatory, Alonso de Córdova 3107, Santiago de Chile, Chile
6
Research School of Astronomy and Astrophysics, Mount Stromlo Observatory, Cotter Road, ACT 2611 Weston Creek, Australia
Received:
7
May
2020
Accepted:
26
January
2021
Context. The Andromeda (M 31) galaxy displays several substructures in its inner halo. Different simulations associate their origin with either a single relatively massive merger, or with a larger number of distinct, less massive accretions.
Aims. The origin of these substructures as remnants of accreted satellites or perturbations of the pre-existing disc would be encoded in the properties of their stellar populations (SPs). The metallicity and star formation history of these distinct populations leave traces on their deep [O III] 5007 Å planetary nebulae luminosity function (PNLF). By characterizing the morphology of the PNLFs, we constrain their origin.
Methods. From our 54 sq. deg. deep narrow-band [O III] survey of M 31, we identify planetary nebulae in six major inner-halo substructures: the Giant Stream, North East Shelf, G1 Clump, Northern Clump, Western Shelf, and Stream D. We obtain their PNLFs and those in two disc annuli, with galactocentric radii of RGC = 10–20 kpc and RGC = 20–30 kpc. We measure PNLF parameters from cumulative fits and statistically compare the PNLFs in each substructure and disc annulus. We link these deep PNLF parameters and those for the Large Magellanic Cloud (LMC) to published metallicities and resolved stellar population-age measurements for their parent SPs.
Results. The absolute magnitudes (M*) of the PNLF bright cut-off for these sub-populations span a significant magnitude range, despite being located at the same distance and having a similar line-of-sight extinction. The M* values of the Giant Stream, W Shelf, and Stream D PNLFs are fainter than those predicted by PN evolution models by 0.6, 0.8, and 1.5 mag, respectively, assuming the measured metallicity of the parent stellar populations. The faint-end slope of the PNLF increases linearly with decreasing fraction of stellar mass younger than 5 Gyr across the M 31 regions and the LMC. From their PNLFs, the Giant Stream and NE Shelf are consistent with being stellar debris from an infalling satellite, while the G1 Clump appears to be linked with the pre-merger disc with an additional contribution from younger stars.
Conclusions. The SPs of the substructures are consistent with those predicted by simulations of a single fairly massive merger event that took place 2–3 Gyr ago in M31. Stream D has an unrelated, distinct origin. Furthermore, this study provides independent evidence that the faint-end of the PNLF is preferentially populated by planetary nebulae evolved from older stars.
Key words: galaxies: individual: M31 / galaxies: evolution / galaxies: structure / planetary nebulae: general
© ESO 2021
1. Introduction
Within the Lambda cold dark matter (ΛCDM) cosmological model, galaxies evolve by hierarchical mass accretion (White & Rees 1978; Bullock & Johnston 2005). Fossil records of these processes are observed in the outskirts of massive galaxies in the form of shells, streams, tidal tails, and other substructures (e.g., Mihos et al. 2005; Martínez-Delgado et al. 2010; Crnojević et al. 2016). The masses and chemical properties of the accreted satellites may be uncovered from the kinematics and chemical abundances of surviving substructures (Johnston et al. 2008). Andromeda (M 31) is the nearest giant spiral galaxy to the Milky Way (MW) at a distance of ∼773 kpc (Conn et al. 2016). The Pan-Andromeda Archaeological Survey (PAndAS; McConnachie et al. 2009, 2018) produced a map of resolved red giant branch (RGB) star counts that revealed multiple substructures (Fig. 1) out to a projected radius of ∼150 kpc around M 31. These features unveiled the tumultuous merger history of M 31. With faint structures detected down to unprecedented surface brightness levels (μV ∼ 33 mag arcsec−2), M 31 provides the best current laboratory for studying the signatures of extended galaxy assembly.
 |
Fig. 1. Position on the sky of PNe (all marked points) identified by Paper I and Bhattacharya et al. (in prep.). Positions are overlaid on the number density map of RGB stars from PAndAS (McConnachie et al. 2018), binned for visual clarity and shown in grey. The PNe selected for the PNLF analysis in the two disc regions and six substructure regions are marked with different colours. North is up, east is left. The HST fields observed by Bernard et al. (2015) to obtain the SFH of four of the M 31 regions have been marked with green squares. |
The Giant Stream is the most prominent substructure in the M 31 halo. It was first discovered by Ibata et al. (2001) who linked its origin to that of an infalling satellite. The subsequent discoveries of other substructures, particularly those near the disc–halo interface, namely the North East Shelf (NE Shelf), G1 Clump, Northern Clump (N Clump), Western Shelf (W Shelf), and Stream D, led to intense speculations as to their origin. Fardal et al. (2013) showed that N-body simulations of a satellite of ∼3.2 × 109 M⊙ infalling along the Giant Stream ∼1 Gyr ago can reproduce the structure and kinematics of the Giant Stream and also of the NE and W shelves.
However, the N and G1 Clump do not arise naturally in models of the dissolution of the Giant Stream progenitors from minor mergers, and they were linked to distinct accretion events of dwarf galaxies (Ferguson & Mackey 2016). Most recently, using hydrodynamical simulations, Hammer et al. (2018) argued that a single merger of a more massive satellite with a total mass of 1.4 × 1010 M⊙ occurring 2–3 Gyr ago is able to perturb the pre-existing M31 disc, leading to the origin of the substructures along its major axis, as well as the origin of the Giant stream and the associated NE and W shelves.
The morphology of the low-surface-brightness substructures, the 2 Gyr-old burst of star formation observed in the M 31 disc and in some inner halo Hubble Space Telescope (HST) pointings (Bernard et al. 2015; Williams et al. 2017), and the dynamical heating of the disc (Dorman et al. 2015; Bhattacharya et al. 2019a, hereafter Paper II) are in line with the predictions from a 1:4 to 1:5 mass merger in M 31 (Hammer et al. 2018). However, further investigation is required to link the origin of any of the observed substructures with either the pre-existing disc or the satellite remnant.
The HST observations by Richardson et al. (2008) and subsequent star formation histories (SFHs) computed by Bernard et al. (2015) for 14 pencil beam pointings, some of which are aligned with the M 31 overdensities, reveal stellar populations similar to that of the Giant Stream while others are more similar to the M 31 disc. Nevertheless, an intrinsic limit of this approach is the very small area coverage of single HST pointings (see Fig. 1) within a significantly more extended subregion in the M 31 inner halo (Williams et al. 2017). Therefore, the SFH measured in such a small area, referred to as the ‘localised SFH’ hereafter, may not provide a robust representation of the SFH over the entire extended subregion if there is a significant variance and/or gradient of the stellar population properties; see for example, the metallicity gradient observed within the Giant Stream (Conn et al. 2016). In this study we then turn to the deep luminosity function of the associated Planetary Nebulae (PNe) population, which provides few constraints on the SFH, but in return these are obtained for an entire subregion.
Planetary Nebulae are identified from their relatively strong [O III] 5007 Å emission and negligible continuum. The characteristic [O III] 5007 Å (M5007) PN luminosity function (PNLF) was first described by Ciardullo et al. (1989). The analytical formula,
was fitted to the bright PNe detected in the centre of M 31 (Ciardullo et al. 1989). The PNLF is a reliable secondary distance indicator for determining galactic distances out to ∼20 Mpc by virtue of its invariant absolute bright cut-off, M*, currently measured at 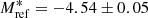 at near-solar metallicities (Ciardullo et al. 2013). While M* gets fainter in low-metallicity populations (e.g., Ciardullo & Jacoby 1992; Ciardullo et al. 2002; Hernández-Martínez & Peña 2009), according to theoretical predictions by Dopita et al. (1992), it seems to be invariant to either the age of the population or galaxy morphological type. The faint end of the PNLF is theoretically expected to follow an exponential function (Jacoby 1980) describing the slow evolution of the central star (CSPN) embedded in a rapidly expanding, optically thin nebula (Henize & Westerlund 1963).
at near-solar metallicities (Ciardullo et al. 2013). While M* gets fainter in low-metallicity populations (e.g., Ciardullo & Jacoby 1992; Ciardullo et al. 2002; Hernández-Martínez & Peña 2009), according to theoretical predictions by Dopita et al. (1992), it seems to be invariant to either the age of the population or galaxy morphological type. The faint end of the PNLF is theoretically expected to follow an exponential function (Jacoby 1980) describing the slow evolution of the central star (CSPN) embedded in a rapidly expanding, optically thin nebula (Henize & Westerlund 1963).
The slope of the PNLF measured at a few magnitudes fainter than its bright cut-off is observed to vary depending on the SFH of the average parent stellar population. In galaxies where the PNLF has been observed to ∼3 mag below M*, steeper PNLF slopes were observed for elliptical galaxies with older stellar populations (e.g., Longobardi et al. 2013; Hartke et al. 2017) and conversely flatter slopes for younger populations (e.g., M33; Ciardullo et al. 2004). In surveys deeper than ∼3 mag below M*, the shape of the PNLF may exhibit further changes in slope, as seen in the Large Magellanic Cloud (LMC; Reid & Parker 2010) or dips, such as for example those in the Small Magellanic Cloud (SMC; Jacoby & De Marco 2002) and NGC 6822 (a Local Group dwarf irregular galaxy; Hernández-Martínez & Peña 2009). Rodríguez-González et al. (2015) describe a two-mode PNLF for NGC 6822 and show that these modes of the PNLF may be associated with the two episodes of star formation, with the younger and older parent stellar population dominating the brighter and fainter PNe respectively. Indeed Valenzuela et al. (2019) showed theoretically that the shape of the PNLF at the faint-end is quite sensitive to the distribution of masses of the PN central stars, which is a product of the SFH in any galaxy. In Bhattacharya et al. (2019b, hereafter Paper I), we observed a rise in the faint-end of the PNLF in the central 16 sq. deg. of M 31 conceivably linked to the SFH of M 31.
Owing to the homogeneous spatial coverage and photometry of the current imaging survey, we detect PNe associated with all the stellar populations in a 54 sq. deg area centred on M31. Thanks to the sensitivity and accuracy, we can quantify the imprints of the variations of these stellar populations on the PNLFs in distinct regions. In Sect. 2, we describe our PN survey of M 31 and set the geometrical boundaries around any regions with RGB overdensities where the PNLFs are measured. In Sect. 3, we obtain the PNLFs, compute the parameters that best describe them, and carry out the quantitative comparisons via statistical methods. In Sect. 4, we correlate the stellar population parameters with the properties of the PNLFs at both their bright and faint ends in the different subregions. In Sect. 5, we discuss the implications of our results on the origin of the M31 inner halo substructures. We draw our conclusions in Sect. 6.
2. Survey of Planetary Nebulae in M31
2.1. Survey characteristics
In Paper I, we identified PNe candidates in a 16 sq. deg. uniform imaging survey of the disc and disc–halo interface of M 31 using the MegaCam wide-field imager (Boulade et al. 2003) mounted on the 3.6-meter Canada-France-Hawaii Telescope (CFHT). M 31 was observed through a narrow-band [O III] filter (λc = 5007 Å, Δλ = 102 Å, on-band) and a broad-band g-filter (λc = 4750 Å, Δλ = 1540 Å, off-band). An additional 38 sq. deg. were obtained in late-2019, providing uniform coverage of the inner halo of M 31 and its substructures reaching a uniform sensitivity down to fluxes equivalent to m5007 = 26.2 mag over the entire area. Details of these observations are presented in Bhattacharya (2020) and Bhattacharya et al. (in prep.).
The zero points for each of the [O III] and g-band frames in AB magnitudes, normalised to a 1 s exposure, are Z[O III] = 23.4 and Zg = 26.5. The photometry was calibrated using observations of spectrophotometric standard stars. The photometric uncertainty (errm, 5007) is well below 0.01 mag at m5007 = 22.5 mag; it increases to errm, 5007∼ 0.15–0.2 mag at m5007 = 26.2 mag.
The PN identification in each of these pointings was also carried out as described in Paper I using the on-off band technique developed and validated in Arnaboldi et al. (2002, 2003), later optimised for large imaging surveys by Longobardi et al. (2013). The PNe are identified as point-like sources with an excess [O III] – g colour. The complete imaging survey led to the identification of 5265 PN candidates in M 31, the largest PN sample in any galaxy (Paper I; Bhattacharya et al., in prep.). Of these, 4085 are newly discovered down to m5007 ≤ 26.7 mag in the deepest pointing. In Paper I, we verified that the identified PNe have counterparts in the HST data from the Panchromatic Hubble Andromeda Treasury (PHAT; Dalcanton et al. 2012) in the regions of overlap, with at most ∼3% possible contamination.
2.2. Substructures in M 31 and their Planetary Nebula subsamples
In Fig. 1 we show all the PNe (all coloured points) identified by the narrow-band imaging survey. These are overlaid on the map of RGB stars from PAndAS (McConnachie et al. 2018). The prominent substructures appear as overdensities in this map of RGB stars. The distances to all of the M 31 substructures are consistent with that of the disc (773 kpc; Conn et al. 2016). Akin to McConnachie et al. (2018), we define the spatial boundaries of these substructures with polygons around the regions of higher spatial density. The identified overdensities, as marked with dashed lines in Fig. 1, are the Giant Stream (red), Northeast Shelf (NE Shelf; black), G1 Clump (dark blue), Northern Clump (N Clump; pink), Western Shelf (W Shelf; yellow), and Stream D (cyan). The PNe included within a given region are considered to belong to that substructure and used for subsequent analysis. Figure 1 also shows elliptical projections of circular annuli in the disc (black dashed) at galactocentric distances of RGC = 10, 20 and 30 kpc covering the disc of M 31. As found in Paper II, the PNe in the 10 < RGC ≤ 20 kpc disc region of M 31 belong both to the (heated) thin and thicker disc, while the PNe in the 20 < RGC ≤ 30 kpc disc region are dominated by PNe belonging to the thicker disc of M 31.
In subsequent sections, we only consider PNe in the disc regions that were selected from the fields with limiting magnitude of m5007 ≥ 26.16 mag1. Figure 1 shows the PNe in the defined 10 < RGC ≤ 20 and 20 < RGC ≤ 30 kpc disc regions in orange and green respectively. Table 1 lists the different regions studied in this work along with the number of PNe identified in those regions, NPN, and those within the magnitude range of m5007 ≤ 26.16 mag used in the subsequent analysis, 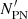 .
.
Number of PNe in each studied region in our M 31 survey.
2.3. Extinction in the M31 survey region
The line-of-sight (LOS) extinction to any subregion in M31 depends on the extinction from the MW halo (Schlegel et al. 1998) and on the internal extinction in M 31 and its substructures. As shown by Ibata et al. (2014) for the PAndAS survey region (see their Fig. 2), which overlaps the area in M 31 covered by this work, the MW halo LOS extinction is largely homogeneous having almost the same value (AV ∼ 0.19 mag) for the entire M31 disc and its substructures. The same can also be observed in the latest foreground reddening map obtained from LAMOST spectra of the MW halo stars to the M31 LOS (Zhang & Yuan 2020, see their Fig. 2).
Regarding the extinction by dust internal to M31, the dust surface density map of Draine et al. (2014) shows a near-exponential radial decrease in the M31 disc, with a scale-length of a few kiloparsec outside an annular radius of Rgc = 15 kpc. Combined with the dust model of Draine & Li (2007), this corresponds to an average AV ∼ 0.3 mag along the LOS at Rgc = 20 kpc and suggests negligible values beyond Rgc = 30 kpc where the inner halo substructures are located (see Fig. 1).
Therefore, dust extinction is present mostly within the Rgc = 20 kpc elliptical isodensity contour of the M31 disc, thereby mainly affecting the PN population in the 10–20 kpc disc region considered in this work. If most of the dust is located together with the gas at very low scale heights, the PNe identified in the 10–20 kpc disc region might miss a fraction of PNe behind the dust layer along the LOS, but the bright cut-off would still reflect the cut-off of the bright PNe in front of the dust. Outside this annulus, the effect of dust internal to M31 is small in the 20–30 kpc disc region and negligible in the substructures further out. From the Pan-Andromeda Archeological survey (PAndAS) CMDs (Ibata et al. 2014; McConnachie et al. 2018) and the CMDs of the small HST fields by Bernard et al. (2015) at Rgc ≥ 30 kpc, there is no evidence for differential reddening. From the recent LAMOST extinction map, the reddening caused by dust in the M31 halo decreases from about 0.01 mag in the central regions to 0.001 mag at a projected distance of 5 R25 (∼100 kpc; Zhang & Yuan 2020). Hence, no further correction is required for internal extinction in any regions other than the 10–20 kpc annulus.
In the subsequent sections, we consider the LOS extinction of A5007 ∼ 0.21 mag (corresponding to AV ∼ 0.19; Cardelli et al. 1989) for the M 31 disc and each of the substructures. We note that the circumstellar extinction of individual PNe is their intrinsic property, and is linked to their progenitor (see Appendix A for details). Therefore, circumstellar extinction is not to be accounted for whenever deriving the absolute magnitude of the PNLF bright cut-off.
3. The Planetary Nebula luminosity function
3.1. Fitting the cumulative PNLF
A quantitative analysis of the luminosity function of the PN subsamples selected in any M 31 region can be performed on the cumulative luminosity function to avoid potential histogram binning issues such as the bin size or position of the first magnitude bin (e.g., Peña et al. 2007, for NGC 3109). For an observed PN population (as in Sects. 3.2 and 3.3), the cumulative PNLF is constructed by taking into account the detection and selection completeness. The detection completeness correction accounts for the non-detection of PNe due to noise. Colour or point-like selection criteria which would exclude those PNe affected by photometric errors is accounted for with the selection completeness correction. See Paper I for further detailed information.
The PNLFs for PN populations in different galaxies are described by the generalised analytical formula introduced by Longobardi et al. (2013), that is,
where c1 is a normalisation constant and c2 is the slope in the intermediate magnitude range. The Ciardullo et al. (1989) LF is therefore a specific case of the generalised formula with c2 = 0.307. The cumulative PNLF corresponding to the generalised analytical PNLF (Paper I) is:
Its free parameters are c1, c2, and M*. Here, M* is theoretically expected to become fainter with decreasing metallicity (Dopita et al. 1992).
In Paper I, we found an additional ubiquitous rise in the faint end of the M 31 PNLF at apparent m5007 magnitudes fainter than m5007 = 25 mag. We describe such a rise with an additional exponential function in the cumulative PNLF, which has the following form:
where cf1 is a normalisation constant and cf2 is the slope of this exponential function. Thus the cumulative PNLF can be described over the entire magnitude range by
For a given PN population, the free parameters in Eq. (3) are fitted to the PN brighter than m5007 = 25 mag2. Once these are determined, they are kept fixed, and the additional parameters cf1 and cf2 for If(M) in Eq. (5) are determined from the PNe with m5007 ≤ 26.04 mag. At the distance and LOS extinction to the main disc of M31, the apparent magnitude of the PNLF bright cut-off is m5007 = 20.16 mag.
3.2. Independent calibration to a large Planetary Nebula sample: Cumulative PNLF of the LMC
Reid & Parker (2010) measured the PNLF in the LMC, reaching ∼8 mag fainter than the bright cut-off. This is one of the deepest surveys of PNe in any galaxy, making it a suitable independent data-set with which to test our fitting procedure. By keeping the absolute bright cut-off of the more metal-poor LMC PNLF constant, M* = −4.44 (Reid & Parker 2010), we obtain the cumulative PNLF of the LMC (Fig. 2) shifted to the distance and average foreground extinction of M 31. It is fitted as previously described to derive the parameter values noted in Table 2. The LMC PNLF is also well described by the Itot(M) function; the faint end of the LMC cumulative PNLF indeed requires the additional exponential component to reproduce the rise at the faint magnitudes.
 |
Fig. 2. Cumulative PNLFs for the LMC PN sample from Reid & Parker (2010) shifted to the apparent bright cut-off of the M 31 disc region at 10 < RGC ≤ 20 kpc. The cumulative PNLFs are fitted by the generalised cumulative function (in blue) for m5007 ≤ 24.5 mag and a function which additionally includes an exponential at the faint end (in orange). The uncertainties of the fits are shaded. The region fainter than the limiting magnitude of the shallowest field (m5007 > 26.16 mag) in our M 31 survey is shown in grey. |
Cumulative PNLF fit parameters and corresponding region properties.
3.3. Cumulative PNLFs of the M 31 regions
We obtain the cumulative PNLF in each identified region of M 31, having corrected for the average foreground extinction. Each magnitude-limited sample reaches m5007 ≤ 26.16 mag, approximately 6 magnitudes fainter than the bright cut-off for M 31. Figure 3 shows the completeness-corrected cumulative PNLFs for the PNe identified in the two disc regions of M 31. Figure 4 shows those computed for the six RGB overdensity regions. The different surface brightness and SFH of each substructure is reflected in the different total number of PNe observed in each region and in turn in the normalisation parameter, c1, of the cumulative PNLF, with brighter regions showing a larger c1 value than the fainter ones. The PNLF in each M 31 region is fitted by the generalised cumulative PNLF (in blue), and with Itot(M) which includes the faint-end exponential (in orange). The fitted parameter values for all regions are shown in Table 2. For the N Clump, the exponential function was unconstrained and hence its cf1 and cf2 values are not listed.
 |
Fig. 3. Completeness-corrected cumulative PNLFs for the disc regions within 10 < RGC ≤ 20 kpc (left) and 20 < RGC ≤ 30 kpc (right). The cumulative PNLFs are fitted by the generalised cumulative function (in blue) for m5007 ≤ 25 mag and a function which additionally includes an exponential at the faint end (in orange). The uncertainties of the fits are shaded. The region fainter than the limiting magnitude of the shallowest field (m5007 > 26.16 mag) is shown in grey. |
 |
Fig. 4. Completeness-corrected cumulative PNLFs for the six different substructures. The cumulative PNLFs are fitted by the generalised cumulative function (in blue) for m5007≤ 25 mag and a function which additionally includes an exponential at the faint end (in orange; except for N Clump). The uncertainties of the fits are shaded. The region fainter than the limiting magnitude of the shallowest field (m5007 > 26.16 mag) is shown in grey. |
We note that while Itot(M) describes the cumulative PNLF of all the M 31 regions well, the fit to the cumulative PNLF of the 10 < RGC ≤ 20 kpc disc region is less optimal in the m5007 ∼ 20.5–21.5 mag interval. While the reason for this is presently unclear, our conjecture is as follows. This region has the largest number of PNe, 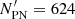 , amongst all the regions studied here. Given the large number statistics, we may be sensitive to sizeable dust attenuation in the 10 < RGC ≤ 20 kpc disc region, as discussed in Sect. 2.3, and possibly to differences in the SFH likely to leave an imprint on the PNLF. Because of the variable dust attenuation in the inner disc, a fraction of the bright PNe would then be more extincted and thus occupy fainter magnitudes in the PNLF, thereby creating a slight paucity of PNe detected in the m5007 ∼ 20.5–21.5 mag interval. Also it is possible that minor features in the cumulative PNLF in the brighter magnitudes (m5007 ∼ 20.5–21.5 mag) are not captured well by Itot(M) and additional functions relating to other specific aspects of the SFH may be required. We discuss the measured effects of the parent stellar population on the M 31 cumulative PNLF in Sects. 4 and 5.1.
, amongst all the regions studied here. Given the large number statistics, we may be sensitive to sizeable dust attenuation in the 10 < RGC ≤ 20 kpc disc region, as discussed in Sect. 2.3, and possibly to differences in the SFH likely to leave an imprint on the PNLF. Because of the variable dust attenuation in the inner disc, a fraction of the bright PNe would then be more extincted and thus occupy fainter magnitudes in the PNLF, thereby creating a slight paucity of PNe detected in the m5007 ∼ 20.5–21.5 mag interval. Also it is possible that minor features in the cumulative PNLF in the brighter magnitudes (m5007 ∼ 20.5–21.5 mag) are not captured well by Itot(M) and additional functions relating to other specific aspects of the SFH may be required. We discuss the measured effects of the parent stellar population on the M 31 cumulative PNLF in Sects. 4 and 5.1.
3.4. Comparison of the shapes of the PNLFs
The differences in the PNLFs obtained for distinct regions reflect diversities in their parent stellar populations (detailed in Sect. 4). We can therefore establish similarities or differences between the stellar populations of different substructures by statistically comparing their PNLFs, even if the colour–magnitude diagram for the resolved RGBs is not available for the entire region. We use the two-sample Anderson-Darling test (AD test; Scholz & Stephens 1987) to compare PNLFs of distinct PN samples. For sample sizes larger than 8 (Lewis 1961), the two-sample AD test is a non-parametric test which checks for the null hypothesis that two samples are extracted from the same distribution. The test statistic is computed from the distance between the cumulative probability distribution of the two samples, and is compared against the critical values3 to derive a significance level of the two samples being drawn from the same distribution. If the significance level is less than 5%, this null hypothesis can be rejected. If the significance level is found to be above 5%, the two samples may or may not be drawn from the same distribution. The AD test has high statistical power compared to other non-parametric tests like the Kolmogorov-Smirnov (KS) test, even for small sample sizes (Mohd Razali & Yap 2011). The AD-test is, in particular, more sensitive than the KS-test at differentiating between two distributions when the differences are most prominent near the beginning or end of the distributions. By comparing the PNLFs of distinct regions, we find which of these have statistically different parent stellar populations.
The cumulative probability of the completeness-corrected PNLF, which is computed by normalizing the PNLF between 0 and 1, is shown for the distinct substructure regions in Fig. 5. We refrain from comparing the PNLF of the N Clump with any other region because it is obtained from smaller sample size than the minimum required for the AD test. The significance level obtained for each compared pair of regions is tabulated in Table 3.
 |
Fig. 5. Cumulative probability of the completeness-corrected PNLF is shown (in log scale for visual clarity) for the five different substructures and the two disc regions. This diagnostic plot illustrates in which magnitude ranges the PNLFs are most different. The region fainter than the limiting magnitude of the shallowest field (m5007 > 26.16 mag) is shown in grey. Here, we report the error bars depicting the photometric errors (multiplied by ten for visual clarity) with magnitudes in our survey, shown as black lines at m5007 = 20, 21, 22 and 23 mag respectively. The M* fitted values for each of the PNLFs are robust in the entire survey area given the photometric accuracy (m5007,err ∼ 0.014 mag at m5007 = 23 mag). Furthermore, the arrow in the upper left corner shows the mean photometric extinction within our survey area (A5007 = 0.21 mag). |
Comparison of PNLF shapes for regions in M 31 with the Anderson-Darling test.
We find that the PNLFs of the disc regions are statistically different from each of the substructure regions. In many cases, the significance level of two PNLFs being drawn from the same distribution is as low as 0.1%. We find that the two disc regions also have different PNLFs from each other as their significance level of being drawn from the same distribution is 4.1%. We also find that Stream D has a PNLF, and hence a parent stellar population, that is different from the Giant Stream, NE Shelf, or G1 Clump. From the AD test results, the other substructure pairs (not marked in italics in Table 3) may or may not have different PNLFs, that is, the test does not support a conclusive answer. If we recompute the AD test on PN subsamples that are brighter than m5007 ≤ 25.9 mag, we find that the significance level of the AD test for the two disc regions is 25% (our capped value), meaning that their stellar populations may or may not be different. This indicates that the PNe in the brighter regions of the PNLF may originate from similar parent stellar populations, while any definite difference in stellar populations is engraved in the faint end. Recomputing the AD tests for the substructures with PN subsamples brighter than m5007 = 25.9 mag, we find that all previous results are robust and not solely driven by the PNe in the faintest magnitude bin in the cumulative PNLFs, with a significance level well below 5%. The exception is the comparison of the Disc (20 < RGC ≤ 30 kpc) and Giant Stream regions, where the significance level increases to 9%.
3.5. Quantitative differences of the PNLFs of distinct subregions in M31
From the deep cumulative PNLFs extracted from the regions associated with the RGB overdensities and disc annuli in M31, we can assess in which magnitude ranges the cumulative PNLFs differentiate the most (see Fig. 5).
-
Bright-end of the PNLF: The apparent magnitude of the PNLF bright cut-off in the M 31 substructures falls in the range m5007 = 20–22.8 mag (Fig. 5) even though all these substructures are at the same LOS distance and have similar extinction values (see Sect. 2.3 for details). In a given M31 subregion, any variation of the fitted PNLF M* value (Table 2) from the reference
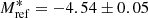 value results from the intrinsic properties of that PN subsample and does not originate from a difference in LOS distance or extinction.
value results from the intrinsic properties of that PN subsample and does not originate from a difference in LOS distance or extinction. -
Intermediate magnitudes of the PNLF: The c2 parameter is the slope of the PNLF at intermediate magnitude (m5007 = 21–25 mag). For some of the M 31 regions, we find c2 ≈ 0 (see Table 2). This occurs when there is a paucity of PNe at intermediate magnitudes and corresponds to a dip in the PNLF.
-
Faint end of the PNLF: The rise in the faint end of the PNLF is ubiquitous amongst the M31 region PNLFs and that of the LMC. However, the slope of the PNLF faint end given by the cf2 parameter covers a wide range of values (see Table 2) indicating differences at the faint end of the PNLF.
Given the negligible effects of LOS distance, extinction, and the uniform and accurate photometry of our survey (Fig. 5), the differences in the PNLFs (as found in Sect. 3.4) are driven by the intrinsic properties of the PN subsamples and are linked to their parent stellar populations.
4. Cumulative PNLFs and stellar populations in the M31 disc and inner halo
We find possible correlations between the parameters that describe the differences among the PNLFs of the M 31 regions and the metallicities ([M/H]; both photometric and spectroscopic as per availability) and SFH obtained from isochrone-fitting of CMDs of resolved stellar populations – mainly RGB stars – in these subregions and also for the LMC.
4.1. Variations of M* in the M31 subregions. Possible correlations with the metallicity of the parent population
The inferred absolute magnitude of the PNLF bright cut-off M* in different galaxies was shown to be independent of morphology (Ciardullo et al. 2013), with a weak dependency on metallicity (see Ciardullo et al. 2002) for galaxies with [M/H] larger than −0.5. In M31 we have the ideal laboratory to investigate this issue further as the PN subsamples and their PNLFs are all at the same distance and with the same LOS extinction for radial distance > 20 kpc from the center of M31.
In Fig. 6, we plot the M* for different M 31 regions against the tabulated [M/H] values of their parent stellar populations listed in Table 2. We provide the [M/H] values in different sub-regions in Appendix B, measured either from isochrone-fitting of the RGB-branch in CMDs or from spectroscopy of individual RGB stars, which are available for some of the regions. In Fig. 6, we also depict the theoretical variation of M* with [M/H]: such variation is computed from the dependency of M* on [O/H] obtained by Ciardullo et al. (2002) from the Dopita et al. (1992) PN evolution models. [O/H] is calibrated to [M/H] by subtracting the solar [O/H] value (=8.69; Asplund et al. 2009) as is done for calibrating stellar and gas phase mass–metallicity relations of galaxies (e.g., Zahid et al. 2017). The theoretical dependence of M* values on [M/H] predicts a dimming of M* with decreasing metallicity.
 |
Fig. 6. [M/H] for the different regions in M31 is plotted against the M* value obtained from fitting their PNLF. The different markers show the different references for the [M/H] measurements – circle: Williams et al. (2017); pentagon: Bernard et al. (2015); triangle: Escala et al. (2020); inverted triangle: Nidever et al. (2020); cross: Tanaka et al. (2010); square: Conn et al. (2016). The theoretical prediction for the values of M* from Dopita et al. (1992) models is shown with the dotted line. Also shown is the variation of photometric errors in our survey (multiplied by a factor of ten for visual clarity) at the magnitudes corresponding to the given M* values (as black lines at M* = −4.74, −3.74 and −2.74 mag). |
We find that the M* for the LMC, the two disc regions, the G1 Clump, and the NE Shelf are in agreement with the theoretical prediction from Dopita et al. (1992) PN models. However, the M* values for the PN samples in the Giant Stream, W Shelf, and Stream D areas are fainter than those predicted on the basis of the measured [M/H] of their parent stellar populations from the Dopita et al. (1992) models. We discuss hereafter in turn the possible origins of the deviant M* values.
Stream D and W Shelf substructures. Only five and ten PNe, respectively, are brighter than m5007 = 25 mag in these regions; see Fig. 4. The low number of PNe in these regions is related to the low luminosity of the substructures. According to Buzzoni et al. (2006), the visibility lifetimes of PNe are short, and the fading of a PN after the maximum brightness plateau is rather fast (Schönberner et al. 2007). Therefore, in these M 31 substructures we may be preferentially detecting slow evolving fainter PNe from less massive, older stars that are entering the PN phase at their own, dimmer M*.
Giant Stream. Differently from the previous two substructures, the Giant Stream is brighter and has a large number (113) of detected PNe. Therefore, statistical uncertainty coupled with short PN visibility lifetime is not a viable alternative explanation for the fainter M* in the Giant Stream. The fainter value of M* for this substructure is further supported by the spectroscopic follow-up of its brightest PN. This PN (PN14 from Fang et al. 2018) has an absolute magnitude M5007 = −3.51 with 12+(O/H) = 8.3 dex, corresponding to [M/H] = −0.39. Hence, in Fig. 6 the M* versus [M/H] point derived from the PNLF fit and RGB metallicities (Escala et al. 2020) coincides with that from the M5007 and [M/H] spectroscopically derived values for the brightest PN in the Giant Stream.
The current investigation indicates a significant discrepancy between the observed dimming of M* at [M/H] ≤ −0.4 and the more modest variations predicted from theoretical models of PN evolution at this [M/H] value. We note that the latter models from either Dopita et al. (1992) or Schönberner et al. (2010) investigate the effect of varying metallicities only for the ionized nebula, while the central star is kept constant with solar metallicity. Planetary Nebula evolution models incorporating the effects of metallicity on the central star as well as on the ionized nebula may provide a better diagnostic for the effect of [M/H] on M*. This is particularly important given the significance of the absolute magnitude of the PNLF bright cut-off, M*, as a reliable secondary distance indicator across the different Hubble galaxy types (Ciardullo et al. 2013), including dwarf galaxies.
4.2. Imprint of star-formation history on the faint end of the PNLFs in M 31
Bernard et al. (2015) obtained the localised SFHs from 14 deep HST pointings in different regions of the M 31 disc and some inner halo substructures. While these latter authors found that M 31 had a ubiquitous burst of star formation ∼2 Gyr ago, they measured significant differences in the percentage of stellar mass formed < 5 Gyr ago (hereafter m*, < 5 Gyr) in distinct HST fields in different substructures. In particular, they found that at the location of the HST pointings in the Giant Stream, NE Shelf, and outer disc, the stellar populations have much smaller m*, < 5 Gyr compared to the G1 Clump. Based on these two-age-bin SFHs (< 5 and > 5 Gyr), they described the Giant Stream and NE Shelf as ‘stream-like’, while the G1 Clump was referred to as ‘disc-like’. The outer-disc field was labelled as a composite field, having a slightly larger m*, < 5 Gyr value compared to the stream-like fields. No SFH measurements are available for the W Shelf4 and Stream D. Williams et al. (2017) used observations from the PHAT survey (Dalcanton et al. 2012) to find that ∼10 − 20% of the stellar mass within Rgc = 20 kpc is formed in a burst of star formation ∼2 Gyr ago with m*, < 5 Gyr ∼ 30%. Using their HST observations in eight scattered fields in the LMC, Weisz et al. (2013) showed that ∼50% of the stellar mass in the LMC was formed in the last 5 Gyr.
Given the extended coverage of the HST fields from which the SFH (from resolved stellar populations) in the LMC and M 31 10 < RGC≤ 20 kpc disc region are derived, the measured m*, < 5 Gyr values are representative of the average stellar population in these regions. As the SFH of the average stellar population leaves an imprint on the global PNLF of any region, the measured m*, < 5 Gyr value for the aforementioned regions can be linked to their PNLF fit parameters. For the other four regions (see Fig. 1), the localised SFH measured from the pencil-beam HST fields obtained by Bernard et al. (2015) may not be representative of the average stellar population for the entire substructure (Williams et al. 2017).
We can assess whether the localised-SFH values determined from the pencil-beam HST fields are representative of the average values for the entire stellar population in any substructure by checking whether the relation between the global PNLF parameters and the measured m*, < 5 Gyr value for these regions lie on the same relation as that for the SFH of the LMC and the M 31 10 < RGC ≤ 20 kpc disc region, whose extended coverage results in measured SFHs from resolved stellar populations that are representative of the entire region. Any region whose average stellar population is vastly different from that found within the tiny HST pointing would diverge significantly from any fitted relation.
We find a correlation between the percentage stellar mass from the HST fields in two age bins (see Table 4), younger and older than 5 Gyr following the age distinction by Bernard et al. (2015), and the exponential function fitting the faint end of the PNLF, cf2 (see Table 2). Figure 7 shows cf2 against m*, < 5 Gyr in the respective HST field of a given subregion. We find that the subregions for which the SFH value is obtained from large spatial HST coverage lie tightly on the same relation as those regions with smaller fields. Fitting the relation between m*, < 5 Gyr and cf2 with a linear function using a Deming regression5 (Kummell 1879), the best fit is given by:
 |
Fig. 7. Linear relation between the slope of exponential function at the faint end of the PNLF, cf2, and the percentage stellar mass formed within the last 5 Gyr, m*, < 5 Gyr. |
Percentage stellar mass formed within the last 5 Gyr, m*, < 5 Gyr, from the PNLF predicted with the pick-one-out test.
As it is not known a priori whether or not the HST field of a particular region could be an outlier influencing the fitted parameters of Eq. (6), we ran a ‘pick-one-out test’ over the parameters for the six regions. The relation between cf2 and m*, < 5 Gyr is fitted for five of the six regions and the m*, < 5 Gyr value is predicted for the selected region from its cf2 value. This process is iterated for each of the six regions. The predicted m*, < 5 Gyr values are noted for each region in Table 4. The predicted quantities are in good agreement with those measured from the HST fields implying that the cf2 – m*, < 5 Gyr relation is applicable to the entire parent stellar population of the PNe in any region. We therefore also use Eq. (6) to predict the m*, < 5 Gyr values for the W Shelf and Stream D (Table 4).
4.3. Stellar population dominating the very faint end of the PNLF
Following this analysis, we infer that the cf2 value of the PNLF increases linearly with decreasing fraction of stellar mass from its parent stellar population that formed in the last 5 Gyr. Hence, the rise at the faint end of the PNLF is driven by the fraction of the stellar mass in the stellar population older than 5 Gyr. This is in agreement with the expectations from the stellar evolution models by Marigo et al. (2004) where the faint end of the PNLF is populated by PNe evolving from older stellar populations and powered by less-massive central stars (see their Figs. 18 and 25 and associated text). However, it is in contrast to the predictions by Méndez et al. (2008) where the faint end of the PNLF is populated by PNe from massive progenitor stars from young stellar populations which have faded rapidly while losing their envelope.
5. Discussion
5.1. Morphology of the PNLFs and stellar population parameters in the M 31 regions
Through the analysis presented in Sects. 3 and 4, we described our efforts to link the differences among the PNLFs of extended M 31 subregions to the diversity of the parameters describing their parent stellar populations. We measured different M* values of the PNLFs in the M 31 subregions. In case of the Giant Stream, W Shelf, and Stream D, we cannot link the measured dimmer M* values of the PNLF to the lower metallicity of the parent stellar populations. We further showed that the cf2 values are clearly associated with the m*, < 5 Gyr. The c2 parameter is also influenced by the SFH of the parent stellar population. Valenzuela et al. (2019) showed theoretically that a dip in the PNLF is also a product of the distribution of masses of the central stars, and hence of the SFH of the parent stellar population. However, a quantitative link is yet to be established between the SFH and a dip in the PNLF, and hence its c2 value.
For each pair of M 31 regions that have different PNLFs (see Table 3), we assessed in which magnitude ranges the PNLFs differentiate the most (Fig. 5) and summarise the differences in their fitted PNLF properties (see Table 2). We link the differences in pairs of M 31 regions to their parent stellar population parameters in Appendix C. The highlights from this analysis are that the Giant Stream and the W Shelf have similarly faint M* values and large cf2 values, with their mass in stars dominated by > 5 Gyr-old populations. Furthermore, the NE Shelf has an M* value that is similar to the inner disc region within the errors, but its stellar mass is dominated by a > 5 Gyr-old population. The G1 clump has a M* value comparable to that of the inner disc region, with a significant contribution from a young < 5 Gyr old population. Finally, Stream D has the faintest M* value amongst the studied subregions.
5.2. The merger origin of the inner-halo substructures in M 31
Having mapped the average properties of the global stellar populations in the substructures of the M 31 inner halo, we now compare our observational results with the predictions from N-body/hydrodynamical simulations of a merger event in M31. On one hand we have the N-body simulations of a minor merger (Fardal et al. 2013 and reference therein). This event, if it took place 1 Gyr ago, successfully reproduces the morphology of the Giant Stream, and NE and W Shelves. The Giant Stream represents the trailing stream of material torn off during the first pericentric passage of the progenitor, while the NE and W Shelf regions contain material torn off in the second and third passages, respectively (Ferguson & Mackey 2016). The largest fraction of stellar mass in all three substructures is made up by the old stellar debris of the satellite. This is consistent with the global PNLF results for these three subregions of M 31: the Giant Stream and NE Shelf have large fractions of older stars, i.e. large cf2 values. The W Shelf also has stellar populations different from the M 31 disc regions but the age of its stellar population is still not very well constrained.
Nevertheless, such an evolution scenario leaves out the formation of the N and G1 clumps. Following their initial discoveries (Ferguson et al. 2002; Ibata et al. 2005), these substructures had been linked to dissolution of dwarf galaxies from distinct accretion events. The G1 Clump is measured to have an absolute V-band magnitude, MV = −12.6 mag (Ferguson et al. 2002), which corresponds to a total V-band luminosity of Ltot = 9.37 × 106 M⊙. If the G1 Clump were the result of a dissolved dwarf, following the luminosity–metallicity relation for Local Group dwarf galaxies (Kirby et al. 2011), its mean [M/H] value would be ∼ − 1.5. Such a value is much lower than its measured [M/H] = −0.37 (Table 2). Thus, the G1 Clump, given its relatively large metallicity, could not have formed from the dissolution of a small dwarf.
The remaining issues regarding the minor merger scenario are the tension between the timing of such an event, ∼1 Gyr ago, and the age of the burst of star formation of ∼2 Gyr in the M31 disc (Bernard et al. 2015; Williams et al. 2017), and particularly the mass of the satellite not being large enough to dynamically heat the M31 disc (Paper II).
We now examine the predictions from the major-merger scenario as simulated by Hammer et al. (2018). In these simulations, a massive gas-rich satellite was accreted with an orbit along the Giant Stream 2–3 Gyr ago. Such a massive satellite would perturb the M 31 disc and produce a thick disc from the pre-existing stars. After the merger, the replenished cold gas would lead to a burst of star formation and the build-up of a less-extended thin disc. Within the 10 < RGC≤ 20 kpc disc region, we observe in the PNLF a superposition of the stellar populations associated with both the newly formed thin disc and the older thicker disc of M 31. This disc region therefore has a larger fraction of younger stars compared to the 20 < RGC≤ 30 kpc disc region where the stellar populations associated with the thicker disc stars dominate.
The simulations by Hammer et al. (2018) also predict that the stellar populations in the Giant Stream, NE Shelf, and W Shelf are dominated by stellar debris from the infalling satellite, while the N and G1 Clumps are associated with the stellar material from the perturbed pre-existing disc. The G1 Clump has a significant fraction of stars younger than 5 Gyr just like the thin disc of M 31. While their stellar populations are statistically different, the younger stars in both the thin disc of M 31 and the G1 Clump may have formed at the same time. Having formed from the perturbed M 31 disc, the PNLF of the G1 Clump is expected to have a M* value similar to that of the inner disc and a slope in the faint end consistent with significant contribution from a young stellar population, in line with the observed values. Unfortunately, we were not able to constrain the stellar population of the N Clump with our data. The major merger scenario therefore simultaneously explains the observed global stellar population properties of the M 31 inner halo substructures, the measured velocity dispersion values (Paper II), and the age of the recent burst of star formation in the disc (Bernard et al. 2015; Williams et al. 2017).
Stream D has a stellar population that is different from both disc regions and the other substructures: it has the faintest value for the PNLF bright cut-off M* and its stellar population is the most metal poor (Conn et al. 2016) of the entire area surveyed around M31. This result points to an independent origin. Indeed this stream does not appear in the simulations by Hammer et al. (2018) and it could have formed in a distinct accretion event, such as for example the disruption of a low-mass dwarf galaxy. Thus we find that the M 31 inner halo substructures, barring Stream D, are consistent with having originated in a single major merger event.
6. Conclusions
This study investigates the properties of the PNLF for the stellar populations in different subregions of M31 based on the largest PN sample ever obtained in any galaxy, including the MW. Because of the unprecedented depth, spatial coverage, and uniform photometry of the survey we were able to empirically investigate the variations of the PNLF across different stellar populations with robust statistics, including the absolute magnitude M* of the bright cut-off, and the faint-end slope cf2. This is greatly aided by the fact that all probed PN subpopulations are at similar distance, and have constant LOS extinction beyond R > 20 kpc from the centre of M31. Furthermore, for the first time we can use the properties of the PNLF to characterise the average stellar populations of the different substructures in M31 and thereby constrain the merger formation history of the galaxy’s inner halo. Our main results are as follows:
-
Statistical comparison of the deep PNLFs in different substructures and disc annuli of M 31 reveals significant differences in the fitted PNLF parameters. In particular M*, the PNLF bright cut-off, is found to vary strongly: for the Giant Stream and W Shelf, M* is nearly one magnitude fainter than for the disc, and the low-metallicity stream D has even fainter M*.
-
The M* values of the PNLFs for the LMC, NE Shelf, G1 Clump, and the two M 31 disc regions are consistent with the theoretical predictions by Dopita et al. (1992) of M* dimming in more-metal-poor populations (see Sect. 4.1). However, the measured M* value for the Giant Stream, W Shelf, and Stream D are much larger than theoretical predictions would suggest. The empirically measured variations of M* in the subregions of M 31 and the LMC can therefore not be conclusively attributed solely to variations in [M/H], thereby highlighting the need for theoretical models of PN evolution with improved treatment for metallicity and other possible effects such as the age of the parent stellar population.
-
Using published HST data, we establish a connection between the PNLF morphology and the stellar mass of the parent stellar population in two age bins, younger and older than 5 Gyr, respectively. We find that the rise in the faint end of the PNLF is driven by the mass-fraction of stellar populations older than 5 Gyr, indicating that PNe evolving from older stars populate the faint end of the PNLF.
-
From their PNLFs we find that the Giant Stream and NE Shelf are consistent with being composed of stellar debris from an in-falling satellite, while the G1 Clump is linked to the pre-merger M 31 disc with a significant contribution of younger stars presumably formed out of the accreted cold gas.
-
The constraints from the deep PNLF on the stellar populations of these substructures point to their origin in a single merger event in M 31. In conjunction with the age–velocity dispersion relation of the M 31 disc (Paper II), this indicates a recent (∼2–3 Gyr ago), fairly massive merger event in M 31, in agreement with predictions from Hammer et al. (2018). We also find that the Stream D was likely formed in a distinct accretion event, probably from a disrupted dwarf satellite.
This work sets the stage for spectroscopic follow-up of the PNe in the outer disc and inner halo of M31, with the goal being to measure their specific metal abundances and accurate LOS velocities. From these discrete measurements, we will then build abundance maps for the substructures and the disc, and correlate variations of metal abundance with kinematics signatures, providing a better understanding of their chemical and dynamical evolution.
The fields in the southwest of the M 31 disc have a brighter limiting magnitude (50% detection completeness limit computed from injection of artificial sources) of m5007 ∼ 25.89 mag. We therefore confine the analysis of the PNLFs in the disc to the fields in the northeast corner of the M 31 disc with sensitivity as deep as that reached in the fields of the substructures. See Paper I for details of limiting magnitudes of different fields.
In hypothesis testing, a critical value is a point on the test distribution that is compared to the test statistic to provide the significance level to reject the null hypothesis. For the AD test, critical values have been defined by Scholz & Stephens (1987).
The HST field linked to the W Shelf by Bernard et al. (2015) does not overlap with the W Shelf spatial over-density as obtained by PAndAS (McConnachie et al. 2018).
The metallicity gradient in the Giant stream is studied by Conn et al. (2016). In their Fig. 3, these latter authors show the spatial coverage of their fields and give the corresponding [Fe/H] (=[M/H] as [α/Fe] = 0) values in their Table 1. With the current PNe survey, we cover a spatial area in the Giant Stream corresponding to their mean metallicity range of [M/H] = −0.4 to −0.7. The [M/H] value for the Giant Stream from Escala et al. (2020) covers the metallicity range observed by Conn et al. (2016) within error and is thus an accurate [M/H] value for parent population of the PN subsample in the Giant Stream.
Acknowledgments
Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique of France, and the University of Hawaii. We acknowledge comments and suggestions from K. Gesicki. We thank the A&A Editor, M. Salaris, for a constructive revision process. SB acknowledges support from the IMPRS on Astrophysics at the LMU Munich. S. B., M. A. and O. G. are grateful for the hospitality of the Mount Stromlo Observatory and the Australian National University (ANU). M. A. and O. G. thank the Research School of Astronomy and Astrophysics at ANU for support through their Distinguished Visitor Program. This work was supported by the DAAD under the Australia-Germany joint research program with funds from the German Federal Ministry for Education and Research. This research made use of Astropy– a community-developed core Python package for Astronomy (Astropy Collaboration 2013), SciPy (Virtanen et al. 2020), NumPy (Oliphant 2015) and Matplotlib (Hunter 2007). This research also made use of NASA’s Astrophysics Data System (ADS; https://ui.adsabs.harvard.edu).
References
- Arnaboldi, M., Aguerri, J. A. L., Napolitano, N. R., et al. 2002, AJ, 123, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Freeman, K. C., Okamura, S., et al. 2003, AJ, 125, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernard, E. J., Ferguson, A. M. N., Richardson, J. C., et al. 2015, MNRAS, 446, 2789 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharya, S. 2020, PhD thesis, Ludwig-Maximilians Universität, Germany [Google Scholar]
- Bhattacharya, S., Arnaboldi, M., Hartke, J., et al. 2019a, A&A, 624, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhattacharya, S., Arnaboldi, M., Caldwell, N., et al. 2019b, A&A, 631, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boulade, O., Charlot, X., Abbon, P., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, A. F. M. Moorwood, et al., 4841, 72 [Google Scholar]
- Bullock, J. S., & Johnston, K. V. 2005, ApJ, 635, 931 [Google Scholar]
- Buzzoni, A., Arnaboldi, M., & Corradi, R. L. M. 2006, MNRAS, 368, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., & Jacoby, G. H. 1992, ApJ, 388, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., & Jacoby, G. H. 1999, ApJ, 515, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Jacoby, G. H., Ford, H. C., & Neill, J. D. 1989, ApJ, 339, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Feldmeier, J. J., Jacoby, G. H., et al. 2002, ApJ, 577, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Durrell, P. R., Laychak, M. B., et al. 2004, ApJ, 614, 167 [Google Scholar]
- Ciardullo, R., Gronwall, C., Adams, J. J., et al. 2013, ApJ, 769, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Conn, A. R., McMonigal, B., Bate, N. F., et al. 2016, MNRAS, 458, 3282 [NASA ADS] [CrossRef] [Google Scholar]
- Crnojević, D., Sand, D. J., Spekkens, K., et al. 2016, ApJ, 823, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Dalcanton, J. J., Williams, B. F., Lang, D., et al. 2012, ApJS, 200, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, B. D., Ciardullo, R., Jacoby, G. H., Feldmeier, J. J., & Indahl, B. L. 2018, ApJ, 863, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Jacoby, G. H., & Vassiliadis, E. 1992, ApJ, 389, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Dorman, C. E., Guhathakurta, P., Seth, A. C., et al. 2015, ApJ, 803, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [Google Scholar]
- Draine, B. T., Aniano, G., Krause, O., et al. 2014, ApJ, 780, 172 [Google Scholar]
- Escala, I., Gilbert, K. M., Kirby, E. N., et al. 2020, ApJ, 889, 177 [Google Scholar]
- Fang, X., García-Benito, R., Guerrero, M. A., et al. 2018, ApJ, 853, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Fardal, M. A., Weinberg, M. D., Babul, A., et al. 2013, MNRAS, 434, 2779 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, A. M. N., & Mackey, A. D. 2016, in Tidal Streams in the Local Group and Beyond, eds. H. J. Newberg, & J. L. Carlin, 420, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, A. M. N., Irwin, M. J., Ibata, R. A., Lewis, G. F., & Tanvir, N. R. 2002, AJ, 124, 1452 [NASA ADS] [CrossRef] [Google Scholar]
- Hammer, F., Yang, Y. B., Wang, J. L., et al. 2018, MNRAS, 475, 2754 [NASA ADS] [Google Scholar]
- Hartke, J., Arnaboldi, M., Longobardi, A., et al. 2017, A&A, 603, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henize, K. G., & Westerlund, B. E. 1963, ApJ, 137, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández-Martínez, L., & Peña, M. 2009, A&A, 495, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R., Irwin, M., Lewis, G., Ferguson, A. M. N., & Tanvir, N. 2001, Nature, 412, 49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ibata, R., Chapman, S., Ferguson, A. M. N., et al. 2005, ApJ, 634, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Lewis, G. F., McConnachie, A. W., et al. 2014, ApJ, 780, 128 [Google Scholar]
- Jacoby, G. H. 1980, ApJS, 42, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H., & De Marco, O. 2002, AJ, 123, 269 [Google Scholar]
- Johnston, K. V., Bullock, J. S., Sharma, S., et al. 2008, ApJ, 689, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, E. N., Lanfranchi, G. A., Simon, J. D., Cohen, J. G., & Guhathakurta, P. 2011, ApJ, 727, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Kummell, C. H. 1879, Analyst, 6, 97 [Google Scholar]
- Lewis, P. A. W. 1961, Ann. Math. Stat., 32, 1118 [Google Scholar]
- Longobardi, A., Arnaboldi, M., Gerhard, O., et al. 2013, A&A, 558, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Girardi, L., Weiss, A., Groenewegen, M. A. T., & Chiosi, C. 2004, A&A, 423, 995 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez-Delgado, D., Gabany, R. J., Crawford, K., et al. 2010, AJ, 140, 962 [Google Scholar]
- McConnachie, A. W., Irwin, M. J., Ibata, R. A., et al. 2009, Nature, 461, 66 [Google Scholar]
- McConnachie, A. W., Ibata, R., Martin, N., et al. 2018, ApJ, 868, 55 [Google Scholar]
- Méndez, R. H., Teodorescu, A. M., Schönberner, D., Jacob, R., & Steffen, M. 2008, ApJ, 681, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C., Harding, P., Feldmeier, J., & Morrison, H. 2005, ApJ, 631, L41 [Google Scholar]
- Mohd Razali, N., & Yap, B. 2011, J. Stat. Model. Anal., 2, [Google Scholar]
- Nidever, D. L., Hasselquist, S., Hayes, C. R., et al. 2020, ApJ, 895, 88 [CrossRef] [Google Scholar]
- Oliphant, T. E. 2015, Guide to NumPy, 2nd edn. (USA: CreateSpace Independent Publishing Platform) [Google Scholar]
- Peña, M., Richer, M. G., & Stasińska, G. 2007, A&A, 466, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, W. A., & Parker, Q. A. 2010, MNRAS, 405, 1349 [NASA ADS] [Google Scholar]
- Richardson, J. C., Ferguson, A. M. N., Johnson, R. A., et al. 2008, AJ, 135, 1998 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-González, A., Hernández-Martínez, L., Esquivel, A., et al. 2015, A&A, 575, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salaris, M., & Cassisi, S. 2005, Evolution of Stars and Stellar Populations (Wiley-VCH) [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Scholz, F. W., & Stephens, M. A. 1987, J. Am. Stat. Assoc., 82, 918 [Google Scholar]
- Schönberner, D., Jacob, R., Steffen, M., & Sandin, C. 2007, A&A, 473, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schönberner, D., Jacob, R., Sandin, C., & Steffen, M. 2010, A&A, 523, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, M., Chiba, M., Komiyama, Y., et al. 2010, ApJ, 708, 1168 [NASA ADS] [CrossRef] [Google Scholar]
- Valenzuela, L. M., Méndez, R. H., & Miller Bertolami, M. M. 2019, ApJ, 887, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Dell’Agli, F., Schneider, R., et al. 2014, MNRAS, 439, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Weisz, D. R., Dolphin, A. E., Skillman, E. D., et al. 2013, MNRAS, 431, 364 [Google Scholar]
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, B. F., Dolphin, A. E., Dalcanton, J. J., et al. 2017, ApJ, 846, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Zahid, H. J., Kudritzki, R.-P., Conroy, C., Andrews, B., & Ho, I. T. 2017, ApJ, 847, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, R., & Yuan, H. 2020, ApJ, 905, L20 [Google Scholar]
Appendix A: Planetary Nebula circumstellar extinction and the PNLF
A fraction of the dust produced in stars during the Asymptotic Giant Branch (AGB) phase (e.g., Ventura et al. 2014) is retained in the PN phase of stellar evolution. This dust production in the AGB phase depends on the initial stellar mass, and hence the SFH, of its parent stellar population (e.g., Ventura et al. 2014, see their Fig. 10). Ciardullo & Jacoby (1999) found that PNe with more massive progenitors have higher measured circumstellar extinction. Davis et al. (2018) found that the M* value of the PNLF in the M 31 bulge is set from a combination of the [O III] 5007 Å flux emitted by the nebula and its circumstellar extinction. PNe with high [O III] 5007 Å flux also have high circumstellar extinction such that the net observed [O III] 5007 Å flux causes the PNe to remain fainter than the M* value of the PNLF (see their Fig. 13). In cases where the de-reddened [O III] 5007 Å flux is considered, the resultant de-reddened PNLF (see Fig. 14 of Davis et al. 2018) does not follow the generalised PNLF functions (Ciardullo et al. 1989; Longobardi et al. 2013). Thus, the SFH-dependent circumstellar extinction (a property of individual PNe) should not be included in obtaining the PNLF and its M* value for any of the regions.
Furthermore, the brightest PN in the Giant Stream (PN14; Fang et al. 2018) has an extinction (LOS plus circumstellar) of 0.37 mag (spectroscopically measured from its Balmer decrement), much lower than the observed difference between the Giant Stream M* value and the predicted value by Dopita et al. (1992) for its [M/H] value (see Fig. 6). This further confirms that any difference in the M* values of the M31 region PNLFs does not result from different extinctions, even if circumstellar extinction is taken into account.
Appendix B: [M/H] measurements for the LMC and M 31 regions
In general, the photometrically measured [Fe/H] is taken to be equal to the [M/H] value, as [α/Fe] is assumed to be zero for the fitted isochrones (e.g., Bernard et al. 2015; Conn et al. 2016; Williams et al. 2017). The [M/H] for the 10 < RGC ≤ 20 kpc disc region was obtained by Bernard et al. (2015) as the mean [M/H] from the PHAT photometry in the radial range RGC = 12–20 kpc, covering one-third of the M 31 disc at this radius. The [M/H] for the NE Shelf and G1 Clump regions is from the pencil-beam HST photometry, with the errors obtained from their metallicity distribution functions. For Stream D, the [M/H] measurement was obtained by Conn et al. (2016) from the CFHT MegaCam observations, covering this entire subregion. The [M/H] for the 20 < RGC ≤ 30 kpc disc region and the Giant Stream6 are obtained from the mean [Fe/H] and mean [α/Fe] values measured from individual stars in small fields observed in these regions by Escala et al. (2020). These values are converted to [M/H] using the following relation from Salaris & Cassisi (2005):
We note that the spectroscopic [M/H] for these two regions agree within errors with that from the pencil-beam HST photometry in these regions by Bernard et al. (2015). For the LMC, we derive the median [M/H] value from the median [Fe/H] and median [α/Fe] values for APOGEE RGB stars spanning a large radial range in the LMC (Nidever et al. 2020). For the W Shelf, Tanaka et al. (2010) construct CMDs for the resolved stellar population in the Subaru Supreme-Cam pointings. The mean [Fe/H] value is measured photometrically from isochrone-fitting to the W Shelf CMD, assuming [α/Fe] = 0.3. We use the measured [Fe/H] and assumed [α/Fe] value in Eq. (B.1) to obtain the measured [M/H] for the W Shelf.
Appendix C: Pair-wise differences in the PNLFs of M 31 regions and their stellar population parameters
For the pairs of M 31 regions that have different PNLFs (see Table 3), we assessed in which magnitude ranges the PNLFs differentiate the most (Fig. 5) and presented the differences in their fitted PNLF properties (see Table 2). We infer the dependencies of these differences in pairs of M 31 regions on their parent stellar population parameters as follows:
The 10 < RGC ≤ 20 kpc and 20 < RGC ≤ 30 kpc disc regions. On the basis of the spectroscopic and kinematic properties of the disc PNe (Paper II), the 10 < RGC ≤ 20 kpc disc region, which contains both young (heated) thin disc and older thicker disc stars, is found to be different from the 20 < RGC ≤ 30 kpc disc region in that the latter has predominantly older and increasingly metal-poor disc stars, reflected in its larger cf2 (see Table 2) and fainter M* values respectively.
The Giant Stream and the 10 < RGC ≤ 20 kpc disc region. The Giant Stream, with a larger cf2 value (see Table 2), has a higher percentage of older stars than the 10 < RGC ≤ 20 kpc disc region. Additionally, the PNLF of the Giant Stream has a fainter M* (see Sect. 4.1) than the 10 < RGC ≤ 20 kpc disc.
The Giant Stream and 20 < RGC ≤ 30 kpc disc region. Here the difference in the deep PNLFs stems mainly from the fainter M* (see Table 2) of the Giant Stream PNLF with respect to that of the outer disc region. Their stellar mass is dominated by older stars according to their large cf2 values.
The NE Shelf and 10 < RGC ≤ 20 kpc disc region. The NE Shelf has a higher cf2 value (see Table 2), and therefore a higher percentage of older stars, than the 10 < RGC ≤ 20 kpc disc region. While the NE Shelf PNLF has a M* value similar to that of the inner disc region within error, it has a c2 ≈ 0 value (see Table 2), indicating further differences in the SFH from the 10 < RGC ≤ 20 kpc disc region.
The NE Shelf and 20 < RGC ≤ 30 kpc disc region. The difference between the two regions originates from the slightly brighter M* of the NE Shelf PNLF and also the fact that the latter has a c2 ≈ 0 value, implying differences in their SFHs.
The G1 Clump and the 10 < RGC ≤ 20 kpc disc region. Both regions have similar m*, < 5 Gyr (see Table 4) but the PNLFs have a different shape owing to the c2 ≈ 0 value (see Table 2) for the G1 Clump, thus indicating a distinct SFH from the 10 < RGC≤ 20 kpc disc region.
The G1 Clump and the 20 < RGC ≤ 30 kpc disc region. The G1 Clump has a higher m*, < 5 Gyr (see Table 4) and lower cf2 value (see Table 2) than the 20 < RGC≤ 30 kpc disc. The difference is further aggravated due to the c2 ≈ 0 value of the G1 Clump PNLF, implying differences in SFHs.
The W Shelf and the two disc regions. We only have an upper limit of m*, < 5Gyr ≤ 42.19% for the W Shelf. The difference from the two disc regions can still be attributed to the c2 ≈ 0 value of the W Shelf PNLF (see Table 2) and thus a difference in SFHs. Additionally, the W Shelf PNLF has a fainter M* (see Sect. 4.1) than the two disc regions.
Stream D. This M 31 substructure is different from both disc regions, the Giant Stream, the NE Shelf, and the G1 Clump because it has the faintest bright cut-off value, M* = −2.689 ± 0.177, among the PN subsamples from the M31 survey (see Sect. 4.1). Its deep PNLF also has c2 ≈ 0 (see Table 2), further implying an SFH that is distinct from some of the M 31 subregions.
A summary of the highlights is provided in Sect. 5.1.
All Tables
Percentage stellar mass formed within the last 5 Gyr, m*, < 5 Gyr, from the PNLF predicted with the pick-one-out test.
All Figures
 |
Fig. 1. Position on the sky of PNe (all marked points) identified by Paper I and Bhattacharya et al. (in prep.). Positions are overlaid on the number density map of RGB stars from PAndAS (McConnachie et al. 2018), binned for visual clarity and shown in grey. The PNe selected for the PNLF analysis in the two disc regions and six substructure regions are marked with different colours. North is up, east is left. The HST fields observed by Bernard et al. (2015) to obtain the SFH of four of the M 31 regions have been marked with green squares. |
| In the text | |
 |
Fig. 2. Cumulative PNLFs for the LMC PN sample from Reid & Parker (2010) shifted to the apparent bright cut-off of the M 31 disc region at 10 < RGC ≤ 20 kpc. The cumulative PNLFs are fitted by the generalised cumulative function (in blue) for m5007 ≤ 24.5 mag and a function which additionally includes an exponential at the faint end (in orange). The uncertainties of the fits are shaded. The region fainter than the limiting magnitude of the shallowest field (m5007 > 26.16 mag) in our M 31 survey is shown in grey. |
| In the text | |
 |
Fig. 3. Completeness-corrected cumulative PNLFs for the disc regions within 10 < RGC ≤ 20 kpc (left) and 20 < RGC ≤ 30 kpc (right). The cumulative PNLFs are fitted by the generalised cumulative function (in blue) for m5007 ≤ 25 mag and a function which additionally includes an exponential at the faint end (in orange). The uncertainties of the fits are shaded. The region fainter than the limiting magnitude of the shallowest field (m5007 > 26.16 mag) is shown in grey. |
| In the text | |
 |
Fig. 4. Completeness-corrected cumulative PNLFs for the six different substructures. The cumulative PNLFs are fitted by the generalised cumulative function (in blue) for m5007≤ 25 mag and a function which additionally includes an exponential at the faint end (in orange; except for N Clump). The uncertainties of the fits are shaded. The region fainter than the limiting magnitude of the shallowest field (m5007 > 26.16 mag) is shown in grey. |
| In the text | |
 |
Fig. 5. Cumulative probability of the completeness-corrected PNLF is shown (in log scale for visual clarity) for the five different substructures and the two disc regions. This diagnostic plot illustrates in which magnitude ranges the PNLFs are most different. The region fainter than the limiting magnitude of the shallowest field (m5007 > 26.16 mag) is shown in grey. Here, we report the error bars depicting the photometric errors (multiplied by ten for visual clarity) with magnitudes in our survey, shown as black lines at m5007 = 20, 21, 22 and 23 mag respectively. The M* fitted values for each of the PNLFs are robust in the entire survey area given the photometric accuracy (m5007,err ∼ 0.014 mag at m5007 = 23 mag). Furthermore, the arrow in the upper left corner shows the mean photometric extinction within our survey area (A5007 = 0.21 mag). |
| In the text | |
 |
Fig. 6. [M/H] for the different regions in M31 is plotted against the M* value obtained from fitting their PNLF. The different markers show the different references for the [M/H] measurements – circle: Williams et al. (2017); pentagon: Bernard et al. (2015); triangle: Escala et al. (2020); inverted triangle: Nidever et al. (2020); cross: Tanaka et al. (2010); square: Conn et al. (2016). The theoretical prediction for the values of M* from Dopita et al. (1992) models is shown with the dotted line. Also shown is the variation of photometric errors in our survey (multiplied by a factor of ten for visual clarity) at the magnitudes corresponding to the given M* values (as black lines at M* = −4.74, −3.74 and −2.74 mag). |
| In the text | |
 |
Fig. 7. Linear relation between the slope of exponential function at the faint end of the PNLF, cf2, and the percentage stellar mass formed within the last 5 Gyr, m*, < 5 Gyr. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



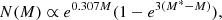
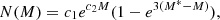
![$$ \begin{aligned}&{I(M)} =c_1e^{c_2M}\left[\frac{1}{c_2}e^{c_2M}+\frac{1}{3-c_2}e^{3(M^{*}+\mu )-(3-c_2)M}\right.\nonumber \\&\qquad \quad \left.-\left(\frac{1}{c_2}+\frac{1}{3-c_2}\right)e^{c_2(M^{*}+\mu )}\right] . \end{aligned} $$](/articles/aa/full_html/2021/03/aa38366-20/aa38366-20-eq7.gif)
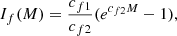
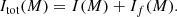
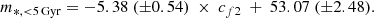
![$$ \begin{aligned} \mathrm [M/H] \sim [Fe/H] + log(0.694\times 10^{[\alpha /Fe]}+0.306). \end{aligned} $$](/articles/aa/full_html/2021/03/aa38366-20/aa38366-20-eq13.gif)