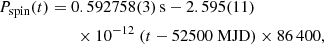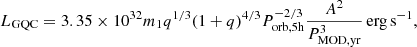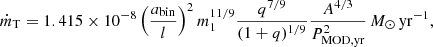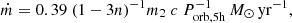| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | L12 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201935665 | |
| Published online | 20 May 2019 | |
Letter to the Editor
Updated orbital ephemeris of the ADC source X 1822-371: a stable orbital expansion over 40 years
1
Dipartimento di Fisica e Chimica – Emilio Segrè, Università di Palermo, via Archirafi 36, 90123 Palermo, Italy
e-mail: simonamichela.mazzola@unipa.it
2
Dipartimento di Fisica, Università degli Studi di Cagliari, SP Monserrato-Sestu, KM 0.7, Monserrato 09042, Italy
3
Istituto Nazionale di Astrofisica, IASF Palermo, Via U. La Malfa 153, 90146 Palermo, Italy
4
IRAP, Université de Toulouse, CNRS, UPS, CNES, Toulouse, France
5
Dipartimento di Fisica e Astronomia “Galileo Galilei”, Università di Padova, Vicolo dell’Osservatorio 3, Padova 35122, Italy
Received:
11
April
2019
Accepted:
8
May
2019
Aims. Source X 1822-371 is an eclipsing compact binary system with a period close to 5.57 h and an orbital period derivative Ṗorb of 1.51(7)×10−10 s s−1. The very high value of Ṗorb is compatible with a super-Eddington mass transfer rate from the companion star, as suggested by X-ray and optical data. The XMM-Newton observation taken in 2017 allows us to update the orbital ephemeris and verify whether the orbital period derivative has been stable over the past 40 yr.
Methods. We added two new values obtained from the Rossi-XTE (RXTE) and XMM-Newton observations performed in 2011 and 2017, respectively, to the X-ray eclipse arrival times from 1977 to 2008. We estimated the number of orbital cycles and the delays of our eclipse arrival times spanning 40 yr, using as reference time the eclipse arrival time obtained from the RXTE observation taken in 1996.
Results. Fitting the delays with a quadratic model, we found an orbital period Porb = 5.57062957(20) h and a Ṗorb value of 1.475(54)×10−10 s s−1. The addition of a cubic term to the model does not significantly improve the fit quality. We also determined a spin-period value of Pspin = 0.5915669(4) s and its first derivative Ṗspin = − 2.595(11) × 10−12 s s−1.
Conclusions. Our results confirm the scenario of a super-Eddington mass transfer rate; we also exclude a gravitational coupling between the orbit and the change in the oblateness of the companion star triggered by the nuclear luminosity of the companion star.
Key words: stars: neutron / stars: individual: X 1822-371 / X-rays: binaries / eclipses / ephemerides
© ESO 2019
1. Introduction
The low-mass X-ray binary system (LMXB) X 1822-371 is a persistent eclipsing source with an orbital period of 5.57 h, hosting an accreting X-ray pulsar with a spin frequency close to 1.69 Hz (Jonker & van der Klis 2001) that is increasing with a derivative of 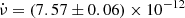 Hz s−1 (Bak Nielsen et al. 2017; Iaria et al. 2015). The mass function of the system is (2.03 ± 0.03) × 10−2 M⊙ (Jonker & van der Klis 2001), with a lower limit on the companion star mass of 0.33 ± 0.05 M⊙ (Jonker et al. 2003). X 1822-371 belongs to the class of accretion disc corona (ADC) sources (White & Holt 1982), with an inclination angle between 81° and 84° (Heinz & Nowak 2001). The distance to this source was estimated to be between 2–2.5 kpc by Mason & Cordova (1982) using infrared and optical observations. The 0.1–100 keV unabsorbed luminosity is 1.2 × 1036 erg s−1 when a distance of 2.5 kpc is adopted (Iaria et al. 2001). The most recent orbital ephemeris of the source X 1822-371 was reported by Chou et al. (2016), who suggested that the orbital period derivative is Ṗorb = (1.464 ± 0.041) × 10−10 s s−1 by adopting quadratic ephemeris, or Ṗorb = (1.94 ± 0.27) × 10−10 s s−1 by adopting cubic ephemeris. The value of Ṗorb is three orders of magnitude higher than what is expected from conservative mass transfer driven by magnetic breaking and gravitational radiation and can be explained only by assuming a mass transfer rate higher than three times the Eddington limit for a neutron star (NS; Burderi et al. 2010; Bayless et al. 2010). Bak Nielsen et al. (2017) suggested that X 1822-371 is a relatively young binary in which the donor is transferring mass on a thermal timescale. The authors suggested that the super-Eddington mass transfer rate generates an outflow of matter from the magnetospheric radius.
Hz s−1 (Bak Nielsen et al. 2017; Iaria et al. 2015). The mass function of the system is (2.03 ± 0.03) × 10−2 M⊙ (Jonker & van der Klis 2001), with a lower limit on the companion star mass of 0.33 ± 0.05 M⊙ (Jonker et al. 2003). X 1822-371 belongs to the class of accretion disc corona (ADC) sources (White & Holt 1982), with an inclination angle between 81° and 84° (Heinz & Nowak 2001). The distance to this source was estimated to be between 2–2.5 kpc by Mason & Cordova (1982) using infrared and optical observations. The 0.1–100 keV unabsorbed luminosity is 1.2 × 1036 erg s−1 when a distance of 2.5 kpc is adopted (Iaria et al. 2001). The most recent orbital ephemeris of the source X 1822-371 was reported by Chou et al. (2016), who suggested that the orbital period derivative is Ṗorb = (1.464 ± 0.041) × 10−10 s s−1 by adopting quadratic ephemeris, or Ṗorb = (1.94 ± 0.27) × 10−10 s s−1 by adopting cubic ephemeris. The value of Ṗorb is three orders of magnitude higher than what is expected from conservative mass transfer driven by magnetic breaking and gravitational radiation and can be explained only by assuming a mass transfer rate higher than three times the Eddington limit for a neutron star (NS; Burderi et al. 2010; Bayless et al. 2010). Bak Nielsen et al. (2017) suggested that X 1822-371 is a relatively young binary in which the donor is transferring mass on a thermal timescale. The authors suggested that the super-Eddington mass transfer rate generates an outflow of matter from the magnetospheric radius.
A suggestion to explain the evolutionary stage of X1822-371 comes also from recent numerical studies of the secular evolution of LMXBs including X-ray irradiation of the donor (Tailo et al. 2018). These models show that when the donor has a mass 0.4 ≲ M/M⊙ ≲ 0.6, like in this system, the evolution is subdivided into cycles of short mass-transfer phases, during which the donor expands on the thermal timescale of its convective envelope and the orbital period increases significantly, followed by long phases of detachments during which thermal relaxation takes place and the donor recovers full thermal equilibrium. The next stage of mass transfer occurs when the orbital period has decreased again so that the stellar radius fills the Roche lobe again, and a new orbital expansion follows. The maximum Ṗorb in the published models is ∼6 × 10−11 s s−1 (see e.g. Tailo et al. 2018), but the specific evolution of X1822-371 may be obtained by reasonable variations of the input parameters.
In this work, we used the eclipse arrival times reported by Iaria et al. (2011), with the addition of two new eclipse arrival times obtained from analysing the RXTE observation performed in 2011 and the XMM-Newton observation performed in 2017; our eclipse arrival times span 41 yr. We investigated the statistical significance for the presence of a second derivative of the orbital period and the possibility that the quadratic term mimics a wide sinusoidal modulation. In the latter case, we excluded that the sinusoidal modulation could be explained as due to a gravitational coupling of the orbit with changes in the oblateness of the magnetically active companion star, the so-called Applegate mechanism (Applegate 1992).
2. Observations and data analysis
The XMM-Newton Observatory (Jansen et al. 2001) observed the source X 1822-371 on 2017 March 3 between 01:10:54 UTC and 19:12:27 UTC (ObsId. 0784820101) for a total observing time of 69 ks. We analysed the data collected by pn-type CCD detector of the European Photon Imaging Camera (Epn; Strüder et al. 2001), operating in Timing Mode, with the aim to estimate the eclipse arrival time. We reprocessed the data using the Science Analysis Software (SAS) v16.1.0, verified the absence of background flaring during the observation, and applied the barycentric correction to the event times.
We extracted the Epn 0.3–10 keV light curve considering only PATTERN≤4 and FLAG = 0 events from a region that included the brightest columns of the detector (RAWX between 30 and 45), while for the background we extracted the events from a region far away from the source (RAWX between 5 and 10). We observe three partial eclipses at 14 ks, 34 ks, and 54 ks from the start time in the Epn background-subtracted light curve. The observation covers almost 3.4 orbital periods of the system.
We folded the background-subtracted light curve, adopting a reference epoch Tfold = 57818.4237 MJD (corresponding to a time close to the mid-time of the observation) and a reference period of Pfold = 0.2321107 days. The folded light curve is shown in Fig. 1.
 |
Fig. 1. XMM-Newton/Epn folded orbital light curve obtained by adopting a period of 0.2321107 days. The period is divided into 128 bins. |
We further added the X-ray eclipse time obtained by analysing the RXTE observations taken from 2011 November 15 to 30 (ObsId. P96344). The same observation was analysed by Chou et al. (2016) using standard 2 data in the energy range 2–9 keV and inferring four eclipse arrival times. In order to make the analysis self-consistent, we re-analysed these data using the X-ray light curves obtained from the standard 1 data products (Std1) of archival RXTE data, that is, the 2–40 keV background-subtracted light curves collected by the PCA with a time resolution of 0.125 s. We applied the barycentric correction to the events using the ftool faxbary and folded the light curve using as epoch Tfold = 55887 MJD and as period Pfold = 0.2321104 days. To estimate the orbital phase at which the eclipse occurred, we adopted the procedure reported by Burderi et al. (2010), finding that the eclipse arrival times are Tecl = 57818.44392(96) MJD/TDB and Tecl = 55887.05307(38) MJD/TDB for the XMM-Newton/Epn and RXTE/PCA observations, respectively. The associated errors are at 68% confidence level.
To update the orbital ephemeris, we included the 2 eclipse arrival times shown above with those reported by Iaria et al. (2011); the 32 eclipse arrival times, the corresponding number of orbital cycles, and the delays are summarised in Table 1. The number of orbital cycles N and the delays associated with the eclipse arrival times were obtained by adopting a reference orbital period of P0 = 0.232109571 days and a reference eclipse time T0 = 50353.08728 MJD, estimated for the RXTE observation of the source performed in 1996 (Parmar et al. 2000).
Journal of available eclipse arrival times for source X 1822-371.
We fitted the delays as function of cycles adopting the quadratic model y = a + bN + cN2 and obtaining a χ2(d.o.f.) of 42.3(29). The uncertainties associated with the best-fit parameters a, b, and c were scaled by a factor 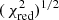 to take into account a
to take into account a 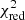 of the best-fit model larger than 1. The best-fit values of the parameters are shown in the second column of Table 2 (upper part); the best-fit quadratic curve (red) and the corresponding residuals in units of σ are shown in the left panel of Fig. 2.
of the best-fit model larger than 1. The best-fit values of the parameters are shown in the second column of Table 2 (upper part); the best-fit quadratic curve (red) and the corresponding residuals in units of σ are shown in the left panel of Fig. 2.
Best-fit modelling parameters of eclipse time delays with different models, including quadratic, cubic, sinusoidal, and quadratic plus sinusoidal ephemeris.
 |
Fig. 2. From left to right: delays vs. cycles for the quadratic (red), cubic (green), and LQS (blue) model. Residuals are in units of σ obtained by adopting the quadratic, cubic, and LQS model, respectively. |
The updated orbital ephemerides are
where the first and the second term represent the new values of the reference epoch T0, orb and orbital period P0, orb, respectively. The third term, equal to (P0Ṗorb)/2, allows us to estimate an orbital period derivative of Ṗorb = 1.475(54) × 10−10 s s−1. Furthermore, we added a cubic term 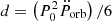 to the quadratic model in order to test the presence of a second derivative of the orbital period. The best-fit curve (green) and the corresponding residuals are shown in Fig. 2 (central panel); the best-fit parameters are shown in the third column of Table 2 (upper part). We obtained a χ2(d.o.f.) of 37.4(28), the F-test probability of chance improvement is 0.065, indicating that the cubic model improves the fitting at a confidence level lower than 2σ, meaning that the cubic term is not significantly required.
to the quadratic model in order to test the presence of a second derivative of the orbital period. The best-fit curve (green) and the corresponding residuals are shown in Fig. 2 (central panel); the best-fit parameters are shown in the third column of Table 2 (upper part). We obtained a χ2(d.o.f.) of 37.4(28), the F-test probability of chance improvement is 0.065, indicating that the cubic model improves the fitting at a confidence level lower than 2σ, meaning that the cubic term is not significantly required.
We investigated also whether the quadratic term could mimic a sinusoidal modulation in the delays: we substituted the quadratic term with a sinusoidal one, using the model y = a + bN + A sin[2π(N − N0)/NMOD] composed of a linear plus sinusoidal term (LS model, hereafter). Keeping the best-fit values of a and b fixed to 8084.33 s and −0.0873931 s to lead the fit to the convergence, we obtained a χ2(d.o.f.) of 37.8(29) with a Δχ2 of 4.9 with respect to the quadratic model, a modulation period PMOD = NMOD P0 = 204 ± 3 yr, and a semi-amplitude of the modulation A = 9289(26) s. The best-fit values are shown in the second column of the lower part of Table 2. We also verified whether a gravitational quadrupole coupling produced by tidal dissipation (Applegate & Shaham 1994) could be detectable in our data; to this aim, we added a quadratic term to the LS model. In the new model (hereafter LQS model) we imposed that NMOD = 0.572 c−1/2A2/3abin/l (this relation is discussed in Sect. 3). The best-fit parameters are shown in the third column of the lower part in Table 2; the best-fit model (blue) and the corresponding residuals are shown in the right panel of Fig. 2. We obtained a χ2(d.o.f.) of 31.2(26), and the F-test probability of chance improvement is 0.045 with respect to the quadratic model, indicating that the LQS model improves the fit at a confidence of about 2σ.
Finally, we searched for the NS spin frequency in the XMM-Newton/Epn data by analysing the 5–12 keV events after applying the barycentric correction using the source coordinates. We corrected the data for the binary orbital motion using a sin i = 1.006(5) lt-s (Jonker & van der Klis 2001) and the value of the orbital period obtained from the quadratic ephemeris shown above. In order to search for the pulsation period, we applied the procedure described by Iaria et al. (2015): we used the ftool efsearch of the XRONOS package (v 5.22), adopting as reference time the start time of the observation and a resolution of the period search of 10−6 s. We explored around a period Pspin of 0.591567 s, estimated using Eq. (6) in Chou et al. (2016), and subsequently, we fitted the peak of the corresponding χ2 curve with a Gaussian function. We assumed that the centroid of the Gaussian was the best estimate of the spin period, and we associated the 68% c. l. error obtained from the best fit with this. We found that the spin period is 0.5915669(4) s, the 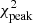 associated with the best period is 44.66 (see the left panel in Fig. 3), and the probability of obtaining a χ2 value greater than or equal to χpeak2 by chance, having seven degrees of freedom, is 1.58 × 10−7 for a single trial. Considering the 1000 trials in our research, we expect almost 1.58 × 10−4 periods with a χ2 value greater than or equal to χpeak2. This implies a detection significance at the 99.984% confidence level.
associated with the best period is 44.66 (see the left panel in Fig. 3), and the probability of obtaining a χ2 value greater than or equal to χpeak2 by chance, having seven degrees of freedom, is 1.58 × 10−7 for a single trial. Considering the 1000 trials in our research, we expect almost 1.58 × 10−4 periods with a χ2 value greater than or equal to χpeak2. This implies a detection significance at the 99.984% confidence level.
 |
Fig. 3. Left panel: folding search for periodicity in the 5–12 keV XMM-Newton/Epn light curve. The horizontal dashed line indicates the χ2 value of 21.85 at which we have the 99.73% confidence level for a single trial, corresponding to a significance of 3σ. Right panel: XMM-Newton/Epn folded light curves obtained by adopting the best period and using 16 phase bins per period. |
Furthermore, we folded the 5–12 keV XMM-Newton/Epn light curve by adopting the obtained Pspin = 0.5915669(4) s and the start time of the observation as reference epoch; we used 16 phase bins per period. We fitted the folded light curve with a constant plus a sinusoidal function with a period kept fixed to one, and we obtained a χ2(d.o.f.) of 9.176(12), a constant value of 19.44(2) c s−1 and a sinusoidal amplitude A = 0.16(2) c s−1. We show the folded light curve and the best-fit curve in the right panel of Fig. 3. We found the fractional amplitude of the pulsation to be 0.83 ± 0.11% for the estimated background count rate of 0.15(1) c s−1. This value is compatible with that reported by Jonker & van der Klis (2001) in the 5–12 keV energy band.
In the end, using the spin period values reported by Iaria et al. (2015) in Table 2, the last value reported by Chou et al. (2016) in Table 4, and the spin-period obtained above, we estimate a spin period derivative of −2.595(11)×10−12 s s−1 with
(see also Jain et al. 2010).
3. Discussion
We updated the orbital ephemeris of source X 1822-371 by adding two eclipse arrival times obtained from the RXTE/PCA observations performed in 2011 and from the XMM-Newton/Epn observation performed in 2017. Our baseline covers almost 40 yr, from 1976 to 2017. We moved the reference epoch of the ephemeris to a more recent time, corresponding to 1996 September 27, which is close to the middle of the baseline. We inferred a Ṗorb of 1.475(54)×10−10 s s−1, compatible with the values in literature. We explored the possibility that a cubic model could improve the fit of the delays, as suggested by Chou et al. (2016); the addition of a cubic term to the quadratic model does not significantly improve the fit yet.
Several authors (Burderi et al. 2010; Bayless et al. 2010; Bak Nielsen et al. 2017) explained the high value of Ṗorb as due to a super-Eddington non-conservative mass transfer rate. This “quadratic model” seems the simplest explanation. We alternatively investigated the possibility that a large sinusoidal modulation could mimic the quadratic trend of the delays. A sinusoidal modulation of the delays could be associated with the gravitational quadrupole coupling (GQC) between the orbit and the changes of the quadrupole moment of the magnetically active companion star (Applegate 1992). The magnetic activity of the secondary generates a torque to the subsurface magnetic field of the companion star (CS); the torque induces a cyclic exchange of angular momentum between the inner and outer regions of the CS, changing its gravitational quadrupole moment, and consequently, the orbital period of the binary system. We assumed that the necessary luminosity LGQC to activate this mechanism comes from the nuclear luminosity Lnuke produced by the CS itself (Applegate 1992). We assumed the mass function f = (2.03 ± 0.03)×10−2 M⊙ (Jonker & van der Klis 2001) and the inclination angle 82.5 ± 1.5 deg (Heinz & Nowak 2001), then we estimated the mass ratio q = M2/M1 = 0.27 ± 0.02 adopting a CS mass M2 of 0.46 ± 0.02 M⊙ and an NS mass M1 of 1.69 ± 0.13 M⊙ (Iaria et al. 2015). Under the reasonable hypothesis that the CS fills its Roche lobe, using Eq. (15) in Sanna et al. (2017),
where m1 is the NS mass in units of M⊙, A is the semiamplitude of the sinusoidal modulation in seconds, PMOD, yr is the modulation period in yr, and Porb, 5h is the orbital period in units of 5 h, we inferred that LGQC = (2.14 ± 0.22)×1033 erg s−1 when we adopted the best-fit values of A and PMOD, yr obtained from the LS model. The nuclear luminosity of a star with mass 0.43 M⊙ < M < 2 M⊙ is given by Lnuke/L⊙ = m4, where m is the stellar mass in units of solar masses (Salaris & Cassisi 2005). Substituting to the latter expression the value of m2, we find that Lnuke = (1.71 ± 0.14)×1032 erg s−1, implying that the nuclear luminosity is a factor of 13 lower than the luminosity needed to activate the GQC process. A large sinusoidal modulation in the delays therefore cannot be explained as results of an Applegate mechanism powered by the nuclear energy of the companion. It is more reasonable that the delays follow a quadratic trend caused by the high value of the orbital period derivative.
It could be possible, on the other hand, that the energy transferred to the CS to trigger the GQC process occurs through tidal dissipation (Applegate & Shaham 1994; Sanna et al. 2017, for a discussion). In this scenario, the magnetic field of the CS, interacting with the mass ejected from the system because of the irradiation from the accreting NS, could produce a torque that is able to slow down the rotation of the CS. The torque, then, holds the CS out of synchronous rotation, generating a tidal dissipation that could furnish the necessary energy to activate the GQC process. In this case, the CS should lose mass, and therefore we should observe an orbital period derivative. Combining Eqs. (17) and (18) of Sanna et al. (2017), we find that the mass transfer rate required to trigger the GQC process through tidal dissipation is
where abin/l represents the ratio between the binary separation and the lever arm of the mass transferred by the CS measured with respect to the centre of mass of the binary system. On the other hand, the mass transfer rate from the CS is linked to the Porb and Ṗorb values as reported in Eq. (4) of Burderi et al. (2010), that is,
where n is the mass-radius index of the CS, and c is the constant of the quadratic term in the model adopted to fit the delays. We assumed n = −1/3 as reported by Burderi et al. (2010). Combining Eqs. (4) and (5), we obtained NMOD = 0.572 c−1/2A2/3abin/l, which we used to constrain the best-fit model (see Sect. 2). The best-fit values obtained from this LQS model suggest that the GQC process is possible through tidal interaction if the mass transfer rate is (9.4 ± 0.3)×10−8 M⊙ y−1, that is, a factor of 6 higher than the Eddington mass accretion rate.
4. Conclusions
Our results confirm the scenario of a super-Eddington mass transfer rate for X 1822-371, where most of the transferred mass is expelled from the system by the X-ray radiation pressure and only a fraction of it accretes onto the NS (see e.g. Iaria et al. 2013). In addition to this simplest “quadratic model”, we note that the GQC mechanism through tidal interaction also predicts a parabolic trend of the delays on which a small modulation with a period of 3.4 ± 1.2 yr and an amplitude of 34 ± 12 s is superimposed. In other words, both the quadratic model and the GQC mechanism through tidal interaction require a large outflow of mass, several times the Eddington limit, from the system.
Acknowledgments
The authors thank Francesca D’Antona for the helpful and kind discussion. The authors acknowledge financial contribution from the agreement ASI-INAF n. 2017-14-H.0, and from the HERMES Project, financed by the Italian Space Agency (ASI) Agreement n. 2016/13 U.O. Part of this work has been funded by the research grant “iPeska” (PI: Andrea Possenti) funded under the INAF national call Prin-SKA/CTA approved with Presidential Decree 70/2016. The authors would like to thank the anonymous referee for their helpful comments.
References
- Applegate, J. H. 1992, ApJ, 385, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Applegate, J. H., & Shaham, J. 1994, ApJ, 436, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Bak Nielsen, A.-S., Patruno, A., & D’Angelo, C. 2017, MNRAS, 468, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Bayless, A. J., Robinson, E. L., Hynes, R. I., Ashcraft, T. A., & Cornell, M. E. 2010, ApJ, 709, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Burderi, L., Di Salvo, T., Riggio, A., et al. 2010, A&A, 515, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chou, Y., Hsieh, H.-E., Hu, C.-P., Yang, T.-C., & Su, Y.-H. 2016, ApJ, 831, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Heinz, S., & Nowak, M. A. 2001, MNRAS, 320, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., & Mason, K. O. 1989, MNRAS, 239, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., & Smale, A. P. 1994, in The Evolution of X-ray Binaries, eds. S. Holt, & C. S. Day, AIP Conf. Ser., 308, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Iaria, R., Di Salvo, T., Burderi, L., & Robba, N. R. 2001, ApJ, 557, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Iaria, R., Di Salvo, T., Burderi, L., et al. 2011, A&A, 534, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iaria, R., Di Salvo, T., D’Aì, A., et al. 2013, A&A, 549, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iaria, R., Di Salvo, T., Matranga, M., et al. 2015, A&A, 577, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jain, C., Paul, B., & Dutta, A. 2010, MNRAS, 409, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jonker, P. G., & van der Klis, M. 2001, ApJ, 553, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Jonker, P. G., van der Klis, M., & Groot, P. J. 2003, MNRAS, 339, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, K. O., & Cordova, F. A. 1982, ApJ, 262, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Parmar, A. N., Oosterbroek, T., Del Sordo, S., et al. 2000, A&A, 356, 175 [NASA ADS] [Google Scholar]
- Salaris, M., & Cassisi, S. 2005, Evolution of stars and stellar populations (J. Wiley) [Google Scholar]
- Sanna, A., Di Salvo, T., Burderi, L., et al. 2017, MNRAS, 471, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tailo, M., D’Antona, F., Burderi, L., et al. 2018, MNRAS, 479, 817 [NASA ADS] [Google Scholar]
- White, N. E., & Holt, S. S. 1982, ApJ, 257, 318 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Best-fit modelling parameters of eclipse time delays with different models, including quadratic, cubic, sinusoidal, and quadratic plus sinusoidal ephemeris.
All Figures
 |
Fig. 1. XMM-Newton/Epn folded orbital light curve obtained by adopting a period of 0.2321107 days. The period is divided into 128 bins. |
| In the text | |
 |
Fig. 2. From left to right: delays vs. cycles for the quadratic (red), cubic (green), and LQS (blue) model. Residuals are in units of σ obtained by adopting the quadratic, cubic, and LQS model, respectively. |
| In the text | |
 |
Fig. 3. Left panel: folding search for periodicity in the 5–12 keV XMM-Newton/Epn light curve. The horizontal dashed line indicates the χ2 value of 21.85 at which we have the 99.73% confidence level for a single trial, corresponding to a significance of 3σ. Right panel: XMM-Newton/Epn folded light curves obtained by adopting the best period and using 16 phase bins per period. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.