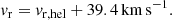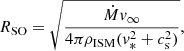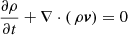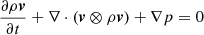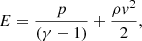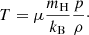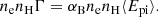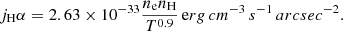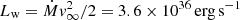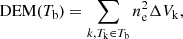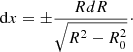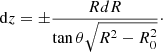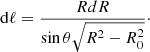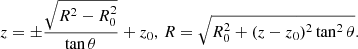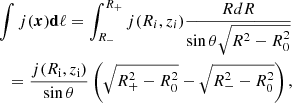| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201834832 | |
| Published online | 29 April 2019 | |
Thermal emission from bow shocks
I. 2D hydrodynamic models of the Bubble Nebula
1
Dublin Institute for Advanced Studies, Astronomy & Astrophysics Section, 31 Fitzwilliam Place, Dublin 2, Ireland
e-mail: green@cp.dias.ie
2
Centre for AstroParticle Physics and Astrophysics, DIAS Dunsink Observatory, Dunsink Lane, Dublin 15, Ireland
3
School of Physics, University College Dublin, Belfield, Dublin 4, Ireland
4
Astrophysics Group, Blackett Laboratory, Imperial College London, Prince Consort Road, London SW7 2AZ, UK
5
Sternberg Astronomical Institute, Lomonosov Moscow State University, Universitetskij Pr. 13, Moscow 119992, Russia
6
Space Research Institute, Russian Academy of Sciences, Profsoyuznaya 84/32, 117997 Moscow, Russia
Received:
11
December
2018
Accepted:
11
March
2019
The Bubble Nebula (or NGC 7635) is a parsec-scale seemingly spherical wind-blown bubble around the relatively unevolved O star BD+60°2522. The young dynamical age of the nebula and significant space velocity of the star suggest that the Bubble Nebula might be a bow shock. We ran 2D hydrodynamic simulations to model the interaction of the wind of the central star with the interstellar medium (ISM). The models cover a range of possible ISM number densities of n = 50−200 cm−3 and stellar velocities of v* = 20−40 km s−1. Synthetic Hα and 24 μm emission maps predict the same apparent spherical bubble shape with quantitative properties similar to observations. The synthetic maps also predict a maximum brightness similar to that from the observations and agree that the maximum brightness is at the apex of the bow shock. The best-matching simulation had v* ≈ 20 km s−1 into an ISM with n ∼ 100 cm−3, at an angle of 60° with respect to the line of sight. Synthetic maps of soft (0.3−2 keV) and hard (2−10 keV) X-ray emission show that the brightest region is in the wake behind the star and not at the bow shock itself. The unabsorbed soft X-rays have a luminosity of ∼1032−1033 erg s−1. The hard X-rays are fainter: ∼1030−1031 erg s−1, and may be too faint for current X-ray instruments to successfully observe. Our results imply that the O star creates a bow shock as it moves through the ISM and in turn creates an asymmetric bubble visible at optical and infrared wavelengths and predicted to be visible in X-rays. The Bubble Nebula does not appear to be unique; it could simply be a favourably oriented, very dense bow shock. The dense ISM surrounding BD+60°2522 and its strong wind suggest that it could be a good candidate for detecting non-thermal emission.
Key words: hydrodynamics / instabilities / radiative transfer / methods: numerical / stars: winds / outflows / ISM: bubbles
© ESO 2019
1. Introduction
Most stars in the universe have winds in the form of gas ejected from their upper atmosphere. The hydrodynamic interaction of such a wind with the surroundings heats the ambient interstellar medium (ISM). For young hot stars with fast winds, a low-density bubble is created from this interaction, expanding with time and displacing the ISM.
The physics governing how a wind-blown bubble expands into the ISM is well understood (Weaver et al. 1977; Castor et al. 1975). A bubble of hot, shocked gas is formed when the wind of a star is converted from kinetic energy to thermal energy as it collides with the surrounding ISM. Around hot stars, a wind bubble expands within the photoionized H II region that surrounds the star (Freyer et al. 2006; Mackey et al. 2015), which is usually isothermal with temperature T ≈ 104 K and isothermal sound speed cs ≈ 10 km s−1. Young bubbles may expand supersonically into this medium generating a shock wave that sweeps up the ISM into a thin, dense shell, which emits at optical, infrared, and radio wavelengths.
A star in motion with respect to the ISM will generate a bow shock on the upstream side and a turbulent wake downstream. Up to 25% of OB stars are indeed moving through space, the so-called runaway stars (Gies 1987; Blaauw et al. 1993), ejected from parent star clusters either because of dynamical encounters with other massive cluster members or due to binary supernova explosions. Prominent examples are ζ Oph (Gull & Sofia 1979; Gvaramadze et al. 2012), Vela X-1 (Kaper et al. 1997; Gvaramadze et al. 2018), and BD+43° 3654 (van Buren et al. 1995; Comerón & Pasquali 2007).
Axisymmetric 2D simulations of bow shocks from hot stars were pioneered by Mac Low et al. (1991) for dense environments and by Comerón & Kaper (1998) for the diffuse ISM. The reverse shock is always adiabatic, as realised by Weaver et al. (1977), and the forward shock is usually radiative and close to isothermal. This can lead to the formation of an unstable thin shell. Thermal conduction may be important at the wind-ISM interface (Comerón & Kaper 1998; Meyer et al. 2014) but may be strongly inhibited by magnetic fields (Meyer et al. 2017). Even slowly moving stars in dense H II regions produce asymmetric wind bubbles (Mackey et al. 2015) with infrared arcs that look like bow shocks (Mackey et al. 2016). Only stars with very strong winds (Freyer et al. 2003) and/or moving through dense gas (Mac Low et al. 1991; Arthur & Hoare 2006) drive wind bubbles that fill their H II region, and therefore we are usually justified in modelling bow shocks as photoionized nebulae where hydrogen is fully ionized (Meyer et al. 2014), but see Rogers & Pittard (2013) for a study in which the surrounding ISM is cold, neutral, and turbulent.
Feedback of radiation and energy from massive stars to molecular clouds and the ISM is a key ingredient in understanding the gas dynamics of galaxies (e.g. Walch et al. 2015). The important contributions of photoionizing radiation and supernovae is well established (Mac Low & Klessen 2004; Matzner 2002), but contributions from stellar winds are much less certain and depend strongly on environment (Haid et al. 2018). If winds are momentum conserving, as argued by McKee et al. (1984), then they are relatively unimportant, whereas energy-conserving winds could inject significant kinetic energy and momentum into the ISM (Matzner 2002). X-ray observations are key to solving this issue, because they directly measure the thermal energy content of the bubble. X-ray observations by Chandra and XMM-Newton have detected diffuse emission from four Wolf-Rayet bubbles (Chu et al. 2003; Toalá et al. 2017a), and a number of nascent bubbles and superbubbles around young star clusters (Townsley et al. 2018). Early predictions of X-ray luminosities of wind bubbles however did not agree with observations quantitatively in that the detected X-ray fluxes were 10–100 times lower than those expected (Chu et al. 2003).
As a star moves through the ISM the interaction between its stellar wind and the surrounding medium can produce instabilities that mix material between the adiabatically shocked wind and the photoionized gas in the wake of the bow shock. This can create a mixing region with plasma temperatures of ∼106 K (Toalá et al. 2016), a strongly cooling boundary layer that efficiently removes thermal pressure support from the bubble. X-rays originating from this thermal plasma are predicted to exist by several numerical simulations (Freyer et al. 2006; Toalá & Arthur 2011; Mackey et al. 2015; Meyer et al. 2014), at a much lower level than previous predictions (e.g. Weaver et al. 1977) because of this wind-ISM mixing. The existence of this layer also has some support from UV observations (Boroson et al. 1997). On larger scales, observations of X-ray emission from hot gas in star clusters, together with other data, show that the majority of the kinetic energy input by stellar winds is absent and must have escaped the cluster (Lopez et al. 2011; Rosen et al. 2014).
Recently, Toalá et al. (2016) detected diffuse emission in the vicinity of the runaway massive star ζ Oph. They conclude the emission similarly has a thermal nature and its cometary shape agrees with radiation-hydrodynamic models of wind bubbles produced by moving stars. It appears that models and observations are slowly converging, in terms of the X-ray emission, towards the conclusion that stellar wind bubbles are closer to the momentum-conserving limit than to the energy-conserving one. Simulations with different physical assumptions can help us understand these mixing processes, as well as non-thermal processes and stellar wind structures.
In this paper, we are starting a project to investigate thermal emission from stellar wind bubbles. To begin with, we model the Bubble Nebula – the only known compact (parsec-scale) seemingly spherical nebula around an O star. The main aim of the modelling is to determine whether the shape of this nebula can be explained in terms of the medium around a runaway star. In Sect. 2, we review observational data on the Bubble Nebula and its associated O star BD+60°2522. In Sect. 3, we describe our model and present the numerical methods and simulation setup. In Sect. 4, we use our preferred model to produce synthetic Hα and infrared emission maps and compare them with observations. In Sect. 5, we construct synthetic maps of X-ray emission from the model Bubble Nebula and assess the possibility of its detection. We discuss our results in Sect. 6 and conclude in Sect. 7.
2. Bubble nebula and BD+60°2522
The Bubble Nebula (or NGC 7635) is an almost perfectly circular emission nebula of angular diameter of ≈3 arcmin. It is clearly visible in infrared and optical wavelengths, as illustrated in Fig. 1 showing the Spitzer Space Telescope 24 μm and the Digitized Sky Survey II (DSS-II) red band (McLean et al. 2000) images of the nebula and its surroundings. Figure 1 also shows that the brightest (northern) side of the Bubble Nebula is orientated towards the more extended emission nebula with bright-rimmed clouds to the north, known as SH 2–162 (Sharpless 1959). Radial-velocity measurements for two nebulae indicate that they are physically associated with each other (Doroshenko & Grachev 1972; Deharveng-Baudel et al. 1973; Maucherat & Vuillemin 1973; Israel et al. 1973).
 |
Fig. 1. Spitzer 24 μm (left-hand panel) and DSS-II red band (right-hand panel) images of the Bubble Nebula and its surroundings. The arrow shows the direction of motion of BD+60°2522 (marked by a circle) as suggested by the Gaia DR2 proper motion and parallax measurements (with 1σ uncertainties shown by dashed arrows). The orientation and the scale of the images are the same. A white spot in the Spitzer image is due to a saturation effect. |
The driving star of the Bubble Nebula is the O6.5 (n)(f)p (Walborn 1973) star BD+60°2522. Conti & Alschuler (1971) derived the luminosity class III for BD+60°2522, but the peculiar shape of the He II λ4686 emission line in the spectrum of this star makes this assertion uncertain Sota et al. (2014); but see below). BD+60°2522 is significantly offset from the geometric centre of the nebula towards its brightest edge. Table 1 shows some properties of BD+60°2522 including the distance to the star and its peculiar transverse velocity based on the Gaia second data release (DR2) (Gaia Collaboration et al. 2018). At the distance of 2.7 ± 0.2 kpc, the linear diameter of the Bubble Nebula is 2.3 ± 0.2 pc.
Summary of the parameters of BD+60°2522.
The Bubble Nebula is the only known parsec-scale wind bubble that has been observed around an O star in optical wavelengths. The morphology of the nebula and its neighbourhood was extensively studied in the 1970s and 1980s where parameters for the central star and the nebula itself were established (see Christopoulou et al. (1995) for a review on the topic). It is generally accepted that the Bubble Nebula is a shell swept up by the stellar wind of BD+60°2522 from the dense (∼100 cm−3) ISM (e.g. Israel et al. 1973; van Buren 1986; Dufour 1989; Christopoulou et al. 1995; Moore et al. 2002a). The inference on the dense ISM follows from the small linear size of the bubble (e.g. Christopoulou et al. 1995; Moore et al. 2002a). It is also evidenced by the presence of dense (≈103−104 cm−3; e.g. Mesa-Delgado & Esteban 2010; Moore et al. 2002b; Esteban et al. 2016), bright-rimmed structures around the Bubble Nebula (one of which even penetrates the bubble; e.g. Moore et al. 2002b), whose “elephant trunk” morphology is typical of H II regions expanding into dense molecular clouds (e.g. Hester et al. 1996). Also, number density estimates based on the [S II] λλ6716, 6731 emission line ratio in the spectrum of the Bubble Nebula showed that the electron number density in its shell is equal to ≈100−300 cm−3 (e.g. Esteban et al. (2016); see their Table 6), which for low-Mach-number shocks (see Sect. 3.2) corresponds to the pre-shock number density of ≈50−100 cm−3.
The wind-blown bubble interpretation of the Bubble Nebula is based on radial-velocity measurements (Deharveng-Baudel et al. 1973; Lynds & Oneil 1983; Christopoulou et al. 1995) showing that the central parts of its shell have more positive radial velocities than the rim. This difference in radial velocities implies that we see the far (receding) side of the nebula and that the Bubble Nebula is located on the near side of the molecular cloud associated with SH 2–162. The illumination of the bright-rimmed clouds surrounding the Bubble Nebula also suggests that BD+60°2522 is on the near side of the cloud. If the observed difference in the radial velocities of ≈20−25 km s−1 (Christopoulou et al. 1995) represents the expansion of the Bubble Nebula as a whole, then its dynamical age can be estimated to be 5 × 104 yr.
Using V magnitude and B − V colour of BD+60°2522 of respectively 8.65 mag and 0.38 mag (Neckel et al. 1980), the intrinsic (B − V)0 colour of O6.5 stars of −0.27 mag (Martins et al. 2005), and assuming the total-to-selective absorption ratio of RV = 3.1, one finds the visual extinction towards the star of AV ≈ 2.0 mag (which agrees with the extinction estimate based on the Balmer decrement in the spectrum of the Bubble Nebula; see Doroshenko 1972) and its absolute visual magnitude of MV = −5.53 mag. The latter value implies (e.g. Walborn 1973; Martins et al. 2005) a luminosity class III for BD+60°2522, in agreement with the result by Conti & Alschuler (1971). The luminosity class III indicates that BD+60°2522 is a relatively unevolved star, meaning that the origin of its associated nebula cannot be explained in the framework of the wind-wind interaction scenario proposed for the origin of circumstellar nebulae around evolved massive stars (e.g. Garcia-Segura et al. 1996a,b). This inference is supported by chemical abundance measurements for the Bubble Nebula, indicating that it is composed of swept-up ISM (Esteban et al. 2016).
The brightness asymmetry of the Bubble Nebula and the off-centred location of BD+60°2522 could be understood if the nebula impinges on a more dense ambient medium in the north direction (e.g. Icke 1973) or interacts with a photoevaporation flow from the nearby molecular cloud (e.g. Moore et al. 2002a), and/or might be caused by motion of BD+60°2522 in the north direction. The latter possibility is supported by the Gaia DR2 data indicating that BD+60°2522 is moving towards the brightest (northern) rim of the Bubble Nebula with a transverse peculiar velocity of 28 ± 3 km s−1 (see Fig. 1 and Appendix A), which is typical of runaway stars. This in turn suggests that the Bubble Nebula could be a bow shock viewed at an appropriate angle.
To derive the total space velocity of BD+60°2522, one needs to know the peculiar radial velocity, vr, of this star, which at the distance of 2.7 kpc, is related to the observed heliocentric radial velocity, vr, hel, as follows:
The radial velocity of BD+60°2522 however is known to be variable (Wilson & Joy 1952), which is most likely caused by the line profile variability due to non-radial pulsations typical of the Ofp stars (Rauw et al. 2003). The SIMBAD data base1 provides several values of vr, hel ranging from −14 to −36 km s−1. These velocities imply that BD+60°2522 is moving either almost in the plane of the sky or receding from us with a velocity comparable to the transverse peculiar velocity. The uncertainty in the stellar velocity relative to the local ISM is aggravated by the possible presence of a photoevaporation flow (whose velocity is of the order of the sound speed, i.e. ∼10 km s−1) from the nearby cloud (cf. Moore et al. 2002a) as well as by the radial-velocity dispersion of H II regions within a spiral arm of ∼10 km s−1 (Georgelin & Georgelin 1976). This means that the total velocity of BD+60°2522 relative to the local ISM, v*, could range from ∼20 to 40 km s−1.
Regardless of whether or not a photoevaporative flow is present, the peculiar space velocity of BD+60°2522 appears sufficient to create a bow shock. The characteristic scale of the bow shock – the stand-off distance – is defined by the balance between the ram pressure of the stellar wind and the ram and thermal pressures of the incoming ISM, and is given by (Baranov et al. 1970):
where Ṁ and v∞ are the stellar mass-loss rate and wind velocity, respectively, and ρISM is the density of the ISM. For bow shocks produced by hot stars (like BD+60°2522), RSO gives the minimum distance to the contact discontinuity, separating the shocked stellar wind from the shocked ISM.
In the following sections, we explore the possibility that a bow shock could produce a circular nebula like the Bubble Nebula, which appears to be a closed bubble.
3. Numerical simulations
3.1. Hydrodynamics and thermodynamics
We solve the Euler equations of classical hydrodynamics including radiative cooling and heating for optically thin plasma. The equations for the conservation of mass, momentum, and energy are:
In Eqs. (2)–(4), υ is the gas velocity in the frame of reference of the star, ρ is the gas mass density, ni, ne and nH are the number density of ions, electrons and hydrogen nuclei, respectively, and p is the thermal pressure. Λ is the rate for optically-thin radiative cooling and Γ is for optically-thin radiative heating. E is the total energy density and is its thermal and kinetic parts summed together,
where γ is the ratio of specific heats for a monatomic ideal gas (i.e. γ = 5/3). The temperature inside a given layer of the bow shock is obtained from the ideal gas law:
The total number density, n, is defined by ρ = μnmH, where μ is the mean mass per particle in units of mH, the mass of a hydrogen atom. We consider a gas composed mostly of hydrogen (0.714 by mass), with one helium atom for every ten atoms of hydrogen, and trace abundances of metals with solar composition. As discussed above, all of the gas is considered to be photoionized, giving μ = 0.61. For doubly ionized helium, the electron, ion, and hydrogen number densities are given by ne = 0.86ρ/mp, ni = 0.79ρ/mp, and nH = 0.71ρ/mp.
The radiative heating is assumed to arise primarily from photoionization of hydrogen atoms that recombine in the H II region and therefore is simply the product of the recombination rate and a mean heating energy per ionization, ⟨Epi⟩, (cf. Meyer et al. 2014):
We take ⟨Epi⟩ = 5 eV, appropriate for an O star, and use the case B recombination rate αB from Hummer (1994). The radiative cooling rate Λ includes:
-
Metal-line cooling taking the minimum of the cooling curve of Wiersma et al. (2009) (collisional ionization equilibrium (CIE), metals only) and the forbidden-line cooling function of Henney et al. (2009) (Eq. (A9), damped exponentially for T > 105 K). This captures cooling of shocked wind assuming CIE, and also the strong forbidden-line cooling of the photoionized ISM that would not arise in CIE.
-
Bremsstrahlung from ionized hydrogen (Hummer 1994) and helium (Rybicki & Lightman 1979).
-
Recombination cooling of H, with rate from Hummer (1994).
3.2. Computational methods and initial conditions
We use the PION radiation hydrodynamics code (Mackey 2012) to model the Bubble Nebula as a propagating O star emitting a stellar wind. The code solves the Euler equations (Eqs. (2)–(4)) in cylindrical coordinates with rotational symmetry on a computational grid in the (R, z) plane. The mass, energy, and momentum densities are defined at the centre of each computational cell, and evolved with time according to the hydrodynamical equations. For a detailed description and explanation of the PION code see Mackey (2012), and for applications of the cylindrical coordinate system see Mohamed et al. (2012) and Mackey et al. (2015). The integration scheme follows Falle (1991) and Falle et al. (1998).
For numerical convenience, a reference frame in which the star is stationary and located at the origin (R, z) = (0, 0) of a rectangular box is chosen. The ISM flows past the star in the negative z-direction, interacting with the stellar wind as it does so. A passive scalar variable is used to distinguish between the ISM and wind gas. For the sake of simplicity, the ISM is assumed to be homogeneous.
A range of ISM densities, nH = 50, 100, and 200 cm−3, were modelled, with corresponding stellar velocities v* = 20, 30, and 40 km s−1 (see Table 1), respectively. These stellar velocities were chosen to account for uncertainty in the relative velocity of the star (see Sect. 2). The ISM densities were chosen because this is the range of observed densities derived from the nebular emission lines (see Sect. 2). The ISM densities and stellar velocities were used to calculate the stand-off distance of the bow shock for each simulation (Eq. (1)). This was then used to estimate the size of the simulation boxes.
3.3. Comparison of simulations
Nine 2D simulations were run using the parameters shown in Table 2, all using the stellar wind properties taken from BD +60°2522 (see Table 1). A snapshot after ∼1 crossing time (time taken for one fluid element to cross the whole simulation box) for each simulation is shown in Fig. 2. Simulation 2a, 2c, 3a, 3b, and 3c could not be used due to the development of an unstable bow shock and gas pile-up at the apex, which is a well-known limitation of 2D simulations (e.g. Meyer et al. 2014). The apex is where the stellar wind and the ISM collide head-on, resulting in a stagnation point of the flow. We compared the remaining four simulations to the Bubble Nebula and found that for simulation 1a the bubble was too big and too faint. Simulations 1c and 2b produced nebulae that were too bright. The 1b model was chosen to be the best simulation to compare with the Bubble Nebula because it evolved into an elliptical shape with a smooth bow shock and its synthetic emission maps showed similarity to the observational data.
Simulations used for post-processing.
 |
Fig. 2. From left to right: snapshot after one crossing time from each simulation in Table 2. The top half shows log10 plots of the gas density (g cm−3) profile of the gas, and the bottom half shows log10 plots of the temperature profile of the gas with white being of higher temperature (K) than black. The star is at the origin. Labels of the different models are shown in white on each panel. |
3.4. Simulation 1b
Snapshots from simulation 1b are shown in Fig. 3. The snapshots are after 0.5 (0.11 Myr), 1 (0.23 Myr), and 2 (0.44 Myr) crossing times. The upper half plane in the plots shows log10 of the gas density profile. The colour-bar on the right of each plot shows that yellow is the highest density (10−20 g cm−3) and dark blue/purple is the lowest density (10−26 g cm−3). The lower half plane in the plots shows log10 of the gas temperature profile. In this case, white is the highest temperature (108 K) and black is the lowest temperature (104 K).
 |
Fig. 3. Top half: log10 plots of the gas density (g cm−3) profile of the gas, and bottom half: log10 plots of the temperature profile of the gas with white being of higher temperature (K) than black. These plots are from the 1b simulation data. The star is at the origin. From left to right: simulation after 0.5, 1, and 2 crossing times, respectively. |
Figure 4 shows snapshots taken from the 1b simulation at the same crossing times as Fig. 3 but plotting gas velocity and the Mach number of the gas in a reference frame where the star is at rest. The upper half plane is a plot of the gas velocity profile of the gas in km s−1. The maximum velocity shown is 30 km s−1 so that the velocity gradients in the bow shock are visible. The velocity of the ISM is initially set to −20 km s−1. The wind bubble has much-higher-velocity gas, comparable to the wind speed of 2500 km s−1. Overlayed are vector arrows showing the direction of the flows. These are used to show the position on the bow shock and how the gas from the ISM is swept backwards around the bubble. The lower half plane is a plot of the isothermal Mach number, ℳ of the gas flow with respect to the star, defined by 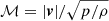 . Overlayed are streamlines showing the direction of the gas.
. Overlayed are streamlines showing the direction of the gas.
 |
Fig. 4. Top half plane: gas velocity (km s−1) with yellow being of higher velocity than dark purple. Bottom half plane: Mach number of the gas with black being of higher Mach number than white. These are from the 1b simulation at the same three time-steps as the density/temperature plots in Fig. 3. |
Early in its evolution, the bow shock is expanding and is not in equilibrium. Later on, the bow shock begins to approach equilibrium where the total pressure (ram pressure + thermal pressure) is constant. However, there is an exception to this where instabilities disturb the flow. We now discuss the simulation results where the bow shock is in its equilibrium state.
At the apex of the bow shock, Fig. 3 shows that the density is ∼10−21 g cm−3. The density remains at approximately this value throughout the entire simulation. The compression factor is largest at the apex because the Mach number (1.94) of the shock is biggest there (dismissing the Mach number of the wind directly from the star). The temperature at the apex of the bow shock is also in equilibrium with the rest of the ISM (∼104 K). The forward shock in the ISM is basically isothermal because the density is high, the post-shock temperature is ∼104 K, cooling is strong, and the cooling time is very short. Figure 4 shows that at the apex of the bow shock the velocity of the gas is 0 km s−1.
Inside the hot bubble, the gas density is as low as ∼10−26 g cm−3 and as high as ∼10−24 g cm−3. The reverse shock in the wind is adiabatic because the density is low, the post-shock temperature is ∼108 K, cooling is weak, and the cooling time is very long. The velocity of the gas reaches 30 km s−1 (and certainly higher because the unshocked part of the stellar wind is moving at 2500 km s−1).
The part of the bow shock at 45° to 90° from the apex (measured from the star) is where the bow shock expands and the density decreases slowly as the velocity increases. Densities and temperatures of this region are similar to the apex of the bow shock with high densities (compared to the inside of the bubble) and temperatures are the same with the surrounding ISM. The velocity of the gas here increases with distance from the apex because the velocity vectors of the ISM and wind do not cancel. The velocity approaches that of the ISM (20 km s−1, Mach number of 1.94) as one moves towards the back of the bow shock.
As the bubble evolves, the bow shock relaxes slowly towards its equilibrium shape (parabolic). However, the bubble itself remains in an elliptic shape. In the later snapshots, the density of the bow shock decreases as R increases. The stellar wind bubble in these simulations also has a periodic change in bubble size. The bubble is at its maximum size roughly every 0.18 Myr (and hence minimum size every 0.09 Myr after a maximum). This can be explained with “Vortex Shedding” and will be discussed further in Sect. 5.
4. Synthetic emission maps and comparison with observations
Synthetic observations are predictions based on theoretical simulations to provide a view of what the astrophysical source in question will appear as to an observer. It is a way of comparing simulations to observational data and to allow the theoretical models to be constrained. Haworth et al. (2018) presented a recent detailed description of the power of synthetic observations in star formation and the impact of stars on the ISM. In this section, we present our synthetic optical, IR, and X-ray images obtained from our simulations to test the hypothesis that the Bubble Nebula formed as a result of a bow shock around BD+60° 2522.
4.1. Observational data used for comparison
The Hα image that we use for comparison with simulations was obtained by the Hubble Space Telescope (HST; Program Id.: 14471, PI: Zolt Levay) on 2016.02.25. We downloaded the level 2 data products (reduced and calibrated images) from the Mikulski Archive for Space Telescopes (MAST)2 at the Space Telescope Science Institute (STScI). The image is composed of four tiled WFC3/UVIS pointings with three images of 500 s exposure per tile (i.e. 1500 s exposure per pixel) and was produced by Avila et al. (2016) as part of the Hubble Heritage Project.
The Spitzer 24 μm image of the Bubble Nebula was downloaded from the NASA/IPAC infrared science archive3. The nebula was observed on 2005.12.05 (Program Id.: 20726, PI: J. Hester), using the Multiband Imaging Photometer for Spitzer (MIPS; Rieke et al. 2004). The image is a level 2 data product, with units of MJy sr−1 and angular resolution of 6 arcsec.
4.2. Calculating Hα emission
Our 2D cylindrical models (in the R − z plane) are rotationally symmetric about the z-axis. We use this symmetry to produce synthetic emission maps of the 3D structure. We developed a raytracing method to calculate synthetic images described in Appendix B, using the symmetry of the simulation to generate projection through 3D space at an angle to the grid (similar to Arthur & Hoare 2006 for radio emission). Synthetic Hα emission maps were generated using this method. The Hα emissivity was calculated by interpolating a table in Osterbrock (1989) as
Figure 5 compares synthetic Hα emission maps taken from the 1b simulation with the HST Hα image. We rotated the HST image so that the x-axis is along the direction of stellar motion as suggested by the Gaia DR2 data (Gaia Collaboration et al. 2018). These images show the Hα brightness of the Bubble Nebula with units of erg cm−2 s−1 arcsec−2 on a logarithmic scale.
 |
Fig. 5. Top two images: synthetic Hα emission maps of the bow shock on a logarithmic colour scale (in units of erg cm−2 s−1 arcsec−2), generated from the 1b simulation for viewing angles of 45° and 60°. Both synthetic images are generated after 0.2135 Myr of evolution. The coordinates are in parsecs relative to the position of the star. The black cross shows the position of the ionizing star. Bottom plot: HST Hα (656 nm) image of the Bubble Nebula. |
The Hα emission therefore traces the densest parts of the bow shock and the forward shock is clearly visible in Fig. 5. At the apex of the bow shock there is a high Hα brightness with intensity 10−12 erg cm−2 s−1 arcsec−2. Even though Fig. 3 shows that the bubble is not closed in the negative z-direction, in Hα it looks like a closed bubble because of projection effects. The brightest pixels in the HST image are from a bright-rimmed cloud near the wind bubble but the brightness of the bubble itself is comparable to the synthetic images.
We made synthetic images at angles from 0° to 90° (with 15° step) between the line of sight and the velocity vector of the star. Visual inspection showed that 45° and 60° were most similar to observations. The other angles can be seen in Fig. 7, where we show synthetic emission maps in 24 μm, Hα, soft and hard X-rays at angles of 0°−90°. The criteria we used were the downstream brightness compared with the apex, and the positioning of the wings of the bow shock on the top and bottom of the nebula. Supporting our visual estimate, the position of the star in the nebula follows the 60° synthetic snapshot (see Fig. 8). Both images also show a high Hα brightness at the apex of the bow shock, the predicted brightness is quantitatively consistent, and the physical appearance of the nebula at the apex is similar. The rings are an artifact of the symmetry of the 2D simulation.
4.3. Calculating dust/infrared emission with TORUS
We simulate dust emission maps from our models by post processing them using the Monte Carlo radiation transport and hydrodynamics code TORUS (e.g. Harries 2000, 2015; Kurosawa et al. 2004). The procedure here is very similar to that described in Mackey et al. (2016). Snapshots from the PION calculations are saved in FITS format and mapped onto the TORUS grid using a bilinear interpolation for 2D models. Because the PION calculations do not compute the dust temperature we first perform a dust radiative equilibrium temperature calculation before producing synthetic observations. For both the radiative equilibrium and synthetic observation calculations we use a Monte Carlo approach based on photon packet propagation introduced by Lucy (1999). Further details of the implementation in TORUS are given in the aforementioned papers.
To ensure a dust-free wind blown region we remove the dust wherever the temperature is more than 106 K. In the remainder of the grid we assume a gas-to-dust mass ratio of 160 (Zubko et al. 2004), which is comprised of 70% silicates (Draine 2003) and 30% carbonaceous (Zubko et al. 1996) grains. We assume that no polycyclic aromatic hydrocarbons survive within the H II region. For both the silicate and carbonaceous grains we assume minimum and maximum grain sizes of 0.005 and 0.25 μm respectively. The size distribution itself between these limits is a power law dn/da ∝ a−q (Mathis et al. 1977), where we take q = 3.3. For the stellar spectrum we use a Kurucz (1993) spectral model with the same temperature as BD+60° 2522.
We take the same snapshot from the 1b simulation to be run with the TORUS code. The code produces dust emission maps (24 μm) at angles from 0°–90° for each snapshot. The top two images in Fig. 6 show the results of the TORUS code for 24 μm emission at angles of 45° and 60° between the line of sight and the velocity vector of the star. The images from the 2D radiative transfer calculations have a length and width of 5 pc and pixel diameter of 0.0195 pc.
 |
Fig. 6. Top two images: synthetic infrared emission maps of the bow shock on a logarithmic colour scale (in units of MJy ster−1), generated from the 1b simulation for viewing angle angles of 45° and 60°. Both synthetic images are generated after 0.2135 Myr of evolution and smoothed to the angular resolution of Spitzer of 6 arcsec. The coordinates are in parsecs relative to the position of the star. The black cross shows the position of the ionizing star. Bottom plot: Spitzer 24 μm image of the Bubble Nebula. |
The synthetic snapshots are smoothed to the resolution of Spitzer to accurately compare the features in the simulated data with the observational data. This has been achieved by convolving the data and does not account for instrumental response. It can be seen that the maximum brightness of the synthetic snapshots (103.51, 103.62 MJy sr−1) matches the maximum brightness of the Spitzer image (103.5 MJy sr−1). The minimum brightness is slightly different because the synthetic maps only simulated the bubble and not the background radiation, whereas Spitzer detected background emission in the field of view.
There are distinct morphological similarities between the synthetic images and the observations. The most noticeable similarity would be the spherical emission surrounding the stellar wind bubble which is at its brightest near the apex of the bow shock. The size of the bubble is consistent with the observations in that it has a radius of ∼2.5–3 pc.
4.4. Position of the star in the Bubble Nebula
Both the Hα and infrared synthetic emission maps are quantitatively and qualitatively consistent with the observational data and bow shock interpretation. The position of the central star in the 60° Hα and infrared images match that of the central star in the retrospective observations. This is shown quantitatively with Fig. 8, where we show the position of the star in the nebula as a function of the angle by which the nebula is rotated about the line of sight. The red line shows the ratio of the position of the star in the observed nebula. The point of intersection of the red line and the black curve gives an indication of the angle the nebula is rotated at, which is shown to be ≈56°. The 60° results are shown as this is close to the estimated angle of rotation. Therefore, the Hα and infrared maps suggest that the star is moving at 20 km s−1 into an ISM with n ∼ 100 cm−3, at an angle of 60° with respect to the line of sight.
 |
Fig. 7. A snapshot (after 1 crossing time) from the 1b simulation was used to generate synthetic images of the Bubble Nebula at angles from 0°−90° with respect to the direction of stellar motion. First row: 24 μm emission, second row: Hα emission, third row: soft X-ray emission, and fourth row: hard X-ray emission. From left to right, the angles are 0°, 15°, 30°, 45°, 60°, 75°, and 90°. For the Hα and X-ray image we plot 1° and 89° instead of 0° and 90° because of technical limitations. Each image is centred on the star (black cross) and is roughly 5 × 5 parsec. |
 |
Fig. 8. Ratio of the stand-off distance RSO to the radius of the bow shock at an angle of 90° from the direction of the stellar motion, as a function of viewing angle, θ. The observed ratio is taken from the Spitzer image and simulation results are from the synthetic infrared images. |
The apparent spherical emission surrounding the stellar wind bubble in each wavelength is consistent with the observations. Also, the brightest part of both emission maps is at the apex of the bow shock, which is again consistent with the observations. The “wings” of the bow shock in the Hα maps however are different to the HST image. This part of the bow shock is less bright and fainter in the observational image. The thickness of the predicted bright emission at the rim of the bubble seems consistent with observations near the apex of the bow shock, but at 90° from the apex we predict a thicker bubble rim than is observed. There are a number of possible reasons for this: a density gradient in the ambient ISM seems to be present (Moore et al. 2002a) but is not modelled here; and ISM magnetic fields could alter the thickness of shocked layers.
5. Calculating X-ray emission
5.1. Synthetic images
The Bubble Nebula was not detected in X-rays by ROSAT (Chu et al. 2003) or since then with any other observations. Now we construct synthetic maps of the soft and hard X-ray emission from this nebula and estimate its X-ray luminosity to generate predictions for which X-ray satellites (e.g. XMM-Newton) could potentially observe at specific energies. The same ray-tracing method (described in Appendix B) was used to generate the soft and hard X-ray emission maps as that used to generate the Hα emission maps. The emissivity as a function of temperature for different X-ray bands was calculated using XSPEC v12.9.1 (Arnaud et al. 1996) and tabulated. Solar abundances from Asplund et al. (2009) as implemented in XSPEC are used. Absorption within the simulation was neglected but we do consider the effect of interstellar absorption from foreground matter.
We generated synthetic soft (0.3−2 keV) and hard (2−10 keV) X-ray emission maps at angles from 0° to 90° (with 15° steps) to the direction of motion for the same snapshot of model 1b as considered in Sects. 4 and 5. Figure 9 shows the soft X-ray emission from simulations at angles of 45° and 60°, and Fig. 10 shows the same for hard X-ray emission. The soft X-ray band shows plasma around the star (and inside the bubble) hot enough to produce soft X-rays with energies between 0.3−2 keV (i.e. temperatures about 106 K). Whereas, the hard X-ray band shows plasma around the star (and inside the bubble) hot enough to produce hard X-rays with energies of 2−10 keV (i.e. temperatures >107 K). Both Figs. 9 and 10 show that the majority of the X-ray emission is in the “tail” of the stellar wind bubble, as observed for ζ Oph by Toalá et al. (2016).
 |
Fig. 9. Synthetic soft X-ray (0.3–2 keV) emission maps of the simulated nebula (unabsorbed). Both images have coordinates in parsecs relative to the position of the star (black cross), and the scale is in erg cm−2 s−1 arcsec−2. Both images are generated from the 1b simulation, after 0.2135 Myr of evolution and are smoothed to the angular resolution of XMM-Newton EPIC cameras (6 arcsec). |
Soft X-rays are about 50 times brighter than the hard X-rays with very weak dependence on orientation. Soft X-rays are mostly emitted at the edges of the bubble and are brightest in the wake behind the star. Hard X-ray emission is from the whole volume of the bubble but is also brightest in the wake behind the star.
The visual extinction towards BD+60°2522 of AV = 2 mag (Sect. 2) means that at 0.5 keV only 0.006 of the radiation from the source will reach Earth. At 1 keV the fraction is 0.40, and at 2 keV it is 0.85. This means that >99% of the soft X-rays with <0.5 keV will be absorbed, unless the extinction is patchy or variable across the nebula. Even with this extinction some bright spectral lines could still be observable (Toalá & Arthur 2016). The hard X-rays are almost unaffected by extinction, and X-rays with 0.5−2 keV are moderately attenuated.
5.2. Total luminosity
Figure 11 demonstrates this with the predicted soft and hard X-ray luminosity of the whole nebula. The left image of Fig. 11 is a plot of the unabsorbed flux (erg cm−2 s−1) and the luminosity (erg s−1) versus the time (Myr) for the whole 1b simulation. The point at each time-step in the graph is the summation of the luminosity/flux over the whole simulated nebula. Each line represents the X-ray luminosity/flux emitted above a certain energy level ranging from 0.1 keV to 10 keV. The right plot shows the X-ray flux that could be detected from Earth with extinction taken into account. X-rays with energies E < 0.5 keV will get absorbed by the ISM, whereas hard X-rays (2−10 keV) are unaffected. The observable X-ray flux corresponds to a luminosity more than 10 000 times less than the mechanical luminosity of the stellar wind. The simulations predict a significant X-ray flux in 0.5−2 keV which could potentially be observed. The total flux received varies from 10−14 to 10−13 erg cm−2 s−1 depending on time4.
 |
Fig. 11. Left-hand panel: synthetic X-ray unabsorbed flux (erg cm−2 s−1) and luminosity (erg −1) plot of the Bubble Nebula as it evolves in time (Myr). Seven X-ray bands simulated from soft to hard X-rays, including 0.1 keV, 0.2 keV, 0.5 keV, 1 keV, 2 keV, 5 keV, and 10 keV. Right-hand panel: absorbed flux (erg cm−2 s−1) and luminosity (erg s−1) plot showing that the 0.1 keV–1 keV X-ray bands get absorbed by the ISM. Mechanical luminosity of the stellar wind (i.e. energy input rate to the wind bubble) is |
The “dips” in the luminosity seen at ∼0.16 Myr, ∼0.35 Myr, and ∼0.5 Myr coincide with minima in the size of the simulated bubble. For example, the middle image in Fig. 3 shows a snapshot of the bubble during one of these “dips” in luminosity. When compared to the left image in the same figure, the size of the bubble in the radial direction is very different. Hence, the larger the bubble, the higher the X-ray luminosity emitted. An explanation for why the bubble shrinks in size is that whenever a vortex forms due to the Kelvin–Helmholtz instability at the boundary layer between the bubble and the ISM, it seems to cause a large part of the gas to flow backwards in the −ẑ direction. This is known as vortex shedding (Wareing et al. 2007). As the vortex travels backwards in the −ẑ direction, it brings all the gas above along with it. The plot in Fig. 11 also shows that this is a periodic event.
5.3. Differential emission measure
The X-ray emission from the hot gas in the 1b simulation is further analysed by calculating the differential emission measure (DEM) as a function of T, and then the emission-weighted mean temperature, TA, following Toalá & Arthur (2018). The DEM profile was calculated using
where ne is the electron number density in cell k and ΔVk is the volume of cell k. All the cells with a gas temperature falling inside a single bin with median temperature Tb are summed together. Figure 12 shows the DEM profile of the simulated nebula (unabsorbed) from the 1b simulation, after 0.2135 Myr of evolution. The DEM shows a profile strongly skewed towards lower temperatures, with a power-law behaviour similar to that shown by Toalá & Arthur (2018) for stellar wind bubbles with turbulent mixing layers and a power-law exponent of approximately −2.
 |
Fig. 12. DEM profile of the simulated nebula (unabsorbed) from the 1b simulation, after 0.2135 Myr of evolution. |
We can use the X-ray emissivity in a given energy band, ϵ, together with the DEM profile, to calculate TA for the simulated wind bubble, defined by
where ϵ(T) is the emission coefficient in the X-ray band and DEM(T) is the DEM at temperature T. The integral is then performed over all the temperature bins in the DEM. Figure 13 shows the evolution of TA as a function of time for different X-ray energy bands. The soft X-ray emission shown in Fig. 9 has a mean temperature of about 106.4 K. Whereas, the hard X-ray emission shown in Fig. 10 has a mean temperature of about 107.4 K. The figure also shows that the X-ray emission between 1 and 2 keV has a mean temperature of 106.8 K. The values of TA are almost constant for the duration of the simulation, apart from the initial expansion phase of the bubble in the first 0.02 Myr.
 |
Fig. 13. Mean temperature (K) of the simulated nebula (unabsorbed) as it evolves in time (Myr) |
6. Discussion
6.1. Comparison with the Bubble Nebula
The original picture, in which the Bubble Nebula is a supersonically expanding wind bubble, is complicated by the fact that the dynamical age of the nebula of 5 × 104 yr is too young for its associated (moderately evolved) star BD+60°2522. For a star moving supersonically through the ISM however, such an issue does not arise because the timescale for the nebula (bow shock) to reach a stationary state is the maximum of the expansion time of the wind (RSO/v∞) and the advection timescale of the flow (RSO/v*). The latter is much longer for hot stars (such as BD+60°2522), but is still less than 105 yr for all feasible values of v*. The bow shock scenario therefore provides an attractive and natural explanation for the apparent youth of the Bubble Nebula. Below we discuss some issues related to this scenario.
The Bubble Nebula is about 3 arcmin in diameter in both the HST and Spitzer images. Using the Gaia distance to BD+60°2522 of d = 2.7 ± 0.2 kpc (see Sect. 2), this corresponds to a linear diameter of 2.3 ± 0.2 pc. Simulation 1b produces a nebula of 3 pc in diameter in both optical and infrared emission (Figs. 5 and 6). The model nebula from the 1b simulation is therefore somewhat bigger compared with the observational data from HST and Spitzer, implying that some of the input parameters are incorrect.
Equation (1) shows that either Ṁ or v∞ is too big, or that ρISM or v* is too small. The stellar peculiar transverse velocity of ≈28 km s−1 together with the inclination angle of the bow shock of 60° imply a total relative velocity of 32 km s−1, which is larger than v* = 20 km s−1 in our preferred model. A larger v* would prevent the nebula from expanding as much as the 1b simulation. Unfortunately our simulations with v* > 30 km s−1 became unstable during the simulation runtime because of gas piling up at the apex of the bow shock. This is a well-known problem with 2D hydrodynamic simulations. This problem could possibly be solved by including a magnetic field (Meyer et al. 2017) and/or running more computationally expensive 3D simulations.
6.2. Mixing/turbulence at the wind/ISM interface
Only a fraction of the energy input from the stellar wind of the massive star goes into the work done to drive the expansion of the bubble. It is thought that the majority of this energy is dissipated by turbulent mixing of the hot shocked wind with the cooler ISM. There is also resultant cooling through line emission or potentially by heat transport through thermal conduction from the wind to the ISM (Rosen et al. 2014). The turbulent mixing is largely driven by Kelvin–Helmholtz instabilities at the contact discontinuity.
The soft X-ray emission is coming from the mixing region between the shocked wind and the ISM. Magnetic fields and thermal conduction are not included in these simulations and therefore the contact discontinuity structure is resolved by numerical diffusion and not by physical processes. Meyer et al. (2014, 2017) showed that both of these processes have some effect, but also that they can cancel each other out somewhat. We will investigate this in future work. The inclusion of a magnetic field can weaken Kelvin–Helmholtz instabilities (Keppens et al. 1999; Frank et al. 1996), reducing the amount of mixing which would in turn reduce the intensity of the soft X-ray emission.
6.3. Limitations of the model
In our simulations, we have not considered the effect of an ISM density gradient on the structure and appearance of our model wind bubble. The observed Hα emission around the Bubble Nebula appears brighter towards the north and gets fainter to the south (see Fig. 1), indicating that there is a density gradient across the nebula. This is also expected on physical grounds because BD+60°2522 photoionizes the surrounding ISM and photoevaporates the molecular cloud to the north. The dense photoevaporated gas expands into the lower-density surroundings, creating a density gradient.
Arthur & Hoare (2006) studied wind bubbles expanding into a stratified medium, both with and without stellar motion. In particular, their models H and I considered a star with a strong wind moving through a stratified medium, and they showed that the density gradient induces higher-velocity flows (up to 30 km s−1) around the wind bubble from the apex to the tail than are obtained from constant-density calculations. The density gradient that is present in the H II region around the Bubble Nebula could be responsible for the discrepancy between our synthetic (Hα and IR) emission maps and observations at the sides of the bubble around 90° from the apex. We will explore this in more detailed future calculations.
6.4. Importance of winds for particle acceleration and non-thermal processes
The winds of massive stars generate fast shocks that can accelerate cosmic rays (CR), possibly making a significant contribution to the total high-energy CR production rate in our Galaxy (Casse & Paul 1980; Cesarsky & Montmerle 1983; Aharonian et al. 2019). It is important to identify systems where this can be tested, and where non-thermal emission from relativistic particles can most easily be detected. The ideal systems have large mass-loss rates with high-velocity winds, but compact nebula surrounded by a relatively dense ISM with a strong magnetic field. The wind properties maximise the number of accelerated particles, and the ISM properties maximise the interaction of relativistic particles with matter, producing non-thermal radiation. Searches for non-thermal emission have for this reason concentrated on runaway stars producing bright bow shocks, where the geometry of the system is well constrained. So far, the only detection is non-thermal radio emission from the bow shock of the star BD+43°3654 (Benaglia et al. 2010), an O4 supergiant (Comerón & Pasquali 2007) whose wind drives a large and well-studied bow shock. Searches for gamma rays (H.E.S.S. Collaboration et al. 2018) and non-thermal X-rays (Toalá et al. 2017b) have so far only produced upper limits. We consider NGC 7635 to be a good target for non-thermal emission given the large mass-loss rate and wind velocity of the driving star, together with the dense surrounding ISM. BD+60°2522 is not as extreme as BD+43°3654 in terms of wind mass-loss rate, but their wind velocities are comparable, and the size and density of their nebulae are similar. This suggests BD+60°2522 is a good target for further radio observations. These would test whether BD+43°3654 is somehow unique or if many bow shocks produce measurable synchrotron emission.
6.5. X-ray emission resolution study
Figure 14 is a plot of the unabsorbed flux (erg cm−2 s−1) and luminosity (erg s−1) of the simulated nebula as it evolves in time (Myr) for the whole 1b simulation (solid lines) and for a lower-resolution (Nzones = 768 × 512) simulation (dashed lines) with the same velocity and ISM density as 1b. This plot compares the two simulations, which differ in resolution, to show that the results are only weakly dependent on spatial resolution.
 |
Fig. 14. Synthetic X-ray unabsorbed flux (erg cm−2 s−1) and luminosity (erg s−1) plot of the Bubble Nebula as it evolves in time (Myr). Seven X-ray bands simulated from soft to hard X-rays, including 0.1 keV, 0.2 keV, 0.5 keV, 1 keV, 2 keV, 5 keV, and 10 keV. Solid lines are from the 1b simulation discussed in this paper, dashed lines are from a lower-resolution (Nzones = 768 × 512) simulation. Mechanical luminosity of the stellar wind (i.e. energy input rate to the wind bubble) is Lw = 3.6 × 1036 erg s−1 (seen as the black line in both plots). |
7. Conclusions
This paper presents the beginning of a project to investigate thermal emission from stellar wind bubbles. For the first time we present simultaneous predictions for X-ray, optical, and infrared emission maps from simulations. Two-dimensional hydrodynamic simulations of the stellar wind bubble NGC 7635 (Bubble Nebula) have been run to model the interaction of the wind of the central star with the ISM. We chose stellar and ISM parameters appropriate for comparison with the Bubble Nebula. The models cover a range of possible ISM densities of 50−200 cm−3 and stellar velocities of 20−40 km s−1. One calculation (1b) was found to be the most plausible candidate to compare with observational data.
The Monte-Carlo radiative-transfer code TORUS was used to post-process this simulation to generate synthetic 24 μm emission-map predictions to compare with observational Spitzer MIPS data. We also post-process the simulation with a ray-tracing projection code to generate synthetic Hα emission maps to compare with HST observational data. The main result is that we find the same morphological spherical bubble shape with similar quantitative aspects. The synthetic maps predict a maximum brightness similar to that from the observations and agree that the maximum brightness is at the apex of the bow shock. The Hα and 24 μm synthetic emission maps are therefore quantitatively and qualitatively consistent with the observational data and bow shock interpretation. The maps therefore suggest that the star is moving at 20 km s−1 into an ISM with n ∼ 100 cm−3, at an angle of 60° with respect to the line of sight.
The ray-tracing projection code was also used to produce soft (0.3−2 keV) and hard (2−10 keV) X-ray emission-map predictions of what an X-ray satellite could observe. These emission maps show that the majority of X-ray emission occurs in the wake behind the star and not with the bow shock itself. The unabsorbed soft X-rays are in the region of ∼1032−1033 erg s−1. However, due to extinction from the ISM in between the nebula and the observer, no X-rays below 0.5 keV can be seen and X-rays in the range (0.5−2 keV) are significantly attenuated. The hard X-rays are faint, ∼1030−1031 ergs s−1, and maybe too faint for current X-ray instruments to successfully observe.
Results from the simulations and the synthetic emission maps allow us to conclude that the O star creates a bow shock as it moves through the ISM and in turn creates an asymmetric bubble visible in optical and infrared wavelengths, and predicted to be visible in X-rays. The Bubble Nebula does not appear to be unique, but does have a favourably oriented and very dense bow shock. Extinction means UV and soft X-rays will be hard to detect and therefore it is difficult to constrain the mixing between the hot and cold plasma. However, the dense ISM surrounding BD+60°2522 together with its strong wind make it a good candidate for detecting non-thermal emission at other wavelengths.
Acknowledgments
SG is funded by a Dublin Institute for Advanced Studies student scholarship. We acknowledge the SFI/HEA Irish Centre for High-End Computing (ICHEC) for the provision of computational facilities and support to run the PION simulations of the Bubble Nebula (project dsast018b). JM acknowledges funding from a Royal Society-Science Foundation Ireland University Research Fellowship (14/RS-URF/3219). TJH is funded by an Imperial College Junior Research Fellowship. VVG acknowledges support from the Russian Science Foundation grant No. 14-12-01096. SG wishes to thank Associate Professor Ben Thornber, from the School of Aerospace, Mechanical and Mechatronic Engineering at the Univeristy of Syndey, for very useful discussions on the concept of vortex shedding. SG and JM also wish to thank Norbert Langer for hosting discussion visits to Bonn. The authors are grateful to the referee, J. Toalá, for constructive suggestions that improved the manuscript. The Darwin Data Analytic system at the University of Cambridge, operated by the University of Cambridge High Performance Computing Service on behalf of the STFC DiRAC HPC Facility (www.dirac.ac.uk) was used to run TORUS to simulate the emission maps. This equipment was funded by a BIS National E-infrastructure capital grant (ST/K001590/1), STFC capital grants ST/H008861/1 and ST/H00887X/1, and DiRAC Operations grant ST/K00333X/1. DiRAC is part of the National E-Infrastructure. Some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. This work has made use of the NASA/IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration, and the SIMBAD database, operated at CDS, Strasbourg, France. This work also has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
References
- Aharonian, F., Yang, R., & de Oña Wilhelmi, E. 2019, Nat. Astron., in press DOI: 10.1038/s41550-019-0724-0 [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
- Arthur, S. J., & Hoare, M. G. 2006, ApJS, 165, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Avila, R., Levay, Z., Christian, C., et al. 2016, High-Level Science Products for the Mikulski Archive for Space Telescopes, http://archive.stsci.edu/prepds/heritage/bubble/ [Google Scholar]
- Baranov, V. B., Krasnobaev, K. V., & Kulikovskii, A. G. 1970, Akademiia Nauk SSSR Doklady, 194, 41 [NASA ADS] [Google Scholar]
- Benaglia, P., Romero, G. E., Martí, J., Peri, C. S., & Araudo, A. T. 2010, A&A, 517, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blaauw, A. 1993, in Massive Stars: Their Lives in the Interstellar Medium, eds. J. P. Cassinelli, & E. B. Churchwell, ASP Conf. Ser., 35, 207 [NASA ADS] [Google Scholar]
- Boroson, B., McCray, R., Clark, O., et al. 1997, ApJ, 478, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Casse, M., & Paul, J. A. 1980, ApJ, 237, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J., McCray, R., & Weaver, R. 1975, ApJ, 200, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Cesarsky, C. J., & Montmerle, T. 1983, Space Sci. Rev., 36, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Christopoulou, P. E., Goudis, C. D., Meaburn, J., Dyson, J. E., & Clayton, C. A. 1995, A&A, 295, 509 [NASA ADS] [Google Scholar]
- Chu, Y. H., Gruendl, R. A., & Guerrero, M. A. 2003, in Revista Mexicana de Astronomia y Astrofisica vol. 27, eds. J. Arthur, & W. J. Henney, Rev. Mex. Astron. Astrofis. Conf. Ser., 15, 62 [NASA ADS] [Google Scholar]
- Comerón, F., & Kaper, L. 1998, A&A, 338, 273 [NASA ADS] [Google Scholar]
- Comerón, F., & Pasquali, A. 2007, A&A, 467, L23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Conti, P. S., & Alschuler, W. R. 1971, ApJ, 170, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Deharveng-Baudel, L. 1973, in Liege International Astrophysical Colloquia, eds. L. Remy-Battiau, J. M. Vreux, & D. H. Menzel, 18, 357 [Google Scholar]
- Doroshenko, V. T. 1972, Soviet Ast., 16, 402 [NASA ADS] [Google Scholar]
- Doroshenko, V. T., & Grachev, N. I. 1972, Soviet Ast., 16, 87 [NASA ADS] [Google Scholar]
- Draine, B. T. 2003, ApJ, 598, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Dufour, R. J. 1989, Rev. Mexicana Astron. Astrofis., 18, 87 [NASA ADS] [Google Scholar]
- Esteban, C., Mesa-Delgado, A., Morisset, C., & García-Rojas, J. 2016, MNRAS, 460, 4038 [NASA ADS] [CrossRef] [Google Scholar]
- Falle, S. A. E. G. 1991, MNRAS, 250, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Falle, S. A. E. G., Komissarov, S. S., & Joarder, P. 1998, MNRAS, 297, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, A., Jones, T. W., Ryu, D., & Gaalaas, J. B. 1996, ApJ, 460, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Freyer, T., Hensler, G., & Yorke, H. W. 2003, ApJ, 594, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Freyer, T., Hensler, G., & Yorke, H. W. 2006, ApJ, 638, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia-Segura, G., Langer, N., & Mac Low, M.-M. 1996a, A&A, 316, 133 [Google Scholar]
- Garcia-Segura, G., Mac Low, M.-M., & Langer, N. 1996b, A&A, 305, 229 [NASA ADS] [Google Scholar]
- Georgelin, Y. M., & Georgelin, Y. P. 1976, A&A, 49, 57 [NASA ADS] [Google Scholar]
- Gies, D. R. 1987, ApJS, 64, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Gull, T. R., & Sofia, S. 1979, ApJ, 230, 782 [NASA ADS] [CrossRef] [Google Scholar]
- Gvaramadze, V. V., Langer, N., & Mackey, J. 2012, MNRAS, 427, L50 [NASA ADS] [CrossRef] [Google Scholar]
- Gvaramadze, V. V., Alexashov, D. B., Katushkina, O. A., & Kniazev, A. Y. 2018, MNRAS, 474, 4421 [NASA ADS] [CrossRef] [Google Scholar]
- H. E. S. S. Collaboration (Abdalla, H., et al.) 2018, A&A, 612, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haid, S., Walch, S., Seifried, D., et al. 2018, MNRAS, 478, 4799 [NASA ADS] [CrossRef] [Google Scholar]
- Harries, T. J. 2000, MNRAS, 315, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Harries, T. J. 2015, MNRAS, 448, 3156 [NASA ADS] [CrossRef] [Google Scholar]
- Haworth, T. J., Glover, S. C. O., Koepferl, C. M., Bisbas, T. G., & Dale, J. E. 2018, New A Rev., 82, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Henney, W. J., Arthur, S. J., de Colle, F., & Mellema, G. 2009, MNRAS, 398, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Hester, J. J., Scowen, P. A., Sankrit, R., et al. 1996, AJ, 111, 2349 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D., & Prinja, R. K. 1989, ApJS, 69, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Hummer, D. G. 1994, MNRAS, 268, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Icke, V. 1973, A&A, 26, 45 [NASA ADS] [Google Scholar]
- Israel, F. P., Habing, H. J., & de Jong, T. 1973, A&A, 27, 143 [NASA ADS] [Google Scholar]
- Kaper, L., van Loon, J. T., Augusteijn, T., et al. 1997, ApJ, 475, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Keppens, R., Tóth, G., Westermann, R. H. J., & Goedbloed, J. P. 1999, J. Plasma Phys., 61, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kurosawa, R., Harries, T. J., Bate, M. R., & Symington, N. H. 2004, MNRAS, 351, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1993, Phys. Scr. Vol. T, 47, 110 [Google Scholar]
- Leitherer, C. 1988, ApJ, 326, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, L. A., Krumholz, M. R., Bolatto, A. D., Prochaska, J. X., & Ramirez-Ruiz, E. 2011, ApJ, 731, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1999, A&A, 344, 282 [NASA ADS] [Google Scholar]
- Lynds, B. T., & Oneil, Jr., E. J. 1983, ApJ, 274, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Mac Low, M.-M., van Buren, D., Wood, D. O. S., & Churchwell, E. 1991, ApJ, 369, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Mackey, J. 2012, A&A, 539, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mackey, J., Gvaramadze, V. V., Mohamed, S., & Langer, N. 2015, A&A, 573, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mackey, J., Haworth, T. J., Gvaramadze, V. V., et al. 2016, A&A, 586, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Matzner, C. D. 2002, ApJ, 566, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Maucherat, A., & Vuillemin, A. 1973, A&A, 23, 147 [NASA ADS] [Google Scholar]
- McKee, C. F., van Buren, D., & Lazareff, B. 1984, ApJ, 278, L115 [NASA ADS] [CrossRef] [Google Scholar]
- McLean, B. J., Greene, G. R., Lattanzi, M. G., & Pirenne, B. 2000, in AstronomicalData Analysis Software and Systems IX, eds. N. Manset, C. Veillet, & D. Crabtree, ASP Conf. Ser., 216, 145 [NASA ADS] [Google Scholar]
- Mesa-Delgado, A., & Esteban, C. 2010, MNRAS, 405, 2651 [NASA ADS] [Google Scholar]
- Meyer, D. M.-A., Mackey, J., Langer, N., et al. 2014, MNRAS, 444, 2754 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, D. M. A., Mignone, A., Kuiper, R., Raga, A. C., & Kley, W. 2017, MNRAS, 464, 3229 [NASA ADS] [CrossRef] [Google Scholar]
- Mohamed, S., Mackey, J., & Langer, N. 2012, A&A, 541, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moore, B. D., Walter, D. K., Hester, J. J., et al. 2002a, AJ, 124, 3313 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B. D., Hester, J. J., Scowen, P. A., & Walter, D. K. 2002b, AJ, 124, 3305 [NASA ADS] [CrossRef] [Google Scholar]
- Neckel, T., Klare, G., & Sarcander, M. 1980, Bulletin d’Information du Centre de Donnees Stellaires, 19, 61 [NASA ADS] [Google Scholar]
- Osterbrock, D. E. 1989, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (University Science Books: Mill Valley, CA) [CrossRef] [Google Scholar]
- Rauw, G., De Becker, M., & Vreux, J.-M. 2003, A&A, 399, 287 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, M. J., Menten, K. M., Zheng, X. W., Brunthaler, A., & Xu, Y. 2009, ApJ, 705, 1548 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., Young, E. T., Engelbracht, C. W., et al. 2004, ApJS, 154, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, H., & Pittard, J. M. 2013, MNRAS, 431, 1337 [NASA ADS] [CrossRef] [Google Scholar]
- Rosen, A. L., Lopez, L. A., Krumholz, M. R., & Ramirez-Ruiz, E. 2014, MNRAS, 442, 2701 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative processes in astrophysics (New York: John Wiley& Sons, Inc.) [Google Scholar]
- Schönrich, R., Binney, J., & Dehnen, W. 2010, MNRAS, 403, 1829 [NASA ADS] [CrossRef] [Google Scholar]
- Sharpless, S. 1959, ApJS, 4, 257 [Google Scholar]
- Sota, A., Maíz Apellániz, J., Morrell, N. I., et al. 2014, ApJS, 211, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Toalá, J. A., & Arthur, S. J. 2011, ApJ, 737, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Toalá, J. A., & Arthur, S. J. 2016, MNRAS, 463, 4438 [NASA ADS] [CrossRef] [Google Scholar]
- Toalá, J. A., & Arthur, S. J. 2018, MNRAS, 478, 1218 [NASA ADS] [CrossRef] [Google Scholar]
- Toalá, J. A., Oskinova, L. M., González-Galán, A., et al. 2016, ApJ, 821, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Toalá, J. A., Marston, A. P., Guerrero, M. A., Chu, Y. H., & Gruendl, R. A. 2017a, ApJ, 846, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Toalá, J. A., Oskinova, L. M., & Ignace, R. 2017b, ApJ, 838, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Townsley, L. K., Broos, P. S., Garmire, G. P., et al. 2018, ApJS, 235, 43 [NASA ADS] [CrossRef] [Google Scholar]
- van Buren, D. 1986, ApJ, 306, 538 [NASA ADS] [CrossRef] [Google Scholar]
- van Buren, D., Noriega-Crespo, A., & Dgani, R. 1995, AJ, 110, 2914 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R. 1973, AJ, 78, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Walch, S., Girichidis, P., Naab, T., et al. 2015, MNRAS, 454, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Wareing, C. J., Zijlstra, A. A., & O’Brien, T. J. 2007, ApJ, 660, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, R., McCray, R., Castor, J., Shapiro, P., & Moore, R. 1977, ApJ, 218, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Wiersma, R. P. C., Schaye, J., & Smith, B. D. 2009, MNRAS, 393, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. E., & Joy, A. H. 1952, ApJ, 115, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Zubko, V., Dwek, E., & Arendt, R. G. 2004, ApJS, 152, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Peculiar transverse velocity of BD+60°2522
Gaia DR2 (Gaia Collaboration et al. 2018) places BD+60°2522 at the distance of 2.7 ± 0.2 kpc and provides highly precise proper-motion measurements for this star (see Table A.1). Using the solar galactocentric distance of 8.0 kpc, the circular Galactic rotation velocity of 240 km s−1 (Reid et al. 2009), and the solar peculiar motion (U⊙, V⊙, W⊙) = (11.1, 12.2, 7.3) km s−1 (Schönrich et al. 2010), we calculated the peculiar transverse velocity 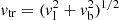 , where vl and vb are the peculiar velocity components of the star along the Galactic longitude and latitude, respectively. For the error calculation, both the uncertainties in the proper motion and the distance measurements were considered. The resulting velocities along with the input data are given in Table A.1.
, where vl and vb are the peculiar velocity components of the star along the Galactic longitude and latitude, respectively. For the error calculation, both the uncertainties in the proper motion and the distance measurements were considered. The resulting velocities along with the input data are given in Table A.1.
Summary of astrometric and kinematic data on BD+60°2522.
Appendix B: Ray-tracing of 2D simulations
Here we describe a ray-tracing method to calculate synthetic images from such simulations. The simplest approach is to take the 2D grid of zones, consider a ray going through each zone-centre in turn, and then produce an image with the same number of pixels as the grid has zones. The grid is then extended in the z-direction to include all rays that intersect some part of the 3D volume created by rotating the 2D plane about the axis of symmetry.
Consider a ray travelling through Cartesian space (x, y, z), in the plane y = R0 (where R0 is the distance from the axis of symmetry), with an angle θ with respect to the positive z-axis, and with the equation x = (z − z0) tan θ. We can place the R − z plane as the upper-half plane x = 0, y ≥ 0. This can be done without loss of generality such that the ray passes through (x, y, z) = (0, R0, z0), corresponding to a grid zone with coordinates (R0, z0).
We now calculate the path of the ray when projected onto the R − z plane. An infinitesimal line element is dℓ = cosθdz + sinθdx and so
Using the equation of the line above, dx = dztanθ, we can get
Therefore, the geometric scaling factor is
Furthermore, it is easy to show that the ray traces a parabola in the R − z plane:
If we approximate our data as a piecewise constant, with each zone having constant values of each variable, then we can analytically integrate the emissivity along a ray segment through a zone, i, as
where the ray enters the zone at R = R− and leaves at R = R+. The sign ambiguity is resolved by considering that the ray is always moving to smaller R on the inward trajectory and larger R on the outward one, but in both cases the emissivity adds to the quantity being integrated.
All Tables
All Figures
 |
Fig. 1. Spitzer 24 μm (left-hand panel) and DSS-II red band (right-hand panel) images of the Bubble Nebula and its surroundings. The arrow shows the direction of motion of BD+60°2522 (marked by a circle) as suggested by the Gaia DR2 proper motion and parallax measurements (with 1σ uncertainties shown by dashed arrows). The orientation and the scale of the images are the same. A white spot in the Spitzer image is due to a saturation effect. |
| In the text | |
 |
Fig. 2. From left to right: snapshot after one crossing time from each simulation in Table 2. The top half shows log10 plots of the gas density (g cm−3) profile of the gas, and the bottom half shows log10 plots of the temperature profile of the gas with white being of higher temperature (K) than black. The star is at the origin. Labels of the different models are shown in white on each panel. |
| In the text | |
 |
Fig. 3. Top half: log10 plots of the gas density (g cm−3) profile of the gas, and bottom half: log10 plots of the temperature profile of the gas with white being of higher temperature (K) than black. These plots are from the 1b simulation data. The star is at the origin. From left to right: simulation after 0.5, 1, and 2 crossing times, respectively. |
| In the text | |
 |
Fig. 4. Top half plane: gas velocity (km s−1) with yellow being of higher velocity than dark purple. Bottom half plane: Mach number of the gas with black being of higher Mach number than white. These are from the 1b simulation at the same three time-steps as the density/temperature plots in Fig. 3. |
| In the text | |
 |
Fig. 5. Top two images: synthetic Hα emission maps of the bow shock on a logarithmic colour scale (in units of erg cm−2 s−1 arcsec−2), generated from the 1b simulation for viewing angles of 45° and 60°. Both synthetic images are generated after 0.2135 Myr of evolution. The coordinates are in parsecs relative to the position of the star. The black cross shows the position of the ionizing star. Bottom plot: HST Hα (656 nm) image of the Bubble Nebula. |
| In the text | |
 |
Fig. 6. Top two images: synthetic infrared emission maps of the bow shock on a logarithmic colour scale (in units of MJy ster−1), generated from the 1b simulation for viewing angle angles of 45° and 60°. Both synthetic images are generated after 0.2135 Myr of evolution and smoothed to the angular resolution of Spitzer of 6 arcsec. The coordinates are in parsecs relative to the position of the star. The black cross shows the position of the ionizing star. Bottom plot: Spitzer 24 μm image of the Bubble Nebula. |
| In the text | |
 |
Fig. 7. A snapshot (after 1 crossing time) from the 1b simulation was used to generate synthetic images of the Bubble Nebula at angles from 0°−90° with respect to the direction of stellar motion. First row: 24 μm emission, second row: Hα emission, third row: soft X-ray emission, and fourth row: hard X-ray emission. From left to right, the angles are 0°, 15°, 30°, 45°, 60°, 75°, and 90°. For the Hα and X-ray image we plot 1° and 89° instead of 0° and 90° because of technical limitations. Each image is centred on the star (black cross) and is roughly 5 × 5 parsec. |
| In the text | |
 |
Fig. 8. Ratio of the stand-off distance RSO to the radius of the bow shock at an angle of 90° from the direction of the stellar motion, as a function of viewing angle, θ. The observed ratio is taken from the Spitzer image and simulation results are from the synthetic infrared images. |
| In the text | |
 |
Fig. 9. Synthetic soft X-ray (0.3–2 keV) emission maps of the simulated nebula (unabsorbed). Both images have coordinates in parsecs relative to the position of the star (black cross), and the scale is in erg cm−2 s−1 arcsec−2. Both images are generated from the 1b simulation, after 0.2135 Myr of evolution and are smoothed to the angular resolution of XMM-Newton EPIC cameras (6 arcsec). |
| In the text | |
 |
Fig. 10. As in Fig. 9, but for hard X-rays (2–10 keV). |
| In the text | |
 |
Fig. 11. Left-hand panel: synthetic X-ray unabsorbed flux (erg cm−2 s−1) and luminosity (erg −1) plot of the Bubble Nebula as it evolves in time (Myr). Seven X-ray bands simulated from soft to hard X-rays, including 0.1 keV, 0.2 keV, 0.5 keV, 1 keV, 2 keV, 5 keV, and 10 keV. Right-hand panel: absorbed flux (erg cm−2 s−1) and luminosity (erg s−1) plot showing that the 0.1 keV–1 keV X-ray bands get absorbed by the ISM. Mechanical luminosity of the stellar wind (i.e. energy input rate to the wind bubble) is |
| In the text | |
 |
Fig. 12. DEM profile of the simulated nebula (unabsorbed) from the 1b simulation, after 0.2135 Myr of evolution. |
| In the text | |
 |
Fig. 13. Mean temperature (K) of the simulated nebula (unabsorbed) as it evolves in time (Myr) |
| In the text | |
 |
Fig. 14. Synthetic X-ray unabsorbed flux (erg cm−2 s−1) and luminosity (erg s−1) plot of the Bubble Nebula as it evolves in time (Myr). Seven X-ray bands simulated from soft to hard X-rays, including 0.1 keV, 0.2 keV, 0.5 keV, 1 keV, 2 keV, 5 keV, and 10 keV. Solid lines are from the 1b simulation discussed in this paper, dashed lines are from a lower-resolution (Nzones = 768 × 512) simulation. Mechanical luminosity of the stellar wind (i.e. energy input rate to the wind bubble) is Lw = 3.6 × 1036 erg s−1 (seen as the black line in both plots). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.