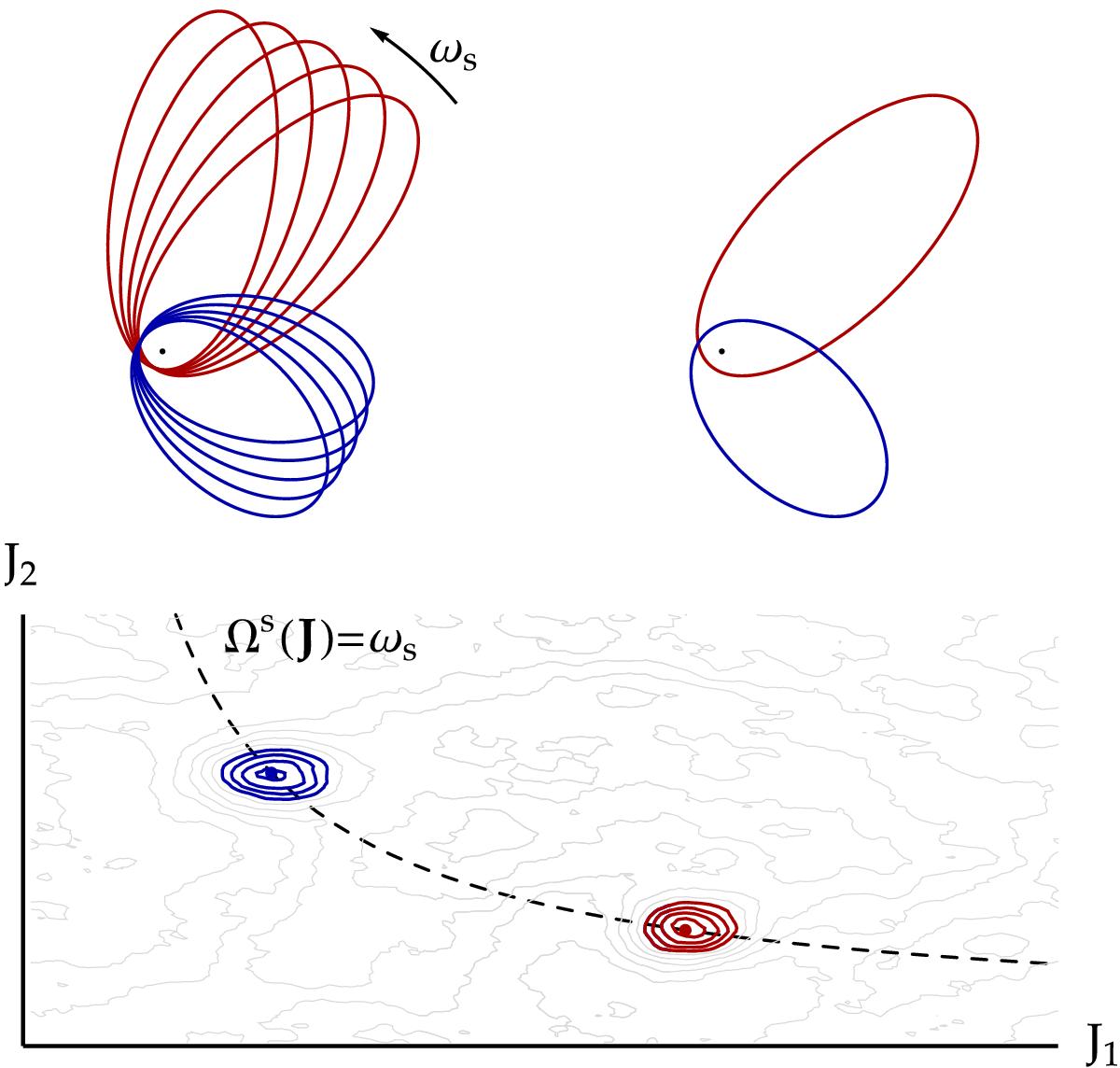
Illustration of the resonance condition appearing in the degenerate inhomogeneous Balescu-Lenard Eq. (58). Top-left: a set of two resonant orbits precessing at the same frequency ω_s. Top-right: in the rotating frame at frequency ω_s in which the two orbits are in resonance. Bottom: fluctuations of the system’s DF in action space caused by finite-N effects and showing overdensities for the blue and red orbits. The dashed line correspond to the critical resonant line in action space along which the resonance condition Ω^s(J) = ω_s is satisfied. The two set of orbits satisfy a resonance condition for their precession frequencies, and uncorrelated sequences of such interactions lead to a secular diffusion of the system’s orbital structure following Eq. (58). Such resonances are non local in the sense that the resonant orbits need not be close in action space nor in position space. As emphasised in Sect. 6.1 for axisymmetric razor-thin discs, symmetry enforces , so that the two orbits are caught in the same resonance.