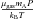| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201424008 | |
| Published online | 14 April 2015 | |
Critical core mass for enriched envelopes: the role of H2O condensation
1 Center for Space and Habitability & Physikalisches Institut, Universitaet Bern, 3012 Bern, Switzerland
e-mail: julia.venturini@space.unibe.ch
2 Observatoire de Besançon, 41 avenue de l’Observatoire, 25000 Besançon, France
3 Department of Earth and Planetary Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, 113-0033 Tokyo, Japan
Received: 16 April 2014
Accepted: 3 February 2015
Context. Within the core accretion scenario of planetary formation, most simulations performed so far always assume the accreting envelope to have a solar composition. From the study of meteorite showers on Earth and numerical simulations, we know that planetesimals must undergo thermal ablation and disruption when crossing a protoplanetary envelope. Thus, once the protoplanet has acquired an atmosphere, not all planetesimals reach the core intact, i.e. the primordial envelope (mainly H and He) gets enriched in volatiles and silicates from the planetesimals. This change of envelope composition during the formation can have a significant effect on the final atmospheric composition and on the formation timescale of giant planets.
Aims. We investigate the physical implications of considering the envelope enrichment of protoplanets due to the disruption of icy planetesimals during their way to the core. Particular focus is placed on the effect on the critical core mass for envelopes where condensation of water can occur.
Methods. Internal structure models are numerically solved with the implementation of updated opacities for all ranges of metallicities and the software Chemical Equilibrium with Applications to compute the equation of state. This package computes the chemical equilibrium for an arbitrary mixture of gases and allows the condensation of some species, including water. This means that the latent heat of phase transitions is consistently incorporated in the total energy budget.
Results. The critical core mass is found to decrease significantly when an enriched envelope composition is considered in the internal structure equations. A particularly strong reduction of the critical core mass is obtained for planets whose envelope metallicity is larger than Z ≈ 0.45 when the outer boundary conditions are suitable for condensation of water to occur in the top layers of the atmosphere. We show that this effect is qualitatively preserved even when the atmosphere is out of chemical equilibrium.
Conclusions. Our results indicate that the effect of water condensation in the envelope of protoplanets can severely affect the critical core mass, and should be considered in future studies.
Key words: planets and satellites: atmospheres / planets and satellites: formation / planets and satellites: interiors / planets and satellites: composition
© ESO, 2015
1. Introduction
The metallicity of the giant planets in our solar system shows that they are considerably enriched in heavy elements compared to the solar composition (Guillot & Gautier 2014, and references therein). Even though this change of composition with respect to solar could be a consequence of an eroding core (Guillot et al. 2004; Wilson & Militzer 2012), numerical studies have shown that the change of composition induced by the disruption of planetesimals in the envelope of growing giant planets can be considerable (Podolak et al. 1988; Mordasini et al. 2006; Iaroslavitz & Podolak 2007; Fortney et al. 2013). For instance, a protoplanet with a core of 6 M⊕ can have an envelope dense enough to completely destroy icy planetesimals of up to 100 km before they reach the core (Baraffe et al. 2006). The dominant size of planetesimals at the time planet formation takes place might even be smaller, as is suggested by studies that incorporate the collisional fragmentation in the evolution of planetesimals (Inaba et al. 2003; Kobayashi et al. 2011; Guilera et al. 2014). This means that a considerable enrichment can readily occur even for protoplanets with small cores. Therefore, the contribution of metals (compounds heavier than H and He) to the total mass of the envelope of a protogiant planet already starts to be relevant in the early stages of growth. We show in this paper that taking into account this early enrichment of the envelope can have a significant effect on the subsequent growth and evolution of a planet.
The aforementioned studies (Podolak et al. 1988; Mordasini et al. 2006; Iaroslavitz & Podolak 2007) have focused on computing the trajectory of planetesimals on their way to the core, as well as their mass and energy deposition in the envelope due to thermal ablation and disruption. However, the resultant metallicity was not included in the thermochemical properties of the envelope, i.e. it was not taken into account to solve the internal structure equations.
The opposite focus was given by Hori & Ikoma (2011; hereafter HI11). In the first part of their work, they assumed a given envelope metallicity and incorporated a consistent equation of state and opacity tables to solve the static internal structure equations; here static means that the only source of energy considered is the release of gravitational energy due to the accretion of planetesimals. This implies that the energy release due to the contraction of the envelope (which necessarily provides a varying luminosity with time) is neglected.
Static internal structure calculations allow for the computation of the critical core mass, which corresponds to the maximum mass of the core able to sustain an envelope in hydrostatic equilibrium (Perri & Cameron 1974; Mizuno et al. 1978; Mizuno 1980). Analytical work by Stevenson (1982) and Wuchterl (1993; for fully radiative and fully convective envelopes, respectively) show that when the core becomes critical, the mass of the envelope is of the same order of magnitude as the core mass. This means that at the critical point the self-gravity of the envelope becomes important. Further, quasi-static studies of planet growth (Bodenheimer & Pollack 1986; Pollack et al. 1996) show that when the energy release due to the contraction of the envelope is taken into account, rapid gas accretion takes place when Mcore ≈ Menv, that is, when the core is around criticality. Since the timescale of gas accretion at critical mass is much shorter than that required to build a critical core, reaching criticality is synonymous with being able to form a giant planet. Hence, the relevance of the critical core mass concept in the core-accretion scenario.
The enrichment of the envelope due to planetesimal disruption causes a reduction of the critical core mass because of the increase in mean molecular weight of the envelope (first pointed out by Stevenson 1982), but more importantly, because of the reduction of the adiabatic temperature gradient that takes place when chemical reactions among volatile molecules occur (HI11). In this work we have included the effect of water latent heat and studied its effect on the critical core mass.
The role played by the condensation of water (i.e. the formation of clouds) in the Earth’s atmosphere is well known among the climate community (see e.g. Pierrehumbert 2010, Chap. 2). When vapour rises above the condensation level, water droplets form and in the phase transition process latent heat is released. This modifies the energy budget of the atmosphere, causing the pressure-temperature profile to switch from dry to moist adiabat. We will show that this change in the temperature profile can actually lead to a severe reduction of the critical core mass.
The paper is organized as follows. The basic equations, assumptions and numerical scheme are described in Sect. 2. The opacities and equation of state implemented are described in Sects. 3 and 4, respectively. Section 5 is devoted to the results concerning the effect on the critical core mass due to water condensation in an envelope of uniform metallicity. In Sect. 6 we justify our assumptions concerning the use of an ideal equation of state and uniform metallicity. We also discuss the dependence of our results on the boundary conditions, and the implications of our results on the diversity of planets that can be formed. Finally, Sect. 7 summarizes our main conclusions.
2. Numerical approach
We have developed a code that solves the static internal structure equations assuming spherical symmetry and a constant luminosity (or constant accretion rate of solids when specified). For better numerical performance, the equations are written as a function of v = r3/Mr, where r is the radial coordinate of the planet, and Mr the mass enclosed inside a sphere of radius r,
![\begin{eqnarray} &&\label{hydeq} \frac{{\rm d}P}{{\rm d}v}= - G \rho_{\rm gas} \bigg(\frac{M_{\text{r}}}{v^2}\bigg)^{2/3} [3 - 4 \pi \rho_{\rm tot} v]^{-1} \\[2mm] && \label{mass_cons} \frac{{\rm d}M_{{r}}}{{\rm d}v}= 4\pi \rho_{\rm tot} M_{{r}} [3 - 4 \pi \rho_{\rm tot} v]^{-1} \\[2mm] &&\label{transport} \frac{{\rm d}T}{{\rm d}v}=\frac{T}{P}\frac{{\rm d}P}{{\rm d}v}\nabla , \end{eqnarray}](/articles/aa/full_html/2015/04/aa24008-14/aa24008-14-eq8.png) where P is the pressure, ρtot the total density and ρgas the gas density1, T the temperature, and G the gravitational constant. The gradient in Eq. (3) is defined as
where P is the pressure, ρtot the total density and ρgas the gas density1, T the temperature, and G the gravitational constant. The gradient in Eq. (3) is defined as 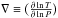 . For the radiative case it is equal to
. For the radiative case it is equal to 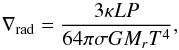 (4)σ being the Stefan-Boltzmann constant, κ the opacity, and L the luminosity. For the convective transport ∇ is the gradient evaluated at constant entropy (adiabatic gradient):
(4)σ being the Stefan-Boltzmann constant, κ the opacity, and L the luminosity. For the convective transport ∇ is the gradient evaluated at constant entropy (adiabatic gradient): 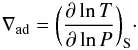 (5)Convection occurs if ∇ad< ∇rad (the Schwarzschild criterion).
(5)Convection occurs if ∇ad< ∇rad (the Schwarzschild criterion).
Parameters used in all simulations.
The three differential equations are solved using a fourth-order Runge-Kutta algorithm. Two boundary conditions are specified at the top of the gaseous envelope (Tout and Pout) and one at the core (core mass or core density). The outer boundary conditions and the position of the planet are listed in Table 1. The total mass of the planet (MP) is defined as the mass inside the Bondi or Hill radius, whichever is smaller. They are, respectively, 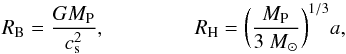 (6)where cs is the sound speed and a the semi-major axis of the planet.
(6)where cs is the sound speed and a the semi-major axis of the planet.
Two different schemes to solve the above equations were implemented. In the first approach (used for the results shown in Fig. 8) the core mass (Mcore), the core density (ρcore), and the accretion rate of solids (Ṁcore) are given. Then the total mass of the planet (MP) is computed through an iterative process. A first value for the total mass is assumed and the structure equations are solved starting from the outer boundary and stopping at the core. The total mass is iterated until the mass of the core is reached within a given tolerance. Since in this approach the core radius (Rcore) and core mass (Mcore) are known a priori, the luminosity of the envelope is given by the release of the gravitational potential energy of the planetesimals, 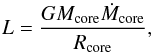 (7)which implies that the energy is assumed to be deposited at the surface of the core. This is not consistent with our assumption of the disruption of the planetesimals occurring before they reach the core, but to do this properly, a varying luminosity in the envelope should be implemented, computed from the mass and energy deposition of the disrupted planetesimals. This will be done in a future work. However, for the cases of highly enriched envelopes (the focus of this work), the envelopes are fully convective (see Sect. 6.1), and hence, the thermal structure is independent on L. Thus, the precise value of L is not expected to affect our results.
(7)which implies that the energy is assumed to be deposited at the surface of the core. This is not consistent with our assumption of the disruption of the planetesimals occurring before they reach the core, but to do this properly, a varying luminosity in the envelope should be implemented, computed from the mass and energy deposition of the disrupted planetesimals. This will be done in a future work. However, for the cases of highly enriched envelopes (the focus of this work), the envelopes are fully convective (see Sect. 6.1), and hence, the thermal structure is independent on L. Thus, the precise value of L is not expected to affect our results.
In the second approach, the total mass of the planet and total luminosity are given. The value of Ṁcore is not known a priori because Mcore is not known. In this case the integration is also performed from the surface to the core, but the difference is that now MP is known, so no iteration is needed. The integration stops when ρr (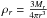 ) is equal to the density of the core. The mass inside this radius is then defined as Mcore. The independent variable v in Eqs. (1)–(3) was introduced with the purpose of making it possible for the integration to stop exactly at ρr = ρcore. Otherwise, an interpolation in r would be required to obtain the mass at which ρr = ρcore. This last method is the one used in all the results shown in this work, except for those shown in Figs. 2, 3, and 8. Its advantage resides in the fact that no iterations are needed to obtain Mcore, which makes the scheme more stable for core masses close to the critical core mass.
) is equal to the density of the core. The mass inside this radius is then defined as Mcore. The independent variable v in Eqs. (1)–(3) was introduced with the purpose of making it possible for the integration to stop exactly at ρr = ρcore. Otherwise, an interpolation in r would be required to obtain the mass at which ρr = ρcore. This last method is the one used in all the results shown in this work, except for those shown in Figs. 2, 3, and 8. Its advantage resides in the fact that no iterations are needed to obtain Mcore, which makes the scheme more stable for core masses close to the critical core mass.
3. Opacities
Most of the opacity tables available in the literature are for solar metallicity. In order to study the effect of enrichment of the envelopes of protoplanets in a consistent way, we must use opacity tables for all ranges of metallicities. In this work we implement, as in HI11, gas opacity tables for all metallicities computed by Ferguson (based on the calculations of Alexander & Ferguson 1994) and Rosseland mean opacities of dust calculated by Semenov et al. (2003).
The Ferguson opacities assume scaled solar abundances (the relative abundances of the various elements is assumed solar, but the total abundance is scaled). The range of validity of the tables is for T ≥ 1000 K and −2 ≤ log R ≤ 6, where 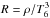 , ρ being the gas density and T6 the temperature in million kelvin. Whenever the envelope values of temperature and density lie outside these ranges, the tables are extrapolated. Using a linear or constant extrapolation does not affect our results.
, ρ being the gas density and T6 the temperature in million kelvin. Whenever the envelope values of temperature and density lie outside these ranges, the tables are extrapolated. Using a linear or constant extrapolation does not affect our results.
As in HI11, we define the total opacity as 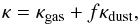 (8)where κgas and κdust are the Rosseland mean opacity of gas and dust grains, respectively. The reduction/enhancement factor f includes the unknown values of the size of the dust grains in protoplanetary envelopes. In principle, the grains released by the ablation of planetesimals could increase the dust opacity with respect to the disc values, but the grains could also rapidly coagulate and hence increase their size, reducing in this way the opacity of the dust (Podolak 2003; Movshovitz & Podolak 2008; Movshovitz et al. 2010; Mordasini 2014; Ormel 2014).
(8)where κgas and κdust are the Rosseland mean opacity of gas and dust grains, respectively. The reduction/enhancement factor f includes the unknown values of the size of the dust grains in protoplanetary envelopes. In principle, the grains released by the ablation of planetesimals could increase the dust opacity with respect to the disc values, but the grains could also rapidly coagulate and hence increase their size, reducing in this way the opacity of the dust (Podolak 2003; Movshovitz & Podolak 2008; Movshovitz et al. 2010; Mordasini 2014; Ormel 2014).
In this work we adopt values of f = 1, since the effect of other reduction/enhancement values was already investigated by HI11. Using f = 10 hardly affects the critical core values with respect to using f = 1, and using lower values of f reduces the critical core mass even further. Therefore, setting f = 1 provides upper values for the critical core mass as far as the effect of dust opacity is concerned. Although these are upper limits, we will show that they become increasingly smaller with increasing metallicity.
In Sect. 6.2.2 we make use of the Freedman et al. (2008) opacities, which are detailed computed opacity tables for H and He and solar metallicity. We use these opacities to illustrate the effect of different opacity tables in the case of envelopes with extended radiative regions. All other results were computed making use of the opacity given by Eq. (8).
4. Equation of state
Beyond suitable opacities, an enriched envelope also needs to be described with a proper equation of state. It turns out that, to the best of our knowledge, there is no equation of state available for an arbitrary metallicity which also takes into account the degeneracy pressure of free electrons. The latter effect plays an important role in the more massive objects. One equation of state (EOS) accounting for these effects is the Saumon et al. (1995) EOS for a mixture of H and He (hereafter SCVH).
In this work we make use of the publicly available software Chemical Equilibrium with Applications (CEA) developed by NASA (Gordon et al. 1994). This program solves the chemical equilibrium equations for an arbitrary gas mixture. It assumes an ideal gas equation of state for the mixture, but takes into account the proper dissociation and ionization temperatures of each compound formed. Although CEA does not consider the pressure of degenerate electrons (which translates into an overestimate of central temperature and pressure for massive objects), we have used it to study the effect of condensation on the envelope structure.
The CEA package has the advantage of containing a database of ~1000 compounds, and that it considers condensed species, like H2O in solid and liquid phase2. The latent heat of phase transitions is included in the calculation of the thermodynamical quantities. For an explanation on the calculation of the density when condensation takes place, see Sect. 4.2. For a discussion on the condensation of species other than water, see Sect. 6.4.
The program can be customized to use as input the pressure, temperature, and composition in molar or mass fraction. In our simulations, the envelope is assumed to be made of hydrogen, helium, carbon and oxygen. We take a fixed C/O mass ratio of 0.24:0.69, which corresponds to Comet Halley (Mumma et al. 1993), a value that we assume is representative of the early solar system. The metallicity, Z, is defined as 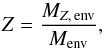 (9)where MZ, env is the mass of elements heavier than H and He in the envelope, and Menv the total mass of the envelope.
(9)where MZ, env is the mass of elements heavier than H and He in the envelope, and Menv the total mass of the envelope.
Carbon and oxygen constitute the Z-component of the envelope; Z is a free parameter in our study, and is assumed to be uniform throughout the envelope. This assumption will be justified in Sect. 6. The mass abundance of H and He (X and Y, respectively) are computed as a weighted average between the solar and Comet Halley values, as in HI113.
The CEA package gives as an output the density, mean molecular weight, internal energy, specific heat, and logarithmic derivatives of certain thermodynamical quantities from which it is possible to compute the adiabatic gradient. The adiabatic gradient (defined by Eq. (5)) is an important quantity because, together with the radiative gradient (Eq. (4)), it determines the type of heat transport present in the envelope. Given its relevance to our study of the structure of planetary envelopes, we present in the next section how we determine this gradient.
4.1. Adiabatic gradient with CEA
One of the outputs of CEA is the log-derivative of the volume with respect to temperature at constant pressure. From this quantity and the specific heat at constant pressure, the adiabatic gradient can easily be calculated.
From the implicit function theorem, it follows 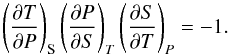 (10)From the definition of the adiabatic gradient, we have
(10)From the definition of the adiabatic gradient, we have 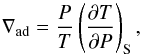 (11)and then
(11)and then 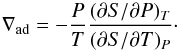 (12)From the definition of the heat capacity at constant pressure (CP), we have
(12)From the definition of the heat capacity at constant pressure (CP), we have 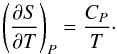 (13)Deriving the Gibbs free energy (G = U − TS + PV) with respect to T and P it can be shown that
(13)Deriving the Gibbs free energy (G = U − TS + PV) with respect to T and P it can be shown that 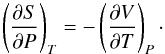 (14)And finally, substituting with the log-derivatives and knowing that the mixture is an ideal gas, we obtain
(14)And finally, substituting with the log-derivatives and knowing that the mixture is an ideal gas, we obtain 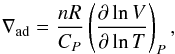 (15)where n is the number of gas moles and R the gas constant.
(15)where n is the number of gas moles and R the gas constant.
4.2. Condensed species in CEA: density calculation
In CEA the mean molecular weight is defined as 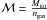 (Mtot being the total mass of the system and ngas the number of moles of the gas), which is not the mean molecular weight of the gas in the case when condensation occurs.
(Mtot being the total mass of the system and ngas the number of moles of the gas), which is not the mean molecular weight of the gas in the case when condensation occurs.
It can be shown that the molecular weight of the gas satisfies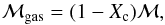 (16)where Xc is the mass fraction of the condensed species, a quantity readily computed with CEA using Eqs. (2.3b) and (2.4a) of Gordon et al. (1994). Since the density computed by the program satisfies
(16)where Xc is the mass fraction of the condensed species, a quantity readily computed with CEA using Eqs. (2.3b) and (2.4a) of Gordon et al. (1994). Since the density computed by the program satisfies 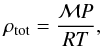 (17)and the gas density must satisfy4
(17)and the gas density must satisfy4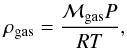 (18)the gas density is readily obtained from
(18)the gas density is readily obtained from 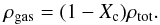 (19)This density enters in the hydrostatic equilibrium equation because the pressure gradient is exerted just by the gas5. For the mass conservation equation, the density that includes the total mass, i.e. ρtot, is the one that must be used (see Sect. 2).
(19)This density enters in the hydrostatic equilibrium equation because the pressure gradient is exerted just by the gas5. For the mass conservation equation, the density that includes the total mass, i.e. ρtot, is the one that must be used (see Sect. 2).
 |
Fig. 1 Critical core mass as a function of metallicity. Green line: results of the “wholly polluted” case of Fig. 2 in HI11; red line: this work, restricted case; blue line: this work, non-restricted case (see main text for the definitions of the different cases). |
5. Critical core mass for different uniform metallicities
5.1. Comparison with HI11
The static internal structure equations were solved for a range of uniform envelope metallicities between 0.1 and 0.95, and a wide range in protoplanetary mass. The planet location, boundary conditions and envelope composition were taken as in HI11 (see Table 1), in order to be able to perform comparison tests. The equality in composition means that we set the same X and Y for a given Z (see Sect. 4), and that we allowed the same 13 species in gaseous phase (H, He, O, C, H2, O2, CO2, H2O, CH4, H+, O−, and e−) to be formed when chemical equilibrium is computed. Hereafter we will refer to this case as the “restricted” case.
A comparison with HI11 is shown in Fig. 1 (green versus red curve). The agreement between the two calculations is remarkable, especially considering that a different way of computing the EOS was used in the different works; for example, HI11 did not use CEA, but computed the thermodynamical quantities partly from the NIST tables.
 |
Fig. 2 Profile of the gas mean molecular weight of the envelope as a function of its temperature for Z = 0.7 when Mcore = Mcrit,NR(Z = 0.7). Solid lines: non-restricted case. Dotted lines: restricted case. We note that in the the non-restricted case, μgas decreases in the outer layers (i.e. low temperature values; see main text). The difference between both profiles at high temperatures is a consequence of a difference in the pressure-temperature profiles (see Fig. 5). |
5.2. Inclusion of H2O condensation
The blue line in Fig. 1 shows the results for the same setup, but in this case no restriction is imposed in the compounds that can be formed when the chemical equilibrium is computed. Hence, CEA makes use of its chemical database, and allows ~50 compounds to be formed from the same proportion of H, He, C, and O as before. It also allows condensed species to be formed. We will refer to this case, where no restriction is imposed in the species that can be formed at equilibrium, as the “non-restricted” case.
Regardless of the case, the most remarkable feature shown by Fig. 1 is the drastic reduction of the critical core mass with increasing Z. Comparing now the non-restricted with the restricted case, it can be seen that the reduction of Mcrit with increasing Z is larger for the first case. Namely, for Z = 0.7, the difference in critical core mass between the restricted and the non-restricted case, is of ΔMcrit ≈ 2 M⊕, and since the critical mass of the non-restricted case is Mcrit,NR ≈ 0.2 M⊕, the relative difference is 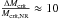 .
.
In order to understand the difference in Mcrit between the restricted and non-restricted cases, we plot the gas mean molecular weight and adiabatic gradient as a function of the envelope temperature for Z = 0.7. For both profiles we assume the same core mass, which corresponds to the critical core of the non-restricted case for Z = 0.7. The purpose of this choice is to ensure the same core gravity. This, in turn, ensures that the differences observed in the atmospheric profiles originate from the chemistry and not from a difference in initial pressure gradients. The results are shown in Figs. 2 and 3. A decrease in the gas mean molecular weight and in the adiabatic gradient in the outer layers are observed when comparing the non-restricted with the restricted case (solid and dotted lines, respectively). By analysing the composition in the outer layers of the envelope of the non-restricted case, we find that the 13 species assumed by HI11 are indeed the dominating ones in the CEA calculations as well, as is shown in Fig. 4 for Z = 0.76. However, we also find that large amounts of water are being condensed in the coldest layers of the envelope of the non-restricted case, which does not occur in the restricted case (see Fig. 4). By observing Figs. 2 and 4, it can be seen that the remarkable difference in mean molecular weight in the outer part of the envelope between the non-restricted and restricted cases lasts as long as H2O coexist in both vapour and solid phase. This is a consequence of what was stated in Sect. 4.2: the larger the mass fraction of condensed species, the lower μgas (see Eq. (16)).
 |
Fig. 3 Profile of the adiabatic gradient of the envelope as a function of its temperature for Z = 0.7. The core mass and labels are set just as in Fig. 2. We note that there is a strong reduction of the adiabatic gradient in the outer layers of the envelope (i.e. low temperature values) in the non-restricted case (see main text). The difference between both profiles at high temperatures has the same explanation as in the previous figure. |
 |
Fig. 4 Envelope composition as a function of temperature for Z = 0.2, 0.4, and 0.7. MP = 0.29 M⊕ for all profiles (planetary mass when Mcore (Z = 0.7) = Mcrit (Z = 0.7)). Left column: non-restricted case. Right column: restricted case. In the non-restricted case water (solid lines) coexists in vapour phase (blue curve), solid phase (cyan curve), and even liquid phase (violet curve) in the case of Z = 0.7. Except H2O in solid and liquid phase, the other 13 species shown here were considered in HI11. In the restricted case, water only exists in vapour phase. |
Water condensation in the outer layers of the envelope modifies the molecular weight and adiabatic gradient. In order to assess which of the two effects plays a role in reducing Mcrit, we performed the following test. We computed the envelope profile for Z = 0.7 and MP = 0.29 M⊕ using μ of the restricted case and ∇ad of the non-restricted case. The profile follows exactly the same profile as the non-restricted case. Therefore, the reduction of the adiabatic gradient is what causes the smaller critical mass.
A straightforward way to understand why the reduction of the adiabatic gradient tends to lower the critical core mass is as follows. Given a fixed core mass (as in the cases shown in Fig. 3), the gravity is fixed, and therefore the pressure gradient (Eq. (1)) is fixed. The thermal profile is established by Eq. (3). From the ideal gas equation we have 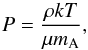 (20)where μ is the mean molecular weight of the gas mixture and mA the atomic mass unit. If the envelope is convective and ∇ad diminishes, the temperature for a given radius diminishes. Hence, in order to keep the same pressure gradient, the density of the envelope has to increase. Since the envelope mass is the integral of the density, if the density increases, the envelope mass increases as well. The more massive an envelope gets for a given core mass, the more likely it is that the core becomes critical (see Fig. 7).
(20)where μ is the mean molecular weight of the gas mixture and mA the atomic mass unit. If the envelope is convective and ∇ad diminishes, the temperature for a given radius diminishes. Hence, in order to keep the same pressure gradient, the density of the envelope has to increase. Since the envelope mass is the integral of the density, if the density increases, the envelope mass increases as well. The more massive an envelope gets for a given core mass, the more likely it is that the core becomes critical (see Fig. 7).
As stated before, the formation of other compounds in the non-restricted case does not play a role, since the 13 compounds assumed by HI11 are the most abundant ones when chemical equilibrium is computed. However, taking into account the condensation changes the picture considerably, as illustrated in Fig. 5. In this figure, the pressure-temperature profile for Z = 0.7 for the non-restricted case, and the restricted case without condensation of water, are shown. Superposed, we plot the case where the composition is restricted, but where water is allowed to condense (hereafter we will refer to this case as “restricted-with-water-condensation”). The vapour pressure for this last case is also plotted. From this figure it is clear that H2O is being condensed from the top of the atmosphere until T = 282 K, since in this range of temperature the vapour pressure is equal to the saturation pressure of water (green dotted line, given by the Clausius-Clapeyron relation). As the temperature increases from the top of the envelope to the surface of the core, there is a location from which water can only exist in vapour phase. For the mass abundance of water when Z = 0.7, this happens at T = 282 K. If the abundance of water is lower than in the Z = 0.7 case, the shift between “moist” and “dry” adiabat (as they are usually called in atmospheric studies; see e.g. Pierrehumbert 2010, chap. 2) occurs for lower temperatures (see Fig. 6) because the vapour pressure is proportional to the mole fraction of vapour (law of partial pressures). This depends on the amount of water present in the outer layers of the envelope, which increases with metallicity, as can be seen in Fig. 4.
 |
Fig. 5 Pressure as a function of temperature for Z = 0.7 and MP = 0.29 M⊕. In the case where water is allowed to condense (orange lines), the vapour pressure follows the Clausius-Clapeyron curve until T = 282 K, which defines the loci where the vapour and liquid phases, and vapour and ice phases, can co-exist (green-dotted line). Hence, in these range of temperatures, water is being condensed, and the pressure-temperature profiles follow the moist adiabat. |
 |
Fig. 6 Pressure as a function of temperature for Z = 0.2, 0.4, and 0.7. MP = 0.29 M⊕ for all cases. The dotted-black lines correspond to regions where the envelope is radiative. This region is extremely small in the case of Z = 0.2 profile. |
Returning to Fig. 5, it can be seen that owing to water condensation, 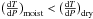 in the coldest layers of the atmosphere. This is the cause of the strong reduction in the adiabatic gradient of the non-restricted case shown in Fig. 3.
in the coldest layers of the atmosphere. This is the cause of the strong reduction in the adiabatic gradient of the non-restricted case shown in Fig. 3.
Figure 5 can also be used to understand why condensation of water reduces Mcrit. If we look at the envelope profile from the surface of the core to the top of the atmosphere, when we compare the non-restricted with the restricted case, we see that at the pressure (equivalent to atmospheric height) where water starts to condense, the temperature of the non-restricted case does not drop as much as in the restricted case. Since latent heat is released in the transition vapour-solid and vapour-liquid, the envelope gets warmer when condensation of water takes place. The release of latent heat is what makes the difference between the moist and dry profiles. It modifies the pressure-temperature profile remarkably, making it possible to have a much higher pressure for a given temperature, which translates to a much higher envelope density and, therefore, to a considerable reduction of critical core mass.
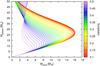 |
Fig. 7 Total mass of the planet as a function of the mass of the core for different uniform metallicities and L = 1027 erg/s. Here the composition of the envelope corresponds to the non-restricted case (see main text). The highest Z shown is 0.5 for aesthetic reasons. |
5.3. Increasing envelope metallicity
In the previous section, we confirmed an earlier finding of Hori & Ikoma (2011) that an enrichment of the envelope leads to a reduction of the mass of the core at which gas can be accreted in a runaway fashion. In addition, we pointed out that when the enrichment leads to condensation, the reduction of the critical core mass is even greater (see Figs. 1 and 7) and can actually become the dominant effect.
To pose this enrichment problem in an evolutionary context, it is interesting to see what would be the total mass of a planet that becomes critical from a gradual enriching process, and how enriched the envelope becomes when reaching the critical core mass. In order to tackle these questions, we performed the following calculation. We assumed that a core grows to 6 M⊕ as a result of the accretion of planetesimals that reach the core without being destroyed in the envelope. In other words, all the planetesimals reach the core without undergoing any physical disruption or thermal ablation until the core acquires a mass of 6 M⊕. Once Mcore = 6 M⊕, we assume that the protoplanet has acquired an atmosphere sufficiently massive to completely disrupt the infalling planetesimals before they reach the core. This choice of 6 M⊕ as a threshold is completely arbitrary. It corresponds to the case of icy planetesimals with a radius of 100 km or less (Baraffe et al. 2006). However, as we explained in Sect. 1, planetesimals could be smaller. In that case, full disruption could already occur for planets with a smaller core; this is analysed at the end of this section.
 |
Fig. 8 Envelope mass as a function of the mass of solids contained in the planet (MZ). The mass of the core is fixed at 6 M⊕. An accretion rate of solids of 3 × 10-6M⊕/yr was assumed, which corresponds to a luminosity of 1027 erg/s (the same used in all the other results). The decrease of Menv for low metallicities (shown in the inset) is due to the increase in the gas opacity and to the fact that for these cases of low Z, a radiative zone develops in the outer layers. For Z> 0.1, the structures are almost fully convective. Therefore, the increase in κgas does not play a role, the dominant effect is the increase in Menv due to the inclusion of Z in the EOS. |
For the case of a fixed core mass of 6 M⊕ as the core threshold for completely disrupting planetesimals in the envelope7, we solved the internal structure equations, and let the envelope metallicity grow gradually until the planet becomes critical. The results are shown in Fig. 8, where the total mass of the envelope as a function of the total mass of the heavy elements acquired by the planet is plotted. If initially, when the full disruption of the planetesimals starts, Z = 0.02 (Z⊙), then the envelope is able to accrete planetesimals until reaching a metallicity of ≈0.48, which represents an envelope mass content of heavy elements of 1.4 M⊕. At this point the core becomes critical, i.e. no further solution to the static internal equations can be found. According to the standard view of the core-accretion model, the subsequent evolution of the protoplanet would imply the accretion of large amounts of gas in a runaway fashion (Mizuno 1980; Bodenheimer & Pollack 1986), making it possible for the protoplanet to become a giant planet soon after the protoplanet becomes critical. The results found here suggest that after the disruption of planetesimals in the envelope begins, the planetary envelope does not need to grow much in order for the planet to become critical. In the particular case of the simulations shown here, a protoplanet with Mcore = 6 M⊕ needs to accrete 1.4 M⊕ of H and He and the same amount of heavy elements to become critical. A consistent evolutionary study, where the metallicity is computed from the accretion rate of solids, will be done in the future to be able to account for the timescales to trigger the runaway of gas when the envelope enrichment is taken into account.
A similar analysis of the enrichment process can also be drawn for cores smaller than 6 M⊕ by just making use of Fig. 1. If we assume, for instance, that the core stops growing at 1 M⊕, then the envelope will get gradually enriched until the core becomes critical at Z ≈ 0.62 (see blue curve in Fig. 1). The corresponding mass of the planet in this critical case is MP = 1.5 M⊕, which means that in this case the mass of heavy elements in the envelope when Mcrit is reached would be ≈0.3 M⊕, and the mass of H–He ≈0.2. M⊕. It would be interesting, also for cases like this where Mcrit is low and the envelopes are heavily polluted, to study the subsequent evolution. The fate of these small but highly enriched critical protoplanets is not easy to assess a priori, since the gravity of the core would not be large enough to trigger gas runaway (Ikoma et al. 2000; Hori & Ikoma 2010). In principle, if runaway of gas accretion cannot be reached, the planet would continue its growth by slowly contracting and therefore, also slowly, accreting gas. If a runaway of gas is not triggered during the lifetime of the gas disc, the result could be the formation of a super-Earth, heavily enriched planet, which would be a very interesting scenario, given the increasing amount of Earth and super-Earth sized planets that are being found (Petigura et al. 2013), and the inference of a very enriched composition for these types of objects (Valencia et al. 2013; Gillon et al. 2012; Nettelmann et al. 2011). A more extended discussion concerning the different type of planets that could be formed when the enrichment of the envelope is considered is presented in Sect. 6.5.
5.4. Dependence on the boundary conditions and semi-major axis
All the results shown before were for a planet whose boundary conditions are those stated in Table 1. In order to check the range in boundary conditions for which condensation can lead to a significant reduction of the critical mass, we perform the following test. We set the outer temperature and pressure of the planet for a given position in the protoplanetary disc making use of the following simple disc model (see e.g. Armitage 2010), ![\begin{eqnarray} \label{Tout} T_{\text{out}} &=& T_0 \left(\frac{a_0}{a}\right)^{1/2} \\[2mm] \label{Pout} P_{\text{out}} &=& P_0 \left(\frac{a_0}{a}\right)^{3}, \end{eqnarray}](/articles/aa/full_html/2015/04/aa24008-14/aa24008-14-eq119.png) where a0, T0, and P0 are the standard boundary conditions used in all previous results, i.e. those given in Table 1. In this section we will refer to the simulations that use boundary conditions at a = a0 as the “reference case”.
where a0, T0, and P0 are the standard boundary conditions used in all previous results, i.e. those given in Table 1. In this section we will refer to the simulations that use boundary conditions at a = a0 as the “reference case”.
The results for the critical core mass as a function of metallicity for different semi-major axes (with the corresponding outer temperature and pressure given by Eqs. (21) and (22)) are shown in Fig. 9 where the results for 2 AU ≤ a ≤ 8.5 AU are shown superposed with the reference cases. The qualitative similarity of the different curves with the reference case where water condenses (blue curve) or with the one where water is not allowed to condense (yellow curve) provides a hint to whether water condensation is taking place or not for the different semi-major axes considered. We note that for a = 2 AU, Tout is always too high for water condensation to take place. For all the other curves condensation of water takes place at some point. The start of the condensation corresponds to the change in the slope of the curves. A particular case takes place for a = 3.0 AU, where a valley in Mcrit occurs for 0.865 <Z< 0.905 (see Fig. 9). The drop in Mcrit corresponds to the start of condensation at Z = 0.865. The same happens for a = 3.2 AU at Z = 0.75 and for a = 3.5 AU at Z = 0.55. The surprising thing about the 3 AU case is that for even higher metallicities, water condensation ceases. The reason for this is that when the minimum in the “valley” of Mcrit is reached, the metallicity has increased so much that there is no more free H2 at the top of the envelope. In other words, H2 starts to be the limiting reactant, so increasing Z (that is, adding more C and O) does not lead to the formation of more water. Instead, more CO2 starts to be formed in this region of the valley (where dMcrit/dZ> 0). At Z = 0.905, the amount of water formed is low enough to make the vapour pressure lower than the saturation vapour pressure for all the P, T values of the envelope. Therefore, for Z ≥ 0.905, the profiles again follow the dry adiabat, water condensation no longer takes place.
Despite this particular case of a = 3 AU, the general trend observed in Fig. 9 is that H2O condensation occurs more readily for planets located further out in the disc. However, while the trend is clear, the exact behaviour is more difficult to predict. For instance, the behaviour of Mcrit changes considerably for 3 ≤ a ≤ 4 AU, but remains very similar for the cases of a = 4, 5.2 and 8.5 AU. To have a better insight on the difference in Mcrit among these cases, we analyse profiles for Z = 0.7 and MP = 0.29 M⊕ for all the different cases shown in Fig. 9. The results of changing a and the corresponding Pout and Tout (as dictated by Eqs. (21) and (22)) are shown in Fig. 108. As expected from the behaviour of Mcrit at Z = 0.7 in Fig. 9, the cases of a ≤ 3.2 AU follow the dry adiabat, whereas the cases of a ≥ 3.5 AU correspond to the moist adiabat. Since there are several factors that could be playing a role in shaping these profiles, we study the effect of changing just one boundary condition and fixing all the others with the standard values (i.e. those given in Table 1) in Figs. 11a, b.
 |
Fig. 9 Critical core mass as a function of metallicity for the specified semi-major axis and corresponding boundary conditions given by Eqs. (21) and (22). Dashed lines correspond to the reference cases (boundary conditions at a = 5.2 AU) plotted in Fig. 1: the yellow curve is the restricted case (i.e. without condensation of water), and the blue curve the non-restricted case (where water condenses). For all the new cases (solid lines) water is allowed to condense. The only case where water does not condense for any value of Z is for a = 2 AU. |
 |
Fig. 10 Pressure-temperature profiles for different positions in the disc for Z = 0.7 and MP = 0.29 M⊕. Tout and Pout correspond to those given by Eqs. (21) and (22) for the semi-major axis specified in the labels. |
 |
Fig. 11 Pressure-temperature profiles for different positions in the disc for Z = 0.7 and MP = 0.29 M⊕. a) Pout given by Eq. (22) for the labelled semi-major axis, but Tout= 150 K (reference case, see Table 1) for all the profiles; b) Tout given by Eq. (21) for the labelled semi-major axis, but Pout corresponds to the reference case for all the profiles. |
Figure 11a shows the effect of changing the outer pressure, Pout. That is, the Pout used to solve the internal structure equations is the one given by Eq. (22), but all the other boundary conditions correspond to the standard case. From this figure we infer that the critical core mass is reduced when Pout increases, since the pressure in the envelope is always higher for higher Pout. This can be understood as follows: from Eqs. (10), (11), and (13) it can be inferred that 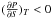 . Hence, at the outer boundary of the planet, the entropy decreases for larger Pout. For these profiles of Z = 0.7, the envelopes are fully convective, so the entropy of the envelope is fixed by Pout, Tout. On the other hand, the temperature at the surface of the core is the same for all the cases because they correspond to the same planetary mass9. Therefore, the pressure at the surface of the core also has to be larger for larger Pout (see Wuchterl 1993; Ikoma et al. 2001, for a discussion on the sensitivity of the critical core mass with the outer boundary conditions for fully convective envelopes).
. Hence, at the outer boundary of the planet, the entropy decreases for larger Pout. For these profiles of Z = 0.7, the envelopes are fully convective, so the entropy of the envelope is fixed by Pout, Tout. On the other hand, the temperature at the surface of the core is the same for all the cases because they correspond to the same planetary mass9. Therefore, the pressure at the surface of the core also has to be larger for larger Pout (see Wuchterl 1993; Ikoma et al. 2001, for a discussion on the sensitivity of the critical core mass with the outer boundary conditions for fully convective envelopes).
In Fig. 11b, the only parameter we change is Tout. The first remarkable observation is that if Tout is larger than the temperature given by the Clausius-Clapeyron relation at P0, no condensation of water occurs. In our particular disc model this happens for a ≤ 3.5 AU. Then, the change in Tout is what gives rise to the two types of profiles observed in the general case (Fig. 10, where all boundary conditions are modified consistently with Eqs. (21) and (22)). The general trend of changing Tout is that Mcrit diminishes when Tout diminishes. This can be explained by drawing similar arguments to those in Fig. 11a. From Eq. (13), we know that 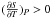 , and hence, at the outer boundary of the planet the profiles with lowest Tout are the ones with lowest entropy. Since the temperature at the surface of the core is the same for all the profiles, the profiles with lowest entropy will have the largest central pressure (because
, and hence, at the outer boundary of the planet the profiles with lowest Tout are the ones with lowest entropy. Since the temperature at the surface of the core is the same for all the profiles, the profiles with lowest entropy will have the largest central pressure (because 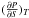 is always negative). Consequently, regarding Tout, the further the planet is from the star, the smaller Mcrit will be.
is always negative). Consequently, regarding Tout, the further the planet is from the star, the smaller Mcrit will be.
We have found, therefore, that the change of Pout and Tout provoke opposite effects in the change of the critical core mass as we move further out in the disc. This is what makes Figs. 9 and 10 difficult to interpret. Looking back at the profiles of Fig. 10, we see that the case of a = 3.5 AU is the only one in which the profile is moist owing to the increase in Pout (compared to the reference case), which places the pressure-temperature curve on the left side of the Clausius-Clapeyron curve. For the cases of a = 2, 3, and 3.2 AU, the increase in Pout that actually occurs with respect to Fig. 11b is not enough to switch the profiles from dry to moist. Hence, in these cases, what makes these profiles follow the dry adiabat (i.e. water does not condense) is the increase in Tout with respect to the reference case.
Concerning the cases of a = 4, 5.2, and 8.5 AU, since (Tout, Pout) always reside in the region where H2O is in solid phase (or in the solid-vapour transition), the profiles follow the moist adiabat. Because of the opposite effects on Mcrit that arise when Pout and Tout decreases as the planet is further from the star, the profiles in these cases are very similar.
We can conclude then that the decrease in Mcrit with increasing metallicity due to the condensation of water in the envelope of protoplanets is robust with respect to changing boundary conditions. The exact location in the disc where H2O starts to condense will depend on the disc model and stellar spectral type, but for distances larger than this, the value of Mcrit will be almost independent of the location of the planet in the disc, as Fig. 9 shows for a ≥ 4 AU.
6. Discussion
6.1. Validity of the uniform metallicity assumption
Although the disruption of planetesimals is more likely to occur in the densest regions close to the surface of the core, the final fate of the metals is not clear a priori. The heavy elements could sink slowly to the core, or get well mixed in the H–He envelope, depending upon the strength of convection and the solubility of the material in the H–He envelope. In Sect. 5.2 we assumed that the metallicity was uniform throughout the envelope, and this may not always be the case. Nevertheless, if the envelope is fully convective, this assumption is a reasonable one. This was the case for all envelopes with Z ≥ 0.45. However, it could also be that the envelopes were fully convective because a uniform Z was assumed. It is important to know if this is the case or not, because if the enrichment does not reach the lowest temperature region of the envelope, no water will be present for temperatures lower than its condensation temperature, and then the condensation of water will not take place (at least for the boundary conditions considered in this work).
To evaluate how well mixed the envelope will be, we performed the following test. We assumed that the enrichment of material occurs at temperatures higher than the condensation temperature of water. Hence, the outermost part of the atmosphere (T<Tcond) is assumed not to be enriched and have a solar composition, whereas the innermost part (T>Tcond) is assumed to have a uniform Z (higher than solar)10. If with this two-layer model atmosphere the envelopes are still fully convective, then a global mixing of material will occur and therefore the envelopes will acquire, eventually, a uniform composition.
Since this initial set-up implies a considerable jump in mean molecular weight at T = Tcond (where the boundary between the solar composition and the high-Z region occurs), the Ledoux criterion for stability against convection should be used (Kippenhahn et al. 2013, Chap. 6), instead of the Schwarschild criterion. Therefore, for our calculation the radiative zones are those for which 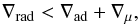 (23)where
(23)where 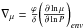 ,
, 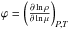 , and
, and 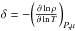 . For an ideal gas ϕ = δ = 1.
. For an ideal gas ϕ = δ = 1.
Because of the finite jump of μ at T = Tcond, ∇μ diverges at this temperature. Hence, to compute the composition gradient, we assumed the same simple prescription used in stellar evolution models to treat the problem of overshooting (Alibert et al. 1999), i.e. we assumed that the change of μ is effective within a distance 0.2H of the radius at which T = Tcond (H is the scale height of the atmosphere at T = Tcond), and we assume ∇μ to be constant in this interval.
For the sake of consistency, we use, for the solar composition layer, the same opacities we used before (i.e., the Ferguson gas opacities), but with a Z = Z⊙. It is important to note that for the range of temperatures of this predominantly H–He region, the Ferguson opacities are extrapolated and, therefore, its values are probably not very accurate. We will discuss the effect of varying this opacity in the next section.
 |
Fig. 12 Planetary mass as a function of the core mass given by solving the internal structure equations for pure H–He envelopes. The red curve uses CEA for the EOS and the blue uses SCVH. Boundary conditions are those from Table 1. ΔMcrit ≈ 1.4 M⊕ |
 |
Fig. 13 Map of the density difference between CEA and SCVH EOS as a function of temperature and pressure, for pure H–He composition. Superposed are shown the profiles of the envelope for the two different EOS for MP = 18.7 M⊕ (planetary mass for which Mcore = Mcrit when CEA is used for the EOS). All units are in cgs. |
The results of the test show that the critical envelopes of the standard, non-restricted case remain fully convective when a layer of solar composition is considered for T<Tcond, provided that Z ≥ 0.6. This means that for these highly enriched cases, the assumption of uniform Z was a good one, and hence that condensation of water is likely to take place, at least for the opacities considered here.
Finally, whatever the fate of the water droplets (depending on the dynamics of the atmosphere and the miscibility of the forming droplets), if the envelope remains convective up to the layer where H2O can condense, it is likely that the continuous saturated state of H2O can sustain a moist-adiabatic pressure-temperature profile11. This will make it possible for the critical core mass to reduce considerably, as Fig. 1 shows. Therefore, for highly enriched envelopes (which should not be so rare during the formation scenario, as shown by Fortney et al. 2013), the effect of condensation of water can play an important role.
6.2. Role of microphysics
6.2.1. Ideal gas assumption
Since in this work an ideal gas equation of state was assumed for the structure calculation, it is relevant to have an estimate of the error introduced by neglecting the degeneracy of the gas at high pressure. For this reason, a comparative test for H–He envelopes implementing CEA and SCVH EOS was performed.
The results of the planetary mass as a function of the core mass (obtained by solving the internal structure equations) are shown in Fig. 12. From this figure, it follows that the differences in planetary mass for a given core mass start to be noticeable when they reach the critical core mass. The critical core masses are 14.18 M⊕ and 15.58 M⊕, for the CEA and SCVH cases, respectively, which implies a relative error of ~10% in the computation of the critical core mass. Even by performing the same test with other boundary conditions or opacities, we find that the error is never larger than ~12%12.
To have a better insight into the effect of degeneracy, we show, in Fig. 13, a map of the difference in density obtained using CEA and SCVH EOS, as a function of (log P, log T). Overlapped are the profiles of the envelope obtained for MP = MP(Mcrit,CEA) for the CEA and SCVH cases (under the same conditions as in Fig. 12). Although the difference between the CEA and SCVH profiles is not easily distinguishable, it can be seen that the CEA profile overestimates the central temperature and pressure, leading, as a consequence, to an also overestimated central density. The difference in central density between these two profiles is of 0.1 g/cm3. The higher density obtained using CEA translates into a higher envelope mass, and hence, a smaller critical core mass, as Fig. 12 shows. We have shown that the change in critical core mass induced by considering the enrichment of the envelope (and in particular, the enrichment by condensable species) is orders of magnitude larger than the changes produced by including non-ideal effects. This justifies our assumption in assessing the effect of condensation on the determination of the critical mass.
6.2.2. Remarks on the opacity
It should be kept in mind that the Ferguson opacities for the gas are extrapolated in the coldest layers of the envelopes computed in this work. In principle this does not affect the profile of envelopes with high and uniform metallicity since they are fully convective, but it could affect the structure for the test described in Sect. 6.1. For instance, if instead of using the extrapolated Ferguson opacities for the H–He region, we used the Freedman et al. (2008) tables, the envelope would become radiative in the H–He region because the Freedman opacity values are lower for the cold regions than the ones extrapolated from Ferguson. This means that the adiabatic gradient becomes larger than the radiative one. In this case, the mixture of the material would probably not occur in the whole envelope. However, because of the use of reduced opacities in the outermost part of the atmosphere, the critical core mass would still remain very low (Ikoma et al. 2000; Hubickyj et al. 2005; Hori & Ikoma 2010), as suggested by Fig. 14. It is interesting to note that even if condensation of water does not take place, the critical core masses shown in Fig. 1 will not be significantly affected.
 |
Fig. 14 Red line: profile for two-layer atmosphere, but using Freedman opacities in the H–He region instead of the Ferguson opacities used in all other results of the paper. Blue line: Z = 0.7 (and uniform in the envelope) where water is allowed to condense. The resemblance of both profiles, compared to the restricted profile of Fig. 5, suggests that for the red curve the corresponding critical core mass will also be very low. Solid lines stand for convective regions and dotted for radiative ones. |
6.3. Chemical equilibrium assumption
There are two processes that can preclude chemical equilibrium in planetary atmospheres: UV-photochemistry in close-in exoplanets, and vertical mixing in cold atmospheres of giant planets (Moses 2014, and references therein). It is well known that the measured CO abundance at the top of Jupiter’s atmosphere is much higher than expected from chemical equilibrium calculations (Lodders 2010). The main reaction producing CO in planetary atmospheres is H2O + CH4 ⇄ 3H2 + CO. The timescale of this reaction is indeed so long for the temperature and pressure at the top of Jupiter’s atmosphere that CO is no longer destroyed by this reaction (Seager 2010). The amount of CO measured at the top of the atmosphere corresponds to that at T ~ 1000 K, where chemical equilibrium still holds (Lodders 2010). The CO produced at this level is carried outwards by vertical mixing. Hence, the CO is frozen in, or “quenched” at T ~ 1000 K (the so-called quench level).
The aforementioned reaction also affects the amount of water at the top of the atmosphere, an issue of major importance for our results, since the effect of water condensation on the critical mass depends on how much water is present in the cold layers of the envelope.
The real amount of water will depend on several mechanisms operating in a planet formation scenario: the amount present in the incoming planetesimals, the depth at which they are completely destroyed, the strength of convection, and the extent of the convective cells, etc. To simplify this complex scenario, we imagine the following picture. We ignore where planetesimals deposit their mass. We assume large-scale convection. Hence, the volatiles provided by planetesimals (whatever their molecular/atomic state) will also be transported to the top of the core, where temperature is high enough to dissociate any water molecule. Then, owing to convection, the bubbles reach the quench level and the abundance of water will remain fixed in that amount up to the top of the atmosphere. Therefore, in order to test in an approximate way the effect of disequilibrium, we assume in the test of this section that the amount of water is the one in equilibrium at a quenching temperature. In reality, the quench level depends on the species present in the atmosphere and their concentrations. Given the similarity of the P − T profiles in our planets and in Jupiter around T = 1000 K, we take Tquench = 1000 K.
In this section we focus on the abundance of water, which is the crucial factor in our results. For this, we consider a fictitious atmosphere that is made only of water and noble gases. Since no reaction occurs between water and noble gases, this scenario provides a good opportunity to study in an approximate way the effect of water condensation in a system where all the species remain quenched until the temperature is high enough for water to dissociate (i.e. for T ≲ 2000 K). We mimic, in this way, what would happen in a disequilibrium scenario.
In Fig. 15 we present temperature-pressure profiles for the “nominal” composition case (the envelope composition assumed so far in this work, i.e. H, He, C and O) and the new “simplified” case, where no chemical reactions take place since the envelope is made of water and noble gases13. Both cases share the same mole fraction of water at the top of the atmosphere. As was explained in Sect. 5.2, this guarantees that the departure from the moist-adiabatic profile occurs at approximately the same (P,T). We note, however, that the profiles follow different tracks after the departure from the moist adiabat. This is due to the lack of chemical reactions in the simplified case. In the nominal case, chemical reactions take place at T ≳ 500 K. This lowers the adiabatic gradient and causes the bump of the blue curve in that range of temperature. Hence, computing the critical core mass with the simplified envelope composition not only provides with a way to simulate a quenched (or disequilibrium) scenario, but also allows us to disentangle the effect of reduction of critical core mass due to chemical reactions and water condensation.
 |
Fig. 15 Comparison of pressure-temperature profile between the simplified envelope composition and the nominal composition for Z = 0.7. In both cases water is allowed to condense. The same mole fraction of water at the top of the atmosphere is assumed for both profiles. Therefore, the departure from the moist adiabat occurs at the same (P, T) in both profiles. |
The effect of water condensation is determined by the point in the temperature-pressure diagram at which the vapour pressure stops being saturated (and this depends just on the mole fraction of vapour). Thus, concerning the effect of water condensation on the critical core mass, the two profiles shown in Fig. 15 are equivalent. We can therefore compute the critical core mass for the simplified case in two steps:
-
1.
We compute the critical core mass as a function of the molefraction of water (xH2O) for the simplified composition (Fig. 16).
-
2.
We compute the mole fraction of water as a function of Z for the nominal composition (Fig. 17, purple curve).
Hence, by combining Figs. 16 and 17 (purple curve) we can express the critical core mass of the simplified composition as a function of an equivalent Z, for which equivalent means having the same mole fraction of water as the one at the top of the atmosphere of the nominal composition. For instance, for a mole fraction of water of 0.29 in the simplified case, Mcrit ≈ 0.5 M⊕ (Fig. 16). For the nominal composition, this mole fraction of water at the top of the atmosphere corresponds to a metallicity of Z = 0.7. Thus, the simplified composition with a mole fraction of water of 0.29 has an equivalent metallicity of 0.7.
 |
Fig. 16 Critical core mass as a function of the mole fraction of water in the simplified case (purple) and nominal case (blue). Water condensation takes place in both cases. |
 |
Fig. 17 Nominal composition case. Relation between the metallicity and the mole fraction of water at the top of the atmosphere (blue) and at T = 1000 K (green). |
Nevertheless, as was explained before, having xH2O = 0.29 at the top of the atmosphere in the nominal case for Z = 0.7 is a result of assuming chemical equilibrium in that layer, which is probably not true. Thus, a more realistic amount of water at the top of the atmosphere should be the one at T = 1000 K (namely, xH2O = 0.22 for Z = 0.7, see green curve in Fig. 17), where chemical equilibrium is a reliable assumption. We therefore compute again the critical core mass for the simplified composition, but assume that the mole fraction of water is that of the nominal composition at T = 1000 K. The critical core mass as a function of the equivalent metallicity for the simplified compositional cases (with and without water condensation) are shown in Fig. 1814.
 |
Fig. 18 Critical core mass as a function of the equivalent metallicity for the simplified composition case. Purple solid line: case where water condenses and the mole fraction of water is the same as the one at the top of the atmosphere of the nominal composition case (purple line in Fig. 17). Green solid line: water condenses, but the mole fraction of water corresponds to that at T = 1000 K of the nominal composition (green line in Fig. 17). Orange dashed line: same as green curve, but in this case water is not allowed to condense. |
From Fig. 18 we can draw the following conclusions. In a chemical disequilibrium scenario (like the one we mimic with our simplified composition), considering or not the condensation of water (green and orange curves in Fig. 18, respectively) still brings a difference in critical core mass of an order of magnitude for large Z, the same that was found considering chemical equilibrium (Fig. 1). The absolute values of Mcrit are larger in the disequilibrium scenario, because the reduction of adiabatic gradient we had for T ≳ 500 K (Fig. 5) due to chemical reactions does not take place in these water/noble gas envelopes. With this simplified composition we exclude all chemical reactions (except dissociation of H2O). This is not justified for T ≳ 1000 K, and in addition, the presence of dust grains may actually increase the rate of chemical reactions (Fegley & Lodders 1994) throughout the envelope. Therefore, the absolute Mcrit values in Fig. 18 are upper limits when translating these into the nominal-composition out-of-chemical equilibrium case.
Finally, we note that we assumed in this test that all water condenses when the pressure and temperature are appropriate for it to occur. This is true in an equilibrium scenario. It is well known within the cloud formation community that in the presence of only one condensible species, the creation of the first condensates (i.e. nucleation) might require a high level of supersaturation (see e.g. the reviews of Helling et al. 2008; Marley et al. 2013). However, if the atmosphere contains pre-existing nucleating seeds, like dust grains, condensations can already occur for saturation ratios close to one. This heterogeneous nucleation is what explains cloud formation on Earth. In the atmospheres to which we refer in this work, dust grains are much more abundant than on Earth because of the constant replenishment by the ablation of planetesimals. Therefore, water can effectively nucleate and condense in the atmospheres of these growing planets.
6.4. Condensation of other species
Apart from water, other compounds could condense in the pressure-temperature regimes considered in this work. In particular, it is known that the atmosphere of Jupiter possesses NH3 clouds. Unfortunately, while CEA does handle NH3 in gaseous form, it does not take into account its condensation. However, we can at least test whether the abundance of NH3 in the atmosphere would be sufficient for its condensation to matter. For this, we consider an atmosphere in which we add nitrogen to the already included H, He, C, and O. We keep the same solar C/O as used throughout, and also assume a solar ratio of N/O. Using CEA, we find that in the coldest layers of the envelope, the mass fraction of NH3 formed is just ~5%. Therefore, even if all the ammonia formed could condense, this would be a minor contribution compared to the amount of condensed water. Even more important, if condensation of other species took place, the effect of reduction of critical core mass would be even larger, since the effect of release of latent heat explained in Sect. 5.2 is not unique to water, but qualitatively general to all vapour-solid (or vapour-liquid) phase transitions.
6.5. Gas accretion timescale
The growth of an enriched, critical protoplanet is not easy to infer. A simple estimation of the gas accretion timescale can be obtained by computing the Kelvin-Helmholtz timescale, which corresponds approximately to (Ikoma et al. 2000) 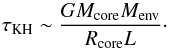 (24)Using Eq. (7), this can be simplified to
(24)Using Eq. (7), this can be simplified to 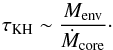 (25)Evaluating this expression when the structures become critical, and using Ṁcore = 10-6M⊕/ yr (which is the approximated planetesimal accretion rate for the cases presented in this paper, as well as a standard value in the planet formation literature; see e.g. Bodenheimer & Pollack 1986; Pollack et al. 1996; Ikoma et al. 2000), we find, for Z = 0.7, that τKH ~ 7 × 104 yr when water condensation takes place, and τKH ~ 106 yr when it does not. In principle, these timescales would indicate that the condensation of water significantly speeds up the accretion of gas. However, two things have to be kept in mind:
(25)Evaluating this expression when the structures become critical, and using Ṁcore = 10-6M⊕/ yr (which is the approximated planetesimal accretion rate for the cases presented in this paper, as well as a standard value in the planet formation literature; see e.g. Bodenheimer & Pollack 1986; Pollack et al. 1996; Ikoma et al. 2000), we find, for Z = 0.7, that τKH ~ 7 × 104 yr when water condensation takes place, and τKH ~ 106 yr when it does not. In principle, these timescales would indicate that the condensation of water significantly speeds up the accretion of gas. However, two things have to be kept in mind:
-
1.
The accretion rate of gas depends on both the self-gravityof the envelope and its ability to cool (and therefore, tocontract). The latter depends on the microphysics of theenvelope. Solving the full planet-growth problem forenriched envelopes would imply, in part, consideringself-consistent grain growth calculation for the opacity(Ormel 2014; Mordasini 2014),because this affects the planet cooling. This, coupled to a code thatsolves the structure with a varying luminosity with time, will beimplemented in a future work.
-
2.
Even if the gas accretion timescale is shorter for the case where water condensation occurs, gas accretion would lead to a decrease of the envelope metallicity (i.e. dilution), and therefore to the increase of the critical core mass.
If a planet reaches the critical mass at a given Zcrit, there are two effects. First, as a result of solid (i.e. planetesimal) accretion, the metal content of the planet (MZ) increases. Second, as a result of gas accretion, the mean Z of the planet will change. According to Ikoma et al. (2000), the gas accretion rate at the critical point is slightly larger than the planetesimal accretion rate. At the time when the critical core mass is reached, the accretion of solids and gas will lead to a decrease of the mean Z in the envelope. As a result, the critical core mass and the total amount of heavy elements for the critical structure MZ,crit increase. A crucial point, for the immediate future of the planet is therefore to compare the increase of MZ (resulting from the accretion of planetesimals) and the increase in the critical amount of heavy elements15.
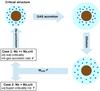 |
Fig. 19 Sketch of the possible phases an enriched protoplanet could follow after reaching the critical mass. Although not illustrated (for not overloading the image), planetesimal accretion is present in all the stages and the material assumed to remain in the envelope. Despite the competition between gas and planetesimal accretion, the immediate result would be dilution, since at this point the accretion of gas is larger than that of solids, as explained in the main text. As a consequence of dilution, Mcrit increases. After this point, depending on the accretion rate of planetesimals (which gives a new MZ) versus the accretion rate of gas from the disc, the planet could become sub-critical or super-critical, as is discussed in Sect. 6.5. |
Thus, two possible scenarios could take place after the critical core mass is reached (see Fig. 19). In the first scenario (case 1), the increase of critical mass is more rapid than the increase of MZ. In this case, the planet will again become subcritical and will no longer accrete gas. Finally, as a result of planetesimal accretion, the metallicty may increase again. In the second scenario (case 2), the increase of critical mass is smaller than the increase of MZ. In this case, the planet will remain super-critical, and might become a giant planet.
The occurrence of case 1 or 2 depends therefore on the relative increase of MZ,crit(Z) and MZ(Z). The steeper the slope of MZ,crit(Z), the larger the increase of MZ,crit for a given reduction of Z and thus, the higher the probability of being in case 1. For instance, as shown in Fig. 20, when comparing the case where water condenses with the one where water does not condense, the former case has a steeper slope than the latter. Therefore, water condensation would probably lead to case 1, and hence to an increase in the heavy element content of the planet.
In reality, which of the two cases takes place depends on the location of the forming planet and solid accretion rate, among other conditions.
 |
Fig. 20 Critical mass of metals (mass content of metals in the planet when Mcore = Mcrit) as a function of metallicity. Red line: restricted case. Blue line: non-restricted case. Boundary conditions given by Table 1. Despite the similarity with Fig. 1, in this case the y-axis represents all the metal content of the planet at criticality, and not just that of the core. Depending on the slope of MZ,crit(Z), for the same planetesimal accretion rate, the planet could become sub- or super-critical. The steeper the slope (water condensation case), the more likely the structure is to become sub-critical, and therefore, to follow case 1 illustrated in Fig. 19. |
7. Conclusions
The critical core mass for envelopes enriched in carbon and oxygen through the disruption of planetesimals was computed, corroborating the reduced values found by Hori & Ikoma (2011). It was found that large amounts of water are formed in the envelope of the enriched protoplanets, and that an important fraction of it can condense for boundary conditions suited for a ≳ 4 AU. Because of the release of latent heat that takes place when H2O condensation occurs, the energy budget of the envelope is dramatically changed. This translates into a drastic pattern shift in the pressure-temperature envelope profile, which implies a remarkable increase in pressure for a given temperature of the envelope. Therefore, compared to the case where H2O condensation is not included, the density of the envelope in the condensed case increases significantly, reducing the critical core to extremely low values, as is shown in Fig. 1.
The reduction of critical core mass due to water condensation depends on the amount of water present in the outer layers of the envelope, which is affected by the assumption of chemical equilibrium. However, we have shown that for a disequilibrium scenario, the critical core mass is still significantly reduced.
This critical core mass is important in the context of the standard models of planet formation because it sets the time required to form a gas giant. Indeed, as is shown in many papers, the gas accretion rate for a critical mass of ~10 M⊕ is so large that the formation time of a giant planet is for practical purposes very close to the time needed to reach the critical mass (see e.g. Bodenheimer & Pollack 1986; Pollack et al. 1996; Alibert et al. 2005).
However, this conclusion only holds for large values of the critical core, as the gas accretion rate at the critical mass is a rapidly increasing function of the planetary mass. As we have shown here, the condensation of water drastically reduces the critical mass, and as a consequence, the gas accretion rate at the critical mass could be in this context very small compared to standard formation models. The work presented here shows that the standard picture of planet formation, including the concept of critical core mass, is overly simplified and should be revised in the future.
ρtot includes the mass of all species and ρgas just the one of the gaseous component. These two densities are equal if no condensation takes place. See Sect. 4.2 for more details.
For the complete list of condensed species considered in CEA, see Appendix B of the User’s Manual from http://www.grc.nasa.gov/WWW/CEAWeb/ceaWhat.htm
It is debated in the literature whether ρgas or ρtot should be used in the hydrostatic equilibrium equation, but recent work suggests that the correct expression is with ρgas (Gorshkov et al. 2012). In any case, we have checked that using either ρgas or ρtot in the hydrostatic equilibrium equation does not affect our results.
The envelope composition for Z = 0.2 and 0.4 are also shown in Fig. 4 to illustrate how the abundance of volatiles, in particular water, increases with increasing metallicity.
Since we need to fix the core mass at the beginning of the simulations, in this case we use the first numerical scheme described in Sect. 2.
Property that can be inferred for stellar structure making use of the virial theorem, see e.g. Kippenhahn et al. (2013). For bodies with a core this is not strictly true, but the changes in central temperature are negligible.
Actually, the condition of a fully convective envelope with perfect mixing is overly severe. In reality, vertical mixing tends to take place in regions well above the convective-radiative boundary. On Earth, for example, the convective region extends for 10 km over the planet surface, but vertical efficient mixing of material occurs up to 80 km height (Goody 1995).
For simplicity, fully convective envelopes were assumed. Since this is the case for the nominal composition for Z ≥ 0.45, we only show results for this range of metallicities, and comparison with Fig. 1 is suitable (possible?).
We are assuming in this discussion (as is illustrated in Fig. 19), that the mass of the core is fixed. Hence, the heavy elements provided by planetesimal accretion remain in the envelope, making Z, and therefore MZ,crit, grow.
Acknowledgments
We thank C. Mordasini for fruitful discussions and the constructive remarks of an anonymous referee who contributed to improving this paper. We acknowledge financial support from the organising committee of the 1st and 2nd ELSI Symposium and of the International Space Science Institute, in the framework of an ISSI Team. This work has been in part carried out within the frame of the National Centre for Competence in Research PlanetS supported by the Swiss National Science Foundation. The authors acknowledge the financial support of the SNSF, the European Research Council under grant 239605, and by Grants-in-Aid for Scientific Research on Innovative Areas (No. 23103005) and Scientific Research (C; No. 25400224) from the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan.
References
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Alibert, Y., Baraffe, I., Hauschildt, P., & Allard, F. 1999, A&A, 344, 551 [NASA ADS] [Google Scholar]
- Alibert, Y., Mordasini, C., Benz, W., & Winisdoerffer, C. 2005, A&A, 434, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Armitage, P. J. 2010, Astrophysics of Planet Formation (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Baraffe, I., Alibert, Y., Chabrier, G., & Benz, W. 2006, A&A, 450, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bodenheimer, P., & Pollack, J. B. 1986, Icarus, 67, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Fegley, Jr., B., & Lodders, K. 1994, Icarus, 110, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Mordasini, C., Nettelmann, N., et al. 2013, ApJ, 775, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, R. S., Marley, M. S., & Lodders, K. 2008, ApJS, 174, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M., Demory, B.-O., Benneke, B., et al. 2012, A&A, 539, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goody, R. 1995, Principles of Atmospheric Physics and Chemistry (New York: Oxford University Press), 324 [Google Scholar]
- Gordon, S., McBride, B. J., & States, U. 1994, Computer program for calculation of complex chemical equilibrium compositions and applications (National Aeronautics and Space Administration, Office of Management, Scientific and Technical Information Program; National Technical Information Service, distributor, Cleveland, Ohio: Springfield, Va) [Google Scholar]
- Gorshkov, V. G., Makarieva, A. M., & Nefiodov, A. V. 2012, J. Exp. Theor. Phys., 115, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Guilera, O. M., de Elía, G. C., Brunini, A., & Santamaría, P. J. 2014, A&A, 565, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., & Gautier, D. 2014, Treatise on Geophysics, 2nd edn., eds. T. Spohn, & G. Schubert, in press [arXiv:1405.3752] [Google Scholar]
- Guillot, T., Stevenson, D. J., Hubbard, W. B., & Saumon, D. 2004, The interior of Jupiter, eds. F. Bagenal, T. E. Dowling, & W. B. McKinnon, 35 [Google Scholar]
- Helling, C., Ackerman, A., Allard, F., et al. 2008, MNRAS, 391, 1854 [NASA ADS] [CrossRef] [Google Scholar]
- Hori, Y., & Ikoma, M. 2010, ApJ, 714, 1343 [NASA ADS] [CrossRef] [Google Scholar]
- Hori, Y., & Ikoma, M. 2011, MNRAS, 416, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Hubickyj, O., Bodenheimer, P., & Lissauer, J. J. 2005, Icarus, 179, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Iaroslavitz, E., & Podolak, M. 2007, Icarus, 187, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Ikoma, M., Nakazawa, K., & Emori, H. 2000, ApJ, 537, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Ikoma, M., Emori, H., & Nakazawa, K. 2001, ApJ, 553, 999 [NASA ADS] [CrossRef] [Google Scholar]
- Inaba, S., Wetherill, G. W., & Ikoma, M. 2003, Icarus, 166, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2013, Stellar Structure and Evolution, 2nd edn. (Berlin, Heidelberg: Springer) [Google Scholar]
- Kobayashi, H., Tanaka, H., & Krivov, A. V. 2011, ApJ, 738, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2010, Geochem News, 142 [Google Scholar]
- Marley, M. S., Ackerman, A. S., Cuzzi, J. N., & Kitzmann, D. 2013, Clouds and Hazes in Exoplanet Atmospheres, eds. S. J. Mackwell, A. A. Simon-Miller, J. W. Harder, & M. A. Bullock, 367 [Google Scholar]
- Mizuno, H. 1980, Prog. Theor. Phys., 64, 544 [Google Scholar]
- Mizuno, H., Nakazawa, K., & Hayashi, C. 1978, Prog. Theor. Phys., 60, 699 [Google Scholar]
- Mordasini, C. 2014, A&A, 572, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., & Benz, W. 2006, in Tenth Anniversary of 51 Peg-b: Status of and prospects for hot Jupiter studies, eds. L. Arnold, F. Bouchy, & C. Moutou, 84 [Google Scholar]
- Moses, J. I. 2014, Roy. Soc. Lond. Phil. Trans. Ser. A, 372, 30073 [Google Scholar]
- Movshovitz, N., & Podolak, M. 2008, in Extreme Solar Systems, eds. D. Fischer, F. A. Rasio, S. E. Thorsett, & A. Wolszczan, ASP Conf. Ser., 398, 257 [Google Scholar]
- Movshovitz, N., Bodenheimer, P., Podolak, M., & Lissauer, J. J. 2010, Icarus, 209, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Mumma, M. J., Weissman, P. R., & Stern, S. A. 1993, in Protostars and Planets III, eds. E. H. Levy, & J. I. Lunine, 1177 [Google Scholar]
- Nettelmann, N., Fortney, J. J., Kramm, U., & Redmer, R. 2011, ApJ, 733, 2 [Google Scholar]
- Ormel, C. W. 2014, ApJ, 789, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Perri, F., & Cameron, A. G. W. 1974, Icarus, 22, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Petigura, E. A., Marcy, G. W., & Howard, A. W. 2013, ApJ, 770, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Pierrehumbert, R. T. 2010, Principles of Planetary Climate (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Podolak, M. 2003, Icarus, 165, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Podolak, M., Pollack, J. B., & Reynolds, R. T. 1988, Icarus, 73, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Saumon, D., Chabrier, G., & van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S. 2010, Exoplanet Atmospheres: Physical Processes (Princeton University Press) [Google Scholar]
- Semenov, D., Henning, T., Helling, C., Ilgner, M., & Sedlmayr, E. 2003, A&A, 410, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stevenson, D. J. 1982, Planet. Space Sci., 30, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Valencia, D., Guillot, T., Parmentier, V., & Freedman, R. S. 2013, ApJ, 775, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, H. F., & Militzer, B. 2012, ApJ, 745, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Wuchterl, G. 1993, Icarus, 106, 323 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Critical core mass as a function of metallicity. Green line: results of the “wholly polluted” case of Fig. 2 in HI11; red line: this work, restricted case; blue line: this work, non-restricted case (see main text for the definitions of the different cases). |
| In the text | |
 |
Fig. 2 Profile of the gas mean molecular weight of the envelope as a function of its temperature for Z = 0.7 when Mcore = Mcrit,NR(Z = 0.7). Solid lines: non-restricted case. Dotted lines: restricted case. We note that in the the non-restricted case, μgas decreases in the outer layers (i.e. low temperature values; see main text). The difference between both profiles at high temperatures is a consequence of a difference in the pressure-temperature profiles (see Fig. 5). |
| In the text | |
 |
Fig. 3 Profile of the adiabatic gradient of the envelope as a function of its temperature for Z = 0.7. The core mass and labels are set just as in Fig. 2. We note that there is a strong reduction of the adiabatic gradient in the outer layers of the envelope (i.e. low temperature values) in the non-restricted case (see main text). The difference between both profiles at high temperatures has the same explanation as in the previous figure. |
| In the text | |
 |
Fig. 4 Envelope composition as a function of temperature for Z = 0.2, 0.4, and 0.7. MP = 0.29 M⊕ for all profiles (planetary mass when Mcore (Z = 0.7) = Mcrit (Z = 0.7)). Left column: non-restricted case. Right column: restricted case. In the non-restricted case water (solid lines) coexists in vapour phase (blue curve), solid phase (cyan curve), and even liquid phase (violet curve) in the case of Z = 0.7. Except H2O in solid and liquid phase, the other 13 species shown here were considered in HI11. In the restricted case, water only exists in vapour phase. |
| In the text | |
 |
Fig. 5 Pressure as a function of temperature for Z = 0.7 and MP = 0.29 M⊕. In the case where water is allowed to condense (orange lines), the vapour pressure follows the Clausius-Clapeyron curve until T = 282 K, which defines the loci where the vapour and liquid phases, and vapour and ice phases, can co-exist (green-dotted line). Hence, in these range of temperatures, water is being condensed, and the pressure-temperature profiles follow the moist adiabat. |
| In the text | |
 |
Fig. 6 Pressure as a function of temperature for Z = 0.2, 0.4, and 0.7. MP = 0.29 M⊕ for all cases. The dotted-black lines correspond to regions where the envelope is radiative. This region is extremely small in the case of Z = 0.2 profile. |
| In the text | |
 |
Fig. 7 Total mass of the planet as a function of the mass of the core for different uniform metallicities and L = 1027 erg/s. Here the composition of the envelope corresponds to the non-restricted case (see main text). The highest Z shown is 0.5 for aesthetic reasons. |
| In the text | |
 |
Fig. 8 Envelope mass as a function of the mass of solids contained in the planet (MZ). The mass of the core is fixed at 6 M⊕. An accretion rate of solids of 3 × 10-6M⊕/yr was assumed, which corresponds to a luminosity of 1027 erg/s (the same used in all the other results). The decrease of Menv for low metallicities (shown in the inset) is due to the increase in the gas opacity and to the fact that for these cases of low Z, a radiative zone develops in the outer layers. For Z> 0.1, the structures are almost fully convective. Therefore, the increase in κgas does not play a role, the dominant effect is the increase in Menv due to the inclusion of Z in the EOS. |
| In the text | |
 |
Fig. 9 Critical core mass as a function of metallicity for the specified semi-major axis and corresponding boundary conditions given by Eqs. (21) and (22). Dashed lines correspond to the reference cases (boundary conditions at a = 5.2 AU) plotted in Fig. 1: the yellow curve is the restricted case (i.e. without condensation of water), and the blue curve the non-restricted case (where water condenses). For all the new cases (solid lines) water is allowed to condense. The only case where water does not condense for any value of Z is for a = 2 AU. |
| In the text | |
 |
Fig. 10 Pressure-temperature profiles for different positions in the disc for Z = 0.7 and MP = 0.29 M⊕. Tout and Pout correspond to those given by Eqs. (21) and (22) for the semi-major axis specified in the labels. |
| In the text | |
 |
Fig. 11 Pressure-temperature profiles for different positions in the disc for Z = 0.7 and MP = 0.29 M⊕. a) Pout given by Eq. (22) for the labelled semi-major axis, but Tout= 150 K (reference case, see Table 1) for all the profiles; b) Tout given by Eq. (21) for the labelled semi-major axis, but Pout corresponds to the reference case for all the profiles. |
| In the text | |
 |
Fig. 12 Planetary mass as a function of the core mass given by solving the internal structure equations for pure H–He envelopes. The red curve uses CEA for the EOS and the blue uses SCVH. Boundary conditions are those from Table 1. ΔMcrit ≈ 1.4 M⊕ |
| In the text | |
 |
Fig. 13 Map of the density difference between CEA and SCVH EOS as a function of temperature and pressure, for pure H–He composition. Superposed are shown the profiles of the envelope for the two different EOS for MP = 18.7 M⊕ (planetary mass for which Mcore = Mcrit when CEA is used for the EOS). All units are in cgs. |
| In the text | |
 |
Fig. 14 Red line: profile for two-layer atmosphere, but using Freedman opacities in the H–He region instead of the Ferguson opacities used in all other results of the paper. Blue line: Z = 0.7 (and uniform in the envelope) where water is allowed to condense. The resemblance of both profiles, compared to the restricted profile of Fig. 5, suggests that for the red curve the corresponding critical core mass will also be very low. Solid lines stand for convective regions and dotted for radiative ones. |
| In the text | |
 |
Fig. 15 Comparison of pressure-temperature profile between the simplified envelope composition and the nominal composition for Z = 0.7. In both cases water is allowed to condense. The same mole fraction of water at the top of the atmosphere is assumed for both profiles. Therefore, the departure from the moist adiabat occurs at the same (P, T) in both profiles. |
| In the text | |
 |
Fig. 16 Critical core mass as a function of the mole fraction of water in the simplified case (purple) and nominal case (blue). Water condensation takes place in both cases. |
| In the text | |
 |
Fig. 17 Nominal composition case. Relation between the metallicity and the mole fraction of water at the top of the atmosphere (blue) and at T = 1000 K (green). |
| In the text | |
 |
Fig. 18 Critical core mass as a function of the equivalent metallicity for the simplified composition case. Purple solid line: case where water condenses and the mole fraction of water is the same as the one at the top of the atmosphere of the nominal composition case (purple line in Fig. 17). Green solid line: water condenses, but the mole fraction of water corresponds to that at T = 1000 K of the nominal composition (green line in Fig. 17). Orange dashed line: same as green curve, but in this case water is not allowed to condense. |
| In the text | |
 |
Fig. 19 Sketch of the possible phases an enriched protoplanet could follow after reaching the critical mass. Although not illustrated (for not overloading the image), planetesimal accretion is present in all the stages and the material assumed to remain in the envelope. Despite the competition between gas and planetesimal accretion, the immediate result would be dilution, since at this point the accretion of gas is larger than that of solids, as explained in the main text. As a consequence of dilution, Mcrit increases. After this point, depending on the accretion rate of planetesimals (which gives a new MZ) versus the accretion rate of gas from the disc, the planet could become sub-critical or super-critical, as is discussed in Sect. 6.5. |
| In the text | |
 |
Fig. 20 Critical mass of metals (mass content of metals in the planet when Mcore = Mcrit) as a function of metallicity. Red line: restricted case. Blue line: non-restricted case. Boundary conditions given by Table 1. Despite the similarity with Fig. 1, in this case the y-axis represents all the metal content of the planet at criticality, and not just that of the core. Depending on the slope of MZ,crit(Z), for the same planetesimal accretion rate, the planet could become sub- or super-critical. The steeper the slope (water condensation case), the more likely the structure is to become sub-critical, and therefore, to follow case 1 illustrated in Fig. 19. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.