| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A127 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321492 | |
| Published online | 12 July 2013 | |
Flux and polarization signals of spatially inhomogeneous gaseous exoplanets
1 SRON – Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
e-mail: T.Karalidi@sron.nl
2 Leiden Observatory, Leiden University, 2300 RA Leiden, The Netherlands
3 Faculty of Aerospace Engineering, Technical University Delft, Kluyverweg 1, 2629 HS Delft, The Netherlands
Received: 18 March 2013
Accepted: 22 May 2013
Aims. We present numerically calculated, disk-integrated, spectropolarimetric signals of starlight that is reflected by vertically and horizontally inhomogeneous gaseous exoplanets. We include various spatial features that are present on Solar System’s gaseous planets: belts and zones, cyclonic spots, and polar hazes, to test whether such features leave traces in the disk-integrated fux and polarization signals.
Methods. Broadband flux and polarization signals of starlight that is reflected by gaseous exoplanets are calculated using an efficient, adding-doubling radiative transfer code, that fully includes single and multiple scattering and polarization. The planetary model atmospheres are vertically inhomogeneous and can be horizontally inhomogeneous, and contain gas molecules and/or cloud and/or aerosol particles.
Results. The broadband flux and polarization signals are sensitive to cloud top pressures, although in the presence of local pressure differences, such as in belts and clouds, the flux and polarization phase functions have similar shapes as those of horizontally homogeneous planets. Fitting flux phase functions of a planet with belts and zones using a horizontally homogeneous planet could theoretically yield cloud top pressures that differ by a few hundred mbar from those derived from fitting polarization phase functions. In practice, however, observational errors and uncertainties in cloud properties would make such a fit unreliable. A cyclonic spot like Jupiter’s Great Red Spot, covering a few percent of the disk, located in equatorial regions, and rotating in and out of the observer’s view yields a temporal variation of a few percent in the broadband flux and a few percent in the degree of polarization. Polar hazes leave strong traces in the polarization of reflected starlight in spatially resolved observations, especially seen at phase angles near 90°. Integrated across the planetary disk, polar hazes that cover only part of the planetary disk, change the broadband degree of polarization of the reflected light by a few percent. Such hazes have only small effects on locally reflected broadband fluxes and negligible effects on disk-integrated broadband fluxes.
Conclusions. Deriving the presence of belts and zones in the atmospheres of gaseous exoplanets from broadband flux and polarization observations will be extremely difficult. Cyclonic spots could leave temporal changes in the broadband flux and polarization signals of a few percent. Polar hazes that cover a fraction of the planetary disk, and that are composed of small, Rayleigh scattering particles, change the broadband degree of polarization by at most a few percent.
Key words: methods: numerical / planets and satellites: atmospheres / polarization
© ESO, 2013
1. Introduction
Since the discovery of the first exoplanet orbiting a main sequence star by Mayor & Queloz (1995), more than 850 exoplanets have been detected up to today. The refinement of the detection methods and the instrumentation, such as the highly successful space missions CoRoT (COnvection, ROtation & planetary Transits; Baglin et al. 2006; Deleuil 2010) and Kepler (Koch et al. 1998), and ground-based telescope instruments like HARPS (High Accuracy Radial Velocity Planet Searcher; Pepe et al. 2004) have led to an almost exponential increase of the number of detected planets per year.
The next step of exoplanet research is the characterization of detected exoplanets: what is the composition and structure of their atmospheres, and, for rocky exoplanets, their surface? In the near future, instruments like SPHERE (Spectro-Polarimetric High-Contrast Exoplanet Research; Dohlen et al. 2008; Roelfsema et al. 2011), on the Very Large Telescope (VLT) and GPI (Gemini Planet Imager; Macintosh et al. 2008) on the Gemini North telescope, and more in the future, EPICS (Exoplanet Imaging Camera and Spectrograph; Kasper et al. 2010) on the E-ELT, will characterize gaseous exoplanets in relatively wide orbits around their stars, and possibly super-Earths around nearby stars, using combinations of spectroscopy and broadband polarimetry.
In exoplanet research, polarimetry helps to detect a planet because the direct stellar light is usually unpolarized (see Kemp et al. 1987), while the starlight that has been reflected by a planet will usually be (linearly) polarized because it has been scattered by atmospheric particles and/or it has been reflected by the planetary surface (if present). Polarimetry helps to confirm the detection of an exoplanet, because background sources will usually be unpolarized, or have a direction of polarization that excludes a relation with the star. A first detection of the polarization signal of an exoplanet was claimed by Berdyugina et al. (2008, 2011). The power of polarization in characterizing planetary atmospheres and surfaces has been demonstrated through observations of Solar System planets (including Earth itself) (see, for example Hansen & Hovenier 1974; Hansen & Travis 1974; Mishchenko 1990; Tomasko et al. 2009). For gaseous and terrestrial-type exoplanets numerical calculations have clearly shown the added information on planetary characteristics that can be derived from polarimetry (e.g. Stam 2003, 2004; Saar & Seager 2003; Seager et al. 2000; Stam 2008; Karalidi et al. 2011).
The numerical studies mentioned above pertain to planetary model atmospheres that are vertically inhomogeneous, but horizontally homogeneous. Partly, this has to do with the computational effort: fully including all orders of scattering and polarization in radiative transfer calculations requires orders more computing time than the scalar radiative transfer calculations that are commonly used to model reflected fluxes (note that ignoring polarization in radiative transfer calculations introduces errors in calculated fluxes, see e.g. Stam & Hovenier 2005, and references therein).
In this paper, we present numerically calculated total flux and polarization signals of unpolarized incident starlight that is reflected by gaseous exoplanets that are both vertically and horizontally inhomogeneous. For the horizontal inhomogeneities, we use banded structures similar to the belts and zones that circle Jupiter and Saturn, cyclonic spots such as the long lived Great Red Spot on Jupiter and the Great Dark Spot that Voyager-2 observed on Neptune, and polar hazes such as those covering the north and south poles of Jupiter and Saturn. In particular the latter hazes are known to strongly polarize the incident sunlight, as observed at small phase angles from Earth (Schmid et al. 2011), and at intermediate phase angles from spacecraft observations (see e.g. West et al. 1983; Smith & Tomasko 1984).
For exoplanets, observations will yield disk-integrated flux and polarization signals. As we will explore in this paper, local horizontal inhomogeneities might reveal themselves through temporal variations in flux and/or polarization signals when planets rotate with respect to the observer, or because the flux and/or polarization signals of the horizontally inhomogeneous planets deviate from those of horizontally homogeneous planets. The dependence of a total flux signal on the composition and structure of a planetary atmosphere is different than that of a polarization signal. Therefore, a horizontally inhomogeneous planet’s total flux and polarization phase functions could be similar to those of different horizontally homogeneous planets. Such differences could be used to detect spatial features like belts and zones, cyclonic spots, and/or polar hazes.
This paper is organized as follows. In Sect. 2, we describe polarized light, our radiative transfer algorithm, and the model planetary atmospheres. In Sect. 3, we present the single scattering properties of the cloud and haze particles in the model atmospheres. Section 4 shows the calculated flux and polarization signals of different types of spatially inhomogeneous model planets: with zones and belts (Sect. 4.1), cyclonic spots (Sect. 4.2), and polar hazes (Sect. 4.3). Section 5, finally, contains a summary and our conclusions.
2. Description of the numerical simulations
2.1. Definitions of flux and polarization
Starlight that has been reflected by a planet can be described by a flux vector πF, as follows ![\begin{equation} \label{eq:first} \pi\vec{F}= \pi\left[\begin{array}{c} F \\ Q \\ U \\ V \end{array}\right], \end{equation}](/articles/aa/full_html/2013/07/aa21492-13/aa21492-13-eq3.png) (1)where parameter πF is the total flux, parameters πQ and πU describe the linearly polarized flux and parameter πV the circularly polarized flux (see e.g. Hansen & Travis 1974; Hovenier et al. 2004). Although not explicitly shown in Eq. (1), all four parameters depend on the wavelength λ, and their dimensions are W m-2 m-1. Parameters πQ and πU are defined with respect to a reference plane, for which we chose the planetary scattering plane, i.e. the plane through the centers of the star, the planet and the observer. Parameter πV of starlight that is reflected by a planet is generally small (Hansen & Travis 1974) and we will ignore it in our simulations. This can be done without introducing significant errors in our calculated fluxes πF, πQ and πU (Stam & Hovenier 2005). The degree of (linear) polarization P of flux vector πF is defined as follows
(1)where parameter πF is the total flux, parameters πQ and πU describe the linearly polarized flux and parameter πV the circularly polarized flux (see e.g. Hansen & Travis 1974; Hovenier et al. 2004). Although not explicitly shown in Eq. (1), all four parameters depend on the wavelength λ, and their dimensions are W m-2 m-1. Parameters πQ and πU are defined with respect to a reference plane, for which we chose the planetary scattering plane, i.e. the plane through the centers of the star, the planet and the observer. Parameter πV of starlight that is reflected by a planet is generally small (Hansen & Travis 1974) and we will ignore it in our simulations. This can be done without introducing significant errors in our calculated fluxes πF, πQ and πU (Stam & Hovenier 2005). The degree of (linear) polarization P of flux vector πF is defined as follows 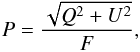 (2)which is independent of the choice of reference plane.
(2)which is independent of the choice of reference plane.
Unless stated otherwise, we assume that the starlight that is incident on a model planet is unpolarized (Kemp et al. 1987) and that the model planets are mirror-symmetric with respect to the planetary scattering plane. In that case, πU equals zero, and we can use an alternative definition for the degree of polarization, namely 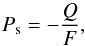 (3)with the subscript s referring to signed. For Ps > 0 (<0), the reflected light is polarized perpendicular (parallel) to the reference plane.
(3)with the subscript s referring to signed. For Ps > 0 (<0), the reflected light is polarized perpendicular (parallel) to the reference plane.
We will present calculated fluxes that are normalized such that at a planetary phase angle α equal to 0° (i.e. seen from the middle of the planet, the angle between the star and the observer equals 0°), the total reflected flux πF equals the planet’s geometric albedo AG (see e.g. Stam et al. 2004). We will indicate the hence normalized total flux by πFn and the associated linearly polarized fluxes by πQn and πUn. The normalized fluxes that we present in this paper can straightforwardly be scaled to absolute fluxes of a particular planetary system by multiplying them with r2/d2, where r is the spherical planet’s radius and d the distance between the planet and the observer, and with the stellar flux that is incident on the planet. In our calculations, we furthermore assume that the distance between the star and the planet is large enough to assume that the incident starlight is uni-directional. Since the degree of polarization P (or Ps) is a relative measure, it doesn’t require any scaling.
Our calculations cover phase angles α from 0° to 180°. Of course, the range of phase angles an exoplanet exhibits as it orbits its star, depends on the orbital inclination angle. Given an orbital inclination angle i (in degrees), one can observe the exoplanet at phase angles ranging from 90° − i to 90° + i. Thus, an exoplanet in a face-on orbit (i = 0°) would always be observed at a phase angle equal to 90°, while the phase angles of an exoplanet in an edge-on orbit (i = 90°) range from 0° to 180°, the complete range that is shown in this paper. Note that the actual range of phase angles an exoplanet can be observed at will depend strongly on the observational technique that is used, and e.g. on the angular distance between a star and its planet.
2.2. Our radiative transfer code
Our radiative transfer code to calculate the total and polarized fluxes that are reflected by model planets is based on the efficient adding-doubling algorithm described by de Haan et al. (1987). It fully includes single and multiple scattering and polarization, and assumes that locally, the planetary atmosphere is plane-parallel. We will use a version of the code that applies to horizontally homogeneous planets (Stam et al. 2004, 2006, 2008), and a (more computing-time-consuming) version that applies to horizontally inhomogeneous planets (Karalidi & Stam 2012). In the latter code, a model planet is divided into pixels that are small enough to be considered horizontally homogeneous. Reflected stellar fluxes are then calculated for all pixels that are both illuminated and visible to the observer and then summed up to acquire the disk-integrated total and polarized reflected fluxes. Since the adding-doubling code uses the local meridian plane (which contains both the local zenith direction and the propagation direction of the reflected light) as the reference plane, we have to rotate locally calculated flux vectors to the planetary scattering plane before summing them up. Following Karalidi & Stam (2012), we divide our model planets into pixels of 2° × 2° (latitude × longitude).
2.3. Our model planets
The atmospheres of our model planets consist of homogeneous, plane-parallel layers that contain gases and, optionally, clouds or hazes. Here, we use the term “haze” for optically thin layers of submicron-sized particles, while “clouds” are thicker and composed of larger particles. The model atmospheres are bounded below by black surfaces, i.e. no light is entering the atmospheres from below. The ambient atmospheric temperature and pressure profiles are representative for midlatitudes on Jupiter (see Stam et al. 2004). Given the temperatures and pressures across an atmospheric layer, and the wavelength λ, the gaseous scattering optical thickness of each atmospheric layer is calculated according to Stam et al. (1999), using a depolarization factor that is representative for hydrogen-gas, namely 0.02 (see Hansen & Travis 1974). At λ = 0.55 μm, the total gaseous scattering optical thickness of our model atmosphere is 5.41. We ignore absorption by methane, and choose wavelengths in the continuum for our calculations. In particular, when broad band filters are being used for the observations, the contribution of reflected flux from continuum wavelengths will contribute most to the measured signal.
The physical properties of the clouds and hazes across a planet like Jupiter vary in time (for an overview, see e.g. West et al. 2004). Here, we use a simple atmosphere model that suffices to show the effects of clouds and hazes on the flux and polarization signals of Jupiter-like exoplanets. Our model atmospheres have an optically thick tropospheric cloud layer that is composed of ammonia ice particles (their properties are presented in Sect. 3). The bottom of this cloud layer is at a pressure of 1.0 bar. We vary the top of the cloud between 0.1 and 0.5 bars. The cloud top pressure of 0.1 bars is representative for the so-called zonal bands on Jupiter. In the zones, the clouds typically rise up higher into the atmosphere than in the adjacent belts where the cloud top pressures can be up to a few hundred mbar higher (see Ingersoll et al. 2004). We set the optical thickness of the clouds in the zones at 21 (at 0.75 μm) and in the belts it varies from 20 to 6.02 as the cloud top pressure varies from 0.1 bar to 0.5 bar. On Jupiter, the clouds are overlaid by a stratospheric, photochemically produced haze layer. The haze layers over in particular both polar regions, provide strong polarization signals indicating that they consist of small aggregated particles (West & Smith 1991). To avoid introducing too many variables, we only use haze layers over the polar regions of our model planets.
We will present results for horizontally homogeneous model planets and for model planets with bands of clouds divided into zones and belts that run parallel to the equator, which lies in the planet’s equatorial plane. Our banded model planets are mirror-symmetric: measured from the equator in either the northern or the southern direction, we chose the latitudes that bound the belts and zones as follows: 0°–8° (zone), 8°–24° (belt), 24°–40° (zone), 40°–60° (belt), 60°–90° (zone). These latitudes correspond roughly to the most prominent cloud bands of Jupiter (see e.g. de Pater & Lissauer 2001). The northern and southern polar hazes extend upward, respectively downward, from a latitude of 60°. Vertically these hazes extend between ~0.0075 bar and ~0.0056 bar, and we give them an optical thickness of 0.2 at 0.55 μm. The single scattering albedo of the haze particles is 0.995 at 0.55 μm.
3. Single scattering properties of the cloud and haze particles
3.1. The tropospheric cloud particles
Thermodynamic models of the jovian atmosphere indicate that the upper tropospheric cloud layers should consist of ammonia ice particles (see for example Sato & Hansen 1979; Simon-Miller et al. 2001; de Pater & Lissauer 2001). Galileo NIMS and Cassini CIRS data, however, indicated that spectrally identifiable ammonia ice clouds cover only very small regions on the planet (see, respectively Baines et al. 2002; Wong et al. 2004). As put forward by e.g. Atreya et al. (2005), this apparent contradiction could be explained if the ammonia ice particles are coated by in particlar hydrocarbon haze particles settling from the stratosphere. Thus, only the highest and freshest ammonia ice clouds would show identifiable spectral features. Atreya et al. (2005) also mention that the strength of the spectral features would depend on the sizes and shapes of the ice crystals. In this paper, we assume that the upper tropospheric clouds in our model atmospheres are indeed composed of ammonia ice particles, without modeling specific spectral features.
Our ammonia ice particles are assumed to be spherical with a refractive index of n = 1.48 + 0.01i (assumed to be constant across the spectral region of our interest) (as adopted from Romanescu et al. (2010) and Gibson et al. (2005), for the real and imaginary part respectively) and with their sizes described by a standard size distribution (see Hansen & Travis 1974) with and effective radius reff of 0.5 μm, and an effective variance veff of 0.1 (Stam et al. 2004). We calculate the single scattering properties of the ammonia ice particles using Mie theory as described by de Rooij & van der Stap (1984).
Figure 1 shows the flux and degree of linear polarization Ps of unpolarized incident light with λ = 0.55 μm, 0.75 μm, and 0.95 μm, respectively, that is singly scattered by the ice particles as functions of the planetary phase angle α. Note that α = 180° − Θ, with Θ the conventional single scattering angle, defined as Θ = 0° for forward scattered light. All scattered fluxes have been normalized such that their average over all scattering directions equals one (see Eq. (2.5) of Hansen & Travis 1974). At α = 0° (180°) the light is scattered in the backward (forward) direction. For comparison, we have added the curves for (Rayleigh) scattering by gas molecules at λ = 0.55 μm (these curves are fairly wavelength independent). As can be seen in the figure, our spherical ice particles are moderately forward scattering and the scattered fluxes show a prominent feature (a local minimum) around α = 12° at λ = 0.55 μm, around 20° at 0.75 μm, and (much less pronounced) around 25° at 0.95 μm.
The degree of polarization Ps of the light that is singly scattered by our ammonia ice particles is negative across almost the whole phase angle range. The light is thus polarized parallel to the scattering plane, which contains both the incident and the scattered beams. The local minima in scattered fluxes have associated local minima in Ps (at slightly shifted values of α).
We should note here that the vast majority of giant planets imaged so far, are too hot to contain ammonia ice particles in their atmospheres (see e.g. Bonnefoy et al. 2013; Konopacky et al. 2013). These planets though, are so far away from their parent star and so hot that the contribution of the reflected starlight to the disk-integrated signal is very small in comparison to the thermal radiation of the planets. Even though the thermal radiation can also be polarized (through scattering from the clouds by the inside, see de Kok et al. 2011) these planets are out of the scope of this paper.
 |
Fig. 1 Single scattering F and Ps of our ammonia (NH3) ice cloud particles and the polar haze particles as functions of the planetary phase angle α at three different wavelengths. The curves for the NH3 ice particles are: black, solid line (λ = 0.55 μm), red, dotted line (0.75 μm), green, dashed-dotted line (0.95 μm). The curves for the polar haze particles are: grey, dashed-triple-dotted line (0.55 μm), orange, long-dashed line (0.75 μm), magenta, dashed line (0.95 μm). The blue, dashed lines are the Rayleigh scattering curves at 0.55 μm. |
3.2. Polar haze particles
 |
Fig. 2 Sketch of the two aggregation-mechanisms to build the polar haze particles. With PCA, identical monomers are sticked together until the maximum distance between two monomers is larger than a given limiting distance dc. With CCA, several PCA-particles are combined until the maximum distance between two monomers of the whole particle is larger than dp. |
We model Jupiter’s polar haze particles as randomly oriented aggregates of equally sized spheres. To generate the aggregates (needed for calculating the single scattering properties of these particles), we use a cluster-cluster aggregation (CCA) method that starts with the formation of particle-cluster aggregates (PCA) by sequentially adding spheres from random directions to an existing cluster, as shown in the upper part of Fig. 2. Next, we combine several PCA-particles, as shown in the lower part of Fig. 2. For both PCA and CCA, the coagulation process finishes when the maximum distance between any pair of monomers of the aggregate exceeds a certain limit (in Fig. 2: dc for PCA and dp for CCA). With the later assumption, we limit the size of the generated particles, which is needed due to the computational limitations of the numerical methods to calculate the single scattering properties of the particles (see below). We use CCA-particles rather than PCA-particles in the model atmospheres because they can yield the high polarization values that have been observed at the poles of Jupiter (see e.g. Schmid et al. 2011). Because PCA-particles are more compact, light is on average scattered more within each particle, which decreases the degree of polarization of the scattered light.
Figure 3 shows a model aggregate haze particle that we generated and for which we calculated the single scattering matrices and other optical properties. The particle consists of 94 spherical monomers. The radius of each monomer is approximately 0.035 μm, and the volume-equivalent-sphere radius of the whole particle 0.16 μm. Calculations of the single scattering matrix and other optical properties of these particles were performed using the T-matrix theory combined with the superposition theorem (Mackowski & Mishchenko 2011), at λ = 0.55, 0.75 and 0.95 μm, and adopting a refractive index of 1.5 + i0.001, which corresponds to that of benzene (suggested to exist on the jovian poles by e.g. Friedson et al. 2002). In Fig. 1 we show the flux and polarization of unpolarized incident light that is singly scattered by the haze particles at the three different wavelengths, together with the Rayleigh curves at λ = 0.55 μm. The single scattering albedo of the particles is 0.995 at 0.55 μm.
 |
Fig. 3 A picture of a model aggregate haze particle that we used for our single light scattering calculations. |
 |
Fig. 4 Total flux πFn and degree of polarization Ps of starlight with λ = 0.55 μm that is reflected by a cloud covered model planet. The bottom of the clouds is at 1.0 bar, while the cloud top pressure varies. For the horizontally homogeneous planets, the cloud top pressures are as follows: 0.1 bar (red, dotted line), 0.2 bar (green, dashed line), 0.3 bar (blue, dashed-dotted line), 0.4 bar (grey, dashed-triple-dotted line), 0.5 bar (magenta, long-dashed line). The spatially inhomogeneous planet (black, solid line) has a cloud top pressure of 0.1 bar in the zones, and 0.2 bar in the belts. |
 |
Fig. 5 Total flux πFn and degree of polarization Ps of starlight with λ = 0.55 μm that is reflected by a spatially inhomogeneous model planet. The cloud top pressure is 0.1 bar in the zones and 0.2 bar (black, solid line), 0.3 bar (red, dashed line), 0.4 bar (blue, dashed-dotted line) or 0.5 bar (grey, dashed-triple-dotted line) in the belts. |
 |
Fig. 8 πFn and Ps as functions of the planet’s rotation angle (in degrees), for a Jupiter-like model planet with a spot on its equator. Curves are shown for spots covering 0.3% (blue, dashed-dotted line), 1% (red, dashed line), 2% (green, dotted line), or 4% (black, solid line) of the planetary disk. The planetary phase angle α is 90° and λ = 0.55 μm. Calculations have been done at rotation angle steps of 20°. |
 |
Fig. 9 Reflected flux πFn at λ = 0.55 μm for every pixel on the disk of a Jupiter-like model planet containing clouds in zones and belts, and polar stratospheric hazes at latitudes above (below) 60° (–60°). The phase angles are: 0° (top) and 90° (below). |
 |
Fig. 11 Disk-integrated πFn and Ps as functions of phase angle α for the Jupiter-like model planet with polar hazes as used in Figs. 9 and 10 at: λ = 0.55 μm (black, solid lines), 0.75 μm (red, dotted lines), and 0.95 μm (green, dashed lines). Also shown are the lines for model planets with the clouds but without the hazes: λ = 0.55 μm (blue, dashed-dotted lines), 0.75 μm (grey, dashed-triple-dotted lines), and 0.95 μm (magenta, long-dashed lines). |
From comparing the different lines in Fig. 1, it is clear that the haze particles are more forward scattering than the ammonia ice particles, and that their scattered flux shows less angular features. The degree of linear polarization of the light scattered by the haze particles is very different from that of the cloud particles: it is positive at almost all phase angles (hence the light is polarized perpendicular to the scattering plane) and it reaches values larger than 0.7 near α = 90°. The main reason that the polarization phase function of the haze particles differs strongly from that of the cloud particles while their flux phase functions are quite similar, is that the latter depends mostly on the size of the whole particle, while the polarization phase function depends more on the size of the smallest scattering particles, which have radii of about 0.035 μm, in the case of the aggregate particles.
The maximum single scattering polarization of our aggregate particles is slightly higher than that derived by West & Smith (1991). This is most likely due to the properties of our haze particles: our monomers are smaller than those used by West & Smith (1991), which have radii near 0.06 μm, sometimes mixed with monomers with radii of 0.03 μm. In addition, the particles in West & Smith (1991) were generated using the diffusion-limited aggregation (DLA) method, in which monomers follow random paths toward the aggregate, and which yields more compact particles than those produced by our CCA-method (see Meakin 1983).
4. Reflected flux and polarization signals of the model planets
In this section, we present fluxes and degrees of linear polarization for three different types of spatial inhomogeneities that occur on gaseous planets in the Solar System: zones and belts (Sect. 4.1), cyclonic spots (Sect. 4.2), and polar hazes (Sect. 4.3). We will compare the flux and polarization signals of the spatially inhomogeneous planets with those of horizontally homogeneous planets to investigate whether or not such spatial inhomogeneities would be detectable.
4.1. Zones and belts
The model atmospheres in this section contain only clouds, no hazes. Figures 4–7 show the flux πFn and the degree of linear polarization Ps as functions of α at λ = 0.55 μm (Fig. 4), 0.75 μm (Fig. 6), and 0.95 μm (Fig. 7), for horizontally homogeneous planets with the bottom of the cloud layer at 1.0 bar, and the top at 0.1, 0.2, 0.3, 0.4, or 0.5 bar. Also shown in these figures, are πFn and Ps for horizontally inhomogeneous model planets each with a cloud top pressure of 0.1 bar in the zones and with cloud top pressures ranging from 0.2 bar (Figs. 4, 6 and 7) to 0.5 bar (Fig. 5) in the belts. The latitudinal borders of the zones and belts have been described in Sect. 2.3.
For each model planet and each wavelength, total flux πFn at α = 0° equals the planet’s geometric albedo AG. With increasing wavelength, AG decreases slightly, because of the decreasing cloud optical thickness with λ, and the decreasing single scattering phase function in the backscattering direction (see Fig. 1). With increasing α, πFn decreases smoothly for all model atmospheres. The angular feature around α = 12° for the horizontally homogeneous planets with the highest cloud layers, can be retraced to the single scattering phase function (Fig. 1). The strength of the feature in the planetary phase functions decreases with λ, just like that in the single scattering phase functions. The decrease of the feature with increasing cloud top pressure is due to the increasing thickness of the gas layer overlying the clouds. With increasing λ, the difference between the total fluxes reflected by the model atmospheres decreases, mostly because of the decrease of Rayleigh scattering above the clouds with λ.
Interestingly, πFn is insensitive to the cloud top pressure around α = 125° at λ = 0.55 μm (Fig. 4). With increasing λ, the phase angle where this insensitivity occurs decreases: from about 110° at λ = 0.75 μm (Fig. 6), to about 90° at λ = 0.95 μm (Fig. 7). Thus precisely across the phase angle range where exoplanets are most likely to be directly detected because they are furthest from their star, reflected fluxes do not give access to the cloud top altitudes.
The degree of linear polarization, Ps, shows the typical bell-shape around approximately α = 90°, that is due to Rayleigh scattering of light by gas molecules (Fig. 4). With increasing cloud top altitude, hence decreasing Rayleigh scattering optical thickness above the clouds, the features of the single scattering phase function of the cloud particles become more prominent. This is especially obvious at the longer wavelengths, i.e. at 0.75 μm and 0.95 μm, where the Rayleigh scattering optical thickness above the clouds is smaller by factors of about (0.55/0.75)4 and (0.55/0.95)4, respectively (Figs. 6 and 7). In particular, the negative polarized feature below α = 30°, that is due to light singly scattered by the cloud particles (see Fig. 1) becomes more prominent.
Figure 4 clearly shows that, unlike the reflected flux, Ps is sensitive to cloud top altitudes across planetary phase angles that are important for direct detections. The reason is that Ps is very sensitive to the Rayleigh scattering optical thickness above the clouds, as has been known for a long time from observations of Solar System planets, such as the ground-based observations of Venus (Hansen & Hovenier 1974), and remote-sensing observations of the Earth by instruments such as POLDER on low-orbit satellites (Knibbe et al. 2000). As expected, with increasing λ, the sensitivity of Ps to the cloud top altitude decreases (see Figs. 6 and 7).
Figures 4–7 also show πFn and Ps of horizontally inhomogeneous planets with zones and belts. In all figures, the cloud top pressure of the zones is 0.1 bar while that at the top of the belts varies from 0.2 bar (Figs. 4, 6, and 7) to 0.5 bar (Fig. 5). The shapes of the flux and polarization phase functions of these horizontally inhomogeneous planets are very similar to those of the horizontally homogeneous planets: one could easily find a horizontally homogeneous model planet with a cloud top pressure between 0.1 and 0.3 bar that would fit the curves pertaining to the horizontally inhomogeneous planets. The cloud top pressure that would provide the best fit would be slightly different when fitting the flux or the polarization curves. For example, fitting the flux reflected by an inhomogeneous planet with cloud top pressures in the belts at 0.4 bar (blue dashed-dotted line of Fig. 5) would require a homogeneous planet with its cloud top pressure at 0.2 bar, while fitting the polarization would require a cloud top pressure of about 0.18 bar. Such small differences would most likely disappear in the measurement errors. With increasing λ, the effects of the cloud top pressure decrease, in particular in πFn. Covering a broad spectral region would thus not help in narrowing the cloud pressures down.
4.2. Cyclonic spots
Other spatial features on giant planets in our Solar System are (anti-)cyclonic storms that show up as oval-shaped spots. Famous examples are Jupiter’s Great Red Spot (GRS) that appears to have been around for several hundreds of years and Neptune’s Great Dark Spot (GDS) that was discovered in 1989 by Voyager-2, but that seems to have disappeared (Hammel et al. 1995). Recent spots on Uranus were presented by Hammel et al. (2009) and Sromovsky et al. (2012). To study the effect of localized spots on reflected flux and polarization signals of exoplanets, we use a Jupiter-like model atmosphere with a spot of NH3 ice clouds extending between 0.75 and 0.13 bar. The clouds in the spot have an optical thickness of 36 at λ = 0.5 μm (Simon-Miller et al. 2001). We model the spot as a square of 26° in longitude by 22° in latitude with an optical thickness of ~30 at 0.55 μm. Additionally, our model planet has zones and belts spatially distributed across the planet as described before, extending between 0.56 to 0.18 bar in the zones, and from 1.0 to 0.5 bar in the belts. The cloud optical thickness in the belts is 6.02, and in the zones 21.0 at λ = 0.75 μm.
Figure 8 shows reflected fluxes πFn and degree of polarization Ps at λ = 0.55 μm, as functions of the planet’s rotation angle. The planet’s phase angle is 90°. The spot is on the planet’s equator (which coincides with the planetary scattering plane). Recall that both Jupiter and Saturn have rotation periods on the order of 10 h, while Uranus and Neptune rotate in about 17 and 16 h, respectively. With a 10-h rotation period and α = 90°, a small spot would cross the illuminated and visible part of the disk in about 2.5 h. Curves are shown for different sizes of the spot: covering at maximum 0.3%, 1%, 2%, or 4% of the planet’s disk, respectively. For comparison: the GRS covers about 6% of Jupiter’s disk. Note that the calculations for Fig. 8 have been done per 20° rotation of the planet, due to computational restrictions.
As can be seen in Fig. 8, the reflected fluxes πFn hardly change upon the passage of the spot across the illuminated and visible part of the planetary disk: even for the largest spot located at the equator, the maximum change in πFn is a few percent. In Ps, the transiting spots also leave a change of at most a few percent (absolute, since Ps is a relative measure itself). For spots located at higher latitudes of the planet, the effects are even smaller. With increasing wavelength, the sensitivity of both πFn and Ps to the cloud top altitude decreases. At longer wavelengths, the effects of a spot would thus be smaller than shown in Fig. 8.
4.3. Polar hazes
The poles of Jupiter and Saturn are covered by stratospheric hazes. In particular, when seen at phase angles around 90°, Jupiter’s polar hazes yield strongly polarized signals. This high polarization can be explained by haze particles that consist of aggregates of particles that are small compared to the wavelength, and that polarize the incident sunlight as Rayleigh scatterers (West & Smith 1991), with a high degree of polarization at scattering angles around 90°. We are interested in whether strongly polarized polar hazes will leave a trace in the disk-integrated polarization signal of a planet.
We use a Jupiter-like model planet with clouds in belts and zones as in Sect. 4.1. The cloud top pressure of the belts is 0.3 bar. Starting at latitudes of 60°, the north and south poles of each model planet are covered by polar haze particles as described in Sect. 3.2. The optical thickness of the haze is 0.2 at λ = 0.55, 0.75, and 0.95 μm.
In Figs. 9 and 10, we show, respectively πFn and P at λ = 0.55 μm of starlight that is locally reflected by pixels on the visible and illuminated part of the planetary disk for α = 0° and 90°. In Fig. 11, we have plotted the disk-integrated reflected flux πFn and degree of polarization Ps as functions of α, for the Jupiter-like model planet with and without polar hazes, and for λ = 0.55, 0.75, and 0.95 μm.
The reflected flux across the planetary disk (Fig. 9) shows clear differences between the zones and the belts, especially around the center of the planetary disk (for both values of α). The reflected fluxes due to the polar hazes do not stand out against those due to the clouds in the belts and the zones. The reflected flux pattern across the visible and illuminated part fo the planetary disk for α = 90° is very similar to that for α = 0°, with the brightest regions in the center, and the darkest at the limb and, for α = 90°, at the terminator. Integrated across the planetary disk (Fig. 11), there is very little difference between πFn of the planets with and without haze. From the disk-integrated reflected fluxes it would thus be impossible to derive the presence of the polar hazes. Note that our simulations pertain to broadband fluxes. Observations across gaseous absorption bands, such as those of methane, could provide more information about the presence of hazes, because the latter would decrease the depths of the bands (see e.g. Stam et al. 2004). Of course, in order to use absorption band depths to derive altitudes of hazes and/or clouds, independent information about the mixing ratios of the absorbing gases would be essential.
The degree of polarization across the planetary disk (Fig. 10), also show clear differences between the zones and the belts, but mostly near the limb and, for α = 90°, the terminator of the planet. For α = 0°, the observed light has been scattered in the backward direction, and the degree of polarization is close to zero across the central region of the disk. Toward the limb, the degree of polarization increases to reach values as high as 0.15 toward the northern and southern limbs, and then it decreases again. The relatively high polarization values are due to significantly polarized second order scattered light (the singly scattered light contributes virtually no polarized light), while the low values at the limb are due to light that has been singly scattered in the backscattering direction (cf. Fig. 1).
For α = 90°, the scattering angle of the singly scattered light is 90° (cf. Fig. 1). The degree of polarization is a few percent at the center of the illuminated and visible part of the planetary disk, where the contribution of multiple scattered light is significant, and increases toward the terminator and the limb. The higher values (up to 0.90 toward the northern and southern limbs, and up to 0.50 toward the western limb and terminator) are due to singly scattered light. We have repeated our calculations for λ = 0.75 (not shown), and found that for α = 0° the polar hazes produce a fractional polarization signal Q/F of ~ 6%, which is similar to what was observed in that wavelength range by Schmid et al. (2011). The degree of polarization due to the polar hazes will depend strongly on the single scattering polarization phase function of the particles and hence on the wavelength. Kolokolova & Mackowski (2012) present calculated polarization phase functions of large fluffy and compact aggregates with application to polarization observations of comets, and clearly show the increase of the maximum degree of polarization around α = 90° (Θ = 90°) with increasing λ for particles built using the CCA-method.
While the polar hazes strongly influence the degree of polarization of local regions on the model planet, integrated across the planetary disk (Fig. 11), they have a small (λ = 0.55 μm) to negligible (λ = 0.95 μm) influence. Like with the reflected fluxes (see above), the polar hazes could have a stronger effect across gaseous absorption bands, where the observed reflected starlight originates from higher altitudes in the planetary atmosphere.
5. Summary and conclusions
In view of upcoming instruments for the direct detections of fluxes and polarization signals of starlight that is reflected by orbiting exoplanets, like SPHERE (Dohlen et al. 2008; Roelfsema et al. 2011) on the VLT, GPI (Macintosh et al. 2008) on the Gemini North telescope, and, further in the future, EPICS (Kasper et al. 2010) on the E-ELT, we have presented numerically calculated disk-integrated, broadband flux and polarization signals of horizontally inhomogeneous gaseous exoplanets in order to investigate whether or not spatial inhomogeneities such as those found on gas giants in the Solar System could be identified on gaseous exoplanets. The spatial inhomogeneities that we have modeled are: cloud top altitudes belts and zones due to varying cloud top altitudes (Sect. 4.1), cyclonic spots (Sect. 4.2), and polar hazes (Sect. 4.3).
We have calculated the total flux and polarization signals of the exoplanets due to the mentioned spatial inhomogeneities using an adding-doubling radiative transfer code that fully includes all orders of scattering and linear and circular polarization. Here, we ignore the circular polarization because it is very small and neglecting it does not introduce significant errors in the calculated total and linearly polarized fluxes (Stam & Hovenier 2005). Circular polarization will also not be measured by the above mentioned instruments. We only consider exoplanets in wide orbits, such that they can be spatially resolved from their parent star, and ignore diffracted light from the parent star and starlight that is scattered by e.g. exozodiacal dust in the planetary system (we thus assume that the observations can be corrected for these two types of background signals).
A version of the adding-doubling radiative transfer code that handles vertically inhomogeneous, but horizontally homogeneous exoplanets has been described by Stam et al. (2004). In our version of the code (see Karalidi & Stam 2012; Karalidi et al. 2012), we divide a horizontally inhomogeneous planet into horizontally homogeneous pixels. For each pixel, we calculate the reflected total and polarized fluxes and add up these local fluxes (including rotations between local and planetary reference planes for the polarized fluxes) to obtain the disk-integrated total and polarized fluxes at a given planetary phase angle. We compare signals calculated for horizontally inhomogeneous planets with those of horizontally homogeneous planets to investigate the appearance of the spatial inhomogeneities in the disk-integrated signals.
Cyclonic spots on a planet will rotate in and out of the view of the observer depending on their daily rotation periods (because we consider exoplanets in wide orbits, they are unlikely to be tidally locked to their star), and will thus give rise to time-varying total and polarized fluxes. Our model exoplanets with zones and belts, and those with the polar hazes are symmetric with respect to their axis of rotation. The total flux and polarization signals of these planets will thus depend on the planetary phase angle, but not on daily rotations of a planet. For these model exoplanets, the presence of horizontal inhomogeneities could presumably be derived from different effects the inhomogeneities have on the total flux and on the degree of linear polarization of the reflected starlight.
Our Jupiter-like model exoplanets have thick cloud layers consisting of spherical ammonia ice particles. In Sect. 4.1, we model belts and zones by choosing different pressure levels for the tops of the clouds, while the base of the clouds is fixed at 1 bar. The pressure at the top of the zonal clouds is fixed at 0.1 bar, while the pressure at the top of the belts is varied between 0.2 bar and 0.5 bar. Comparing the total and polarized fluxes of the horizontally inhomogeneous planets with those of horizontally homogeneous cloudy planets, it is clear that both the reflected total fluxes and the polarization are sensitive to the cloud top altitude. The polarization appears to be more useful to derive cloud top altitudes than the reflected flux, because the polarization is most sensitive to the cloud top altitude at planetary phase angles around 90°, which are favorable for direct imaging of exoplanets. At these phase angles, the sensitivity of the total flux to the cloud top altitude is small, and it decreases with increasing wavelength, because of the decreasing Rayleigh scattering optical thickness above the clouds.
The shape of the polarization phase function for a planet with belts and zones is very similar to that of a horizontally homogeneous planet with a cloud top pressure between that of the zones and the belts (the precise value depends on the latitudes covered by the belts and zones and by the cloud top pressures across the belts and the zones). Combining polarization phase functions at different broadband wavelengths will not help to reveal the presence of horizontal inhomogeneities. Combining total flux phase functions with polarization phase functions will also fail to reveal the presence of inhomogeneities because of the lack of sensitivity of the total flux phase functions to the cloud top pressures, especially at the phase angles that are favorable for polarimetry (by lack of independent information about the planet radius, the total flux phase functions will also have error bars that preclude deriving meaningful cloud top pressures from them).
We model a cyclonic spot as a localized cloudy region with a lower cloud top pressure than the surrounding clouds: in the spot, the cloud top pressure is 0.13 bar, while outside the spot, the cloud top pressure is 0.5 bar at the edges and 0.18 bar at the central latitudes. Our results for model planets with a cyclonic spot on the planet’s equator that covers about 4% of the planetary disk show that the change in the reflected total flux as the spot moves in and out of view of the observer is less than a percent at a planetary phase angle of 90°. The change in the degree of polarization is a few percent (in absolute sense). The temporal changes in the total flux and the degree of polarization decrease if the spot is located further away from the planetary scattering plane. If a planet has more than one spot, a temporal analysis of flux and polarization time series might reveal the locations and sizes of the most prominent spots.
Polar hazes that very likely consist of aggregates of small monomers cover the poles of Jupiter and Saturn, yielding a locally relatively high degree of polarization (West & Smith 1991). We modeled polar hazes on Jupiter-like planets using fluffy aggregates covering latitudes north and southwards of, respectively, 60° and –60°. In the locally reflected total fluxes (i.e. spatially resolved across the planet), the polar hazes do not leave a significant trace, and, not surprisingly, neither do they in the disk-integrated total fluxes. In the degree of polarization of the locally reflected light, the polar hazes do show up. At a phase angle of 0°, light that has been scattered twice by the haze particles has a relatively high degree of polarization (compared to the light that has been singly scattered in the backward direction by the gas molecules or the haze particles, and that is virtually unpolarized). At a phase angle of 90°, light that has been singly scattered by the haze particles has a high degree of polarization, because the monomers that form the aggregated haze particles scatter like Rayleigh scatterers.
When integrated over the planetary disk, however, the polar hazes change the degree of linear polarization by only a few percent when compared to a planet without polar hazes at λ = 0.55 μm, and less at longer wavelengths. The shape of the polarization phase function of the planet with polar hazes is similar to that without hazes.
Finally, we note that the vast majority of giant planets discovered so far are very hot (see e.g. Knutson et al. 2012; de Mooij et al. 2013) and their atmospheric chemistry and temperature-pressure profiles vary considerably from those of the giant planets of our solar system (see e.g. Moses et al. 2011; Huitson et al. 2012; Madhusudhan 2012, and references there in). While these close-in planets orbit too close to their parent star to be directly detectable and are thus out of the scope of this paper, they have taught us that giant planets can exhibit a large variety of properties. Even the exoplanets that orbit a few AU from their parent star, and that could thus be directly detectable, might be shown in the near future to vary considerably in their properties.
References
- Atreya, S. K., Wong, A. S., Baines, K. H., Wong, M. H., & Owen, T. C. 2005, Planet. Space Sci., 53, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., Auvergne, M., Barge, P., et al. 2006, in ESA SP, 1306, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, 33 [Google Scholar]
- Baines, K. H., Carlson, R. W., & Kamp, L. W. 2002, Icarus, 159, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V., Berdyugin, A. V., Fluri, D. M., & Piirola, V. 2008, ApJ, 673, L83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V., Berdyugin, A. V., Fluri, D. M., & Piirola, V. 2011, ApJ, 728, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnefoy, M., Boccaletti, A., Lagrange, A.-M., et al. 2013, A&A, 555, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Haan, J. F., Bosma, P. B., & Hovenier, J. W. 1987, A&A, 183, 371 [NASA ADS] [Google Scholar]
- de Kok, R. J., Helling, C., Stam, D. M., Woitke, P., & Witte, S. 2011, A&A, 531, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mooij, E. J. W., Brogi, M., de Kok, R. J., et al. 2013, A&A, 550, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Pater, I., & Lissauer, J. J. 2001, Planetary Sciences [Google Scholar]
- de Rooij, W. A., & van der Stap, C. C. A. H. 1984, A&A, 131, 237 [NASA ADS] [Google Scholar]
- Deleuil, M. 2010, in COSPAR, Plenary Meeting, 2, 38th COSPAR Scientific Assembly. Held 18–15 July 2010, in Bremen, Germany, 2509 [Google Scholar]
- Dohlen, K., Langlois, M., Saisse, M., et al. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- Friedson, A. J., Wong, A.-S., & Yung, Y. L. 2002, Icarus, 158, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, J., Welch, W. J., & de Pater, I. 2005, Icarus, 173, 439 [Google Scholar]
- Hammel, H. B., Lockwood, G. W., Mills, J. R., & Barnet, C. D. 1995, Science, 268, 1740 [NASA ADS] [CrossRef] [Google Scholar]
- Hammel, H. B., Sromovsky, L. A., Fry, P. M., et al. 2009, Icarus, 201, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, J. E., & Hovenier, J. W. 1974, J. Atmosph. Sci., 31, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, J. E., & Travis, L. D. 1974, Space Sci. Rev., 16, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Hovenier, J. W., Van der Mee, C., & Domke, H. 2004, Transfer of polarized light in planetary atmospheres: basic concepts and practical methods, Astrophys. Space Sci. Lib., 318 [Google Scholar]
- Huitson, C. M., Sing, D. K., Vidal-Madjar, A., et al. 2012, MNRAS, 422, 2477 [NASA ADS] [CrossRef] [Google Scholar]
- Ingersoll, A. P., Dowling, T. E., Gierasch, P. J., et al. 2004, Dynamics of Jupiter’s atmosphere, eds. F. Bagenal, T. E. Dowling, & W. B. McKinnon, 105 [Google Scholar]
- Karalidi, T., & Stam, D. M. 2012, A&A, 546, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karalidi, T., Stam, D. M., & Hovenier, J. W. 2011, A&A, 530, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karalidi, T., Stam, D. M., & Hovenier, J. W. 2012, A&A, 548, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kasper, M., Beuzit, J.-L., Verinaud, C., et al. 2010, in SPIE Conf. Ser., 7735 [Google Scholar]
- Kemp, J. C., Henson, G. D., Steiner, C. T., & Powell, E. R. 1987, Nature, 326, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Knibbe, W. J. J., de Haan, J. F., Hovenier, J. W., et al. 2000, J. Quant. Spec. Radiat. Transf., 64, 173 [Google Scholar]
- Knutson, H. A., Lewis, N., Fortney, J. J., et al. 2012, ApJ, 754, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, D. G., Borucki, W., Webster, L., et al. 1998, in SPIE Conf. Ser. 3356, eds. P. Y. Bely, & J. B. Breckinridge, 599 [Google Scholar]
- Kolokolova, L., & Mackowski, D. 2012, J. Quant. Spec. Radiat. Transf., 113, 2567 [NASA ADS] [CrossRef] [Google Scholar]
- Konopacky, Q. M., Barman, T. S., Macintosh, B. A., & Marois, C. 2013, Science, 339, 1398 [NASA ADS] [CrossRef] [Google Scholar]
- Macintosh, B. A., Graham, J. R., Palmer, D. W., et al. 2008, in SPIE Conf. Ser., 7015 [Google Scholar]
- Mackowski, D. W., & Mishchenko, M. I. 2011, J. Quant. Spec. Radiat. Transf., 112, 2182 [Google Scholar]
- Madhusudhan, N. 2012, ApJ, 758, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Meakin, P. 1983, Phys. Rev. A (General Physics), 27, 1495 [Google Scholar]
- Mishchenko, M. I. 1990, Icarus, 84, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Moses, J. I., Visscher, C., Fortney, J. J., et al. 2011, ApJ, 737, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Mayor, M., Queloz, D., et al. 2004, A&A, 423, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roelfsema, R., Gisler, D., Pragt, J., et al. 2011, in SPIE Conf. Ser., 8151 [Google Scholar]
- Romanescu, C., Marschall, J., Kim, D., Khatiwada, A., & Kalogerakis, K. S. 2010, Icarus, 205, 695 [Google Scholar]
- Saar, S. H., & Seager, S. 2003, in Scientific Frontiers in Research on Extrasolar Planets, eds. D. Deming, & S. Seager, ASP Conf. Ser., 294, 529 [Google Scholar]
- Sato, M., & Hansen, J. E. 1979, J. Atmosph. Sci., 36, 1133 [Google Scholar]
- Schmid, H. M., Joos, F., Buenzli, E., & Gisler, D. 2011, Icarus, 212 [Google Scholar]
- Seager, S., Whitney, B. A., & Sasselov, D. D. 2000, ApJ, 540, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Simon-Miller, A. A., Banfield, D., & Gierasch, P. J. 2001, Icarus, 154, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, P. H., & Tomasko, M. G. 1984, Icarus, 58, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Sromovsky, L. A., Hammel, H. B., de Pater, I., et al. 2012, Icarus, 220, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Stam, D. M. 2003, in Earths: DARWIN/TPF and the Search for Extrasolar Terrestrial Planets, eds. M. Fridlund, T. Henning, & H. Lacoste, ESA SP, 539, 615 [Google Scholar]
- Stam, D. M. 2008, A&A, 482, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stam, D. M., & Hovenier, J. W. 2005, A&A, 444, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stam, D. M., De Haan, J. F., Hovenier, J. W., & Stammes, P. 1999, J. Geophys. Res., 104, 16843 [NASA ADS] [CrossRef] [Google Scholar]
- Stam, D. M., Hovenier, J. W., & Waters, L. B. F. M. 2004, A&A, 428, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stam, D. M., de Rooij, W. A., Cornet, G., & Hovenier, J. W. 2006, A&A, 452, 669 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Tomasko, M. G., Doose, L. R., Dafoe, L. E., & See, C. 2009, Icarus, 204, 271 [NASA ADS] [CrossRef] [Google Scholar]
- West, R. A., & Smith, P. H. 1991, Icarus, 90, 330 [NASA ADS] [CrossRef] [Google Scholar]
- West, R. A., Hart, H., Hord, C. W., et al. 1983, J. Geophys. Res., 88, 8679 [NASA ADS] [CrossRef] [Google Scholar]
- West, R. A., Baines, K. H., Friedson, A. J., et al. 2004, in Jupiter. The planet, satellites and magnetosphere, eds. F. Bagenal, T. E. Dowling, & W. B. McKinnon (CUP), 79 [Google Scholar]
- Wong, M. H., Bjoraker, G. L., Smith, M. D., Flasar, F. M., & Nixon, C. A. 2004, Planet. Space Sci., 52, 385 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Single scattering F and Ps of our ammonia (NH3) ice cloud particles and the polar haze particles as functions of the planetary phase angle α at three different wavelengths. The curves for the NH3 ice particles are: black, solid line (λ = 0.55 μm), red, dotted line (0.75 μm), green, dashed-dotted line (0.95 μm). The curves for the polar haze particles are: grey, dashed-triple-dotted line (0.55 μm), orange, long-dashed line (0.75 μm), magenta, dashed line (0.95 μm). The blue, dashed lines are the Rayleigh scattering curves at 0.55 μm. |
| In the text | |
 |
Fig. 2 Sketch of the two aggregation-mechanisms to build the polar haze particles. With PCA, identical monomers are sticked together until the maximum distance between two monomers is larger than a given limiting distance dc. With CCA, several PCA-particles are combined until the maximum distance between two monomers of the whole particle is larger than dp. |
| In the text | |
 |
Fig. 3 A picture of a model aggregate haze particle that we used for our single light scattering calculations. |
| In the text | |
 |
Fig. 4 Total flux πFn and degree of polarization Ps of starlight with λ = 0.55 μm that is reflected by a cloud covered model planet. The bottom of the clouds is at 1.0 bar, while the cloud top pressure varies. For the horizontally homogeneous planets, the cloud top pressures are as follows: 0.1 bar (red, dotted line), 0.2 bar (green, dashed line), 0.3 bar (blue, dashed-dotted line), 0.4 bar (grey, dashed-triple-dotted line), 0.5 bar (magenta, long-dashed line). The spatially inhomogeneous planet (black, solid line) has a cloud top pressure of 0.1 bar in the zones, and 0.2 bar in the belts. |
| In the text | |
 |
Fig. 5 Total flux πFn and degree of polarization Ps of starlight with λ = 0.55 μm that is reflected by a spatially inhomogeneous model planet. The cloud top pressure is 0.1 bar in the zones and 0.2 bar (black, solid line), 0.3 bar (red, dashed line), 0.4 bar (blue, dashed-dotted line) or 0.5 bar (grey, dashed-triple-dotted line) in the belts. |
| In the text | |
 |
Fig. 6 Same as in Fig. 4, except for λ = 0.75 μm. |
| In the text | |
 |
Fig. 7 Same as in Fig. 4, except for λ = 0.95 μm. |
| In the text | |
 |
Fig. 8 πFn and Ps as functions of the planet’s rotation angle (in degrees), for a Jupiter-like model planet with a spot on its equator. Curves are shown for spots covering 0.3% (blue, dashed-dotted line), 1% (red, dashed line), 2% (green, dotted line), or 4% (black, solid line) of the planetary disk. The planetary phase angle α is 90° and λ = 0.55 μm. Calculations have been done at rotation angle steps of 20°. |
| In the text | |
 |
Fig. 9 Reflected flux πFn at λ = 0.55 μm for every pixel on the disk of a Jupiter-like model planet containing clouds in zones and belts, and polar stratospheric hazes at latitudes above (below) 60° (–60°). The phase angles are: 0° (top) and 90° (below). |
| In the text | |
 |
Fig. 10 Same as in Fig. 9 except for Ps. Note the different color scales. |
| In the text | |
 |
Fig. 11 Disk-integrated πFn and Ps as functions of phase angle α for the Jupiter-like model planet with polar hazes as used in Figs. 9 and 10 at: λ = 0.55 μm (black, solid lines), 0.75 μm (red, dotted lines), and 0.95 μm (green, dashed lines). Also shown are the lines for model planets with the clouds but without the hazes: λ = 0.55 μm (blue, dashed-dotted lines), 0.75 μm (grey, dashed-triple-dotted lines), and 0.95 μm (magenta, long-dashed lines). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


