| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321473 | |
| Published online | 28 June 2013 | |
Understanding angular momentum transport in red giants: the case of KIC 7341231
1
Laboratoire AIM Paris-Saclay, CEA/DSM/IRFU/SAp – CNRS – Université
Paris Diderot, Centre de
Saclay, 91191
Gif-sur-Yvette Cedex,
France
e-mail: tugdual.ceillier@cea.fr
2
Observatoire de Genève, Université de Genève,
51 chemin des Maillettes,
1290
Sauverny,
Suisse
Received: 14 March 2013
Accepted: 21 May 2013
Context. Thanks to recent asteroseismic observations, it has been possible to infer the radial differential rotation profile of subgiants and red giants.
Aims. We want to reproduce the observed rotation profile of the early red giant KIC 7341231 through modeling and constrain the physical mechanisms responsible for angular momentum transport in stellar interiors.
Methods. We computed models of KIC 7341231 including a treatment of shellular rotation, and we compared the rotation profiles obtained with the one derived from observations. We then modify some modeling parameters in order to quantify their effect on the obtained rotation profile. Moreover, we mimicked a powerful angular momentum transport during the main sequence and studied its effect on the evolution of the rotation profile during the subgiant and red giant phases.
Results. We show that meridional circulation and shear mixing alone produce a rotation profile for KIC 7341231 that is too steep compared to the observed one. An additional mechanism is then needed to increase the internal transport of angular momentum. We find that this undetermined mechanism has to be efficient not only during the main sequence but also during the much quicker subgiant phase. Moreover, we point out the importance of studying the whole rotational history of a star to explain its rotation profile during the red giant evolution.
Key words: stars: rotation / stars: oscillations / stars: evolution
© ESO, 2013
1. Introduction
Stellar evolution is a very complex process, still not fully understood. It is driven by many different physical mechanisms, among which rotation is known to be playing a very important part (e.g. Pinsonneault et al. 1990; Eggenberger et al. 2010b; Maeder 2009). The transport of chemical elements and angular momentum by the large-scale meridional circulation and shear mixing, both induced by rotation, can strongly modify the global evolution of a star (Zahn 1992; Maeder & Zahn 1998; Mathis & Zahn 2004). That is why this transport has been included in stellar evolution codes. This implementation follows the shellular rotation hypothesis, which assumes that a strong horizontal turbulent transport in stably stratified stellar radiation zones leads to an angular velocity constant on the isobars that thus depends almost only on the radius (Meynet & Maeder 2000; Decressin et al. 2009). To validate these models, it is now necessary to compare their results to observations.
Observational characteristics of KIC 7341231.
The first constraints that can be used to evaluate the efficiency of rotational mixing in stars are the surface abundances. The influence of rotation has indeed been studied on the abundances of light elements (e.g. Pinsonneault 2010) and on the evolution of the lithium depletion (e.g. Eggenberger et al. 2012a). That the models including shellular rotation are unable to reproduce lithium abundance in certain cases (Talon & Charbonnel 2003) is a first clue that an additional physical process is at work in the internal layers of low-mass stars (Charbonnel & Talon 2005).
Another way to compare the results of modeling on angular momentum transport with reality is to look directly at observations of rotation in stars. The more straightforward way of doing so is to study the measurements of surface rotation. Such studies tend to show that young solar-type stars in rapid rotation would demonstrate a solid-body rotation (see for instance Denissenkov et al. 2010), which is a sign of a strong coupling between the core and the envelope, which is not accounted for by meridional circulation and shear mixing alone (Eggenberger et al. 2010a). This is yet another indication that models are missing another transport and mixing process.
One can then go deeper into stars by means of helio- and asteroseimology. The study of stellar oscillations is indeed used to probe their internal layers. As for the Sun, the vast amount of seismological observations have made it possible to derive its rotation profile from the surface to the most inner parts (e.g. Mathur et al. 2008; García et al. 2007; Thompson et al. 1996; Elsworth et al. 1995). The resulting profile is almost flat down to 0.2 R⊙, while solar models tend to produce a steeper profile (e.g. Turck-Chièze et al. 2010; Pinsonneault et al. 1989), showing once again the need for an additional coupling process.
To this day, two possible mechanisms have been investigated. The first one implies fossil magnetic fields trapped during the early phases of the star evolution (Braithwaite & Spruit 2004; Duez & Mathis 2010). These magnetic fields are able to transport angular momentum thanks to Maxwell stresses, large-scale torques and magnetic instabilities (e.g. Gough & McIntyre 1998; Mathis & Zahn 2005; Garaud & Garaud 2008; Strugarek et al. 2011; Eggenberger et al. 2005). The second one consists of internal gravity waves, excited at the limit between the convective and radiative zones. These waves can indeed transport angular momentum through radiative zones (e.g. Press 1981; Goldreich & Nicholson 1989; Schatzman 1993; Zahn et al. 1997; Talon & Charbonnel 2005; Mathis & de Brye 2012).
The launch of space missions such as CoRoT (Baglin et al. 2006) and Kepler (Borucki et al. 2010) have given access to long high-precision light curves for a huge number of stars. Many of these stars exhibit solar-like oscillations at different evolutionary stages, from the main sequence (see for instance Appourchaux et al. 2008; García et al. 2009; Chaplin et al. 2011; Ballot et al. 2011; Metcalfe et al. 2012; Mathur et al. 2013) to more advanced stages, such as subgiants (Mathur et al. 2011; Campante et al. 2011, among others) and red giants (e.g. Huber et al. 2011; Bedding et al. 2010; Mosser et al. 2010, 2012; Di Mauro et al. 2011) which allowed probing stellar interiors. Moreover, the study of the dynamics of stars requires such long time series. The existence of surface magnetic activity, for instance, has made it possible to constrain the surface rotation (Mathur et al. 2010; Fröhlich et al. 2012), as well as to measure activity cycles (García et al. 2010).
Furthermore, precise analysis of the rotational splittings of the oscillations modes can strongly constrain the internal rotation profile of main sequence stars (Ballot et al. 2011), young red giants (Deheuvels et al. 2012) and evolved red giants (Beck et al. 2012; Mosser et al. 2012). These splittings have been precisely determined for the red giant KIC 8366239 by Beck et al. (2012). Eggenberger et al. (2012b) and Marques et al. (2013) have shown that models including shellular rotation predict a steep rotation profile that is incompatible with the measured splittings. Eggenberger et al. (2012b) also demonstrated that the asteroseismic measurements strongly constrain the efficiency of the needed additional mechanism for the angular momentum transport.
In this work, we study the case of KIC 7341231, a low-mass and low-metallicity halo early red giant. The very fine observations of this star by Kepler have allowed precise measurement of rotational splittings of mixed modes by Deheuvels et al. (2012), who were able to constrain the radial rotation profile of this star by deriving the core’s rotation rate and an upper limit for the surface’s rotation rate. In the present paper we present modeling of KIC 7341231 in order to compare the modeled radial rotation profile with the observed one. In Sect. 2, we present the known characteristics of KIC 7341231. We then explain how we modeled the star and discuss our first results in Sect. 3, while the influence of varying various parameters of the model on the obtained radial differential profile is studied in Sect. 4. Section 5 then presents the modifications of the modeling so as to mimic a strong angular momentum transport on the main sequence and their consequences on the deduced rotation, and in Sect. 6 we focus on the subgiant evolution and the different angular momentum transports during this phase. Finally, our conclusions are given in Sect. 7.
2. Modeled star: KIC 7341231
KIC 7341231, also known as HIP 92775 and G205-42, is an early red giant with a mass of about 0.84 M⊙. Its Kepler magnitude is 9.910. It has an effective temperature comprised between 5470 K (Casagrande et al. 2010) and 5483 K (Ammons et al. 2006) and a log g between 3.55 (Deheuvels et al. 2012) and 4.06 (Molenda-Zakowicz et al. 2008). Its metallicity [Fe/H] is very low and ranges from −2.18 (Laird et al. 1988) to −0.79 (Ammons et al. 2006). This low metallicity, combined with its high proper motion (39.18 mas/yr in RA and 255.25 in Dec according to van Leeuwen 2007) and its high radial velocity (−269.16 km s-1, Latham et al. 2002), indicates that KIC 7341231 is a halo star. All these caracteristics are summarized in Table 1.
The radial rotation profile of KIC 7341231 has been derived by Deheuvels et al. (2012). They use a one-year-long Kepler short-cadence photometric light curve, corrected following the procedures described by García et al. (2011). Their analysis of this light curve led first to obtaining the values of the global seismic parameters: a large separation of Δν = 28.9 ± 0.2 μHz and a period spacing (for dipole g-modes) of ΔΠ1 = 107.1 ± 2.3 s. They then measured 40 individual eigenmodes of both acoustic and mixed natures, making it possible to study the individual rotational splittings of these modes. It allowed them to derive the core’s rotation rate and an upper limit for the surface’s rotation rate, and to constrain the radial rotation profile of the star. Deheuvels et al. (2012) have shown that the core of KIC 7341231 is rotating at a frequency Ωc = 710 ± 51 nHz (averaged on the innermost 1.4% of the stellar radius, corresponding to 17% of the total mass) while its surface rotates at a much slower rate Ωs < 150 ± 19 nHz. These properties are summarized in Table 2.
Seismically derived properties of KIC 7341231 (Deheuvels et al. 2012).
KIC 7341231 also has a much lower mass and a much lower metallicity than the red giant KIC 8366239 observed by Beck et al. (2012), which has a mass of about 1.5 M⊙ and a solar metallicity. It is then particularly interesting to compare the rotation profile of KIC 7341231 inferred by observations and the ones predicted by theoretical models to investigate if the conclusions of Eggenberger et al. (2012b) on KIC 8366239 about the efficiency of the internal transport of angular momentum in red giants are still valid for a low-mass, low-metallicity red giant like KIC 7341231, located near the base of the red giant branch.
3. Modeling and first results
Characteristics of the computed models.
To compute models of KIC 7341231, we use the Geneva stellar evolution code. (Eggenberger et al. 2008) in which the effects of
shellular rotation and the associated meridional circulation and turbulence on stellar
evolution have been implemented (Eggenberger et al.
2010b). In this work, we do not consider internal gravity waves or magnetic fields
(e.g. Talon & Charbonnel 2005; Mathis & Zahn 2005). All computed models start at the
zero age main sequence (ZAMS). We assume a metallicity [Fe/H] = −1 dex and an initial
helium abundance Yini = 0.260. The stop point we select for the
computed models corresponds to when the models’ asymptotic value of the large separation
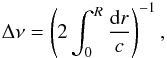 (1)where c is the sound speed, is
equal to the observed one – without computing surface corrections. We then compare the
models’ asymptotic value of the period spacing
(1)where c is the sound speed, is
equal to the observed one – without computing surface corrections. We then compare the
models’ asymptotic value of the period spacing
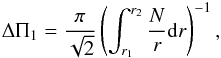 (2)where N is the Brunt-Väisälä
frequency and N(r) > 0 for
r1 < r < r2
, to verify that it has the same value as the observed one. To best reproduce the observed
surface rotation, we focus on models with a low initial rotational velocity on the ZAMS of
vini = 2 km s-1.
(2)where N is the Brunt-Väisälä
frequency and N(r) > 0 for
r1 < r < r2
, to verify that it has the same value as the observed one. To best reproduce the observed
surface rotation, we focus on models with a low initial rotational velocity on the ZAMS of
vini = 2 km s-1.
In accordance with Deheuvels et al. (2012), we find that a model with a mass M = 0.84 M⊙ reproduces both the observed large separation and period spacing at the same age T = 13.01 Gyr. The characteristics of this model are recalled in Table 3. Its evolutionary track (Figs. 1 and 2) shows that KIC 7341231 is an early red giant that has recently finished the subgiant phase.
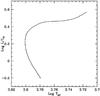 |
Fig. 1 Evolutionary track of the 0.84 M⊙ model from the ZAMS, including the effects of rotation. The end point corresponds to the selected model of the star, matching both the observed large separation and period spacing. |
 |
Fig. 2 Evolutionary track of the 0.84 M⊙ model in the asteroseismic H.-R. diagram (blue). The black diamond indicates the position of the selected model. The dashed red and green lines correspond to the errors bars on the observed large separation and period spacing, respectively, from Deheuvels et al. (2012). These error bars have been magnified 40 times for the large separation and 400 times for the period spacing to be visible. |
 |
Fig. 3 Rotation profile of the selected model at the end of the evolutionary track (solid line). The two dashed lines correspond to the core and the surface rotation rates derived by Deheuvels et al. (2012). |
Characteristics of the modified models.
We find that the obtained radial differential rotation profile is much steeper than the observed one, as can be seen in Fig. 3: the rotation rate of the core is almost two orders of magnitude higher than the observed value (33 μHz for the model versus 0.71 μHz for the observations).This is in complete agreement with the results obtained by Eggenberger et al. (2012b) for the more massive star KIC 8366239, by Pinsonneault et al. (1989) and Turck-Chièze et al. (2010) for the Sun and also by Marques et al. (2013) for a 1.3 M⊙ star. It shows that, for a low-mass and low-metallicity red giant like KIC 7341231, the shellular rotation and the subsequent meridional circulation and shear mixing alone produce an internal coupling insufficient to explain the observed rotation profile.
4. Influence of modeling parameters
In order to investigate the effects of varying different modeling parameters on the rotation profile we compute models with the same global properties (mass, vini, metallicity...) but with modified properties (see also Marques et al. 2013). We study the influence of the magnetic braking during the main sequence, the atomic diffusion, the value of the mixing-length parameter, the value of initial helium abundance and the metallicity. The resulting characteristics of these modified models are summarized in Table 4. The reasons why these parameters were chosen are detailed in the following paragraphs.
We first wanted to study the influence of magnetic braking on the modeled rotation profile, as it modifies directly the surface rotation of the star. As a result, switching on the magnetic braking during the main sequence reduces the surface rotation rate, which amplifies the radial differential rotation and thus modifies the structure of the star and increases the strength of the meridional circulation.
We then investigated the effect of atomic diffusion – or microscopic diffusion – on the rotation profile. To calculate the reference model, we had only taken transport mecanisms linked to the rotation into account, while we add atomic diffusion here. This would modify the transport of chemicals in the star, changing its structure and thus, indirectly, the angular momentum transport.
A parameter that is often fixed to a solar value in stellar models is the mixing length parameter αMLT. It is however very difficult to be sure that this parameter can be set to the same value for a whole range of different stars. Indeed, when modeling red giants, one can wonder if the vast differences between the Sun’s and red giants’ structures cannot prevent us from using the solar value. That is why we wanted to see the effect of a change in αMLT. We thus calculated a model similar to the reference one in every aspect except for the mixing-length parameter that we set to 1.7 instead of 1.6. The extension of the convective zone being increased by this change, the distribution of angular momentum should be altered as well.
As a halo star, KIC 7341231 is assumed to have a low initial helium abundance. It is however difficult to have a precise estimate of its value. To evaluate the influence of this quantity on the internal differential rotation profile, we calculated a model with a slightly higher Yini: 0.3 instead of 0.26. This model would correspond to a star born later than KIC 7341231 and could show the differences in angular momentum transport between two stars formed at two different epochs. This change also has a strong influence on the age of the model, which is 9.71 Gyr. While this difference with the reference model is logical, it results in a higher luminosity and a slightly higher log g.
For the same reasons KIC 7341231 is assumed to have a low initial helium abundance, it is also assumed to have a very low metallicity. Once again, it remains quite difficult to estimate accurately this quantity. That is why we decided to assess the influence of the metallicity on the obtained rotation profile. To do so, we computed a model with a metallicity of [Fe/H] = −0.8 (in accordance with Ammons et al. 2006) instead of −1. Like the helium-richer model, this metal-richer model would correspond to a star formed later than KIC 7341231. Here again, the age of the model is strongly modified: 14.16 Gyr, far from the 13.01 Gyr of the reference model. This leads to a higher effective temperature, a lower luminosity and a slightly more elevated log g.
All these modifications are bound to influence the structure and evolution of the modeled star, thus resulting in different values of the large separation and period spacing. Nevertheless, these changes are relatively small and the obtained values are always compatible with the observed ones, as can be seen in Table 4.
 |
Fig. 4 Differences between the rotation profiles of the modified models and the rotation profile of the reference model. Black, solid: Model 1 (Magnetic braking On). Blue, short-dashed: Model 2 (Atomic diffusion On). Red, long-dashed: Model 3 (modified αMLT). Green, dot-short-dashed: Model 4 (modified Yini). Magenta, dot-long-dashed: Model 5 (modified [Fe/H]). |
Modifications of the rotation rates of the modified models.
The changes implied in the rotation profile are however more significant. In Fig. 4, we show the difference between the rotation profiles of the modified models and the reference model’s one. The modifications of the core rotation rate and the surface rotation rate are also summarized in Table 5. It is then clear that modifying the modeling parameters induces small changes in the rotation profile compared to the gap between the modeled and observed core rotation rates. We are still far from reproducing the relatively flat rotation profile deduced from asteroseimic measurements. Once again, this suggests that another and yet undetermined physical process is at work in stellar interiors to increase angular momentum transport, in addition to meridional circulation and shear mixing.
For the time being, it would seem that the two best candidates for angular momentum transport from the core to the more external layers are internal gravity waves excited by the turbulent convective envelope (Zahn et al. 1997; Talon & Charbonnel 2005, 2008; Mathis 2009; Schatzman 1993) and fossil magnetic field with related MHD processes (Gough & McIntyre 1998; Eggenberger et al. 2005; Mathis & Zahn 2005; Zahn et al. 2007; Strugarek et al. 2011; Spada et al. 2010). These two processes would tend to damp the differential rotation gradient inside stars and might explain the internal rotation profile of the Sun and red giants.
5. Simulating a strong angular momentum transport on the Main Sequence
It is then clear that another process is needed to account for the important angular momentum transport in stellar interiors. While it is still unclear what this process is precisely, we wanted to study the possible effects of such a process on the rotation profile of the early red giant KIC 7341231. What we know is that this mechanism would flatten the rotation profile of the star. As the longuest evolutionary phase in stellar life is the main sequence, the unknown process would probably strongly impact the rotation profile of the star during this phase. Following this hypothesis, we decided to consider an extreme case, corresponding to a complete homogenization of angular momentum during the main sequence. This homogenization is indeed similar to the effects of a very strong and highly efficient angular momentum transport mechanism. The efficiency of such an additional process being unknown on smaller timescales such as the subgiant phase, we decided to let the star evolve normally as soon as the end of the main sequence. We are well aware that this approach is slightly crude and that the real effects of an additional phenomenon would be more subtle but we chose this methodology as an extreme case, in order to put constraints on the aformentioned process and have a first quantitative evaluation of such a process.
To simulate a strong homogenizing mechanism, we therefore forced in the evolution code a solid-body rotation of the star during the main sequence, allowing the transport of angular momentum through meridional circulation and shear mixing only during the post-main sequence evolution. The initial rotational velocity on the ZAMS was still fixed at vini = 2 km s-1. We have computed two such models: for the first one the solid-body rotation is maintained until the hydrogen abundance in the core reaches Xc = 0.1, while for the second it stops when there is no more hydrogen in the core. The first case does not correspond to the exact end of the main sequence but allowed us to observe the influence of the rotation of the star during the main sequence on the red giant’s rotation profile. The resulting rotation profiles (Fig. 5) were much less steep than previously, as could be expected. Without surprise, the later we switch off the solid-body rotation, the flatter the rotation profile. This shows the sensitivity of the red giant rotation profile to the efficiency of the angular momentum transport during the main sequence. Nevertheless, the gap is still huge between what we obtain and what is observed: the models’ core rotation rates are at least one order of magnitude higher than the observed one (Ωc = 3.5 and 13.2 μHz for models versus 0.71 μHz for observations). This suggests that the required process, whatever what it might be, has to be efficient also on small time scales such as the subgiant evolution.
 |
Fig. 5 Rotational profiles of the models with and without solid-body rotation during the main sequence. Black: same as Fig. 3. Blue, short-dashed: model with solid-body rotation until Xc = 0.1. Magenta, long-dashed: model with solid-body rotation until Xc = 0. |
 |
Fig. 6 Rotational profiles of the models with and without solid-body rotation during the main sequence, but after the subgiant phase (at an age T = 13.40 Gyr). Black: normal case (no solid-body rotation). Blue, short-dashed: model with solid-body rotation until Xc = 0.1. Magenta, long-dashed: model with solid-body rotation until Xc = 0. |
Another remarkable consequence of the solid-body rotation during the main sequence is that even in the later evolution of the star (i.e. the red giant phase) the rotation profiles obtained strongly differ from the one corresponding to the normal case (i.e. without solid-body rotation). This discrepancy can be seen in Fig. 6. In particular, we can observe a decrease of the rotational rate in the core of the star, which was already visible in Fig. 5 but less prominent. This shows that, in these models, the rotational history of the star is not completely erased by its evolution during the subgiant and red giant phases. To fully understand red giants’ rotation profiles it is thus adamant to study the evolution of the rotation inside the star during its whole evolution.
6. Subgiant evolution and angular momentum transport
 |
Fig. 7 Rotational profiles of the reference model at different evolution times. Blue, solid: end of Main Sequence. Green, short-dashed: end of Subgiant evolution considering all angular momentum transport phenomenons. Red, long-dashed: end of subgiant evolution considering only conservation of angular momentum during the subgiant phase. |
 |
Fig. 8 Rotational profiles of the model with solid-body rotation during Main Sequence (until Xc = 0.1) at different evolution times. Colors: same as Fig. 7. |
We have seen that the missing angular momentum transport mechanism has to be efficient during the short-lived subgiant phase. But what of the transport processes already considered? In order to quantify their effect during this phase, we compared the evolution of the rotational profile during the subgiant phase in two different cases. For the first one, we took into account rotationaly induced processes such as meridional circulation and shear mixing. For the second one, we considered only angular momentum conservation. Thus the difference between the obtained rotational profiles at the end of the subgiant phase is a good proxy of the efficiency of the transport processes.
This has been done for the reference model and for the model with solid-body rotation during the main sequence until Xc = 0.1. The resulting profiles are shown in Figs. 7 and 8. While considering rotationaly induced transport reduces indeed the core’s rotation rate, the effect is of very small magnitude (1.5 μHz maximum compared to Ωc = 33 μHz, a 4.5% change). The evolution of the star’s rotation profile during subgiant evolution is therefore completely dominated by the sheer conservation of angular momentum due to the profound modifications of the star’s structure.
This comparison emphasizes that any angular momentum transport phenomenon considered must be considerably more efficient than meridional circulation and shear mixing on small timescales. More precisely, during the subgiant phase, this phenomenon has to be strong enough to counterbalance angular momentum conservation. Once again, this is a rather important constraint for the studied additional processes such as internal gravity waves and magnetic fields.
7. Conclusion
The comparison between the radial rotation profile of the red giant KIC 7341231 inferred from asteroseismic measurements with profiles predicted by stellar models – including shellular rotation, meridional circulation and shear mixing – have shown that such models are unable to reproduce the observed internal rotational rates. The theoretical rotation profiles are indeed too steep compared to the one deduced from observations: in the case of KIC 7341231 the model’s core is rotating at least 30 times faster than what has been deduced through asteroseismic means. This is in perfect agreement with the conclusions of Eggenberger et al. (2012b), Marques et al. (2013) and Ceillier et al. (2012) and shows that this discrepancy is also found for a low-mass, low-metallicity red giant like KIC 7341231 (see also Palacios et al. 2006).
These results illustrate the need to progress in our understanding and modeling of (magneto-)hydrodynamical processes at work in stellar interiors and to implement new physical processes into stellar evolution codes, such as internal gravity waves or magnetic fields. We have demonstrated here that these processes, however efficient during the long-lasting main sequence, have to be very effective during the rapid evolution of the subgiant phase. Furthermore, we have also shown that their effect on internal rotation must be considered over the whole evolution of the star and that the rapid evolution during the subgiant phase does not completely erase all the previous rotational history of the star.
It would be interesting to determine the efficiency of the unknown physical process needed for the internal transport of angular momentum to correctly reproduce the observed rotation profile of KIC 7341231. This would allow a comparison with the effective viscosity of 3 × 104 cm2 s-1 found for the more massive red giant KIC 8366239 (Eggenberger et al. 2012b), although we would like to remind the reader that neither internal gravity waves nor fossil magnetic fields have an effect comparable with an effective viscosity (see Mathis 2013).
We have no doubt that codes in which the effects on angular momentum transport of processes like internal gravity waves or magnetic fields have been implemented will allow us to understand more accurately the various physical mechanisms at work in stars. In such improvement of our vision of the dynamical evolution of stars, asteroseismology is then one of the most promising ways to get strong constraints as demonstrated here with the case of KIC 7341231.
Acknowledgments
T.C., R.A.G. and S.M. acknowledge the CNES support of CoRoT and of asteroseismic activities at the SAp – CEA/Saclay and the CNRS/INSU PNPS support. T.C. and S.M. thank the Geneva Observatory for its hospitality. P.E. was partly supported by the Swiss National Science Foundation. The authors would like to thank the referee for her/his suggestions which helped improving the paper.
References
- Ammons, S. M., Robinson, S. E., Strader, J., et al. 2006, ApJ, 638, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Appourchaux, T., Michel, E., Auvergne, M., et al. 2008, A&A, 488, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baglin, A., Auvergne, M., Barge, P., et al. 2006, in ESA SP, 1306, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, 33 [Google Scholar]
- Ballot, J., Gizon, L., Samadi, R., et al. 2011, A&A, 530, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Bedding, T. R., Huber, D., Stello, D., et al. 2010, ApJ, 713, L176 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Braithwaite, J., & Spruit, H. C. 2004, Nature, 431, 819 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Campante, T. L., Handberg, R., Mathur, S., et al. 2011, A&A, 534, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceillier, T., Eggenberger, P., García, R. A., & Mathis, S. 2012, Astron. Nachr., 333, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., Kjeldsen, H., Christensen-Dalsgaard, J., et al. 2011, Science, 332, 213 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Charbonnel, C., & Talon, S. 2005, Science, 309, 2189 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Decressin, T., Mathis, S., Palacios, A., et al. 2009, A&A, 495, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenkov, P. A., Pinsonneault, M., Terndrup, D. M., & Newsham, G. 2010, ApJ, 716, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Di Mauro, M. P., Cardini, D., Catanzaro, G., et al. 2011, MNRAS, 415, 3783 [NASA ADS] [CrossRef] [Google Scholar]
- Duez, V., & Mathis, S. 2010, A&A, 517, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Maeder, A., & Meynet, G. 2005, A&A, 440, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Astrophys. Space Sci., 316, 43 [Google Scholar]
- Eggenberger, P., Maeder, A., & Meynet, G. 2010a, A&A, 519, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Miglio, A., Montalban, J., et al. 2010b, A&A, 509, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Haemmerlé, L., Meynet, G., & Maeder, A. 2012a, A&A, 539, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Montalbán, J., & Miglio, A. 2012b, A&A, 544, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elsworth, Y., Howe, R., Isaak, G. R., et al. 1995, Nature, 376, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Fröhlich, H.-E. E., Frasca, A., Catanzaro, G., et al. 2012, A&A, 543, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garaud, P., & Garaud, J.-D. 2008, MNRAS, 391, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- García, R. A., Turck-Chièze, S., Jiménez-Reyes, S. J., et al. 2007, Science, 316, 1591 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- García, R. A., Régulo, C., Samadi, R., et al. 2009, A&A, 506, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García, R. A., Mathur, S., Salabert, D., et al. 2010, Science, 329, 1032 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- García, R. A., Hekker, S., Stello, D., et al. 2011, MNRAS, 414, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Nicholson, P. D. 1989, ApJ, 342, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Gough, D., & McIntyre, M. 1998, Nature, 394, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Laird, J. B., Carney, B. W., & Latham, D. W. 1988, AJ, 95, 1843 [NASA ADS] [CrossRef] [Google Scholar]
- Latham, D. W., Stefanik, R. P., Torres, G., et al. 2002, AJ, 124, 1144 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Berlin, Heidelberg: Springer) [Google Scholar]
- Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
- Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S. 2009, A&A, 506, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S. 2013, Lect. Notes Phys., 865, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, S., & de Brye, N. 2012, A&A, 540, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & Zahn, J.-P. 2004, A&A, 425, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & Zahn, J.-P. 2005, A&A, 440, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., Eff-Darwich, A., García, R. A., & Turck-Chièze, S. 2008, A&A, 484, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., García, R. A., Catala, C., et al. 2010, A&A, 518, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., Handberg, R., Campante, T. L., et al. 2011, ApJ, 733, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., García, R. A., Morgenthaler, A., et al. 2013, A&A, 550, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Metcalfe, T. S., Chaplin, W. J., Appourchaux, T., et al. 2012, ApJ, 748, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS] [Google Scholar]
- Molenda-Zakowicz, J., Frasca, A., & Latham, D. W. 2008, Acta Astron., 58, 419 [NASA ADS] [Google Scholar]
- Mosser, B., Belkacem, K., Goupil, M.-J. J., et al. 2010, A&A, 517, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palacios, A., Charbonnel, C., Talon, S., & Siess, L. 2006, A&A, 453, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinsonneault, M. H. 2010, Proc. IAU, 5, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Pinsonneault, M. H., Kawaler, S. D., Sofia, S., & Demarque, P. 1989, ApJ, 338, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Pinsonneault, M. H., Kawaler, S. D., & Demarque, P. 1990, ApJS, 74, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H. 1981, ApJ, 245, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Schatzman, E. 1993, A&A, 279, 431 [NASA ADS] [Google Scholar]
- Spada, F., Lanzafame, A. C., & Lanza, A. F. 2010, MNRAS, 404, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Strugarek, A., Brun, A. S., & Zahn, J.-P. 2011, A&A, 532, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talon, S., & Charbonnel, C. 2003, A&A, 405, 1025 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talon, S., & Charbonnel, C. 2005, A&A, 440, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talon, S., & Charbonnel, C. 2008, A&A, 482, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, M. J., Toomre, J., Anderson, E. R., et al. 1996, Science, 272, 1300 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Turck-Chièze, S., Palacios, A., Marques, J. P., & Nghiem, P. A. P. 2010, ApJ, 715, 1539 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 12 [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
- Zahn, J.-P., Talon, S., & Matias, J. 1997, A&A, 322, 320 [Google Scholar]
- Zahn, J.-P., Brun, A. S., & Mathis, S. 2007, A&A, 474, 145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Evolutionary track of the 0.84 M⊙ model from the ZAMS, including the effects of rotation. The end point corresponds to the selected model of the star, matching both the observed large separation and period spacing. |
| In the text | |
 |
Fig. 2 Evolutionary track of the 0.84 M⊙ model in the asteroseismic H.-R. diagram (blue). The black diamond indicates the position of the selected model. The dashed red and green lines correspond to the errors bars on the observed large separation and period spacing, respectively, from Deheuvels et al. (2012). These error bars have been magnified 40 times for the large separation and 400 times for the period spacing to be visible. |
| In the text | |
 |
Fig. 3 Rotation profile of the selected model at the end of the evolutionary track (solid line). The two dashed lines correspond to the core and the surface rotation rates derived by Deheuvels et al. (2012). |
| In the text | |
 |
Fig. 4 Differences between the rotation profiles of the modified models and the rotation profile of the reference model. Black, solid: Model 1 (Magnetic braking On). Blue, short-dashed: Model 2 (Atomic diffusion On). Red, long-dashed: Model 3 (modified αMLT). Green, dot-short-dashed: Model 4 (modified Yini). Magenta, dot-long-dashed: Model 5 (modified [Fe/H]). |
| In the text | |
 |
Fig. 5 Rotational profiles of the models with and without solid-body rotation during the main sequence. Black: same as Fig. 3. Blue, short-dashed: model with solid-body rotation until Xc = 0.1. Magenta, long-dashed: model with solid-body rotation until Xc = 0. |
| In the text | |
 |
Fig. 6 Rotational profiles of the models with and without solid-body rotation during the main sequence, but after the subgiant phase (at an age T = 13.40 Gyr). Black: normal case (no solid-body rotation). Blue, short-dashed: model with solid-body rotation until Xc = 0.1. Magenta, long-dashed: model with solid-body rotation until Xc = 0. |
| In the text | |
 |
Fig. 7 Rotational profiles of the reference model at different evolution times. Blue, solid: end of Main Sequence. Green, short-dashed: end of Subgiant evolution considering all angular momentum transport phenomenons. Red, long-dashed: end of subgiant evolution considering only conservation of angular momentum during the subgiant phase. |
| In the text | |
 |
Fig. 8 Rotational profiles of the model with solid-body rotation during Main Sequence (until Xc = 0.1) at different evolution times. Colors: same as Fig. 7. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


