| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321276 | |
| Published online | 09 July 2013 | |
Detection of 15NNH+ in L1544: non-LTE modelling of dyazenilium hyperfine line emission and accurate 14N/15N values⋆,⋆⋆
1 Centro de Astronomia e Astrofísica, Observatório Astronómico de Lisboa, Tapada da Ajuda 1349-018, Lisboa Portugal
e-mail: bizzocchi@oal.ul.pt; elle@oal.ul.pt
2 School of Physics and Astronomy, University of Leeds, Leeds LS2 9JT, UK
e-mail: P.Caselli@leeds.ac.uk
3 Dipartimento di Chimica “G. Ciamician”, Università di Bologna, via F. Selmi 2, 40126 Bologna, Italy
e-mail:
luca.dore@unibo.it
Received: 11 February 2013
Accepted: 17 May 2013
Context. Samples of pristine solar system material found in meteorites and interplanetary dust particles are highly enriched in 15N. Conspicuous nitrogen isotopic anomalies have also been measured in comets, and the 14N/15N abundance ratio of the Earth is itself higher than the recognised presolar value by almost a factor of two. Low-temperature ion/molecule reactions in the proto-solar nebula have been repeatedly indicated as being responsible for these 15N-enhancements.
Aims. We have searched for 15N variants of the N2H+ ion in L1544, a prototypical starless cloud core that is one of the best candidate sources for detection owing to its low central core temperature and high CO depletion. The goal is to evaluate accurate and reliable 14N/15N ratio values for this species in the interstellar gas.
Methods. A deep integration of the 15NNH+(1−0) line at 90.4 GHz was obtained with the IRAM 30 m telescope. Non-LTE radiative transfer modelling was performed on the J = 1−0 emissions of the parent and 15N-containing dyazenilium ions, using a Bonnor-Ebert sphere as a model for the source.
Results. A high-quality fit of the N2H+(1−0) hyperfine spectrum has allowed us to derive a revised value of the N2H+ column density in L1544. Analysis of the observed N15NH+ and 15NNH+ spectra yielded an abundance ratio N(N15NH+)/N(15NNH+) = 1.1 ± 0.3. The obtained 14N/15N isotopic ratio is ~1000 ± 200, suggestive of a sizeable 15N depletion in this molecular ion. Such a result is not consistent with the prediction of the current nitrogen chemical models.
Conclusions. Since chemical models predict high 15N fractionation of N2H+, we suggest that 15N14N, or 15N in some other molecular form, tends to deplete onto dust grains.
Key words: ISM: clouds / ISM: molecules / ISM: individual objects: L1544 / radio lines: ISM
Based on observations carried out with the IRAM 30 m Telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain).
Full Tables B.1−B.6 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/555/A109
© ESO, 2013
1. Introduction
Determination of the abundance ratios of the stable isotopes of the light elements in different objects of the solar system is one of the key elements in understanding its origin and early history (see, e.g. Caselli & Ceccarelli 2012). Nitrogen, the fifth or sixth most abundant element in the Sun (after H, He, C, O, and maybe Ne, Asplund et al. 2009), is particularly intriguing because its isotopic composition shows large variations whose interpretation is still controversial (Aléon 2010; Adande & Ziurys 2012).
Recent laboratory analysis of the solar wind particles collected by the Genesis spacecraft (Marty et al. 2011) yielded a 14N/15N ratio of 441 ± 6, higher than in any solar system object, but probably representative of the proto-solar nebula value, being comparable to the one measured in Jupiter’s atmosphere (435 ± 57, Owen et al. 2001; Fouchet et al. 2004) and in the osbornite (TiN) inclusions (Ca-Al rich) from the CH/CB chondrite Isheyevo (424 ± 3, Meibom et al. 2007). The 14N/15N value of the terrestrial atmosphere is significantly lower (~272), and larger 15N enrichments have been measured in cometary nitrile-bearing molecules (Arpigny et al. 2003; Bockelée-Morvan et al. 2008; Manfroid et al. 2009) and in primitive chondritic materials (up to 50, see e.g., Briani et al. 2009; Bonal et al. 2010).
A common but still debated interpretation considers such variations as an inheritance from the proto-solar chemistry: low-temperature ion/molecule reactions (e.g., Millar 2002) in the interstellar medium (ISM) were proven to cause large isotopic excesses for D in organic molecules, and have repeatedly been proposed as the cause of the observed 15N excesses, too. However, in molecular clouds, gas-phase chemistry continually cycles nitrogen between atomic and molecular forms, equating the composition of the isotopic reservoirs. Indeed, classical ion/molecule reaction models fail to predict major 15N enrichments (Terzieva & Herbst 2000). Specific conditions, such as strong and selective CO freeze-out (Charnley & Rodgers 2002; Rodgers & Charnley 2008), might overcome this difficulty and produce a “nitrogen super-fractionation” in cold ISM, in principle capable of accounting for the largest measured enhancements.
A way to assess the isotopic composition of the presolar gas is to measure the 14N/15N ratio in other proto-stellar systems. Recent observations of 15N-bearing molecules have found no significant fractionation in NH3 (14N/15N = 350−500, Gerin et al. 2009; 334 ± 50, Lis et al. 2010) toward prestellar cores and proto-stellar envelopes, and in N2H+ (14N/15N = 446 ± 71, Bizzocchi et al. 2010) toward the prototypical starless cloud core L1544. Conversely, various preliminary measurements on nitrile species towards prestellar cores have shown that they are highly enriched in 15N (between 70 and 380, Milam & Charnley 2012; Hily-Blant et al. 2013; Bizzocchi, unpublished). Also, similar values have been found by Adande & Ziurys (2012) in HNC observations of massive star-forming regions across the Galaxy.
Another problem with directly linking prestellar core chemistry and the solar system composition comes from the poor correlation between D- and 15N-enhancements observed in some pristine materials (Busemann et al. 2006; Robert & Derenne 2006), whereas it is clear that the chemical processes invoked to account for nitrogen fractionation should also produce enormous deuterium enhancements.
Wirström et al. (2012) have considered the spin-state dependence in ion/molecule reactions involving the ortho and para forms of H2 and succeeded in reproducing the differential 15N-fractionation observed in amine- and nitrile-bearing compounds, as well as the overall lack of correlation with hydrogen isotopic anomalies. The authors point out that, in cold interstellar environments, the ortho-to-para ratio of H2 plays a pivotal role in producing a diverse range of D–15N fractionation in precursors molecules, thus providing a strong support for the astrochemical origin of nitrogen isotopic anomalies. However, this hypothesis still requires a sound verification, since so far observations of 15N-isotopologues in the ISM are rather sparse. An extended survey of the 14N/15N ratio targeting starless clouds in different evolutionary phases, and possibly in different environmental conditions, is thus desirable.
Obtaining accurate determinations of the nitrogen isotopic ratio in the ISM is problematic: 15N-bearing species typically produce very weak emissions, which requires time-consuming high-sensitivity observations. Moreover, the rotational spectra of common N-containing species are usually optically thick, and the line intensities are not reliable indicators of the molecular abundance. For nitrile molecules, this difficulty may be overcome by using less abundant 13C variants as proxies for the parent species and then deriving the 14N/15N ratio from an assumption for the 12C/13C (e.g., Dahmen et al. 1995). Another route is to use the hyperfine structure analysis to evaluate the optical depth of the parent species, thus allowing for a more direct determination of the nitrogen isotope ratio (Savage et al. 2002; Adande & Ziurys 2012).
In a previous letter, Bizzocchi et al. (2010) report the detection of N15NH+ in L1544. The analysis was carried out assuming local thermodynamic equilibrium (LTE) conditions and yielded a 14N/15N ratio of 446 ± 71. This indicates the absence of nitrogen fractionation in the dyazenilium ion, a result not consistent with the prediction of the chemical model of Gerin et al. (2009) and Wirström et al. (2012).
The chosen target, L1544, is a prototypical starless core on the verge of star formation (Ward-Thompson et al. 1999; Caselli et al. 2002a). Its density structure, low central temperature, and high CO depletion make it an ideal laboratory for studying the isotopic fractionation processes. Also, an accurate model for its internal structure and dynamics has been proposed by Keto & Caselli (2010) and then successfully used to analyse the H2O emission observed by Herschel (Caselli et al. 2012). In this paper we present the detection of the  isotopologue in L1544, together with a full non-LTE radiative transfer treatment of the dyazenilium ions aimed at evaluating accurate and reliable values of the 14N/15N ratio in this species.
isotopologue in L1544, together with a full non-LTE radiative transfer treatment of the dyazenilium ions aimed at evaluating accurate and reliable values of the 14N/15N ratio in this species.
The paper is organised as follows. In Sect. 2 we describe the technique used for observations, and in Sect. 3 we summarise our direct observational results. Section 4 is devoted to describing the Monte Carlo radiative transfer modelling of N2H+ and its 15N-variants and to deriving their molecular abundances. In Sect. 5 we discuss the implications for the chemical models, and in Sect. 6 we summarise our conclusions.
2. Observations
The observations towards L1544 were carried out with the IRAM 30 m antenna, located at Pico Veleta (Spain) during observing sessions in June 2009 and July 2010. The J = 1 − 0 transition of  was observed with the EMIR receiver in the E090 configuration tuned at 90 263.8360 MHz and using the lower-inner sideband. The hyperfine-free rest frequencies were taken from the most recent laboratory investigation of 15N-dyazenilium species (Dore et al. 2009). Scans were performed in frequency-switching mode, with a throw of ±7 MHz; the backend used was the VESPA correlator set to a spectral resolution of 20 kHz (corresponding to 0.065 km s-1) and spectral bandpass of 20 MHz. We tracked the L1544 continuum dust emission peak at 1.3 mm, where we previously detected the other 15N-containing isotopologue, N15NH+ (Bizzocchi et al. 2010). The J2000 coordinates are RA = 05h04m17.21s, Dec = 25°10′42.8′′ (Caselli et al. 2002a). The telescope pointing was checked every two hours on nearby bright radio quasars and was found to be accurate to 3−4′′; the half power beam width (HPBW) at the line frequency is 27′′.
was observed with the EMIR receiver in the E090 configuration tuned at 90 263.8360 MHz and using the lower-inner sideband. The hyperfine-free rest frequencies were taken from the most recent laboratory investigation of 15N-dyazenilium species (Dore et al. 2009). Scans were performed in frequency-switching mode, with a throw of ±7 MHz; the backend used was the VESPA correlator set to a spectral resolution of 20 kHz (corresponding to 0.065 km s-1) and spectral bandpass of 20 MHz. We tracked the L1544 continuum dust emission peak at 1.3 mm, where we previously detected the other 15N-containing isotopologue, N15NH+ (Bizzocchi et al. 2010). The J2000 coordinates are RA = 05h04m17.21s, Dec = 25°10′42.8′′ (Caselli et al. 2002a). The telescope pointing was checked every two hours on nearby bright radio quasars and was found to be accurate to 3−4′′; the half power beam width (HPBW) at the line frequency is 27′′.
In May 2009 we spent 4.25 h on source with average atmospheric condition (τ ~ 0.1), while during the summer 2010 session we observed a further 23.9 hours with good weather conditions (τ < 0.05); all those scans were summed together for a total of 28.15 hours of on-source telescope time. Horizontal and vertical polarisations were simultaneously observed and averaged together to produce the final spectrum, which was then rescaled in units of Tmb assuming a source-filling factor of unity and using the forward and main beam efficiencies appropriate for : Feff = 0.95 and Beff = 0.75, respectively. The rms noise level achieved was about 3 mK, close to what was obtained for the J = 1−0 line of the species N15NH+ toward the same line of sight (Bizzocchi et al. 2010).
The same backend configuration was also employed to collect new data for the J = 1 − 0 transition of the main isotopologue, N2H+, with the EMIR receiver tuned at 93 173.4013 MHz. This line was observed shortly at the beginning of each telescope session for a total integration time of ~56 min. The final rms noise level is 15 mK, resulting in a high signal-to-noise spectrum, well suited to modelling purposes.
Predicted hyperfine frequencies, estimated 1σ uncertainties, and relative line intensities for the J = 1 − 0 transition of N15NH+ and  (Dore et al. 2009).
(Dore et al. 2009).
Results of the CLASS HFS fit on the observed spectral profile of the 15N-bearing dyazenilium isotopologues observed towards L1544.
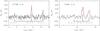 |
Fig. 1 Spectra of the 15N-containing dyazenilium isotopologues observed towards L1544 (black histogram), and computed spectral profiles resulting from the HFS fits (red dashed curves). Superimposed black lines indicate the position and relative intensity of the hyperfine components. Left panel: N15NH+(1−0) transition (reproduced from Bizzocchi et al. 2010). Right panel: |
3. Results
The two 15N-dyazenilium spectra observed in L1544 are presented in Fig. 1. Due to the smaller magnitude of the electric quadrupole coupling constant or the inner 14N atom, the hyperfine triplet of the  (1−0) transition is spread over ~1 MHz, much less than the other 15N-isotopologue. For the sake of completeness, the frequencies and relative intensities of the J = 1 − 0 hyperfine transition of both 15N-bearing dyazenilium variants are reported in Table 1 (Dore et al. 2009).
(1−0) transition is spread over ~1 MHz, much less than the other 15N-isotopologue. For the sake of completeness, the frequencies and relative intensities of the J = 1 − 0 hyperfine transition of both 15N-bearing dyazenilium variants are reported in Table 1 (Dore et al. 2009).
The data were processed using the GILDAS1 software (Pety 2005). After polynomial baseline subtraction, average line parameters were estimated by fitting Gaussian line profiles to the detected components using the HFS routine implemented in CLASS. The hyperfine splittings and relative intensities of the J = 1 − 0 transitions of both 15N isotopologues were taken from Table 1 and kept fixed in the least-squares procedure. Since the lines are optically thin within the HFS fitting errors, we forced the optical depth to have the value of 0.1, the minimum allowed in CLASS. This method has been adopted in the past (e.g., Caselli et al. 2002b) to avoid highly uncertain values of the optical depth to affect the intrinsic line width, as the error on τ is not propagated in the evaluation of the line width.
The derived parameters for  (1−0) are gathered in Table 2, where the results obtained from the previous N15NH+(1−0) observations are also reported for completeness. From these data one can derive a systemic velocity VLSR = 7.203 ± 0.010 km s-1 for
(1−0) are gathered in Table 2, where the results obtained from the previous N15NH+(1−0) observations are also reported for completeness. From these data one can derive a systemic velocity VLSR = 7.203 ± 0.010 km s-1 for  (1−0), which compares well with the value derived previously for the N15NH+(1−0), i.e., VLSR = 7.299 ± 0.014 km s-1 (Bizzocchi et al. 2010). The small discrepancies observed in source velocity and in the line width between the 15N-species (these quantities agree within 5σ) are likely to be attributed to the low signal-to-noise ratio (S/N) and the spectral resolution (0.067 km s-1).
(1−0), which compares well with the value derived previously for the N15NH+(1−0), i.e., VLSR = 7.299 ± 0.014 km s-1 (Bizzocchi et al. 2010). The small discrepancies observed in source velocity and in the line width between the 15N-species (these quantities agree within 5σ) are likely to be attributed to the low signal-to-noise ratio (S/N) and the spectral resolution (0.067 km s-1).
4. L1544 modelling and radiative transfer
In the following sections we describe the radiative transfer treatment carried out on L1544 to model the J = 1 − 0 emission of N2H+, N15NH+, and  , and to derive accurate molecular abundances and 14N/15N ratios. The physical model is based on the one proposed by Keto & Caselli (2010) and updated by including oxygen to interpret the far infrared emission of the water vapour in the same source (Caselli et al. 2012). Briefly, the core is described as a gravitationally contracting Bonnor-Ebert sphere; the model includes radiative equilibrium from dust, gas cooling via both molecular emission lines and grain collisional coupling, as well as a simplified molecular chemistry (Keto & Caselli 2008).
, and to derive accurate molecular abundances and 14N/15N ratios. The physical model is based on the one proposed by Keto & Caselli (2010) and updated by including oxygen to interpret the far infrared emission of the water vapour in the same source (Caselli et al. 2012). Briefly, the core is described as a gravitationally contracting Bonnor-Ebert sphere; the model includes radiative equilibrium from dust, gas cooling via both molecular emission lines and grain collisional coupling, as well as a simplified molecular chemistry (Keto & Caselli 2008).
First, we used the original model with a central density of 2 × 107 cm-3: its temperature, density, and inward velocity profile are shown in Fig. 2. The H2 column density, averaged over the 30 m telescope main beam FWHM at 3 mm, is 6.57 × 1022 cm-2. This value compares well with the one derived by Crapsi et al. (2005) through dust continuum emission observation at 1.2 mm; once averaged over the same beam (11′′), our model yields 11.5 × 1022 cm-2, consistent with the observed value of (9.4 ± 1.6) × 1022 cm-2.
The radiative transfer calculations have been performed using the non-local thermodynamic equilibrium (non-LTE) numerical code MOLLIE (Keto 1990; Keto et al. 2004). We used the updated version of the algorithm, able to proper treating the overlapping lines, thus allowing better reproduction of the non-LTE hyperfine ratios (excitation anomalies) observed in the N2H+ spectra of L1544 and in a number of other starless cores (Caselli et al. 1995; Daniel et al. 2007). For the present modelling we mostly relied on the hyperfine rates calculations of Daniel et al. (2004, 2005) for N2H+/He collisions, and the appropriate rate coefficients for H2 partner were then obtained using a suitable scaling relation (see Appendix A).
 |
Fig. 2 Temperature, density, and inward velocity profiles of L1544 used as model in the present radiative transfer modelling. The red dotted curve indicates the gas temperature in K, the blue curve is the log of density in cm-3, and the purple dashed curve represents the inward velocity in units of 0.01 km s-1. |
The cloud structure of L1544 was modelled with three nested grids, each composed of 48 cells. The cell linear dimensions of each nested level are decreasing; i.e., the level 1 covers the whole source out to a radius of 66 000 AU, whereas the finer level 3 maps the inner 16 000 AU of the core. In each cell, the temperature, density, and gas kinematic parameters were taken from the model shown in Fig. 2 and assumed constant. A constant turbulent FWHM line width of 0.13 km s-1 (as found by Tafalla et al. 2002) was added in quadrature to the thermal line width calculated in each model cell.
4.1. N2H+(1−0)
Radiative transfer modelling of N2H+ is not an easy task. Because of the two 14N nuclei, each rotational level is split by quadrupole interactions into nine sub-levels and the rotational transitions exhibit a complex structure of hyperfine components (i.e., 15 for J = 1 − 0, 38 for J = 2 − 1, etc.) with varying degrees of overlap between them. The presence of the hyperfine structure (HFS) complicates the modelling. The relative populations of the hyperfine sub-levels may depart from their statistical weights, producing non-LTE intensity ratios (e.g., Caselli et al. 1995). Indeed, collisional coefficients for each individual hyperfine component typically have different values (e.g., Buffa 2012), thus producing hyperfine selective collisional excitation (Stutzki & Winnewisser 1985). A second effect is the hyperfine line trapping, i.e., various components may have different optical depths, thus getting different amounts of radiative excitation. The trapping becomes important at high optical depths and is accentuated by the overlap of the various hyperfine components.
A Monte Carlo modelling of the N2H+(1−0) emission line in L1544 and other starless cores was previously performed by Tafalla et al. (2002). They adopted a simplified treatment in which the above-mentioned effects are ignored: all the hyperfine sub-levels were assumed to be populated according to their statistical weights (no hyperfine selective collisional excitation was considered), and the hyperfine line trapping was neglected. To justify such a simple approach, it was argued that line trapping is only significant at very large optical depths and, in any case, non-LTE intensity effects typically involved only 10−15% of the emerging flux. For most sources this modelling provided N2H+ spectra that are in good agreement with observations, but it yielded a less satisfactory result for L1544. Notably, the predicted spectrum was unable to reproduce the non-Gaussian line shape of the hyperfine lines, which was attributed to the presence of two velocity components in the core (Tafalla et al. 1998). They were thus roughly modelled using a broader profile.
Another issue involves the N2H+ abundance profile. So far, the source model used in radiative transfer studies of L1544 assumed a constant N2H+ abundance throughout the source (Tafalla et al. 1998, 2002; Keto & Rybicki 2010). This hypothesis is reasonable, given the similarity between the observed L1544 dust continuum and N2H+(1−0) emission maps (see, e.g. Tafalla et al. 2002). Also, the observed radial profiles of the integrated line emission intensity (see Fig. 2 of Caselli et al. 1999), show that the abundance behaviour of N2H+ is markedly different from that of CO, which is known to suffer considerable depletion at the high gas densities toward the core centre. However, Caselli et al. (2002b) suggest that a certain amount of nitrogen depletion is also expected in the dense gas, thus the dyazenilium abundance is also likely to show a drop toward the L1544 centre (see also Bergin et al. 2002).
 |
Fig. 3 Abundance trends (normalised to the maximum values) predicted by the Aikawa et al. (2011) models for dyazenilium and chemically related species. The N2H+ abundance decreases toward the cloud centre following the N2 freeze-out (green curve) onto dust mantels at high gas density. The concomitant steeper drops of free electron (grey curve) and CO (brown curve) give rise to the N2H+ abundance maxima at radii of ~104 and ~103 astronomical units. N2D+ shows similar behaviour (blue curve), but it features a much stronger inner peak owing to the strong deuterium fractionation existing in the highly-CO depleted central region. |
Given the uncertainties in the spatial distribution of N2H+ (due to the poor spatial resolution), we investigated both constant and central-drop abundance profiles. In either instance, we ran a grid of models with varying standard N2H+ abundance, and sought the best fit of the observed line profiles.
In the first set of models we used a constant dyazenilium abundance with respect to H2, then we tested the N2H+ radial abundance profile calculated using the hydro-dynamical−chemical model of Aikawa et al. (2011). The employed chemical network is the same as in Aikawa et al. (2012), but not the dynamics. In this paper, we assume that the physical structure is fixed at the model shown in Fig. 2, and the chemistry is run until the C18O column density reaches the observed value within the IRAM 30 m beam. The predicted trends for a selection of chemical species are illustrated in Fig. 3. Dyazenilium is formed by proton transfer to N2 and scavenged by reaction with CO and recombination with electron. As expected, the nitrogen freeze-out at smaller radii produces a overall decreasing N2H+ abundance trend, while the secondary peak at ~1000 AU is due to the concomitant faster drop in the main depleting reactants.
 |
Fig. 4 Weighted χ2 of the N2H+(1−0) modellings using different standard dyazenilium abundances and radial profiles. Blue curve: constant N2H+ abundance with respect to H2; red curve: constant abundance and modified cloud infall velocity (see text). Green curve: radial N2H+ abundance profile shown in Fig. 3; yellow curve: radial profile with modified cloud infall velocity. |
The “goodness” of each modelling was estimated using the quantity ![\begin{equation} \label{eq:chi2} \chi^2 = \sum_i^{N}\left\{\frac{1}{\sigma_\mrm{obs}} \left[T_\mrm{mb,obs}(i) - T_\mrm{mb,model}(i)\right] \right\}^2 , \end{equation}](/articles/aa/full_html/2013/07/aa21276-13/aa21276-13-eq67.png) (1)where Tmb(i) are the brightness temperature of the observed and modelled spectra at the ith velocity channel and σobs is the actual rms noise of the observation which is estimated to be 0.015 K. The sum in Eq. (1)runs over all the velocity channels calculated by MOLLIE, covering an interval of 2 km s-1 around each hyperfine component.
(1)where Tmb(i) are the brightness temperature of the observed and modelled spectra at the ith velocity channel and σobs is the actual rms noise of the observation which is estimated to be 0.015 K. The sum in Eq. (1)runs over all the velocity channels calculated by MOLLIE, covering an interval of 2 km s-1 around each hyperfine component.
 |
Fig. 5 Observed N2H+(1−0) spectrum in L1544 modelled with non-LTE code MOLLIE. The histograms show our observation data. The red curve shows the model spectrum computed using the “altered” dark cloud model and N2H+ constant abundance throughout the core (see text). |
Figure 4 plots the resulting χ2 for varying standard N2H+ abundance and different abundance profiles. Both constant and centrally decreasing abundance models yield fits of comparable but not satisfactory quality, since both fail in reproducing the observed brightness of the thinner F1,F = (1,0) − (1,1) component. Another weakness of these simulations is the overall poor agreement of the spectral profile; i.e., the calculated lines are systematically narrower than the observed ones. This suggests that the inward velocity profile adopted as a model (see Fig. 2) could be underestimated. In fact, the hydrodynamic calculations of Keto & Caselli (2010) result in idealised models of contracting Bonnor-Ebert spheres in quasi-static equilibrium, and the contraction velocity was derived from noisier data.
We have thus altered the L1544 cloud model by increasing its inward velocity profile by a constant factor, and again sought the minimum χ2 by varying the N2H+ standard abundance. Both constant and centrally decreasing N2H+ abundance profiles were tested. Best fits were obtained using a velocity profile scaled with a constant 1.75 factor, as illustrated in Fig. 4. A significant improvement was achieved for both profiles; the model with constant abundance drops to a narrow χ2 minimum of 76.2 and supersedes the best fit obtained with the centrally decreasing profile, which is almost twice poorer (χ2 ~ 140). The obtained best χ2 for the two models correspond to weighted rms of 0.54 and 0.98, indicating that in both cases the observed profile is reproduced within the average spectral noise.
We regard the spectrum obtained with the constant N2H+ abundance profile and a standard abundance value of 6.5 × 10-10 as the “best-fit” model, which corresponds to the minimum of the red curve of Fig. 4. The comparison between the observed and calculated N2H+(1−0) spectral profiles is shown in Fig. 5. The quality of the fit is remarkable: the double-peaked profile of all the hyperfine components is reproduced with high accuracy, including that of the weakest F1,F = (1,0) − (1,1) line, which exhibits only a minor asymmetry due to the low optical opacity. The N2H+ column density averaged over the IRAM 30 m main beam is N = 4.06 × 1013 cm-2.
Figure 6 illustrates the optimal calculated N2H+(1−0) spectrum adopting the centrally decreasing N2H+ abundance profile of Aikawa et al. (2011), and higher infall velocity (yellow curve in Fig. 4). It can be seen that this modelling is also of reasonable quality, although the line profiles of the partially resolved velocity doublets is reproduced less well. For this model, the standard abundance value is 3.0 × 10-9 (value of 1 in Fig. 3), yielding an N2H+ beam-averaged column density of N = 3.32 × 1013 cm-2.
Clearly, the values of N(N2H+) obtained through this method are affected by uncertainties that are difficult to evaluate. In principle, given the least-squares procedure adopted, one may derive the variance-covariance matrix of the system by evaluating the Jacobian of the optimised variables, i.e.: the N2H+ standard abundance, the turbulent line-width, and the scaling factor applied to the hydro-dynamical velocity field.
Such a purely statistical procedure yields rather small errors (<1%), very likely to be negligible compared to the systematic uncertainties associated to the choice of the spherically symmetric hydro-dynamical model − which we expect to be an over-simplified description of the real core structure − or to those produced by the inaccuracies of the collision data. To estimate the latter point, we ran various radiative transfer models, using artificially altered hyperfine rate coefficients by factors of 2 to 5. The resulting optimal N2H+ abundance showed only moderate changes (10−15%, 20% in the most extreme case), but the fits were systematically poorer (χ2 = 200 − 300) with the calculated spectral profile being increasingly unable to reproduce the observed infall asymmetry.
On the other hand, we have shown that one may adopt a completely different choice of N2H+ radial abundance profile still obtaining an acceptable fit (compare Figs. 5 and 6), and this ultimately provides a mean to do an approximate evaluation of the N(N2H+) error bar. The column densities derived using different abundance profiles differ by 0.74 × 1013 cm-2, i.e., 18% of our “best-fit” value. Assuming that this discrepancy represents the maximum 2σ dispersion of the actual N(N2H+), and adding in quadrature a conservative 10% calibration error, we ended with an estimated 13% relative uncertainty on the final results, N(N2H+) = (4.1 ± 0.5) × 1013 cm-2.
 |
Fig. 6 Observed N2H+(1−0) spectrum in L1544 modelled with non-LTE code MOLLIE. The black histograms show our observation data. The blue curve shows the model spectrum computed using the “altered” dark cloud model and the N2H+ radial abundance profile of Aikawa et al. (2011). |
4.2. N15NH+(1−0) and 15NNH+(1−0)
Given the high-quality fit to the N2H+(1−0) hyperfine components, we adopt the velocity “augmented” L1544 model with constant molecular abundance to fit the observed spectra of the 15N-containing isotopologues. Due to the lack of one 14N nucleus, the HFS of the N15NH+(1−0) and  (1−0) lines are simpler than that of the parent species; i.e. they consist of triplets of hyperfine components. In addition, owing to the different quadrupole coupling constants, the N15NH+(1−0) HFS is spread over 4.2 MHz (14 km s-1), whereas the N15NH+(1−0) triplet is contained in a ~1 MHz (3.3 km s-1) interval.
(1−0) lines are simpler than that of the parent species; i.e. they consist of triplets of hyperfine components. In addition, owing to the different quadrupole coupling constants, the N15NH+(1−0) HFS is spread over 4.2 MHz (14 km s-1), whereas the N15NH+(1−0) triplet is contained in a ~1 MHz (3.3 km s-1) interval.
The best simulations of the two lines were obtained by varying independently the N15NH+ and  standard abundance until minimum χ2 is achieved. The best fit dyazenilium abundances are 6.2 × 10-13 for N15NH+ and 6.0 × 10-13, for
standard abundance until minimum χ2 is achieved. The best fit dyazenilium abundances are 6.2 × 10-13 for N15NH+ and 6.0 × 10-13, for  .
.
The fit results are shown in Figs. 7 and 8. The model computed spectra are characterised by symmetrical line profiles. They also show a small but very apparent velocity doubling as expected in the case of a contracting centrally concentrated core. However, the S/N achieved by the present observations is not enough to reveal this feature in the L1544 spectra. The low S/N plus the background effects are responsible for the peculiar line profile asymmetry exhibited by the detected components of both 15N-bearing dyazenilium variants. A detail of the central F = 2 − 1 component of the N15NH+(1−0) and  (1−0) spectra is presented in Fig. 9, where the data obtained with the horizontal and vertical polarisation units of the EMIR receiver are plotted using different curves. It is apparent that the “red asymmetry” noticeable in the observed spectra is produced by the more disturbed signal profiles provided by the vertical polarisation unit (red curves in Fig. 9).
(1−0) spectra is presented in Fig. 9, where the data obtained with the horizontal and vertical polarisation units of the EMIR receiver are plotted using different curves. It is apparent that the “red asymmetry” noticeable in the observed spectra is produced by the more disturbed signal profiles provided by the vertical polarisation unit (red curves in Fig. 9).
 |
Fig. 7 Observed N15NH+(1−0) spectrum in L1544 modelled with non-LTE code MOLLIE. The black histogram shows our observation data. The red curve shows the model spectrum computed using the best fit model (see text). |
Compared to the N2H+(1−0), observations of the 15N dyazenilium variants are considerably noisier and optimum molecular abundances are to be sought over broad χ2 minimums. The estimated column densities are thus affected by comparable larger error. Our optimisation procedure showed that the uncertainty of the 15N-species abundance determination is at most ~10%. This adds in quadrature, together with the other error contributions considered previously for the modelling of the normal isotopologue, yielding a final estimate of a 17% relative uncertainty of the N15NH+ and  column densities.
column densities.
 |
Fig. 8 Observed |
 |
Fig. 9 Detail of the central F = 2 − 1 component for N15NH+(1−0) (upper panel) and |
5. Discussion
5.1. Dyazenilium column densities
Table 3 shows the dyazenilium column densities determined toward L1544 by our radiative transfer modelling and the resulting 14N/15N ratios. Within the estimated error bar, the abundances of N15NH+ and  are coincident:
are coincident: 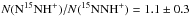 . The newly derived value of the 14N/15N ratio for dyazenilium is ~1000 ± 200, higher than the value of 446 ± 71 previously evaluated adopting the LTE approximation (Bizzocchi et al. 2010).
. The newly derived value of the 14N/15N ratio for dyazenilium is ~1000 ± 200, higher than the value of 446 ± 71 previously evaluated adopting the LTE approximation (Bizzocchi et al. 2010).
Column densities determined for dyazenilium isotopologues toward L1544 and derived 14N/15N abundance ratios.
In our previous letter we analysed the N15NH+(1−0) line emission in LTE assuming constant excitation temperature, Tex = 5 K and optical thin emission. The obtained N(N15NH+) value was (4.1 ± 0.5) × 1010 cm-2, which compares favourably with the one derived by the present full radiative transfer modelling. In fact, owing to the associated low optical opacity, photons emitted by 15N-species can escape easily, and the emerging flux is not affected much by the source structure and dynamics. LTE treatment is thus expected to yield reliable results provided that the assumed Tex is a good approximation of the average core gas temperature.
On the other hand, the N2H+ column density derived here is twice as large as the literature value of (1.8 ± 0.2) × 1013 cm-2 obtained by Crapsi et al. (2005) through an LTE approach. They derived the total optical depth, τ, and Tex directly from the fitting of the J = 1 − 0 hyperfine spectrum and assumed constant excitation temperature for all the quadrupole components. A similar result was also obtained earlier by Caselli et al. (2002b), employing the integrated intensity of the “weak” and moderately thick F1,F = (1,0 − 1,1) component to determine the total column density using the optical thin approximation. Both these treatment are likely to be affected by sizeable inaccuracies. The latter method may underestimate the actual column density by a factor of ~τ/ [1 − exp( − τ1,0 − 1,1)] (≲2, see Appendix in Caselli et al. 2002b); similarly, the above estimate of the total optical depth is significantly uncertain as it does not take the possible presence of excitation anomalies into account.
Indeed, as pointed out by Daniel et al. (2006), for the typical gas condition prevailing in dark clouds, the LTE approximation is inadequate for assessing molecular abundances from observed emission lines; in particular, the assumption of constant excitation temperatures among the hyperfine components of a given rotational transition fails for high opacities. It follows that non-local computation of the radiative transfer is required to reproduce the intensities of the N2H+(1−0) hyperfine spectrum and to retrieve reliable dyazenilium abundance. We are thus confident that our revised N(N2H+) value presented in Table 3 represents a robust estimate of the actual column density of N2H+ toward the L1544 core.
5.2. Nitrogen fractionation in L1544
The dyazenilium 14N/15N abundance ratio derived in the present study is approximately twice as large as previously inferred (Bizzocchi et al. 2010), leading us to reconsider the picture of nitrogen fractionation in L1544 and the implications for the chemical models. Although only a few measurements of the 14N/15N isotopic ratio are available, they clearly show a chemical differentiation. Nitrile-bearing species (molecule carrying the –CN group or its isomer) have been found to be considerably enriched in 15N (Ikeda et al. 2002; Milam & Charnley 2012; Hily-Blant et al. 2013), whereas ammonia derivatives show no 15N enhancements or even a substantial depletion (e.g., 15NH2D in various pre-stellar cores, Gerin et al. 2009). This chemical dichotomy has been treated in detail by Hily-Blant et al. (2013), who proposes a distict genesis for the 15N-enhancement in nitrile- and amine-bearing interstellar molecules. Briefly, nitriles derive from atomic nitrogen, while ammonia is formed via N+, which in turns come from N2 (Wirström et al. 2012, see also Fig. 3 of Hily-Blant et al. 2013). The chemical networks responsible for their 15N enrichment are thus well separated.
The spin-state-dependent chemical model of Wirström et al. (2012) predicts that the 15N-enrichment of ammonia is highly sensitive to the H2ortho-to-para (OPR) ratio, while the fractionation evolution of nitriles is not significantly affected. The production of NH3 is initiated by the ion-neutral reaction 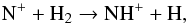 (2)whose activation energy barrier of ~200 K can be efficiently overcome by the o-H2 internal energy. On the other hand, ammonia fractionation gets much less efficient as the OPR decreases, and then an increasing quantity of 15N+ is circulated back into molecular nitrogen by the equilibrium
(2)whose activation energy barrier of ~200 K can be efficiently overcome by the o-H2 internal energy. On the other hand, ammonia fractionation gets much less efficient as the OPR decreases, and then an increasing quantity of 15N+ is circulated back into molecular nitrogen by the equilibrium 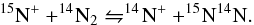 (3)The time evolution of the system shows that the o-H2 drop is paralleled by a substantial rise in the ammonia 14N/15N ratio up to doubling the original elemental fraction (≲800), while 15N enhancement of nitrile compounds keeps increasing, reaching values in the range ≈100 − 300.
(3)The time evolution of the system shows that the o-H2 drop is paralleled by a substantial rise in the ammonia 14N/15N ratio up to doubling the original elemental fraction (≲800), while 15N enhancement of nitrile compounds keeps increasing, reaching values in the range ≈100 − 300.
The above reasoning matches nicely with what is observed in L1544. Low 14N/15N ratios have been measured for HCN (~260, Hily-Blant et al. 2010) and HNC (>27, Milam & Charnley 2012); in contrast, 15N is under-abundant in ammonia, i.e. [NH2D]/[15NH2D] > 700 (Gerin et al. 2009), suggesting an age >2 × 105 yr for the fractionated gas (Wirström et al. 2012).
In this context, our result for N2H+ is puzzling. The low abundances found for 15N-variants suggest that the fractionation behaviour of this ion is very similar to that of ammonia. Their formation pathways are however distinct,because NH3 is generated from N+ through the parent process (2), whereas N2H+ derives from the molecular nitrogen via the protonation reaction 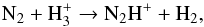 (4)which should not be affected much by the relative abundance of o-H2, as (2)does. One thus might expect that the dyazenilium 15N content simply reflects the degree of fractionation of N2.
(4)which should not be affected much by the relative abundance of o-H2, as (2)does. One thus might expect that the dyazenilium 15N content simply reflects the degree of fractionation of N2.
The molecular nitrogen 14N/15N ratio is predicted to lie in the interval 100−200 by the Wirström et al. (2012) model, matching the previous calculation of the same authors perfectly (Rodgers & Charnley 2008). Essentially the same result has been also obtained by Gerin et al. (2009) using a gas-phase only network. We thus conclude that the N2H+ fractionation cannot be explained in the framework of present nitrogen chemical models.
A way to reconcile our observational results with chemical modelling is to allow selective freeze-out of 15N in some molecular form − possibly 15N14N − on the surface of dust grains, something that needs to be tested in future models that include 15N-bearing species and surface chemistry, as well with laboratory work.
6. Conclusion
In this article we have reported on the detection of  in L1544 and we also presented a full non-LTE radiative transfer modelling of dyazenilium J = 1 − 0 emission in this starless core. Our main findings are summarised below.
in L1544 and we also presented a full non-LTE radiative transfer modelling of dyazenilium J = 1 − 0 emission in this starless core. Our main findings are summarised below.
-
1.
The optically thick N2H+(1−0) spectrum has been reproduced with a high degree of accuracy using a slowly contracting Bonor-Ebert sphere to describe the cloud core. The best match between observed and modelled spectra is obtained using a constant molecular abundance throughout the source. The skewed double peak-profile of the various hyperfine lines was correctly predicted by this simple model, and no evidence of multiple velocity components was found.
-
2.
Our revised estimate of the N2H+ column density in L1544 is ~4 × 1013 cm-2, about two times higher than those determined in a previous investigation using simpler approaches, e.g. LTE: 1.8 × 1013 cm-2, LVG: 2.7 × 1013 cm-2 (Crapsi et al. 2005).
-
3.
N15NH+ and
 spectra were modelled using the same method and yielded column densities that agree well with our previous LTE estimates (~4 × 1010 cm-2, Bizzocchi et al. 2010). The abundance ratio between the two isotopologues is
spectra were modelled using the same method and yielded column densities that agree well with our previous LTE estimates (~4 × 1010 cm-2, Bizzocchi et al. 2010). The abundance ratio between the two isotopologues is 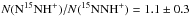 , consistent with the value of 1.25 tentatively determined by Linke et al. (1983) in DR 21 (OH) interstellar cloud. The N15NH+ enhancement predicted by Rodgers & Charnley (2004) is not observed in L1544.
, consistent with the value of 1.25 tentatively determined by Linke et al. (1983) in DR 21 (OH) interstellar cloud. The N15NH+ enhancement predicted by Rodgers & Charnley (2004) is not observed in L1544. -
4.
The dyazenilium 14N/15N ratio determined in L1544 is ~1000 ± 200. This value is similar to what is found for NH3 (>700 Gerin et al. 2009), and is thus suggestive of a common fractionation pathway for the two molecules. This behaviour is not consistent with chemical models, which predict high 15N fractionation of N2H+. We suggest that 15N14N, the precursor of 15N-bearing N2H+ molecular ions, is significantly depleted in the gas phase.
-
5.
A set of hyperfine rate coefficients for N2H+/H2,
 /H2 and
/H2 and  /H2 collisions has been obtained from the N2H+/He close-coupling calculations of Daniel et al. (2004, 2005) and using a transition-dependent scaling relation derived from HCO+/He/H2 studies.
/H2 collisions has been obtained from the N2H+/He close-coupling calculations of Daniel et al. (2004, 2005) and using a transition-dependent scaling relation derived from HCO+/He/H2 studies.
See GILDAS home page at the URL: http://www.iram.fr/IRAMFR/GILDAS
In this appendix the lower case symbol j is used for the quantum number associated to the molecule end-over-end rotation. This follows the convention used in Daniel et al. (2004, 2005) papers, in which the upper case letters are reserved to the angular momenta of the whole collisional system (molecule plus atom).
Acknowledgments
The authors wish to thank the anonymous referee and the editor for the meticulous reading of the manuscript and the useful suggestions. We are indebted to Eric Keto for his help with the MOLLIE code, Yuri Aikawa for supplying the molecular abundance profiles, and to Steve Charnley and Eva Wirstrom who provided the N2H+ fractionation curves calculated with their models. We are also grateful to the IRAM staff for their support during the observations. L.B. and E.L. gratefully acknowledge support from the Science and Technology Foundation (FCT, Portugal) through the Fellowships SFRH/BPD/62966/2009 and SFRH/BPD/71278/2010. L.B. also acknowledges travel support to Pico Veleta from the TNA Radio Net project funded by the European Commission within the FP7 Programme.
References
- Adande, G. R., & Ziurys, L. M. 2012, ApJ, 744, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Aikawa, Y., Furuya, K., Wakelam, V., et al. 2011, in IAU Symp., 280, 33 [Google Scholar]
- Aikawa, Y., Wakelam, V., Hersant, F., Garrod, R. T., & Herbst, E. 2012, ApJ, 760, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Aléon, J. 2010, ApJ, 722, 1342 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, M. H. 1979, J. Chem. Phys., 71, 5212 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, M. H., & Davis, S. L. 1983, J. Chem. Phys., 78, 6754 [NASA ADS] [CrossRef] [Google Scholar]
- Amano, T., Hirao, T., & Takano, J. 2005, J. Mol. Spectrosc., 234, 170 [Google Scholar]
- Arpigny, C., Jehin, E., Manfroid, J., et al. 2003, Science, 301, 1522 [CrossRef] [PubMed] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Balakrishnan, N., Forrey, R. C., & Dalgarno, A. 1999, ApJ, 514, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Alves, J., Huard, T., & Lada, C. J. 2002, ApJ, 570, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Bizzocchi, L., Caselli, P., & Dore, L. 2010, A&A, 510, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bockelée-Morvan, D., Biver, N., Jehin, E., et al. 2008, ApJ, 679, 49 [Google Scholar]
- Bonal, L., Huss, G. R., Krot, A. N., et al. 2010, Geochim. Cosmochim. Acta, 74, 6590 [NASA ADS] [CrossRef] [Google Scholar]
- Briani, G., Gounelle, M., Marrocchi, Y., et al. 2009, in Lunar and Planetary Institute Science Conference Abstracts, 40, 1642 [Google Scholar]
- Buffa, G. 2012, MNRAS, 421, 719 [NASA ADS] [Google Scholar]
- Buffa, G., Dore, L., & Meuwly, M. 2009, MNRAS, 397, 1909 [NASA ADS] [CrossRef] [Google Scholar]
- Busemann, H., Alexander, C. M. O., Nittler, L. R., et al. 2006, Meteor. Planet. Sci. Supp., 41, 5327 [Google Scholar]
- Caselli, P., & Ceccarelli, C. 2012, A&ARv, 20, 56 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Caselli, P., Myers, P. C., & Thaddeus, P. 1995, ApJ, 455, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Zucconi, A., et al. 2002a, ApJ, 565, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Zucconi, A., et al. 2002b, ApJ, 565, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Keto, E., Bergin, E. A., et al. 2012, ApJ, 759, L37 [Google Scholar]
- Charnley, S. B., & Rodgers, S. D. 2002, ApJ, 569, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Corey, G. C., & McCourt, F. R. 1983, J. Phys. Chem., 87, 2723 [CrossRef] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
- Dahmen, G., Wilson, T. L., & Matteucci, F. 1995, A&A, 295, 194 [NASA ADS] [Google Scholar]
- Daniel, F., Dubernet, M.-L., & Meuwly, M. 2004, J. Chem. Phys., 121, 4540 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Daniel, F., Dubernet, M.-L., Meuwly, M., Cernicharo, J., & Pagani, L. 2005, MNRAS, 363, 1083 [NASA ADS] [CrossRef] [Google Scholar]
- Daniel, F., Cernicharo, J., & Dubernet, M.-L. 2006, ApJ, 648, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Daniel, F., Cernicharo, J., Roueff, E., Gerin, M., & Dubernet, M. L. 2007, ApJ, 667, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Dore, L., Bizzocchi, L., Degli Esposti, C., & Tinti, F. 2009, A&A, 496, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubernet, M.-L., & Grosjean, A. 2002, A&A, 390, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubernet, M. L., Alexander, M. H., Ba, Y. A., et al. 2013, A&A, 553, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, D. R. 1999, MNRAS, 305, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Fouchet, T., Irwin, P. G. J., Parrish, P., et al. 2004, Icarus, 172, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Gerin, M., Marcelino, N., Biver, N., et al. 2009, A&A, 498, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grosjean, A., Dubernet, M.-L., & Ceccarelli, C. 2003, A&A, 408, 1197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hily-Blant, P., Walmsley, M., Pineau Des Forêts, G., & Flower, D. 2010, A&A, 513, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hily-Blant, P., Bonal, L., Faure, A., & Quirico, E. 2013, Icarus, 223, 582 [Google Scholar]
- Ikeda, M., Hirota, T., & Yamamoto, S. 2002, ApJ, 575, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E., & Caselli, P. 2008, ApJ, 683, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E., & Caselli, P. 2010, MNRAS, 402, 1625 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E., & Rybicki, G. 2010, ApJ, 716, 1315 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E., Rybicki, G. B., Bergin, E. A., & Plume, R. 2004, ApJ, 613, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E. R. 1990, ApJ, 355, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Linke, R. A., Langer, W. D., & Guelin, M. 1983, ApJ, 271, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Lique, F., Toboła, R., Kłos, J., et al. 2008, A&A, 478, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lis, D. C., Wootten, A., Gerin, M., & Roueff, E. 2010, ApJ, 710, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Manfroid, J., Jehin, E., Hutsemékers, D., et al. 2009, A&A, 503, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marty, B., Chaussidon, M., Wiens, R. C., Jurewicz, A. J. G., & Burnett, D. S. 2011, Science, 332, 1533 [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, A., Krot, A. N., Robert, F., et al. 2007, ApJ, 656, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Milam, S. N., & Charnley, S. B. 2012, in Lunar and Planetary Inst. Technical Report, 43, 2618 [Google Scholar]
- Millar, T. J. 2002, P&SS, 50, 1189 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, T., Mahaffy, P. R., Niemann, H. B., Atreya, S., & Wong, M. 2001, ApJ, 553, L77 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pagani, L., Bourgoin, A., & Lique, F. 2012, A&A, 548, L4 [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J. 2005, in EDP Sciences Conf. Ser., eds. F. Casoli, T. Contini, J. Hameury, & L. Pagani, Vol. SF2A-2005, 721 [Google Scholar]
- Robert, F., & Derenne, S. 2006, Meteor. Planet. Sci. Supp., 41, 5259 [Google Scholar]
- Rodgers, S. D., & Charnley, S. B. 2004, MNRAS, 352, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Rodgers, S. D., & Charnley, S. B. 2008, MNRAS, 385, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, C., Apponi, A. J., Ziurys, L. M., & Wyckoff, S. 2002, ApJ, 578, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stutzki, J., & Winnewisser, G. 1985, A&A, 144, 1 [NASA ADS] [Google Scholar]
- Tafalla, M., Mardones, D., Myers, P. C., et al. 1998, ApJ, 504, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., Walmsley, C. M., & Comito, C. 2002, ApJ, 569, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Terzieva, R., & Herbst, E. 2000, MNRAS, 317, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Ward-Thompson, D., Motte, F., & André, P. 1999, MNRAS, 305, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Wirström, E. S., Charnley, S. B., Cordiner, M. A., & Milam, S. N. 2012, ApJ, 757, L11 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Hyperfine rate coefficients for diazenylium
Appendix A.1: The general case
Hyperfine de-excitation rate coefficients for 15N-containing dyazenilium can be derived using the scattering calculations performed by Daniel et al. (2004, 2005) for the parent species which has two 14N quadrupolar nuclei. Using a CCSD(T) theoretically calculated potential energy surface for the N2H+–He system, these authors derived thermal averages of the opacity factor tensor elements 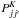 up to j = 6 and fitted them to an analytical form, whose coefficients were presented in a table for the ease of rapid evaluation of the collisional rates at various temperatures2. Unfortunately, some of the equations given in Daniel et al. (2005) are affected by typographic errors, thus preventing recovery of the correct values for the collisional rate coefficients from the given data. With the aim of emending such inconsistencies, we fully reproduce the derivation of the hyperfine rate coefficients from the data of that paper and report all the relevant equations in their correct form. The reader is referred to the original papers (and references therein) for the explanation of the quantities and symbols not explicitly defined here.
up to j = 6 and fitted them to an analytical form, whose coefficients were presented in a table for the ease of rapid evaluation of the collisional rates at various temperatures2. Unfortunately, some of the equations given in Daniel et al. (2005) are affected by typographic errors, thus preventing recovery of the correct values for the collisional rate coefficients from the given data. With the aim of emending such inconsistencies, we fully reproduce the derivation of the hyperfine rate coefficients from the data of that paper and report all the relevant equations in their correct form. The reader is referred to the original papers (and references therein) for the explanation of the quantities and symbols not explicitly defined here.
A convenient starting point is the expression of the hyperfine de-excitation cross-section (see Eq. (15) of Daniel et al. 2004): ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:xsect} \sigma_{jF_1F\rightarrow j'F'_1F'} = \frac{\pi}{k_j^2}[F_1\,F'_1\,F'] \nonumber\\ \times \sum_K \wsxj{F_1}{F'_1}{K}{F'}{F}{I_2}^2 \wsxj{j}{j'}{K}{F'_1}{F_1}{I_1}^2 P^K_{jj'} ; \end{eqnarray}](/articles/aa/full_html/2013/07/aa21276-13/aa21276-13-eq120.png) (A.1)where kj is the wave vector for the energy channel E,
(A.1)where kj is the wave vector for the energy channel E, 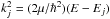 ; the terms in braces are the Wigner-6j symbols; and the notation [xy...] is handy shorthand for the product (2x + 1)(2y + 1)... Each j → j′ transition comprises up to [I1I2] 2 = 81 components and can be described by means of [Min(j,j′)] tensor elements
; the terms in braces are the Wigner-6j symbols; and the notation [xy...] is handy shorthand for the product (2x + 1)(2y + 1)... Each j → j′ transition comprises up to [I1I2] 2 = 81 components and can be described by means of [Min(j,j′)] tensor elements 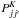 with rank ranging from | j − j′ | to j + j′ (Daniel et al. 2004; Alexander 1979; Alexander & Davis 1983). This tensor contains the whole dynamics of the collisional system and is expressed in terms of the full atom-molecule spinless transition matrix elements
with rank ranging from | j − j′ | to j + j′ (Daniel et al. 2004; Alexander 1979; Alexander & Davis 1983). This tensor contains the whole dynamics of the collisional system and is expressed in terms of the full atom-molecule spinless transition matrix elements 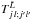 (Daniel et al. 2004; Corey & McCourt 1983):
(Daniel et al. 2004; Corey & McCourt 1983): ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:PKjj} P^K_{jj'} = [K] \sum_{ll'}\sum_{\tilde{L}\tilde{L}'} (-1)^{-\tilde{L}-\tilde{L}'} [\tilde{L}\,\tilde{L}'] \wsxj{j}{j'}{K}{l'}{l}{\tilde{L}} \wsxj{j}{j'}{K}{l'}{l}{\tilde{L}'} \nonumber\\ \times T^{\tilde{L}'}_{j\,l;j'l'}{}^\ast \: T^{\tilde{L}}_{j\,l;j'l'} . \end{eqnarray}](/articles/aa/full_html/2013/07/aa21276-13/aa21276-13-eq133.png) (A.2)At a given temperature, hyperfine de-excitation rates
(A.2)At a given temperature, hyperfine de-excitation rates 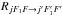 are then obtained by the convolution of the corresponding cross-sections with the Boltzmann-Maxwell distribution of kinetic energies:
are then obtained by the convolution of the corresponding cross-sections with the Boltzmann-Maxwell distribution of kinetic energies: 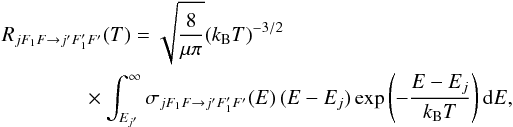 (A.3)where the safe approximation
(A.3)where the safe approximation 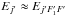 has been used for the lower energy in the integration limits.
has been used for the lower energy in the integration limits.
By substituting Eq. (A.1)for the cross sections into the integral, the expression of the hyperfine rate coefficients can be recast as ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:Rates} R_{jF_1F \rightarrow j'F'_1F'} = [F_1\,F'_1\,F'] \sum_K \wsxj{F_1}{F'_1}{K}{F'}{F}{I_2}^2 \wsxj{j}{j'}{K}{F'_1}{F_1}{I_1}^2 \nonumber\\ \times \left\langle \frac{\pi}{k_j^2} P^K_{jj'} \right\rangle_T \mrm{e}^{E_j/k_{\rm B} T} . \end{eqnarray}](/articles/aa/full_html/2013/07/aa21276-13/aa21276-13-eq137.png) (A.4)Here, the so-called Maxwellian averaged opacity factors are introduced. Following Daniel et al. (2005), they take the form
(A.4)Here, the so-called Maxwellian averaged opacity factors are introduced. Following Daniel et al. (2005), they take the form 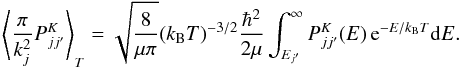 (A.5)The constant exponential factor eEj/kBT is removed from the thermal average (A.3)and thus appears explicitly in the definition of the collisional rate (A.4).
(A.5)The constant exponential factor eEj/kBT is removed from the thermal average (A.3)and thus appears explicitly in the definition of the collisional rate (A.4).
Daniel et al. (2005) calculated the Maxwellian averaged opacity factors 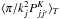 and then fitted them to a analytical form similar to that used by Grosjean et al. (2003) (see also Balakrishnan et al. 1999; Dubernet & Grosjean 2002), i.e.
and then fitted them to a analytical form similar to that used by Grosjean et al. (2003) (see also Balakrishnan et al. 1999; Dubernet & Grosjean 2002), i.e. 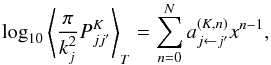 (A.6)where x = T1/3. This equation is to be regarded as the formally correct expression of Eq. (7) in Daniel et al. (2005), and the coefficients
(A.6)where x = T1/3. This equation is to be regarded as the formally correct expression of Eq. (7) in Daniel et al. (2005), and the coefficients 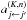 are those presented in Tables 3−5 of that paper. However, the reader has to consider that, for consistency, the correct header of the first column is j ← j′, and the arrows in all its entries must be reversed.
are those presented in Tables 3−5 of that paper. However, the reader has to consider that, for consistency, the correct header of the first column is j ← j′, and the arrows in all its entries must be reversed.
Given a temperature T, one can thus derive the corresponding Maxwellian averaged opacity factors from Eq. (A.6), and then substitute it back into Eq. (A.4)to obtain the N2H+ hyperfine de-excitation rates. If needed, the corresponding excitation rates can be obtained either with Eq. (A.4)with the appropriate quantum number sets (the 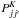 tensor is symmetrical by definition (A.2)) or from de-excitation rates through the detailed balance relation:
tensor is symmetrical by definition (A.2)) or from de-excitation rates through the detailed balance relation: ![\appendix \setcounter{section}{1} \begin{equation} \label{eq:detbal} R_{jF_1F \leftarrow j'F'_1F'} = \frac{[F]}{[F']} R_{jF_1F \rightarrow j'F'_1F'} \, \mrm{e}^{-\Delta E/k_{\rm B} T} , \end{equation}](/articles/aa/full_html/2013/07/aa21276-13/aa21276-13-eq146.png) (A.7)where ΔE represents the energy difference between the hyperfine levels (jF1F) and
(A.7)where ΔE represents the energy difference between the hyperfine levels (jF1F) and 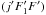 . By summing Eq. (A.4)over all the final states
. By summing Eq. (A.4)over all the final states 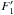 , F′, and making use of the 6j-symbol orthogonality relation, one can derive the equality
, F′, and making use of the 6j-symbol orthogonality relation, one can derive the equality 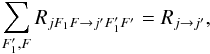 (A.8)with the rotational de-excitation collisional rates defined as
(A.8)with the rotational de-excitation collisional rates defined as ![\appendix \setcounter{section}{1} \begin{equation} \label{eq:jrates} R_{j \rightarrow j'} = [j]^{-1} \sum_K \left\langle \frac{\pi}{k_j^2} P^K_{jj'} \right\rangle_T \mrm{e}^{E_j/k_{\rm B} T} . \end{equation}](/articles/aa/full_html/2013/07/aa21276-13/aa21276-13-eq154.png) (A.9)These values coincide with those obtainable from the expansion coefficients reported in Table 2 of Daniel et al. (2005) if one considers that they define excitation rates and not “de-excitation rates” as is incorrectly stated in the caption.
(A.9)These values coincide with those obtainable from the expansion coefficients reported in Table 2 of Daniel et al. (2005) if one considers that they define excitation rates and not “de-excitation rates” as is incorrectly stated in the caption.
Appendix A.2: 15N-species
The 15N-variants of diazenylium contain a single quadrupolar nucleus, thus the coupling scheme is 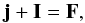 (A.10)and each hyperfine level is labelled by the two quantum numbers j and F. The corresponding de-excitation rates can be derived from Maxwellian-averaged opacity factors
(A.10)and each hyperfine level is labelled by the two quantum numbers j and F. The corresponding de-excitation rates can be derived from Maxwellian-averaged opacity factors 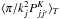 by adapting Eqs. (A.4)to the single spin case. This is done simply by summing the right-hand side of the expression over all final states F′ and again, making use of the orthogonality relation of the 6j-symbols. At this point, F1 become the new F and it results in
by adapting Eqs. (A.4)to the single spin case. This is done simply by summing the right-hand side of the expression over all final states F′ and again, making use of the orthogonality relation of the 6j-symbols. At this point, F1 become the new F and it results in ![\appendix \setcounter{section}{1} \begin{equation} \label{eq:R1spin} R_{jF \rightarrow j'F'} = [F'] \sum_K \wsxj{j}{j'}{K}{F'}{F}{I}^2 \left\langle \frac{\pi}{k_j^2} P^K_{jj'} \right\rangle_T \mrm{e}^{E_j/k_{\rm B} T} . \end{equation}](/articles/aa/full_html/2013/07/aa21276-13/aa21276-13-eq158.png) (A.11)The desired rates RjF → j′F′ at a given T are thus obtained by using the Maxwellian average opacity factors
(A.11)The desired rates RjF → j′F′ at a given T are thus obtained by using the Maxwellian average opacity factors 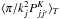 derived from the coefficients of Daniel et al. (2005) through Eq. (A.6).
derived from the coefficients of Daniel et al. (2005) through Eq. (A.6).
Appendix A.3: Scaling of hyperfine rates
Since all the above data deal with the the dyazenilium/He system, we had to choose a reliable scaling relation to evaluate the appropriate rates for H2 collisions. A widely used approximation is to consider identical cross sections for these two colliding systems, and then apply a scaling factor of 1.37 to the rate coefficients in order to correct for the difference in reduced mass (Lique et al. 2008; Schöier et al. 2005); however, it has been pointed out by many authors (see, e.g. Daniel et al. 2006; Pagani et al. 2012) that this correction is not appropriate for molecular ions, since the in electrostatic interaction with H2 is markedly different from that with He. This is indeed the case for HCO+: the comparison between the HCO+/He rotational rates calculated by Buffa et al. (2009) and those for the HCO+/H2 system (Flower 1999) shows that the latter are higher by a factor of about 2−5, depending on the rotational quantum number j and the temperature.
N2H+/H2 hyperfine rates (cm3 s-1) for temperatures ranging from 5 K to 50 K.
N15NH+/H2 hyperfine rates (cm3 s-1) for temperatures ranging from 5 K to 50 K.
15NNH+/H2 hyperfine rates (cm3 s-1) for temperatures ranging from 5 K to 50 K.
On the other hand, the HCO+/He rates are practically indistinguishable from those of N2H+/He (hyperfine free, Daniel et al. 2005), owing to the similarity in the ion electronic structure. This suggests that accurate values of the hyperfine coefficients for the dyazenilium/H2 system can be obtained at any given temperature as follows: 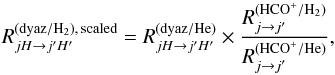 (A.12)where H represents the set of spin quantum numbers used to label a given hyperfine level. We derived j → j′ transition dependent scaling factors from the available HCO+ rotational data (Flower 1999; Buffa et al. 2009) and then applied them to the hyperfine rates of the N2H+/He, N15NH+/He, and
(A.12)where H represents the set of spin quantum numbers used to label a given hyperfine level. We derived j → j′ transition dependent scaling factors from the available HCO+ rotational data (Flower 1999; Buffa et al. 2009) and then applied them to the hyperfine rates of the N2H+/He, N15NH+/He, and  /He systems calculated from the data of Daniel et al. (2005). We used Eq. (A.12)to evaluate only scaled de-excitation hyperfine rates, whereas the corresponding coefficients for the excitation transitions were obtained through the detailed balance equality
/He systems calculated from the data of Daniel et al. (2005). We used Eq. (A.12)to evaluate only scaled de-excitation hyperfine rates, whereas the corresponding coefficients for the excitation transitions were obtained through the detailed balance equality 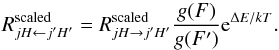 (A.13)It should be noted that to use Eq. (A.12)one also needs the elastic Δj = 0 rates for both hyperfine-free data sets. These coefficients are required to properly scale the hyperfine rates for transitions among various F1, F sublevels of a given j. Elastic rates for HCO+/H2 collisions from Flower (1999) calculations are available in the basecol3 database (Dubernet et al. 2013). Conversely, elastic coefficients were not provided for the HCO+/He system in the Buffa et al. (2009) paper, so we evaluated these rates from a set of Δj = 0 cross-sections provided by the author.
(A.13)It should be noted that to use Eq. (A.12)one also needs the elastic Δj = 0 rates for both hyperfine-free data sets. These coefficients are required to properly scale the hyperfine rates for transitions among various F1, F sublevels of a given j. Elastic rates for HCO+/H2 collisions from Flower (1999) calculations are available in the basecol3 database (Dubernet et al. 2013). Conversely, elastic coefficients were not provided for the HCO+/He system in the Buffa et al. (2009) paper, so we evaluated these rates from a set of Δj = 0 cross-sections provided by the author.
N2H+ hyperfine level energies (MHz).
N15NH+ hyperfine level energies (MHz).
15NNH+ hyperfine level energies (MHz).
Appendix B: Rate coefficient tables
We calculated a full set of hyperfine de-excitation rates for the N2H+/H2, N15NH+/H2, and  /H2 collision systems in the temperature range 5−50 K. Since these data are not included in the collisional databases, we make them available at the CDS. Tables B.1−B.3 contain the hyperfine de-excitation collisional rates for N2H+/H2, N15NH+/H2, and
/H2 collision systems in the temperature range 5−50 K. Since these data are not included in the collisional databases, we make them available at the CDS. Tables B.1−B.3 contain the hyperfine de-excitation collisional rates for N2H+/H2, N15NH+/H2, and  /H2, respectively. Elastic rates (ΔJ = 0,ΔF = 0) are also included in the tables. The energy levels used for the calculation are reported in Tables B.4−B.6. Energy values for N15NH+ and
/H2, respectively. Elastic rates (ΔJ = 0,ΔF = 0) are also included in the tables. The energy levels used for the calculation are reported in Tables B.4−B.6. Energy values for N15NH+ and  were taken from Dore et al. (2009), whereas for the parent species they were derived through a spectral fitting of the hyperfine frequencies of Caselli et al. (1995) and the submillimetre transitions of Amano et al. (2005).
were taken from Dore et al. (2009), whereas for the parent species they were derived through a spectral fitting of the hyperfine frequencies of Caselli et al. (1995) and the submillimetre transitions of Amano et al. (2005).
In this section we reproduce an excerpt of each table (the first five lines) with the appropriate column headings.
All Tables
Predicted hyperfine frequencies, estimated 1σ uncertainties, and relative line intensities for the J = 1 − 0 transition of N15NH+ and  (Dore et al. 2009).
(Dore et al. 2009).
Results of the CLASS HFS fit on the observed spectral profile of the 15N-bearing dyazenilium isotopologues observed towards L1544.
Column densities determined for dyazenilium isotopologues toward L1544 and derived 14N/15N abundance ratios.
All Figures
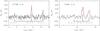 |
Fig. 1 Spectra of the 15N-containing dyazenilium isotopologues observed towards L1544 (black histogram), and computed spectral profiles resulting from the HFS fits (red dashed curves). Superimposed black lines indicate the position and relative intensity of the hyperfine components. Left panel: N15NH+(1−0) transition (reproduced from Bizzocchi et al. 2010). Right panel: |
| In the text | |
 |
Fig. 2 Temperature, density, and inward velocity profiles of L1544 used as model in the present radiative transfer modelling. The red dotted curve indicates the gas temperature in K, the blue curve is the log of density in cm-3, and the purple dashed curve represents the inward velocity in units of 0.01 km s-1. |
| In the text | |
 |
Fig. 3 Abundance trends (normalised to the maximum values) predicted by the Aikawa et al. (2011) models for dyazenilium and chemically related species. The N2H+ abundance decreases toward the cloud centre following the N2 freeze-out (green curve) onto dust mantels at high gas density. The concomitant steeper drops of free electron (grey curve) and CO (brown curve) give rise to the N2H+ abundance maxima at radii of ~104 and ~103 astronomical units. N2D+ shows similar behaviour (blue curve), but it features a much stronger inner peak owing to the strong deuterium fractionation existing in the highly-CO depleted central region. |
| In the text | |
 |
Fig. 4 Weighted χ2 of the N2H+(1−0) modellings using different standard dyazenilium abundances and radial profiles. Blue curve: constant N2H+ abundance with respect to H2; red curve: constant abundance and modified cloud infall velocity (see text). Green curve: radial N2H+ abundance profile shown in Fig. 3; yellow curve: radial profile with modified cloud infall velocity. |
| In the text | |
 |
Fig. 5 Observed N2H+(1−0) spectrum in L1544 modelled with non-LTE code MOLLIE. The histograms show our observation data. The red curve shows the model spectrum computed using the “altered” dark cloud model and N2H+ constant abundance throughout the core (see text). |
| In the text | |
 |
Fig. 6 Observed N2H+(1−0) spectrum in L1544 modelled with non-LTE code MOLLIE. The black histograms show our observation data. The blue curve shows the model spectrum computed using the “altered” dark cloud model and the N2H+ radial abundance profile of Aikawa et al. (2011). |
| In the text | |
 |
Fig. 7 Observed N15NH+(1−0) spectrum in L1544 modelled with non-LTE code MOLLIE. The black histogram shows our observation data. The red curve shows the model spectrum computed using the best fit model (see text). |
| In the text | |
 |
Fig. 8 Observed |
| In the text | |
 |
Fig. 9 Detail of the central F = 2 − 1 component for N15NH+(1−0) (upper panel) and |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


