| Issue |
A&A
Volume 544, August 2012
|
|
|---|---|---|
| Article Number | A5 | |
| Number of page(s) | 7 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201219531 | |
| Published online | 19 July 2012 | |
Ram pressure effects in the galactic plane and galactic dynamos in the no-z approximation
1 School of Mathematics, University of Manchester, Oxford Road, Manchester, M13 9PL, UK
e-mail: moss@ma.man.ac.uk
2 Department of Physics, Moscow University, 119992 Moscow, Russia
3 MPI für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
Received: 3 May 2012
Accepted: 20 June 2012
Context. The magnetic field of galaxies is believed to be produced by internal dynamo action, but can be affected by motion of the galaxy through the surrounding medium. Observations of polarized radio emission of galaxies located in galaxy clusters have revealed noticeable features of large-scale magnetic configurations, including displacements of the magnetic structures from the optical images and tails, which are possible imprints of ram pressure effects arising from motion of the galaxies through the intracluster medium.
Aims. We present a quantitative dynamo model, which attempts to describe the above effects. In contrast, to the traditional problem of a wind affecting a body with a prescribed magnetic field, we investigate how a non-magnetized wind flow affects a magnetic field that is being self-excited by galactic dynamo action.
Methods. To isolate the leading physical effects, we exploit a simple dynamo model that can describe relevant effects. In particular, we use what is known as the “no-z” approximation for the mean-field dynamo equations.
Results. In a suitable parametric range we obtain displacements of the large-scale magnetic field, as well as magnetic tails. However, the specific details of their locations are quite counterintuitive. The direction of displacement is perpendicular to, rather than parallel to, the wind direction. The point at which the tail emerges from the galaxy depends on details of the model. The tail is eventually directed downstream. In the simplest case the magnetic tail begins in the region where the wind decreases the total gas velocity. Any wind that penetrates the galaxy modifies the intrinsic dynamo action. These features are different from those found in ram-pressure models.
Conclusions. Any determination of galactic motion through the cluster medium from observational data needs to take the effects of dynamo action into account.
Key words: galaxies: clusters: intracluster medium / galaxies: magnetic fields / dynamo / galaxies: individual: Virgo cluster / magnetic fields / galaxies: interactions
© ESO, 2012
1. Introduction
The formation and subsequent evolution of large-scale galactic magnetic fields are believed to be a result of galactic physical processes, mainly induction effects of differential rotation and mirror-asymmetric galactic turbulence (e.g. Beck et al. 1996). Galaxies are surrounded by the intergalactic medium and participate in various intergalactic interactions which somehow modify the “intrinsic” magnetic properties of galaxies. The corresponding effects on galactic magnetic structures naturally attract interest (e.g. Williams et al. 2002). A straightforward example of this is provided by the propagation of galaxies through the medium pervading galaxy clusters. It appears quite natural to attempt to attribute the existence of various galactic tails to the effects of such propagation. Such a morphological interpretation a priori appears natural; however it requires verification by modelling, including effects of galactic dynamo action.
Contemporary radio polarimetric observations provide several examples of large-scale galactic magnetic configurations which appear possibly to be affected by such propagation effects. In particular, Vollmer et al. (2007) and Weżgowiec et al. (2007) observed magnetic fields of large spiral galaxies in the Virgo Cluster in order to study interactions of galaxies with the cluster environment. (Further relevant results can be found in Kantharia et al. 2008; Vollmer et al. 2010; Weżgowiec et al. 2011; see also Yoshida et al. 2012.) A straightforward intention of this work was to use the proximity of the Virgo Cluster to isolate effects of the high-velocity tidal interactions and the effects of ram pressure stripping by the intracluster gas.
Indeed, the observational results presented by Weżgowiec et al. (2007) demonstrate a magnetic configuration that impressively mimics the naive expectation of the effects of ram pressure arising from galactic motion through the surrounding intracluster gas. In particular, the distribution of total radio intensity in NGC 4535 at 6.3 cm wavelength (Fig. 5 in the above cited paper) practically coincides with the optical image while the measures of polarized emission (Fig. 6 of that paper) are markedly displaced from the optical image towards the west. This displacement has been confirmed by observations at 3.6 cm wavelength (Weżgowiec et al. 2012) and hence cannot be caused by Faraday depolarization. Possible interpretations of this displacement include: (1) the spiral magnetic field generated in NGC 4535 by a galactic dynamo is compressed on the western side by ram pressure; (2) a weakening of the galactic dynamo on the eastern side by ram pressure; (3) amplification and ordering of the magnetic field by shear in the HI envelope of the galaxy (Vollmer et al. 2010). Note that NGC 4535 is observed almost face-on, so that if the asymmetry in PI is due to ram pressure effects then its motion through the intracluster medium (ICM) is expected to be at a small or moderate angle with respect to the galactic plane; in this case the direction of motion can hardly be inferred from spectroscopic data which gives radial velocities.
We present as an instructive example a map of polarized intensity and magnetic vectors of NGC 4535 overlaid on the optical image of this galaxy (Fig. 1). Note that the maximum of polarized intensity is located at the periphery of the optical image while the magnetic field vectors cover the entire optical image.
 |
Fig. 1 Polarized radio emission (contours) and B-vectors of the spiral galaxy NGC 4535 in the Virgo Cluster, observed at 3.6 cm wavelength with the Effelsberg 100-m telescope, smoothed to 3′ resolution and overlaid onto a DSS optical image (kindly provided by Marek Weżgowiec). |
Another example comes from the observations of NGC 4501. (Figure 3 in Weżgowiec et al. 2007, shows the total intensity and Fig. 4 the polarized intensity.) Again, the total intensity practically coincides with the optical image while the polarized emission is displaced from the optical image. The displacement is less pronounced than for NGC 4535. NGC 4501 is more inclined towards the line of sight than NGC 4535, which makes the interpretation less straightforward. Displacements towards one side of the disc are also detected in other galaxies observed edge-on, e.g. in NGC 4402 (Vollmer et al. 2007) and in NGC 4388 (Weżgowiec et al. 2012). On the other hand, several face-on galaxies of the Virgo Cluster with large-scale spiral patterns of their magnetic fields, like NGC 4303 and NGC 4321, show no displacement at all, presumably indicating that they move “head-on” through the cluster medium, i.e. almost along the line of sight (Weżgowiec et al. 2012).
 |
Fig. 2 Polarized radio emission (contours) and B-vectors of the spiral galaxy NGC 4535 in the Virgo Cluster, observed at 6.3 cm wavelength with the VLA at 18′′ resolution and overlaid onto a DSS optical image (from Vollmer et al. 2007). |
Each galaxy needs a specific model of gas stripping, gas back-flow and the effects of the flow on the magnetic field, and these can explain the observations in many cases (e.g. Vollmer et al. 2009, 2012). However, these models consider only magnetic fields which are sheared and amplified by the distorted velocity field of the gas and neglect the ongoing dynamo action in the galaxy. Not surprisingly, several features of the magnetic field patterns, such as a large-scale asymmetry out of the disc plane as in NGC 4192 (Weżgowiec et al. 2012) or a long magnetic tail in NGC 4438 (Fig. 2) remained unexplained in these papers.
An interpretation of the displacement as an effect of the ram pressure interacting with galactic dynamo action needs quantitative investigation and verification; this is the aim of this paper.
Our idea is to test the interpretation in the most straightforward way. We present the effect of ram pressure (in the coordinate system of the galaxy) as a non-magnetized flow of the intracluster gas which moves through the galaxy parallel to the galactic plane and interacts with the dynamo-generated magnetic field. We assume that this motion does not destroy the main drivers of galactic dynamo, i.e. differential rotation and helical interstellar turbulence, that are responsible for the generation of the large-scale magnetic field and subsequently for the polarized emission. We expect to see that the gas motion (“wind”) displaces the dynamo-generated magnetic field so that it is no longer centred on the galaxy.
The effect of a wind on magnetic structures around various celestial bodies is a classical topic that originated in investigations of interactions between the solar wind and the Earth’s magnetic field. Obviously, the solar wind has a significant effect on the shape of the Earth’s magnetic field, but not on its generation. We consider here the problem where a flow directly affects the region of magnetic field generation. We do not consider the galactic magnetic field to be prescribed a priori, but rather investigate how the generation process is modified by the wind.
2. The dynamo model
We assume that the ram pressure effects under investigation are quite robust and their modelling does not require knowledge of finer details of hydrodynamics and MHD of a particular galaxy (which are hardly known for NGC 4535 and NGC 4501). Correspondingly, we choose the simplest galactic dynamo model and include the effects of interests.
We use a version of the “no-z” model (Subramanian & Mestel 1993; Moss 1995), implemented in cartesian coordinates in the αω approximation (see Moss et al. 2012, for more details). The dynamo-active disc is embedded in an external diffusive medium, chosen to be large enough that a further increase in size does not affect the results.
The code solves in the αω approximation explicitly for the field components parallel to the disc plane while the component perpendicular to this plane (i.e. in the z-direction) is given by the solenoidality condition. The key parameters are the aspect ratio λ = h/R, where h corresponds to the semi-thickness of the warm gas disc and R is its radius, and the dynamo numbers Rα = α0h/η,Rω = Ω0h2/η. λ must be a small parameter. η is the turbulent diffusivity, for simplicity assumed uniform throughout the computational region, and α0,Ω0 are typical values of the α-coefficient and angular velocity respectively. Thus the dynamo equations become in cylindrical polar coordinates (r,φ,z) ![\begin{eqnarray} \frac{\partial B_r}{\partial t} & = & -R_\alpha B_\phi-\frac{\pi^2}{4} B_r\nonumber \\ &&+\,\lambda^2\left(\frac{\partial}{\partial r}\left[\frac{1}{r}\frac{\partial}{\partial r}(rB_r)\right]+\frac{1}{r^2}\frac{\partial^2B_r}{\partial\phi^2}-\frac{2}{r^2}\frac{\partial B_\phi}{\partial\phi}\right), \label{evolBr} \end{eqnarray}](/articles/aa/full_html/2012/08/aa19531-12/aa19531-12-eq15.png) (1)
(1)![\begin{eqnarray} \frac{\partial B_\phi}{\partial t} & = & R_\omega r B_r\frac{{\rm d}\Omega}{{\rm d}r}-R_\omega\Omega\frac{\partial B_\phi}{\partial \phi}-\frac{\pi^2}{4} B_\phi \nonumber \\ && +\,\lambda^2\left(\frac{\partial}{\partial r}\left[\frac{1}{r}\frac{\partial}{\partial r}(rB_\phi)\right] +\frac{1}{r^2}\frac{B_\phi^2}{\partial \phi^2}-\frac{2}{r^2}\frac{\partial B_r}{\partial \phi}\right), \label{evolBphi} \end{eqnarray}](/articles/aa/full_html/2012/08/aa19531-12/aa19531-12-eq16.png) (2)here z does not appear explicitly. This equation has been calibrated by introduction of the factors π2/4 in the vertical diffusion terms. These factors arise from a pragmatic examination of the z-dependence of the solutions in the local approximation (e.g. Ruzmaikin et al. 1988), and their inclusion improves significantly the agreement between the no-z and local approximations. In principle in the αω approximation the parameters Rα,Rω can be combined into a single dynamo number D = RαRω, but we choose to keep them separate.
(2)here z does not appear explicitly. This equation has been calibrated by introduction of the factors π2/4 in the vertical diffusion terms. These factors arise from a pragmatic examination of the z-dependence of the solutions in the local approximation (e.g. Ruzmaikin et al. 1988), and their inclusion improves significantly the agreement between the no-z and local approximations. In principle in the αω approximation the parameters Rα,Rω can be combined into a single dynamo number D = RαRω, but we choose to keep them separate.
We assume a uniform alpha-effect over the disc region x2 + y2 ≤ 1, and the rotation law in r < r3 is given by 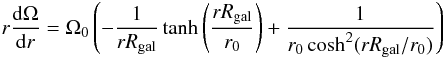 (3)(see also Moss et al. 2012). This rotation law is truncated at the fractional radius r3 ~ 1, and in
(3)(see also Moss et al. 2012). This rotation law is truncated at the fractional radius r3 ~ 1, and in 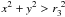 the value at r = r3 decays smoothly to zero by r = 3. There is a smooth transition between the forms in r < r3 and r > r3.
the value at r = r3 decays smoothly to zero by r = 3. There is a smooth transition between the forms in r < r3 and r > r3.
A uniform wind U = −U0i blowing in the negative x-direction is imposed. The governing parameter for the wind is Rm = U0h/η0, where η0 is the value of the diffusivity in the disc x2 + y2 ≤ 1. Thus we add to the right hand sides of the dimensionless Eqs. (1) and (2) terms corresponding to the r and φ components of Rm λ ∇ × ( − U0 i × B) – see Moss (1996) for further details. We note that the treatment of the “external” region r > 1 is subject to increased uncertainty. At larger galacto-centric distances outside of the “galaxy”, the no-z approximation is likely to become more inaccurate in the absence of a well defined disc. Also the value of the diffusivity in this region is uncertain – see also Sect. 4.
 |
Fig. 3 Magnetic field vectors for the steady state field without wind. Rα = 1, Rω = 20, r3 = 0.9. The galaxy is assumed to rotate counterclockwise in this and all other examples. |
3. Results
We performed extensive numerical simulations. We first evolve the model with no wind until an approximately steady state is reached – see Fig. 3. (This normally occurs by τ ≈ 3 − 4.) The initial conditions are a comparitively weak ( ≲ 1% of equipartition strength) quasi-uniform field (however the steady saturated field configuration is not sensitive to the initial field provided that it is relatively weak and more-or-less homogeneous). We then turn on the wind, and evolve until a steady state is again reached. (In practice, the details of the start-up procedure make no difference to the final configuration.)
Putting Rα = 1, for two values of r3 (the rotation law transition radius), we computed models with several values of Rω and Rm. With r3 = 0.9 we show in Fig. 4 the final states of the magnetic field for Rω = 20,Rm = 100,150, Rα = 1. (Rm = 200 kills dynamo action for these parameters.) For comparison, in Fig. 5 we show a model with r3 = 1.4, Rω = 20,Rm = 150, Rα = 1. In all models, the magnetic pattern is displaced perpendicular to the wind direction and a spectacular magnetic tail can appear.
Of course, dynamo action is significant for the results obtained. For comparison we performed a simulation with Rα = 0 to confirm that the magnetic field rapidly decays for such a flow.
We appreciate that a homogeneous wind velocity profile is certainly a severe oversimplification, given the substantial density contrast between the exterior medium and the galactic disc. Thus we implement a wind profile that decays inside the galaxy. In order to mimic it we multiply the originally uniform wind velocity by the factor exp( − l/ld) where l is the distance a wind particle has traveled since encountering the nominal edge of the galaxy at r = rw (with a natural choice rw = 1). To be specific, we choose ld = 4.
This wind strongly reduces the efficiency of the dynamo and this reduction grows with smaller ld. Even for ld = 4 we have to use Rα = 2 and Rω = 30 to obtain a growing field instead of Rα = 1 and Rω = 20 for which magnetic field becomes decaying.
Magnetic field evolution with an x-dependent wind velocity results in a minor displacement of the magnetic structure from the galactic centre, which is almost invisible in the plot (Fig. 6), and the magnetic tail disappears.
 |
Fig. 4 Vectors of the steady state distribution of magnetic field, overlaid on circles indicating the location of the dynamo sources (solid) and r = r3 (broken). a) r3 = 0.9, Rω = 20,Rm = 100, b) r3 = 0.9, Rω = 20,Rm = 150, c) r3 = 0.9, Rω = 10,Rm = 150. The streaming velocity is in the negative x-direction. |
 |
Fig. 5 Vectors of the steady state distribution of magnetic field, overlaid on circles indicating the location of the dynamo sources (solid) and r = r3 (broken), r3 = 1.4, Rα = 1, Rω = 20,Rm = 150. The streaming velocity is in the negative x-direction. |
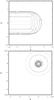 |
Fig. 6 Model with wind decelerating through the galaxy: Rα = 2.0, Rω = 30, Rm = 150. Upper panel – contours of velocity field; below – the stationary magnetic configuration. Note that in the upper panel the centre of the plot is the centre of the galaxy. |
The velocity field shown in Fig. 6 has a nonvanishing divergency. In principle, it can be argued that a z-component of velocity would compensate this divergency. In the no-z context, such a component might be represented by an additional loss term. However, to obtain some idea of the possible importance of this omission, we added a term vy, determined from the condition ∂vx/∂x + ∂vy/∂y = 0. The effect of this change was found to be negligible.
To explore an additional possibility, we follow a suggestion of Pfrommer & Dursi (2010) and also consider a wind that is deflected around the galaxy, i.e. a case of a “magnetic drape” (Fig. 7, upper panel). Of course, we have to add extra terms involving uy to Eqs. (1), (2). An example of a stationary magnetic structure (Fig. 7, middle panel) resulting from such a flow shows again a general displacement of magnetic structure in the direction perpendicular to the wind.
Details of the elongated magnetic structure are strongly model dependent, as demonstrated in Fig. 7, for example, compare the lower and middle panels (Rm = 75 and 100, respectively).
 |
Fig. 7 Model with wind deflected around the galaxy (“draping flow”, top panel) and the corresponding magnetic structures. Governing parameters are Rα = 1,Rω = 10,r3 = 1.4, with Rm = 100 in the middle panel, and Rm = 75 in the lower. Note that in the uppermost plot, the centre of the plot is the centre of the galaxy. |
Our modelling includes ongoing dynamo action, rather than prescribing the initial magnetic structure, and allowing it to evolve passively, subject to the ram pressure flow. We demonstrate a distinction between two cases by considering a model with evolution of an initially prescribed magnetic field which is affected by a wind and is not supported by further dynamo action (Fig. 8). Such a magnetic configuration decays and is transported by the wind further and further away from the galaxy centre. For cases with dynamo action, for some wind profiles the magnetic configuration becomes a straight tail emerging from the side of the galaxy in the direction downstream of the wind, while the tail in the model shown in middle panel of Fig. 7 emerges on the upstream side, and is twisted around the galaxy. In Fig. 7, lower panel, the tail originates on the left side and is wound around the galaxy over about 270 degrees. Note that the end of the tail detaches from the galaxy and continues downstream at the side of the galaxy where the wind decreases the total gas velocity (negative y, “south” side). It is debatable whether we should refer to a “tail” in these cases when describing a “wound around” field, rather than considering this to be an immediate result of the modified dynamo action within the galaxy.
 |
Fig. 8 Model with the draping flow interacting with a magnetic configuration that is initially prescribed by dynamo action, but then the dynamo action is switched off. A snapshot for just one instant is presented. As in the other figures, the mean streaming velocity is in the negative x-direction. |
4. Discussion
We have presented the results of modelling of the effects of ram pressure on the stationary, dynamo-generated, magnetic field configuration in spiral galaxies. We recognize a general displacement of the magnetic configuration from the galaxy centre as well as, in some cases (not always, see Fig. 6), magnetic tails propagating from the galaxy into the surrounding medium. These effects are rather nontrivial and have not been recognized in previous modelling attempts (Roediger 2009; Vollmer et al. 2009, 2012).
Figures 4 and 5 show that the wind displaces the centre of the magnetic field pattern in a galaxy from the nominal centre of mass. Surprisingly, this displacement is not in the downstream direction of the wind flow, but perpendicular to this direction. As the galaxy is assumed to rotate counterclockwise, the wind increases the total gas velocity on the “north” side of the galaxy and decreases it on the “south” side. It thus appears that the large-scale field is displaced towards the galaxy in the region where the gas velocity is reduced. The small-scale (turbulent) magnetic field component, related to the star-formation activity in a galaxy and hence the gas distribution, is not affected, in agreement with the observation that the total radio emission is not displaced.
If the ram speed of the wind is too large, it evacuates the large-scale magnetic field from the galaxy and dynamo action is killed. The critical velocity U∗ at which dynamo action is still possible can be estimated as follows. Accepting for a crude estimate that the maximal linear velocity of differential rotation V = ΩR and taking into account the definitions of Rω and Rm we obtain 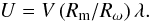 (4)For Rm = 150, Rω = 20 (close to the maximal wind velocity for which dynamo still works) and λ = 0.05, V = 250 km s-1 we obtain U∗ ≈ 100 km s-1.
(4)For Rm = 150, Rω = 20 (close to the maximal wind velocity for which dynamo still works) and λ = 0.05, V = 250 km s-1 we obtain U∗ ≈ 100 km s-1.
Comparing the estimate U∗ = 100 km s-1 with the observed velocities of galaxies relative to the ICM it is necessary to take into account that the majority of our models do not include the density contrast between the interstellar medium (ISM) in the galaxy and ICM. Estimating the limiting velocity of a galaxy W in the cluster medium that is just sufficient to kill dynamo action from the condition ρISMU∗ = ρICMW, and taking ρISM/ρICM ≈ 10-2 cm-3/10-4 cm-3 ≈ 100 we derive W ≈ 104 km s-1 (here ρISM and ρICM are typical ionized gas densities in the galactic disc and the ICM respectively).
If U > U∗, the wind pushes the dynamo-generated magnetic field out of the region where dynamo is active and hence kills the dynamo. If U ≪ U∗, the wind almost does not affect the dynamo-generated magnetic field. If U is slightly less than U∗, the main effect is a less efficient dynamo action in the “northmost” part of the galaxy where wind and rotation velocities reinforce. In contrast, the magnetic field is larger in the “south” part of the galaxy where the velocities tend to cancel and dynamo action is stronger. As a result, the magnetic configuration is shifted across rather along the wind direction. There is thus a substantial difference between the effect of a wind on a magnetic configuration generated in situ (i.e. by dynamo action) from that on a magnetic configuration generated before the wind impacts on the galaxy. In our models the dynamo operates contemporaneously with the wind, and so the wind modifies the dynamo velocity field, and hence the dynamo properties.
The wind direction and the general displacement of the main magnetic structure are mutually perpendicular. This must be into account in determinations of galactic motion through the cluster medium from observational data (cf. e.g. Pfrommer & Dursi 2010).
The displacements obtained in the models are quite moderate. It is impossible to push the centre of the magnetic configuration far beyond the galaxy centre, or the boundary of the region occupied by the bulk of the field far beyond its original position. This is partly at least because in the absence of external dynamo sources (here alpha-effect) the field rapidly decays. Note that the magnetic vectors in the map of NGC 4535 cover the centre of the optical structure of the galaxy, i.e. the displacement of magnetic structure from the optical image is still quite modest.
Another unexpected result is the location of the magnetic tail: it emerges from different regions of the disc depending on the details of the model, and then propagates into the area where the wind decreases the total velocity. The dynamo-generated field propagates due to turbulent diffusion out of the area which rotates significantly, and is caught by the wind, producing a tail.
Observations (Weżgowiez et al. 2007) do not show the presence of magnetic tails in NGC 4535 and NGC 4501. On the other hand, the spectacular magnetic tails presented in Fig. 4 may be related to the tail of polarized emission in NGC 4438 (Fig. 2; Vollmer et al. 2007, 2010). Our simple model does not describe gas flows which might be associated with the magnetic tails. It appears plausible that gas is also carried along in the magnetic tail. Chung et al. (2007) found seven spiral galaxies in the Virgo cluster with long, one-sided tails of neutral gas.
The various features of magnetic field structures associated with the ram pressure effects obtained in the models presented above have different ranges of robustness. The magnetic structure is displaced perpendicularly to the wind direction in all models. Magnetic tails are quite “fragile” and disappear when the turbulent magnetic diffusivity in the surrounding space is increased. The value of turbulent magnetic diffusivity in galactic halos and ICMs is an important dynamo governing parameter, but is difficult to estimate (e.g. Sokoloff & Shukurov 1990). If we include a deceleration of the wind in the disc, the tails are smaller and its recognition becomes difficult – see Sect. 3. The tail disappears if an x-dependence is imposed on the wind velocity (Sect. 3). Furthermore, the no-z approximation can no longer be expected to be valid far outside of the disc region, where inter alia the estimate of − B/h2 for the z-diffusion may in turn be an over-estimate. Given that the dynamo does not operate in the external region, the latter uncertainty can probably be formally absorbed into the uncertainty concerning the external diffusivity. Thus the presence of a magnetic tail cannot be considered a robust feature of our simulations.
A statistical investigation of magnetic tails in cluster galaxies could contribute to elucidation of the problem. Of course, further details such as elongated magnetic structures and their particular forms are even more uncertain and need further more detailed modelling.
Our simulations are necessarily restricted to considering flows parallel to the galactic plane. Real flows will be inclined at arbitrary angles. We can split such a general flow into components parallel to and perpendicular to the plane. We have separately modelled the effects of a perpendicular flow (parallel to the z-axis) in an axisymmetric dynamo model with dynamo effect confined to the disc region. Here the effect is more clearly an advection of the field structure in the direction of the flow, effectively “lifting” the field from the galactic midplane. As the field is moved out of the disc region, where the alpha-effect is assumed to operate, in the absence of dynamo action the field decays. The advection is thus naturally limited in extent. A somewhat faster flow removes the field from the dynamo-active region more rapidly than it can be regenerated, and so kills the dynamo completely. Thus we feel our results are reasonably representative of flows that are not too strongly inclined to the galactic plane. In contrast, strong flows at large angles to the disc plane will seriously weaken dynamo action.
Finally, we wish to stress again that the problem under discussion is different from the classical problem of a magnetized wind affecting a body with prescribed magnetic field (this problem in the galactic context is addressed e.g. by Ruszkowski et al. 2012). The interaction between the wind and the internal velocity field, and hence the effect of the wind on dynamo action, cannot be avoided, unless the internal magnetic field is completely shielded from the external flow – which however is unrealistic. The problem is no longer that of a dynamo with a simple circular flow. Hence, the interpretation of an asymmetry in polarized radio intensity as a naive effect of ram pressure is similarly unrealistic. A compression of the internal field is possible only if the wind penetrates the galaxy, which in turn must affect dynamo action. Clearly there are plausible improvements that could be made to our no-z model, but we believe our results are generic. We have investigated a magnetic field that is self-excited in a region that is directly affected by the wind, i.e. the flow generating the dynamo is altered. This problem has not attracted attention so far. In this preliminary study we have attempted to isolate the basic physical effects. We assume that the wind itself is non-magnetized and flows parallel to the galactic plane, and use simple models to describe the wind profile. These assumptions allowed us to use the simple no-z approach. A more detailed modelling, including a magnetized wind inclined to the galactic plane and extension to a 3D model, and/or to go beyond a mean-field formulation of the problem, would be instructive and should be investigated in future.
Acknowledgments
We thank Marek Weżgowiec for providing Fig. 1 and Bernd Vollmer for Fig. 2, and Marita Krause for a number of useful comments on the text. R.B. acknowledges support from the DFG Research Unit FOR1254. An anonymous referee also helped to improve the paper. The research was partially supported by the grant DFG-RFBR 08-02-92881.
References
- Beck, R., Brandenburg, A., Moss, D., Shukurov, & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Chung, A., van Gorkom, J. H., Kenney, J. D. P., & Vollmer, B. 2007, ApJ, 659, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Kantharia, N. G., Pramesh, R. A., & Sirothia, S. K. 2008, MNRAS, 383, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D. 1995, MNRAS, 275, 191 [NASA ADS] [Google Scholar]
- Moss, D. 1996, A&A, 315, 63 [NASA ADS] [Google Scholar]
- Moss, D., Stepanov, R., Arshakian, T. G., et al. 2012, A&A, 537, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfrommer, C., & Dursi, L. J. 2010, Nature Physics, 6, 520 [Google Scholar]
- Roediger, E. 2009, Astron. Nachr., 330, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Ruszkowski, M., Brüggen, M., Lee, D., & Shin, M.-S. 2012, ApJ, submitted [arXiv:1203.1343] [Google Scholar]
- Ruzmaikin, A. A., Shukurov, A. M., & Sokoloff, D. D. 1988, Magnetic Fields of Galaxies (Kluwer) [Google Scholar]
- Sokoloff, D., & Shukurov, A. 1990, Nature, 347, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Subramanian, K., & Mestel, L. 1993, MNRAS, 265, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Vollmer, B., Soida, M., Beck, R., et al. 2007, A&A, 464, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Soida, M., Chung, A., et al. 2009, A&A, 496, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Soida, M., Chung, A., et al. 2010, A&A, 512, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Soida, M., Braine, J., et al. 2012, A&A, 537, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weżgowiec, M., Urbanik, M., Vollmer, B., et al. 2007, A&A, 471, 93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weżgowiec, M., Vollmer, B., Ehle, M., et al. 2011, A&A, 531, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weżgowiec, M., Urbanik, M., Beck, R., Chyży, K. T., & Soida, M., 2012, A&A, submitted [Google Scholar]
- Yoshida, M., Yagi, M., Komiyama, Y., et al. 2012, ApJ, 749, 43 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Polarized radio emission (contours) and B-vectors of the spiral galaxy NGC 4535 in the Virgo Cluster, observed at 3.6 cm wavelength with the Effelsberg 100-m telescope, smoothed to 3′ resolution and overlaid onto a DSS optical image (kindly provided by Marek Weżgowiec). |
| In the text | |
 |
Fig. 2 Polarized radio emission (contours) and B-vectors of the spiral galaxy NGC 4535 in the Virgo Cluster, observed at 6.3 cm wavelength with the VLA at 18′′ resolution and overlaid onto a DSS optical image (from Vollmer et al. 2007). |
| In the text | |
 |
Fig. 3 Magnetic field vectors for the steady state field without wind. Rα = 1, Rω = 20, r3 = 0.9. The galaxy is assumed to rotate counterclockwise in this and all other examples. |
| In the text | |
 |
Fig. 4 Vectors of the steady state distribution of magnetic field, overlaid on circles indicating the location of the dynamo sources (solid) and r = r3 (broken). a) r3 = 0.9, Rω = 20,Rm = 100, b) r3 = 0.9, Rω = 20,Rm = 150, c) r3 = 0.9, Rω = 10,Rm = 150. The streaming velocity is in the negative x-direction. |
| In the text | |
 |
Fig. 5 Vectors of the steady state distribution of magnetic field, overlaid on circles indicating the location of the dynamo sources (solid) and r = r3 (broken), r3 = 1.4, Rα = 1, Rω = 20,Rm = 150. The streaming velocity is in the negative x-direction. |
| In the text | |
 |
Fig. 6 Model with wind decelerating through the galaxy: Rα = 2.0, Rω = 30, Rm = 150. Upper panel – contours of velocity field; below – the stationary magnetic configuration. Note that in the upper panel the centre of the plot is the centre of the galaxy. |
| In the text | |
 |
Fig. 7 Model with wind deflected around the galaxy (“draping flow”, top panel) and the corresponding magnetic structures. Governing parameters are Rα = 1,Rω = 10,r3 = 1.4, with Rm = 100 in the middle panel, and Rm = 75 in the lower. Note that in the uppermost plot, the centre of the plot is the centre of the galaxy. |
| In the text | |
 |
Fig. 8 Model with the draping flow interacting with a magnetic configuration that is initially prescribed by dynamo action, but then the dynamo action is switched off. A snapshot for just one instant is presented. As in the other figures, the mean streaming velocity is in the negative x-direction. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


