© ESO, 2011

1. Introduction

Interest in gyroresonant radiation transfer arose with the first observations of cyclotron lines in the spectra of astrophysical objects, such as neutron stars and white dwarfs. For a firmly grounded interpretation of these observations, the study of all physical processes that take part in the cyclotron line formation is needed. In the present work, we analyze the processes that lead to the spectral redistribution of gyroresonant photons within and outside the line core. Owing to the strong magnetic field, this redistribution is a one-dimensional (1D) process, what makes it different from the well-known three-dimensional (3D) redistribution in the case of atomic (ion) line formation (see Mihalas 1978, and references therein). The net results, however, are qualitatively (but non quantitatively) similar: the redistribution dramatically influences the cyclotron line profile and the distribution of outgoing photons over their optical depth of origin.

Depending on the atmospheric parameters, different effects can govern the transport of gyroresonant radiation in the strong magnetic field. For example, the vacuum polarization and linear mode coupling can change the dispersive characteristics and propagation of electromagnetic waves in magnetized plasma (Adler 1971; Pavlov & Shibanov 1979; Zheleznyakov et al. 1983; Kirk & Cramer 1985; Ho & Lai 2001). Another potentially important effect is the redistribution of the gyroresonant photons over frequencies and their subsequent escape from the line. This is the effect that we closly examine below for a broad range of parameters. The comprehensive treatment of radiation transfer with due account for the photon redistribution is beyond the scope of this work and will be presented elsewhere.

Since the motion of electrons in the strong magnetic field is essentially 1D, the spectral redistribution of photons is strongly suppressed compared to the common case of atomic and ion lines, where the motion of scatterers is 3D. However, the escape of radiation from the cyclotron line becomes increasingly important as the average number of scatterings that a photon takes to leave the line (usually a very large number) exceeds the number of scatterings it takes to get absorbed. This, as we show below, appears to be a common situation in magnetized atmospheres of compact stars. The frequency redistribution plays a decisive role not only for neutron stars, but also (somewhat counterintuitively) for white dwarfs, where the temperatures are very far from relativistic values and the magnetic field strength is several orders of magnitude smaller than the Schwinger limit.

We note that Wasserman & Salpeter (1980) presented an analysis of cyclotron radiation transfer in the limit of a strong magnetic field, where the recoil effect is of crucial importance. Here we focus on other mechanisms of frequency redistribution that are important in the weaker magnetic fields such as the redistribution caused by both the relativistic Doppler effect and the natural line broadening. We analyze, in terms of Monte-Carlo simulations, how the frequency redistribution affects the radiation transfer in the magnetized plasma with parameters that are typical of compact stars atmospheres of B ~ 10⁸−10¹⁴ G, T ~ 1−1000 eV.

One particularly important application of our work is to cyclotron-driven winds. Mitrofanov & Pavlov (1981, 1982) drew attention to the radiation pressure force in the atmospheres of compact stars is becoming amplified because of an electron cyclotron resonance in the same way as it becomes amplified in the presence of ion resonance lines in the atmospheres of early-type stars. A number of estimates indicated that the critical luminosity of compact stars with strong magnetic fields can be many orders of magnitude below the Eddington limit (Braun & Yahel 1984; Bespalov & Zheleznyakov 1990; Zheleznyakov et al. 1996). The exact magnitude of the resonant radiation pressure force remains an open question; apparently one should take into consideration the spectral redistribution of gyroresonant photons, as well as some other effects.

2. Model setup

Our numerical models are set up as follows. For the atmosphere, we take the thin slab geometry, pure hydrogen composition, and 100 percent ionization. The magnetic field B is assumed to be constant, so the cyclotron frequency does not change during the transfer. We assume a constant temperature T, which corresponds to the Maxwellian distribution of electrons over longitudinal (with respect to the magnetic field) velocities 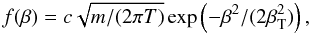$\mathit{f}\mathrm{\left(}\mathit{\beta }\mathrm{\right)}\mathrm{=}\mathit{c}\sqrt{\mathit{m}\mathit{/}\mathrm{\left(}\mathrm{2}\mathit{\pi T}\mathrm{\right)}}\exp \mathrm{(}\mathrm{-}{\mathit{\beta }}^{\mathrm{2}}\mathit{/}\mathrm{(}\mathrm{2}{\mathit{\beta }}_{\mathrm{T}}^{\mathrm{2}}{\mathrm{\left)}}^{\mathrm{\right)}}\mathit{,}$(1)where c is the speed of light, m the electron mass, and β = v/c the dimensionless longitudinal velocity, β_T = (T/(mc²))^1/2 the thermal velocity. The transverse temperature is taken to be zero (all electrons are at the ground Landau level). In principle, strong gyroresonant radiation can alter the electron distribution over the longitudinal velocities and Landau levels; this as well as possible temperature inhomogeneity will be discussed elsewhere. We use the optical depth at the cyclotron line center 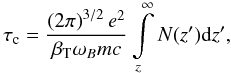${\mathit{\tau }}_{\mathrm{c}}\mathrm{=}\frac{{\mathrm{(}\mathrm{2}{\mathit{\pi }}^{\mathrm{)}}}^{\mathrm{3}\mathit{/}\mathrm{2}}{\mathit{e}}^{\mathrm{2}}}{{\mathit{\beta }}_{\mathrm{T}}{\mathit{\omega }}_{\mathit{B}}\mathit{mc}}\underset{\mathit{z}}{\overset{\mathrm{\infty }}{\mathrm{\int }}}\mathit{N}\mathrm{\left(}{\mathit{z}}^{\mathrm{\prime }}\mathrm{\right)}\mathrm{d}{\mathit{z}}^{\mathrm{\prime }}\mathit{,}$(2)as a definition of the local optical depth. Here e is the elementary charge, ω_B = eB/(mc) the electron gyrofrequency, N the number density of electrons and the z-axis is perpendicular to the stellar surface and directed outwards.

3. Photon redistribution over frequencies

We now consider first the photon redistribution via the relativistic Doppler effect. Here we use the word “relativistic” to stress the necessity to keep second order terms in the resonance condition, regardless of how small the velocity of a scatterer is. The non-relativistic resonance condition for 1D electron motion 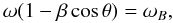$\mathit{\omega }\mathrm{(}\mathrm{1}\mathrm{-}\mathit{\beta }\cos \mathit{\theta }\mathrm{)}\mathrm{=}{\mathit{\omega }}_{\mathit{B}}\mathit{,}$(3)means that a photon with given frequency ω and propagation angle θ is scattered resonantly by electrons whose longitudinal velocity is (ω − ω_B)/(ωcosθ). When the photon scatters off such an electron, it acquires different parameters ω′ and θ′, but these quantities are related by the same resonant condition, with the same value of resonant velocity. Thus, by an appropriate choice of variables the equation of radiation transfer reduces to an equivalent of monochromatic scattering by immovable particles. This implies that escape of photons from the cyclotron resonance line due to the Doppler frequency shift is absolutely forbidden as long as the non-relativistic approximation is used.

From the fully relativistic resonance condition for photon-electron interaction one can find that for each frequency ω there are, in general, two groups of resonant electrons. Under the conditions typical for neutron stars and white dwarfs, the thermal velocity of electrons is much smaller than the speed of light and the energy of gyroresonant photons is much smaller than the electron’s rest energy, ħω_B ≪ m_ec². In this case, it is sufficient to expand the cyclotron resonance condition into a power-law series, keeping terms up to the second order in β and up to the first order in the recoil parameter κ = ħω_B/(2mc²): 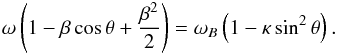$\mathit{\omega }\left(\mathrm{1}\mathrm{-}\mathit{\beta }\cos \mathit{\theta }\mathrm{+}\frac{{\mathit{\beta }}^{\mathrm{2}}}{\mathrm{2}}\right)\mathrm{=}{\mathit{\omega }}_{\mathit{B}}\mathrm{(}\mathrm{1}\mathrm{-}\mathit{\kappa }{\sin }^{\mathrm{2}}{\mathit{\theta }}^{\mathrm{)}}\mathit{.}$(4)The velocities of resonant electrons are: 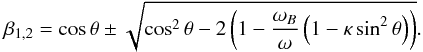${\mathit{\beta }}_{\mathrm{1}\mathit{,}\mathrm{2}}\mathrm{=}\cos \mathit{\theta }\mathrm{\pm }\sqrt{{\cos }^{\mathrm{2}}\mathit{\theta }\mathrm{-}\mathrm{2}\left(\mathrm{1}\mathrm{-}\frac{{\mathit{\omega }}_{\mathit{B}}}{\mathit{\omega }}\mathrm{(}\mathrm{1}\mathrm{-}\mathit{\kappa }{\sin }^{\mathrm{2}}{\mathit{\theta }}^{\mathrm{)}}\right)}\mathit{.}$(5)If |cosθ| ~ 1, one of the roots becomes unphysical (| β| > 1), which is of no real importance since the number of electrons in a Maxwellian distribution at |β| ≫ β_T is negligible anyway. In the case of quasitransverse propagation (| cosθ| ≲ β_T), both roots are of the order of β_T and should be taken into account together, since both groups of resonant electrons are numerous enough.

Resonant interaction with two separate groups of electrons at once can lead to an efficient escape of radiation from the line center. We consider, for example, a photon, that resonantly scatters off an electron with velocity β₂, and that is also in resonance with electrons whose velocity is β₁ (where we assume that |β₂| > |β₁| for definiteness). Upon scattering, the photon acquires frequency ω′ and propagation angle θ′. This photon will be in resonance with electrons which have either the velocity

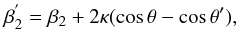${\mathit{\beta }}_{\mathrm{2}}^{\mathrm{\prime }}\mathrm{=}{\mathit{\beta }}_{\mathrm{2}}\mathrm{+}\mathrm{2}\mathit{\kappa }\mathrm{(}\cos \mathit{\theta }\mathrm{-}\cos {\mathit{\theta }}^{\mathrm{\prime }}\mathrm{)}\mathit{,}$which is nearly the same as the initial one except for the small (because usually κ ≪ β_T) recoil correction, or the velocity 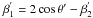${\mathit{\beta }}_{\mathrm{1}}^{{}^{\mathrm{\prime }}}\mathrm{=}\mathrm{2}\cos {\mathit{\theta }}^{\mathrm{\prime }}\mathrm{-}{\mathit{\beta }}_{\mathrm{2}}^{{}^{\mathrm{\prime }}}$, which, in general, differs a lot from the initial resonance at β₁. Furthermore, the relation 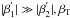$\mathrm{\left|}{\mathit{\beta }}_{\mathrm{1}}^{{}^{\mathrm{\prime }}}\mathrm{\right|}\mathrm{\gg }\mathrm{\left|}{\mathit{\beta }}_{\mathrm{2}}^{{}^{\mathrm{\prime }}}\mathrm{\right|}\mathit{,}{\mathit{\beta }}_{\mathrm{T}}$ holds for almost all possible scattering directions. In effect, the photon makes a jump from one group of resonant electrons (those with β = β₁, which are the most abundant resonant electrons before the scattering) to another (those with 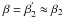$\mathit{\beta }\mathrm{=}{\mathit{\beta }}_{\mathrm{2}}^{{}^{\mathrm{\prime }}}\mathrm{\approx }{\mathit{\beta }}_{\mathrm{2}}$, which are the most abundant resonant electrons after the scattering).

A typical outcome of such a scattering is a decrease in the optical depth because the number of electrons with relatively high velocities β₂ is smaller than that with low velocities β₁. For the Maxwellian distribution, the optical depth τ drops from 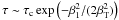$\mathit{\tau }\mathrm{~}{\mathit{\tau }}_{\mathrm{c}}\exp {}^{\mathrm{(}}\mathrm{-}{\mathit{\beta }}_{\mathrm{1}}^{\mathrm{2}}\mathit{/}\mathrm{(}\mathrm{2}{\mathit{\beta }}_{\mathrm{T}}^{\mathrm{2}}{\mathrm{\left)}}^{\mathrm{\right)}}$ to $\mathit{\tau }\mathrm{~}{\mathit{\tau }}_{\mathrm{c}}\exp {}^{\mathrm{(}}\mathrm{-}{\mathit{\beta }}_{\mathrm{2}}^{\mathrm{2}}\mathit{/}\mathrm{(}\mathrm{2}{\mathit{\beta }}_{\mathrm{T}}^{\mathrm{2}}{\mathrm{\left)}}^{\mathrm{\right)}}$.

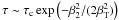The jump mechanism causes photons to escape from the line mainly in a single scattering. This happens if a photon after the scattering has both resonant groups far enough from zero velocity, β = 0, so that the optical depth becomes less than unity. For the Maxwellian distribution, this condition takes the form

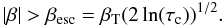$\mathrm{\left|}\mathit{\beta }\mathrm{\right|}\mathit{>}{\mathit{\beta }}_{\mathrm{esc}}\mathrm{=}{\mathit{\beta }}_{\mathrm{T}}\mathrm{\left(}\mathrm{2}\ln \mathrm{\right(}{\mathit{\tau }}_{\mathrm{c}}\mathrm{)}{\mathrm{)}}^{\mathrm{1}\mathit{/}\mathrm{2}}\mathit{.}$We consider a photon that has a resonance at β₁ = 0; its second resonant group is therefore at β₂ = 2cosθ. If |β₂| > β_esc, then a single scattering off an electron with velocity β₂ will allow the photon to escape. The probability of this scattering relative to the total scattering probability equals $\mathit{P}\mathrm{=}{\mathrm{[}\mathrm{1}\mathrm{+}\exp {\mathrm{(}\mathrm{2}{\cos }^{\mathrm{2}}\mathit{\theta }\mathit{/}{{\mathit{\beta }}_{\mathrm{T}}^{\mathrm{2}}}^{\mathrm{)}}}^{\mathrm{]}}}^{-1}$(6)and rapidly drops to zero at |cosθ| ≫ β_T. Averaging Eq. 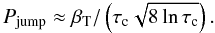(6) over isotropical propagation directions yields the escape probability ${\mathit{P}}_{\mathrm{jump}}\mathrm{\approx }{\mathit{\beta }}_{\mathrm{T}}\mathit{/}\left({\mathit{\tau }}_{\mathrm{c}}\sqrt{\mathrm{8}\ln {\mathit{\tau }}_{\mathrm{c}}}\right)\mathit{.}$(7)Two other mechanisms of photon escape from the cyclotron line are the recoil and the off-resonance scattering, which become possible because of the line broadening. The recoil mechanism operates only under the condition 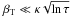${\mathit{\beta }}_{\mathrm{T}}\mathrm{\ll }\mathit{\kappa }\sqrt{\ln \mathit{\tau }}$. In this case, the recoil velocity is so large that after the scattering the electron finds itself far in the tail of the Maxwellian distribution and therefore escapes from the line. In the opposite case, the frequency shift attained due to recoil is compensated at subsequent scatterings and the photon remains within the line (Wang et al. 1988).

The probability of escape from the line via radiative broadening can be calculated as follows. If after the scattering the optical depth for the photon becomes less than unity, we assume that this photon has escaped from the line. We define P_Σ(β_T,γ,τ_c) to be the probability of such an event, where 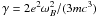$\mathit{\gamma }\mathrm{=}\mathrm{2}{\mathit{e}}^{\mathrm{2}}{\mathit{\omega }}_{\mathit{B}}^{\mathrm{2}}\mathit{/}\mathrm{\left(}\mathrm{3}\mathit{m}{\mathit{c}}^{\mathrm{3}}\mathrm{\right)}$ is the natural line width. If the natural line width were equal to zero, then the probability of escape would be equal to the probability of escape due to relativistic jumps: P_Σ = P_jump. If we neglect relativistic effects, then P_Σ = P_γ(γ/(ω_Bβ_T),τ_c) where in the non-relativistic limit the cyclotron line has a pure Voigt shape (Wasserman & Salpeter 1980), thus it depends only on the ratio of the natural line width to the Doppler width. Here P_γ is the probability of escape due to the finite natural line width. There is no simple formula for this probability, but it can be calculated numerically, the result being presented in Fig. 1.

Fig. 1 The probability of escape via line broadening, Pγ (per scattering), for a photon with frequency ω = ωB residing at the optical depth τ. Solid line is for γ/(ωBβT) = 10-3, dashed line is for γ/(ωBβT) = 10-4, and dot-dashed line is for γ/(ωBβT) = 10-5.

Under the condition that the natural line width is much smaller than the Doppler width, the overall probability of escape is P_Σ ≈ P_γ + P_jump. This expression is approximate because of the relativistic corrections to P_γ and finite line-width corrections to P_jump, whose influence is minor, as confirmed by numerical simulations. We note that P_γ(τ) is a much slower function of optical depth τ than P_jump(τ), which means that at sufficiently high optical depths the probability of escape due to natural line broadening becomes dominant.

4. Monte Carlo simulations

We consider a semi-infinite atmosphere with an exponential density profile, where scattering strongly prevails over absorption. The probability of absorption in a single photon-electron interaction grows linearly with the optical depth P_abs = ε₀τ, provided that $\mathit{\tau }\mathrm{\ll }{\mathit{\epsilon }}_{\mathrm{0}}^{-1}$. Using a Monte Carlo code based on the Lucy (1999) algorithm, we calculate the probability of escape for a photon initially emitted at the optical depth τ. The results (Fig. 2) show that the probability of escape increases considerably because of redistribution effects, especially at large optical depths. Therefore, the impact of these deep layers on the emergent spectra can be crucial.

Fig. 2 The function τ2Pesc(τ) for the semi-infinite atmosphere. Model atmosphere parameters are ε0 = 10-6, βT = 0.01, and γ/ωB = 10-6. Solid line represents data with both relativistic Doppler effect and natural line broadening taken into account, and dashed line that where only non-relativistic Doppler effect (3) is included in the simulation.

At smaller optical depths, where the probability of absorption is very low, the escape probability is close to 1. Thus, almost all photons have enough time to escape from the atmosphere. Starting from the depth τ₁ ≈ (ε₀) ^− 1/3, which is equal to the so-called thermalization depth in the limit of coherent scattering, photons are more readily absorbed than let to leave the atmosphere via diffusion. Here the photons escape from the atmosphere primarily through the wings of the line, as a result of redistribution. Furthermore, if the optical depth for a photon at its place of origin were larger than τ₂ = 1/ε₀, then the mean free path would be determined not by the scattering, but rather by the absorption. In this case, the photon has an exponentially small probability of escaping from the atmosphere. We note that the majority of emerging radiation is generated at τ < τ₂. This means that, for the comprehensive analysis of cyclotron radiation transfer, one should include frequency redistribution effects in the simulations and run them for all optical depths up to the large value τ₂.

Fig. 3 Schematic view of the regions of dominance for various mechanisms of photon escape on the magnetic field – temperature plane, I – diffusion escape, II – relativistic jumps, III – natural line broadening, IV – recoil. The region where cyclotron driven wind is possible is above the dashed lines. The left figure is for a white dwarf (MWD = 1   M⊙), and the right figure is for a neutron star (MNS = 1.4   M⊙, R = 12 km).

On the basis of the Monte Carlo calculations, we identify regions of the magnetic field – temperature plane, where particular mechanisms of photon escape dominate (Fig. 3). These results are given for the optical depth where the probability of photon absorption is equal to the probability of photon escape. Since a significant part of the emergent radiation originates at larger depths, the frequency effects can be important under even less restrictive conditions. Hence, the exact location of the border lines in Fig. 3 cannot be defined in a model-independent way.

Altogether, there are four zones with different cyclotron radiation escape dynamics. In zone I, the spatial diffusion of photons leads them out of the atmosphere without any significant changes to their mean free paths. In this case, we can neglect both relativistic jumps and escape due to the natural line broadening. In zone II, the majority of the cyclotron radiation leaves the line because of relativistic jumps, whereas in zone III it leaves the line because of off-resonance scatterings at the Lorentzian wings of broadened cyclotron line. In zone IV, the recoil effect becomes important. We note that these zones are determined according to the main escape mechanism of a photon, which, generally speaking, differs from the main frequency redistribution mechanism (cf. Fig. 1 in Garasyov et al. 2008).

The region where a cyclotron driven wind is possible, is above the dashed lines. The line is drawn assuming a maximum possible cyclotron radiation pressure, i.e. assuming that the emerging intensity is equal to the blackbody’s value with temperature T. The wind region in Fig. 3 encompasses the first three zones. Thus, both a relativistic correction to the resonance condition and natural line broadening should be taken into account, whereas the recoil effect can be neglected for cyclotron-driven winds.

5. Conclusions

We have analyze the effects of the frequency redistribution of gyroresonant radiation in the atmospheres of magnetized compact stars, particularly the region of parameters around ħω_B ~ kT, where the formation of a cyclotron radiation-driven wind is possible. At the same time, our study is equally well suited to obtaining the cyclotron line profiles in the case of low intensities, where no wind-like outflow is expected.

The redistribution under such conditions differs essentially from the well-studied mechanisms that are typical of the atomic and ion spectral lines, primarily because of the 1D character of electron motion in a strong magnetic field. The inclusion of sophisticated physics and the interplay between various mechanisms of the gyrophoton redistribution over frequencies make the problems of the gyroresonant radiation transfer and the cyclotron radiation-driven wind highly non-trivial. The resolution of both problems may greatly enrich our understanding of compact star observations.

Our finding is that the main (for typical compact-star parameters) cause of the redistribution of gyrophotons over frequencies, is the relativistic Doppler effect. It is responsible for two roots in the gyroresonance condition, such that a photon can experience huge changes in opacity by resonantly scattering off faster electrons whose longitudinal velocity is offset from the Maxwell distribution core. The finite linewidth and the recoil effect turn out to be less important when the energy of cyclotron quanta is of the order of the thermal energy, but can be crucial if the cyclotron line is located far in the Wien tail of thermal spectrum or the optical depth is sufficiently large.

Statistically, the redistribution of photons out of the cyclotron line results in a boosted probability of their escape from a large optical depth. As our simulations show, the emerging radiation is gathered over a large interval of optical depths, spanning one or two orders of magnitude. Potentially, this causes all sorts of inhomogeneities to show up in the resulting spectrum in a more pronounced way, and the radiation transfer equation in these situations should be solved over a range of optical depths sufficiently large to capture the origin of the major part of outgoing photons.

Acknowledgments

This work was supported by RFBR (grant 11-02-00364-a).

References

All Figures

	Fig. 1 The probability of escape via line broadening, Pγ (per scattering), for a photon with frequency ω = ωB residing at the optical depth τ. Solid line is for γ/(ωBβT) = 10-3, dashed line is for γ/(ωBβT) = 10-4, and dot-dashed line is for γ/(ωBβT) = 10-5.
In the text

	Fig. 2 The function τ2Pesc(τ) for the semi-infinite atmosphere. Model atmosphere parameters are ε0 = 10-6, βT = 0.01, and γ/ωB = 10-6. Solid line represents data with both relativistic Doppler effect and natural line broadening taken into account, and dashed line that where only non-relativistic Doppler effect (3) is included in the simulation.
In the text

Fig. 3 Schematic view of the regions of dominance for various mechanisms of photon escape on the magnetic field – temperature plane, I – diffusion escape, II – relativistic jumps, III – natural line broadening, IV – recoil. The region where cyclotron driven wind is possible is above the dashed lines. The left figure is for a white dwarf (MWD = 1   M⊙), and the right figure is for a neutron star (MNS = 1.4   M⊙, R = 12 km).

In the text