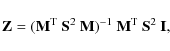Imaging of stellar surfaces with the Occamian approach and the least-squares deconvolution technique

S. P. Järvinen; S. V. Berdyugina

doi:10.1051/0004-6361/200912574

Home

All issues

Volume 521 (October 2010)

A&A, 521 (2010) A86

Full HTML

Free Access

Issue		A&A Volume 521, October 2010


Article Number		A86
Number of page(s)		11
Section		Numerical methods and codes
DOI		https://doi.org/10.1051/0004-6361/200912574
Published online		25 October 2010

A&A 521, A86 (2010)

Imaging of stellar surfaces with the Occamian approach and the least-squares deconvolution technique

S. P. Järvinen¹ - S. V. Berdyugina^2,3

1 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
2 - Kiepenheuer-Institut für Sonnenphysik, Schöneckstr. 6, 79104 Freiburg, Germany
3 - Tuorla Observatory, University of Turku, 21500 Piikkiö, Finland

Received 26 May 2009 / Accepted 3 August 2010

Abstract
Context. We present in this paper a new technique for the indirect imaging of stellar surfaces (Doppler imaging, DI), when low signal-to-noise spectral data have been improved by the least-squares deconvolution (LSD) method and inverted into temperature maps with the Occamian approach. We apply this technique to both simulated and real data and investigate its applicability for different stellar rotation rates and noise levels in data.
Aims. Our goal is to boost the signal of spots in spectral lines and to reduce the effect of photon noise without loosing the temperature information in the lines.
Methods. We simulated data from a test star, to which we added different amounts of noise, and employed the inversion technique based on the Occamian approach with and without LSD. In order to be able to infer a temperature map from LSD profiles, we applied the LSD technique for the first time to both the simulated observations and theoretical local line profiles, which remain dependent on temperature and limb angles. We also investigated how the excitation energy of individual lines effects the obtained solution by using three submasks that have lines with low, medium, and high excitation energy levels.
Results. We show that our novel approach enables us to overcome the limitations of the two-temperature approximation, which was previously employed for LSD profiles, and to obtain true temperature maps with stellar atmosphere models. The resulting maps agree well with those obtained using the inversion code without LSD, provided the data are noiseless. However, using LSD is only advisable for poor signal-to-noise data. Further, we show that the Occamian technique, both with and without LSD, approaches the surface temperature distribution reasonably well for an adequate spatial resolution. Thus, the stellar rotation rate has a great influence on the result. For instance, in a slowly rotating star, closely situated spots are usually recovered blurred and unresolved, which affects the obtained temperature range of the map. This limitation is critical for small unresolved cool spots and is common for all DI techniques. Finally the LSD method was carried out for high signal-to-noise observations of the young active star V889 Her: the maps obtained with and without LSD are found to be consistent.
Conclusions. Our new technique provides meaningful information on the temperature distribution on the stellar surfaces, which was previously inaccessible in DI with LSD. Our approach can be easily adopted for any other multi-line techniques.

Key words: stars: imaging - stars: activity - methods: data analysis

1 Introduction

$\begin{figure} \resizebox{18cm}{!}{\includegraphics{12574fg1.eps}} \end{figure}$	Figure 1: Spot distribution on the test star with $T_{\rm phot}=5750$ K and $T_{\rm spot}=4500$ K.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=15cm,clip]{12574fg2.eps} \end{figure}$

Figure 2:

Surface temperature maps of the test star rotating with $v\sin i=45~$ km s^-1 using the Occamian approach without LSD. The temperature scale has been chosen so that it is easier to compare results without and with LSD as well as with different $v\sin i$ values. The temperatures on the left side of the scale denote minimum and maximum temperatures of the individual cases. Top panel: infinite S/N. Middle panel: S/N=150. Bottom panel: S/N=100.

Open with DEXTER

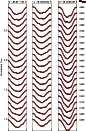
$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{12574fg3.eps}} \end{figure}$	Figure 3: Calculated (red lines) and observed (crosses) spectral lines for the set with $v\sin i=45~$ km s^-1 and infinite S/N.
Open with DEXTER

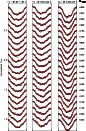
$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{12574fg4.eps}} \end{figure}$	Figure 4: Calculated (red lines) and observed (crosses) spectral lines for the set with $v\sin i=45~$ km s^-1 and S/N=150.
Open with DEXTER

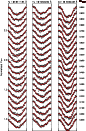
$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{12574fg5.eps}} \end{figure}$	Figure 5: Calculated (red lines) and observed (crosses) spectral lines for the set with $v\sin i=45~$ km s^-1 and S/N=100.
Open with DEXTER

We have developed a new technique for mapping temperature distribution on the stellar surface from spectral line profiles (Doppler imaging, DI) based on the Occamian approach (Berdyugina 1998) and using the least-squares deconvolution (LSD) algorithm elaborated by Semel (1989) and Donati et al. (1997). The motivation for developing LSD was that even in the best cases, the relative noise level from a single line in a single spectrum was higher than the relative noise level required in Stokes V profiles in order to detect and invert the Zeeman signatures. Moreover, active stars rotate quite rapidly and may vary on time-scales of a few rotations, which prevents phase-binning with more than a few spectra in order to decrease the noise level.

The idea of LSD is to extract the polarisation information from as many lines as possible in a single spectrum, since most of the lines are expected to exhibit Zeeman signatures with more or less the same shape. Note that Donati et al. (1997) were mainly concentrated on improving Zeeman signatures in Stokes V line profiles, whereas in this paper we are interested in decreasing the noise in Stokes I line profiles. Doppler imaging with LSD was so far employed to recover maps of the spot filling factor under some limiting assumptions. It was elaborated by Donati et al. (1997), and subsequently used by many other authors (see, e.g., Donati & Collier Cameron 1997; Barnes et al. 1998; Donati & Wade 1999), even though according to Donati et al. (1997) LSD is often less efficient for intensity spectra. However, for Doppler imaging purposes the sufficient gain in signal-to-noise ratio (S/N) is from $S/N\approx50$ to $S/N\approx300$ .

A drawback of improving S/N with the LSD technique by averaging many spectral lines is that the resulting profile looses its identity and blurs the thermodynamic and magnetic sensitivity of contributing lines. The interpretation of such a profile becomes a challenge. So far, it was based on assumptions of a two-temperature distribution on the stellar surface and the weak-field approximation, both of which are far too simple for inferring the complexity of stellar surface structures owing to magnetic fields. In the present paper we show that LSD can be employed with an inversion technique without loosing the temperature information contained in spectral lines. For the first time, the LSD technique is applied to both observed line profiles and a set of theoretical local line profiles, using the same mask of spectral lines. This enables us to obtain temperature-dependent LSD local line profiles and to overcome the limitations of the two-temperature approximation when interpreting Stokes I profiles. An analogous approach can be applied to other Stokes parameters as well but is not discussed here. The other aspect of this paper is to investigate the effect of the stellar rotation and noise level on resulting Doppler images.

The structure of the paper is as follows. The LSD method is described in Sect. 2. The results with simulated data from a test star are shown in Sect. 3, while in Sect. 4 the method is applied to real observations. Finally, the results and implications are discussed in Sect. 5.

2 Doppler imaging with LSD

2.1 Basic principles of LSD

Let us briefly describe basics of the LSD technique following Donati et al. (1997). First, we define a local intensity line profile $I_{{\rm loc}}(v)$ , where v represents the velocity coordinate ( $v=c\Delta\lambda/\lambda$ ) associated with a wavelength shift $\Delta\lambda$ from the line centre wavelength $\lambda$ . Assuming that this profile is similar in shape for all lines and simply scales up in depth with the local line central depth d, we can express it as

$\begin{displaymath}I_{{\rm loc}}(v)=d\: k_{\rm B}(v), \end{displaymath}$

where $k_{\rm B}$ is a proportionality function (equal for all lines). In principle, this is strictly valid only for optically thin lines (Sennhauser et al. 2009), but it is acceptable for a rotationally broadened line profile if strong absorption lines are excluded. Integrating the previous equation over the visible surface of a rotating star, i.e., over all points M of brightness $b_{\rm M}$ and radial velocity $v_{\rm M}$ , gives

I(v)	=	$\displaystyle \int \! \! \! \int b_{\rm M}\: I_{{\rm loc}}~ (v-v_{\rm M})\: {\rm d} S$
	=	$\displaystyle {\rm d} \int \! \! \! \int b_{\rm M}\: k_{\rm B}~ (v-v_{\rm M})\: {\rm d} S {}$
	=	$\displaystyle {\rm d} \: Z(v).$

If also limb darkening is assumed to be independent on wavelength, the integral function Z(v) - called mean Zeeman signature - is constant for all lines, and its shape is reproduced by all Stokes I(v) profiles with a scaling by d.

The line pattern function, called a line mask, M(v) is defined as

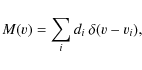
$\begin{displaymath}M(v)=\sum_{i}d_{i}\: \delta(v-v_{i}), \end{displaymath}$

where v_i and d_i are the position in velocity space and weight of each spectral line, respectively. Now, the spectrum I can be written as a convolution expression (I=M*Z) or equivalently as a linear system (I= M Z). The least-squares solution in Z yields

$\begin{displaymath}\mathbf{Z} = (\mathbf{M}^{\rm T}~ \mathbf{S}^{2}~ \mathbf{M})^{-1}~ \mathbf{M}^{\rm T}~ \mathbf{S}^{2}~ \mathbf{I}, \end{displaymath}$

(1)

where S is the diagonal matrix whose element S_jj contains the inverse error $1/\sigma_{j}$ of spectral pixel j. $\mathbf{M}^{\rm T}~ \mathbf{S}^{2}~ \mathbf{I}$ is a cross-correlation of the observed spectrum I with a line pattern M, i.e., a weighted mean of all lines selected for analysis, while $\mathbf{M}^{\rm T}~ \mathbf{S}^{2}~ \mathbf{M}$ is the autocorrelation matrix.

2.2 Line mask

To perform LSD, one needs a line mask containing positions, relative strengths, and in case of other Stokes profiles also magnetic sensitivities (e.g., Landé factors). Donati et al. (1997) introduced a selection criterion for useful lines. They suggested that only lines which have the central depth without line rotational broadening exceeding 40 per cent should be used to avoid overpresenting weak lines. We have omitted this criterion at the moment. However, as suggested by Donati et al. (1997), we exclude the very strong lines. Also, because blends strongly affect the LSD profile, we have chosen least blended lines with best known parameters based on the solar spectrum. This resulted in the total number of 189 lines selected from the wavelength region 4750 Å to 6850 Å. They are mainly Fe I, Ni I, and Ca I lines. This mask is suitable for the analysis of spectra of G-K stars. Even though the total number of selected lines is relatively small, this mask well preserves the temperature information, as we can use only lines which we know how to model. On the other hand, our choice was limited by the echelle orders of the SOFIN spectrograph, which at the moment provides us with most of our observations. However, the mask can certainly be extended for other spectrographs with a wider wavelength range.

Furthermore, to test which lines are best for LSD and to preserve their temperature sensitivity as well as possible, we created additional submasks from the main mask, where transitions were divided into three groups according to the low level excitation energies. The first submask has all lines with $\chi <2.5$ eV (45 transitions), the second submask has lines with $\chi =2.5{-}4.5$ eV (99), and the third one the lines with $\chi >4.5$ eV (45). Our tests have shown that this relatively small number of lines in the mask is sufficient for spectra with $S/N \ge 100$ .

2.3 Local line profiles

The quality of Doppler imaging strongly depends on how much is known about the local line profile $I_{\rm loc}$ , i.e., the intensity profile at a given point on the stellar disc. Here local line profiles for all spectral lines in the mask were calculated with the code by Berdyugina (1991), which includes calculations of opacities in the continuum and in atomic and molecular lines, although we here omitted molecular lines. Atomic line parameters were obtained from the Vienna Atomic Line Database (VALD; Piskunov et al. 1995; Kupka et al. 1999). To account for blends in a given wavelength region (around the main lines from the mask), all lines with a central depth of 1% or more were included in the spectral synthesis. The local line profiles were calculated for a grid of Kurucz models (Kurucz 1993) with temperature $T_{\rm eff}$ ranging from 3500 K to 6000 K in steps of 250 K and for 20 values of $\mu=\cos \theta$ from the disc centre to the limb. The spectral resolution ( $\lambda/\Delta\lambda$ ) of about 200 000 was adopted. The LSD was applied to the calculated profiles for each $T_{\rm eff}$ and $\mu$ separately, so that the obtained Z-solutions depend on these parameters. Below the Doppler imaging technique was employed using sets of local line profiles without LSD, I, and with LSD, Z.

2.4 Inversion

The Occamian approach was employed for inversions of observed line profiles into stellar images (Berdyugina 1998). A $6\hbox{$^\circ$ }\times6\hbox{$^\circ$ }$ grid on the stellar surface was used for integrating local line profiles into normalised flux profiles. With a set of stellar atmosphere models, the stellar image is considered as the distribution of effective temperature across the stellar surface, as is usually done in the surface imaging. Using LSD profiles required only minor changes in the inversion code. As before, the code was fed with sets of observed and local line profiles, but in this case they were pre-processed by the LSD algorithm, i.e., both were Z-solutions depending on used model atmosphere parameters.

It is known that uncertainties in various stellar parameters as well as spot locations have an effect on the resulting temperature map (for details, see Berdyugina 1998). In particular, spots near the equator are usually reconstructed with a reduced spot area and contrast, which is reflected in the temperature scale of the image.

$\begin{figure} \par\includegraphics[width=15cm,clip]{12574fg6.eps} \end{figure}$	Figure 6: Surface temperature maps of the test star rotating with $v\sin i=17~$ km s^-1 using the Occamian approach without LSD. The temperature scale as in Fig. 2. Top panel: infinite S/N. Middle panel: S/N=150. Bottom panel: S/N=100.
Open with DEXTER

3 Test star

3.1 Input parameters

The assumed spot configuration on the test star is shown in Fig. 1. The photospheric temperature is $T_{\rm phot}=5750$ K, and the temperature of all spots is set to $T_{\rm spot}=4500$ K. ``Observed'' spectra of the star were simulated with high spatial resolution on the stellar surface (with a grid $1\hbox{$^\circ$ }\times1\hbox{$^\circ$ }$ ) for 20 evenly distributed rotational phases. Several sets of profiles were generated: with rotation velocities $v\sin i=45~$ km s^-1 and 17 km s^-1, and assuming the signal-to-noise ratio (S/N) to be infinite, 150, and 100.

3.2 Doppler images without LSD

Three atomic lines were selected for Doppler imaging without LSD: Fe I 6411.64 Å, Fe I 6430.80 Å, and Ca I 6439.08 Å. Their local line profiles were calculated as described above.

First, we applied the inversion to the sets of profiles with $v\sin i=45~$ km s^-1. For the case with the infinite S/N (Fig. 2, top panel) the Occamian approach is able to reconstruct the spot distribution with high accuracy. The two other reconstructed images with S/N=150 and S/N=100 (Fig. 2, middle and bottom panel, respectively) demonstrate the importance of good observational data quality. The spots are usually at the correct positions, but the images become noisier and more blurred. Furthermore, the errors in the temperature scale increase with decreasing S/N. The fits to the observed spectra for all the three lines used in the inversions and for all the S/N cases are shown in Figs. 3-5.

$\begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{12574fg7.eps}} \end{figure}$	Figure 7: Calculated (red lines) and observed (crosses) spectral lines for the set with $v\sin i=17~$ km s^-1 and infinite S/N.
Open with DEXTER

$\begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{12574fg8.eps}} \end{figure}$	Figure 8: Calculated (red lines) and observed (crosses) spectral lines for the set with $v\sin i=17~$ km s^-1 and S/N=150.
Open with DEXTER

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12574fg9.eps}} \end{figure}$	Figure 9: Calculated (red lines) and observed (crosses) spectral lines for the set with $v\sin i=17~$ km s^-1 and S/N=100.
Open with DEXTER

The sets with $v\sin i=17~$ km s^-1 represent a challenge for Doppler imaging. At the moment it is the lowest rotational velocity of a real target for which temperature maps were obtained with Doppler imaging from intensity spectra (EK Dra, see, e.g., Strassmeier & Rice 1998; Järvinen et al. 2007). The temperature maps recovered from the sets with this $v\sin i$ (Fig. 6) reveal the following effects. First, even with the perfect data, the recovered spots are clearly noisier and more blurred than in the case of higher $v\sin i$ . Second, the resolution is better in the longitudinal than in latitudinal direction. Furthermore, with a good phase coverage and resolution, the spot temperature is recovered with a larger error for lower S/N, similar to the case of a more rapidly rotating test star. Also, the maps show persistent artificial brighter regions. The fits to the observed spectra are shown in Figs. 7-9 for noiseless spectra and for S/N=150 and S/N=100, respectively.

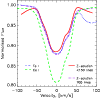
3.3 Doppler images with LSD

Before performing the LSD for all cases presented in Sect. 3.2, we studied the effects of the excitation energy of individual lines on the LSD Doppler imaging results. In Fig. 10 Doppler imaging is performed for noiseless simulated spectra of the test star rotating with $v\sin i=45~$ km s^-1 using four different masks as described in Sect. 2.2. It is remarkable that the spot places are well recovered regardless of which mask is used, even though a very different amount of lines are included in these four cases. Note that the spots are well recovered also for lines with $\chi >4.5$ eV, although the contrast of the image is poor because the same colour scale was used for all images. The temperature range closest to the temperature distribution of the input star was achieved when using the main mask with all lines (189). Also the submask with $\chi <2.5$ eV results in a very good temperature range, although a small number of lines (45) was used. However, the near equatorial spots are clearly too warm. Almost a similar result is achieved when using the submask with $\chi =2.5{-}4.5$ eV (99 lines). Now also the equatorial spots have a better contrast, similar to the first case when all lines were used. With the last mask, i.e., lines with $\chi >4.5$ eV, the reconstructed spots are too warm, and also the unspotted photospheric temperature is too high. However, if lines with $\chi >4.5$ eV were dropped from the main mask, the result was not as good as the one obtained with all lines. Therefore, we conclude that all lines, covering a wide range of excitation energies, should be used in the line mask to achieve the best result.

$\begin{figure} \par\includegraphics[width=17cm]{12574fg10.eps} \end{figure}$

Figure 10:

Surface temperature maps of the test star using different line masks for obtaining the Z-solution. Four different masks are used: including all selected transitions (main mask), and using lines with $\chi <2.5$ eV, with $\chi =2.5{-}4.5$ eV, and with $\chi >4.5$ eV (submasks). All maps are plotted in the same temperature scale - the two temperatures on left side of the scale show the minimum and the maximum temperature recovered for individual submasks.

Open with DEXTER

In Fig. 11 two example Z-profiles calculated with a different number of lines are compared with the Fe I and Ca I lines used in Doppler imaging without LSD. Even though the depths of the profiles are different, the main features due to spots are well visible in each of them. The figure shows that with a small line mask the blends are not fully accounted for and the continuum adjacent to the line profiles is not flat. However, the result is improved when more lines are considered.

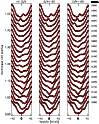
Now we apply the LSD for the same cases as in Sect. 3.2 while obtaining the Z-solutions with the main mask, based on the results described above. For individual spectra with the original S/N of 150 and 100, LSD boosts it up to approximately 320 and 230, respectively.

The resulting temperature maps for the sets of profiles with $v\sin i=45~$ km s^-1 are shown in Fig. 12, while LSD profiles with three different S/N values are plotted in Fig. 13. As expected, the places of the spots are well recovered. The infinite S/N case appears to be better for DI without LSD, which indicates that LSD profiles do blur the information. However, for the cases with low S/N the spot shapes are recovered significantly better with LSD than without, which reflects the effect of the boosted S/N (Fig. 2). The temperature ranges in the three cases are not identical, but still rather close to each other. The coolest spot temperature does not reach the input value even with the best S/N, which again indicates that some information is still lost. Furthermore, there are some small hotter regions, which can be considered as artifacts. If these hottest areas are excluded, the average photospheric temperature corresponds well with the surface temperature of the test star.

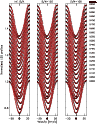
Figures 14 and 15 show the resulting temperature maps and obtained LSD profiles for the data sets with $v\sin i=17~$ km s^-1 and different S/N values. As in the case without LSD, the two high-latitude spots are still unresolved and appear merged, which is the consequence of a lower spatial resolution for slower rotators. However, the spot temperatures are very close to the true value. The low latitude spots are not clearly recovered - without foreknowledge of their positions one would miss them. Furthermore, a hot equatorial ring is formed below the two high-latitude spots.

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12574fg11.eps}} \end{figure}$	Figure 11: Two example Z-profiles using 148 lines (solid red line) and 700 lines (dash-dot purple line) are plotted for comparison with Fe I 6430.80 Å (dotted blue line) and Ca I 6439.08 Å (dashed green line). The stellar rotation velocity is 45 km s^-1 and S/N is infinite.
Open with DEXTER

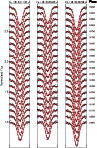
3.4 Effects of the spatial resolution

To analyse how much information is lost owing to low spatial resolution we created an additional test with a pair of test images (see, Fig. 16, top row). The photospheric temperature is again set to $T_{\rm phot}=5750$ K and $v\sin i=45~$ km s^-1. The lines used are the same as in Sect. 3.2 for without LSD and as in Sect. 3.3 for with LSD. In both test cases, the spots have the same visual brightness, but one has $T_{\rm spot}=5300$ K with the filling factor of 100% while another has $T_{\rm spot}=3700$ K with the filling factor of 25%. To better visualise the temperature distribution, we also plotted the cumulative surface area as a function of pixel temperature for both cases. The input images have again high spatial resolution ( $1\hbox{$^\circ$ }\times1\hbox{$^\circ$ }$ ) while we used a grid of $6\hbox{$^\circ$ }\times6\hbox{$^\circ$ }$ for the inversions.

In both test cases, the overall spot location is again well recovered. However, as expected, the obtained temperature distribution is not perfect. The differentiation in latitude is poor in equatorial regions. Therefore, the features are more smeared towards the equator, and only the strongest features are properly recovered. This is an old problem and is discussed in many papers (see, for example, Rice et al. 1989 or Rice 2002). The case with a warm solid spot shows that its contrast is smoothed: the middle area of the spot is somewhat cooler than the given input temperature, while the rim of the spot is too warm. However, the cumulative surface area versus temperature plot demonstrates that the solution approximates the input well for both DI with and without LSD. The recovered images for the case with unresolved, small, cool spots show a blurred spot centred at the spot group, as expected for low spatial resolution data. The temperature scale and cumulative surface area plot show that we do not reach the input spot temperature. Nevertheless, the recovered spot is clearly cooler than in in the first test, but without knowing the difference between the two inputs it is impossible to decide whether we resolve real spots.

These two tests clearly demonstrate that improving the S/N of the data with LSD does not compensate for the lack of the spatial resolution. We emphasise that this is common for all DI techniques and not specific to the Occamian approach. Therefore, Doppler images of slowly rotating stars (whether with temperature or magnetic field distribution) should be analysed and interpreted with great care.

$\begin{figure} \par\resizebox{18cm}{!}{\includegraphics{12574fg12.eps}} \end{figure}$	Figure 12: Surface temperature maps of the test star rotating with $v\sin i=45~$ km s^-1 using LSD profiles. The temperature scale as in Fig. 2. Top panel: infinite S/N. Middle panel: S/N=150 boosted to $S/N \approx 320$ . Bottom panel: S/N=100 boosted to $S/N \approx 230$ .
Open with DEXTER

4 Doppler imaging of V889 Her

The successful results of testing the Occamian approach to Doppler imaging combined with the LSD technique applied to simulated data in Sect. 3 encouraged us to employ this new technique for the analysis of real data. We now apply LSD to observations which originally had a good S/N. There we can expect that the obtained temperature maps should be almost identical regardless of whether the Occamian approach is used with or without LSD.

For our purpose, we took the spectra of the young solar analogue V889 Her obtained in July 2005 with the Nordic Optical Telescope (NOT, La Palma) and the SOFIN echelle spectrograph. The signal-to-noise ratio of the original spectra was on average above 250. A more detailed description of the observations is given by Järvinen et al. (2008), who carried out an analysis of the data and obtained temperature maps using the Occamian approach without LSD.

A line mask containing 95 spectral lines is built with lines from 15 spectral orders within a wavelength range of 4770-7067 Å. As for the inversion without LSD (Järvinen et al. 2008), the local line profiles are calculated for a grid of Kurucz models (Kurucz 1993) with temperatures ranging from 4000 K to 6500 K in steps of 250 K and for 20 values of $\mu=\cos \theta$ from the disc centre to the limb.

The resulting surface temperature map of V889 Her obtained with the Occamian approach with LSD is shown in Fig. 17 and, for comparison, the map obtained without LSD from the same data is shown in Fig. 18. As seen from the maps, the temperature range is smaller for the case with LSD than without it. However, the spot occupancy does not change dramatically. The polar spot recovered with LSD is more compact than the one recovered without LSD and is comparable with the one by Jeffers & Donati (2008) obtained from data taken only about a month earlier.

5 Discussion and conclusions

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12574fg13.eps}} \end{figure}$	Figure 13: Calculated (red lines) and observed (crosses) LSD profiles for $v\sin i=45~$ km s^-1 with different original S/N values. Left panel: infinite S/N. Middle panel: S/N=150 boosted to $S/N \approx 320$ . Right panel: S/N=100 boosted to $S/N \approx 230$ .
Open with DEXTER

$\begin{figure} \par\resizebox{18cm}{!}{\includegraphics{12574fg14.eps}} \end{figure}$	Figure 14: Surface temperature maps of the test star rotating with $v\sin i=17~$ km s^-1 using LSD profiles. The temperature scale as in Fig. 2. Top panel: infinite S/N. Middle panel: S/N=150 boosted to $S/N \approx 320$ . Bottom panel: S/N=100 boosted to $S/N \approx 220$ .
Open with DEXTER

We have shown that it is possible to preserve the temperature information in spectral lines while performing Doppler imaging with LSD. This is achieved by applying for the first time the LSD technique to both observed line profiles and a set of local line profiles, while using the same mask of spectral lines. This approach enables us to obtain temperature and limb distance dependent LSD local line profiles and to overcome the limitations of the widely employed two-temperature approximation when interpreting Stokes I LSD profiles (e.g., Donati et al. 1997). We combined the Occamian approach with the LSD technique and investigated the sensitivity of recovered images to the noise level and spatial resolution. We demonstrated that the Occamian approach is truly temperature sensitive when an adequate spatial resolution is provided by the data.

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12574fg15.eps}} \end{figure}$	Figure 15: Calculated (red lines) and observed (crosses) LSD profiles for $v\sin i=17~$ km s^-1 with different original S/N values. Left panel: infinite S/N. Middle panel: S/N=150 boosted to $S/N \approx 220$ . Right panel: S/N=100 boosted to $S/N \approx 180$ .
Open with DEXTER

We found that the obtained solution is sensitive to the excitation energies of the used lines. This is illustrated in Fig. 10. The submask, which only has lines with $\chi >4.5$ eV, results in a clearly worse map than the submask with lines with $\chi <2.5$ eV (both have the same amount of lines). Even though the positions of the spots are well recovered, lines with high excitation energies produce more blurred spots and the temperature range is shifted towards higher values. The best solution is obtained using all lines independent of their excitation energies. However, one has to keep in mind that the result is dominated by the lines with $\chi =2.5{-}4.5$ eV, which by themselves give almost as good a result as when using all the lines.

$\begin{figure} \par\resizebox{18cm}{!}{\includegraphics{12574fg16.eps}} \end{figure}$

Figure 16:

Top panel: two tests where the spot area has the same visual brightness: on the left $T_{\rm spot}=5300$ K with the filling factor of 100%, and on the right $T_{\rm spot}=3700$ K with the filling factor of 25%. Next to the map is plotted the cumulative surface area as a function of pixel temperature. Note that the cumulative surface area of input images has been scaled to correspond to the resolution of output images. Middle panel: recovered maps and cumulative surface area plots when the Occamian approach is used without LSD. Bottom panel: recovered maps and cumulative surface area plots when the Occamian approach is used with LSD. All maps have again the same temperature scale, and the minimum and maximum temperature of each map is marked on the left side of the temperature scales. The Y-axis is in logarithmic scale to emphasise the lower part of the cumulative plot showing the spot-covered area.

Open with DEXTER

An important outcome of our tests is that inversions with LSD do not produce better results than those without LSD for reasonable noise levels in the data. In all cases with LSD, the spot temperature is recovered to be higher than the input value, and bright artificial features appear in the maps. This is probably because of non-linear effects that arise when lines of different strengths are averaged together, which is not taken into account in the LSD technique. Therefore, we conclude that for temperature mapping, LSD is only advisable when the observations have a poor signal-to-noise ratio, perhaps $\le$ 100. For data of a better quality the simultaneous inversions of several spectral lines with various temperature sensitivity is a more reliable approach. Alternatively, non-linear multi-line techniques, such as non-linear deconvolution with deblending (NDD, Sennhauser et al. 2009), can be adopted using the same approach as described in this paper.

$\begin{figure} \par\resizebox{6cm}{!}{\includegraphics{12574fg17.eps}} \end{figure}$	Figure 17: Surface temperature map of V889 Her obtained with the Occamian approach with LSD. The temperature scale is chosen to match that of Fig. 18, and the minimum and maximum temperatures of the LSD solution are marked to the left side of the scale.
Open with DEXTER

$\begin{figure} \par\resizebox{6cm}{!}{\includegraphics{12574fg18.eps}} \end{figure}$	Figure 18: Surface temperature map of V889 Her obtained using the Occamian approach without LSD. Adapted from Järvinen et al. (2008).
Open with DEXTER

Furthermore, we have shown that boosting the S/N with LSD does not compensate for the lack of spatial resolution on stars with low $v\sin i$ values. For a slowly rotating star, spots do not leave a clear signature (a hump) in the line profile, but merely cause a shift of the line centre. A lack of spatial resolution leads to merging of nearby spots, which form a larger, often blurred, structure. Also, low-latitude spots remain undetectable in a slowly rotating star.

Acknowledgements

S.P.J. acknowledges the support from Alfred Kordelin Foundation, Finland. S.V.B. acknowledges the EURYI (European Young Investigator) Award provided by the European Science Foundation (see www.esf.org/euryi) and SNF grant PE002-104552. This work was also supported by the Academy of Finland, grant 115417.

References

Barnes, J. R., Collier Cameron, A., Unruh, Y. C., Donati, J.-F., & Hussain, G. A. J. 1998, MNRAS, 299, 904 [NASA ADS] [CrossRef] [Google Scholar]
Berdyugina, S. V. 1991, Bull. Crimean Astrophys. Obs., 83, 89 [NASA ADS] [Google Scholar]
Berdyugina, S. V. 1998, A&A, 338, 97 [NASA ADS] [Google Scholar]
Donati, J.-F., & Collier Cameron, A. 1997, MNRAS, 291, 1 [NASA ADS] [CrossRef] [Google Scholar]
Donati, J.-F., & Wade, G. A. 1999, A&A, 341, 216 [NASA ADS] [Google Scholar]
Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & Cameron, A. C. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
Donati, J.-F., Collier Cameron, A., Hussain, G. A. J., & Semel, M. 1999, MNRAS, 302, 437 [NASA ADS] [CrossRef] [Google Scholar]
Järvinen, S. P., Berdyugina, S. V., Korhonen, H., Ilyin, I., & Tuominen, I. 2007, A&A, 472, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Järvinen, S. P., Korhonen, H., Berdyugina, S. V., et al. 2008, A&A, 488, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Jeffers, S. V., & Donati, J.-F. 2008, MNRAS, 390, 635 [NASA ADS] [CrossRef] [Google Scholar]
Kupka, F., Piskunov, N. E., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
Kurucz, R. L. 1993, Kurucz CD No. 13 [Google Scholar]
Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [Google Scholar]
Rice, J. B. 2002, AN, 323, 220 [Google Scholar]
Rice, J. B., Wehlau, W. H., & Khokhlova, V. 1989, A&A, 208, 179 [NASA ADS] [Google Scholar]
Semel, M. 1989, A&A, 225, 456 [NASA ADS] [Google Scholar]
Sennhauser, C., Berdyugina, S. V., & Fluri, D. M. 2009, A&A, 507, 1711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Strassmeier, K. G., & Rice, J. B. 1998, A&A, 330, 685 [NASA ADS] [Google Scholar]

All Figures

$\begin{figure} \resizebox{18cm}{!}{\includegraphics{12574fg1.eps}} \end{figure}$	Figure 1: Spot distribution on the test star with $T_{\rm phot}=5750$ K and $T_{\rm spot}=4500$ K.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=15cm,clip]{12574fg2.eps} \end{figure}$	Figure 2: Surface temperature maps of the test star rotating with $v\sin i=45~$ km s^-1 using the Occamian approach without LSD. The temperature scale has been chosen so that it is easier to compare results without and with LSD as well as with different $v\sin i$ values. The temperatures on the left side of the scale denote minimum and maximum temperatures of the individual cases. Top panel: infinite S/N. Middle panel: S/N=150. Bottom panel: S/N=100.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{12574fg3.eps}} \end{figure}$	Figure 3: Calculated (red lines) and observed (crosses) spectral lines for the set with $v\sin i=45~$ km s^-1 and infinite S/N.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{12574fg4.eps}} \end{figure}$	Figure 4: Calculated (red lines) and observed (crosses) spectral lines for the set with $v\sin i=45~$ km s^-1 and S/N=150.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{12574fg5.eps}} \end{figure}$	Figure 5: Calculated (red lines) and observed (crosses) spectral lines for the set with $v\sin i=45~$ km s^-1 and S/N=100.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=15cm,clip]{12574fg6.eps} \end{figure}$	Figure 6: Surface temperature maps of the test star rotating with $v\sin i=17~$ km s^-1 using the Occamian approach without LSD. The temperature scale as in Fig. 2. Top panel: infinite S/N. Middle panel: S/N=150. Bottom panel: S/N=100.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{12574fg7.eps}} \end{figure}$	Figure 7: Calculated (red lines) and observed (crosses) spectral lines for the set with $v\sin i=17~$ km s^-1 and infinite S/N.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{12574fg8.eps}} \end{figure}$	Figure 8: Calculated (red lines) and observed (crosses) spectral lines for the set with $v\sin i=17~$ km s^-1 and S/N=150.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12574fg9.eps}} \end{figure}$	Figure 9: Calculated (red lines) and observed (crosses) spectral lines for the set with $v\sin i=17~$ km s^-1 and S/N=100.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=17cm]{12574fg10.eps} \end{figure}$	Figure 10: Surface temperature maps of the test star using different line masks for obtaining the Z-solution. Four different masks are used: including all selected transitions (main mask), and using lines with $\chi <2.5$ eV, with $\chi =2.5{-}4.5$ eV, and with $\chi >4.5$ eV (submasks). All maps are plotted in the same temperature scale - the two temperatures on left side of the scale show the minimum and the maximum temperature recovered for individual submasks.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12574fg11.eps}} \end{figure}$	Figure 11: Two example Z-profiles using 148 lines (solid red line) and 700 lines (dash-dot purple line) are plotted for comparison with Fe I 6430.80 Å (dotted blue line) and Ca I 6439.08 Å (dashed green line). The stellar rotation velocity is 45 km s^-1 and S/N is infinite.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{18cm}{!}{\includegraphics{12574fg12.eps}} \end{figure}$	Figure 12: Surface temperature maps of the test star rotating with $v\sin i=45~$ km s^-1 using LSD profiles. The temperature scale as in Fig. 2. Top panel: infinite S/N. Middle panel: S/N=150 boosted to $S/N \approx 320$ . Bottom panel: S/N=100 boosted to $S/N \approx 230$ .
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12574fg13.eps}} \end{figure}$	Figure 13: Calculated (red lines) and observed (crosses) LSD profiles for $v\sin i=45~$ km s^-1 with different original S/N values. Left panel: infinite S/N. Middle panel: S/N=150 boosted to $S/N \approx 320$ . Right panel: S/N=100 boosted to $S/N \approx 230$ .
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{18cm}{!}{\includegraphics{12574fg14.eps}} \end{figure}$	Figure 14: Surface temperature maps of the test star rotating with $v\sin i=17~$ km s^-1 using LSD profiles. The temperature scale as in Fig. 2. Top panel: infinite S/N. Middle panel: S/N=150 boosted to $S/N \approx 320$ . Bottom panel: S/N=100 boosted to $S/N \approx 220$ .
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{12574fg15.eps}} \end{figure}$	Figure 15: Calculated (red lines) and observed (crosses) LSD profiles for $v\sin i=17~$ km s^-1 with different original S/N values. Left panel: infinite S/N. Middle panel: S/N=150 boosted to $S/N \approx 220$ . Right panel: S/N=100 boosted to $S/N \approx 180$ .
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{18cm}{!}{\includegraphics{12574fg16.eps}} \end{figure}$	Figure 16: Top panel: two tests where the spot area has the same visual brightness: on the left $T_{\rm spot}=5300$ K with the filling factor of 100%, and on the right $T_{\rm spot}=3700$ K with the filling factor of 25%. Next to the map is plotted the cumulative surface area as a function of pixel temperature. Note that the cumulative surface area of input images has been scaled to correspond to the resolution of output images. Middle panel: recovered maps and cumulative surface area plots when the Occamian approach is used without LSD. Bottom panel: recovered maps and cumulative surface area plots when the Occamian approach is used with LSD. All maps have again the same temperature scale, and the minimum and maximum temperature of each map is marked on the left side of the temperature scales. The Y-axis is in logarithmic scale to emphasise the lower part of the cumulative plot showing the spot-covered area.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{6cm}{!}{\includegraphics{12574fg17.eps}} \end{figure}$	Figure 17: Surface temperature map of V889 Her obtained with the Occamian approach with LSD. The temperature scale is chosen to match that of Fig. 18, and the minimum and maximum temperatures of the LSD solution are marked to the left side of the scale.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{6cm}{!}{\includegraphics{12574fg18.eps}} \end{figure}$	Figure 18: Surface temperature map of V889 Her obtained using the Occamian approach without LSD. Adapted from Järvinen et al. (2008).
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Barnes, J. R., Collier Cameron, A., Unruh, Y. C., Donati, J.-F., & Hussain, G. A. J. 1998, MNRAS, 299, 904 [NASA ADS] [CrossRef] [Google Scholar]

[2] Berdyugina, S. V. 1991, Bull. Crimean Astrophys. Obs., 83, 89 [NASA ADS] [Google Scholar]

[3] Berdyugina, S. V. 1998, A&A, 338, 97 [NASA ADS] [Google Scholar]

[4] Donati, J.-F., & Collier Cameron, A. 1997, MNRAS, 291, 1 [NASA ADS] [CrossRef] [Google Scholar]

[5] Donati, J.-F., & Wade, G. A. 1999, A&A, 341, 216 [NASA ADS] [Google Scholar]

[6] Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & Cameron, A. C. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]

[7] Donati, J.-F., Collier Cameron, A., Hussain, G. A. J., & Semel, M. 1999, MNRAS, 302, 437 [NASA ADS] [CrossRef] [Google Scholar]

[8] Järvinen, S. P., Berdyugina, S. V., Korhonen, H., Ilyin, I., & Tuominen, I. 2007, A&A, 472, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[9] Järvinen, S. P., Korhonen, H., Berdyugina, S. V., et al. 2008, A&A, 488, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[10] Jeffers, S. V., & Donati, J.-F. 2008, MNRAS, 390, 635 [NASA ADS] [CrossRef] [Google Scholar]

[11] Kupka, F., Piskunov, N. E., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]

[12] Kurucz, R. L. 1993, Kurucz CD No. 13 [Google Scholar]

[13] Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [Google Scholar]

[14] Rice, J. B. 2002, AN, 323, 220 [Google Scholar]

[15] Rice, J. B., Wehlau, W. H., & Khokhlova, V. 1989, A&A, 208, 179 [NASA ADS] [Google Scholar]

[16] Semel, M. 1989, A&A, 225, 456 [NASA ADS] [Google Scholar]

[17] Sennhauser, C., Berdyugina, S. V., & Fluri, D. M. 2009, A&A, 507, 1711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[18] Strassmeier, K. G., & Rice, J. B. 1998, A&A, 330, 685 [NASA ADS] [Google Scholar]