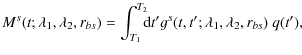EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 519 (September 2010) A&A, 519 (2010) A36 Full HTML
Free Access
Issue
A&A
Volume 519, September 2010
Article Number A36
Number of page(s) 7
Section The Sun
DOI https://doi.org/10.1051/0004-6361/200913963
Published online 09 September 2010
A&A 519, A36 (2010)

Solar near-relativistic electron observations as a proof of a back-scatter region beyond 1 AU during the 2000 February 18 event

N. Agueda1,2 - R. Vainio1 - D. Lario3 - B. Sanahuja4

1 - Department of Physics, University of Helsinki, 00014 Helsinki, Finland
2 - Space Sciences Laboratory, University of California, Berkeley, CA 94720, USA
3 - Applied Physics Laboratory, The Johns Hopkins University, Laurel, MD 20723, USA
4 - Departament d'Astronomia i Meteorologia & Institut de Ciències del Cosmos, Universitat de Barcelona, 08028 Barcelona, Spain

Received 23 December 2009 / Accepted 3 May 2010

Abstract
Aims. We study the near-relativistic (NR; >30 keV) electron event observed on 2000 February 18 by near-Earth spacecraft. Previous works have explained this event by assuming that the propagation of NR electrons is essentially ``scatter-free'' at heliocentric radial distances r<1 AU, and that beyond 1 AU particles are ``back-scattered'' by magnetic field irregularities.
Methods. Our aim is to re-visit this interplanetary propagation scenario and infer the injection profile at the Sun by fitting the electron directional intensities observed by the Advanced Composition Explorer.
Results. We use a Monte Carlo transport model to explore this approach. We assume that the interplanetary magnetic field is an Archimedean spiral and that the interplanetary transport of NR electrons is characterized by a large radial mean free path ( $\lambda_r>0.5$ AU) and anisotropic pitch-angle scattering for r<1 AU, and a small radial mean free path ( $\lambda_r<0.5$ AU) and isotropic scattering in the back-scatter region.
Conclusions. The event cannot be explained without assuming a back-scatter region beyond 1 AU. The best fit is obtained by assuming $\lambda_r=3.2$ AU in the inner heliosphere and a back-scatter region characterized by a small mean free path $\lambda_{r} =0.2$ AU located beyond 1.2 AU.

Key words: Sun: particle emission - Sun: flares - Sun: coronal mass ejections (CMEs) - interplanetary medium

1 Introduction

Pitch-angle distributions (PADs) highly collimated along the interplanetary magnetic field (IMF) during the rising phase of solar energetic particle (SEP) events have usually been interpreted as evidence that the propagation of SEPs in the heliosphere can be under some circumstances nearly ``scatter-free''. The Advanced Composition Explorer (ACE) and the Wind spacecraft have observed these ``beam-like'' PADs during solar near-relativistic (NR; >30 keV) electron events, and many studies have used them to extract information about the duration of the solar particle injection, and hence got insights into the mechanisms of electron acceleration close to the Sun (e.g. Krucker et al. 1999; Haggerty & Roelof 2002; Simnett et al. 2002; Kahler et al. 2007).

We here re-visit the 2000 February 18 NR electron event observed by ACE. Highly collimated PADs were observed at the onset of this electron event (Haggerty & Roelof 2002; Simnett et al. 2002). Two previous works have inferred the solar injection function from observations at 1 AU by assuming that either NR electrons were reflected from beyond 1 AU or that the interplanetary scattering strength increased with radial distance (Roelof 2008; Dröge & Kartavykh 2009). One approach assumed that particles propagate ``scatter-free'' along the IMF line connecting the coronal injection region to the observer, but further out particles are ``back-scattered'' inward from beyond 1 AU by magnetic field compressions and irregularities (Roelof 2008). Thus the propagation was assumed not to be scatter-free beyond 1 AU. This approximation allowed the inference of the injection history of the first-crossing solar electrons (directly from the data, without any propagation modeling) by utilizing unidirectional intensities from two preferred directions (sunward and anti-sunward) and taking into account that the particle pitch-angle cosines are inter-related by the conservation of the magnetic moment (Roelof 2008).

The second approach involved numerically solving the focused transport equation and a visual fit of the solution to the observations, allowing an estimation of the solar injection function as well as the interplanetary transport parameters (Dröge & Kartavykh 2009). Dröge & Kartavykh (2009) modeled the intensity- and first-order anisotropy-time profiles of 107 keV electrons observed by Wind and obtained a good fit by assuming a constant parallel mean-free path of $\lambda_\parallel=1.2$ AU. The assumption of a constant parallel mean free path leads to efficient back-scattering when the focusing length becomes more extended than $\lambda_{\parallel}$, i.e. with increasing heliocentric radial distance.

Agueda et al. (2010) explored the first approach by using Monte Carlo simulations of the particle transport along an Archimedean interplanetary magnetic field. Their goal was to fit the 2000 February 18 electron event observed by the LEFS60 telescope of the EPAM experiment on board ACE (Gold et al. 1998) making use of observational sectored intensities. This ensures that the directional information contained in the data is used in full to explain the event. Agueda et al. (2010) concluded that the electron directional intensities observed on 2000 February 18 could not be explained without the assumption of a back-scatter region beyond 1 AU. But scatter-free propagation inside 1 AU predicted PADs more collimated than the observed ones.

Our goal is to use the same Monte Carlo transport model to consider a new transport scenario that allows some degree of scattering inside 1 AU. We assume that the IMF is an Archimedean spiral and that the interplanetary transport of NR electrons is characterized by a large radial mean free path ( $\lambda_r>0.5$ AU) and anisotropic scattering in the inner heliosphere (heliocentric radial distances r<1 AU). We assume a small radial mean free path ( $\lambda_r<0.5$ AU) and isotropic scattering in the back-scatter region beyond 1 AU.

We review the transport model and the fitting technique in Sect. 2. The results of deconvolving the directional intensities observed during the 2000 February 18 NR electron event are given in Sect. 3. We discuss the results in Sect. 4 and summarize this work in Sect. 5.

2 Transport and injection modeling

2.1 Interplanetary transport model

We simulate the interplanetary transport of SEPs injected at the root of an Archimedean spiral magnetic field line using the Monte Carlo technique (Agueda et al. 2008). The model includes particle streaming along the magnetic field lines, pitch-angle focusing by the diverging IMF, pitch-angle scattering by magnetic fluctuations, adiabatic deceleration resulting from the interplay of scattering and focusing, and solar wind convection (Kocharov et al. 1998; Vainio et al. 2000). The model provides us with the directional distribution of particles at 1 AU as a function of time and the energy range of interest (see Agueda et al. 2008, for details).

Electrons are assumed to be injected instantaneously at two solar radii from the center of the Sun. Therefore, the results of the simulation are expressed in terms of Green's functions of particle transport. We describe the energy spectrum of the solar source by a power law ( ${\rm d}N/{\rm d}E\propto E^{-\gamma_{\rm s}}$) with the spectral index $\gamma_{\rm s}$, which we estimate from the observations.

The pitch-angle diffusion coefficient can be expressed as $D_{\mu \mu}=\nu(1-\mu^2)/2$ in the solar wind frame, where $\nu$ is the scattering frequency and $\mu $ is the particle pitch-angle cosine. We assume

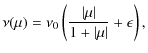
$\displaystyle % \nu(\mu)=\nu_0 \left (\frac{\vert\mu\vert}{1+\vert\mu\vert} +\epsilon \right),$     (1)

where $\epsilon$ is the parameter that allows us to simulate different scattering conditions from quasi-isotropic ( $\epsilon \ge 1$) to fully anisotropic ( $\epsilon=0$). The relation of the scattering rate, $\nu_0$, to the mean free path parallel to the field $\lambda_{\vert\vert}$, or the radial mean free path $\lambda_r$, is given by
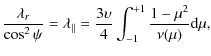
$\displaystyle % \frac{\lambda_r}{\cos^2\psi}=\lambda_{\vert\vert}=\frac{3 \upsilon}{4}\int_{-1}^{+1}\frac{1-\mu^2}{\nu(\mu)}{\rm d}\mu,$     (2)

where $\upsilon$ is the particle speed and $\psi$ is the angle between the magnetic field and the radial direction (Hasselmann & Wibberenz 1968). Following the procedure adopted in previous works, we assume the radial mean free path to be constant, independent of the radial distance and energy (Kallenrode et al. 1992; Dröge 2003). We neglect particle transport perpendicular to the magnetic field.

For isotropic scattering, the scattering frequency is constant ($\nu=\nu_0$) and $\lambda_{\vert\vert}=\upsilon/\nu_0$. For a $\mu $-dependent scattering model, the parallel mean free path can be expressed in terms of $\nu_0$ and $\epsilon$, as

$\displaystyle % \lambda_{\parallel}=\frac{\upsilon}{\nu_0} \phi(\epsilon)$   (3)

where $\phi(\epsilon)$ is given in an analytical form (see Appendix A in Agueda et al. 2008). For $\epsilon \ll 1$
$\displaystyle % \phi(\epsilon) = \frac{3}{2} \ln \frac{1}{\epsilon}$   (4)

and the scattering frequency is given by
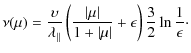
$\displaystyle % \nu (\mu) = \frac{\upsilon}{\lambda_\parallel} \left(\frac{\ver... ...rt}{1+\vert\mu\vert} + \epsilon \right) \frac{3}{2} \ln \frac{1}{\epsilon}\cdot$   (5)

Figure 1 shows the scattering frequency ratio between the isotropic and a $\mu $-dependent scattering model. If we assume $\epsilon =0.01$, then $\nu(\mu=1) = 3.5 \upsilon/\lambda_{\parallel}$, which means that the scattering frequency at $\mu=1$ is 3.5 times larger than the scattering frequency for isotropic scattering. Equivalently, it means that electrons with $\mu=1$ undergo pitch-angle scattering with the same frequency as a particle with a mean free path 3.5 times smaller for isotropic pitch-angle scattering.

The model is adapted to be able to differentiate between two different transport regimes. We assume that in the inner heliosphere (at heliospheric distances r<1 AU) the scattering is $\mu $-dependent with $\epsilon =0.01$ and $\lambda_r = \lambda_1$. For $\epsilon =0.01$, the form of the pitch-angle diffusion coefficient features reduced but finite scattering through $\mu=0$, as predicted by current models of particle scattering (Dröge 2000). The back-scatter region is assumed to be located beyond $r_{\rm bs}$ (where $r_{\rm bs}>1$ AU). We assume isotropic scattering and $\lambda_r = \lambda_2$ in the back-scatter region.

\begin{figure} \par\includegraphics[width=8cm,clip]{13963fg1.eps} \end{figure} Figure 1:

Scattering frequency ratio between the $\mu $-dependent scattering model with $\epsilon =0.01$ and the isotropic scattering model.

Open with DEXTER

2.2 Fitting technique

We infer the interplanetary transport conditions and the injection time profile at the Sun from a set of in-situ measured sectored intensities by using the inversion technique presented in Agueda et al. (2008) and Agueda et al. (2009b). By taking the angular response of the sectors scanned by the LEFS60 telescope into account, it is possible to transform the simulated PADs into sectored intensities measured by the telescope (Agueda et al. 2008). The modeled sectored intensities in sector s, $M^{s}(t;\lambda_1,\lambda_2,r_{\rm bs})$, are given by
$\displaystyle % M^{s}(t;\lambda_1,\lambda_2,r_{bs})=\int_{T_1}^{T_2}\!\!\! {\rm d}t'g^{s}(t,t';\lambda_1,\lambda_2,r_{bs})~ q(t'),$   (6)

where q(t) denotes the electron injection function and $g^{s}(t,t';\lambda_1,\lambda_2,r_{\rm bs})$ is the contribution of an impulsive injection to the modeled intensities for a given sector s at a given time t, when the injection of NR electrons took place at time t'.

Let b be the background intensity and Is(t) be the intensity measured at time t by sector s in a given energy channel. The best-fit injection function can be determined by comparing the modeled intensities with the observations, taking all sectors of the telescope into account.

The inversion problem is to derive the injection m-vector $\vec{q}$ that minimizes the length of the n-vector $\vec{J}-\vec{M}$, where Js(t)=Is(t)-b. This means minimizing the value of $\vert\vert\vec{J}-\vec{M}\vert\vert \equiv \vert\vert\vec{J}-{\vec g}\cdot\vec{q}\vert\vert,$ subject to the constraint that $q(t) \geq 0$. We use the non-negative least-squares method (Lawson & Hanson 1974) to solve the inversion problem for a given set of transport parameters (i.e. $\lambda_1$, $\lambda_2$ and $r_{\rm bs}$), and obtain the best-fit injection profile. This method always converges to a solution. Therefore there is a mathematically preferred injection profile for each set of transport parameters that can be obtained from the data. Note however that in some cases this fit reproduces the observations rather poorly (see Sect. 3). Thus the goodness of the fit needs to be determined with an estimator that can quantitatively compare the results from the different transport scenarios.

We explored a wide range of transport parameters ($\lambda_1$, $\lambda_2$ and $r_{\rm bs}$). We found the one that best fits the observations by minimizing a goodness-of-fit estimator $\zeta=\sum_i (\log I_i - \log (M_i+b))^2$, which computes the sum of the squared logarithmic differences between the observational Ii and the modeled Mi sectored intensities in each energy channel. The calculation of the goodness of the fit is restricted to the time interval selected. The goodness-of-fit estimator of the whole fit was obtained by adding the values for each energy channel. It is important to note that $\zeta$ allows us to identify the set of parameters that can better explain the data with an automated, quantitative, and reproducible method, which is more objective than an eye-ball fit.

3 Results

We used electron intensities measured by the LEFS60 telescope of the EPAM experiment on the ACE spacecraft in three energy channels: E'2 (62-102 keV), E'3 (102-175 keV) and E'4 (175-312 keV) (Gold et al. 1998). The LEFS60 telescope utilizes the spin of the spacecraft to define eight sectors (Gold et al. 1998), so that particle flux anisotropy can be studied by comparing counting rates from each sector.

We studied the NR electron event observed on 2000 February 18 by LEFS60 from 09:30 UT to 11:15 UT. During this period there was a data gap in the solar wind observations of the plasma instrument SWEPAM on board ACE (McComas et al. 1998). The solar wind speed observed by Wind ranged from 370 to 390 km s-1. To model the event we assumed that the spacecraft was embedded in a 380 km s-1 solar wind stream, with the nominal magnetic footpoint at the Sun located at W63. The IMF vector at ACE was very stable throughout the selected time interval and each sector scanned roughly the same pitch-angle cosine range. The LEFS60 telescope scanned $\sim$82% of the total pitch-angle cosine range. This can be considered a very high sample of pitch-angle cosines and makes the event adequate for simulation (Agueda et al. 2009a).

The first NR electrons were detected above the pre-event background at 09:32 UT in the E'4 channel. The onset of the event was observed during the decay phase of a smaller event on the previous day and the background had a residual anisotropy at the beginning of the event. We took this into account by allowing the background b (see previous section) to depend on the sector. During the event, highly collimated PADs were observed (Haggerty & Roelof 2002; Simnett et al. 2002; Dröge & Kartavykh 2009), i.e. the peak intensity observed in the sector scanning particles propagating from the Sun along the IMF direction was more than one order of magnitude higher than the peak intensity measured by the sector which mainly scanned electrons propagating sunward (see Fig. 1 in Simnett et al. 2002). The maximum intensity was observed at 09:45/09:47/09:52 UT in the E'4/E'3/E'2 energy channels, respectively. The spectral index of the maximum spin-averaged differential intensities was 2.2.

Table 1:   Best-fit parameters for different transport scenarios (see text for details).

The event was associated with a C1.1 X-ray solar flare observed in the NOAA active region #8867 at approximately S16 W78 (Maia & Pick 2004). The soft X-ray emission (1-8 Å) was observed from 09:21 to 09:38 UT, peaking at 09:27 UT. The WAVES experiment on the Wind spacecraft (Bougeret et al. 1995) observed a type III radio burst starting at 09:23 UT at 14 MHz (Maia & Pick 2004). The solar radio event included a series of type II radio bursts, first seen at 70 MHz around 09:24 UT and lasting for more than 20 min (Maia & Pick 2004). A CME was also associated with this event, first seen in a LASCO/C2 image at 09:54 UT, when its leading edge was at 4.15 $R_\odot$ from the center of the Sun.

The SOHO/LASCO CME Catalog (Yashiro et al. 2004) estimates the plane-of-sky speed of the CME to be 890 km s-1 from a linear fit to all data points. A second-order fit to the same data points indicates some deceleration (-9.6 m s-2) of the CME below 4 $R_\odot$. Maia & Pick (2004) provided further evidence of the CME deceleration in the low corona from the analysis of EIT data.

\begin{figure} \par\includegraphics[height=.24\textheight,clip]{13963fg2.eps} \end{figure} Figure 2:

Near-relativistic electron event on 2000 February 18 as observed by five of the sectors of the LEFS60 telescope. Electron sectored intensities E'4 175-312 keV, E'3 102-175 keV ($\times $10), and E'2 62-102 keV ($\times $100). The sectors are labeled from 1 to 5. The curves show the modeled sector intensities for scenario A and dots show the observational data. Low panels show the pitch-angle cosine of the midpoint clock-angle zenith direction of the sector (curve) and the scanned pitch-angle cosine range (gray area) as a function of time. The last panel shows the omnidirectional intensities and the mean pitch-angle cosine deduced from the simulation. The gray area shows the pitch-angle cosine range scanned by the telescope.

Open with DEXTER

\begin{figure} \par\includegraphics[height=.24\textheight,clip]{13963fg3.eps} \end{figure} Figure 3:

Same as in Fig. 2 for scenario B.

Open with DEXTER

\begin{figure} \par\includegraphics[height=.24\textheight,clip]{13963fg4.eps} \end{figure} Figure 4:

Same as in Fig. 2 for scenario C.

Open with DEXTER

We considered three different propagation scenarios in the simulations. In scenario A we assume that there is no back-scatter region (i.e. it can be considered to be located at $r_{\rm bs} \rightarrow \infty$) and consider six values of $\lambda_1$ logarithmically spaced between 0.5 and 1.5 AU. In scenario B we assume scatter-free propagation in the inner heliosphere ( $\lambda_1 \rightarrow \infty$) and consider six values of $\lambda_2$ logarithmically spaced between 0.01 and 0.5 AU, and six radial positions of the back-scatter region $r_{\rm bs}\in [1.1,1.6]$ AU with step intervals of 0.1 AU. In scenario C we assume six values of $\lambda_1$ logarithmically spaced between 2.2 and 4.2 AU, the back-scatter region is assumed to be located at $r_{\rm bs}\in [1.1,1.6]$ AU and $\lambda_2 \in [0.01,0.5]$ AU.

The best-fit transport parameters for each transport scenario (i.e., those minimizing $\zeta$) are listed in Table 1. Figures 2-4 show the observations along with the simulation results for scenarios A, B, and C, respectively. These figures display the electron intensities for five of the eight sectors, which are representative of the directional information contained in the data owing to the stability of the IMF vector and the symmetry of the system.

\begin{figure} \par\includegraphics[width=8cm,clip]{13963fg5.eps} \end{figure} Figure 5:

Electron injection profiles derived for the three modeled scenarios in the E'3 energy range (injection times are shifted by 500 s to account for the light travel time). In addition to the fit result (histogram), smoothed curves obtained by four-point moving averaging are shown. The soft X-ray flux observed by GOES and the time-height plot of the CME leading edge (right axis) are given, as are the linear fit (dashed) and the second-order fit (dotted) to the CME height-time data. The radio flux observed by Wind and local electron plasma frequency at the height of the CME leading edge is shown by the dotted curve.

Open with DEXTER

It can be seen from Fig. 2 that the observed sectored intensities cannot be explained by assuming an Archimedean IMF and no back-scatter region beyond 1 AU (scenario A) because the observations from the sectors that scan particles propagating mainly sunward cannot be reproduced (sectors 1 and 2). If we assume scatter-free propagation in the inner heliosphere and a back-scatter region beyond 1 AU (scenario B), the best possible fit does not succeed either in reproducing the directional intensities (see Fig. 3). In this case, the PADs predicted by the model at 1 AU are too collimated along the IMF vector to explain the intensities observed by those sectors scanning mainly particles with $0\le \mu < 1$ (sectors 3 and 4 in Fig. 3). The best-fit scenario corresponds to scenario C, which assumes weak scattering in the inner heliosphere and a back-scatter region beyond 1 AU. The lowest value of $\zeta$ is obtained for $\lambda_1=3.2$ AU, $r_{\rm bs}=1.2$ AU and $\lambda_2=0.2$ AU. In this case, the fit succeeds in reproducing most of the features of the sectored intensity profiles (see Fig. 4). Some discrepancy however remains between the observations and the electron intensities predicted by the model for $\mu \le 0$ (sectors 1 and 2).

The three top panels of Fig. 5 display the best-fit injection profiles inferred for each scenario in the E'3 energy channel. The injection profile appears patchy, but the fit would practically not differ from the best fit if we assumed a smoothed injection profile (smoothed curves in Fig. 5, calculated with a 4-point moving average). The injection profiles inferred for scenarios A, B, and C last at least 1.5 h and peak at 09:30/09:40/09:36 UT, respectively. Scenarios B and C predict very similar injection profiles, i.e., peak intensities differing by a factor of 3 and occurring within 4 min of each other.

The two lower panels in Fig. 5 compare the timing of the electron injection with the timing of the solar event electromagnetic emissions. The first panel shows the soft X-ray flux observed by the GOES satellite in the 1-8 Å band together with the CME height-time plot together with the linear and second-order fit to the SOHO/LASCO observations, as reported in the CME Catalog (Yashiro et al. 2004). The bottom panel shows the 14 MHz-20 kHz radio emission observed by Wind/WAVES together with the frequency of emission of the plasma at the height of the CME leading-edge if the density model of Vrsnak et al. (2004) is used (dotted curve).

The best-fit injection profile inferred for scenario C begins at $\sim$09:26 UT and lasts at least 1.5 h. We observe a 2-3 min delay between the beginning of the injection and the timing of the metric and decametric radio bursts. Previous works have reported delays between the metric type III bursts and the electron release times of up to 30 min (Krucker et al. 1999), with a median delay of 13 min (Haggerty et al. 2003). For the 2000 February 18 event, the $\sim$3 min delay that we observe could also be related to high background intensities.

Simnett et al. (2002) compared the release time of 47 NR electron events with the launch time of the associated CMEs, and found that at the time of electron injection the height of the CME was most of the times between 1.5 and $3.5~R_\odot$. The position of the CME leading-edge observed by SOHO/LASCO on 2000 February 18 is uncertain at the time of the beginning of the injection. The CME leading-edge was at $2.6~R_\odot$ if the CME propagated radially with constant speed, or at $2~R_\odot$ if the CME decelerated in the low corona. Simnett et al. (2002) suggested that most NR electrons are accelerated by the shock driven by a coronal transient and are released at a radial distance around 2-$3~R_\odot$. The long duration of the injection profile inferred for the 2000 February 18 event and the estimated height of the CME leading-edge at the beginning of the injection support this hypothesis.

4 Discussion

We find a good agreement between the modeled and observed electron intensities if we assume a $\mu $-dependent scattering model with $\epsilon =0.01$ for the propagation of 62-312 keV electrons in the inner heliosphere. This kind of scattering model ensures suppressed scattering of electrons with $\mu=0$ and reduced diffusion between the two $\mu $ hemispheres. The large value of the inferred radial mean free path ( $\lambda_r=3.2$ AU) implies that electrons with $\mu \sim 0$ propagated under scatter-free conditions, whereas electrons with $\mu=1$ propagated with an effective isotropic radial mean free path of $\sim$0.9 AU.

Dröge & Kartavykh (2009) found an excellent fit to both 107 keV electron intensity and first-order anisotropy-time profiles by assuming $\lambda_\parallel=1.2$ AU and no back-scatter region beyond 1 AU. However, when they compared the PAD of 107 keV electrons observed around the time of maximum intensity with the model predictions, they found that the observed distribution was stronger peaked toward $\mu=1$. We attribute this disagreement to the interplanetary transport scenario. Dröge & Kartavykh (2009) assumed a constant parallel mean free path in order to resemble the increasing scattering strength with radial distance, but it seems that the scattering conditions increased much more drastically beyond 1 AU.

We examined the IMF and solar wind measurements previous to the NR electron event to find out whether the presence of a nearby back-scatter region during the 2000 February 18 event can be inferred from the observations. Figure 6 shows the magnetic field and solar wind parameters (from top to bottom magnetic field magnitude, proton solar wind speed, density and temperature) over a 6-day interval beginning on February 13. The data were obtained from the OMNI Web Plus browser[*],[*] with 1-h time resolution. There was a data gap in the ACE solar wind observations during the period under study, but measurements from the Wind spacecraft were available. The NR electron event period analyzed in this paper is indicated on the plot by the thin gray bar.

\begin{figure} \par\includegraphics[width=8cm,clip]{13963fg6.eps} \end{figure} Figure 6:

IMF and solar wind speed, density and temperature 1-h measurements by ACE (black) and Wind (red) for a 6-day interval beginning on February 13. The gray shaded intervals show the shock downstream region and the duration of the NR electron event, respectively.

Open with DEXTER

An interplanetary shock was observed at 1 AU on 2000 February 14 at 07:31 UT (Cane & Richardson 2003). The downstream region observed immediately after the shock passage was characterized by high plasma temperature and density (see Fig. 6). According to Cane & Richardson (2003), the interplanetary counterpart of a CME (ICME) was observed from 2000 February 14 at 12:00 UT to 2000 February 16 at 08:00 UT; but the boundary times of the ICME were indicated to be somehow ``ill-defined''. As pointed out by several authors (e.g. Hundhausen 1972), the presence of an ICME in interplanetary space modifies the IMF topology, because field lines get draped around the traveling interplanetary structure. Enhanced magnetic fluctuations and a non-Archimedean field configuration are expected throughout the ICME, which may affect the transport of solar energetic particles.

At the measured solar wind speed of 380 km s-1, the trailing edge of the ICME would have been convected to a radial distance of about 0.4 AU beyond the Earth's orbit by the beginning of the NR electron event. From the fitting of the directional intensities observed by ACE at 1 AU, we inferred that substantial pitch-angle scattering was taking place beyond 1.2 AU. The inferred position of the back-scattering region agrees with the trailing edge position of the ICME inferred from the solar wind and IMF observations, if we take into account the uncertainties in the estimation of the boundary times of the ICMEs, and the single-point nature of the IMF and solar wind observations.

Previous observational studies (e.g. Anderson et al. 1995; Roelof et al. 1992; Bieber et al. 2002; Tan et al. 2009) have provided evidence of the presence of discrete solar wind-interplanetary magnetic field structures beyond 1 AU, which are able to reflect SEPs back to the inner heliosphere. The present study provides another example in which the electron propagation is influenced by a similar structure. It also provides further support for the idea that the evolving global configuration of the heliosphere, as it is disturbed by the transit of ICMEs, can shape the characteristic of the SEP events observed at 1 AU.

5 Summary

We simulated the 2000 February 18 NR electron event observed by the ACE spacecraft and discussed the hypothesis that the propagation of the solar NR electrons was influenced by a back-scatter region located beyond 1 AU. We used a Monte Carlo transport model to explore this approach by simulating two transport regimes along an Archimedean IMF: 1) anisotropic scattering in the inner heliosphere and large radial mean free path ( $\lambda_r>0.5$ AU) of the electrons; and 2) isotropic scattering in the back-scatter region and a small radial mean free path ( $\lambda_r<0.5$ AU) of the electrons.

We found evidence in the directional intensities observed during this event of a back-scatter region beyond 1 AU. The best fit is obtained by assuming $\mu $-dependent scattering conditions in the inner heliosphere with $\lambda_r=3.2$ AU and a back-scatter region beyond 1.2 AU with $\lambda_{r} =0.2$ AU. The inferred solar injection profile lasts more than 1.5 h.

The IMF and solar wind measurements prior to the NR electron event provide evidence of an ICME that convected beyond 1 AU by the time of the beginning of the NR electron event observed by ACE.

In future work we plan to explore other transport scenarios. Because we observe some discrepancy in the sectors with $\mu \le 0$, it would be interesting to further explore the $\mu $-dependence of the pitch-angle scattering frequency. We also plan to investigate a propagation scenario where the interplanetary magnetic field beyond 1 AU is not an Archimedean spiral.

Acknowledgements
N.A. and R.V. acknowledge the financial support of the Academy of Finland under the projects 110021, 121650 and 124837. B.S. is grateful for the financial support of the Spanish Ministerio de Ciencia y Tecnología (project AYA2007-60724). D.L. was supported by NSF under SHINE research grant ATM-0648181 and by NASA under HGI grant NNX09AG30G. Computational support has been provided by the Finnish IT center for science.

References

  1. Agueda, N., Vainio, R., Lario, D., & Sanahuja, B. 2008, ApJ, 675, 1601 [Google Scholar]
  2. Agueda, N., Vainio, R., Lario, D., & Sanahuja, B. 2009a, Adv. Space Res., 44, 794 [Google Scholar]
  3. Agueda, N., Lario, D., Vainio, R., et al. 2009b, A&A, 507, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Agueda, N., Vainio, R., Lario, D., & Sanahuja, B. 2010, AIP Conf. Proc. 1216, 596 [CrossRef] [Google Scholar]
  5. Anderson, K. A., Sommers, J., Lin, R. P., et al. 1995, J. Geophys. Res., 100, 3 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bieber, J. W., Dröge, W., Evenson, P. A., et al. 2002, ApJ, 567, 622 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bougeret, J. L., Kaiser, M. L., Kellogg, P. J., et al. 1995, Space Sci. Rev., 71, 231 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cane, H. V., & Richardson, I. G. 2003, Geophys. Res. Lett., 108, SSH 6-1 [Google Scholar]
  9. Dröge, W. 2000, Space Sci. Rev., 93, 121 [NASA ADS] [CrossRef] [Google Scholar]
  10. Dröge, W. 2003, ApJ, 589, 1027 [Google Scholar]
  11. Dröge, W., & Kartavykh, Y. Y. 2009, ApJ, 639, 69 [NASA ADS] [CrossRef] [Google Scholar]
  12. Gold, R. E., Krimigis, S. M., Hawkins, S. E., III, et al. 1998, Space Sci. Rev., 86, 541 [Google Scholar]
  13. Haggerty, D. K., & Roelof, E. C. 2002, ApJ, 579, 841 [NASA ADS] [CrossRef] [Google Scholar]
  14. Haggerty, D. K., Roelof, E. C., & Simnett, G. M. 2003, ApJ, 32, 2673 [Google Scholar]
  15. Hasselmann, K., & Wibberenz, G. 1968, Z. Geophys., 34, 3533 [Google Scholar]
  16. Hundhausen, A. J. 1972, Coronal Expansion and Solar Wind (Berlin: Springer-Verlag) [Google Scholar]
  17. Kahler, S. W., Aurass, H., Mann, G., & Klassen, A. 2007, ApJ, 656, 567 [NASA ADS] [CrossRef] [Google Scholar]
  18. Kallenrode, M. B., Wibberenz, G., & Hucke, S. 1992, ApJ, 394, 351 [NASA ADS] [CrossRef] [Google Scholar]
  19. Kocharov, L., Vainio, R., Kovaltsov, G. A., & Torsti, J. 1998, Sol. Phys., 182, 195 [NASA ADS] [CrossRef] [Google Scholar]
  20. Krucker, S., Larson, D. E., Lin, R. P., & Thompson, B. J. 1999, ApJ, 519, 864 [NASA ADS] [CrossRef] [Google Scholar]
  21. Lawson, C. L., & Hanson, R. J. 1974, Solving Least Squares Problems (Englewood Cliffs: Prentice-Hall) [Google Scholar]
  22. Maia, D. J. F., & Pick, M. 2004, ApJ, 609, 1082 [NASA ADS] [CrossRef] [Google Scholar]
  23. McComas, D. J., Bame, S. J., Barker, P., et al. 1998, Space Sci. Rev., 86, 563 [NASA ADS] [CrossRef] [Google Scholar]
  24. Roelof, E.C. 2008, AIP Conf. Proc. 1039, 174 [NASA ADS] [CrossRef] [Google Scholar]
  25. Roelof, E. C., Gold, R. E., Simnett, G. M., et al. 1992, Geophys. Res. Lett., 19, 1243 [NASA ADS] [CrossRef] [Google Scholar]
  26. Simnett, G. M., Roelof, E. C., & Haggerty, D. K. 2002, ApJ, 579, 854 [NASA ADS] [CrossRef] [Google Scholar]
  27. Tan, L. C., Reames, D. V., Ng, C. K., Saloniemi, O., & Wang, L. 2009, ApJ, 701, 1753. [NASA ADS] [CrossRef] [Google Scholar]
  28. Vainio, R., Kocharov, L., & Laitinen, T. 2000, ApJ, 528, 1015 [NASA ADS] [CrossRef] [Google Scholar]
  29. Vrsnak, B., Magdalenic, J., & Zlobec, P. 2004, A&A, 413, 753 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Yashiro, S., Gopalswamy, N., Michalek, G., et al. 2004, J. Geophys. Res., 109, 7105 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... browser[*]
http://ftpbrowser.gsfc.nasa.gov/mag_iwa.html
...[*][*]
http://ftpbrowser.gsfc.nasa.gov/pla_iwa.html

All Tables

Table 1:   Best-fit parameters for different transport scenarios (see text for details).

All Figures

  \begin{figure} \par\includegraphics[width=8cm,clip]{13963fg1.eps} \end{figure} Figure 1:

Scattering frequency ratio between the $\mu $-dependent scattering model with $\epsilon =0.01$ and the isotropic scattering model.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=.24\textheight,clip]{13963fg2.eps} \end{figure} Figure 2:

Near-relativistic electron event on 2000 February 18 as observed by five of the sectors of the LEFS60 telescope. Electron sectored intensities E'4 175-312 keV, E'3 102-175 keV ($\times $10), and E'2 62-102 keV ($\times $100). The sectors are labeled from 1 to 5. The curves show the modeled sector intensities for scenario A and dots show the observational data. Low panels show the pitch-angle cosine of the midpoint clock-angle zenith direction of the sector (curve) and the scanned pitch-angle cosine range (gray area) as a function of time. The last panel shows the omnidirectional intensities and the mean pitch-angle cosine deduced from the simulation. The gray area shows the pitch-angle cosine range scanned by the telescope.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=.24\textheight,clip]{13963fg3.eps} \end{figure} Figure 3:

Same as in Fig. 2 for scenario B.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=.24\textheight,clip]{13963fg4.eps} \end{figure} Figure 4:

Same as in Fig. 2 for scenario C.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13963fg5.eps} \end{figure} Figure 5:

Electron injection profiles derived for the three modeled scenarios in the E'3 energy range (injection times are shifted by 500 s to account for the light travel time). In addition to the fit result (histogram), smoothed curves obtained by four-point moving averaging are shown. The soft X-ray flux observed by GOES and the time-height plot of the CME leading edge (right axis) are given, as are the linear fit (dashed) and the second-order fit (dotted) to the CME height-time data. The radio flux observed by Wind and local electron plasma frequency at the height of the CME leading edge is shown by the dotted curve.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13963fg6.eps} \end{figure} Figure 6:

IMF and solar wind speed, density and temperature 1-h measurements by ACE (black) and Wind (red) for a 6-day interval beginning on February 13. The gray shaded intervals show the shock downstream region and the duration of the NR electron event, respectively.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.