| Issue |
A&A
Volume 509, January 2010
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 9 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/200912857 | |
| Published online | 19 January 2010 | |
Astrometry with Carte du Ciel plates, San Fernando zone
II. CdC-SF: a precise proper motion catalogue![[*]](/icons/foot_motif.png)
B. Vicente1,5 - C. Abad2 - F. Garzón1,3 - T. M. Girard4
1 - Instituto de Astrofísica de Canarias (IAC), 38200
La Laguna (S/C de Tenerife), Spain
2 - Centro de Investigaciones de Astronomía (CIDA),
Apdo. 264, Mérida, 3101-A Venezuela
3 - Departamento de Astrofísica, Universidad de La Laguna, 38200 La Laguna (S/C de Tenerife), Spain
4 - Department of Astronomy, Yale University, PO Box 208101,
New Haven, CT 06520, USA
5 - Instituto de Astrofísica de Andalucía (IAA-CSIC), Apdo. 3004, 18080 Granada, Spain
Received 8 July 2009 / Accepted 5 November 2009
Abstract
Context. The historic plates of the Carte du Ciel, an
international cooperative project launched in 1887, offer valuable
first-epoch material for the determination of absolute proper motions.
Aims. We present the CdC-SF, an astrometric catalogue of positions and proper motions derived from the Carte du Ciel plates of the San Fernando zone, photographic material with a mean epoch of 1901.4 and a limiting magnitude of ![]() ,
covering the declination range of
,
covering the declination range of
![]() .
.
Methods. Digitization has been made using a conventional flatbed
scanner. Special techniques have been developed to handle the
combination of plate material and the large distortion introduced by
the scanner. The equatorial coordinates are on the ICRS defined by
Tycho-2, and proper motions are derived using UCAC2 as second-epoch
positions.
Results. The result is a catalogue with positions and proper motions for 560 000 stars, covering 1080 degrees2. The mean positional uncertainty is 0
![]() 20 (0
20 (0
![]() 12 for well-measured stars) and the proper-motion uncertainty is 2.0 mas/yr (1.2 mas/yr for well-measured stars).
12 for well-measured stars) and the proper-motion uncertainty is 2.0 mas/yr (1.2 mas/yr for well-measured stars).
Conclusions. The proper motion catalogue CdC-SF is effectively a
deeper extension of Hipparcos, in terms of proper motions, to a
magnitude of 15.
Key words: astrometry - catalogs - reference systems - surveys - stars: kinematics and dynamics
1 Introduction
The Hipparcos Catalogue (Perryman et al. 1997) contains the positions, parallaxes and proper motions of 118 218 stars with great precision (proper motions precision is 1 mas/year), complete up to a magnitude of V=7.3. Due to its precision and homogeneity, this catalogue constitutes an important source of information and has provided a useful tool in numerous kinematic studies. However, its relatively bright magnitude limit restricts it to very nearby stars, with the number of stars per unit area also being lower than what is often desired in kinematic analyses of the Galaxy.
For this reason, various efforts have been made to develop astrometric catalogues that are more dense and reach deeper magnitudes, becoming in effect an extension of the Hipparcos catalogue. It is necessary that such catalogues contain proper motions besides positions in order to provide the essential information with the quality and completeness needed.
The Tycho-2 Catalogue (Høg et al. 2000) can be considered
an extension of Hipparcos in the way that it contains positions and
proper motions for stars brighter than ![]() with errors of 2.5 mas/year. At the present time the Hipparcos and
Tycho-2 catalogues are the largest high-quality proper motion surveys.
with errors of 2.5 mas/year. At the present time the Hipparcos and
Tycho-2 catalogues are the largest high-quality proper motion surveys.
Other proper motion catalogues available at the present time are UCAC2 catalogues (Zacharias et al. 2004, 2-7 mas/yr depending on the magnitude and current version has systematic errors of the order of 3 mas/yr), NPM (Hanson et al. 2004, 5 mas/yr, 8 < B < 18) and SPM (Girard et al. 2004, 4 mas/yr, 5 < V < 18.5). For an overview in detail of the current astrometric catalogues, see Girard (2008).
When determining proper motions, a long time-baseline is highly desirable. Historical photographic records provide ideal material for the calculation of proper motions. This is a prime motivation for the digitization and reduction of the collections of photographic plates that were accumulated in observatories at the end of the 19th century.
In 1887, the first great astronomical project of international cooperation
in history was planned in Paris. Its objective was
the construction of a complete catalogue up to a magnitude of ![]() ,
the Astrographic Catalogue (AC), and to map the sky up to
,
the Astrographic Catalogue (AC), and to map the sky up to ![]() ,
the Carte du Ciel (CdC).
A total of twenty observatories around the world participated in
the task of taking the necessary observations.
This material represents the first existing photographic record of the
complete sky and is an extremely important potential resource for
determining proper motions due to the long time-baseline relative to
modern observations,
,
the Carte du Ciel (CdC).
A total of twenty observatories around the world participated in
the task of taking the necessary observations.
This material represents the first existing photographic record of the
complete sky and is an extremely important potential resource for
determining proper motions due to the long time-baseline relative to
modern observations,
![]() 100 years in most cases.
100 years in most cases.
This study is part of a larger project, the goal of which is to produce
an astrometric catalogue with proper motions for a variety of applications
in Galactic kinematics, as well as to provide a
dense, faint reference frame by recovering and utilizing the historical CdC plates.
In order to construct the catalogue, the first necessary step is
to digitize these plates.
The digitization and measurement process is discussed in detail in a previous paper (Vicente et al. 2007,
hereafter Paper I), where an innovative method of digitization
using a commercial flatbed scanner was presented. It was demonstrated
that this device, together with the techniques developed to remove the
distortion it introduces, is an alternative to more specialized
measuring machines that are less available, while yielding similar
measuring errors of 0
![]() 18 as
other groups, deriving astrometry from similar plate material,
although from other CdC collections (Rapaport 2006; Ortiz-Gil 1998; Geffert 1996).
18 as
other groups, deriving astrometry from similar plate material,
although from other CdC collections (Rapaport 2006; Ortiz-Gil 1998; Geffert 1996).
The main scientific value of positions at the epoch of 1900 resides in their usefulness in providing positions to serve as the first epoch in proper motion determinations involving the compilation of several catalogues of different epochs.
The current paper explains the various steps and procedures used during the construction of the CdC-SF proper-motion catalogue. The catalogue's properties are described in detail, including an estimation of uncertainties in the positions and proper motions. For the convenience of the reader, some of the figures and tables from Paper I are reproduced here for their relevance to the catalogue description.
2 Digitization of the plate material with a flatbed scanner
The plate material used in this work corresponds to the CdC collection stored in the Real Instituto y Observatorio de la Armada in San Fernando, Spain (ROA), which was charged with observing the area between the -2The plates are a historical patrimony of the institution,
and as such they could not be extracted from the museum to
be measured with specialized instrumentation.
Initially, reproductions were made in acetate and these were to be digitized
with a measuring machine, a microdensitometer PDS.
After performing several test scans of the acetate copies using
the PDS at Yale University (USA)
and the PDS at the CIDA (Venezuela), it was concluded
that large unpredictable distortions due to the copying process
(up to 15 ![]() m) together with the slowness of the PDS (1 plate / day)
would prohibit the successful completion of the project.
m) together with the slowness of the PDS (1 plate / day)
would prohibit the successful completion of the project.
For this reason, we used a commercial flatbed scanner as an alternative for the digitalization. Though its internal precision is much inferior to that obtained from a PDS, it is possible to measure the original plates with the scanner and, because of its faster speed (1 plate/8 min.), it allowed us to repeat the digitalization to improve the final precision. At present, ROA has completed the digitization of its collection of 2520 AC/CdC plates.
The main problem to be addressed when using a measuring device such as a
scanner for astrometric work is the significant distortion introduced
(![]() 100
100 ![]() m, Fig. 1) by the scanner itself.
To make matters worse, this distortion is not consistent, as
has been confirmed by repeated sans.
Vicente et al. (2007) described the method developed to calibrate and
correct for scanner distortion in detail yielding excellent results.
The resultant final single-measurement internal error-estimate per exposure is
3
m, Fig. 1) by the scanner itself.
To make matters worse, this distortion is not consistent, as
has been confirmed by repeated sans.
Vicente et al. (2007) described the method developed to calibrate and
correct for scanner distortion in detail yielding excellent results.
The resultant final single-measurement internal error-estimate per exposure is
3 ![]() m (0
m (0
![]() 2) for single-exposures plates
and 5
2) for single-exposures plates
and 5 ![]() m (0
m (0
![]() 3) for triple-exposures ones.
3) for triple-exposures ones.
| Figure 1:
Positional differences obtained from two digitalizations of the same plate, rotated one with regard to the other by 90 |
|
| Open with DEXTER | |
3 Measurement of the plates
The most important characteristics of the plates that complicate the determination of precise astrometry include:
- 1)
- the blending of the triple-exposure images on the odd-numbered declination plates;
- 2)
- the blending and confusion of stars that fall on the superposed réseau grid lines;
- 3)
- the false detections due to plate flaws, spurious dust and degradations that have accumulated during storage, and;
- 4)
- typical effects in photographic material caused by optical aberrations and by non-linear detectors.
For the resolution of all these problems it has been necessary to develop the necessary programmes from scratch since available commercial software packages are not optimized for photographic material. All of the effects mentioned above have been successfully treated. Details can be found in Paper I.
Currently, the algorithms have been applied to only one third of the San Fernando zone; the one with a right ascension between 6 and 14 h, constituting 420 plates (180 simple-exposures plates and 240 triple-exposures plates). The measurement of the remaining plates in the future will be straightforward, based on the information developed and presented here and in Paper I.
4 Astrometric reduction of the plates
The transformation from the (x,y) coordinates into celestial
coordinates (
![]() )
was performed by the
block-adjustment technique (Stock 1981)
including a determination of the field distortion (Abad 1993).
This technique utilizes images which overlapping plates have in common
in addition to positional information from an external reference catalogue.
A linear plate model is used in combination with a residuals-based
corrective mask that is common to all plates.
These are derived and applied in an iterative process.
)
was performed by the
block-adjustment technique (Stock 1981)
including a determination of the field distortion (Abad 1993).
This technique utilizes images which overlapping plates have in common
in addition to positional information from an external reference catalogue.
A linear plate model is used in combination with a residuals-based
corrective mask that is common to all plates.
These are derived and applied in an iterative process.
Residuals consist of the differences between individual positions and the averages, for multiply measured stars, in addition to differences between the averages and the external catalogue for the reference stars. Figure 2 shows a sample of the stacked residuals. The pattern represents the systematic field distortion remaining in the plates. This empirical function is applied to the positions, and a new iteration of the linear plate solution plus mask is performed. For more details about the procedure and other considerations in the determination of positions see Paper I. The overlapping technique allows for the simultaneous reduction of all plates. Nevertheless, we decide to divide the set of plates into four zones grouped by right ascension in order to compare the results as a function of the sky position and stellar density. Every zone covers two hours in right ascension and seven complete zones of declination.
The Tycho-2 Catalogue (Høg et al. 2000) was used as a reference catalogue,
using its proper motions to take the positions backward to the epoch
of each plate. Its proper motions have a precision of 2.5 mas/year and
an accuracy somewhat less than that, making it a suitable reference source.
It also has a sufficient density of stars and a magnitude limit of
![]() .
An alternative reference catalogue, the UCAC2, was not adopted due to
its lower precision in proper motions, and also because its positions
will be used as second-epoch data in the proper motion determination,
and we prefer a totally independent reduction of the first-epoch
material.
.
An alternative reference catalogue, the UCAC2, was not adopted due to
its lower precision in proper motions, and also because its positions
will be used as second-epoch data in the proper motion determination,
and we prefer a totally independent reduction of the first-epoch
material.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12857fig02.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg20.png)
|
Figure 2: Position residuals as a function of coordinates after a linear plate model is applied, showing the systematic errors in the plates due to the telescope optics. |
| Open with DEXTER | |
4.1 Magnitude-equation correction
Magnitude-equation is the term used to describe the bias in star image positions as a function of stellar magnitude that is present in virtually all photographic plates. In order to correct for it, it is necessary to obtain not only the Cartesian positions (x, y), of each stellar image but also a magnitude index for the image, to allow a magnitude calibration. The estimated magnitude we use is the photographic one, the measured flux under the 2D Gaussian fitting, calibrated with the approximate R magnitudes of the UCAC2 catalogue. For each plate we calculate the coefficients of the transformation needed as a least-squared fitting with a second-order polynomial (Fig. 3).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12857fig03.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg21.png)
|
Figure 3: Example of the magnitude calibration for one plate. A second-order polynomial fitting is applied (red line). |
| Open with DEXTER | |
The common magnitude equation within the plates is handled by stacking residuals and deriving correction masks. Different correction masks are constructed by binning stars into one-magnitude wide intervals to determine the magnitude dependence of the systematic errors (some examples in Fig. 4). The distortion is found to be more pronounced at bright magnitudes.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12857fig04.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg22.png)
|
Figure 4: Vector residuals are shown for four exemplary magnitude ranges. Positions within a given magnitude range are corrected using the appropriate mask. The exact correction for a star is calculated as an interpolation in magnitude between the two masks nearest in magnitude. |
| Open with DEXTER | |
After the mask correction is applied, a slight residual magnitude equation was detected based on differences with the reference Tycho-2 catalogue (Fig. 5). However, it is possible that these systematic effects are actually inherent in the Tycho-2 proper motions and propagated into the Tycho-2 positions at epoch 1900. After a thorough study of our derived proper motions for open cluster members, we decided for this to be the case and did not make a further adjustment in the magnitude-equation based on the trends seen in the differences with Tycho-2.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12857fig05.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg23.png)
|
Figure 5:
Systematic trend in the positional differences for Tycho-2 reference
stars depending on the magnitude. The straight line is a least-squares
linear fit. These data correspond to the group of the plates with
|
| Open with DEXTER | |
5 Determination of the proper motions
The early-epoch CdC positions are combined with modern positions from the UCAC2 catalogue to derive relative proper motions. We have confirmed previously that both catalogues are free of significant systematic errors with respect to Tycho-2, minus the residual magnitude trend discussed above. Thus, both are ostensibly on the same system.
The relative proper motions are placed on the ICRS system via a direct comparison to the Hipparcos proper motions for common stars with our catalogue, applying a local correction for systematic effects. The value to be corrected is calculated as an average of the differences between our proper motions and those of the 50 nearest Hipparcos stars. We have preferred using the accumulative distribution function (Hamaker 1978) to calculate the average and the dispersion of the Hipparcos proper-motion differences for the 50 nearby stars. In general, this method is much more consistent and immune to atypical values for the estimation of the average and dispersion using the property of which the sample fits a Gaussian distribution.
Figure 6 shows a vector field with the differences in proper motions between the two sets of proper motions as a function of sky position, employing for the plot the technique of the ``weighted sliding polynomial'' (Stock & Abad 1988). The source of the systematic trend seen in the differences between the preliminary CdC-SF proper motions and those of Hipparcos is unknown. It is difficult to explain trends with a scale length of tens of degrees when our individual plates cover just two degrees. We speculate that it may be due to systematics in the Tycho-2 proper motions that were used in deriving our first-epoch positions. Systematics of this amplitude, of 1 to 2 mas/yr, have been noticed during the construction of the soon to be released Southern Proper Motion catalogue (SPM4) when compared to Tycho-2. Noticeable fixed-pattern trends of 1 to 2 mas/yr in amplitude and a scale length of one to two degrees were observed across the six-degree wide SPM fields, even though Tycho-2 had been used as a reference in the cubic polynomial plate models. Whether larger scale-length systematics are present in the Tycho-2 proper motions is not known (and could not have been detected during the SPM4 analysis, as they would have been absorbed by the cubic polynomial), but this is a possibility (Girard 2009, private comm.). It is also demonstrated in Rapaport (2006) that the propagated Tycho-2 errors are non-negligible, becoming equal to or even greater than the measurement errors due to the long interval of time between the epochs of Tycho-2 positions and CdC plates (about 100 years). For now, the cause of the pattern seen in Fig. 6 is unclear. Nevertheless, the best course of action is to correct for it as we have done, placing us more firmly on the proper-motion system of Hipparcos, which we consider to be reliable.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12857fig06.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg24.png)
|
Figure 6: Differences in the proper motions of CdC-SF and Hipparcos as a function of right ascension and declination before the local correction has been applied. After the application the differences become random and less than 1 mas/yr. |
| Open with DEXTER | |
We have also confirmed that the magnitude equation is not present for the common stars with Hipparcos. Thus we conclude that our absolute proper motions are indeed in the Hipparcos system, at least for the common magnitude range.
6 Error estimation
As an example of the astrometric quality of the final catalogue which we have extensively described, we will present here the errors and uncertainties of its positions and proper motions.
6.1 Errors in positions
An estimated internal error for each star in the catalogue is derived based on the rms of the positional differences of each image in the overlapping plates to the average position. This value, considered as the internal positional error of the star, is included in the catalogue. The distribution of the errors as a function of magnitude is given in Table 1, repeated here from Paper I for the convenience of the reader.
Table 1: Final internal positional uncertainties as a function of magnitude for the derived CdC-SF coordinates, grouped by right ascension.
The mean values of these uncertainties are
![]() for the entire catalogue, and for stars brighter than 14, the mean values are
for the entire catalogue, and for stars brighter than 14, the mean values are
![]() .
For completeness, triple exposure plates with a measuring error of better
than 7
.
For completeness, triple exposure plates with a measuring error of better
than 7 ![]() m are included in the catalogue.
Nevertheless, for minimizing the effect of their lower precision,
a lesser weight has been assigned to them.
The mean error of the catalogue including
only simple exposure plates is 0
m are included in the catalogue.
Nevertheless, for minimizing the effect of their lower precision,
a lesser weight has been assigned to them.
The mean error of the catalogue including
only simple exposure plates is 0
![]() 14, in each coordinate.
The individual uncertainty estimates are based on a handful of
measures per star. Therefore, one should not place too much weight
on the variation of uncertainty estimates within a given magnitude range,
and the median uncertainty at a given magnitude may possibly be a better estimate for any particular star.
14, in each coordinate.
The individual uncertainty estimates are based on a handful of
measures per star. Therefore, one should not place too much weight
on the variation of uncertainty estimates within a given magnitude range,
and the median uncertainty at a given magnitude may possibly be a better estimate for any particular star.
The final line in Table 1 also lists the rms differences between our derived positions and the Tycho-2 catalogue, at the CdC-SF epoch. These rms differences are expected to have a significant, possibly dominant, contribution from the errors in the Tycho-2 positions at this epoch.
A comparison of our catalogue with the Tycho-2 positions at the CdC plates' epoch as a function of magnitude (Fig. 7) shows no systematic pattern, the mean differences remaining constant over all magnitudes. Thus our catalogue can be considered to have been successfully placed on the system ICRS, as defined by Hipparcos, via Tycho-2. Note that this is not inconsistent with our earlier discovery of trends in the proper motion differences with Tycho-2. It simply means that applying our proper motions to our 1900-epoch positions and bringing them into a modern epoch will yield modern postions that do disagree with Tycho-2. However, it is the integrity of our proper motions that is the highest priority. We have little other choice but to adopt the Tycho-2 positional system, at the epoch 1900, for our positional reference system.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12857fig07.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg35.png)
|
Figure 7: Differences in positions
between CdC-SF positions and Tycho-2 catalogue at the CdC epoch as
a function of magnitude for stars in common. The fitted line indicates
the moving-mean standard deviation. The plot for
|
| Open with DEXTER | |
Figure 8 shows that the dispersion of
these positional differences with Tycho-2 is
![]() and is well described by a Gaussian distribution.
This agrees with the mean value obtained for the standard deviation 0
and is well described by a Gaussian distribution.
This agrees with the mean value obtained for the standard deviation 0
![]() 34 (final line in the Table 1), that it is
1.414 times the spread of a Gaussian function.
34 (final line in the Table 1), that it is
1.414 times the spread of a Gaussian function.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12857fig08.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg39.png)
|
Figure 8: Reference star residuals
of CdC-SF catalogue based on a comparison with the Tycho-2 positions at
the epoch of the plates. We obtain a well defined Gaussian
distribution, the standard deviations of which are
|
| Open with DEXTER | |
We note that our uncertainty values compare well with results from other studies based on similar plate material, but digitized with precision measuring machines specialized for photographic plates (Table 2, repeated here from Paper I).
Table 2: Comparison of various astrometric studies involving CdC plate material.
6.2 Internal and external errors in proper motions
In cases where the proper motion is calculated using the positions of several catalogues of different epochs, one can estimate the proper-motion uncertainties from the dispersion of the individual data fittings. But in the investigation of the CdC-SF we have compared the positions only with one more catalogue, UCAC2. This means we have the adjustment of a straight line to two points. Nevertheless, for each star we have included in the catalogue an estimate of the uncertainties of the proper motions obtained from the quadrature sum of the stated positional uncertainties in the catalogue CdC-SF and in the UCAC2 divided by the epoch difference.
The average of the uncertainties in the two proper-motion
components is (2.0, 1.9) mas/yr for all the stars in the catalogue. For stars brighter than ![]() it is (1.2, 1.1) mas/yr, as is shown in Fig. 9. The mean uncertainties tabulated by magnitude bins of
it is (1.2, 1.1) mas/yr, as is shown in Fig. 9. The mean uncertainties tabulated by magnitude bins of
![]() are given in Table 3.
are given in Table 3.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12857fig09.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg46.png)
|
Figure 9:
Proper-motion uncertainties as a function of magnitude.
Each point represents 25 stars, and the grey line indicates a moving mean.
|
| Open with DEXTER | |
Table 3: Internal estimation of the proper motion errors binned by magnitude, including the number of stars per magnitude interval.
6.3 External comparison with Hipparcos proper motions
The evaluation of the external errors in the proper motions
of the CdC-SF is obtained by means of comparison with the
Hipparcos catalogue (ESA 1997), although obviously this comparison can only
be made for the bright stars. The uncertainty of the Hipparcos proper motions is on average ![]() 1 mas/yr (Fig. 10).
1 mas/yr (Fig. 10).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12857fig10.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg49.png)
|
Figure 10:
Uncertainties of the proper motions as a function of magnitude from the Hipparcos catalogue (ESA 1997). The plot for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12857fig11.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg50.png)
|
Figure 11: Differences of CdC-SF absolute proper motions compared with Hipparcos as a funcion of magnitude. The fitted line indicates the moving-average differences. |
| Open with DEXTER | |
In Fig. 11 the differences between our absolute proper motions and those of Hipparcos are shown for the 701 common stars. No systematic trends are seen, neither depending on the magnitude nor on the position.
The observed dispersion of the mean differences,
![]() = 2.5 mas/yr and
= 2.5 mas/yr and
![]() = 2.7 mas/yr,
includes the errors of our catalogue and
those of Hipparcos, added in quadrature.
Since the Hipparcos proper motion errors are on average
1.5 mas/yr, in the common sky area and magnitude range,
we can deduce an estimation of the external accuracy of the CdC-SF for the bright objects of up to
= 2.7 mas/yr,
includes the errors of our catalogue and
those of Hipparcos, added in quadrature.
Since the Hipparcos proper motion errors are on average
1.5 mas/yr, in the common sky area and magnitude range,
we can deduce an estimation of the external accuracy of the CdC-SF for the bright objects of up to ![]() ,
of 2.0 mas/yr.
,
of 2.0 mas/yr.
Note that this comparison is done for the brightest stars of our catalogue, which are precisely those that suffer from saturation problems, but at least it gives us an upper limit of our external errors.
6.4 Proper motion errors using open clusters
The internal velocity dispersion of all but the very nearest open clusters is too small to be measured with proper motions. Thus, the observed dispersion is a good estimate of the individual proper-motion errors for members of the cluster.
A handful of open clusters within our catalogue allow us to estimate the the proper-motion errors and also confirm that a magnitude equation is not present.
For each cluster utilized, Table 4 shows the dispersion of our proper motions of the most probable members according to the Dias et al. (2006) database. Unfortunately, the membership information available comes from either bright catalogues (Hipparcos, Tycho-2) or from less precise proper-motion sources (UCAC2). Thus, some stars may be erroneously identified as members. Still, the dispersions of the mean proper motion of the clusters provide an estimate of at least an upper limit to our internal error. We verify that this limit of the error is consistent with the estimation we made earlier (Sect. 6.2).
Table 4: Dispersion of proper motions for each open cluster studied.
7 Description of the CdC-SF Catalogue
The resulting catalogue, called CdC-SF Catalogue, contains positions and proper motions for approximately 500 000 stars in the ICRS system. It is constructed from 420 plates, one third of the full CdC-SF collection. The mean epoch is 1901.4, although the positions are presented in the epoch 1900 for convenience. The mean epoch of observation for each star is also listed. Thus, the original-epoch position of each star can be retrieved from the proper motions, should one wish to include these data in the compilation of other proper-motion catalogues.
The CdC-SF sky coverage is illustrated in Fig. 12. The gaps correspond to plates that had problems during the reduction or that were not included because of their poor quality and would have adversely affected neighbouring fields in the catalogue. The contents of the CdC-SF Catalogue is given in Table 6, and a summary of its main characteristics is described in Table 5.
| Figure 12: Sky coverage of the CdC-SF Catalogue. |
|
| Open with DEXTER | |
Table 5: CdC-SF Catalogue properties.
Table 6: Contents of the CdC-SF Catalogue.
In the final catalogue we have rejected stars that come from just one measure, because, at minimum, every real stellar image should have at least two measures owing to the fact that we have digitized every plate twice. The two scans of the same plate were considered as separate measures, as a justifiable simplification. Even if those two scans are not truly independent, they are still significantly enough independent because of the dominant contribution of the measuring process to the total error. So, we think that treating them as independent measures for the purposes of computing averages and uncertainties might be roughly correct. As far as the uncertainty estimates goes, the validity of this approximation is shown to be reasonable by the external checks on the error estimates, i.e., the open clusters and the comparison with the Hipparcos data. We have also removed uncertain or failed matches with stars in the UCAC2, which were needed to calculate proper motions. For this reason, the UCAC2 completeness sets our completeness. In addition to this we have further losses due to the detection pipeline in combination with the problematical plates.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12857fig13.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg73.png)
|
Figure 13:
Correlation between the
|
| Open with DEXTER | |
Besides the photometric magnitude calculated and calibrated during
the reduction, we have included the photometry from other catalogues:
BV magnitudes for the common stars with Tycho-2,
R magnitude from UCAC2 and
![]() from the 2MASS catalogue.
Tycho-2 magnitudes,
from the 2MASS catalogue.
Tycho-2 magnitudes, ![]() and
and ![]() ,
have been transformed into the the UBV photometric system using the equations (ESA SP-1200 1997):
,
have been transformed into the the UBV photometric system using the equations (ESA SP-1200 1997):
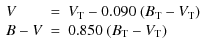
|
(1) |
An extrapolated V estimate has been derived from 2MASS
The catalogue includes also cross-identifications with the Hipparcos, Tycho-2, UCAC2 and 2MASS catalogues in order to access complementary information from these catalogues. We are aware that CdC-SF does not include all Hipparcos stars in our area (bright objects are saturated on the plates), nor all Tycho-2 stars (lost on the grid or on rejected plates). For this reason, we annex two files with the identification numbers of these missing stars, 3170 Hipparcos's stars and 39 611 stars of Tycho-2 not included in Hipparcos.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12857fig14.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg79.png)
|
Figure 14: Completeness of the CdC-SF catalogue: magnitude distribution compared to other astrometric catalogues. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12857fig15.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg80.png)
|
Figure 15: Moving-average error of CdC-SF proper motions, as a function of magnitude, compared with Hipparcos, Tycho-2 and UCAC2. |
| Open with DEXTER | |
Future versions of the CdC-SF catalogue with expanded coverage to the full 24 h of right ascension will be constructed by applying the techniques presented here to the remainder of the digitized plate material.
8 Conclusions
We have presented the CdC-SF Catalogue, an astrometric catalogue
with positions and proper motions for more than 500 000 stars,
in the ICRS system, with a mean epoch of 1901.4,
to V=16, covering 1080 degrees2 in the sky area
between
![]() .
The mean uncertainty in positions is 0
.
The mean uncertainty in positions is 0
![]() 20
(0
20
(0
![]() 12 for well-measured stars),
and in proper motions it is 2 mas/yr (1.1 mas/yr for well-measured stars).
The catalogue is based on the reduction of the original
Carte du Ciel photographic plates, San Fernando zone,
that have been ``revived'' by digitization with a commercial flatbed scanner.
12 for well-measured stars),
and in proper motions it is 2 mas/yr (1.1 mas/yr for well-measured stars).
The catalogue is based on the reduction of the original
Carte du Ciel photographic plates, San Fernando zone,
that have been ``revived'' by digitization with a commercial flatbed scanner.
External comparison of the data has been made with the catalogues Hipparcos and UCAC2, as well as a study of the proper-motion errors using open clusters. The catalogue achieves approximately the same precision in proper motions as the Hipparcos catalogue, but it extends to seven magnitudes fainter.
Finally, the CdC-SF catalogue covers -10![]() to +60
to +60![]() galactic latitude and will provide an excellent basis for studies
of the kinematics of different components of our Galaxy.
The positions at the epoch 1900 should prove to be useful for
other proper-motion determinations.
galactic latitude and will provide an excellent basis for studies
of the kinematics of different components of our Galaxy.
The positions at the epoch 1900 should prove to be useful for
other proper-motion determinations.
We are very grateful to the Observatorio de San Fernando for making available to us the Carte du Ciel plates from their historical archive. We also want to thank all of the people who have participated in the digitizationof the collection, with special mention of José Muiños, Fernando Belizón and Miguel Vallejo.
References
- Abad, C. 1993, A&AS, 98, 1 [Google Scholar]
- Dias, W. S., Assafin, M., Flório, V., Alessi, B. S., & Líbero, V. 2006, A&A, 389, 871 [Google Scholar]
- ESA 1997, ESA SP-1200, 1-7 (ESA97) [Google Scholar]
- Geffert, M., Bonnefond, P., Maintz, G., et al. 1996, A&AS, 118, 277 [Google Scholar]
- Girard, T. M., Dinescu, D. I., van Altena, W. F., et al. 2004, AJ, 127, 3060 [NASA ADS] [CrossRef] [Google Scholar]
- Girard, T. M. 2008, IAU Sysmp., 248, 303 [NASA ADS] [Google Scholar]
- Hamaker, H. C. 1978, Applied Statistics 27, 76 [CrossRef] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V., et al. 2000, A&A, 357, 367 [Google Scholar]
- Ortiz-Gil, A., Hiesgen, M., & Brosche, P. 1998, A&AS, 128, 621 [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, 49 [Google Scholar]
- Rapaport, M., Ducourant, C., Le Campion, J., et al. 2006, A&A, 449, 435 [Google Scholar]
- Stock, J. 1981, Rev. Mex. Astron. Astrofis., 6, 115 [Google Scholar]
- Stock, J., & Abad, C. 1988, Rev. Mex. Astron. Astrofis., 16, 63 [Google Scholar]
- Vicente, B., Abad, C., & Garzón, F. 2007, A&A, 471, 1077 [Google Scholar]
- Zacharias, N., Urban, S., Zacharias, M., Wycoff, G., Hall, D., Monet, D., & Rafferty, T. 2004, AJ, 127, 3043 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... catalogue
![[*]](/icons/foot_motif.png)
- The Astrometric catalog is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/509/A62
All Tables
Table 1: Final internal positional uncertainties as a function of magnitude for the derived CdC-SF coordinates, grouped by right ascension.
Table 2: Comparison of various astrometric studies involving CdC plate material.
Table 3: Internal estimation of the proper motion errors binned by magnitude, including the number of stars per magnitude interval.
Table 4: Dispersion of proper motions for each open cluster studied.
Table 5: CdC-SF Catalogue properties.
Table 6: Contents of the CdC-SF Catalogue.
All Figures
| |
Figure 1:
Positional differences obtained from two digitalizations of the same plate, rotated one with regard to the other by 90 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12857fig02.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg20.png)
|
Figure 2: Position residuals as a function of coordinates after a linear plate model is applied, showing the systematic errors in the plates due to the telescope optics. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12857fig03.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg21.png)
|
Figure 3: Example of the magnitude calibration for one plate. A second-order polynomial fitting is applied (red line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12857fig04.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg22.png)
|
Figure 4: Vector residuals are shown for four exemplary magnitude ranges. Positions within a given magnitude range are corrected using the appropriate mask. The exact correction for a star is calculated as an interpolation in magnitude between the two masks nearest in magnitude. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12857fig05.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg23.png)
|
Figure 5:
Systematic trend in the positional differences for Tycho-2 reference
stars depending on the magnitude. The straight line is a least-squares
linear fit. These data correspond to the group of the plates with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12857fig06.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg24.png)
|
Figure 6: Differences in the proper motions of CdC-SF and Hipparcos as a function of right ascension and declination before the local correction has been applied. After the application the differences become random and less than 1 mas/yr. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12857fig07.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg35.png)
|
Figure 7: Differences in positions
between CdC-SF positions and Tycho-2 catalogue at the CdC epoch as
a function of magnitude for stars in common. The fitted line indicates
the moving-mean standard deviation. The plot for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12857fig08.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg39.png)
|
Figure 8: Reference star residuals
of CdC-SF catalogue based on a comparison with the Tycho-2 positions at
the epoch of the plates. We obtain a well defined Gaussian
distribution, the standard deviations of which are
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12857fig09.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg46.png)
|
Figure 9:
Proper-motion uncertainties as a function of magnitude.
Each point represents 25 stars, and the grey line indicates a moving mean.
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12857fig10.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg49.png)
|
Figure 10:
Uncertainties of the proper motions as a function of magnitude from the Hipparcos catalogue (ESA 1997). The plot for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12857fig11.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg50.png)
|
Figure 11: Differences of CdC-SF absolute proper motions compared with Hipparcos as a funcion of magnitude. The fitted line indicates the moving-average differences. |
| Open with DEXTER | |
| In the text | |
| |
Figure 12: Sky coverage of the CdC-SF Catalogue. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12857fig13.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg73.png)
|
Figure 13:
Correlation between the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12857fig14.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg79.png)
|
Figure 14: Completeness of the CdC-SF catalogue: magnitude distribution compared to other astrometric catalogues. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12857fig15.ps}
\end{figure}](/articles/aa/full_html/2010/01/aa12857-09/Timg80.png)
|
Figure 15: Moving-average error of CdC-SF proper motions, as a function of magnitude, compared with Hipparcos, Tycho-2 and UCAC2. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


