- ... populations
![[*]](/icons/foot_motif.gif)
- As a ``normal'' SSP we define a
coeval stellar population of a single metallicity and characterised by
either a Salpeter (1955) or a Kroupa (2001)-type stellar initial mass
function (IMF), i.e., a two-part power law covering the stellar mass
range from
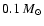 to
to 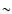
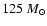 ,
depending on
metallicity.
,
depending on
metallicity.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... radii
![[*]](/icons/foot_motif.gif)
- Assuming that
light traces mass, the observed half-light radii must be corrected for
projection onto the sky by applying a correction factor of 3/4 (e.g.,
Fleck et al. 2006).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... stars
![[*]](/icons/foot_motif.gif)
- Although, strictly speaking, Eq. (1)
is valid for line-of-sight velocity dispersions instead of the
equivalent dispersions based on proper-motion studies, the effect of
ignoring this will be mass overestimates by a factor of 2 (or
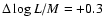 )
if the clusters' kinematics are isotropic. This does
not affect our conclusions.
)
if the clusters' kinematics are isotropic. This does
not affect our conclusions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... only
![[*]](/icons/foot_motif.gif)
- Despite the extent of
the error bar associated with the age estimate of the Pleiades, Kroupa
et al. (2001) showed this cluster to have re-virialised by an age of
50 Myr, so that it is unlikely affected by the aftermath of the
gas-expulsion phase.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
clusters
![[*]](/icons/foot_motif.gif)
- For a quantitative estimate of this effect, let us
assume that our clusters are well represented by Plummer
models. However, we note that this is an unproven assumption; younger
clusters are likely more extended (e.g. Elson et al. 1987),
whereas older clusters (particularly lower-mass objects) may be
significantly depleted in their outer regions and hence could be much
more compact. A back-of-the-envelope calculation shows then that the
following relations apply (from Heggie & Hut 2003):
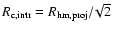 ,
,
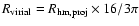 ,
and
,
and
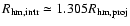 .
This
leads, approximately, to
.
This
leads, approximately, to
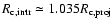 ,
and therefore
,
and therefore
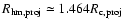 .
Here, the
subscripts ``c'', ``hm'', ``intr'', and ``proj'' stand for core, half mass,
intrinsic, and projected. This result only holds approximately
for a Plummer model; it gives us a rough idea of the errors involved
in our analysis, leading to
.
Here, the
subscripts ``c'', ``hm'', ``intr'', and ``proj'' stand for core, half mass,
intrinsic, and projected. This result only holds approximately
for a Plummer model; it gives us a rough idea of the errors involved
in our analysis, leading to
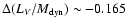 (in
solar units).
(in
solar units).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... lines
![[*]](/icons/foot_motif.gif)
- However, we need an unbiased sample to
explore this option statistically and in more detail.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Tacconi-Garman
![[*]](/icons/foot_motif.gif)
- Although these authors
published a mass determination of
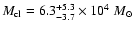 for Westerlund 1, they recently redetermined its
velocity dispersion and hence its mass, at
for Westerlund 1, they recently redetermined its
velocity dispersion and hence its mass, at
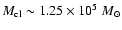 (Mengel & Tacconi-Garman 2007b).
(Mengel & Tacconi-Garman 2007b).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...2001)
![[*]](/icons/foot_motif.gif)
- NGC 3532 is also strongly flattened (Gieseking 1981),
roughly orthogonal to the Galactic plane. Both theory and N-body
simulations suggest that the effects of the Galactic tidal field give
rise to a flattening of cluster outskirts in the direction towards the
Galactic Centre and perpendicular to the Galactic plane (see Mathieu
1985).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.