... conditions

Throughout the paper, evolutionary conditions mean the age, metallicity, and star formation history of the stellar ensemble.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... transformations

In the following, we assume 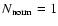$N_{\rm norm}=1$ and we do not include the subindex 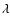$\lambda$ in the luminosities to simplify the notation. We also omit the subindex 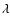$\lambda$ in the following equations.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... function

This function provides the probability that a single star has a given luminosity, and it is only defined by the evolutionary conditions of a stellar sample.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... element

The higher the number of stars, the larger the possible fluctuation, as we see below (cf. Eq. (13)).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... mixes

This is a simplification of the original theory, in which IMF sampling is but one of several causes of dispersion; it is, however, sufficient to develop our argument. See Cerviño & Luridiana (2006) for more details.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.