Table 1:
Predicted temporal slopes 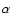 for various afterglow scenarios
based on the measured spectral slopes
for various afterglow scenarios
based on the measured spectral slopes
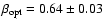 (Sect. 3.2) and
(Sect. 3.2) and
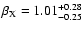 (Sect. 3.1). These values have to be compared with the measured
(Sect. 3.1). These values have to be compared with the measured
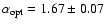 and
and
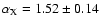 .
Assuming a
jet, for
.
Assuming a
jet, for
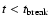 the isotropic model holds, whereas for
the isotropic model holds, whereas for
 the jet model applies (e.g. Zhang & Mészáros 2004). The
the jet model applies (e.g. Zhang & Mészáros 2004). The
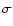 -level represents the difference between the predicted and the
observed temporal slope, normalized to the square root of the sum of their
quadratic errors. The favoured model is highlighted.
-level represents the difference between the predicted and the
observed temporal slope, normalized to the square root of the sum of their
quadratic errors. The favoured model is highlighted.
| Afterglow model |
Optical |
X-ray |
| |
 |
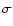 -level -level |
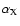 |
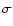 -level -level |
| Iso |
ISM, wind,
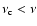 |
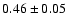 |
-14.54 |
 |
-1.14 |
ISM,
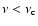 |
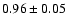 |
-8.53 |
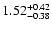 |
-0.01 |
wind,
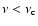 |
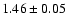 |
-2.52 |
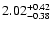 |
1.24 |
|---|
| Jet |
ISM, wind,
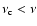 |
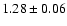 |
-4.23 |
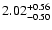 |
0.96 |
ISM, wind,
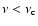 |
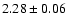 |
6.62 |
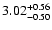 |
2.89 |
Source LaTeX |
All tables |
In the text