Table 5:
Model photospheres.
| Case |
R |
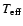 |
log g |
T0a |
db |
log FLc |
log RLd |
| |
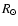 |
K |
|
K |
|
|
|
| M = |
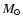 |
|
|
|
|
|
|
|
a |
50 |
4000 |
1.04 |
2196 |
1.06 |
12.206 |
-2.542 |
| a |
50 |
3900 |
1.04 |
2185 |
1.08 |
12.193 |
-2.572 |
| a |
75 |
3800 |
0.69 |
2117 |
1.13 |
12.185 |
-2.609 |
| a |
75 |
3700 |
0.69 |
2094 |
1.13 |
12.171 |
-2.641 |
| a |
100 |
3600 |
0.44 |
2023 |
1.18 |
12.160 |
-2.679 |
|
b |
100 |
3600 |
0.44 |
2074 |
1.18 |
12.159 |
-2.677 |
| b |
100 |
3500 |
0.44 |
2037 |
1.18 |
12.144 |
-2.711 |
| b |
150 |
3400 |
0.09 |
1857 |
1.30 |
12.137 |
-2.755 |
| b |
150 |
3300 |
0.09 |
1628 |
1.29 |
12.118 |
-2.787 |
| b |
200 |
3200 |
-0.16 |
1396 |
1.40 |
12.102 |
-2.825 |
|
b |
200 |
3100 |
-0.16 |
1291 |
1.38 |
12.064 |
-2.842 |
| b |
250 |
3000 |
-0.36 |
1079 |
1.51 |
12.031 |
-2.866 |
| b |
250 |
2900 |
-0.36 |
1021 |
1.47 |
11.974 |
-2.868 |
| b |
300 |
2800 |
-0.52 |
895 |
1.58 |
11.931 |
-2.886 |
|
M = |
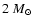 |
|
|
|
|
|
|
|
a |
50 |
4000 |
1.34 |
2251 |
1.04 |
12.200 |
-2.536 |
| a |
50 |
3900 |
1.34 |
2234 |
1.04 |
12.187 |
-2.566 |
| a |
75 |
3800 |
0.99 |
2172 |
1.06 |
12.178 |
-2.602 |
| a |
75 |
3700 |
0.99 |
2152 |
1.06 |
12.163 |
-2.634 |
| a |
100 |
3600 |
0.74 |
2089 |
1.08 |
12.152 |
-2.670 |
|
b |
100 |
3600 |
0.74 |
2142 |
1.08 |
12.151 |
-2.668 |
| b |
100 |
3500 |
0.74 |
2107 |
1.08 |
12.135 |
-2.702 |
| b |
150 |
3400 |
0.39 |
2003 |
1.13 |
12.124 |
-2.742 |
| b |
150 |
3300 |
0.39 |
1884 |
1.12 |
12.104 |
-2.773 |
| b |
200 |
3200 |
0.14 |
1652 |
1.17 |
12.083 |
-2.806 |
|
b |
200 |
3100 |
0.14 |
1525 |
1.16 |
12.041 |
-2.819 |
| b |
250 |
3000 |
-0.06 |
1342 |
1.20 |
11.998 |
-2.833 |
| b |
250 |
2900 |
-0.06 |
1234 |
1.19 |
11.936 |
-2.830 |
| b |
300 |
2800 |
-0.22 |
1102 |
1.22 |
11.882 |
-2.837 |
a Temperature at
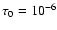 where
where 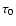 is the optical depth defined by the continuous
opacity at
is the optical depth defined by the continuous
opacity at
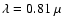 m;
b m;
b
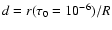 is a measure
of the extension of the photosphere;
c FL is the flux in the L band in unit of
erg cm-2 s-1 per
is a measure
of the extension of the photosphere;
c FL is the flux in the L band in unit of
erg cm-2 s-1 per
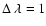 cm;
d cm;
d
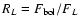 where
where
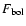 is the bolometric flux.
is the bolometric flux.
|
Source LaTeX |
All tables |
In the text